Stepwise Evolution of Photocatalytic Spinel-Structured (Co,Cr,Fe,Mn,Ni)3O4 High Entropy Oxides from First-Principles Calculations to Machine Learning
Abstract
:1. Introduction
2. Methods
2.1. First-Principles Calculations
2.2. Machine Learning (ML) Algorithms
3. Results and Discussion
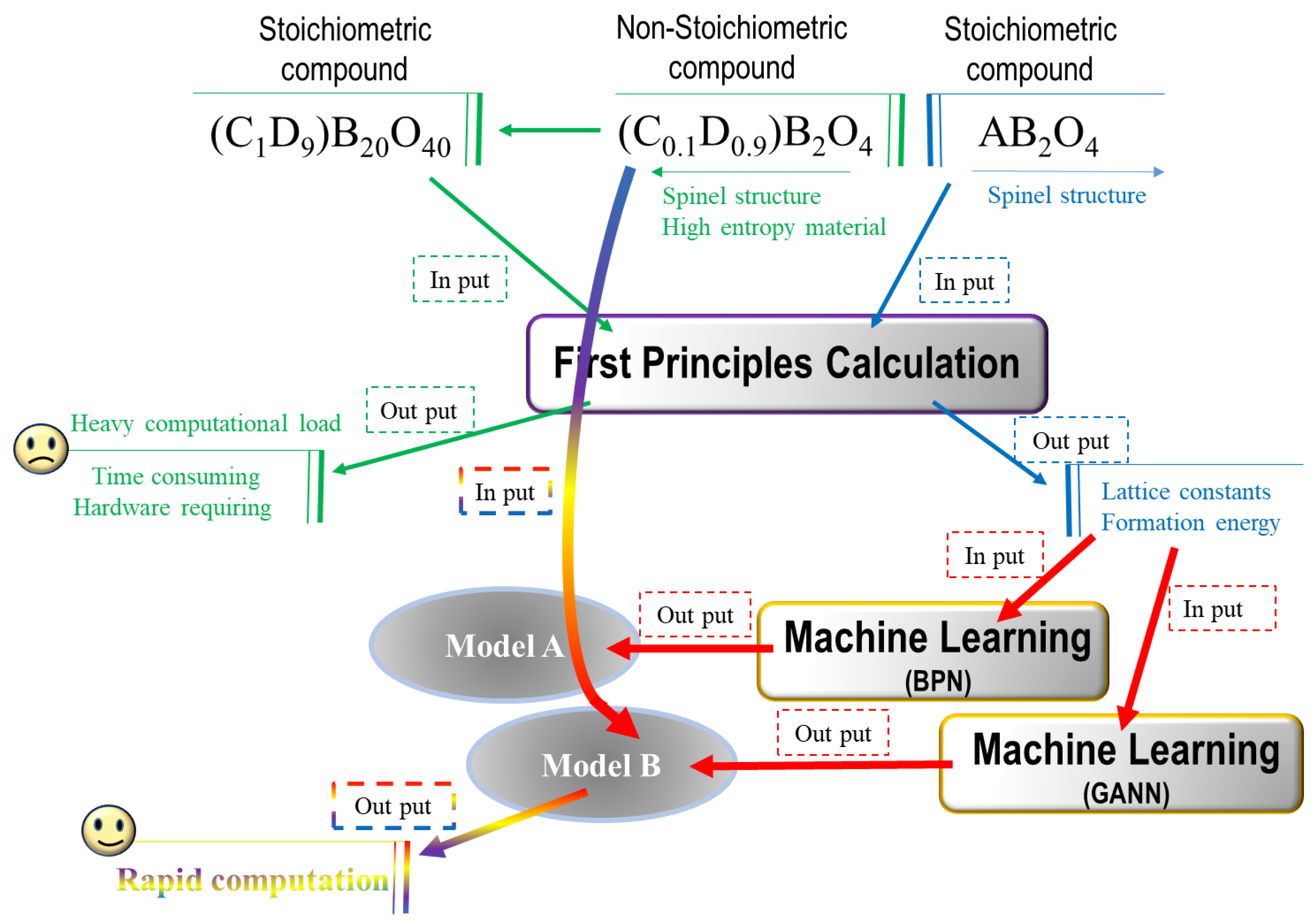
3.1. Decision Flow
3.2. ML-Model Selection and Performance
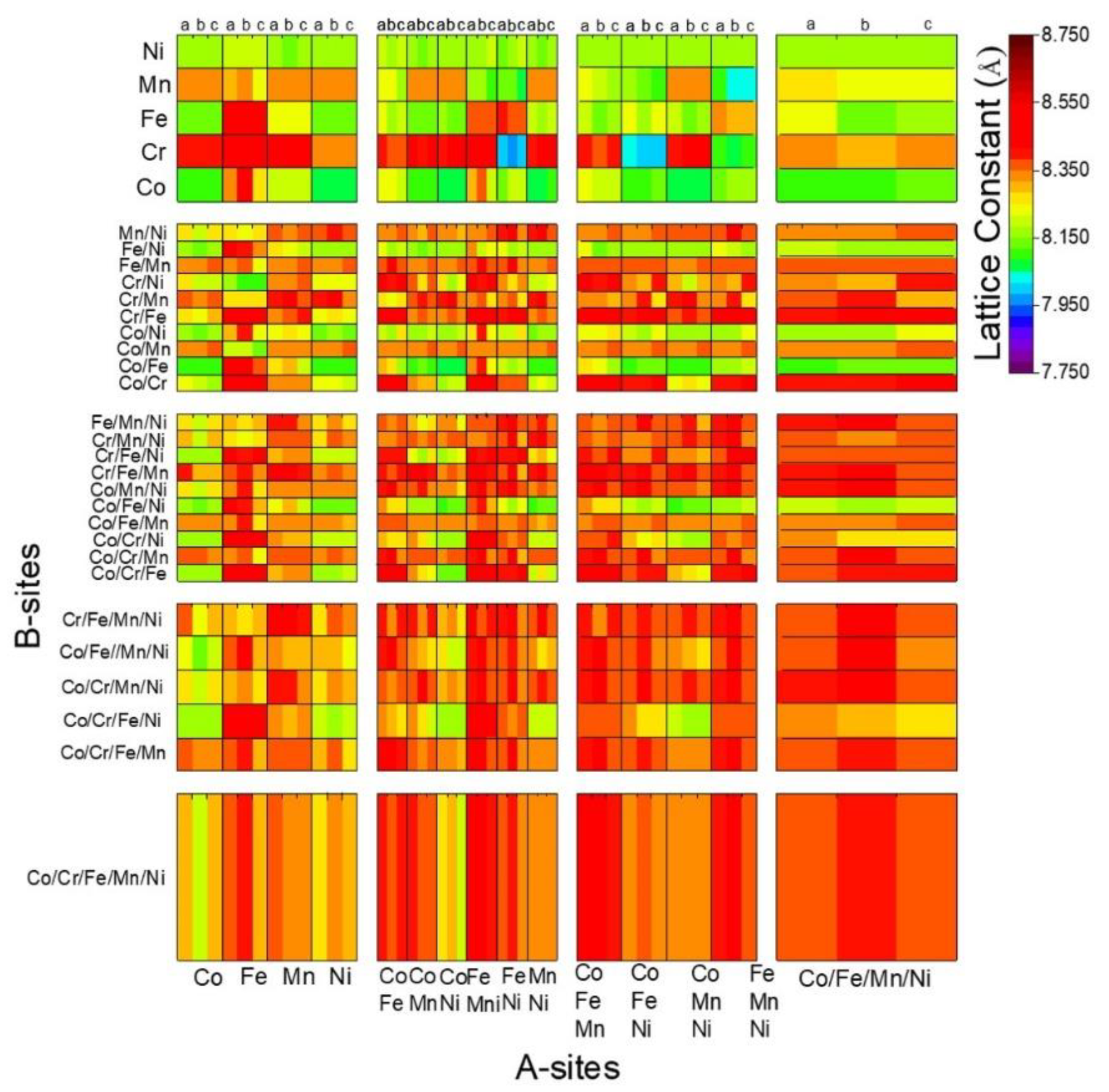
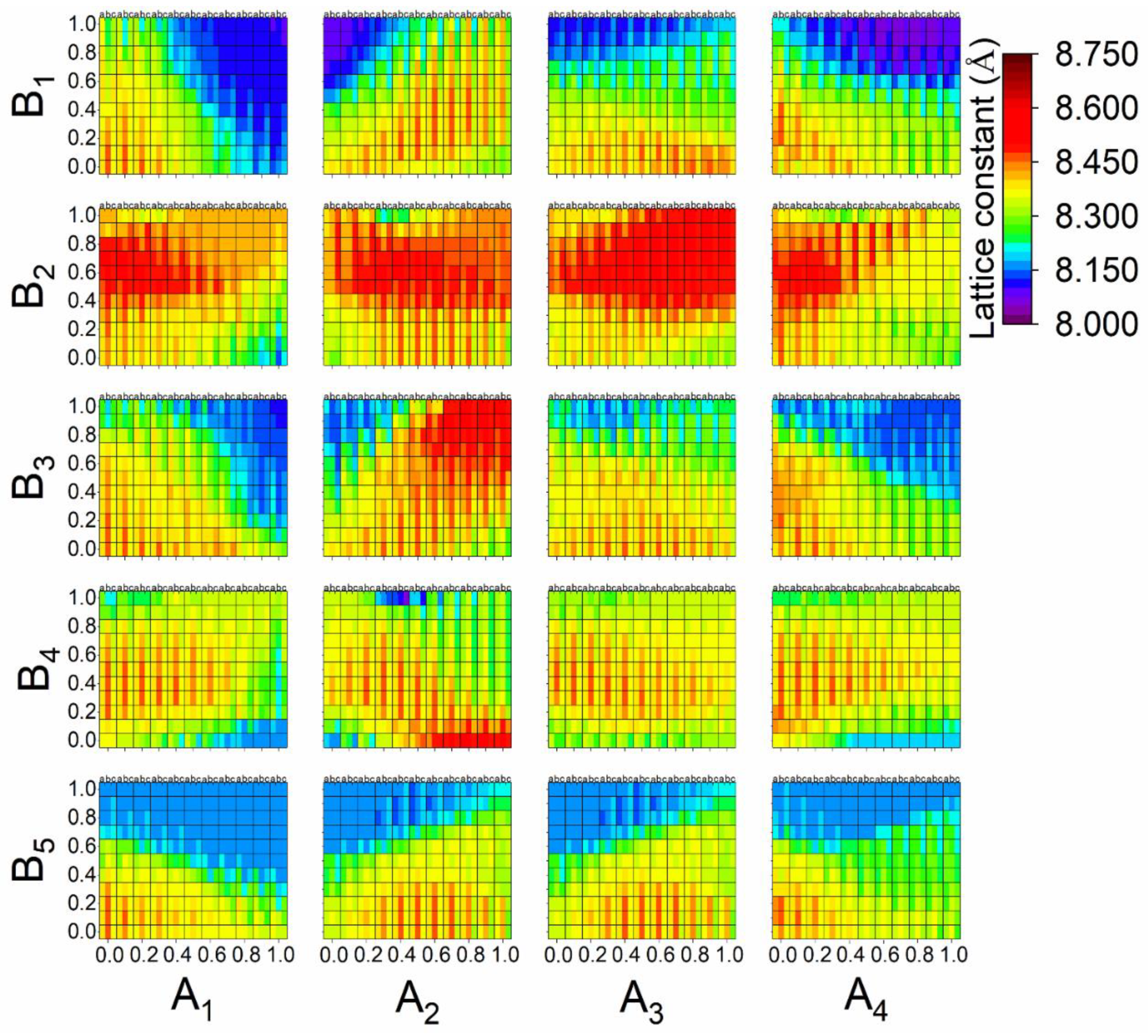
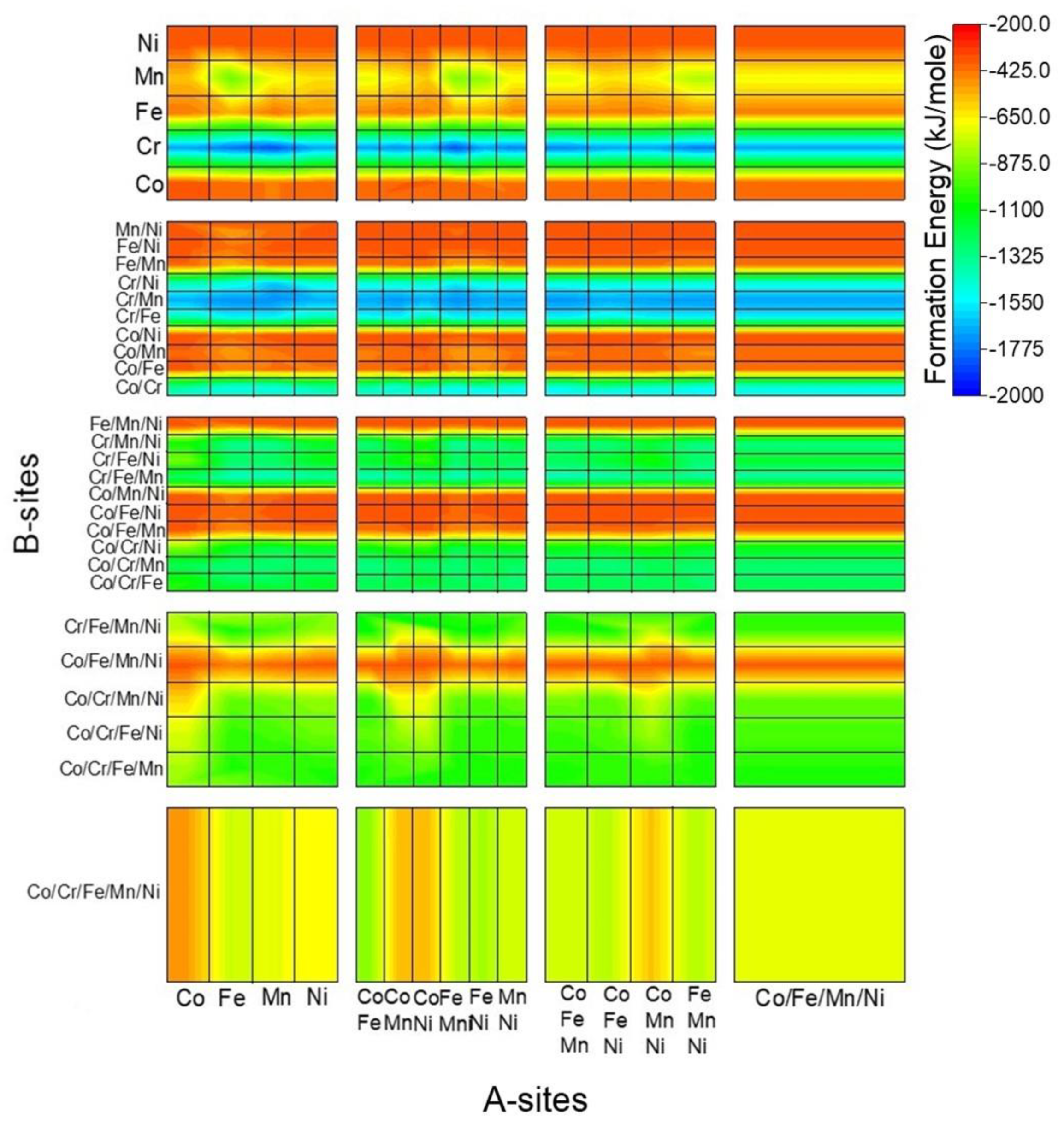
3.3. Prediction of the New Spinel Structure
3.4. Comparison of the Calculated and Predicted Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dragoe, N.; Bérardan, D. Order emerging from disorder. Science 2019, 366, 573. [Google Scholar] [CrossRef] [PubMed]
- Sarkar, A.; Velasco, L.; Wang, D.; Wang, Q.; Talasila, G.; de Biasi, L.; Kübel, C.; Brezesinski, T.; Bhattacharya, S.S.; Hahn, H.; et al. High entropy oxides for reversible energy storage. Nat. Commun. 2018, 9, 3400. [Google Scholar] [CrossRef] [Green Version]
- Qiu, N.; Chen, H.; Yang, Z.; Sun, S.; Wang, Y.; Cui, Y. A high entropy oxide (Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O) with superior lithium storage performance. J. Alloy. Compd. 2019, 777, 767–774. [Google Scholar] [CrossRef]
- Wang, Q.; Sarkar, A.; Li, Z.; Lu, Y.; Velasco, L.; Bhattacharya, S.S.; Brezesinski, T.; Hahn, H.; Breitung, B. High entropy oxides as anode material for Li-ion battery applications: A practical approach. Electrochem. Commun. 2019, 100, 121–125. [Google Scholar] [CrossRef]
- Wang, Q.; Sarkar, A.; Wang, D.; Velasco, L.; Azmi, R.; Bhattacharya, S.S.; Bergfeldt, T.; Düvel, A.; Heitjans, P.; Brezesinski, T.; et al. Multi-anionic and -cationic compounds: New high entropy materials for advanced Li-ion batteries. Energy Environ. Sci. 2019, 12, 2433–2442. [Google Scholar] [CrossRef] [Green Version]
- Dai, W.; Lu, T.; Pan, Y. Novel and promising electrocatalyst for oxygen evolution reaction based on MnFeCoNi high entropy alloy. J. Power Sources 2019, 430, 104–111. [Google Scholar] [CrossRef]
- Huang, K.; Zhang, B.; Wu, J.; Zhang, T.; Peng, D.; Cao, X.; Zhang, Z.; Li, Z.; Huang, Y. Exploring the impact of atomic lattice deformation on oxygen evolution reactions based on a sub-5 nm pure face-centred cubic high-entropy alloy electrocatalyst. J. Mater. Chem. A 2020, 8, 11938–11947. [Google Scholar] [CrossRef]
- Chen, H.; Fu, J.; Zhang, P.; Peng, H.; Abney, C.W.; Jie, K.; Liu, X.; Chi, M.; Dai, S. Entropy-stabilized metal oxide solid solutions as CO oxidation catalysts with high-temperature stability. J. Mater. Chem. A 2018, 6, 11129–11133. [Google Scholar] [CrossRef]
- Chen, H.; Lin, W.; Zhang, Z.; Jie, K.; Mullins, D.R.; Sang, X.; Yang, S.-Z.; Jafta, C.J.; Bridges, C.A.; Hu, X.; et al. Mechanochemical Synthesis of High Entropy Oxide Materials under Ambient Conditions: Dispersion of Catalysts via Entropy Maximization. ACS Mater. Lett. 2019, 1, 83–88. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, S.; Hu, X.; Xu, H.; Peng, H.; Liu, M.; Thapaliya, B.P.; Jie, K.; Zhao, J.; Liu, J.; et al. Mechanochemical Nonhydrolytic Sol–Gel-Strategy for the Production of Mesoporous Multimetallic Oxides. Chem. Mater. 2019, 31, 5529–5536. [Google Scholar] [CrossRef]
- Okejiri, F.; Zhang, Z.; Liu, J.; Liu, M.; Yang, S.; Dai, S. Room-Temperature Synthesis of High-Entropy Perovskite Oxide Nanoparticle Catalysts through Ultrasonication-Based Method. ChemSusChem 2020, 13, 111–115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rost, C.M.; Sachet, E.; Borman, T.; Moballegh, A.; Dickey, E.C.; Hou, D.; Jones, J.L.; Curtarolo, S.; Maria, J.-P. Entropy-stabilized oxides. Nat. Commun. 2015, 6, 8485. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berardan, D.; Meena, A.K.; Franger, S.; Herrero, C.; Dragoe, N. Controlled Jahn-Teller distortion in (MgCoNiCuZn)O-based high entropy oxides. J. Alloy. Compd. 2017, 704, 693–700. [Google Scholar] [CrossRef]
- Dąbrowa, J.; Stygar, M.; Mikuła, A.; Knapik, A.; Mroczka, K.; Tejchman, W.; Danielewski, M.; Martin, M. Synthesis and microstructure of the (Co,Cr,Fe,Mn,Ni)3O4 high entropy oxide characterized by spinel structure. Mater. Lett. 2018, 216, 32–36. [Google Scholar] [CrossRef]
- Bérardan, D.; Franger, S.; Dragoe, D.; Meena, A.K.; Dragoe, N. Colossal dielectric constant in high entropy oxides. Phys. Status Solidi (RRL)—Rapid Res. Lett. 2016, 10, 328–333. [Google Scholar] [CrossRef] [Green Version]
- Jimenez-Segura, M.P.; Takayama, T.; Bérardan, D.; Hoser, A.; Reehuis, M.; Takagi, H.; Dragoe, N. Long-range magnetic ordering in rocksalt-type high-entropy oxides. Appl. Phys. Lett. 2019, 114, 122401. [Google Scholar] [CrossRef] [Green Version]
- Bérardan, D.; Franger, S.; Meena, A.K.; Dragoe, N. Room temperature lithium superionic conductivity in high entropy oxides. J. Mater. Chem. A 2016, 4, 9536–9541. [Google Scholar] [CrossRef] [Green Version]
- Osenciat, N.; Bérardan, D.; Dragoe, D.; Léridon, B.; Holé, S.; Meena, A.K.; Franger, S.; Dragoe, N. Charge compensation mechanisms in Li-substituted high-entropy oxides and influence on Li superionic conductivity. J. Am. Ceram. Soc. 2019, 102, 6156–6162. [Google Scholar] [CrossRef]
- Zheng, Y.; Yi, Y.; Fan, M.; Liu, H.; Li, X.; Zhang, R.; Li, M.; Qiao, Z.-A. A high-entropy metal oxide as chemical anchor of polysulfide for lithium-sulfur batteries. Energy Storage Mater. 2019, 23, 678–683. [Google Scholar] [CrossRef]
- Sarkar, A.; Djenadic, R.; Wang, D.; Hein, C.; Kautenburger, R.; Clemens, O.; Hahn, H. Rare earth and transition metal based entropy stabilised perovskite type oxides. J. Eur. Ceram. Soc. 2018, 38, 2318–2327. [Google Scholar] [CrossRef]
- Chen, K.; Pei, X.; Tang, L.; Cheng, H.; Li, Z.; Li, C.; Zhang, X.; An, L. A five-component entropy-stabilized fluorite oxide. J. Eur. Ceram. Soc. 2018, 38, 4161–4164. [Google Scholar] [CrossRef]
- Gild, J.; Samiee, M.; Braun, J.L.; Harrington, T.; Vega, H.; Hopkins, P.E.; Vecchio, K.; Luo, J. High-entropy fluorite oxides. J. Eur. Ceram. Soc. 2018, 38, 3578–3584. [Google Scholar] [CrossRef]
- Mao, A.; Quan, F.; Xiang, H.-Z.; Zhang, Z.-G.; Kuramoto, K.; Xia, A.-L. Facile synthesis and ferrimagnetic property of spinel (CoCrFeMnNi)3O4 high-entropy oxide nanocrystalline powder. J. Mol. Struct. 2019, 1194, 11–18. [Google Scholar] [CrossRef]
- Grzesik, Z.; Smoła, G.; Miszczak, M.; Stygar, M.; Dąbrowa, J.; Zajusz, M.; Świerczek, K.; Danielewski, M. Defect structure and transport properties of (Co,Cr,Fe,Mn,Ni)3O4 spinel-structured high entropy oxide. J. Eur. Ceram. Soc. 2020, 40, 835–839. [Google Scholar] [CrossRef]
- McCormack, S.J.; Navrotsky, A. Thermodynamics of high entropy oxides. Acta Mater. 2021, 202, 1–21. [Google Scholar] [CrossRef]
- Bragg, W.H. The Structure of Magnetite and the Spinels. Nature 1915, 95, 561. [Google Scholar] [CrossRef]
- Hill, R.J.; Craig, J.R.; Gibbs, G.V. Systematics of the spinel structure type. Phys. Chem. Miner. 1979, 4, 317–339. [Google Scholar] [CrossRef]
- Sickafus, K.E.; Wills, J.M.; Grimes, N.W. Structure of Spinel. J. Am. Ceram. Soc. 1999, 82, 3279–3292. [Google Scholar] [CrossRef]
- Laguna-Bercero, M.A.; Sanjuán, M.L.; Merino, R.I. Raman spectroscopic study of cation disorder in poly- and single crystals of the nickel aluminate spinel. J. Phys. Condens. Matter 2007, 19, 186217. [Google Scholar] [CrossRef] [PubMed]
- O’Quinn, E.C.; Shamblin, J.; Perlov, B.; Ewing, R.C.; Neuefeind, J.; Feygenson, M.; Gussev, I.; Lang, M. Inversion in Mg1–xNixAl2O4 Spinel: New Insight into Local Structure. J. Am. Chem. Soc. 2017, 139, 10395–10402. [Google Scholar] [CrossRef]
- Musicó, B.; Wright, Q.; Ward, T.Z.; Grutter, A.; Arenholz, E.; Gilbert, D.; Mandrus, D.; Keppens, V. Tunable magnetic ordering through cation selection in entropic spinel oxides. Phys. Rev. Mater. 2019, 3, 104416. [Google Scholar] [CrossRef]
- Mao, A.; Xiang, H.-Z.; Zhang, Z.-G.; Kuramoto, K.; Zhang, H.; Jia, Y. A new class of spinel high-entropy oxides with controllable magnetic properties. J. Magn. Magn. Mater. 2020, 497, 165884. [Google Scholar] [CrossRef]
- Mao, A.; Xie, H.-X.; Xiang, H.-Z.; Zhang, Z.-G.; Zhang, H.; Ran, S. A novel six-component spinel-structure high-entropy oxide with ferrimagnetic property. J. Magn. Magn. Mater. 2020, 503, 166594. [Google Scholar] [CrossRef]
- Wang, D.; Jiang, S.; Duan, C.; Mao, J.; Dong, Y.; Dong, K.; Wang, Z.; Luo, S.; Liu, Y.; Qi, X. Spinel-structured high entropy oxide (FeCoNiCrMn)3O4 as anode towards superior lithium storage performance. J. Alloy. Compd. 2020, 844, 156158. [Google Scholar] [CrossRef]
- Middleburgh, S.C.; King, D.M.; Lumpkin, G.R.; Cortie, M.; Edwards, L. Segregation and migration of species in the CrCoFeNi high entropy alloy. J. Alloy. Compd. 2014, 599, 179–182. [Google Scholar] [CrossRef]
- Navrotsky, A.; Kleppa, O.J. Thermodynamics of formation of simple spinels. J. Inorg. Nucl. Chem. 1968, 30, 479–498. [Google Scholar] [CrossRef]
- Navrotsky, A.; Kleppa, O.J. The thermodynamics of cation distributions in simple spinels. J. Inorg. Nucl. Chem. 1967, 29, 2701–2714. [Google Scholar] [CrossRef]
- Navrotsky, A. Thermodynamics of A3O4-B3O4 spinel solid solutions. J. Inorg. Nucl. Chem. 1969, 31, 59–72. [Google Scholar] [CrossRef]
- Müller, F.; Kleppa, O.J. Thermodynamics of formation of chromite spinels. J. Inorg. Nucl. Chem. 1973, 35, 2673–2678. [Google Scholar] [CrossRef]
- Jasiewicz, K.; Cieslak, J.; Kaprzyk, S.; Tobola, J. Relative crystal stability of AlxFeNiCrCo high entropy alloys from XRD analysis and formation energy calculation. J. Alloy. Compd. 2015, 648, 307–312. [Google Scholar] [CrossRef]
- Jiang, L.Q.; Guo, J.K.; Liu, H.B.; Zhu, M.; Zhou, X.; Wu, P.; Li, C.H. Prediction of lattice constant in cubic perovskites. J. Phys. Chem. Solids 2006, 67, 1531–1536. [Google Scholar] [CrossRef]
- Emery, A.A.; Wolverton, C. High-throughput DFT calculations of formation energy, stability and oxygen vacancy formation energy of ABO3 perovskites. Sci. Data 2017, 4, 170153. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Takahashi, K.; Takahashi, L.; Baran, J.D.; Tanaka, Y. Descriptors for predicting the lattice constant of body centered cubic crystal. J. Chem. Phys. 2017, 146, 204104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dubey, P.; Kaurav, N. Stoichiometric and Non-Stoichiometric compounds. In Structure Processing Properties Relationships in Stoichiometric and Nonstoichiometric Oxides; IntechOpen: London, UK, 2019. [Google Scholar]
- Lo, K.-C.; Chang, Y.-J.; Murakami, H.; Yeh, J.-W.; Yeh, A.-C. An oxidation resistant refractory high entropy alloy protected by CrTaO4-based oxide. Sci. Rep. 2019, 9, 7266. [Google Scholar] [CrossRef]
- Ye, B.; Wen, T.; Huang, K.; Wang, C.-Z.; Chu, Y. First-principles study, fabrication, and characterization of (Hf0.2Zr0.2Ta0.2Nb0.2Ti0.2)C high-entropy ceramic. J. Am. Ceram. Soc. 2019, 102, 4344–4352. [Google Scholar] [CrossRef] [Green Version]
- Wen, C.; Zhang, Y.; Wang, C.; Xue, D.; Bai, Y.; Antonov, S.; Dai, L.; Lookman, T.; Su, Y. Machine learning assisted design of high entropy alloys with desired property. Acta Mater. 2019, 170, 109–117. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.; Martin, P.; Zhuang, H.L. Machine-learning phase prediction of high-entropy alloys. Acta Mater. 2019, 169, 225–236. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef] [Green Version]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B Condens. Matter 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, M.C.; Niu, C.; Jiang, C.; Irving, D.L. Applications of Special Quasi-random Structures to High-Entropy Alloys. In High-Entropy Alloys: Fundamentals and Applications; Gao, M.C., Yeh, J.-W., Liaw, P.K., Zhang, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 333–368. [Google Scholar]
- Available online: https://www.ce.tku.edu.tw/~icyeh/spcn/ (accessed on 15 September 2018).
- Zhao, Q.; Yan, Z.; Chen, C.; Chen, J. Spinels: Controlled Preparation, Oxygen Reduction/Evolution Reaction Application, and Beyond. Chem. Rev. 2017, 117, 10121–10211. [Google Scholar] [CrossRef] [PubMed]
- Ong, S.P.; Richards, W.D.; Jain, A.; Hautier, G.; Kocher, M.; Cholia, S.; Gunter, D.; Chevrier, V.L.; Persson, K.A.; Ceder, G. Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis. Comput. Mater. Sci. 2013, 68, 314–319. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-C.; Chang, C.-W.; Kaun, C.-C.; Su, Y.-H. Stepwise Evolution of Photocatalytic Spinel-Structured (Co,Cr,Fe,Mn,Ni)3O4 High Entropy Oxides from First-Principles Calculations to Machine Learning. Crystals 2021, 11, 1035. https://doi.org/10.3390/cryst11091035
Lin C-C, Chang C-W, Kaun C-C, Su Y-H. Stepwise Evolution of Photocatalytic Spinel-Structured (Co,Cr,Fe,Mn,Ni)3O4 High Entropy Oxides from First-Principles Calculations to Machine Learning. Crystals. 2021; 11(9):1035. https://doi.org/10.3390/cryst11091035
Chicago/Turabian StyleLin, Chia-Chun, Chia-Wei Chang, Chao-Cheng Kaun, and Yen-Hsun Su. 2021. "Stepwise Evolution of Photocatalytic Spinel-Structured (Co,Cr,Fe,Mn,Ni)3O4 High Entropy Oxides from First-Principles Calculations to Machine Learning" Crystals 11, no. 9: 1035. https://doi.org/10.3390/cryst11091035
APA StyleLin, C.-C., Chang, C.-W., Kaun, C.-C., & Su, Y.-H. (2021). Stepwise Evolution of Photocatalytic Spinel-Structured (Co,Cr,Fe,Mn,Ni)3O4 High Entropy Oxides from First-Principles Calculations to Machine Learning. Crystals, 11(9), 1035. https://doi.org/10.3390/cryst11091035






