Interplay of Active Stress and Driven Flow in Self-Assembled, Tumbling Active Nematics
Abstract
:1. Introduction
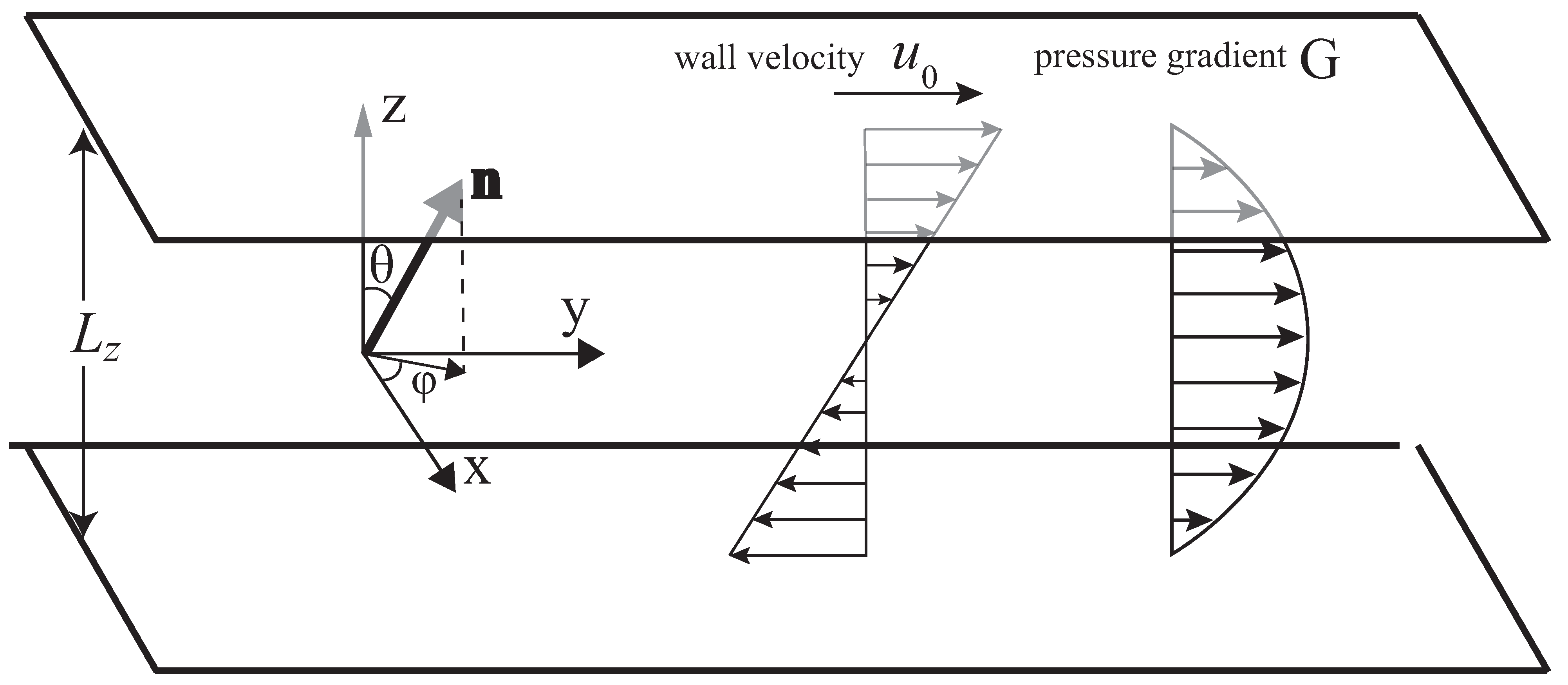
2. Methods
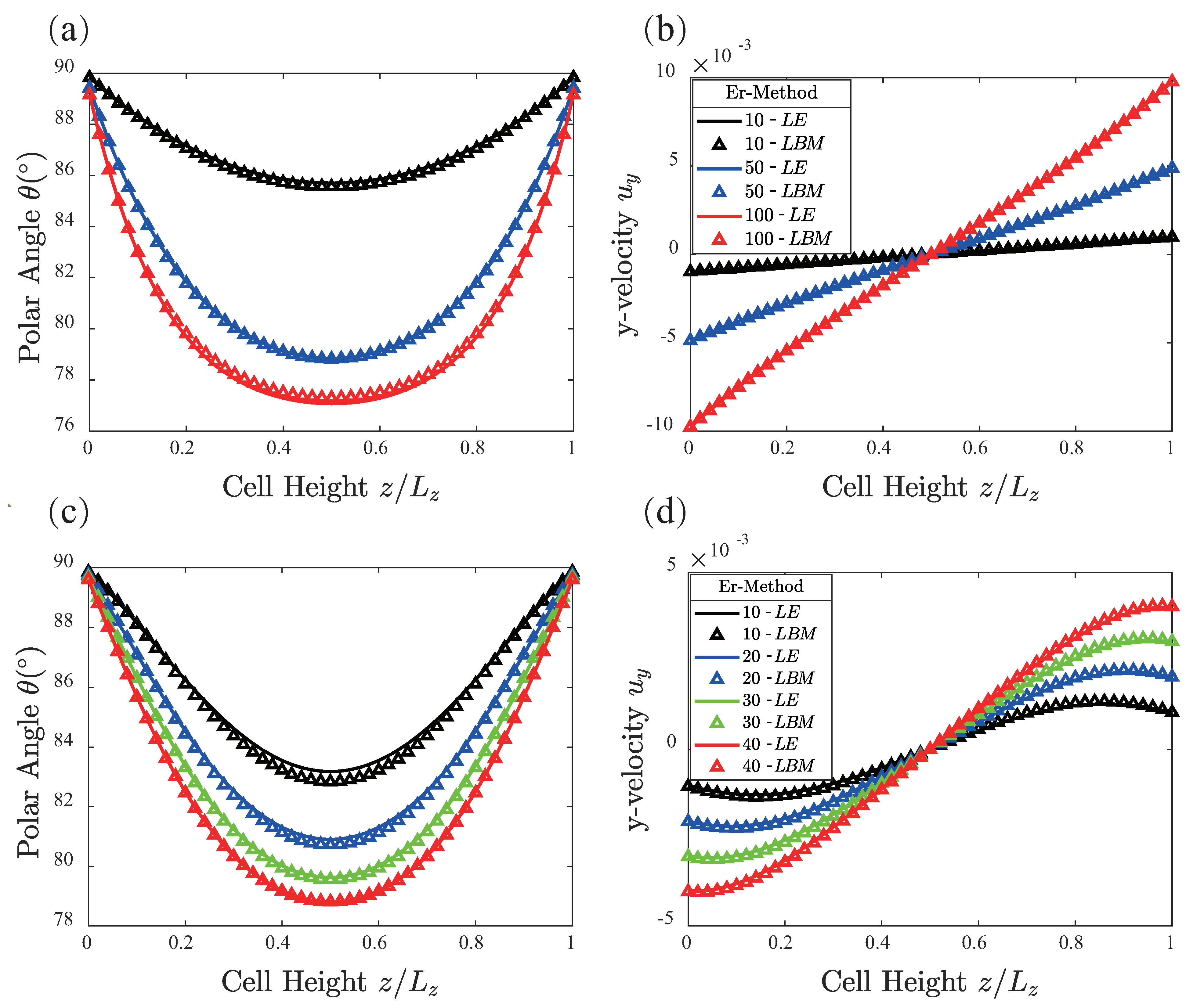
2.1. Hybrid Lattice Boltzmann Method
2.2. Leslie–Ericksen Theory
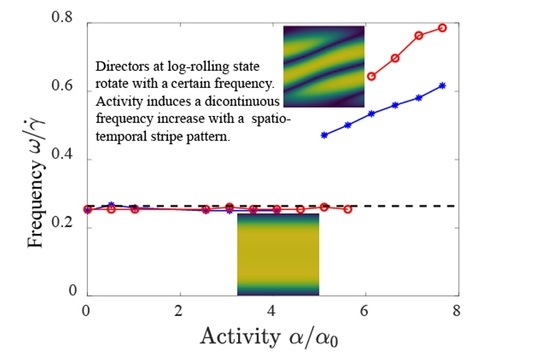
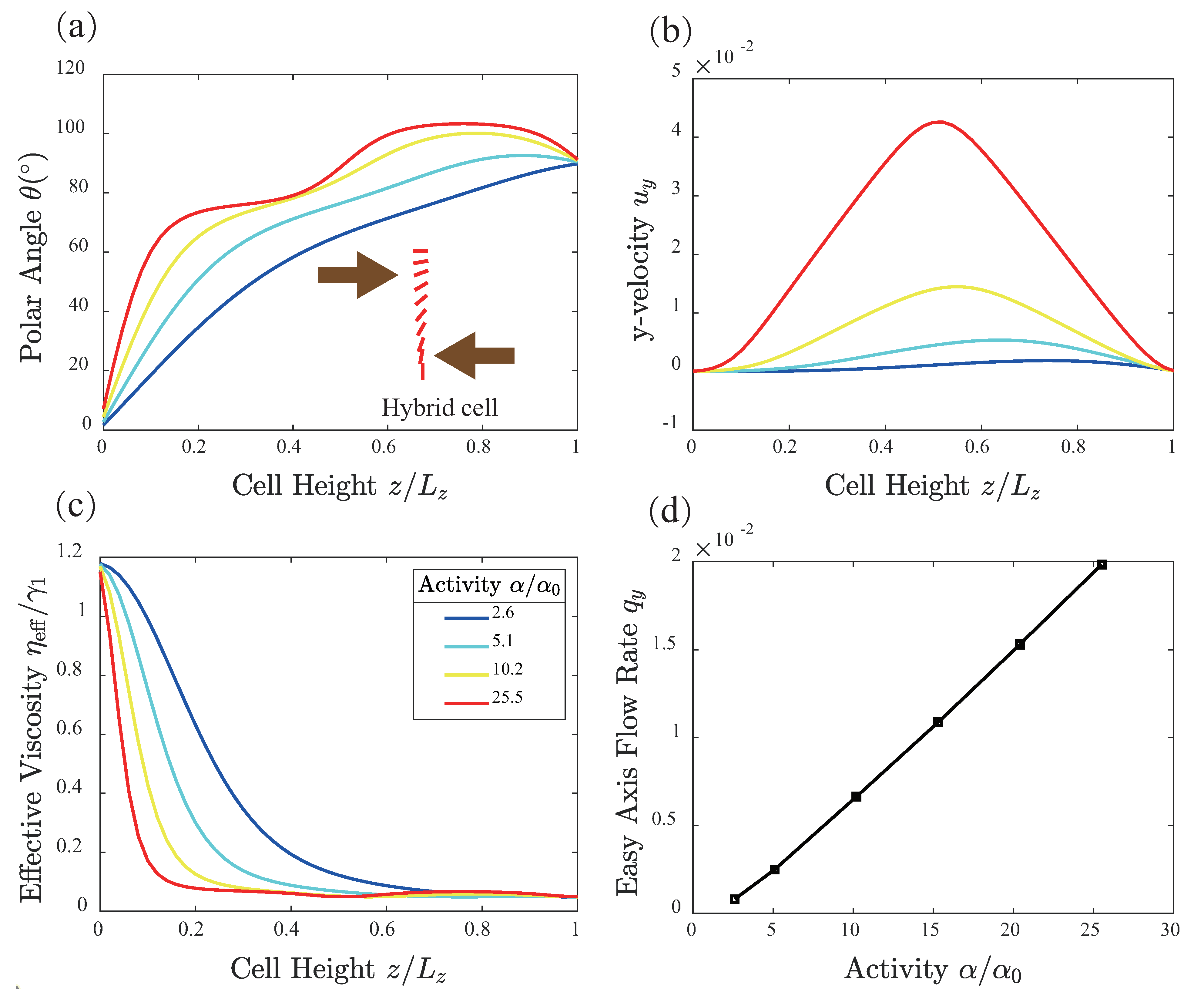
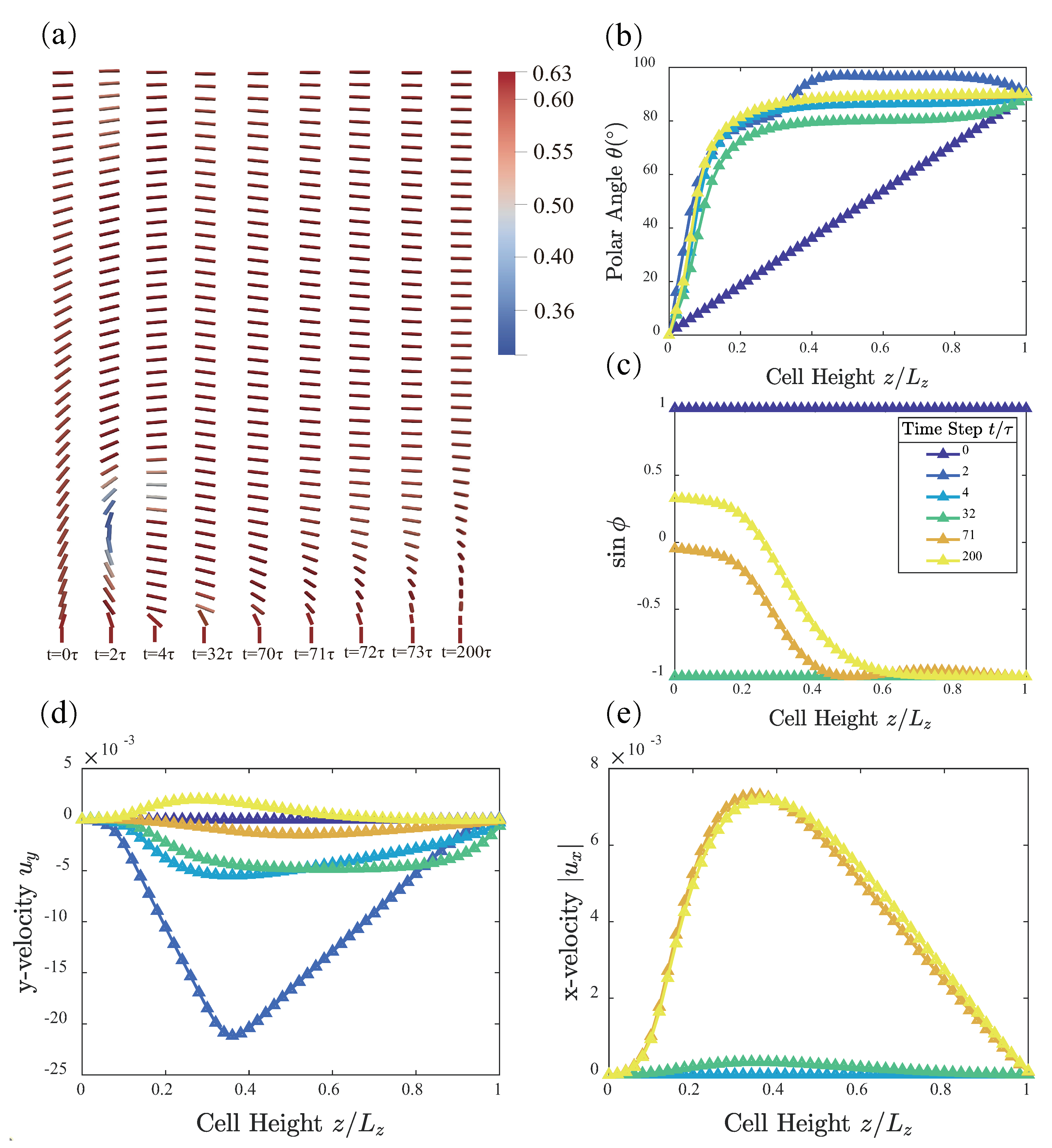
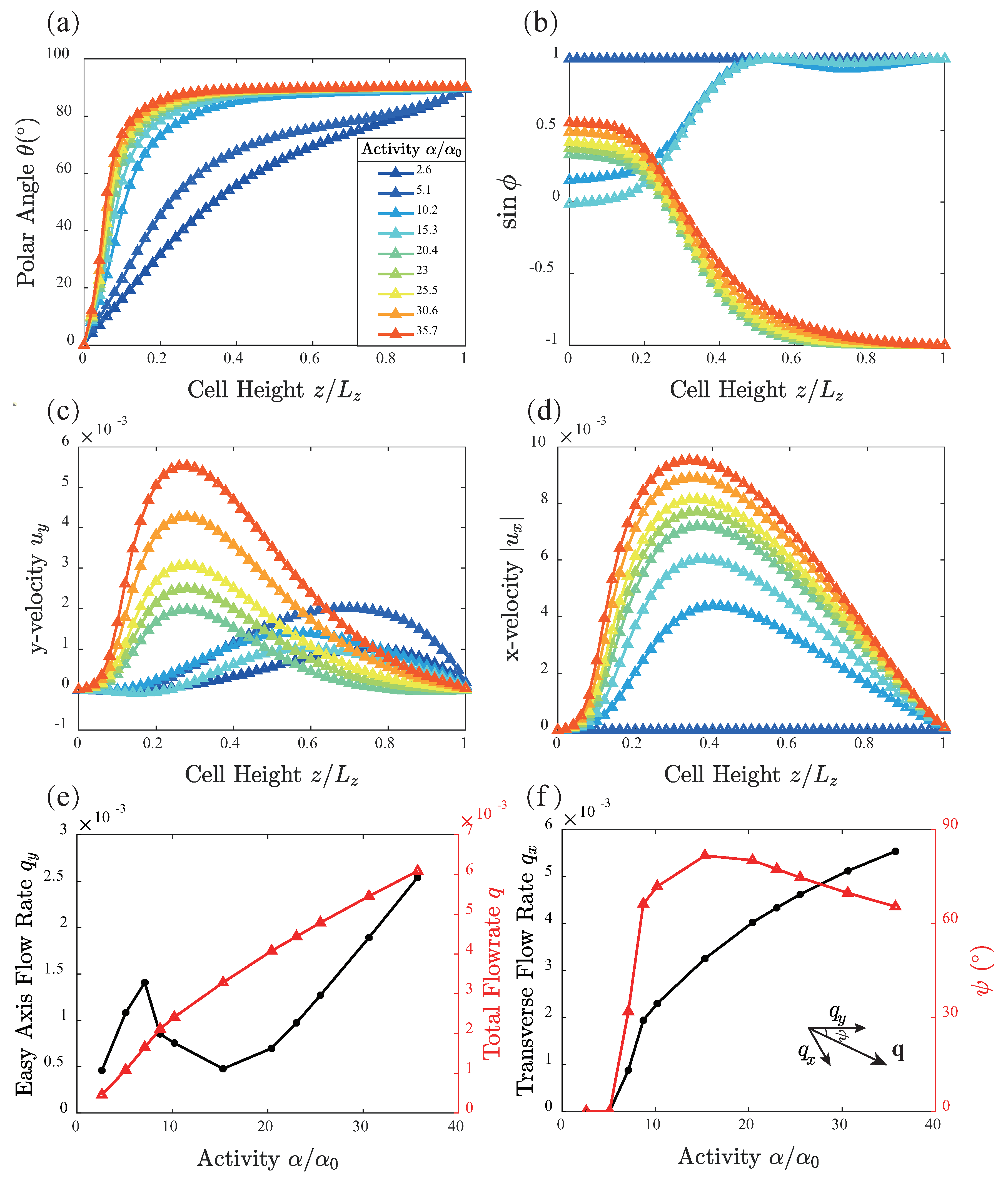
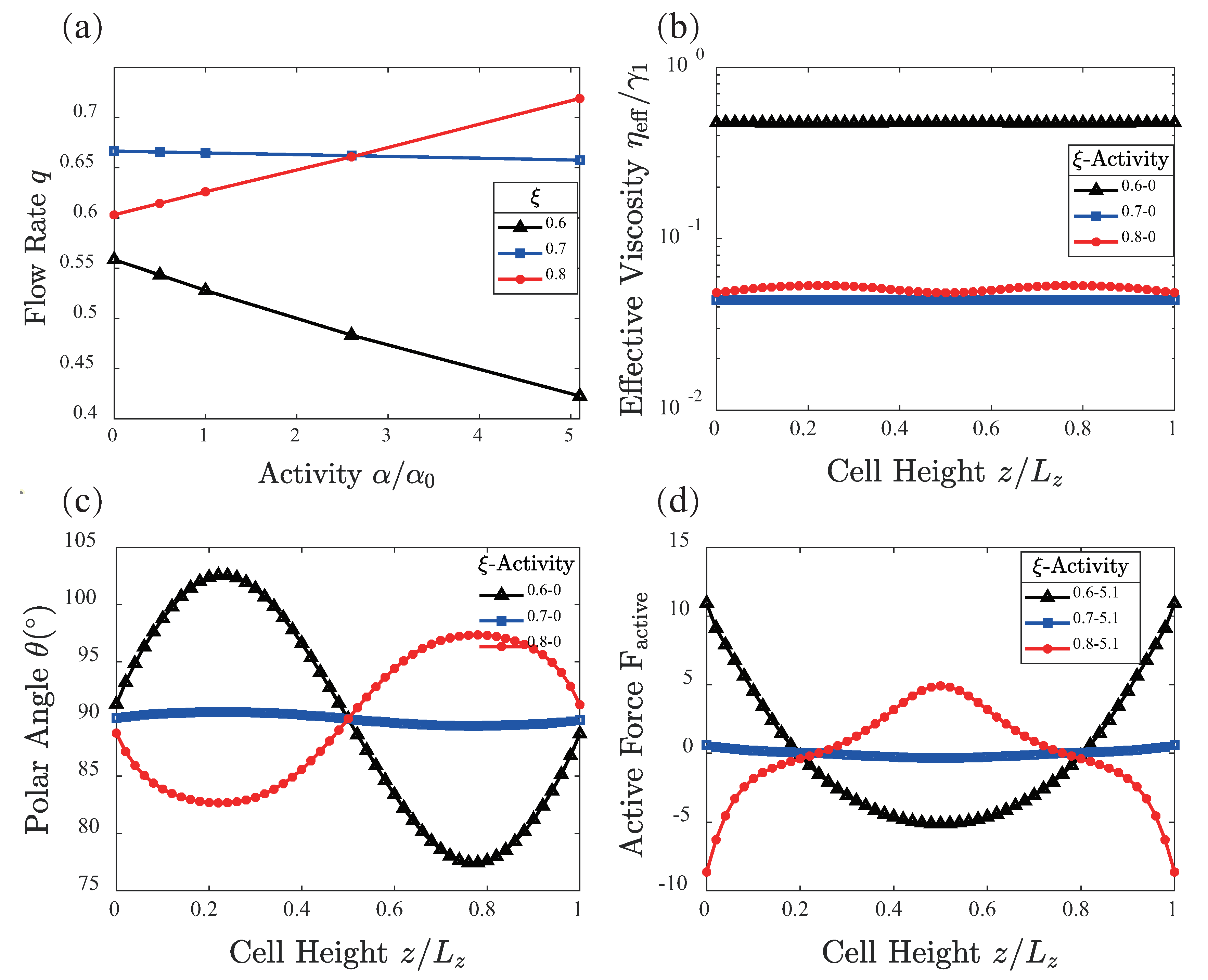
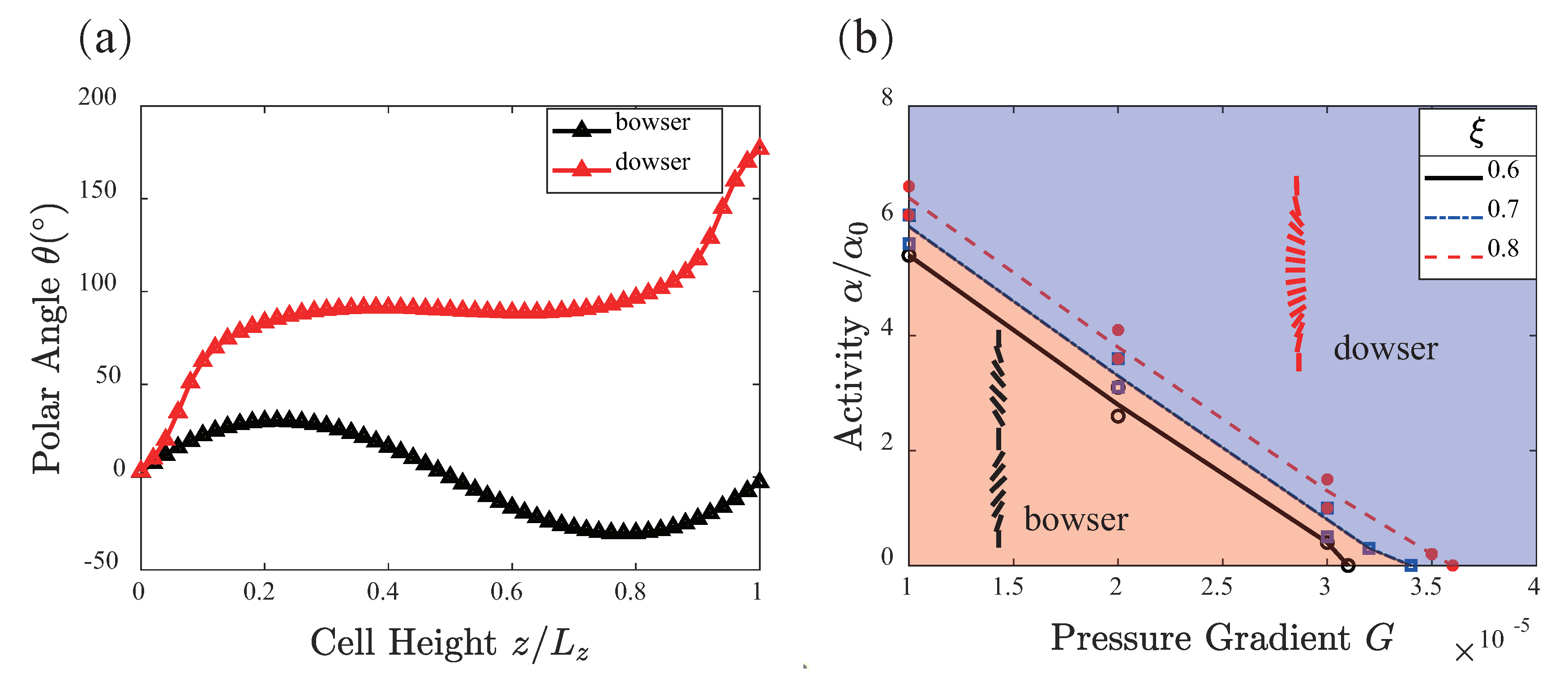
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Mapping of Leslie Viscosity Coefficients
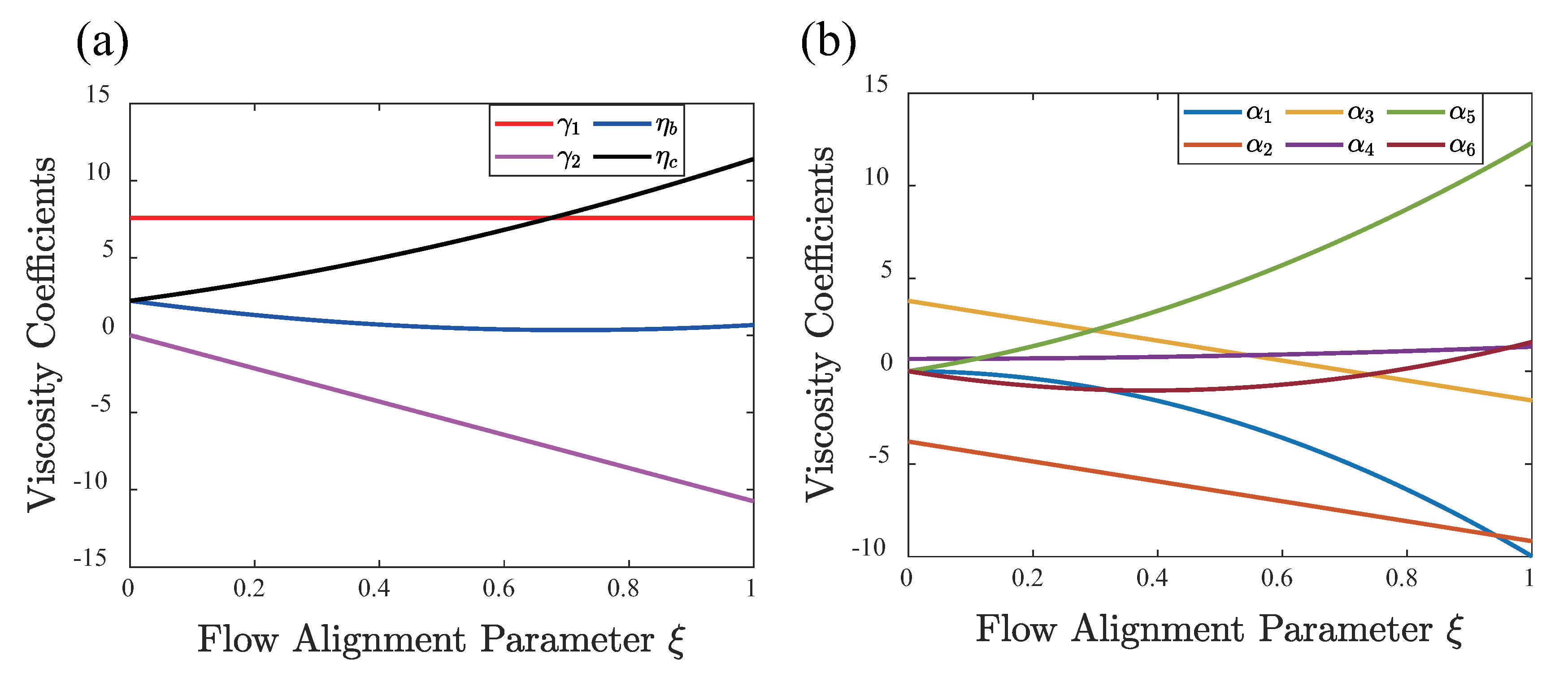
Appendix A.2. Derivation of Tumbling Frequency
References
- de Gennes, P.; Prost, J. The Physics of Liquid Crystals; Oxford University Press, Inc.: Oxford, UK, 1995. [Google Scholar]
- Kleman, M.; Laverntovich, O.D. Soft Matter Physics: An Introduction; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar]
- Lin, I.H.; Miller, D.S.; Bertics, P.J.; Murphy, C.J.; De Pablo, J.J.; Abbott, N.L. Endotoxin-induced structural transformations in liquid crystalline droplets. Science 2011, 332, 1297–1300. [Google Scholar] [CrossRef] [Green Version]
- Sadati, M.; Apik, A.I.; Armas-Perez, J.C.; Martinez-Gonzalez, J.; Hernandez-Ortiz, J.P.; Abbott, N.L.; de Pablo, J.J. Liquid crystal enabled early stage detection of beta amyloid formation on lipid monolayers. Adv. Funct. Mater. 2015, 25, 6050–6060. [Google Scholar] [CrossRef]
- Muševič, I.; Škarabot, M.; Tkalec, U.; Ravnik, M.; Žumer, S. Two-Dimensional Nematic Colloidal Crystals Self-Assembled by Topological Defects. Science 2006, 313, 954–958. [Google Scholar] [CrossRef] [PubMed]
- Whitmer, J.K.; Wang, X.; Mondiot, F.; Miller, D.S.; Abbott, N.L.; de Pablo, J.J. Nematic-Field-Driven Positioning of Particles in Liquid Crystal Droplets. Phys. Rev. Lett. 2013, 11, 227801. [Google Scholar] [CrossRef] [Green Version]
- Rahimi, M.; Roberts, T.F.; Armas-Pérez, J.C.; Wang, X.; Bukusoglu, E.; Abbott, N.L.; de Pablo, J.J. Nanoparticle self-assembly at the interface of liquid crystal droplets. Proc. Natl. Acad. Sci. USA 2015, 112, 5297–5302. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Miller, D.S.; Bukusoglu, E.; de Pablo, J.J.; Abbott, N.L. Topological defects in liquid crystals as templates for molecular self-assembly. Nat. Mater. 2015, 15, 106. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Kim, Y.K.; Bukusoglu, E.; Zhang, B.; Miller, D.S.; Abbott, N.L. Experimental Insights into the Nanostructure of the Cores of Topological Defects in Liquid Crystals. Phys. Rev. Lett. 2016, 116, 147801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lavrentovich, O.D. Transport of particles in liquid crystals. Soft Matter 2014, 10, 1264–1283. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mo, J.; Milleret, G.; Nagaraj, M. Liquid crystal nanoparticles for commercial drug delivery. Liq. Cryst. Rev. 2017, 5, 69–85. [Google Scholar] [CrossRef]
- Lavrentovich, O.D. Design of nematic liquid crystals to control microscale dynamics. Liq. Cryst. Rev. 2020, 8, 59–129. [Google Scholar] [CrossRef]
- Sengupta, A.; Tkalec, U.; Bahr, C. Nematic textures in microfluidic environment. Soft Matter 2011, 7, 6542–6549. [Google Scholar] [CrossRef]
- Sengupta, A.; Tkalec, U.; Ravnik, M.; Yeomans, J.M.; Bahr, C.; Herminghaus, S. Liquid crystal microfluidics for tunable flow shaping. Phys. Rev. Lett. 2013, 110, 048303. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, A.; Herminghaus, S.; Bahr, C. Liquid crystal microfluidics: Surface, elastic and viscous interactions at microscales. Liq. Cryst. Rev. 2014, 2, 73–110. [Google Scholar] [CrossRef]
- Giomi, L.; Kos, Ž.; Ravnik, M.; Sengupta, A. Cross-talk between topological defects in different fields revealed by nematic microfluidics. Proc. Natl. Acad. Sci. USA 2017, 114, E5771–E5777. [Google Scholar] [CrossRef] [Green Version]
- Emeršič, T.; Zhang, R.; Kos, Ž.; Čopar, S.; Osterman, N.; De Pablo, J.J.; Tkalec, U. Sculpting stable structures in pure liquids. Sci. Adv. 2019, 5, eaav4283. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Čopar, S.; Kos, Ž.; Emeršič, T.; Tkalec, U. Microfluidic control over topological states in channel-confined nematic flows. Nat. Commun. 2020, 11, 1–10. [Google Scholar] [CrossRef]
- Rey, A.D. Liquid crystal models of biological materials and processes. Soft Matter 2010, 6, 3402–3429. [Google Scholar] [CrossRef]
- Saw, T.B.; Doostmohammadi, A.; Nier, V.; Kocgozlu, L.; Thampi, S.; Toyama, Y.; Marcq, P.; Lim, C.T.; Yeomans, J.M.; Ladoux, B. Topological defects in epithelia govern cell death and extrusion. Nature 2017, 544, 212–216. [Google Scholar] [CrossRef] [PubMed]
- Kawaguchi, K.; Kageyama, R.; Sano, M. Topological defects control collective dynamics in neural progenitor cell cultures. Nature 2017, 545, 327–331. [Google Scholar] [CrossRef]
- Marchetti, M.C.; Joanny, J.F.; Ramaswamy, S.; Liverpool, T.B.; Prost, J.; Rao, M.; Simha, R.A. Hydrodynamics of soft active matter. Rev. Mod. Phys. 2013, 85, 1143. [Google Scholar] [CrossRef] [Green Version]
- Doostmohammadi, A.; Ignés-Mullol, J.; Yeomans, J.M.; Sagués, F. Active nematics. Nat. Commun. 2018, 9, 3246. [Google Scholar] [CrossRef]
- Needleman, D.; Dogic, Z. Active matter at the interface between materials science and cell biology. Nat. Rev. Mater. 2017, 2, 1–14. [Google Scholar] [CrossRef]
- Zhang, R.; Mozaffari, A.; de Pablo, J.J. Autonomous materials systems from active liquid crystals. Nat. Rev. Mater. 2021, 6, 437–453. [Google Scholar] [CrossRef]
- Sanchez, T.; Chen, D.T.; DeCamp, S.J.; Heymann, M.; Dogic, Z. Spontaneous motion in hierarchically assembled active matter. Nature 2012, 491, 431–434. [Google Scholar] [CrossRef] [Green Version]
- Kumar, N.; Zhang, R.; de Pablo, J.J.; Gardel, M.L. Tunable structure and dynamics of active liquid crystals. Sci. Adv. 2018, 4, eaat7779. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Shi, X.; Huang, M.; Chen, X.; Xiao, M.; Liu, C.; Chaté, H.; Zhang, H. Data-driven quantitative modeling of bacterial active nematics. Proc. Natl. Acad. Sci. USA 2019, 116, 777–785. [Google Scholar] [CrossRef] [Green Version]
- Zhou, S.; Sokolov, A.; Lavrentovich, O.D.; Aranson, I.S. Living liquid crystals. Proc. Natl. Acad. Sci. USA 2014, 111, 1265–1270. [Google Scholar] [CrossRef] [Green Version]
- Genkin, M.M.; Sokolov, A.; Lavrentovich, O.D.; Aranson, I.S. Topological defects in a living nematic ensnare swimming bacteria. Phys. Rev. X 2017, 7, 011029. [Google Scholar] [CrossRef] [Green Version]
- Sokolov, A.; Mozaffari, A.; Zhang, R.; De Pablo, J.J.; Snezhko, A. Emergence of radial tree of bend stripes in active nematics. Phys. Rev. X 2019, 9, 031014. [Google Scholar] [CrossRef] [Green Version]
- Turiv, T.; Koizumi, R.; Thijssen, K.; Genkin, M.M.; Yu, H.; Peng, C.; Wei, Q.H.; Yeomans, J.M.; Aranson, I.S.; Doostmohammadi, A.; et al. Polar jets of swimming bacteria condensed by a patterned liquid crystal. Nat. Phys. 2020, 16, 481–487. [Google Scholar] [CrossRef] [Green Version]
- Duclos, G.; Adkins, R.; Banerjee, D.; Peterson, M.S.; Varghese, M.; Kolvin, I.; Baskaran, A.; Pelcovits, R.A.; Powers, T.R.; Baskaran, A.; et al. Topological structure and dynamics of three-dimensional active nematics. Science 2020, 367, 1120–1124. [Google Scholar] [CrossRef] [Green Version]
- Giomi, L.; Liverpool, T.B.; Marchetti, M.C. Sheared active fluids: Thickening, thinning, and vanishing viscosity. Phys. Rev. E 2010, 81, 051908. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guillamat, P.; Ignés-Mullol, J.; Shankar, S.; Marchetti, M.C.; Sagués, F. Probing the shear viscosity of an active nematic film. Phys. Rev. E 2016, 94, 060602. [Google Scholar] [CrossRef] [Green Version]
- Lydon, J. Chromonic liquid crystalline phases. Liq. Cryst. 2011, 38, 1663–1681. [Google Scholar] [CrossRef]
- Zimmermann, N.; Jünnemann-Held, G.; Collings, P.J.; Kitzerow, H.S. Self-organized assemblies of colloidal particles obtained from an aligned chromonic liquid crystal dispersion. Soft Matter 2015, 11, 1547–1553. [Google Scholar] [CrossRef] [Green Version]
- Park, H.S.; Kang, S.W.; Tortora, L.; Nastishin, Y.; Finotello, D.; Kumar, S.; Lavrentovich, O.D. Self-assembly of lyotropic chromonic liquid crystal Sunset Yellow and effects of ionic additives. J. Phys. Chem. B 2008, 112, 16307–16319. [Google Scholar] [CrossRef]
- Zhou, S.; Neupane, K.; Nastishin, Y.A.; Baldwin, A.R.; Shiyanovskii, S.V.; Lavrentovich, O.D.; Sprunt, S. Elasticity, viscosity, and orientational fluctuations of a lyotropic chromonic nematic liquid crystal disodium cromoglycate. Soft Matter 2014, 10, 6571–6581. [Google Scholar] [CrossRef]
- Davidson, Z.S.; Kang, L.; Jeong, J.; Still, T.; Collings, P.J.; Lubensky, T.C.; Yodh, A. Chiral structures and defects of lyotropic chromonic liquid crystals induced by saddle-splay elasticity. Phys. Rev. E 2015, 91, 050501. [Google Scholar] [CrossRef] [Green Version]
- Nayani, K.; Chang, R.; Fu, J.; Ellis, P.W.; Fernandez-Nieves, A.; Park, J.O.; Srinivasarao, M. Spontaneous emergence of chirality in achiral lyotropic chromonic liquid crystals confined to cylinders. Nat. Commun. 2015, 6, 1–7. [Google Scholar] [CrossRef]
- Jeong, J.; Davidson, Z.S.; Collings, P.J.; Lubensky, T.C.; Yodh, A. Chiral symmetry breaking and surface faceting in chromonic liquid crystal droplets with giant elastic anisotropy. Proc. Natl. Acad. Sci. USA 2014, 111, 1742–1747. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Park, G.; Čopar, S.; Suh, A.; Yang, M.; Tkalec, U.; Yoon, D.K. Periodic Arrays of Chiral Domains Generated from the Self-Assembly of Micropatterned Achiral Lyotropic Chromonic Liquid Crystal. ACS Cent. Sci. 2020, 6, 1964–1970. [Google Scholar] [CrossRef]
- Lavrentovich, M.; Sergan, T.; Kelly, J. Planar and twisted lyotropic chromonic liquid crystal cells as optical compensators for twisted nematic displays. Liq. Cryst. 2003, 30, 851–859. [Google Scholar] [CrossRef]
- Shiyanovskii, S.V.; Lavrentovich, O.D.; Schneider, T.; Ishikawa, T.; Smalyukh, I.I.; Woolverton, C.J.; Niehaus, G.D.; Doane, K.J. Lyotropic chromonic liquid crystals for biological sensing applications. Mol. Cryst. Liq. Cryst. 2005, 434, 259–587. [Google Scholar] [CrossRef]
- Sharma, A.; Ong, I.L.H.; Sengupta, A. Time dependent lyotropic chromonic textures in microfluidic confinements. Crystals 2021, 11, 35. [Google Scholar] [CrossRef]
- Peng, C.; Turiv, T.; Guo, Y.; Wei, Q.H.; Lavrentovich, O.D. Command of active matter by topological defects and patterns. Science 2016, 354, 882–885. [Google Scholar] [CrossRef] [Green Version]
- Baza, H.; Turiv, T.; Li, B.X.; Li, R.; Yavitt, B.M.; Fukuto, M.; Lavrentovich, O.D. Shear-induced polydomain structures of nematic lyotropic chromonic liquid crystal disodium cromoglycate. Soft Matter 2020, 16, 8565–8576. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, R.; Ge, B.; Yaqoob, Z.; So, P.T.C.; Bischofberger, I. Structures and topological defects in pressure-driven lyotropic chromonic liquid crystals. Proc. Natl. Acad. Sci. USA 2021, 118, e2108361118. [Google Scholar] [CrossRef]
- Thampi, S.P.; Golestanian, R.; Yeomans, J.M. Driven active and passive nematics. Mol. Phys. 2015, 113, 2656–2665. [Google Scholar] [CrossRef] [Green Version]
- Thijssen, K.; Metselaar, L.; Yeomans, J.M.; Doostmohammadi, A. Active nematics with anisotropic friction: The decisive role of the flow aligning parameter. Soft Matter 2020, 16, 2065–2074. [Google Scholar] [CrossRef] [Green Version]
- Chandragiri, S.; Doostmohammadi, A.; Yeomans, J.M.; Thampi, S.P. Flow states and transitions of an active nematic in a three-dimensional channel. Phys. Rev. Lett. 2020, 125, 148002. [Google Scholar] [PubMed]
- Pieranski, P.; Guyon, E.; Pikin, S. Nouvelles instabilités de cisaillement dans les nématiques. J. Phys. Colloq. 1976, 37, C1-3. [Google Scholar] [CrossRef]
- Denniston, C.; Orlandini, E.; Yeomans, J.M. Lattice Boltzmann simulations of liquid crystal hydrodynamics. Phys. Rev. E 2001, 63, 056702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beris, A.N.; Edwards, B.J. Thermodynamics of Flowing Systems: With Internal Microstructure; Number 36, Oxford University Press on Demand: Oxford, UK, 1994. [Google Scholar]
- Ravnik, M.; Žumer, S. Landau–de Gennes modelling of nematic liquid crystal colloids. Liq. Cryst. 2009, 36, 1201–1214. [Google Scholar] [CrossRef]
- Denniston, C.; Marenduzzo, D.; Orlandini, E.; Yeomans, J. Lattice Boltzmann algorithm for three–dimensional liquid–crystal hydrodynamics. Philos. Trans. R. Soc. London. Ser. Math. Phys. Eng. Sci. 2004, 362, 1745–1754. [Google Scholar] [CrossRef]
- Zhang, R.; Roberts, T.; Aranson, I.S.; De Pablo, J.J. Lattice Boltzmann simulation of asymmetric flow in nematic liquid crystals with finite anchoring. J. Chem. Phys. 2016, 144, 084905. [Google Scholar] [CrossRef]
- Giomi, L.; Bowick, M.J.; Ma, X.; Marchetti, M.C. Defect annihilation and proliferation in active nematics. Phys. Rev. Lett. 2013, 110, 228101. [Google Scholar] [CrossRef]
- Marenduzzo, D.; Orlandini, E.; Cates, M.; Yeomans, J. Steady-state hydrodynamic instabilities of active liquid crystals: Hybrid lattice Boltzmann simulations. Phys. Rev. E 2007, 76, 031921. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ravnik, M.; Yeomans, J.M. Confined active nematic flow in cylindrical capillaries. Physical review letters 2013, 110, 026001. [Google Scholar] [CrossRef]
- Green, R.; Toner, J.; Vitelli, V. Geometry of thresholdless active flow in nematic microfluidics. Phys. Rev. Fluids 2017, 2, 104201. [Google Scholar] [CrossRef]
- Zhou, S.; Nastishin, Y.A.; Omelchenko, M.M.; Tortora, L.; Nazarenko, V.G.; Boiko, O.P.; Ostapenko, T.; Hu, T.; Almasan, C.C.; Sprunt, S.N.; et al. Elasticity of lyotropic chromonic liquid crystals probed by director reorientation in a magnetic field. Phys. Rev. Lett. 2012, 109, 037801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Strübing, T.; Khosravanizadeh, A.; Vilfan, A.; Bodenschatz, E.; Golestanian, R.; Guido, I. Wrinkling instability in 3D active nematics. Nano Lett. 2020, 20, 6281–6288. [Google Scholar] [CrossRef] [PubMed]
- Nejad, M.R.; Yeomans, J.M. Extensile stress promotes out-of-plane flows in active layers. arXiv 2021, arXiv:2105.10812. [Google Scholar]
- Jewell, S.A.; Cornford, S.L.; Yang, F.; Cann, P.; Sambles, J.R. Flow-driven transition and associated velocity profiles in a nematic liquid-crystal cell. Phys. Rev. E 2009, 80, 041706. [Google Scholar] [CrossRef] [PubMed]
- Batista, V.M.; Blow, M.L.; da Gama, M.M.T. The effect of anchoring on the nematic flow in channels. Soft Matter 2015, 11, 4674–4685. [Google Scholar] [CrossRef] [PubMed] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Zhang, R. Interplay of Active Stress and Driven Flow in Self-Assembled, Tumbling Active Nematics. Crystals 2021, 11, 1071. https://doi.org/10.3390/cryst11091071
Wang W, Zhang R. Interplay of Active Stress and Driven Flow in Self-Assembled, Tumbling Active Nematics. Crystals. 2021; 11(9):1071. https://doi.org/10.3390/cryst11091071
Chicago/Turabian StyleWang, Weiqiang, and Rui Zhang. 2021. "Interplay of Active Stress and Driven Flow in Self-Assembled, Tumbling Active Nematics" Crystals 11, no. 9: 1071. https://doi.org/10.3390/cryst11091071
APA StyleWang, W., & Zhang, R. (2021). Interplay of Active Stress and Driven Flow in Self-Assembled, Tumbling Active Nematics. Crystals, 11(9), 1071. https://doi.org/10.3390/cryst11091071