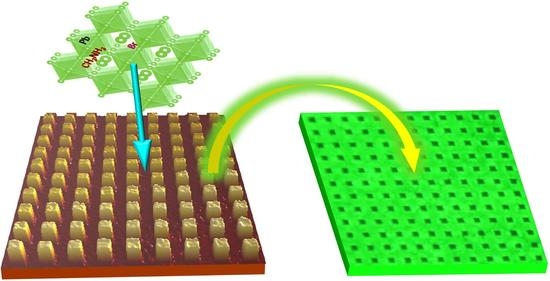
Two-Dimensional Crystalline Gridding Networks of Hybrid Halide Perovskite for Random Lasing
Abstract
:1. Introduction
2. The Network of Squarely Gridded Thin Film of MAPbBr3
3. Optical Spectroscopic Performance of the Gridded Crystalline Film
3.1. Absorption and Photoluminescence
3.2. Random Lasing
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Thomas, M.B.; David, A.E.; Leeor, K.; Gary, H.; David, C.H. Hybrid organic–inorganic perovskites: Low-cost semiconductors with intriguing charge-transport properties. Nat. Rev. Mater. 2016, 1, 15007. [Google Scholar]
- Jena, A.K.; Kulkarni, A.; Miyasaka, T. Halide Perovskite Photovoltaics: Background, Status, and Future Prospects. Chem. Rev. 2019, 119, 3036–3103. [Google Scholar] [CrossRef]
- Gu, Z.; Zhou, Z.; Huang, Z.; Wang, K.; Cai, Z.; Hu, X.; Li, L.; Li, M.; Zhao, Y.S.; Song, Y. Controllable Growth of High-Quality Inorganic Perovskite Microplate Arrays for Functional Optoelectronics. Adv. Mater. 2020, 32, e1908006. [Google Scholar] [CrossRef]
- Wang, K.; Xing, G.; Song, Q.; Xiao, S. Micro- and Nanostructured Lead Halide Perovskites: From Materials to Integrations and Devices. Adv. Mater. 2020, 33, e2000306. [Google Scholar] [CrossRef]
- Ahmad, R.; Surendran, A.; Harikesh, P.C.; Haselsberger, R.; Jamaludin, N.F.; John, R.; Koh, T.M.; Bruno, A.; Leong, W.L.; Mathews, N.; et al. Perturbation-Induced Seeding and Crystallization of Hybrid Perovskites over Surface-Modified Substrates for Optoelectronic Devices. ACS Appl. Mater. Interfaces 2019, 11, 27727–27734. [Google Scholar] [CrossRef]
- Cao, L.Z.; Hu, F.R.; Zhang, C.F.; Zhu, S.N.; Xiao, M.; Wang, X.Y. Optical studies of semiconductor perovskite nanocrystals for classical optoelectronic applications and quantum information technoloies: A review. Adv. Photon. 2020, 2, 054001. [Google Scholar] [CrossRef]
- Congreve, D.N.; Weidman, M.C.; Seitz, M.; Paritmongkol, W.; Dahod, N.S.; Tisdale, W.A. Tunable Light-Emitting Diodes Utilizing Quantum-Confined Layered Perovskite Emitters. ACS Photon. 2017, 4, 476–481. [Google Scholar] [CrossRef]
- Cho, H.; Jeong, S.-H.; Park, M.-H.; Kim, Y.-H.; Wolf, C.; Lee, C.-L.; Heo, J.H.; Sadhanala, A.; Myoung, N.; Yoo, S.; et al. Overcoming the electroluminescence efficiency limitations of perovskite light-emitting diodes. Science 2015, 350, 1222–1225. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Cui, J.; Du, K.; Tian, H.; He, Z.; Zhou, Q.; Yang, Z.; Deng, Y.; Chen, D.; Zuo, X.; et al. Efficient blue light-emitting diodes based on quantum-confined bromide perovskite nanostructures. Nat. Photon. 2019, 13, 760–764. [Google Scholar] [CrossRef]
- Yang, W.S.; Park, B.-W.; Jung, E.H.; Jeon, N.J.; Kim, Y.C.; Lee, D.U.; Shin, S.S.; Seo, J.; Kim, E.K.; Noh, J.H.; et al. Iodide management in formamidinium-lead-halide–based perovskite layers for efficient solar cells. Science 2017, 356, 1376–1379. [Google Scholar] [CrossRef] [Green Version]
- Arora, N.; Dar, M.I.; Hinderhofer, A.; Pellet, N.; Schreiber, F.; Zakeeruddin, S.M.; Grätzel, M. Perovskite solar cells with CuSCN hole extraction layers yield stabilized efficiencies greater than 20%. Science 2017, 358, 768–771. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ergen, O.; Gilbert, S.M.; Pham, T.; Turner, S.J.; Tan, M.T.Z.; Worsley, M.A.; Zettl, A. Graded bandgap perovskite solar cells. Nat. Mater. 2016, 16, 522–525. [Google Scholar] [CrossRef]
- Kao, T.S.; Chou, Y.-H.; Hong, K.-B.; Huang, J.-F.; Chou, C.-H.; Kuo, H.-C.; Chen, F.-C.; Lu, T.-C. Controllable lasing performance in solution-processed organic–inorganic hybrid perovskites. Nanoscale 2016, 8, 18483–18488. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.; Zhang, C.; Liu, X.; Yao, J.; Zhao, Y.S. Materials chemistry and engineering in metal halide perovskite lasers. Chem. Soc. Rev. 2020, 49, 951–982. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, S.; Huang, C.; Yisheng, G.; Wang, K.; Xiao, S.; Song, Q. Room temperature three-photon pumped CH3NH3PbBr3 perovskite microlasers. Sci. Rep. 2017, 7, 45391. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Duan, Z.; Wang, S.; Yi, N.; Gu, Z.; Gao, Y.; Song, Q.; Xiao, S. Miscellaneous Lasing Actions in Organo-Lead Halide Perovskite Films. ACS Appl. Mater. Interfaces 2017, 9, 20711–20718. [Google Scholar] [CrossRef]
- Gu, Z.; Wang, K.; Sun, W.; Li, J.; Liu, S.; Song, Q.; Xiao, S. Two-Photon Pumped CH3NH3PbBr3 Perovskite Microwire Lasers. Adv. Opt. Mater. 2015, 4, 472–479. [Google Scholar] [CrossRef]
- Jeon, T.; Kim, S.J.; Yoon, J.; Byun, J.; Hong, H.R.; Lee, T.-W.; Kim, J.-S.; Shin, B.; Kim, S.O. Hybrid Perovskites: Effective Crystal Growth for Optoelectronic Applications. Adv. Energy Mater. 2017, 7, 1602596. [Google Scholar] [CrossRef]
- Liu, C.; Cheng, Y.-B.; Ge, Z. Understanding of perovskite crystal growth and film formation in scalable deposition processes. Chem. Soc. Rev. 2020, 49, 1653–1687. [Google Scholar] [CrossRef]
- Choi, J.J.; Khan, M.E.; Hawash, Z.; Kim, K.J.; Lee, H.; Ono, L.K.; Qi, Y.B.; Kim, Y.-H.; Park, J.Y. Atomic-scale view of stability and degradation of single-crystal MAPbBr3 surfaces. J. Mater. Chem. A 2019, 7, 20760. [Google Scholar] [CrossRef]
- Wang, K.-H.; Li, L.-C.; Shellaiah, M.; Sun, K.W. Structural and Photophysical Properties of Methylammonium Lead Tribromide (MAPbBr3) Single Crystals. Sci. Rep. 2017, 7, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.P.; Wang, M.; Ma, L.; Fu, Y.L.; Fu, Y.L.; Guo, J.X.; Ma, H.; Zhang, Y.W.; Yan, Z.G.; Han, X.D. Ultrafast two-photon optical switch using singlecrystal hybrid halide perovskites. Optica 2021, 8, 735–742. [Google Scholar] [CrossRef]
- Weng, G.; Tian, J.; Chen, S.; Xue, J.; Yan, J.; Hu, X.; Chen, S.; Zhu, Z.; Chu, J. Giant reduction of the random lasing threshold in CH3NH3PbBr3 perovskite thin films by using a patterned sapphire substrate. Nanoscale 2019, 11, 10636–10645. [Google Scholar] [CrossRef]
- Shi, Z.-F.; Sun, X.-G.; Wu, D.; Xu, T.-T.; Tian, Y.-T.; Zhang, Y.-T.; Li, X.-J.; Du, G.-T. Near-infrared random lasing realized in a perovskite CH3NH3PbI3 thin film. J. Mater. Chem. C 2016, 4, 8373–8379. [Google Scholar] [CrossRef]
- Wang, Y.-C.; Li, H.; Hong, Y.-H.; Hong, K.-B.; Chen, F.-C.; Hsu, C.-H.; Lee, R.-K.; Conti, C.; Kao, T.S.; Lu, T.-C. Flexible Organometal–Halide Perovskite Lasers for Speckle Reduction in Imaging Projection. ACS Nano 2019, 13, 5421–5429. [Google Scholar] [CrossRef] [PubMed]
- Saouma, F.O.; Stoumpos, C.C.; Wong, J.; Kanatzidis, M.G.; Jang, J.I. Selective enhancement of optical nonlinearity in two-dimensional organic-inorganic lead iodide perovskites. Nat. Commun. 2017, 8, 742. [Google Scholar] [CrossRef]
- Hu, J.; Wang, M.; Tang, F.; Liu, M.; Mu, Y.; Fu, Y.; Guo, J.; Song, X.; Zhang, X. Threshold Size Effects in the Patterned Crystallization of Hybrid Halide Perovskites for Random Lasing. Adv. Photon. Res. 2020, 2, 2000097. [Google Scholar] [CrossRef]
- Oded, M.; Kelly, S.T.; Gilles, M.K.; Mueller, A.H.E.; Shenhar, R. Periodic nanoscale patterning of polyelectrolytes over square centimeter areas using block copolymer templates. Soft Matter 2016, 12, 4595–4602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Coutts, M.J.; Zareie, H.M.; Cortie, M.; Phillips, M.; Wuhrer, R.; McDonagh, A. Exploiting Zinc Oxide Re-emission to Fabricate Periodic Arrays. ACS Appl. Mater. Interfaces 2010, 2, 1774–1779. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Petit, C.A.P.; Carbeck, J.D. Combing of nolecules in microchannels (COMMIC): A method for micropatterning and orienting stretched molecules of DNA on a surface. Nano Lett. 2003, 3, 1141. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, X.; Li, W.; Jiang, C.; Wang, Z.; Xiao, X. Recent progress in periodic patterning fabricated by self-assembly of colloidal spheres for optical applications. Sci. China Mater. 2020, 63, 1418–1437. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Xue, H.; Zhang, X. Two-Dimensional Crystalline Gridding Networks of Hybrid Halide Perovskite for Random Lasing. Crystals 2021, 11, 1114. https://doi.org/10.3390/cryst11091114
Hu J, Xue H, Zhang X. Two-Dimensional Crystalline Gridding Networks of Hybrid Halide Perovskite for Random Lasing. Crystals. 2021; 11(9):1114. https://doi.org/10.3390/cryst11091114
Chicago/Turabian StyleHu, Jingyun, Haibin Xue, and Xinping Zhang. 2021. "Two-Dimensional Crystalline Gridding Networks of Hybrid Halide Perovskite for Random Lasing" Crystals 11, no. 9: 1114. https://doi.org/10.3390/cryst11091114