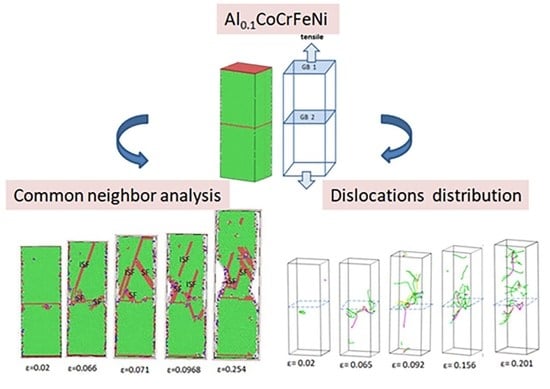
The Influence of Grain Boundaries on Crystal Structure and Tensile Mechanical Properties of Al0.1CoCrFeNi High-Entropy Alloys Studied by Molecular Dynamics Method
Abstract
:1. Introduction
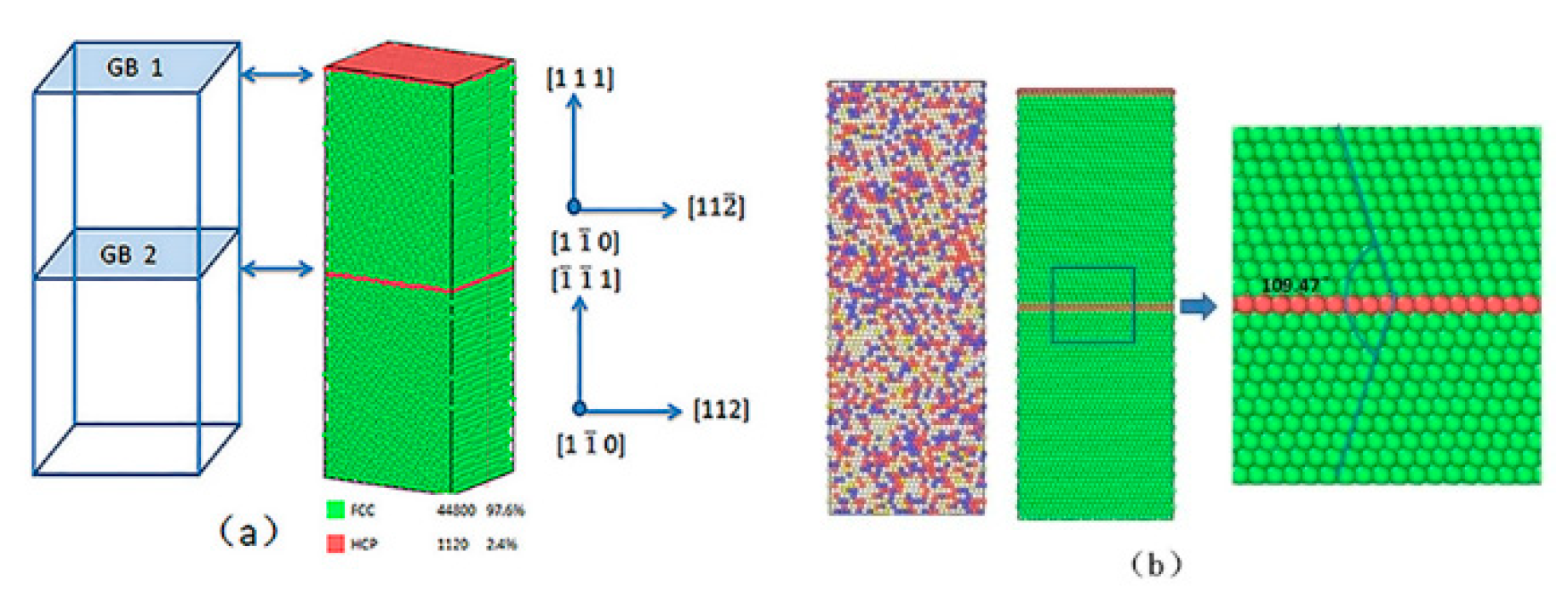
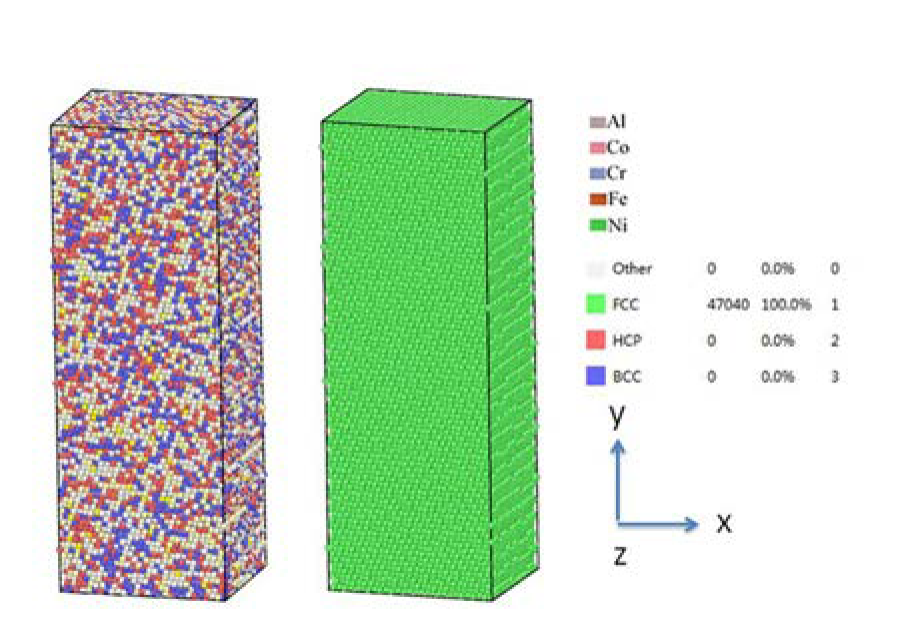
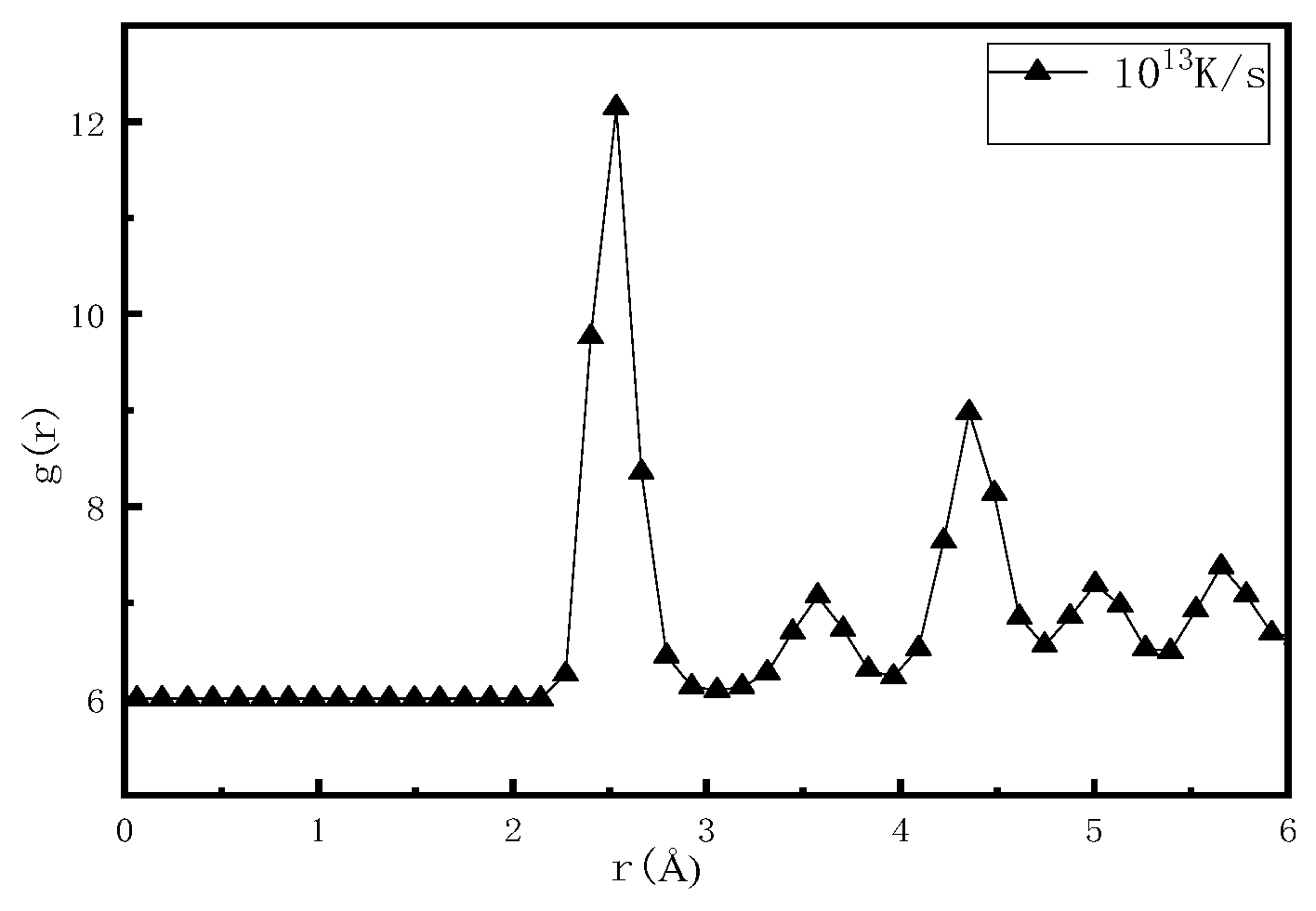
2. Computational Methods
3. Results
3.1. Effect of Σ3 GBs HEAs and Non-GBs HEAs at Different Strain Rates at Room Temperature (300 K)
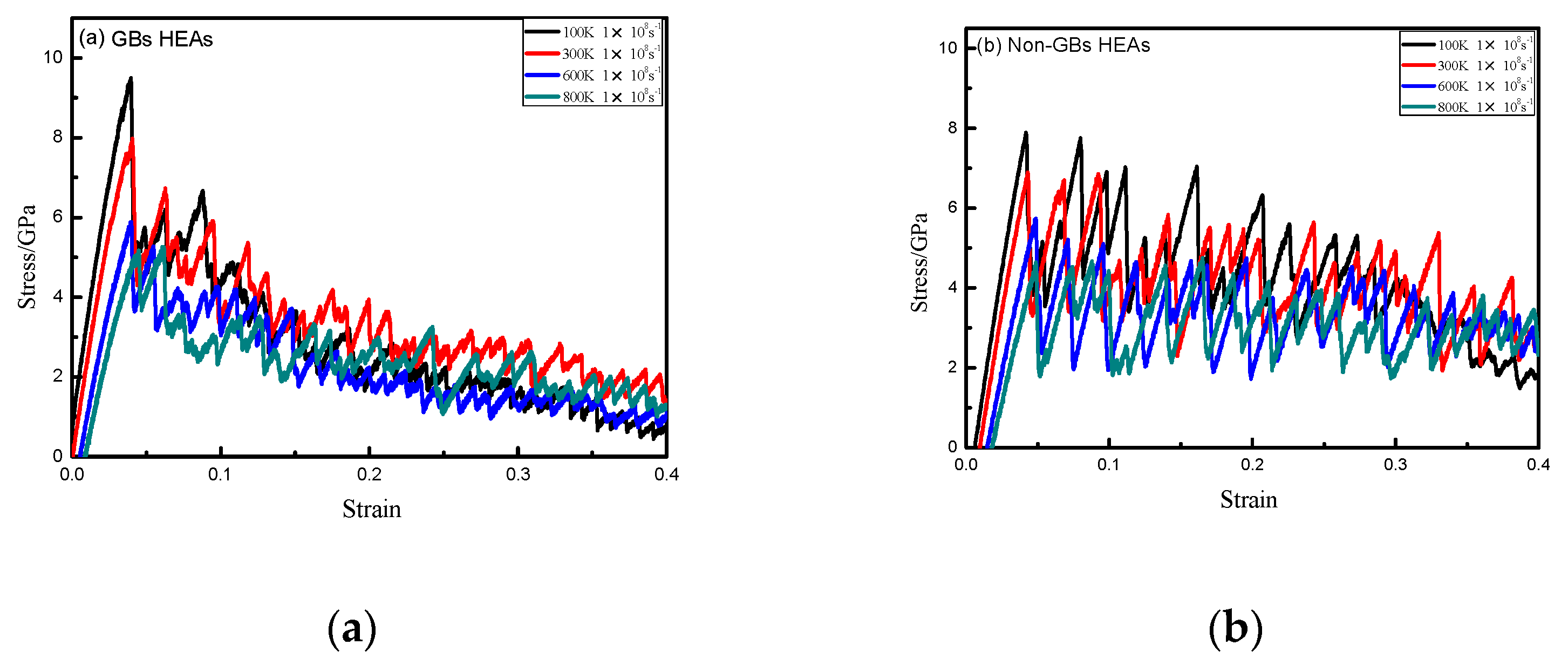
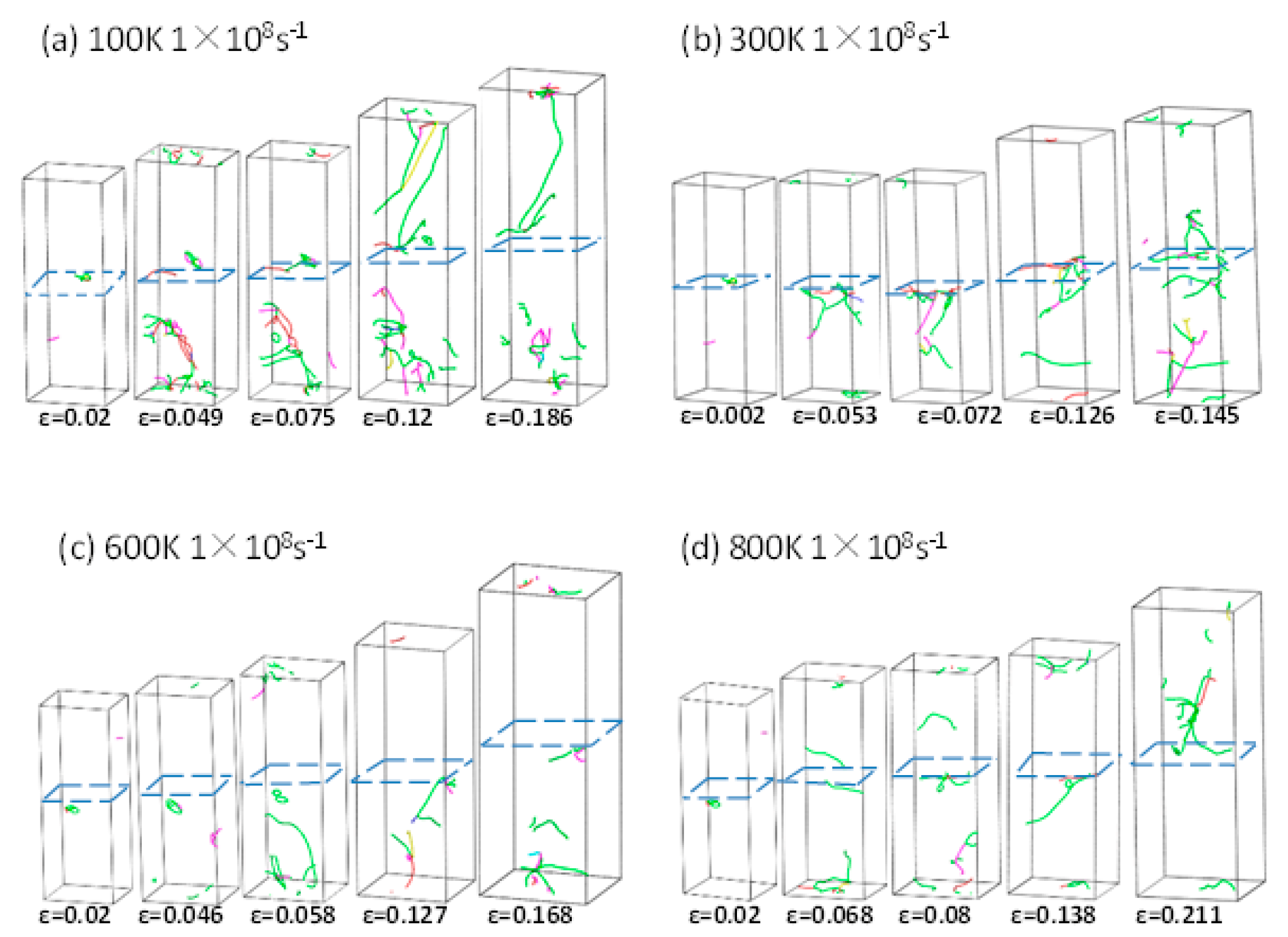
3.2. Tensile Properties of Σ3 GBs HEAs and Without Non-GBs HEAs at the Same Strain Rate at Different Temperatures
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chou, Y.-L.; Wang, Y.-C.; Yeh, J.-W.; Shih, H.-C. Pitting corrosion of the high-entropy alloy Co1.5CrFeNi1.5Ti0.5Mo0.1 in chloride-containing sulphate solutions. Corros. Sci. 2010, 52, 3481–3491. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, B.; Xie, X.; Brechtl, J.; Dahmen, K.A.; Liaw, P.K. Corrosion of AlxCoCrFeNi High-entropy alloys: Al-content and potential scan-rate dependent pitting behavior. Corros. Sci. 2017, 119, 33–45. [Google Scholar] [CrossRef]
- Chuang, M.-H.; Tsai, M.-H.; Wang, W.-R.; Lin, S.-J.; Yeh, J.-W. Microstructure and wear behavior of AlxCo1.5CrFeNi1.5Tiy high-entropy alloys. Acta Mater. 2011, 59, 6308–6317. [Google Scholar] [CrossRef]
- Poulia, A.; Georgatis, E.; Lekatou, A. Microstructure and wear behavior of a refractory high entropy alloy. Int. J. Refract. Met. Hard Mater. 2016, 57, 50–63. [Google Scholar] [CrossRef]
- Yeh, J.-W.; Chen, S.-K.; Lin, S.-J.; Gan, J.-Y.; Chin, T.-S.; Shun, T.-T.; Tsau, C.-H.; Chang, S.-Y. Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes. Adv. Eng. Mater. 2004, 5, 299–303. [Google Scholar] [CrossRef]
- Qiu, X.-W.; Zhang, Y.-P.; He, L.; Liu, C.-G. Microstructure and corrosion resistance of AlCrFeCuCo high entropy alloy. J. Alloys Compd. 2013, 549, 195–199. [Google Scholar] [CrossRef]
- Yen, J.-W.; Lin, S.-J.; Chin, T.-S.; Gan, J.-Y.; Chen, S.-K.; Shun, T.-T.; Tsau, C.-H.; Chou, S.-Y. Formation of simple crystal structures in Cu-Co-Ni-Cr-Al-Fe-Ti-V alloys with multi principal metallic elements. Metall. Mater. Trans. A 2004, 35, 2533–2536. [Google Scholar]
- Tong, C.-J.; Chen, Y.-L.; Yeh, J.-W.; Shun, T.-T.; Tsau, C.-H.; Lin, S.-J.; Chang, S.-Y. Microstructure characterization of AlxCoCrCuFeNi high-entropy alloy system with multi-principal elements. Metall. Mater. Trans. A 2005, 36, 881–893. [Google Scholar] [CrossRef]
- Wu, Z.; Bei, H.; Pharr, G.-M.; George, E.-P. Temperature dependence of the mechanical properties of equiatomic solid solution alloys with face-centered cubic crystal structures. Acta Mater. 2014, 81, 428–441. [Google Scholar] [CrossRef]
- Liu, W.-H.; Wu, Y.; He, J.-Y.; Nieh, T.-G.; Lu, Z.P. Grain growth and the Hall–Petch relationship in a high-entropy FeCrNiCoMn alloy. Scr. Mater. 2013, 68, 526–529. [Google Scholar] [CrossRef]
- Thota, H.; Jeyaraam, R.; Bairi, L.-R.; Tirunilaic, A.-S.; Kauffmann, A.; Freudenberger, J.; Heilmaier, M.; Mandal, S.; Vadlamani, S.-S. Grain boundary engineering and its implications on corrosion behavior of equiatomic CoCrFeMnNi high entropy alloy. J. Alloys Compd. 2020, 888, 161500. [Google Scholar] [CrossRef]
- Chen, B.-R.; Yeh, A.-C.; Yeh, J.-W. Effect of one-step recrystallization on the grain boundary evolution of CoCrFeMnNi high entropy alloy and its subsystems. Sci. Rep. 2016, 6, 22306. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.-M.; Tasan, C.-C.; Pradeep, K.-G.; Raabe, D. A TRIP-assisted dual-phase high-entropy alloy: Grain size and phase fraction effects on deformation behavior. Acta Mater. 2017, 131, 323–335. [Google Scholar] [CrossRef]
- Zhao, S.-J. Effects of local elemental ordering on defect-grain boundary interactions in high-entropy alloys. J. Alloys Compd. 2021, 887, 161314. [Google Scholar] [CrossRef]
- Kumar, N.; Ying, Q.; Nie, X.; Mishra, R.-S.; Tang, Z.; Liaw, P.-K.; Brennan, R.-E.; Doherty, K.-J.; Cho, K.-C. High Strain-Rate Compressive Deformation Behavior of the Al0.1CrFeCoNi High Entropy Alloy. Mater. Des. 2015, 86, 598–602. [Google Scholar] [CrossRef]
- Bulatov, V.-V.; Reed, B.-W.; Kumar, M. Grain boundary energy function for fcc metals. Acta Mater. 2014, 65, 161–175. [Google Scholar] [CrossRef]
- Yang, J.; Qiao, W.-J.; Ma, G.-S.; Wu, Y.-G.; Zhao, D. Revealing the Hall-Petch relationship of Al0.1CoCrFeNi high-entropy alloy and its deformation mechanisms. J. Alloys Compd. 2019, 795, 269–274. [Google Scholar] [CrossRef]
- Yang, T.; Xia, S.; Liu, S.; Wang, C.; Wang, L. Effects of Al addition on microstructure and mechanical properties of AlxCoCrFeNi High-entropy alloy. Mater. Sci. Eng. A 2015, 648, 15–22. [Google Scholar] [CrossRef]
- Xia, S.; Zhang, Y. Deformation mechanisms of Al0.1CoCrFeNi high entropy alloy at ambient and cryogenic temperatures. Mater. Sci. Eng. A 2018, 733, 408–413. [Google Scholar] [CrossRef]
- Yang, T.-F.; Tang, Z.; Xie, X.; Carroll, R.; Wang, G.-Y.; Wang, Y.-G.; Dahmen, K.-A.; Liaw, P.-K.; Zhang, Y.-W. Deformation mechanisms of Al0.1CoCrFeNi at elevated temperatures. Mater. Sci. Eng. A 2017, 684, 552–558. [Google Scholar] [CrossRef] [Green Version]
- Jia, L.; Fang, Q.-H.; Liu, B.; Liu, Y.-W.; Liu, Y. Mechanical behaviors of AlCrFeCuNi high-entropy alloys under uniaxial tensile via molecular dynamics simulation. RSC Adv. 2016, 6, 76409–76419. [Google Scholar]
- Brandon, D.-G. The structure of high-angle grain boundaries. Acta Metall. 1966, 14, 1479–1484. [Google Scholar] [CrossRef]
- Yang, Y.-C.; Liu, C.-X.; Lin, C.-Y.; Xia, Z.-H. The effect of local atomic configuration in high-entropy alloys on the dislocation behaviors and mechanical properties. Mater. Sci. Eng. A 2021, 815, 141253. [Google Scholar] [CrossRef]
- Sharma, A.; Balasubramanian, G. Dislocation dynamics in Al0.1CoCrFeNi high-entropy alloy under tensile loading. Intermetallics 2017, 91, 31–34. [Google Scholar] [CrossRef]

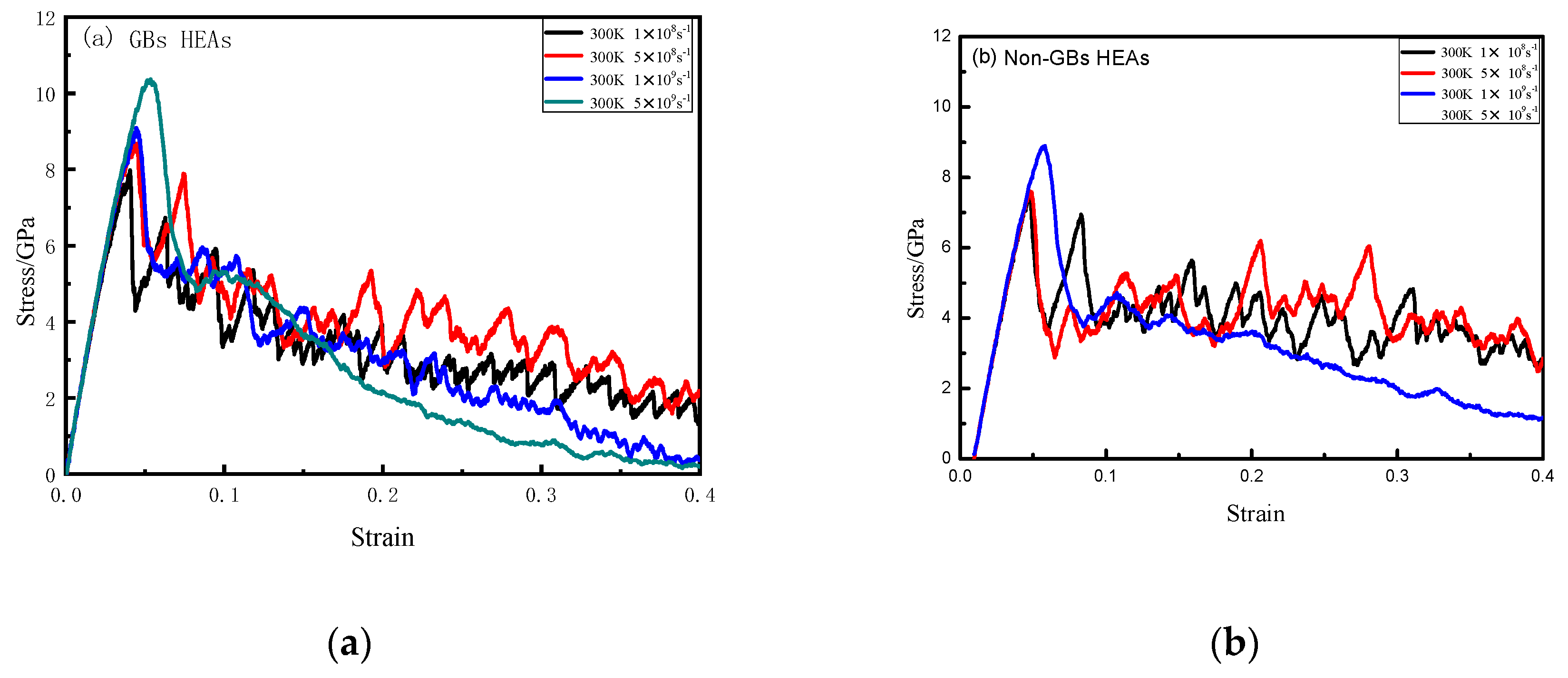
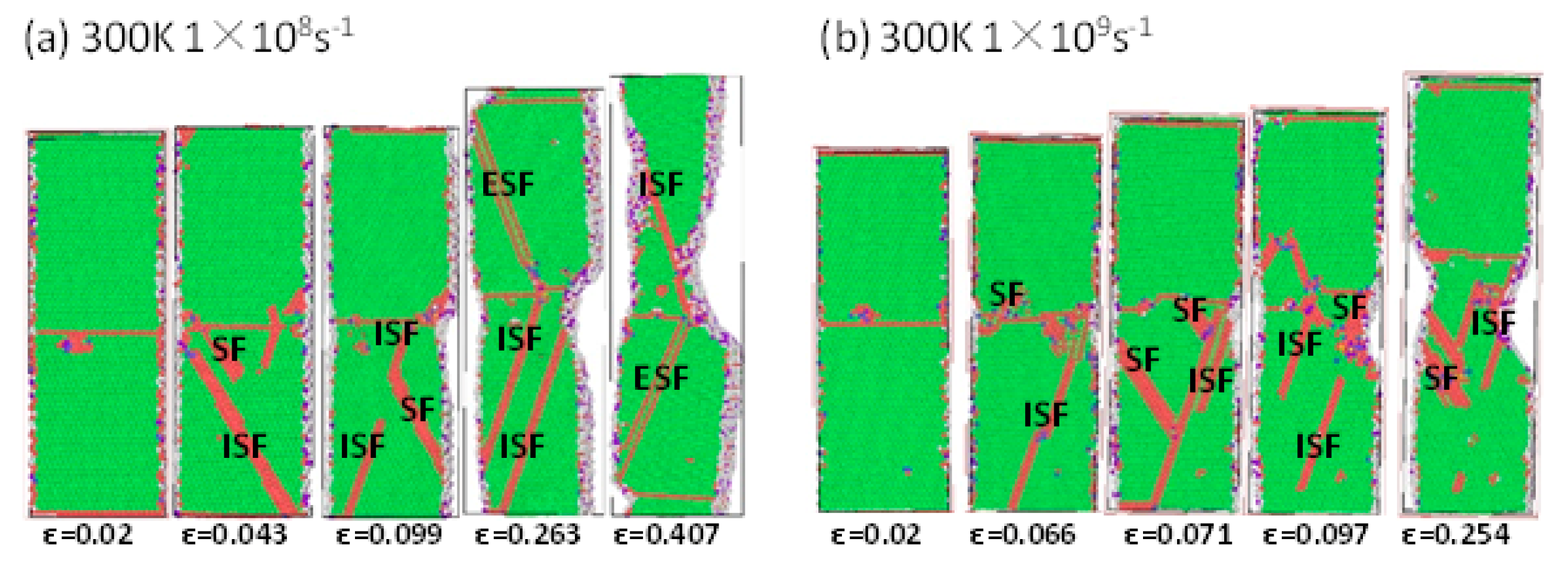
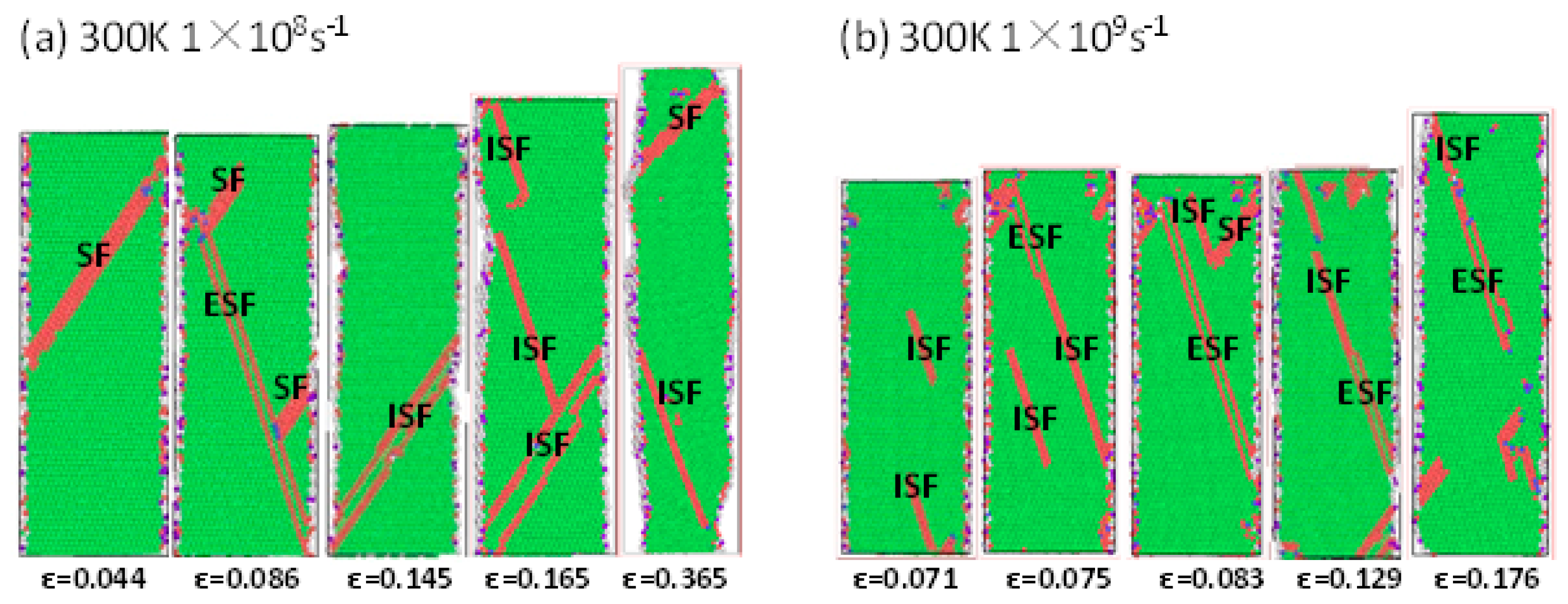
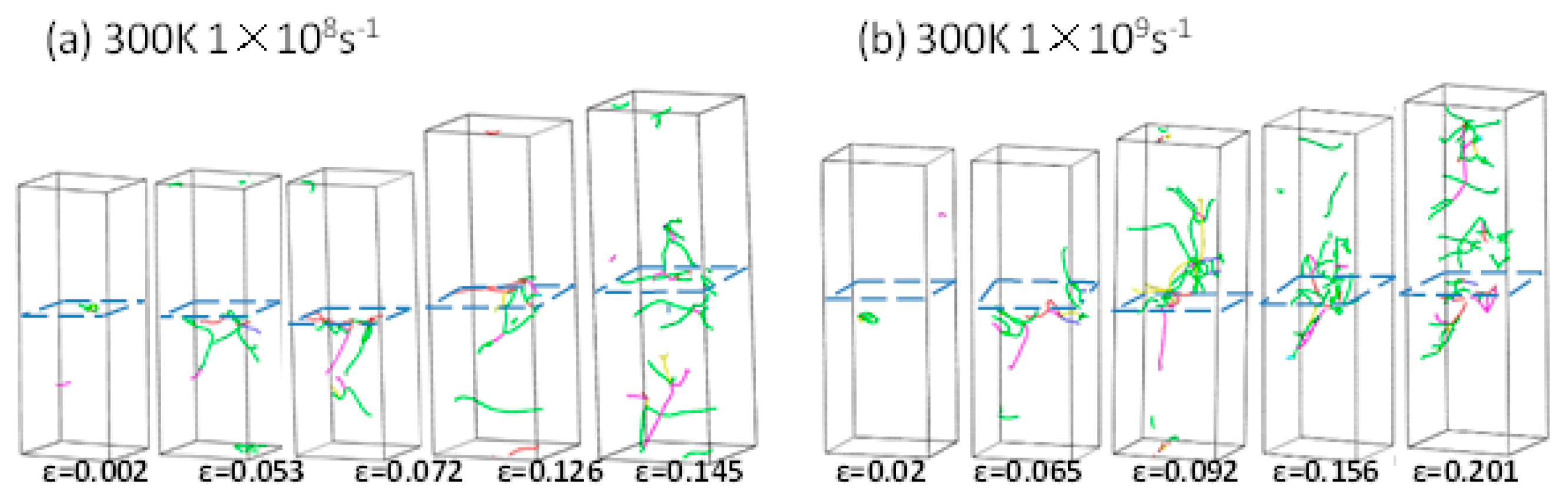




| Rate/s−1 | Non-GBs Yield Strength/GPa | GBsyield Strength/GPa | Non-GBs Young’s Modulus/GPa | GBsYoung’s Modulus/GPa |
|---|---|---|---|---|
| 1 × 108 | 6.89 | 7.97 | 219.12 | 230.57 |
| 5 × 108 | 7.51 | 8.67 | 219.24 | 231.63 |
| 1 × 109 | 7.54 | 9.03 | 219.71 | 235.08 |
| 5 × 109 | 8.84 | 10.34 | 221.07 | 235.76 |
| Temperature/K | Non-GBs Yield Strength/GPa | GBsyield Strength/GPa | Non-GBsYoung’s Modulus/GPa | GBsYoung’s Modulus/GPa |
|---|---|---|---|---|
| 100 | 7.86 | 9.47 | 226.09 | 242.84 |
| 300 | 6.89 | 7.97 | 219.12 | 230.57 |
| 600 | 5.67 | 5.86 | 180.52 | 188.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Wang, R.; Jian, Z. The Influence of Grain Boundaries on Crystal Structure and Tensile Mechanical Properties of Al0.1CoCrFeNi High-Entropy Alloys Studied by Molecular Dynamics Method. Crystals 2022, 12, 48. https://doi.org/10.3390/cryst12010048
Liu C, Wang R, Jian Z. The Influence of Grain Boundaries on Crystal Structure and Tensile Mechanical Properties of Al0.1CoCrFeNi High-Entropy Alloys Studied by Molecular Dynamics Method. Crystals. 2022; 12(1):48. https://doi.org/10.3390/cryst12010048
Chicago/Turabian StyleLiu, Cuixia, Rui Wang, and Zengyun Jian. 2022. "The Influence of Grain Boundaries on Crystal Structure and Tensile Mechanical Properties of Al0.1CoCrFeNi High-Entropy Alloys Studied by Molecular Dynamics Method" Crystals 12, no. 1: 48. https://doi.org/10.3390/cryst12010048
APA StyleLiu, C., Wang, R., & Jian, Z. (2022). The Influence of Grain Boundaries on Crystal Structure and Tensile Mechanical Properties of Al0.1CoCrFeNi High-Entropy Alloys Studied by Molecular Dynamics Method. Crystals, 12(1), 48. https://doi.org/10.3390/cryst12010048