Effects of Grain Boundary Angles on Initial Deformation of 304 Austenitic Stainless Steel under Nanoindentation: A Molecular Dynamics Simulation
Abstract
:1. Introduction
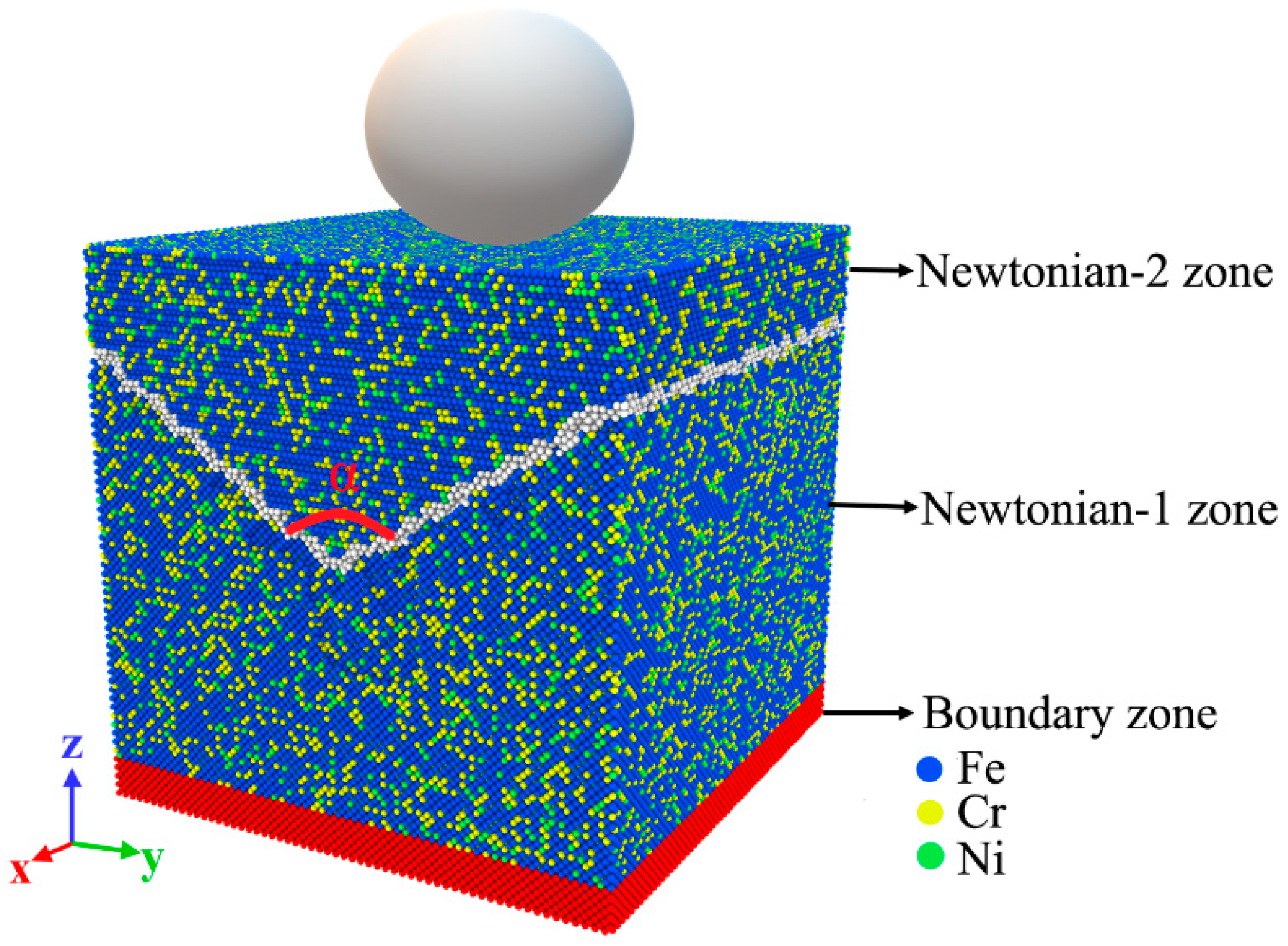
2. Simulation Methods
3. Results and Discussion
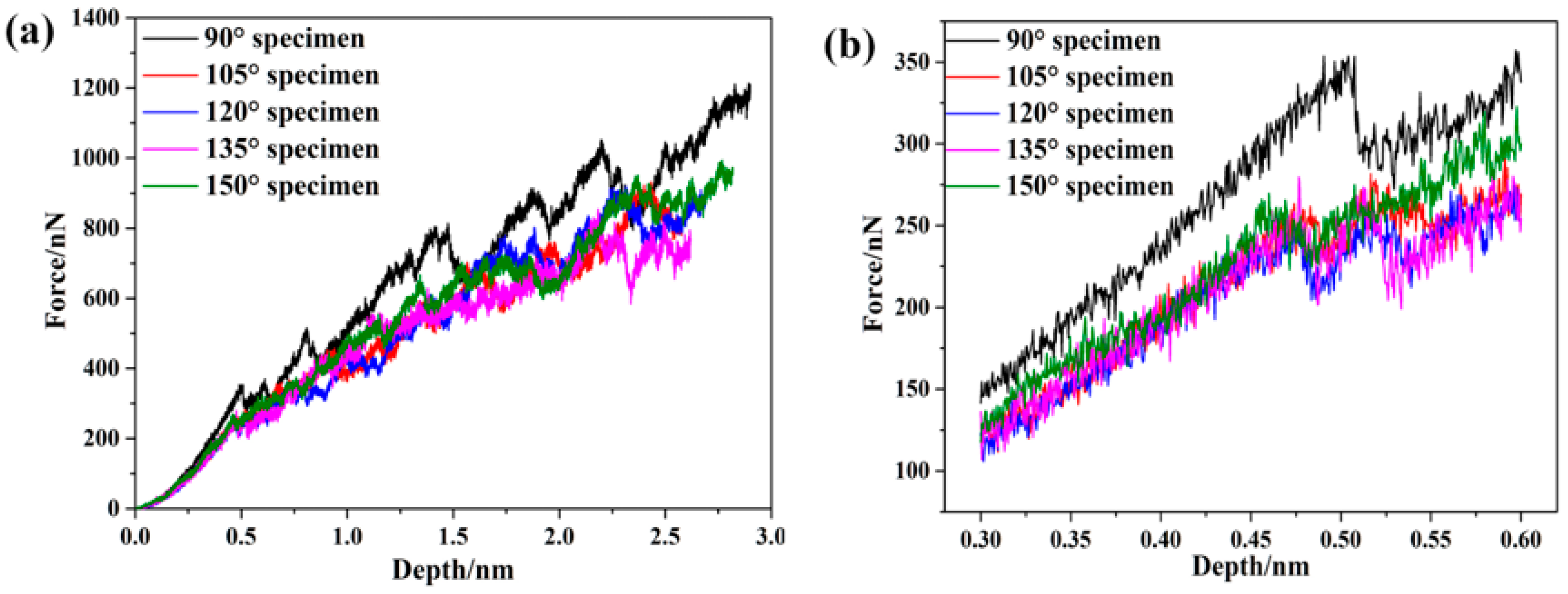
3.1. The Force and Depth Curves of Nanoindentation
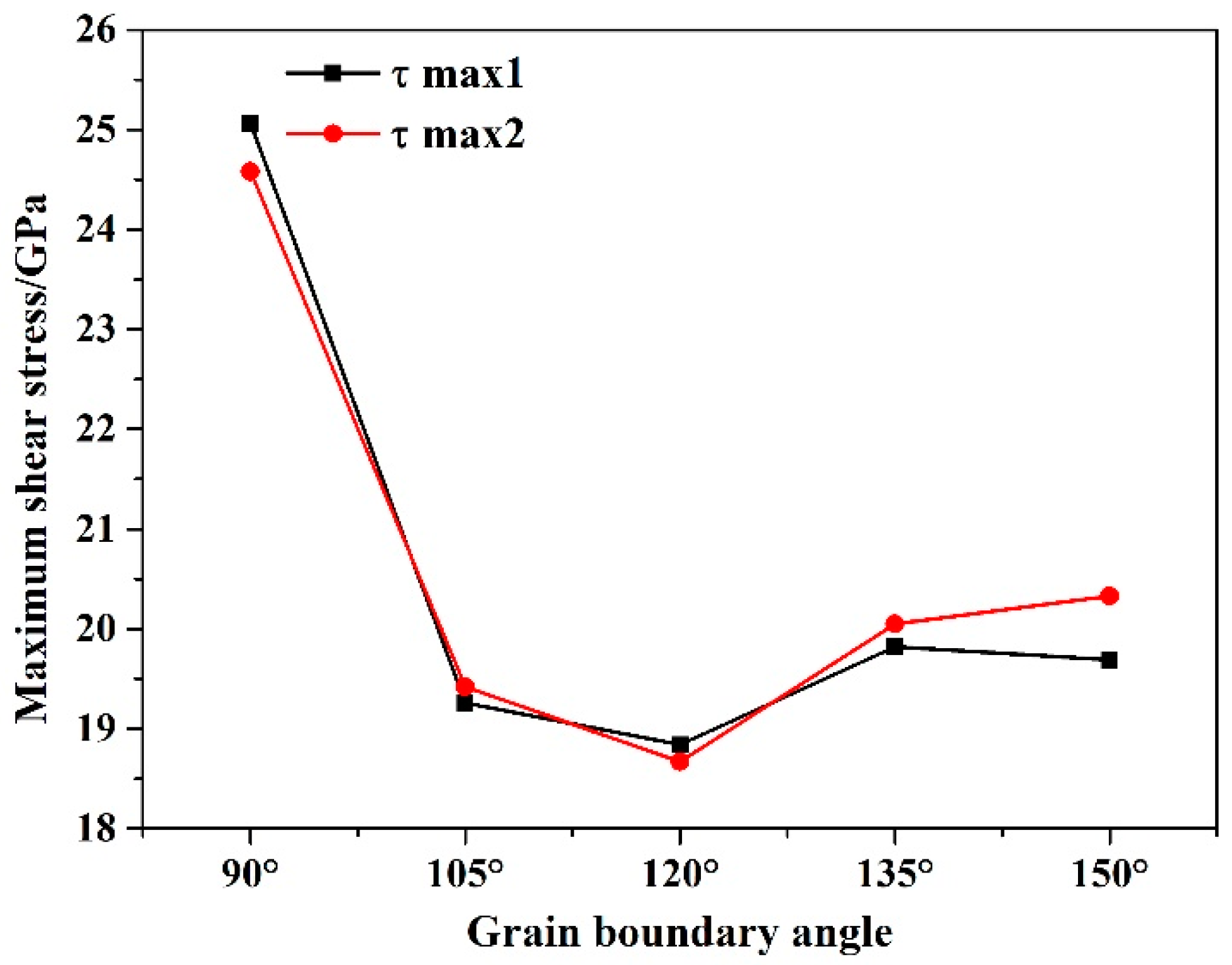
3.2. The Typical Mechanical Parameters of Nanoindentation
3.3. The Effect of GBs on the Dislocation Slip
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Wu, X.; Liu, Y.; Sun, Y.; Dai, N.; Li, J.; Jiang, Y. A discussion on evaluation criteria for crevice corrosion of various stainless steels. J. Mater. Sci. Technol. 2021, 64, 29–37. [Google Scholar] [CrossRef]
- Sun, H.; Yang, H.; Wang, M.; Giron-Palomares, B.; Zhou, Z.; Zhang, L.; Zhang, G. The corrosion and stress corrosion cracking behavior of a novel alumina-forming austenitic stainless steel in supercritical water. J. Nucl. Mater. 2017, 484, 339–346. [Google Scholar] [CrossRef]
- Takakuwa, O.; Soyama, H. Effect of residual stress on the corrosion behavior of austenitic stainless steel. Adv. Chem. Eng. Sci. 2015, 5, 62–71. [Google Scholar] [CrossRef] [Green Version]
- Ziemniak, S.; Hanson, M. Zinc treatment effects on corrosion behavior of 304 stainless steel in high temperature, hydrogenated water. Corros. Sci. 2006, 48, 2525–2546. [Google Scholar] [CrossRef] [Green Version]
- Hu, S.; Mao, Y.; Liu, X.; Han, E.-H.; Hänninen, H. Intergranular corrosion behavior of low-chromium ferritic stainless steel without Cr-carbide precipitation after aging. Corros. Sci. 2020, 166, 108420. [Google Scholar] [CrossRef]
- Nair, A.P.; Arafat, S.; Farhan; Vincent, S. Corrosion characteristics of zinc coated SS304 stainless steel. Mater. Today Proc. 2020, 28, 1210–1215. [Google Scholar] [CrossRef]
- Cheng, M.; He, P.; Lei, L.; Tan, X.; Wang, X.; Sun, Y.; Li, J.; Jiang, Y. Comparative studies on microstructure evolution and corrosion resistance of 304 and a newly developed high Mn and N austenitic stainless steel welded joints. Corros. Sci. 2021, 183, 109338. [Google Scholar] [CrossRef]
- Natesan, K.; Majumdar, S.; Shankar, P.S.; Shah, V.N. Preliminary Materials Selection Issues for the Next Generation Nuclear Plant Reactor Pressure Vessel; OSTI.GOV: Argonne, IL, USA, 2007.
- Špirit, Z.; Chocholoušek, M.; Šíma, M. Influence of mechanical stress at high temperatures on the properties of steels intended for the manufacture of fuel cladding for generation IV reactors. Solid State Phenom. 2017, 270, 246–252. [Google Scholar] [CrossRef]
- Luo, Q.; Chen, Y.; Liu, S. The studies on the corrosion behaviors of 316NG and 304 NG nitrogen-containing stainless steels made in China. Procedia Eng. 2012, 27, 1560–1567. [Google Scholar] [CrossRef] [Green Version]
- Wei, Y.-J.; Xia, D.-H.; Song, S.-Z. Detection of SCC of 304 NG stainless steel in an acidic NaCl solution using electrochemical noise based on chaos and wavelet analysis. Russ. J. Electrochem. 2016, 52, 560–575. [Google Scholar] [CrossRef]
- Bruchhausen, M.; Dundulis, G.; McLennan, A.; Arrieta, S.; Austin, T.; Cicero, R.; Chitty, W.-J.; Doremus, L.; Ernestova, M.; Grybenas, A.; et al. Characterization of austenitic stainless steels with regard to environmentally as-sisted fatigue in simulated light water reactor conditions. Metals 2021, 11, 307. [Google Scholar] [CrossRef]
- Tan, J.; Zhang, Z.; Zheng, H.; Wang, X.; Gao, J.; Wu, X.; Han, E.-H.; Yang, S.; Huang, P. Corrosion fatigue model of austenitic stainless steels used in pressurized water reactor nuclear power plants. J. Nucl. Mater. 2020, 541, 152407. [Google Scholar] [CrossRef]
- Hong, I.T.; Koo, C.H. Antibacterial properties, corrosion resistance and mechanical properties of Cu-modified SUS 304 stainless steel. Mater. Sci. Eng. A 2005, 393, 213–222. [Google Scholar] [CrossRef]
- Wang, K.; Song, Y.; La, P.; Wei, F.; Ma, F.; Sheng, J.; Shi, Y.; Guo, X.; Li, Z. Effect of rolling deformation on nanograins and mechanical properties of exceptional nano/microcrystalline 304 stainless steel. Steel Res. Int. 2018, 89, 1700490. [Google Scholar] [CrossRef]
- Thi, P.H.; Takeshi, I. An evaluation of fracture properties of type-304 austenitic stainless steel at high deformation rate using the small punch test. Int. J. Mech. Sci. 2018, 144, 249–261. [Google Scholar]
- Luu, H.-T.; Dang, S.-L.; Hoang, T.-V.; Gunkelmann, N. Molecular dynamics simulation of nanoindentation in Al and Fe: On the influence of system characteristics. Appl. Surf. Sci. 2021, 551, 149221. [Google Scholar] [CrossRef]
- AlMotasem, A.T.; Posselt, M.; Bergstrom, J. Nanoindentation and nanoscratching of a ferrite/austenite iron bi-crystal: An at-omistic study. Tribol. Int. 2018, 127, 231–239. [Google Scholar] [CrossRef]
- Qu, S.; Zhou, H. Hardening by twin boundary during nanoindentation in nanocrystals. Nanotechnology 2010, 21, 335704. [Google Scholar] [CrossRef]
- Talaei, M.; Nouri, N.; Ziaei-Rad, S. Grain boundary effects on nanoindentation of Fe bicrystal using molecular dynamic. Mech. Mater. 2016, 102, 97–107. [Google Scholar] [CrossRef]
- Faken, D.; Jónsson, H. Systematic analysis of local atomic structure combined with 3D computer graphics. Comput. Mater. Sci. 1994, 2, 279–286. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Daw, M.S. Model of metallic cohesion: The embedded-atom method. Phys. Rev. B 1989, 39, 7441–7452. [Google Scholar] [CrossRef]
- Johnson, R.A. Alloy models with the embedded-atom method. Phys. Rev. B 1989, 39, 12554–12559. [Google Scholar] [CrossRef]
- Bonny, G.; Terentyev, D.; Pasianot, R.C.; Poncé, S.; Bakaev, A. Interatomic potential to study plasticity in stainless steels: The FeNiCr model alloy. Model. Simul. Mater. Sci. Eng. 2011, 19, 085008. [Google Scholar] [CrossRef]
- Andoh, C.N.; Gyeabour, A.A.I.; Banini, G.K. Molecular dynamics simulation of mechanical deformation of austenitic stainless steels (Fe-Ni-Cr alloys) at supercritical water conditions. J. Appl. Sci. Technol. 2017, 22, 1–13. [Google Scholar]
- Haslam, A.J.; Phillpot, S.R.; Wolf, D. Mechanisms of grain growth in nanocrystalline fcc metals by molecular-dynamics simulation. Mater. Sci. Eng. A 2001, 318, 293–312. [Google Scholar] [CrossRef]
- Voter, A.F. A method for accelerating the molecular dynamics simulation of infrequent events. J. Chem. Phys. 1997, 106, 4665–4677. [Google Scholar] [CrossRef]
- Tuckerman, M.E.; Alejandre, J.; Lopez-Rendon, R.; Jochim, A.L.; Martyna, G.J. A Liouville-operator derived measure-preserving integrator for molecular dynamics simulations in the isothermal–isobaric ensemble. J. Phys. A Math. Gen. 2006, 39, 5629–5651. [Google Scholar] [CrossRef]
- Evans, D.J.; Holian, B.L. The Nose–Hoover thermostat. J. Chem. Phys. 1985, 83, 4069. [Google Scholar] [CrossRef]
- Stukowski, A.; Bulatov, V.V.; Arsenlis, A. Automated identification and indexing of dislocations in crystal interfaces. Model. Simul. Mater. Sci. Eng. 2012, 20, 085007. [Google Scholar] [CrossRef]
- Stukowski, A.; Albe, K. Extracting dislocations and non-dislocation crystal defects from atomistic simulation data. Model. Simul. Mater. Sci. Eng. 2010, 18, 085001. [Google Scholar] [CrossRef]
- Tsuzuki, H.; Branicio, P.S.; Rino, J.P. Structural characterization of deformed crystals by analysis of common atomic neighborhood. Comput. Phys. Com. 2007, 177, 518–523. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Fu, T.; Peng, X.; Weng, S.; Zhao, Y.; Gao, F.; Deng, L.; Wang, Z. Molecular dynamics simulation of effects of twin interfaces on Cu/Ni multilayers. Mater. Sci. Eng. A 2016, 658, 1–7. [Google Scholar] [CrossRef]
- Meyersm, M.A.; Ashworth, E. A model for the effect of grain size on the yield stress of metals. Philos. Mag. A 1982, 46, 737–759. [Google Scholar] [CrossRef]
- Benson, D.J.; Fu, H.H.; Meyers, M.A. On the effect of grain size on yield stress: Extension into nanocrystalline domain. Mater. Sci. Eng. A 2001, 319, 854–861. [Google Scholar] [CrossRef]
- Machado, M.; Moreira, P.; Flores, P.; Lankarani, H.M. Compliant contact force models in multibody dynamics: Evolution of the Hertz contact theory. Mech. Mach. Theory 2012, 53, 99–121. [Google Scholar] [CrossRef]
- Gupta, R.K.; Darling, K.S.; Raman, R.K.S.; Ravi, K.R.; Koch, C.C.; Murty, B.S.; Scattergood, R.O. Synthesis, characterization and mechanical behaviour of an in situ consolidated nanocrystalline FeCrNi alloy. J. Mater. Sci. 2011, 47, 1562–1566. [Google Scholar] [CrossRef]
- Ng, T.; Pandurangan, V.; Li, H. Multiscale modeling of nanoindentation in copper thin films via the concurrent coupling of the meshless Hermite–Cloud method with molecular dynamics. Appl. Surf. Sci. 2011, 257, 10613–10620. [Google Scholar] [CrossRef]
- Guillonneau, G.; Wheeler, J.; Wehrs, J.; Philippe, L.; Baral, P.; Höppel, H.W.; Göken, M.; Michler, J. Determination of the true projected contact area by in situ indentation testing—ERRATUM. J. Mater. Res. 2019, 34, 4086. [Google Scholar] [CrossRef]
- De las Cuevas, F.; Reis, M.; Ferraiuolo, A.; Pratolongo, G.; Karjalainen, L.P.; Alkorta, J.; Gil Sevillano, J. Hall-Petch relationship of a TWIP steel. Key Eng. Mater. 2010, 867, 147–152. [Google Scholar] [CrossRef]
- Kumar, N.N.; Tewari, R.; Durgaprasad, P.V.; Dutta, B.K.; Dey, G.K. Active slip systems in bcc iron during nanoindentation: A molecular dynamics study. Comput. Mater. Sci. 2013, 77, 260–263. [Google Scholar] [CrossRef]
- Cottrell, A.H. Theory of brittle fracture in steel and similar metals. Trans. Met. Soc. AIME 1958, 212, 192–203. [Google Scholar]
- Zaefferer, S.; Kuo, J.-C.; Zhao, Z.; Winning, M.; Raabe, D. On the influence of the grain boundary misorientation on the plastic deformation of aluminum bicrystals. Acta Mater. 2003, 51, 4719–4735. [Google Scholar] [CrossRef]


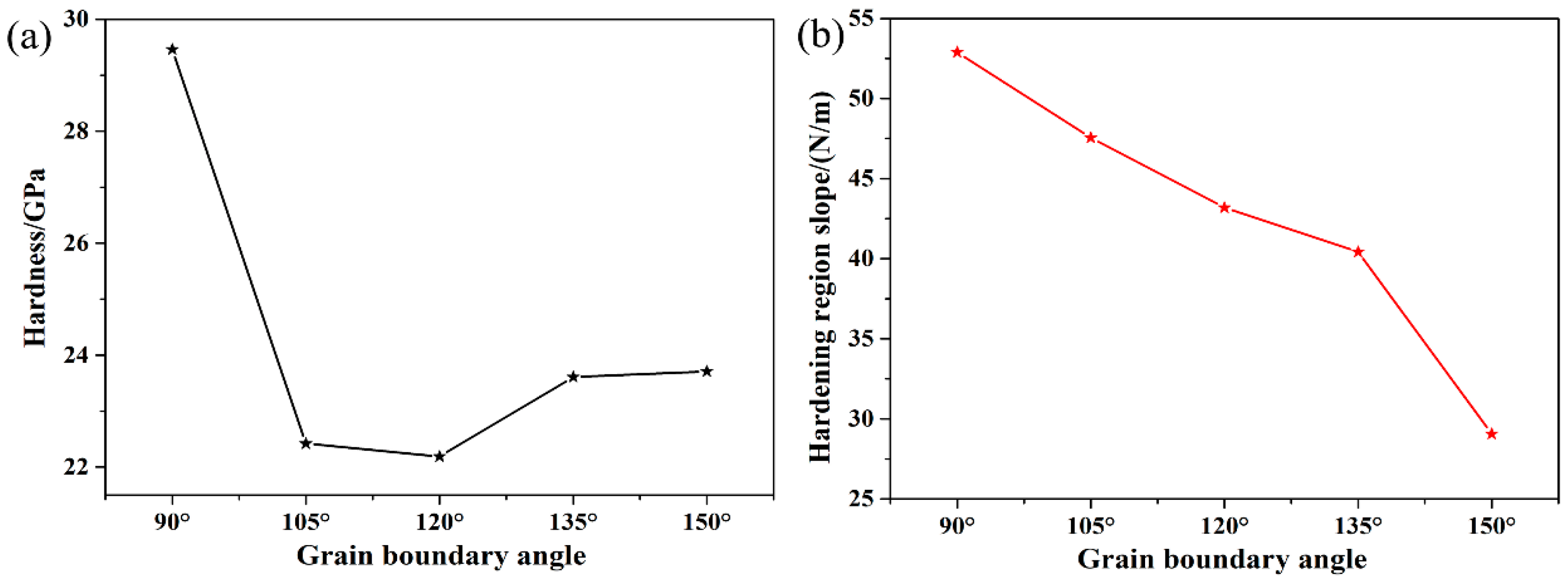


| Parameters | 90° Sample | 105° Sample | 120° Sample | 135° Sample | 150° Sample |
|---|---|---|---|---|---|
| Young’s modulus by Equations (4) and (5) (GPa) | 351.52 | 279.89 | 273.61 | 288.39 | 293.53 |
| Young’s modulus by Equation (6) (GPa) | 340.41 | 286.22 | 266.46 | 296.53 | 308.59 |
| Maximum shear stress by Equation (7) (GPa) | 25.06 | 19.26 | 18.84 | 19.82 | 19.96 |
| Maximum shears tress by Equation (8) (GPa) | 24.58 | 19.42 | 18.67 | 20.05 | 20.33 |
| Hardness at yielding point (GPa) | 29.46 | 22.42 | 22.19 | 23.61 | 23.71 |
| Hardness region slope (N/m) | 52.89 | 47.55 | 43.19 | 40.42 | 29.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Sun, K.; Peng, W.; Li, X.; Zhang, L. Effects of Grain Boundary Angles on Initial Deformation of 304 Austenitic Stainless Steel under Nanoindentation: A Molecular Dynamics Simulation. Crystals 2022, 12, 58. https://doi.org/10.3390/cryst12010058
Yang L, Sun K, Peng W, Li X, Zhang L. Effects of Grain Boundary Angles on Initial Deformation of 304 Austenitic Stainless Steel under Nanoindentation: A Molecular Dynamics Simulation. Crystals. 2022; 12(1):58. https://doi.org/10.3390/cryst12010058
Chicago/Turabian StyleYang, Longlong, Kun Sun, Weixiang Peng, Xuejie Li, and Liang Zhang. 2022. "Effects of Grain Boundary Angles on Initial Deformation of 304 Austenitic Stainless Steel under Nanoindentation: A Molecular Dynamics Simulation" Crystals 12, no. 1: 58. https://doi.org/10.3390/cryst12010058