Charge Compensation by Iodine Covalent Bonding in Lead Iodide Perovskite Materials
Abstract
:1. Introduction
2. Materials and Methods
2.1. Density Functional Theory Simulations
2.2. X-ray Photoelectron Spectroscopy
3. Results
3.1. Defect Simulations
3.2. Bader Charges
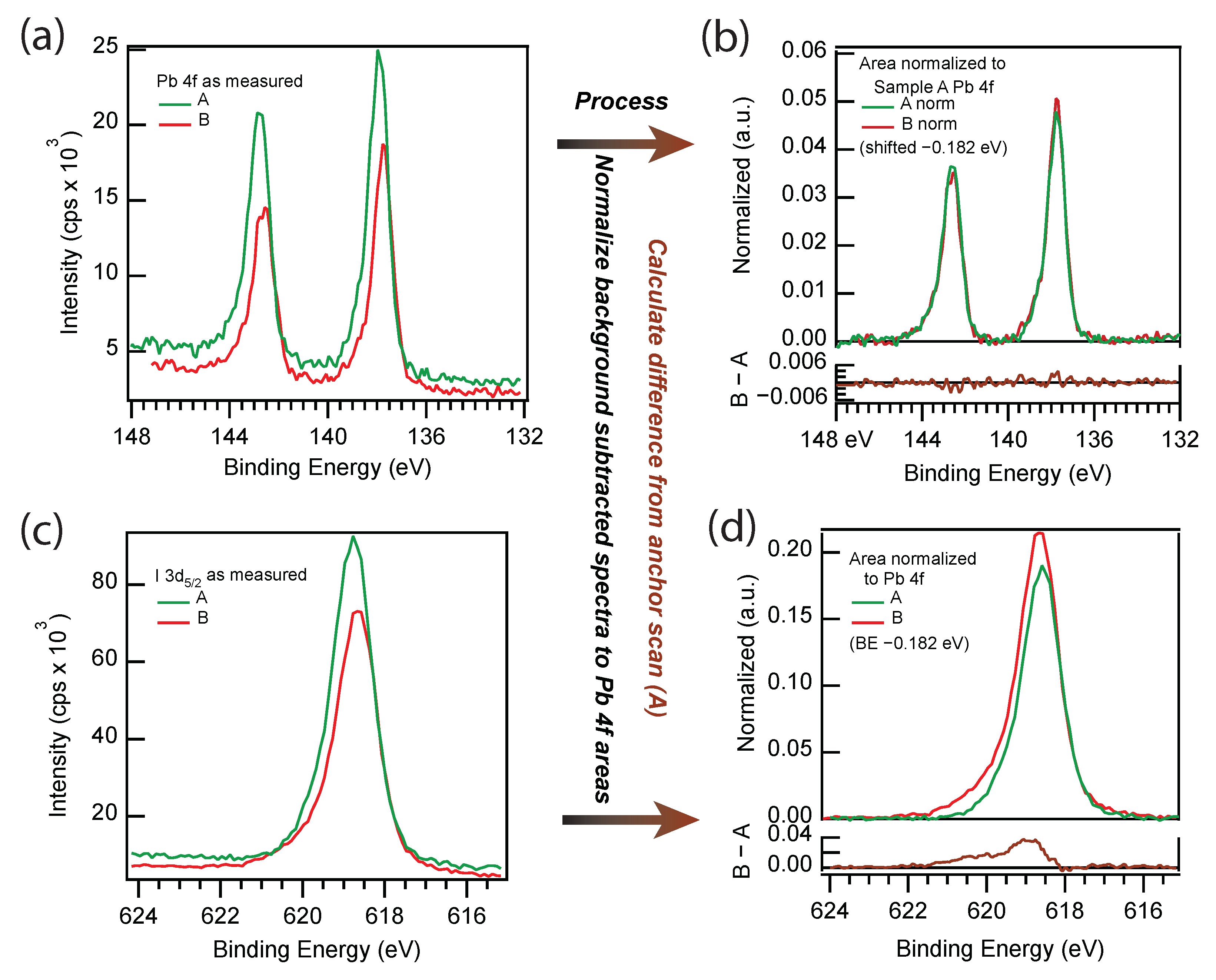
3.3. X-ray Photoelectron Spectroscopy
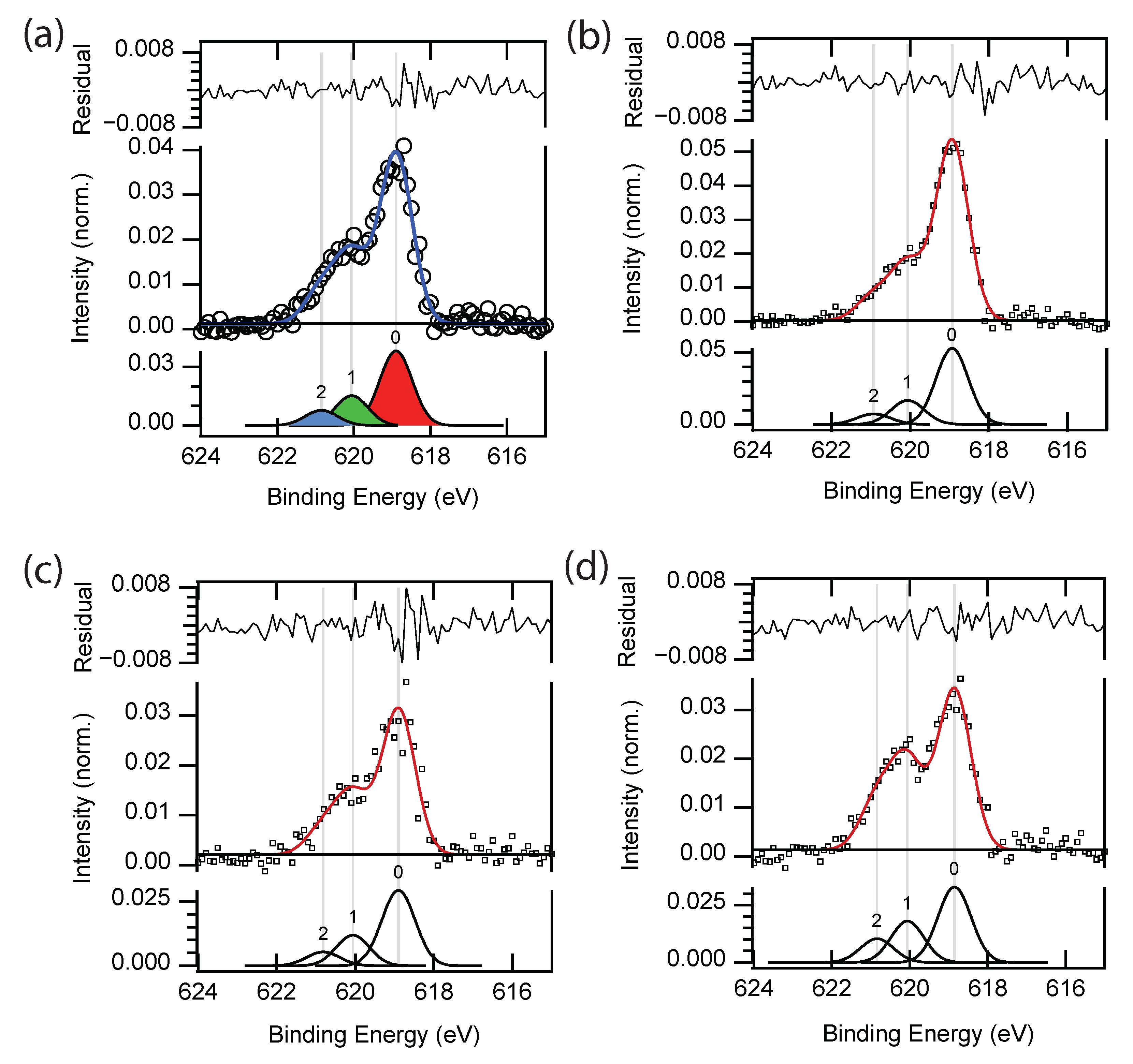
3.4. Three-Peak Model
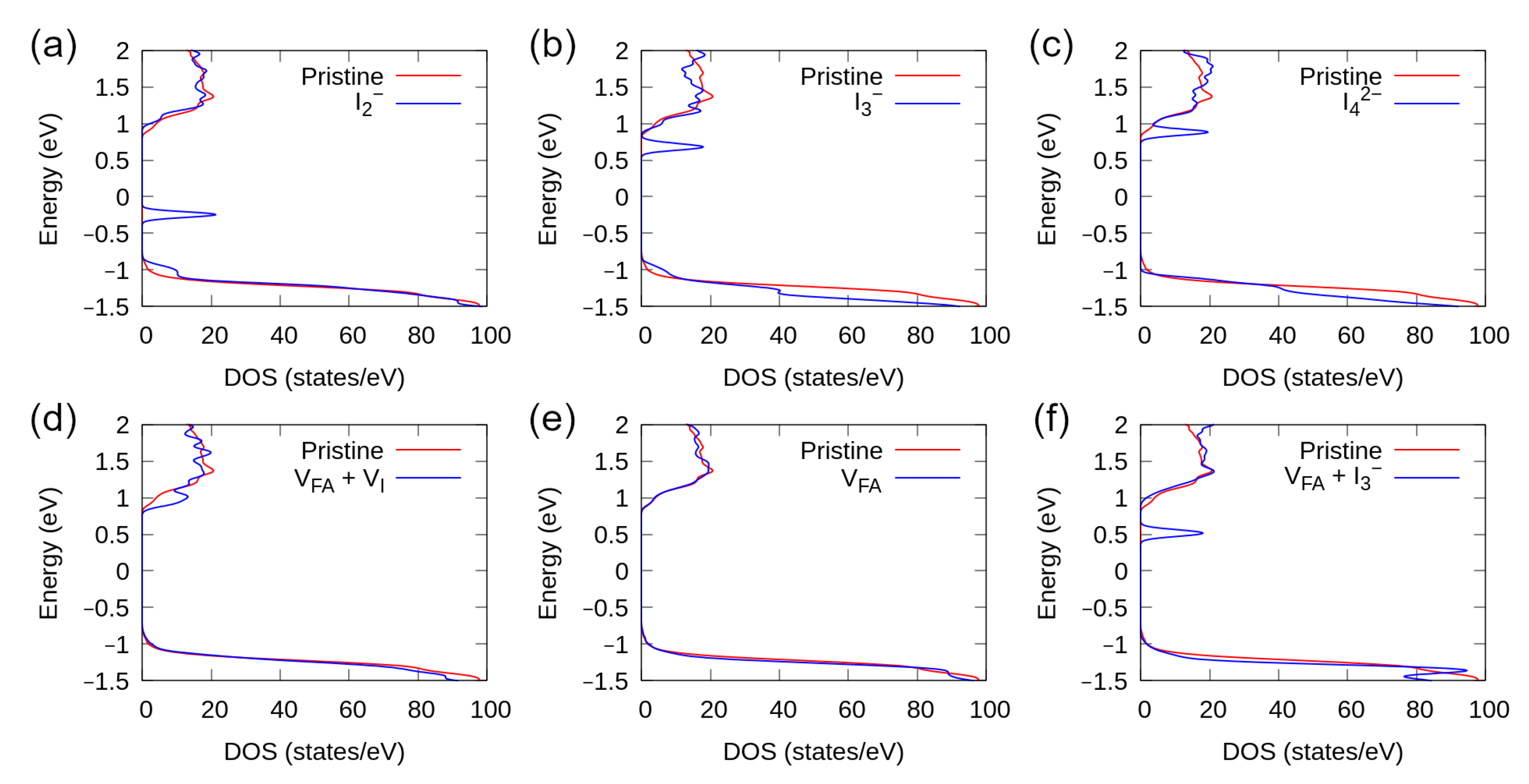
3.5. Density of States
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MHPs | Metal halide perovskite materials |
| XPS | X-ray photoelectron spectroscopy |
| BE | Binding energy |
| FWHM | Full width half max |
| VASP | Vienna Ab Initio Software Package |
| DFT | Density functional theory |
| GGA-PBE | The Perdew, Burke, Erzenhof formulation of the generalized gradient approximation |
| VDW | van der Waals |
| PAW | Projector augmented wave |
| DOS | Density of states |
| CB | Conduction band |
| VB | Valence band |
References
- Zhang, J.; Chen, R.; Wu, Y.; Shang, M.; Zeng, Z.; Zhang, Y.; Zhu, Y.; Han, L. Extrinsic Movable Ions in MAPbI3 Modulate Energy Band Alignment in Perovskite Solar Cells. Adv. Energy Mater. 2018, 8, 1701981. [Google Scholar] [CrossRef]
- Liu, N.; Yam, C. First-principles study of intrinsic defects in formamidinium lead triiodide perovskite solar cell absorbers. Phys. Chem. Chem. Phys. 2018, 20, 6800–6804. [Google Scholar] [CrossRef]
- Miller, D.W.; Eperon, G.E.; Roe, E.T.; Warren, C.W.; Snaith, H.J.; Lonergan, M.C. Defect states in perovskite solar cells associated with hysteresis and performance. Appl. Phys. Lett. 2016, 109, 153902. [Google Scholar] [CrossRef]
- Kim, H.S.; Jang, I.H.; Ahn, N.; Choi, M.; Guerrero, A.; Bisquert, J.; Park, N.G. Control of I – V Hysteresis CH3NH3PbI3 Perovskite Solar Cell. J. Phys. Chem. Lett. 2015, 6, 4633–4639. [Google Scholar] [CrossRef]
- Calado, P.; Telford, A.M.; Bryant, D.; Li, X.; Nelson, J.; O’Regan, B.C.; Barnes, P.R.F. Evidence for ion migration in hybrid perovskite solar cells with minimal hysteresis. Nat. Commun. 2016, 7, 13831. [Google Scholar] [CrossRef]
- Zarazua, I.; Bisquert, J.; Garcia-Belmonte, G. Light-Induced Space-Charge Accumulation Zone as Photovoltaic Mechanism in Perovskite Solar Cells. J. Phys. Chem. Lett. 2016, 7, 525–528. [Google Scholar] [CrossRef] [Green Version]
- Moia, D.; Gelmetti, I.; Calado, P.; Fisher, W.; Stringer, M.; Game, O.; Hu, Y.; Docampo, P.; Lidzey, D.; Palomares, E.; et al. Ionic-to-electronic current amplification in hybrid perovskite solar cells: Ionically gated transistor-interface circuit model explains hysteresis and impedance of mixed conducting devices. Energy Environ. Sci. 2019, 12, 1296–1308. [Google Scholar] [CrossRef]
- Watts, C.L.; Aspitarte, L.; Lin, Y.H.; Li, W.; Elzein, R.; Addou, R.; Hong, M.J.; Herman, G.S.; Snaith, H.J.; Labram, J.G. Light soaking in metal halide perovskites studied via steady-state microwave conductivity. Commun. Phys. 2020, 3, 73. [Google Scholar] [CrossRef]
- Mosconi, E.; Meggiolaro, D.; Snaith, H.J.; Stranks, S.D.; De Angelis, F. Light-induced annihilation of Frenkel defects in organo-lead halide perovskites. Energy Environ. Sci. 2016, 9, 3180–3187. [Google Scholar] [CrossRef]
- Knight, A.J.; Wright, A.D.; Patel, J.B.; McMeekin, D.P.; Snaith, H.J.; Johnston, M.B.; Herz, L.M. Electronic Traps and Phase Segregation in Lead Mixed-Halide Perovskite. ACS Energy Lett. 2019, 4, 75–84. [Google Scholar] [CrossRef]
- Brennan, M.C.; Ruth, A.; Kamat, P.V.; Kuno, M. Photoinduced anion segregation in mixed Halide perovskites. Trends Chem. 2020, 2, 282–301. [Google Scholar] [CrossRef] [Green Version]
- Hoke, E.T.; Slotcavage, D.J.; Dohner, E.R.; Bowring, A.R.; Karunadasa, H.I.; McGehee, M.D. Reversible photo-induced trap formation in mixed-halide hybrid perovskites for photovoltaics. Chem. Sci. 2015, 6, 613–617. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kerner, R.A.; Rand, B.P. Ionic–Electronic Ambipolar Transport in Metal Halide Perovskites: Can Electronic Conductivity Limit Ionic Diffusion? J. Phys. Chem. Lett. 2018, 9, 132–137. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Zhou, H. Defects chemistry in high-efficiency and stable perovskite solar cells. J. Appl. Phys. 2020, 128, 060903. [Google Scholar] [CrossRef]
- Yang, J.H.; Yin, W.J.; Park, J.S.; Wei, S.H. Fast self-diffusion of ions in CH3NH3PbI3: The interstiticaly mechanism versus vacancy-assisted mechanism. J. Mater. Chem. A 2016, 4, 13105–13112. [Google Scholar] [CrossRef]
- Eames, C.; Frost, J.M.; Barnes, P.R.F.; O’Regan, B.C.; Walsh, A.; Islam, M.S. Ionic transport in hybrid lead iodide perovskite solar cells. Nat. Commun. 2015, 6, 7497. [Google Scholar] [CrossRef] [Green Version]
- Ruth, A.; Brennan, M.C.; Draguta, S.; Morozov, Y.V.; Zhukovskyi, M.; Janko, B.; Zapol, P.; Kuno, M. Vacancy-Mediated Anion Photosegregation Kinetics in Mixed Halide Hybrid Perovskites: Coupled Kinetic Monte Carlo and Optical Measurements. ACS Energy Lett. 2018, 3, 2321–2328. [Google Scholar] [CrossRef]
- Rothmann, M.U.; Kim, J.S.; Borchert, J.; Lohmann, K.B.; O’Leary, C.M.; Sheader, A.A.; Clark, L.; Snaith, H.J.; Johnston, M.B.; Nellist, P.D.; et al. Atomic-scale microstructure of metal halide perovskite. Science 2020, 370, eabb5940. [Google Scholar] [CrossRef] [PubMed]
- Meggiolaro, D.; Mosconi, E.; De Angelis, F. Modeling the Interaction of Molecular Iodine with MAPbI3: A Probe of Lead-Halide Perovskites Defect Chemistry. ACS Energy Lett. 2018, 3, 447–451. [Google Scholar] [CrossRef]
- Walsh, A.; Scanlon, D.O.; Chen, S.; Gong, X.G.; Wei, S. Self-Regulation Mechanism for Charged Point Defects in Hybrid Halide Perovskites. Angew. Chem. Int. Ed. 2015, 54, 1791–1794. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Evarestov, R.A.; Senocrate, A.; Kotomin, E.A.; Maier, J. First-principles calculations of iodine-related point defects in CsPbI 3. Phys. Chem. Chem. Phys. 2019, 21, 7841–7846. [Google Scholar] [CrossRef]
- Meggiolaro, D.; Mosconi, E.; De Angelis, F. Formation of Surface Defects Dominates Ion Migration in Lead-Halide Perovskites. ACS Energy Lett. 2019, 4, 779–785. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Bai, S.; Tress, W.; Hagfeldt, A.; Gao, F. Defects engineering for high-performance perovskite solar cells. NPJ Flex. Electron. 2018, 2, 22. [Google Scholar] [CrossRef] [Green Version]
- Samu, G.F.; Balog, A.; De Angelis, F.; Meggiolaro, D.; Kamat, P.V.; Janáky, C. Electrochemical Hole Injection Selectively Expels Iodide from Mixed Halide Perovskite Films. J. Am. Chem. Soc. 2019, 141, 10812–10820. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Park, J.S.; Calbo, J.; Jung, Y.K.; Whalley, L.D.; Walsh, A. Accumulation of Deep Traps at Grain Boundaries in Halide Perovskites. ACS Energy Lett. 2019, 4, 1321–1327. [Google Scholar] [CrossRef]
- Naskar, A.; Khanal, R.; Choudhury, S. Role of Chemistry and Crystal Structure on the Electronic Defect States in Cs-Based Halide Perovskites. Materials 2021, 14, 1032. [Google Scholar] [CrossRef] [PubMed]
- Das, C.; Wussler, M.; Hellmann, T.; Mayer, T.; Jaegermann, W. In situ XPS study of the surface chemistry of MAPI solar cells under operating conditions in vacuum. Phys. Chem. Chem. Phys. 2018, 20, 17180–17187. [Google Scholar] [CrossRef] [PubMed]
- Doherty, T.A.S.; Winchester, A.J.; Macpherson, S.; Johnstone, D.N.; Pareek, V.; Tennyson, E.M.; Kosar, S.; Kosasih, F.U.; Anaya, M.; Abdi-Jalebi, M.; et al. Performance-limiting nanoscale trap clusters at grain junctions in halide perovskites. Nature 2020, 580, 360–366. [Google Scholar] [CrossRef] [PubMed]
- Reichert, S.; An, Q.; Woo, Y.W.; Walsh, A.; Vaynzof, Y.; Deibel, C. Probing the ionic defect landscape in halide perovskite solar cells. Nat. Commun. 2020, 11, 6098. [Google Scholar] [CrossRef]
- Steirer, K.X.; Schulz, P.; Teeter, G.; Stevanovic, V.; Yang, M.; Zhu, K.; Berry, J.J. Defect Tolerance in Methylammonium Lead Triiodide Perovskite. ACS Energy Lett. 2016, 1, 360–366. [Google Scholar] [CrossRef]
- Park, B.w.; Kwon, H.W.; Lee, Y.; Lee, D.Y.; Kim, M.G.; Kim, G.; Kim, K.j.; Kim, Y.K.; Im, J.; Shin, T.J.; et al. Stabilization of formamidinium lead triiodide α-phase with isopropylammonium chloride for perovskite solar cells. Nat. Energy 2021, 6, 419–428. [Google Scholar] [CrossRef]
- Cacovich, S.; Messou, D.; Bercegol, A.; Béchu, S.; Yaiche, A.; Shafique, H.; Rousset, J.; Schulz, P.; Bouttemy, M.; Lombez, L. Light-Induced Passivation in Triple Cation Mixed Halide Perovskites: Interplay between Transport Properties and Surface Chemistry. ACS Appl. Mater. Interfaces 2020, 12, 34784–34794. [Google Scholar] [CrossRef]
- Boyd, C.C.; Shallcross, R.C.; Moot, T.; Kerner, R.; Bertoluzzi, L.; Onno, A.; Kavadiya, S.; Chosy, C.; Wolf, E.J.; Werner, J.; et al. Overcoming Redox Reactions at Perovskite-Nickel Oxide Interfaces to Boost Voltages in Perovskite Solar Cells. Joule 2020, 4, 1759–1775. [Google Scholar] [CrossRef]
- Kot, M.; Kegelmann, L.; Köbler, H.; Vorokhta, M.; Escudero, C.; Kúš, P.; Šmíd, B.; Tallarida, M.; Albrecht, S.; Abate, A.; et al. In situ Near-Ambient Pressure X-ray Photoelectron Spectroscopy Reveals the Influence of Photon Flux and Water on the Stability of Halide Perovskite. ChemSusChem 2020, 13, 5722–5730. [Google Scholar] [CrossRef]
- Donakowski, A.; Miller, D.W.; Anderson, N.C.; Ruth, A.; Sanehira, E.M.; Berry, J.J.; Irwin, M.D.; Rockett, A.; Steirer, K.X. Improving Photostability of Cesium-Doped Formamidinium Lead Triiodide Perovskite. ACS Energy Lett. 2021, 6, 574–580. [Google Scholar] [CrossRef]
- Haruyama, J.; Sodeyama, K.; Han, L.; Tateyama, Y. Surface Properties of CH3NH3PbI3 for Perovskite Solar Cells. Acc. Chem. Res. 2016, 49, 554–561. [Google Scholar] [CrossRef] [PubMed]
- Weller, M.T.; Weber, O.J.; Frost, J.M.; Walsh, A. Cubic Perovskite Structure of Black Formamidinium Lead Iodide, α-[HC(NH2)2]PbI3, at 298 K. J. Phys. Chem. Lett. 2015, 6, 3209–3212. [Google Scholar] [CrossRef]
- Dalpian, G.M.; Zhao, X.G.; Kazmerski, L.; Zunger, A. Formation and Composition-Dependent Properties of Alloys of Cubic Halide Perovskites. Chem. Mater. 2019, 31, 2497–2506. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Lee, S.H.; Lee, J.H.; Hong, K.H. The Role of Intrinsic Defects in Methylammonium Lead Iodide Perovskite. J. Phys. Chem. Lett. 2014, 5, 1312–1317. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F. Atoms in Molecules: A Quantum Theory; Clarendon Pr Oxford: Cary, NC, USA, 1990. [Google Scholar]
- Code: Bader Charge Analysis. Available online: http://theory.cm.utexas.edu/henkelman/code/bader/ (accessed on 19 December 2021).
- Kerner, R.A.; Xu, Z.; Larson, B.W.; Rand, B.P. The role of halide oxidation in perovskite halide phase separation. Joule 2021, 5, 2273–2295. [Google Scholar] [CrossRef]
- Irwin, M.D.; Dhas, V.V.; Mielczarek, K. Doped Nickel Oxide Interfacial Layer. U.S. Patent 10189998B2, 29 January 2019. [Google Scholar]
- Irwin, M.D.; Chute, J.A.; Dhas, V.V. Method of Formulating Perovskite Solar Cell Materials. U.S. Patent 9305715B2, 5 April 2016. [Google Scholar]
- Irwin, M.D.; Chute, J.A.; Dhas, V.V. Perovskite Material Layer Processing. U.S. Patent 9425396B2, 23 August 2016. [Google Scholar]
- Irwin, M.D.; Chute, J.A.; Dhas, V.V.; Mielczarek, K. Mixed Cation Perovskite Material Devices. U.S. Patent 10316196B2, 11 June 2019. [Google Scholar]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pack, J.D.; Monkhorst, H.J. “Special points for Brillouin-zone integrations”—A reply. Phys. Rev. B 1977, 16, 1748–1749. [Google Scholar] [CrossRef]
- Pavlovetc, I.M.; Brennan, M.C.; Draguta, S.; Ruth, A.; Moot, T.; Christians, J.A.; Aleshire, K.; Harvey, S.P.; Toso, S.; Nanayakkara, S.U.; et al. Suppressing Cation Migration in Triple-Cation Lead Halide Perovskites. ACS Energy Lett. 2020, 5, 2802–2810. [Google Scholar] [CrossRef]
- Li, Z.; Yang, M.; Park, J.S.; Wei, S.H.; Berry, J.J.; Zhu, K. Stabilizing Perovskite Structures by Tuning Tolerance Factor: Formation of Formamidinium and Cesium Lead Iodide Solid-State Alloys. Chem. Mater. 2016, 28, 284–292. [Google Scholar] [CrossRef]
- Zhao, X.G.; Dalpian, G.M.; Wang, Z.; Zunger, A. Polymorphous nature of cubic halide perovskites. Phys. Rev. B 2020, 101, 155137. [Google Scholar] [CrossRef]
- MedeA. Available online: https://www.materialsdesign.com/ (accessed on 19 December 2021).
- Lide, D.R. Handbook of Chemistry and Physics: CRC Handbook; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Csm-Xps. minespex. Available online: https://github.com/csm-xps/minespex (accessed on 19 December 2021).
- Schulz, P.; Whittaker-Brooks, L.L.; MacLeod, B.A.; Olson, D.C.; Loo, Y.L.; Kahn, A. Electronic Level Alignment in Inverted Organometal Perovskite Solar Cells. Adv. Mater. Interfaces 2015, 2, 1400532. [Google Scholar] [CrossRef]
- Heo, S.; Seo, G.; Lee, Y.; Lee, D.; Seol, M.; Lee, J.; Park, J.B.; Kim, K.; Yun, D.J.; Kim, Y.S.; et al. Deep level trapped defect analysis in CH3NH3PbI3 perovskite solar cells by deep level transient spectroscopy. Energy Environ. Sci. 2017, 10, 1128–1133. [Google Scholar] [CrossRef]
- Kearney, K.; Seo, G.; Matsushima, T.; Adachi, C.; Ertekin, E.; Rockett, A. Computational Analysis of the Interplay between Deep Level Traps and Perovskite Solar Cell Efficiency. J. Am. Chem. Soc. 2018, 140, 15655–15660. [Google Scholar] [CrossRef]
- Sharma, K.; Sharma, V.; Sharma, S.S. Dye-Sensitized Solar Cells: Fundamentals and Current Status. Nanoscale Res. Lett. 2018, 13, 381. [Google Scholar] [CrossRef]
- Luongo, A.; Brunetti, B.; Vecchio Ciprioti, S.; Ciccioli, A.; Latini, A. Thermodynamic and Kinetic Aspects of Formamidinium Lead Iodide Thermal Decomposition. J. Phys. Chem. C 2021, 125, 21851–21861. [Google Scholar] [CrossRef] [PubMed]
- Du, M.H. Density Functional Calculations of Native Defects in CH3NH3PbI3: Effects of Spin–Orbit Coupling and Self-Interaction Error. J. Phys. Chem. Lett. 2015, 6, 1461–1466. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Zhou, H.; Hu, J.; Huang, B.; Sun, M.; Dong, B.; Zheng, G.; Huang, Y.; Chen, Y.; Li, L.; et al. A Eu3+-Eu2+ ion redox shuttle imparts operational durability to Pb-I perovskite solar cells. Science 2019, 363, 265–270. [Google Scholar] [CrossRef] [PubMed]
- Zhidkov, I.S.; Boukhvalov, D.W.; Akbulatov, A.F.; Frolova, L.A.; Finkelstein, L.D.; Kukharenko, A.I.; Cholakh, S.O.; Chueh, C.C.; Troshin, P.A.; Kurmaev, E.Z. XPS spectra as a tool for studying photochemical and thermal degradation in APbX3 hybrid halide perovskites. Nano Energy 2021, 79, 105421. [Google Scholar] [CrossRef]
- Kerner, R.A.; Schulz, P.; Christians, J.A.; Dunfield, S.P.; Dou, B.; Zhao, L.; Teeter, G.; Berry, J.J.; Rand, B.P. Reactions at noble metal contacts with methylammonium lead triiodide perovskites: Role of underpotential deposition and electrochemistry. APL Mater. 2019, 7, 041103. [Google Scholar] [CrossRef]
- Mundt, L.E.; Tong, J.; Palmstrom, A.F.; Dunfield, S.P.; Zhu, K.; Berry, J.J.; Schelhas, L.T.; Ratcliff, E.L. Surface-Activated Corrosion in Tin–Lead Halide Perovskite Solar Cells. ACS Energy Lett. 2020, 5, 3344–3351. [Google Scholar] [CrossRef]
- Boschloo, G.; Hagfeldt, A. Characteristics of the Iodide/Triiodide Redox Mediator in Dye-Sensitized Solar Cells. Acc. Chem. Res. 2009, 42, 1819–1826. [Google Scholar] [CrossRef]
- Jia, Y.H.; Neutzner, S.; Zhou, Y.; Yang, M.; Tapia, J.M.F.; Li, N.; Yu, H.; Cao, J.; Wang, J.P.; Petrozza, A.; et al. Role of Excess FAI in Formation of High-Efficiency FAPbI3-Based Light-Emitting Diodes. Adv. Funct. Mater. 2020, 30, 1906875. [Google Scholar] [CrossRef]
- Yang, W.S.; Park, B.W.; Jung, E.H.; Jeon, N.J.; Kim, Y.C.; Lee, D.U.; Shin, S.S.; Seo, J.; Kim, E.K.; Noh, J.H.; et al. Iodide management in formamidinium-lead-halide–based perovskite layers for efficient solar cells. Science 2017, 356, 1376–1379. [Google Scholar] [CrossRef] [Green Version]

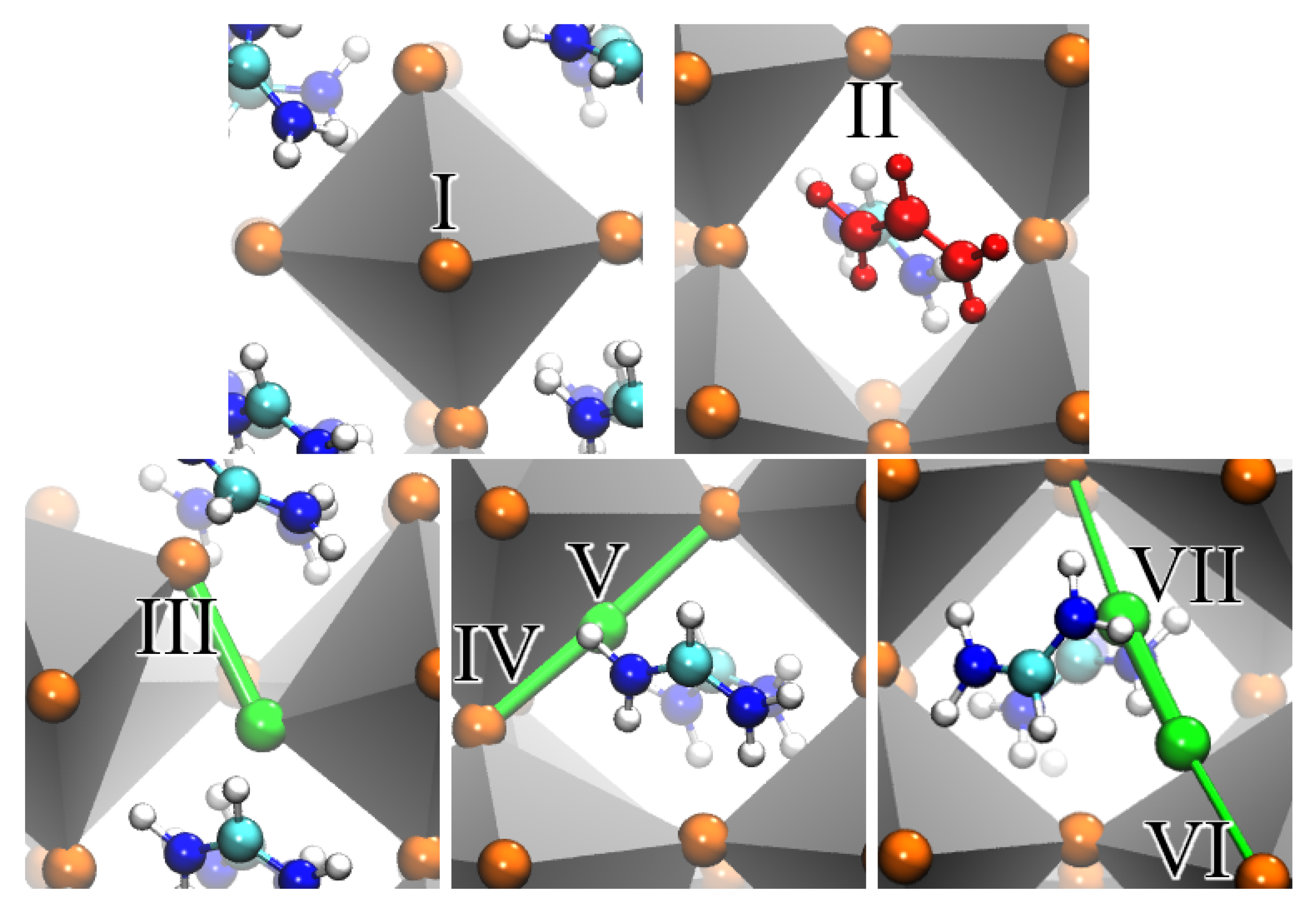
| Iodine Environment | Defect | DFT Structure | Bader Charge |
|---|---|---|---|
| I | Pristine | a–g | −0.57 |
| II | V | f | −0.50 |
| III | I | b | −0.34, −0.31 |
| IV | I | c | −0.36, −0.26 |
| V + I | g | −0.34, −0.23 | |
| V | I | c | −0.04 |
| V + I | g | 0.00 | |
| VI | I | d | −0.47, −0.45 |
| VII | I | d | −0.12, −0.11 |
| Sample | I:Pb | N:Pb |
|---|---|---|
| A | 2.9 | 2.0 |
| B | 3.5 | 2.9 |
| C | 3.6 | 2.5 |
| D | 3.6 | 2.6 |
| Peak | BE | Assignment | Bader (q) | from Pb 4f 137.75 eV | Area |
|---|---|---|---|---|---|
| Peak 0 | 618.90 ± 0.03 | I | −0.57 | 481.14 | 0.040 ± 0.010 |
| Peak 1 | 620.06 | I(IV) | −0.26, −0.36 | 482.31 | 0.0165 ± 0.0028 |
| Peak 2 | 620.85 ± 0.05 | I(V) | −0.04 | 483.11 | 0.0082 ± 0.0022 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruth, A.; Holland, M.; Rockett, A.; Sanehira, E.; Irwin, M.D.; Steirer, K.X. Charge Compensation by Iodine Covalent Bonding in Lead Iodide Perovskite Materials. Crystals 2022, 12, 88. https://doi.org/10.3390/cryst12010088
Ruth A, Holland M, Rockett A, Sanehira E, Irwin MD, Steirer KX. Charge Compensation by Iodine Covalent Bonding in Lead Iodide Perovskite Materials. Crystals. 2022; 12(1):88. https://doi.org/10.3390/cryst12010088
Chicago/Turabian StyleRuth, Anthony, Michael Holland, Angus Rockett, Erin Sanehira, Michael D. Irwin, and K. Xerxes Steirer. 2022. "Charge Compensation by Iodine Covalent Bonding in Lead Iodide Perovskite Materials" Crystals 12, no. 1: 88. https://doi.org/10.3390/cryst12010088
APA StyleRuth, A., Holland, M., Rockett, A., Sanehira, E., Irwin, M. D., & Steirer, K. X. (2022). Charge Compensation by Iodine Covalent Bonding in Lead Iodide Perovskite Materials. Crystals, 12(1), 88. https://doi.org/10.3390/cryst12010088






