Autofocusing and Self-Healing Optical Vortices Realized via Circular Cubic Phase Modulation
Abstract
:1. Introduction
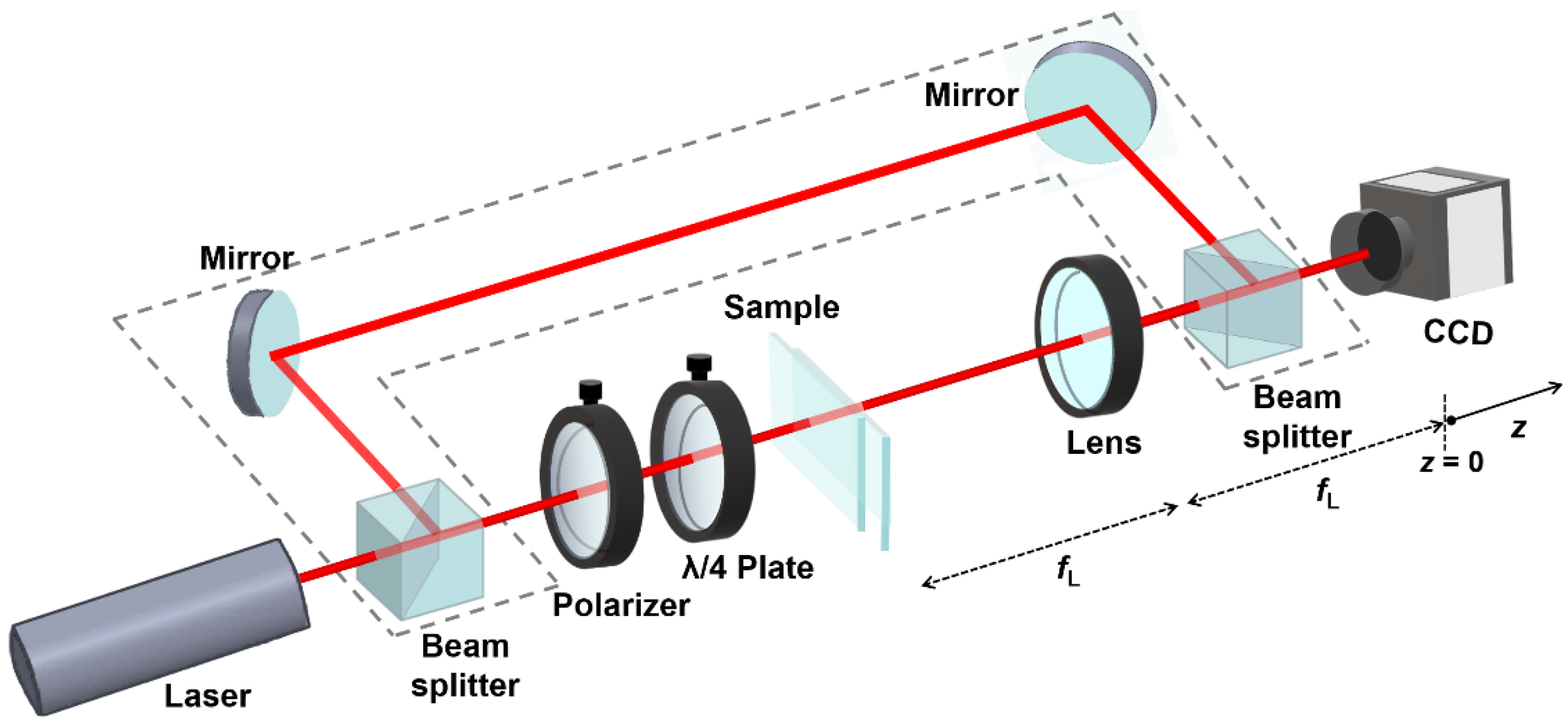
2. Design and Principle
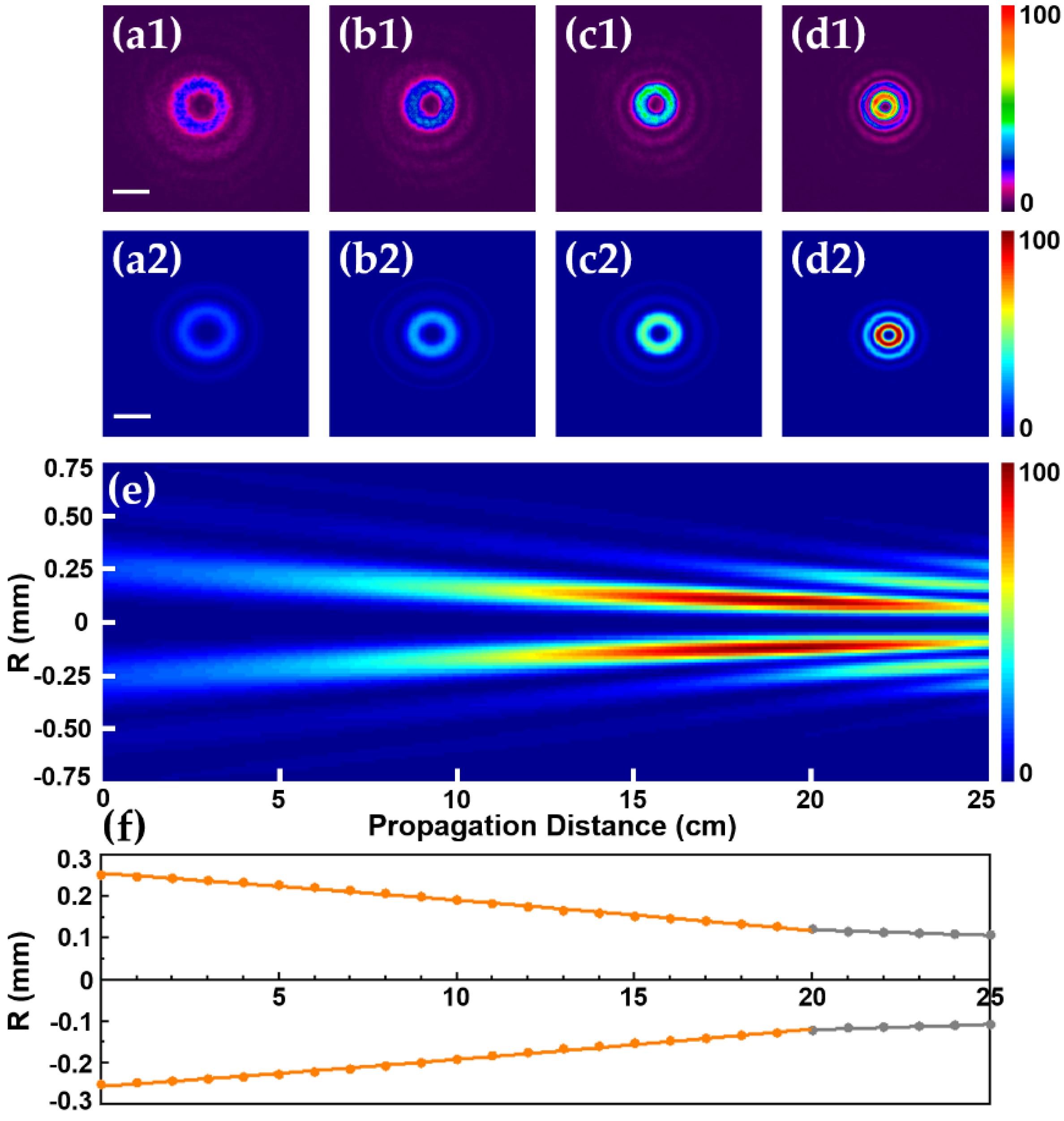
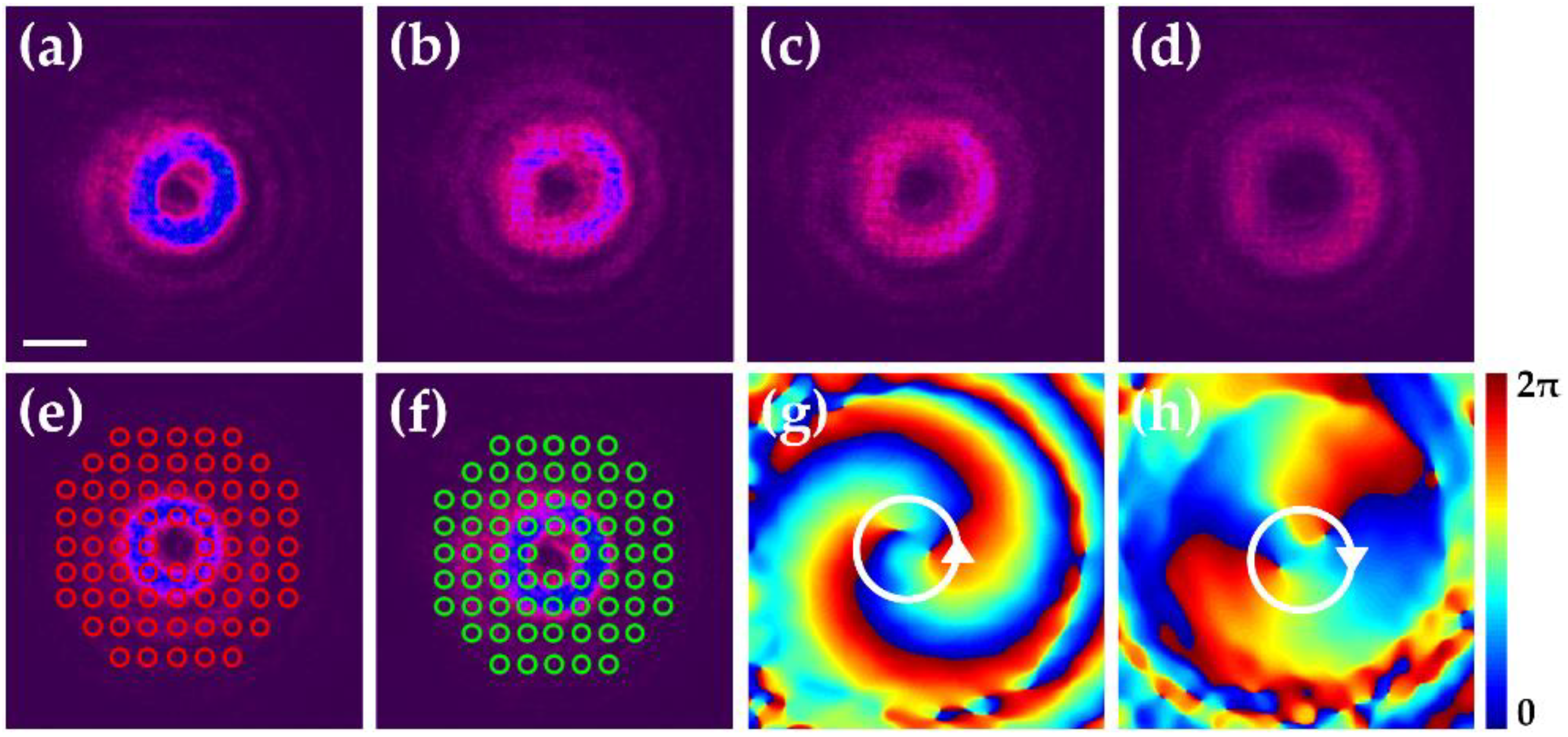
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Forbes, A.; Oliveira, M.; Dennis, M.R. Structured light. Nat. Photonics 2021, 15, 253–262. [Google Scholar] [CrossRef]
- Yao, A.M.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photonics 2011, 3, 161–204. [Google Scholar] [CrossRef]
- Fu, S.; Shang, Z.; Hai, L.; Huang, L.; Lv, Y.; Gao, C. Orbital angular momentum comb generation from azimuthal binary phases. Adv. Photonics Nexus 2022, 1, 016003. [Google Scholar] [CrossRef]
- Paterson, L.; MacDonald, M.P.; Arlt, J.; Sibbett, W.; Bryant, P.E.; Dholakia, K. Controlled rotation of optically trapped microscopic particles. Science 2001, 292, 912–914. [Google Scholar] [CrossRef]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Ren, Y.X.; Chen, M.; Arita, Y.; Rosales-Guzmán, C. Optical trapping with structured light: A review. Adv. Photonics 2021, 3, 034001. [Google Scholar] [CrossRef]
- Molina-Terriza, G.; Torres, J.P.; Torner, L. Twisted photons. Nat. Phys. 2007, 3, 3050–3310. [Google Scholar] [CrossRef]
- Wang, X.L.; Cai, X.D.; Su, Z.E.; Chen, M.C.; Wu, D.; Li, L.; Liu, N.L.; Lu, C.Y.; Pan, J.W. Quantum teleportation of multiple degrees of freedom of a single photon. Nature 2015, 518, 516–519. [Google Scholar] [CrossRef]
- Hell, S.W.; Wichmann, J. Breaking the diffraction resolution limit by stimulated emission: Stimulated-emission depletion fluorescence microscopy. Opt. Lett. 1994, 19, 780–782. [Google Scholar] [CrossRef]
- Yan, L.; Gregg, P.; Karimi, E.; Rubano, A.; Marrucci, L.; Boyd, R.; Ramachandran, S. Q-plate enabled spectrally diverse orbital-angular-momentum conversion for stimulated emission depletion microscopy. Optica 2015, 2, 900–903. [Google Scholar] [CrossRef] [Green Version]
- Fang, X.; Ren, H.; Gu, M. Orbital angular momentum holography for high-security encryption. Nat. Photonics 2020, 14, 102–108. [Google Scholar] [CrossRef]
- Lee, J.H.; Foo, G.; Johnson, E.G.; Swartzlander, G.A. Experimental verification of an optical vortex coronagraph. Phys. Rev. Lett. 2006, 97, 053901. [Google Scholar] [CrossRef]
- Zhou, Y.; Cui, Z.; Han, Y. Polarization and coherence properties in self-healing propagation of a partially coherent radially polarized twisted beam. Opt. Express 2022, 30, 23448–23462. [Google Scholar] [CrossRef]
- Žukauskas, A.; Malinauskas, M.; Brasselet, E. Monolithic generators of pseudo-nondiffracting optical vortex beams at the microscale. Appl. Phys. Lett. 2013, 103, 181122. [Google Scholar] [CrossRef]
- Gutiérrez-Vega, J.C.; López-Mariscal, C. Nondiffracting vortex beams with continuous orbital angular momentum order dependence. J. Opt. A Pure Appl. Opt. 2008, 10, 015009. [Google Scholar] [CrossRef]
- Vetter, C.; Steinkopf, R.; Bergner, K.; Ornigotti, M.; Nolte, S.; Gross, H.; Szameit, A. Realization of free-space long-distance self-healing Bessel beams. Laser Photonics Rev. 2019, 13, 1900103. [Google Scholar] [CrossRef]
- Bouchal, Z.; Courtial, J. The connection of singular and nondiffracting optics. J. Opt. A Pure Appl. Opt. 2004, 6, S184–S188. [Google Scholar] [CrossRef]
- Kovalev, A.A.; Kotlyar, V.V. Orbital angular momentum of superpositions of optical vortices perturbed by a sector aperture. Photonics 2022, 9, 531. [Google Scholar] [CrossRef]
- Tsukamoto, Y.; Yoshida, H.; Ozaki, M. Generation of a focused optical vortex beam using a liquid crystal spiral zone plate. Opt. Express 2022, 30, 8667–8675. [Google Scholar] [CrossRef]
- Kovalev, A.A.; Kotlyar, V.V.; Porfirev, A.P. Auto-focusing accelerating hyper-geometric laser beams. J. Opt. 2016, 18, 025610. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, C.; Lin, Z.; Wu, Y.; Wu, Y.; Wu, L.; Deng, D. Auto-focusing and self-healing of symmetric odd-Pearcey Gauss beams. Opt. Lett. 2020, 45, 2957–2960. [Google Scholar] [CrossRef]
- Dai, H.T.; Liu, Y.J.; Luo, D.; Sun, X.W. Propagation dynamics of an optical vortex imposed on an Airy beam. Opt. Lett. 2010, 35, 4075–4077. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, Y.; Ke, Y.; Luo, H.; Wen, S. Generation of Airy vortex and Airy vector beams based on the modulation of dynamic and geometric phases. Opt. Lett. 2015, 40, 3193–3196. [Google Scholar] [CrossRef]
- Wei, B.Y.; Chen, P.; Ge, S.J.; Duan, W.; Hu, W.; Lu, Y.Q. Generation of self-healing and transverse accelerating optical vortices. Appl. Phys. Lett. 2016, 109, 121105. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, W.; Tang, J.; Xu, X.; Chen, P.; Ma, C.Q.; Zhang, W.; Wei, B.Y.; Ming, Y.; Cui, G.X.; et al. Switchable second-harmonic generation of Airy beam and Airy vortex beam. Adv. Opt. Mater. 2021, 9, 2001776. [Google Scholar] [CrossRef]
- Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D.N. Observation of accelerating Airy beams. Phys. Rev. Lett. 2007, 99, 213901. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A. Airy beam with a hyperbolic trajectory. Opt. Commun. 2014, 313, 290–293. [Google Scholar] [CrossRef]
- Efremidis, N.K.; Chen, Z.; Segev, M.; Christodoulides, D.N. Airy beams and accelerating waves: An overview of recent advances. Optica 2019, 6, 686–701. [Google Scholar] [CrossRef]
- Baumgartl, J.; Mazilu, M.; Dholakia, K. Optically mediated particle clearing using Airy wavepackets. Nat. Photonics 2008, 2, 675–678. [Google Scholar] [CrossRef]
- Polynkin, P.; Kolesik, M.; Moloney, J.V.; Siviloglou, G.A.; Christodoulides, D.N. Curved plasma channel generation using ultraintense Airy beams. Science 2009, 324, 229–232. [Google Scholar] [CrossRef]
- Chong, A.; Renninger, W.H.; Christodoulides, D.N.; Wise, F.W. Airy-Bessel wave packets as versatile linear light bullets. Nat. Photonics 2010, 4, 103–106. [Google Scholar] [CrossRef]
- Gu, Y.; Gbur, G. Scintillation of Airy beam arrays in atmospheric turbulence. Opt. Lett. 2010, 35, 3456–3458. [Google Scholar] [CrossRef]
- Vettenburg, T.; Dalgarno, H.I.C.; Nylk, J.; Coll-Lladó, C.; Ferrier, D.E.K.; Cižmár, T.; Gunn-Moore, F.J.; Dholakia, K. Light-sheet microscopy using an Airy beam. Nat. Methods 2014, 11, 541–544. [Google Scholar] [CrossRef]
- Guo, W.L.; Chen, K.; Wang, G.M.; Luo, X.Y.; Cai, T.; Zhang, C.B.; Feng, Y. Airy beam generation: Approaching ideal efficiency and ultra wideband with reflective and transmissive metasurfaces. Adv. Opt. Mater. 2020, 8, 2000860. [Google Scholar] [CrossRef]
- Wei, B.Y.; Liu, S.; Chen, P.; Qi, S.X.; Zhang, Y.; Hu, W.; Lu, Y.Q.; Zhao, J.L. Vortex Airy beams directly generated via liquid crystal q-Airy-plates. Appl. Phys. Lett. 2018, 112, 121101. [Google Scholar] [CrossRef]
- Zhan, Q. Cylindrical vector beams: From mathematical concepts to applications. Adv. Opt. Photonics 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Wei, B.; Qi, S.; Liu, S.; Li, P.; Zhang, Y.; Han, L.; Zhong, J.; Hu, W.; Lu, Y.; Zhao, J. Auto-transition of vortex- to vector-Airy beams via liquid crystal q-Airy-plates. Opt. Express 2019, 27, 18848–18857. [Google Scholar] [CrossRef]
- Li, H.; Liu, H.; Chen, X. Nonlinear generation of Airy vortex beam. Opt. Express 2018, 26, 21204–21209. [Google Scholar] [CrossRef]
- Dai, H.T.; Liu, Y.J.; Luo, D.; Sun, X.W. Propagation properties of an optical vortex carried by an Airy beam: Experimental implementation. Opt. Lett. 2011, 36, 1617–1619. [Google Scholar] [CrossRef]
- Wei, B.Y.; Hu, W.; Ming, Y.; Xu, F.; Rubin, S.; Wang, J.G.; Chigrinov, V.; Lu, Y.Q. Generating switchable and reconfigurable optical vortices via photopatterning of liquid crystals. Adv. Mater. 2014, 26, 1590–1595. [Google Scholar] [CrossRef]
- Chen, P.; Wei, B.Y.; Ji, W.; Ge, S.J.; Hu, W.; Xu, F.; Chigrinov, V.; Lu, Y.Q. Arbitrary and reconfigurable optical vortex generation: A high-efficiency technique using director-varying liquid crystal fork gratings. Photon. Res. 2015, 3, 133–139. [Google Scholar] [CrossRef]
- Chen, P.; Wei, B.Y.; Hu, W.; Lu, Y.Q. Liquid-crystal-mediated geometric phase: From transmissive to broadband reflective planar optics. Adv. Mater. 2019, 32, 1903665. [Google Scholar] [CrossRef]
- Liu, S.; Qi, S.; Li, P.; Wei, B.; Chen, P.; Hu, W.; Zhang, Y.; Gan, X.; Zhang, P.; Lu, Y.; et al. Analogous optical activity in free space using a single Pancharatnam-Berry phase element. Laser Photonics Rev. 2022, 16, 2100291. [Google Scholar] [CrossRef]
- Liu, S.J.; Chen, P.; Ge, S.J.; Zhu, L.; Zhang, Y.H.; Lu, Y.Q. 3D engineering of orbital angular momentum beams via liquid-crystal geometric phase. Laser Photonics Rev. 2022, 16, 2200118. [Google Scholar] [CrossRef]
- Zhu, L.; Xu, C.T.; Chen, P.; Zhang, Y.H.; Liu, S.J.; Chen, Q.M.; Ge, S.J.; Hu, W.; Lu, Y.Q. Pancharatnam-Berry phase reversal via opposite-chirality-coexisted superstructures. Light Sci. Appl. 2022, 11, 135. [Google Scholar] [CrossRef]
- Yuan, R.; Xu, C.T.; Cao, H.; Zhang, Y.H.; Wang, G.Y.; Chen, P.; Lu, Y.Q.; Hu, W. Spin-decoupled transflective spatial light modulations enabled by a piecewise-twisted anisotropic monolayer. Adv. Sci. 2022, 9, 2202424. [Google Scholar] [CrossRef]
- Liu, S.; Qi, S.; Li, Y.; Wei, B.; Li, P.; Zhao, J. Controllable oscillated spin Hall effect of Bessel beam realized by liquid crystal Pancharatnam-Berry phase elements. Light Sci. Appl. 2022, 11, 219. [Google Scholar] [CrossRef]
- Zhang, Y.; Wei, B.; Liu, S.; Li, P.; Chen, X.; Wu, Y.; Dou, X.; Zhao, J. Circular Airy beams realized via the photopatterning of liquid crystals. Chin. Opt. Lett. 2020, 18, 080008. [Google Scholar] [CrossRef]
- Wei, B.; Zhang, Y.; Li, P.; Liu, S.; Hu, W.; Lu, Y.; Wu, Y.; Dou, X.; Zhao, J. Liquid-crystal splitter for generating and separating autofocusing and autodefocusing circular Airy beams. Opt. Express 2020, 28, 26151–26160. [Google Scholar] [CrossRef]
- Slussarenko, S.; Murauski, A.; Du, T.; Chigrinov, V.; Marrucci, L.; Santamato, E. Tunable liquid crystal q-plates with arbitrary topological charge. Opt. Express 2011, 19, 4085–4090. [Google Scholar] [CrossRef] [Green Version]
- Pregla, R.; Reden, W.V.; Hoekstra, H.J.W.M.; Baghdasaryan, H.V. Beam propagation methods. In Book Photonic Devices for Telecommunications; Guekos, G., Ed.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 35–65. [Google Scholar]
- Li, P.; Liu, S.; Peng, T.; Xie, G.; Gan, X.; Zhao, J. Spiral autofocusing Airy beams carrying power-exponent-phase vortices. Opt. Express 2014, 22, 7598–7606. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Han, L.; Li, P.; Zhang, Y.; Cheng, H.; Zhao, J. A method for simultaneously measuring polarization and phase of arbitrarily polarized beams based on Pancharatnam-Berry phase. Appl. Phys. Lett. 2017, 110, 171112. [Google Scholar] [CrossRef]
- Wang, K.; Kemao, Q.; Di, J.; Zhao, J. Deep learning spatial phase unwrapping: A comparative review. Adv. Photonics Nexus 2022, 1, 014001. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, H.; Wei, B.; Zhang, Y.; Liu, S.; Li, P.; Wu, Y.; Zhao, J. Autofocusing and Self-Healing Optical Vortices Realized via Circular Cubic Phase Modulation. Crystals 2022, 12, 1356. https://doi.org/10.3390/cryst12101356
Xiong H, Wei B, Zhang Y, Liu S, Li P, Wu Y, Zhao J. Autofocusing and Self-Healing Optical Vortices Realized via Circular Cubic Phase Modulation. Crystals. 2022; 12(10):1356. https://doi.org/10.3390/cryst12101356
Chicago/Turabian StyleXiong, Haozhe, Bingyan Wei, Yuan Zhang, Sheng Liu, Peng Li, Yunlong Wu, and Jianlin Zhao. 2022. "Autofocusing and Self-Healing Optical Vortices Realized via Circular Cubic Phase Modulation" Crystals 12, no. 10: 1356. https://doi.org/10.3390/cryst12101356




