Next Article in Journal
Double-Layer Superhydrophobic Anti-Icing Coating Based on Carbon Nanoparticles
Next Article in Special Issue
Local Probing ErCrO3
Previous Article in Journal
Nickel-Assisted Transfer-Free Technology of Graphene Chemical Vapor Deposition on GaN for Improving the Electrical Performance of Light-Emitting Diodes
Previous Article in Special Issue
Local Crystalline Structure of Doped Semiconductor Oxides Characterized by Perturbed Angular Correlations: Experimental and Theoretical Insights
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 12
Issue 10
10.3390/cryst12101499
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Structure and Properties of Cubic PuH2 and PuH3: A Density Functional Theory Study

by
Thomas Smith
1,
Samuel Moxon
1,
David J. Cooke
1,
Lisa J. Gillie
1,
Robert M. Harker
2,
Mark T. Storr
2,
Estelina Lora da Silva
3 and
Marco Molinari
1,*
1
Department of Chemical Sciences, University of Huddersfield, Queensgate, Huddersfield HD1 3DH, UK
2
AWE Aldermaston, Reading RG7 4PR, UK
3
IFIMUP, Department of Physics and Astronomy, Faculty of Science, University of Porto, Rua do Campo Alegre 687, 6169-007 Porto, Portugal
*
Author to whom correspondence should be addressed.
Crystals 2022, 12(10), 1499; https://doi.org/10.3390/cryst12101499
Submission received: 5 October 2022 / Revised: 17 October 2022 / Accepted: 19 October 2022 / Published: 21 October 2022
(This article belongs to the Special Issue Radioactive Isotopes Based Materials Characterization)
Browse Figures
Versions Notes

Abstract

:
The presence of cubic PuH2 and PuH3, the products of hydrogen corrosion of Pu, during long-term storage is of concern because of the materials’ pyrophoricity and ability to catalyse the oxidation reaction of Pu to form PuO2. Here, we modelled cubic PuH2 and PuH3 using Density Functional Theory (DFT) and assessed the performance of the PBEsol+U+SOC (0 ≤ U ≤ 7 eV) including van der Waals dispersion using the Grimme D3 method and the hybrid HSE06sol+SOC. We investigated the structural, magnetic and electronic properties of the cubic hydride phases. We considered spin–orbit coupling (SOC) and non-collinear magnetism to study ferromagnetic (FM), longitudinal and transverse antiferromagnetic (AFM) orders aligned in the <100>, <110> and <111> directions. The hybrid DFT confirmed that FM orders in the <110> and <111> directions were the most stable for cubic PuH2 and PuH3, respectively. For the standard DFT, the most stable magnetic order is dependent on the value of U used, with transitions in the magnetic order at higher U values (U > 5 eV) seen for both PuH2 and PuH3.

1. Introduction

The UK has a long history of nuclear power generation dating from the opening of Calder Hall reactor at Sellafield in 1956 [1], with a range of reactor types generating plutonium as a by-product of the power generation [2,3]. Throughout this history, the dominant plutonium material type for both research and use has been the dioxide, PuO2: its chemical stability makes it useful as a fuel and for storage.
Plutonium hydrides are less studied in comparison [4] but are nevertheless an important class of compounds. Firstly, metallic plutonium corrodes in the presence of hydrogen or water (gas or liquid) to form hydrides and hydride containing mixtures, and similar products are formed if plutonium metallic materials are held in close proximity to hydrogenous materials (polymers, oils, etc.), which can radiolytically decay and generate hydrogen. The hydrides formed in such scenarios are often friable, high surface area materials that react vigorously with air, presenting a pyrophoric hazard [5]. Additionally, the volume increase associated with formation of hydrides could theoretically lead to mechanical strain on storage containers [6,7,8]. Thus, waste packages that might contain plutonium metallic materials could present specific hazards if they are generating hydrides during long periods of storage: the subsequent opening in a controlled or uncontrolled fashion in an air environment could ignite plutonium hydride materials. Secondly, plutonium hydrides are a component of mixed hydride fuels such as PUZH (PuH2-U-ZrH1.6) that are reported to have a higher burnup opportunity (103 vs. 50 GWD/MTiHM for mixed oxide fuels (MOX)) [9]. In addition, a PUZH core is estimated to cost ~13% less than a MOX core, and to be superior to mixed oxide fuels MOX in terms of transmutation effectiveness and proliferation resistance [10].
There are two accepted phase diagrams for the Pu+H system. Firstly, that of Wicke [11] and of Flotow [12] and secondly that of Haschke et al. [5] The earlier work implies that the PuH2+x cubic form is present from PuH2 to PuH3 although is non-committal at high temperatures. Alternatively, the Haschke phase diagram indicates that increasing complexity creeps in above PuH2.7 with first a mixed phase region (cubic + hexagonal), then hexagonal and then orthorhombic (an unidentified further phase is also suggested in this phase range). These two-phase diagrams are not necessarily in disagreement and Haschke himself notes that the discrepancy is probably due to preparation methods (the cubic form would appear to be observed above PuH2.7 if the hydride is prepared at higher temperatures). So, to summarise the literature consensus that the cubic form of PuHx is observed between PuH1.95 and PuH2.7 and the cubic form may or may not be found at higher hydrogen stoichiometries depend on the preparation conditions. In PuH2, hydrogen occupies the tetrahedral sites (HT), and the additional hydrogen in a PuH3 cubic structure is accommodated within the octahedral sites (HO) (Figure 1). A large activation energy prevents the cubic to hexagonal phase transition at lower temperatures [5,13].
Experimental studies on Pu materials are challenging due to the toxic and radioactive nature of the materials [14,15]. Computational studies, utilising first principles techniques, have been employed with different levels of complexity, for instance using DFT including on-site Coulombic correction Hubbard parameter U [16,17,18,19,20,21,22,23,24,25,26], spin–orbit coupling (SOC) [18,20,21,24,25,26,27], and hybrid [28] functionals. Theoretical studies have shown the ability to produce accurate descriptions of the properties of cubic PuH2 and PuH3. For example, the lattice contraction that occurs in PuHx as x increases from x = 2 to 3 [17,21,26,28] agreeing with experimental X-ray diffraction (XRD) [29] data, and the metal-insulator transition (MIT) [21,27] agreeing with a DC experiment [30].
In this study, we model cubic PuH2 and PuH3 using Density Functional Theory (DFT) using two levels of theory PBEsol+U+SOC (0 ≤ U ≤ 7 eV) and hybrid HSE06sol+SOC, including spin orbit coupling (SOC) and non-collinear magnetism, to investigate their structure, and magnetic and electronic properties. In particular, the order of stability of ferromagnetic (FM), longitudinal antiferromagnetic (AFM) and transverse AFM orders in the <100>, <110>, and <111> directions.

2. Computational Methodology

PuHx was investigated using a non-collinear relativistic computational method employing DFT within the Vienna Ab initio Simulation Package (VASP) [31]. Our simulations use a plane-wave basis set incorporating relativistic core potentials and ion-electron interactions described using the project augmented wave (PAW) method [32]. The inclusion of spin–orbit coupling (SOC) [33] is deemed important in the previous literature [26], thus is included in this study. We applied the generalised gradient approximation (GGA) with the Perdew–Burke–Ernzerhof for solids (PBEsol) [34] functional and the hybrid functional of Heyd–Scuseria–Ernzerhof for solids (HSE06sol) [35]. To describe the strong on-site Columbic repulsion of Pu 5f electrons using the PBEsol functional, the Hubbard U correction was applied. In the Liechtenstein method [36], the Coulombic (U) and the exchange (J) parameters are treated as independent variables. We evaluated values of U between 0 and 7 eV with J = 0 eV, and hence this method becomes equivalent to the Dudarev method [37]. The effective U parameter, Ueff = U – J, is referred to as U from now on. Following convergence testing, see Table S1, the cut-off energy for the planewave basis set is 1000 eV (PBEsol+U+SOC) and 500 eV (HSE06sol+SOC). The Brillouin zone was sampled using a k-point grid of 11 × 11 × 11 for PBEsol+U+SOC for both the calculations for the geometry optimisation and the electronic density of states, and 5 × 5 × 5 for HSE06sol+SOC calculations. The electronic and ionic iteration convergence criteria for the bulk structures of cubic PuH2 and PuH3 were 1 × 10−5 eV per atom and 1 × 10−3 eV Å−1, respectively. A total of nine magnetic orders were considered, consisting of ferromagnetic, longitudinal antiferromagnetic and transverse antiferromagnetic orders in the <100>, <110> and <111> alignments. The non-collinear magnetic wave vectors are as shown in Figure 2. The terminology 1k, 2k and 3k refers to the alignment of the magnetic moments in the <100>, <110> and <111> directions, respectively, and is common terminology when it comes to UO2, NpO2 and PuO2 [38,39,40].

3. Results and Discussion

The most stable magnetic order amongst ferromagnetic <100>, <110> and <111>, longitudinal antiferromagnetic 1k, 2k and 3k, and transverse antiferromagnetic 1k, 2k and 3k orders, which we will refer to as FM <100>, FM <110>, FM <111>, L1kAFM, L2kAFM, L3kAFM, T1kAFM, T2kAFM and T3kAFM, respectively, was determined using HSE06sol+SOC and PBEsol+U+SOC (0 ≤ U ≤ 7 eV) functionals considering non-collinear magnetic contributions. The advantage of computational techniques is that they allow one to simulate different structural models and impose structural constraints to evaluate whether they are or could be stable. For example, a small distortion of the oxygen sublattice has been reported in fluorite UO2, which caused a lowering of symmetry from Fm 3 ¯ m to Pa 3 ¯ [40,41]. We have also applied such distortion on the hydrogen sublattice in both cubic PuH2 and PuH3. However, all our attempts to geometry optimise these structures removed the distortion in the hydrogen sublattice for all magnetic orders and for all values of the Hubbard U parameter used (0 ≤ U ≤ 7 eV). We have also studied the inclusion of van der Waals (vdW) dispersions using the D3 method of Grimme et al. [42] (PBEsol+U+SOC+D3) considering non-collinear magnetic contributions. Our results using vdW corrections are consistent to those without vdW in terms of energy differences (Table S2), magnetism (Table S3), symmetry (Table S4), and lattice parameters for PuH2 (Table S5) and PuH3 (Table S6) and their average values (Figure S1), thus PBEsol+U+SOC+D3 results are presented in the SI.

3.1. Thermodynamic Stability

The relative energetics of cubic PuH2 and PuH3 calculated using HSE06sol+SOC are reported in Figure 3.
For both structures, our data indicates that the FM order is the most stable. For PuH2, the most stable alignment is in the <110> direction followed by <111> and then <100> for each of the three magnetisms, i.e. FM, longitudinal AFM, and transverse AFM. The most stable magnetic order overall for PuH2 is FM <110>; however only a very small difference (6.0 × 10−3 eV/PuH2) is predicted to the next most stable order T2kAFM. For PuH3, alignment in the <111> direction is most stable for FM orders, followed by <100> and <110> directions. For longitudinal and transverse AFM orders, the alignment in the <110> direction is most stable followed by the ones in the <100> and <111> directions. The most stable magnetic order overall is FM <111>; however only a 1.0 × 10−2 eV/PuH3 difference is predicted to the next most stable order FM <100>. Such small differences in relative energy are mostly of the order of kbT at room temperatures, i.e., 2.6 × 10−2 eV, suggesting that magnetic orders could co-exist. This is supported by both experimental [30,43] and computational [21,26,28] investigations where either FM and AFM orders are predicted as most stable for PuH2, and only very small energy differences exist between both orders for PuH2 and PuH3.
Experimentally, using a vibrating sample magnetometer (VSM), Willis et al. [30] (PuHx with x = 1.93, 45 K) and Kim et al. [44] (PuHx with x = 1.9, 40 K) found the FM order to be the most stable. Whilst, the AFM order was also experimentally determined as most stable for PuH2 by Aldred et al. [43] (PuHx with x = 1.99, 30 K) using the Faraday method in agreement with the nuclear magnetic resonance (NMR) results of Cinader et al. [45] Such a difference in magnetic order obtained by the experiments was attributed to differences in samples and compositions by Willis et al. [30] However, the determination of the correct composition and magnetic properties of PuHx is difficult to obtain experimentally as thermodynamic equilibrium has to be reached, in addition to a possible oxidation of the sample, i.e., where the fluorite PuO2 structure may also be present as a surface layer onto the Pu metal [43].
Computationally, the hybrid PBE0 (without SOC) of Li et al. [28] found that the FM <100> order is more stable than the 1k AFM order for both cubic PuH2 and PuH3 with only small energy differences, i.e., EFM-EAFM of −5.4 × 10−2 eV for PuH2 and −4.1 × 10−2 eV for PuH3. For PuH2, using HSE06sol+SOC we found the order of stability in the <100> alignment is FM <100> > L1kAFM > T1kAFM, which agrees with findings from an alternative hybrid method of Li et al. [28]. The energy differences we predict between orders are very small with only −2.2 × 10−3 eV between FM <100> and L1kAFM, and −3.1 × 10−3 eV between FM <100> and T1kAFM. For PuH3, using HSE06sol+SOC we found that the order of stability in the <100> direction is FM <100> > T1kAFM > L1kAFM, with small energy differences of −2.4 × 10−2 eV between FM <100> and T1kAFM, and −4.9 × 10−2 eV between FM <100> and L1kAFM. Furthermore, the GGA+U+SOC study of Guo et al. [21] found FM to be more stable than AFM for both PuH2 and PuH3, agreeing with the present work and Li et al. [28] Although the alignment of the magnetic order is not specified, small differences in energy are reported, i.e. EFM-EAFM was only −2.7 × 10−3 eV for PuH2 and −2.7 × 10−2 eV for PuH3, respectively [21]. The AFM order was found to be more stable than FM using LDA(GGA)+U (unstated alignment) for cubic PuH2 and PuH3 [26] and using PBE+U (spin magnetic moments aligned in a simple “up down up down” alternative manner along the <111> direction, U = 3.25 eV) for PuH2 [46]. A transition is observed in the magnetic order of PuH2 from AFM to FM when U = 4 eV for LDA+U and from FM to AFM when U = 1 eV for GGA+U. The introduction of SOC was deemed important, with FM state predicted as more stable for PuH3; however, the AFM order was still most stable for PuH2 [26].
We calculate only very small differences in relative energies amongst all the magnetic orders for each value of the Hubbard U using PBEsol+U+SOC for both cubic PuH2 and PuH3 (Figure 4). We find a transition between the most stable magnetic orders in both PuH2 and PuH3, which is dependent on the value of U used.
For PuH2, and considering PBEsol+U+SOC when 0 ≤ U ≤ 4 eV, T2kAFM is the most stable magnetic order but when 5 ≤ U ≤ 7 eV FM <110> order is the most stable, implying that a transition occurs at U = 5 eV from AFM to FM, which is comparable to that obtained by Zheng et al. [26] at U = 4 eV using LDA+U. When comparing with our results from HSE06sol+SOC, FM <110> and T2kAFM are the most stable and next most stable orders, displaying how sensitive the magnetism is upon the choice of the Hubbard correction.
As for PuH3, only a very small difference in energy (6.2 × 10−2 eV) was predicted between the most stable magnetic order FM <111> and the least stable L3kAFM using HSE06sol+SOC. By employing PBEsol+U+SOC, the relative energies display a more complicated behaviour for PuH3. There is a transition in stability between the FM and AFM order at U = 6 eV. However, when U = 0 eV, U = 1 eV, 2 ≤ U ≤ 5 eV the most stable orders are FM <100>, FM <110>, and FM <111>, respectively, whereas when 6 ≤ U ≤ 7 eV the most stable order is T2kAFM.
Instabilities in the energy trends of PuH2 where found, for example in L3kAFM at U = 6 and T3kAFM at U = 7 which do not follow the trend. This may be due to the DFT+U methodology, which has issues in stabilising metastable states as the degeneracy of the f orbitals is broken. The energy minimisation that optimised the geometry may thus lead the system to be “trapped” in a metastable state. There are methodologies, such as occupation matrix control (OMC) [47] and U-ramping [48] that can help with the DFT+U localisation issues to reach the ground state. Applying DFT+U+OMC would require the consideration of all possible initial occupation matrices, making the method time consuming and complicated for a system such as cubic PuHx with a high number of electronic configurations. On the other hand, by choosing the U-ramping method, one has to consider that it can only be applied when the selected U value does not change the orbital ordering. We tested U-ramping on selected structures and yet could not eliminate the instabilities in the energy trend.

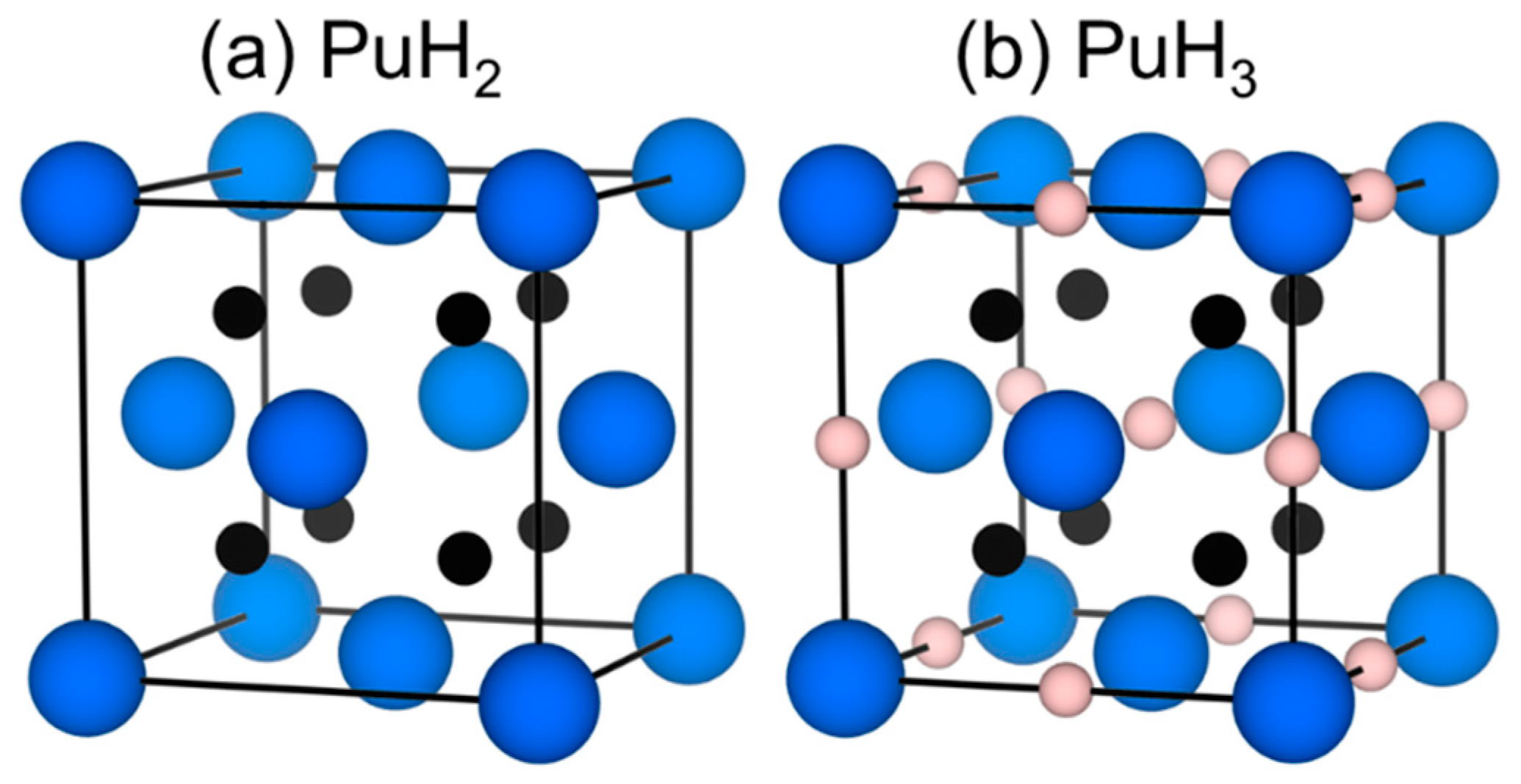
3.2. Symmetry and Structure

Space groups of the optimised cubic PuH2 and PuH3 phases using FM and AFM magnetic orders are shown in Table 1 for both HSE06sol+SOC and PBEsol+U+SOC calculations. Only the L3kAFM order maintained the cubic experimentally derived Fm 3 ¯ m symmetry for both PuH2 and PuH3. Supported by both our hybrid and standard DFT calculations, the space group symmetry of PuH2 and PuH3 are the same but display a lowering of symmetry with a distortion on one of the three lattice parameters (see Tables S8 and S9 for full details).
Good agreement is found between HSE06sol+SOC and PBEsol+U+SOC with the same symmetry predicted for all phases apart from a small difference in FM <110> and T2kAFM orders. Between PuH2 and PuH3 the same symmetry is determined, except for HSE06sol+SOC FM <110> and T2kAFM and PBEsol+U+SOC T2kAFM where U = 2 eV. Using HSE06sol+SOC, the cell lengths for the most stable magnetic order of PuH2 (FM <110>) are a = b = 5.33 Å and c = 5.28 Å, and for the most stable magnetic order of PuH3 (FM <111>) is 5.24 Å. Only a difference of 0.59% was calculated between the hybrid value obtained for the lattice parameters of cubic PuH2 and the experimental value of Mulford et al. [49,50] (5.359 Å). For cubic PuH3, a 1.97% difference in the lattice parameters was determined compared to the experimental value of Muromura et al. [29] (5.34 Å).
In Figure 5 the average cell length and angles for each magnetism are plotted as a function of the U value (0–7 eV) for the PBEsol+U+SOC calculations, along with the values from HSE06sol+SOC and experiments. The individual values for cell lengths, cell angle and cell volumes are shown in Tables S8 and S9 for PuH2 and PuH3, respectively. At least U = 2–3 eV is required to reproduce the values from the HSE06sol+SOC, but U > 4 eV are the minimum satisfactory values to gain experimental comparison; although this comparison is more accurate for PuH2 (Figure 5a) than for PuH3 since a contraction of the simulated cell at all U values (Figure 5b) is evidenced. A lattice contraction is observed between x = 2 and x = 3, as the ionic character increases with an increase in x, resulting in a lattice contraction due to an increase cell cohesion [16,17,19,20,21].
Cell lengths for cubic PuH2 with the FM order as 5.454 Å and the AFM order as 5.388 Å, and for PuH3 with FM as 5.35 Å and AFM as 5.35 Å (all magnetic orders where in the [001] direction) were reported by Li et al. [28] using PBE0. For a magnetism aligned in the [001], a distortion in the lattice would be expected in a cubic structure, see the work on UO2, NpO2 and PuO2 [38,39,40]. Our lattice parameter predicted using HSE06sol+SOC are comparable to those obtained by Li et al. [28]. When comparing our values in the same alignment for each magnetism (i.e., FM <100>, L1kAFM and T1kAFM) we find only small percentage differences of between 0.8 and 3.2% for PuH2 and 0.44–7.82% for PuH3.
As for PBEsol+U+SOC (U = 5 eV), the cell length obtained for the L3kAFM magnetic order of cubic PuH2 is 5.36 Å, which agrees perfectly well with the experimental findings of 5.36 Å from Mulford et al. [49,50] for PuH2. L3kAFM was chosen for comparison as it was the only magnetic order to retain Fm 3 ¯ m symmetry and U = 5 eV was chosen as cell lengths are accurately described. As the Hubbard U parameter increased from 0 to 7 eV using L3kAFM, a 3.96% increase in cell length is seen; this is due to the 5f electrons becoming more localised leading to a reduction in cohesion energies and an increase in cell length. For cubic PuH3 with the L3kAFM magnetic order using PBEsol+U+SOC when U = 5, a cell length of 5.32 Å is in good agreement (0.34% difference) with the experimental finding of 5.34 Å from Muromura et al. [29] All magnetic orders are in good agreement with the experimental value when U = 5 eV For L3kAFM, a 3.28% increase in cell length is seen when U is increased from 0 to 7 eV.

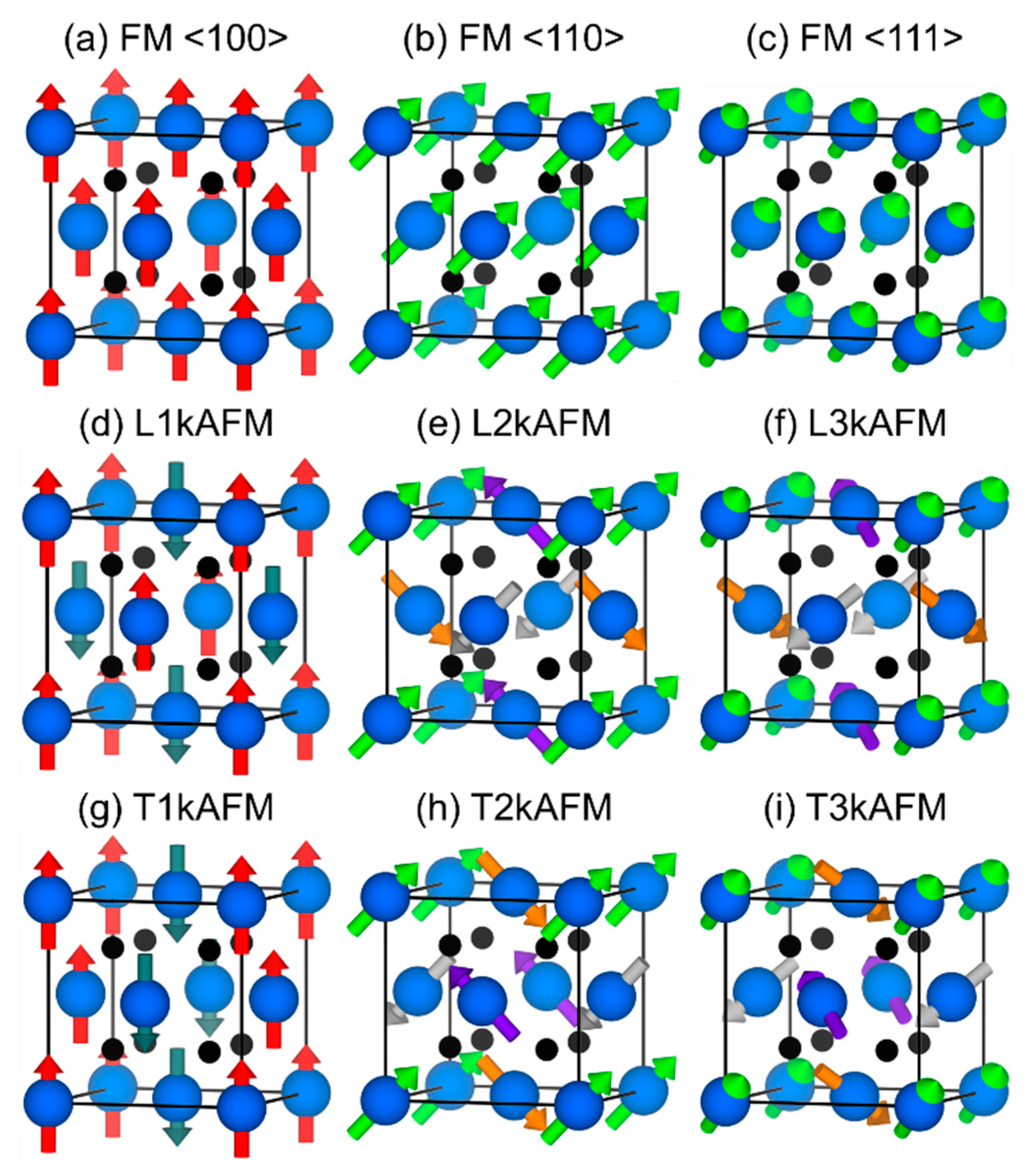
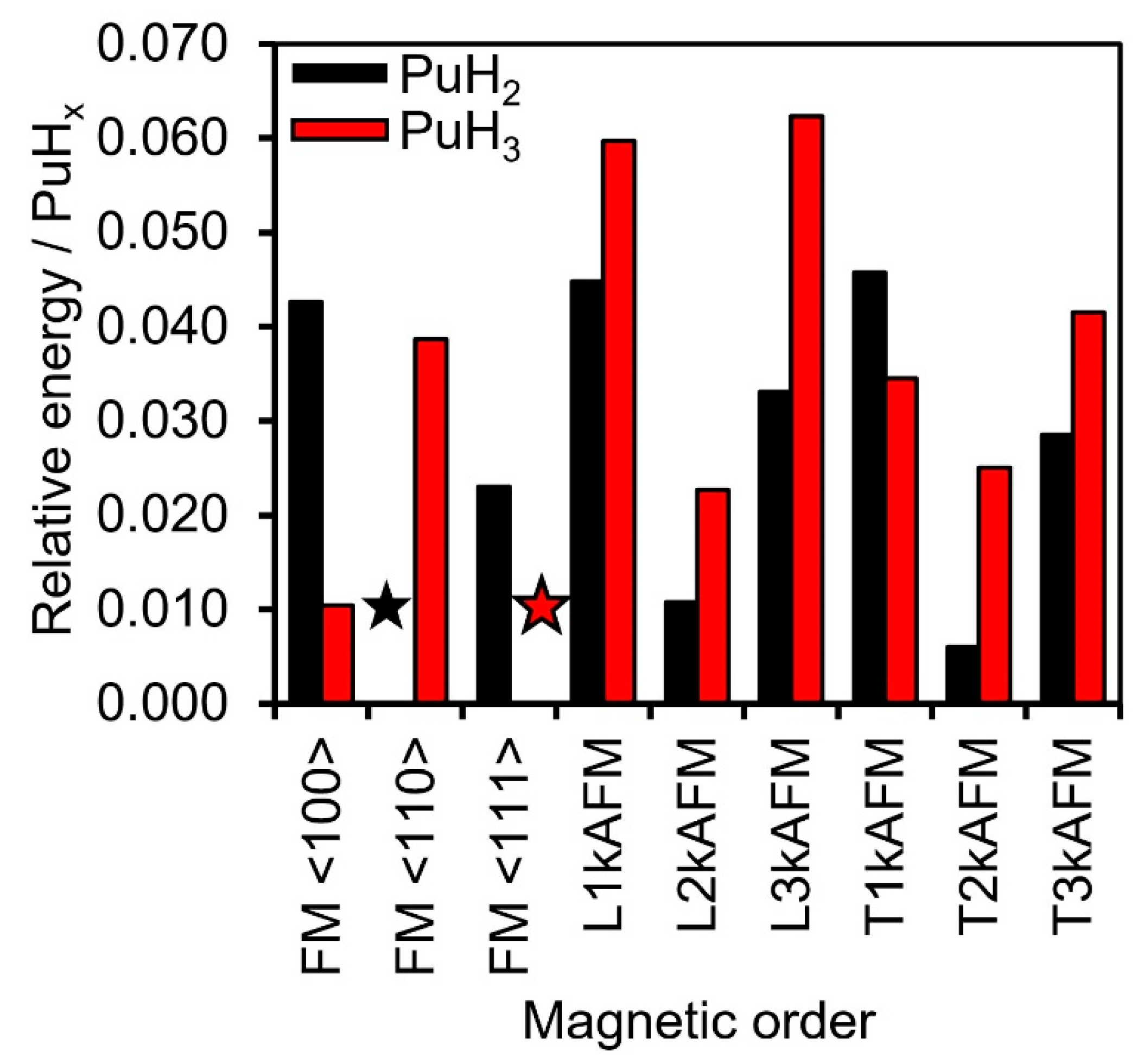
3.3. Magnetic Moments

The spin (μs), orbital (μl) and total (μtotal) magnetic moments for cubic PuH2 and PuH3 calculated with HSE06sol+SOC and PBEsol+U+SOC are shown in Figure 6. Values of magnetic moments are consistent in magnitude regardless of the magnetic structure imposed on the system when using HSE06sol+SOC. The optimised magnetic wavevectors of PuH2 predicted using HSE06sol+SOC are presented in Table S7. By considering PBEsol+U+SOC, the average values for all magnetic orders of PuH2 the total magnetic moments decrease from 2.06 to 1.26 μB/atom (38% decrease) when U increased from 0 to 7 eV. For the spin magnetic moment an increase from 4.54 to 4.86 μB/atom (7% increase) occurs, whilst for the orbital moment a change from −2.48 to −3.60 μB/atom (45% decrease) takes place when U increases from 0 to 7 eV. We find good agreement between hybrid and standard DFT methods.
Spin, orbital, and total magnetic moments were calculated by Zheng et al. [26] using LDA+U+SOC (U = 4 eV); which were found to be 4.58, −3.69 and 0.89 μB/atom, respectively for PuH2 with an AFM order. These are comparable to the values we obtained for the spin, orbital, and total magnetic moments using PBEsol+U+SOC (U = 4 eV) for PuH2 with the T2kAFM order (the most stable for that particular value of U) of 4.73, −3.43 and 1.30 μB/atom, respectively. All DFT studies overestimate the total magnetic moments in comparison to experimental values for saturated moment of 0.44 μB/ion of Aldred et al. [43] for cubic PuH1.99, and 0.43 μB/ion of Willis et al. [30].

3.4. Electronic Structure

As we compare the performance of the PBEsol+U+SOC depending on the value of U, the electronic density of states (eDOS) for cubic PuH2 and PuH3 are shown in Figure 7. As the previous session has shown that values of U = 4–6 eV give the best answer in terms of lattice parameters, we have only reported the eDOS for U = 5 eV here. eDOS for U = 4 and 6 eV for both PuH2 and PuH3 can be found in Figures S2 and S3, respectively. Our findings suggest that independent of the value of the U parameter, and of all magnetic orders imposed to the hydrides, cubic PuH2 and PuH3 are both metallic, as there is a non-zero occupancy at the Fermi level, EF. The valence band and conduction band are dominated by Pu 5f states, as is observed in the literature [16,17,20,21]. The non-zero occupancy at the Fermi level in PuH3 is much less pronounced compared to PuH2. The covalent character result from Pu 6d and H 1s hybridisation is observed in the projected DOS for cubic PuHx (x = 2 and 3) (Figure 7). The on-site Hubbard parameter U increases the localisation of Pu 5f electrons, which separates and sharpens the 5f states [16,17,19,20,21].
Many computational studies agree with our PBEsol+U+SOC results for cubic PuH2, i.e., LDA/LDA+U [16,17,19,26] and GGA/GGA+U [20,21], and for PuH3, i.e., LDA/LDA+U [17,26], GGA/GGA+U [20,21] and PBE+U [22] where it is reported that only a small number of electrons crosses the Fermi level. However, there is also some controversy. The GGA+sp+U (U = 4 eV) of Guo et al. [21] using the full potential linearised augmented plane wave method (FP-LAPW) reports semiconductor behaviour with a bandgap of 0.35 eV for cubic PuH3. If the introduction of SOC changes the nature of the electronic behaviour, we do not see such change in agreement with the LDA+U+SOC (U = 4 eV) of Zheng et al. [26]. In addition to the metallic behaviour for cubic PuH2, Li et al. [27] reported semiconductor behaviour also cubic PuH3 at 300K using DFT+U (U = 4.2 eV) and the Dynamical Mean-Field Theory (DMFT). However, somehow their predictions suggest that the occupancy of Pu 5f states would result in Pu3+ valence for both PuH2 and PuH3 phases. To note, the Pu 5f electrons are at the boundary between the early actinides with itinerant 5f electrons and the late actinides with localised 5f electrons. Any change in temperature, pressure and chemical potential (i.e., composition) may result in the transition between itinerancy and localisation, causing mixed-valent states or valence fluctuations. This poses issue when simulating PuHx phases using DFT.
Experimentally, a metal to insulator (MIT) transition was observed by Willis et al. [30] and Ward et al. [51] for cubic PuHx between x = 1.93 and 2.65. Cubic PuHx phases were grown on metallic support (Ga doped δ-Pu metal) as described by Haschke et al. [52], but information on sample thickness and support thickness was not reported. Using a four-terminal DC method, a possible transition is recorded at x = 2.14 while a definite transition occurred at x = 2.65 as the rate change in resistivity against temperature becomes negative [30,51].

4. Conclusions

Cubic PuH2 and PuH3 were investigated computationally using DFT with two levels of theory: the hybrid HSE06sol+SOC and PBEsol+U+SOC (0 ≤ U ≤ 7 eV) considering spin–orbit coupling (SOC) and non-collinear magnetism. The structural, magnetic and electronic properties were investigated for nine magnetic orders: ferromagnetic <100>, <110> and <111>; longitudinal antiferromagnetic 1k, 2k and 3k; and transverse antiferromagnetic 1k, 2k and 3k magnetic orders.
Our data suggests that only a very small difference exists between FM and AFM magnetic orders, and that they may coexist. Using HSE06sol+SOC, we found FM <110> and FM <111> orders to be the most stable for PuH2 and PuH3, respectively. Using PBEsol+U+SOC, the order of stability is dependent on the value of the Hubbard parameter U, with a transition from AFM to FM seen in PuH2 at U = 5 eV, whilst an FM to AFM transition is observed at U = 6 eV in PuH3. Of the nine magnetic orders investigated, we determined that only the L3kAFM order retains the experimentally measured Fm 3 ¯ m structure. We determined that both cubic PuH2 and PuH3 have metallic behaviour using PBEsol+U+SOC (U = 5 eV).

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst12101499/s1. The SI contains three sections, organised as follows: Section S1: Convergence testing of cubic PuH2 and PuH3 using PBEsol+U+SOC. Section S2: Energetics and structural properties of cubic PuH2 and PuH3 calculated with PBEsol+U+SOC+D3; Section S3: Magnetic, structural and electronic properties of cubic PuH2 and PuH3. References [29,42,49] are cited in the Supplementary Materials.

Author Contributions

T.S., S.M. and M.M. performed the calculations and data analysis. D.J.C., L.J.G. and E.L.d.S. provided support and discussion. R.M.H. and M.T.S. provided comment on the comparison with experiments. M.M. and T.S. devised the research project. All authors have read and agreed to the published version of the manuscript.

Funding

We would like to acknowledge the EPSRC DTP 2018-19 University of Huddersfield (EP/R513234/1). Analysis was performed on the Orion computing facility at the University of Huddersfield. Calculations were run on the ARCHER and ARCHER2 UK National Supercomputing Services via our membership of the UK HEC Materials Chemistry Consortium (MCC; EPSRC EP/L000202, EP/R029431). EldS acknowledges the Network of Extreme Conditions Laboratories (NECL), financed by FCT and co-financed by NORTE 2020, through the programme Portugal 2020 and FEDER. To the extent that this paper relies on the contribution of RMH/MTS, then the copyright vests in the @British Crown Copyright 2020/AWE.

Institutional Review Board Statement

Not Applicable.

Informed Consent Statement

Not Applicable.

Data Availability Statement

The data presented in this study is available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Patterson, W. Fifty years of hopes and fears. Nature 2007, 449, 664. [Google Scholar] [CrossRef]
  2. Hyatt, N.C. Safe management of the UK separated plutonium inventory: A challenge of materials degradation. NPJ Mater. Degrad. 2020, 4, 1. [Google Scholar] [CrossRef]
  3. Nuclear Decommissioning Authority. Progress on Plutonium Consolidation, Storage and Disposition; Nuclear Decommissioning Authority: Moor Row, UK, 2019.
  4. Oetting, F.L. The Chemical Thermodynamic Properties of Plutonium Compounds. Chem. Rev. 1967, 67, 261. [Google Scholar] [CrossRef]
  5. Haschke, J.M.; Hodges, A.E.; Lucas, R.L. Equilibrium and structural properties of the PuH system. J. Less-Common Met. 1987, 133, 155. [Google Scholar] [CrossRef]
  6. Allen, T.H.; Haschke, J.M. Hydride-Catalyzed Corrosion of Plutonium by Air: Initiation by Plutonium Monoxide Monohydride; LA-13462-MS; Los Alamos National Lab.: Los Alamos, NM, USA, 1998. [Google Scholar] [CrossRef] [Green Version]
  7. Haschke, J.M.; Allen, T.H. Plutonium hydride, sesquioxide and monoxide monohydride: Pyrophoricity and catalysis of plutonium corrosion. J. Alloys Compd. 2001, 320, 58. [Google Scholar] [CrossRef]
  8. Hecker, S.S.; Martz, J.C. Plutonium Aging: From Mystery to Enigma. In Ageing Studies and Lifetime Extension of Materials; Springer: Boston, MA, USA, 2001; pp. 23–52. [Google Scholar]
  9. Ganda, F.; Greenspan, E. Incineration of Plutonium in PWR Using Hydride Fuel. In Proceedings of the 2005 International Conference on Advances in Nuclear Power Plants, ARWIF-2005, Oak Ridge, TN, USA, 6–18 February 2005. [Google Scholar]
  10. Ganda, F.; Greenspan, E. Plutonium recycling in hydride fueled PWR cores. Nucl. Eng. Des. 2009, 239, 1489. [Google Scholar] [CrossRef]
  11. Wicke, O.J. (Ed.) Plutonium Handbook: A Guide to the Technology; American Nuclear Society: La Grange Park, IL, USA, 1992. [Google Scholar]
  12. Flotow, H.E.; Haschke, J.M.; Yamauchi, S. Part 9—The Actinide Hydrides. In The Chemical Thermodynamics of Actinide Elements and Compounds; IAEA: Vienna, Austria, 1984; p. 115. [Google Scholar]
  13. Haschke, J.M.; Stakebake, J.L. Handling, Storage, and Disposition of Plutonium and Uranium. In The Chemistry of the Actinide and Transactinide Elements; Springer: Dordrecht, The Netherlands, 2007; pp. 3199–3272. [Google Scholar]
  14. Stakebake, J.L. The storage behavior of plutonium metal, alloys, and oxide: A review. J. Nucl. Mater. 1971, 38, 241. [Google Scholar] [CrossRef]
  15. Hecker, S.S. Plutonium—An element never at equilibrium. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2008, 39, 1585. [Google Scholar] [CrossRef]
  16. Ai, J.; Liu, T.; Gao, T.; Ao, B. First-principles study of electronic structure and metal-insulator transition of plutonium dihydride and trihydride. Comput. Mater. Sci. 2012, 51, 127. [Google Scholar] [CrossRef]
  17. Ao, B.Y.; Wang, X.L.; Shi, P.; Chen, P.H.; Ye, X.Q.; Lai, X.C.; Gao, T. First-principles LDA + U calculations investigating the lattice contraction of face-centered cubic Pu hydrides. J. Nucl. Mater. 2012, 424, 183. [Google Scholar] [CrossRef]
  18. Li, S.; Ao, B.; Ye, X.; Qiu, R.; Gao, T. New Insights into the Crystal Structures of Plutonium Hydrides from First-Principles Calculations. J. Phys. Chem. C 2018, 122, 10103. [Google Scholar] [CrossRef]
  19. Ao, B.Y.; Ai, J.J.; Gao, T.; Wang, X.L.; Shi, P.; Chen, P.H.; Ye, X.Q. Metal-insulator transition of plutonium hydrides: DFT + U calculations in the FPLAPW basis. Chin. Phys. Lett. 2012, 29, 017102. [Google Scholar] [CrossRef]
  20. Ao, B.Y.; Shi, P.; Guo, Y.; Gao, T. The abnormal lattice contraction of plutonium hydrides studied by first-principles calculations. Chin. Phys. B 2013, 22, 037103. [Google Scholar] [CrossRef]
  21. Guo, Y.; Ai, J.J.; Gao, T.; Ao, B.Y. Structural, magnetic, electronic, and elastic properties of face-centered cubic PuHx (x = 2, 3): GGA (LSDA) + U + so. Chin. Phys. B 2013, 22, 057103. [Google Scholar] [CrossRef]
  22. Sudhapriyanga, G.; Santhosh, M.; Rajeswarapalanichamy, R.; Iyakutti, K. First Principles Study of Pressure Induced Phase Transition, Electronic and magnetic Properties of Plutonium trihydride. Int. J. Sci. Eng. Res. 2014, 5, 114. [Google Scholar]
  23. Zhang, C.; Yang, Y.; Zhang, P. Thermodynamics Study of Dehydriding Reaction on the PuO2(110) Surface from First Principles. J. Phys. Chem. C 2018, 122, 7790. [Google Scholar] [CrossRef]
  24. Yang, Y.; Zhang, P. Hydriding and dehydriding energies of PuHx from ab initio calculations. Phys. Lett. A 2015, 379, 1649. [Google Scholar] [CrossRef]
  25. Zheng, J.J.; Li, W.D.; Li, S.N.; Zhang, P.; Wang, B.T. Mechanical and thermodynamic properties of plutonium dihydride. J. Alloys Compd. 2018, 750, 258. [Google Scholar] [CrossRef]
  26. Zheng, J.J.; Wang, B.T.; Di Marco, I.; Li, W.D. Electronic structure and phase stability of plutonium hydrides: Role of Coulomb repulsion and spin-orbital coupling. Int. J. Hydrogen Energy 2014, 39, 13255. [Google Scholar] [CrossRef]
  27. Li, R.S.; Lu, X.; Wang, J.T.; Xin, D.Q.; Yao, X.G. A many-body perspective on dual 5f states in two plutonium hydrides. Chem. Phys. Lett. 2020, 740, 137079. [Google Scholar] [CrossRef]
  28. Li, S.; Guo, Y.; Ye, X.; Gao, T.; Ao, B. Structural, magnetic, and dynamic properties of PuH2+x (x = 0, 0.25, 0.5, 0.75, 1): A hybrid density functional study. Int. J. Hydrogen Energy 2017, 42, 30727–30737. [Google Scholar] [CrossRef]
  29. Muromura, T.; Yahata, T.; Ouchi, K.; Iseki, M. The variation of lattice parameter with hydrogen content of non-stoichiometric plutonium dihydride. J. Inorg. Nucl. Chem. 1972, 34, 171. [Google Scholar] [CrossRef]
  30. Willis, J.O.; Ward, J.W.; Smith, J.L.; Kosiewicz, S.T.; Haschke, J.M.; Hodges, A.E. Electronic properties and structure of the plutonium-hydrogen system. Phys. B C 1985, 130, 527. [Google Scholar] [CrossRef]
  31. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
  32. Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207. [Google Scholar] [CrossRef] [Green Version]
  33. Steiner, S.; Khmelevskyi, S.; Marsmann, M.; Kresse, G. Calculation of the magnetic anisotropy with projected-augmented-wave methodology and the case study of disordered Fe1-xCox alloys. Phys. Rev. B 2016, 93, 224425. [Google Scholar] [CrossRef]
  34. Csonka, G.I.; Perdew, J.P.; Ruzsinszky, A.; Philipsen, P.H.T.; Lebègue, S.; Paier, J.; Vydrov, O.A.; Ángyán, J.G. Assessing the performance of recent density functionals for bulk solids. Phys. Rev. B 2009, 79, 155107. [Google Scholar] [CrossRef]
  35. Schimka, L.; Harl, J.; Kresse, G. Improved hybrid functional for solids: The HSEsol functional. J. Chem. Phys. 2011, 134, 024116. [Google Scholar] [CrossRef]
  36. Liechtenstein, A.I.; Anisimov, V.I.; Zaanen, J. Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators. Phys. Rev. B 1995, 52, R5467. [Google Scholar] [CrossRef] [Green Version]
  37. Dudarev, S.; Botton, G. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA + U study. Phys. Rev. B 1998, 57, 1505. [Google Scholar] [CrossRef]
  38. Moxon, S.; Symington, A.R.; Tse, J.S.; Dawson, J.; Flitcroft, J.M.; Parker, S.C.; Cooke, D.J.; Harker, R.M.; Molinari, M. The energetics of carbonated PuO2 surfaces affects nanoparticle morphology: A DFT+: U study. Phys. Chem. Chem. Phys. 2020, 22, 7728. [Google Scholar] [CrossRef] [PubMed]
  39. Pegg, J.T.; Shields, A.E.; Storr, M.T.; Wills, A.S.; Scanlon, D.O.; de Leeuw, N.H. Hidden magnetic order in plutonium dioxide nuclear fuel. Phys. Chem. Chem. Phys. 2018, 20, 20943. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  40. Pegg, J.T.; Aparicio-Anglès, X.; Storr, M.; de Leeuw, N.H. DFT + U study of the structures and properties of the actinide dioxides. J. Nucl. Mater. 2017, 492, 269. [Google Scholar] [CrossRef]
  41. Desgranges, L.; Ma, Y.; Garcia, P.; Baldinozzi, G.; Siméone, D.; Fischer, H.E. What Is the Actual Local Crystalline Structure of Uranium Dioxide, UO2? A New Perspective for the Most Used Nuclear Fuel. Inorg. Chem. 2017, 56, 321. [Google Scholar] [CrossRef] [PubMed]
  42. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
  43. Aldred, A.T.; Cinader, G.; Lam, D.J.; Weber, L.W. Magnetic properties of neptunium and plutonium hydrides. Phys. Rev. B 1979, 19, 300. [Google Scholar] [CrossRef]
  44. Kim, J.W.; Mun, E.D.; Baiardo, J.P.; Smith, A.I.; Richmond, S.; Mitchell, J.; Schwartz, D.; Zapf, V.S.; Mielke, C.H. Detecting low concentrations of plutonium hydride with magnetization measurements. J. Appl. Phys. 2015, 117, 053905. [Google Scholar] [CrossRef]
  45. Cinader, G.; Zamir, D.; Hadari, Z. NMR study of the plutonium hydride system. Phys. Rev. B 1976, 14, 912. [Google Scholar] [CrossRef]
  46. Yang, X.; Yang, Y.; Lu, Y.; Sun, Z.; Hussain, S.; Zhang, P. First-principles GGA + U calculation investigating the hydriding and diffusion properties of hydrogen in PuH2+x, 0 ≤ x ≤ 1. Int. J. Hydrogen Energy 2018, 43, 13632. [Google Scholar] [CrossRef]
  47. Dorado, B.; Amadon, B.; Freyss, M.; Bertolus, M. DFT + U calculations of the ground state and metastable states of uranium dioxide. Phys. Rev. B 2009, 79, 235125. [Google Scholar] [CrossRef]
  48. Meredig, B.; Thompson, A.; Hansen, H.A.; Wolverton, C.; Van De Walle, A. Method for locating low-energy solutions within DFT + U. Phys. Rev. B 2010, 82, 195128. [Google Scholar] [CrossRef] [Green Version]
  49. Mulford, R.N.R.; Sturdy, G.E. The Plutonium-Hydrogen System. I. Plutonium Dihydride and Dideuteride. J. Am. Chem. Soc. 1955, 77, 3449. [Google Scholar] [CrossRef]
  50. Mulford, R.N.R.; Sturdy, G.E. The Plutonium-Hydrogen System. II. Solid Solution of Hydrogen in Plutonium Dihydride. J. Am. Chem. Soc. 1956, 78, 3897. [Google Scholar] [CrossRef]
  51. Ward, J.W. Electronic structure and bonding in transuranics: Comparison with lanthanides. J. Less-Common Met. 1983, 93, 279. [Google Scholar] [CrossRef] [Green Version]
  52. Haschke, J.M.; Hodges, A.E.; Smith, C.M.; Oetting, F.L. Equilibria and thermodynamic properties of the plutonium-hydrogen system. J. Less-Common Met. 1980, 73, 41. [Google Scholar] [CrossRef]
Crystals 12 01499 g001 550
Figure 1. Crystal structures of cubic (a) PuH2 and (b) PuH3. Pu in blue and H occupying tetrahedral sites (HT) in black and octahedral sites (HO) in pink.
Figure 1. Crystal structures of cubic (a) PuH2 and (b) PuH3. Pu in blue and H occupying tetrahedral sites (HT) in black and octahedral sites (HO) in pink.
Crystals 12 01499 g001
Crystals 12 01499 g002 550
Figure 2. Magnetic structure of cubic PuHx with FM (a) <100>, (b) <110>, (c) <111>, longitudinal AFM (d) 1k, (e) 2k, (f) 3k, and transverse AFM (g) 1k, (h) 2k and (i) 3k. Pu in blue and H occupying tetrahedral sites (HT) in black for PuH2. The presence of H occupying octahedral sites (HO) in PuH3 would not change the directions of the magnetisation on Pu atoms.
Figure 2. Magnetic structure of cubic PuHx with FM (a) <100>, (b) <110>, (c) <111>, longitudinal AFM (d) 1k, (e) 2k, (f) 3k, and transverse AFM (g) 1k, (h) 2k and (i) 3k. Pu in blue and H occupying tetrahedral sites (HT) in black for PuH2. The presence of H occupying octahedral sites (HO) in PuH3 would not change the directions of the magnetisation on Pu atoms.
Crystals 12 01499 g002
Crystals 12 01499 g003 550
Figure 3. Relative energies of FM <100>, <110> and <111>, longitudinal AFM 1k, 2k and 3k, and transverse AFM 1k, 2k and 3k magnetic orders per PuHx for PuH2 in black and for PuH3 in red, calculated using HSE06sol+SOC. Black and red stars represent the most stable magnetic order for PuH2 and PuH3, respectively.
Figure 3. Relative energies of FM <100>, <110> and <111>, longitudinal AFM 1k, 2k and 3k, and transverse AFM 1k, 2k and 3k magnetic orders per PuHx for PuH2 in black and for PuH3 in red, calculated using HSE06sol+SOC. Black and red stars represent the most stable magnetic order for PuH2 and PuH3, respectively.
Crystals 12 01499 g003
Crystals 12 01499 g004 550
Figure 4. Relative energies per formula unit for cubic PuH2 (a) FM <100>, <110>, <111>, (b) longitudinal AFM 1k, 2k and 3k, and (c) transverse AFM 1k, 2k and 3k, and for PuH3 (d) FM <100>, <110> and <111>, (e) longitudinal AFM 1k, 2k and 3k, and (f) transverse AFM 1k, 2k and 3k calculated with PBEsol+U+SOC (0 ≤ U ≤ 7 eV).
Figure 4. Relative energies per formula unit for cubic PuH2 (a) FM <100>, <110>, <111>, (b) longitudinal AFM 1k, 2k and 3k, and (c) transverse AFM 1k, 2k and 3k, and for PuH3 (d) FM <100>, <110> and <111>, (e) longitudinal AFM 1k, 2k and 3k, and (f) transverse AFM 1k, 2k and 3k calculated with PBEsol+U+SOC (0 ≤ U ≤ 7 eV).
Crystals 12 01499 g004
Crystals 12 01499 g005 550
Figure 5. Average cell lengths a-b-c (Å) for cubic (a) PuH2 and (b) PuH3 and average cell angles α-β-γ (degree) for (c) PuH2 and (d) PuH3. Where PBEsol+U+SOC (U = 0–7 eV) method is represented by circles, triangles and squares symbols for <100>, <110> and <111> alignments, respectively, and HSE06sol+SOC method is represented by solid, dash and square dotted lines for <100>, <110> and <111>, respectively. FM in blue, LAFM in red, TAFM in black. Experimental cell lengths represented in green for PuH2 (Mulford et al. [49,50]) and PuH3 (Muromura et al. [29]).
Figure 5. Average cell lengths a-b-c (Å) for cubic (a) PuH2 and (b) PuH3 and average cell angles α-β-γ (degree) for (c) PuH2 and (d) PuH3. Where PBEsol+U+SOC (U = 0–7 eV) method is represented by circles, triangles and squares symbols for <100>, <110> and <111> alignments, respectively, and HSE06sol+SOC method is represented by solid, dash and square dotted lines for <100>, <110> and <111>, respectively. FM in blue, LAFM in red, TAFM in black. Experimental cell lengths represented in green for PuH2 (Mulford et al. [49,50]) and PuH3 (Muromura et al. [29]).
Crystals 12 01499 g005
Crystals 12 01499 g006 550
Figure 6. Spin (green), orbital (red) and total (blue) magnetic moments calculated using HSE06sol+SOC for (a) cubic PuH2 and for (e) PuH3 and using PBEsol+U+SOC for cubic PuH2 and for PuH3 (b,f) FM <100>, <110> and <111>, (c,g) longitudinal AFM 1k, 2k and 3k, and (d,h) transverse AFM 1k, 2k and 3k.
Figure 6. Spin (green), orbital (red) and total (blue) magnetic moments calculated using HSE06sol+SOC for (a) cubic PuH2 and for (e) PuH3 and using PBEsol+U+SOC for cubic PuH2 and for PuH3 (b,f) FM <100>, <110> and <111>, (c,g) longitudinal AFM 1k, 2k and 3k, and (d,h) transverse AFM 1k, 2k and 3k.
Crystals 12 01499 g006
Crystals 12 01499 g007 550
Figure 7. eDOS plots calculated using PBEsol+U+SOC (U = 5 eV) for cubic PuH2/PuH3 with: FM (a,d) <100>, (b,e) <110> and (c,f) <111>; longitudinal AFM (g,j) 1k, (h,k) 2k, and (i,l) 3k; and transverse AFM (m,p) 1k, (n,q) 2k, and (o,r) 3k. The Fermi level is at 0 eV denoted by a vertical dashed line.
Figure 7. eDOS plots calculated using PBEsol+U+SOC (U = 5 eV) for cubic PuH2/PuH3 with: FM (a,d) <100>, (b,e) <110> and (c,f) <111>; longitudinal AFM (g,j) 1k, (h,k) 2k, and (i,l) 3k; and transverse AFM (m,p) 1k, (n,q) 2k, and (o,r) 3k. The Fermi level is at 0 eV denoted by a vertical dashed line.
Crystals 12 01499 g007
Table
Table 1. Space groups calculated with HSE06sol+SOC and PBEsol+U+SOC with a tolerance of 10−5 Å for FM <100>, <110> and <111>, longitudinal and transverse AFM 1k, 2k and 3k order for cubic PuH2. For cubic PuH3, the space groups are the same apart from the ones in brackets, which refers to the space group for PuH3 when it differs from that of PuH2. Space group numbers: I4/mmm (139), P 1 ¯ (2), C2/m (12), Immm (71), R 3 ¯ m (166), Fm 3 ¯ m (225), Fmmm (69), Cmca (64), Pbca (61) and Pa 3 ¯ (205).
Table 1. Space groups calculated with HSE06sol+SOC and PBEsol+U+SOC with a tolerance of 10−5 Å for FM <100>, <110> and <111>, longitudinal and transverse AFM 1k, 2k and 3k order for cubic PuH2. For cubic PuH3, the space groups are the same apart from the ones in brackets, which refers to the space group for PuH3 when it differs from that of PuH2. Space group numbers: I4/mmm (139), P 1 ¯ (2), C2/m (12), Immm (71), R 3 ¯ m (166), Fm 3 ¯ m (225), Fmmm (69), Cmca (64), Pbca (61) and Pa 3 ¯ (205).
Magnetic
Order		PBEsol+U+SOC—U (eV)HSE06sol
+SOC
01234567
FM <100>I4/mmmI4/mmmI4/mmmI4/mmmI4/mmmI4/mmmI4/mmmI4/mmmI4/mmm
FM <110>P 1 ¯ C2/mC2/mC2/mC2/mC2/mC2/mC2/mImmm
(C2/m)
FM <111>R 3 ¯ mR 3 ¯ mR 3 ¯ mR 3 ¯ mR 3 ¯ mR 3 ¯ mR 3 ¯ mR 3 ¯ mR 3 ¯ m
L1kAFMI4/mmmI4/mmmI4/mmmI4/mmmI4/mmmI4/mmmI4/mmmI4/mmmI4/mmm
L2kAFMI4/mmmI4/mmmI4/mmmI4/mmmI4/mmmI4/mmmI4/mmmI4/mmmI4/mmm
L3kAFMFm 3 ¯ mFm 3 ¯ mFm 3 ¯ mFm 3 ¯ mFm 3 ¯ mFm 3 ¯ mFm 3 ¯ mFm 3 ¯ mFm 3 ¯ m
T1kAFMFmmmFmmmFmmmFmmmFmmmFmmmFmmmFmmmFmmm
T2kAFMCmcaCmcaCmca (Pbca)CmcaCmcaCmcaCmcaCmcaPbca (Fmmm)
T3kAFMPa 3 ¯ Pa 3 ¯ Pa 3 ¯ Pa 3 ¯ Pa 3 ¯ Pa 3 ¯ Pa 3 ¯ Pa 3 ¯ Pa 3 ¯
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Smith, T.; Moxon, S.; Cooke, D.J.; Gillie, L.J.; Harker, R.M.; Storr, M.T.; da Silva, E.L.; Molinari, M. Structure and Properties of Cubic PuH2 and PuH3: A Density Functional Theory Study. Crystals 2022, 12, 1499. https://doi.org/10.3390/cryst12101499

AMA Style

Smith T, Moxon S, Cooke DJ, Gillie LJ, Harker RM, Storr MT, da Silva EL, Molinari M. Structure and Properties of Cubic PuH2 and PuH3: A Density Functional Theory Study. Crystals. 2022; 12(10):1499. https://doi.org/10.3390/cryst12101499

Chicago/Turabian Style

Smith, Thomas, Samuel Moxon, David J. Cooke, Lisa J. Gillie, Robert M. Harker, Mark T. Storr, Estelina Lora da Silva, and Marco Molinari. 2022. "Structure and Properties of Cubic PuH2 and PuH3: A Density Functional Theory Study" Crystals 12, no. 10: 1499. https://doi.org/10.3390/cryst12101499

APA Style

Smith, T., Moxon, S., Cooke, D. J., Gillie, L. J., Harker, R. M., Storr, M. T., da Silva, E. L., & Molinari, M. (2022). Structure and Properties of Cubic PuH2 and PuH3: A Density Functional Theory Study. Crystals, 12(10), 1499. https://doi.org/10.3390/cryst12101499

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop