Estimation of the Critical Value of the Second-Phase Particles in the Microstructure of AZ31 Mg Alloy by Phase-Field Methods
Abstract
:1. Introduction
2. Model Description
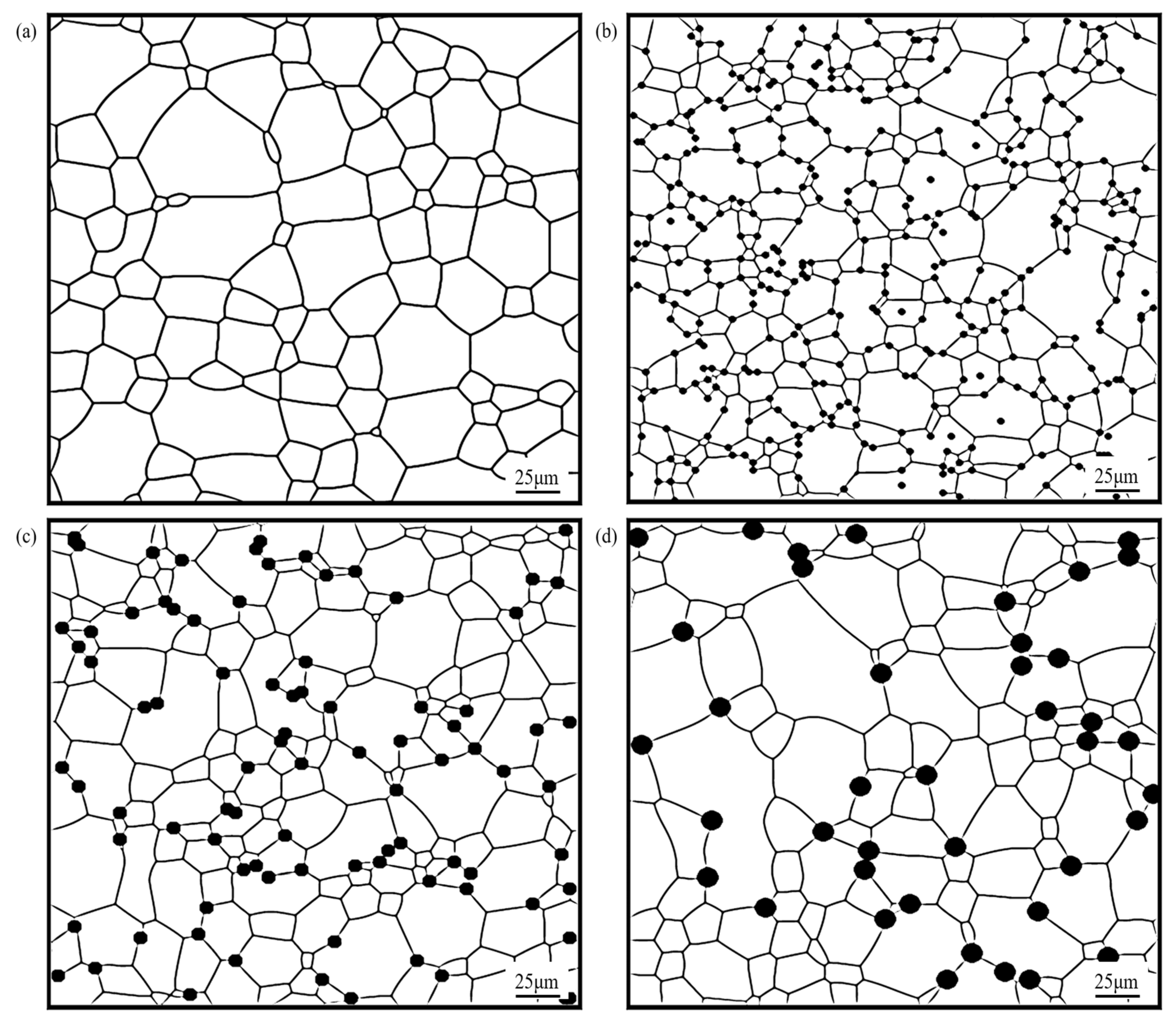
3. Simulation Results of the AZ31 Mg Alloy
4. Analysis and Discussion
4.1. Effect of SPP on the Grain Growth of Mg Alloy
4.2. Critical Value of SPP for Grain Boundary Pinning
4.2.1. Critical Volume Fraction of SPP for Grain Boundary Pinning
4.2.2. Critical Size of SPP for Grain Boundary Pinning
4.3. Zener Relationship Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, G.H.; Chen, Y.S.; Ding, W.J. Current research, application and future prospect of Magnesium alloys in aerospace industry. Manned Spacefl. 2016, 22, 281–292. [Google Scholar]
- Yang, Y.X.; Yang, W.F.; Mao, D.L.; Peng, J.H. Research and mechanical properties of Tantalum Carbide (TaC) reinforced AZ91 magnesium matrix composites. Hot Work. Technol. 2021, 50, 70–74. [Google Scholar]
- Shi, Z.Z.; Chen, H.T.; Zhang, K.; Dai, F.Z.; Liu, X.F. Crystallography of precipitates in Mg alloys. J. Magnes. Alloys 2021, 9, 416–431. [Google Scholar] [CrossRef]
- Zhang, J.; Jian, Y.; Zhao, X.; Meng, D.; Pan, F.; Han, Q. The tribological behavior of a surface-nanocrystallized magnesium alloy AZ31 sheet after ultrasonic shot peening treatment. J. Magnes. Alloys 2021, 9, 1187–1200. [Google Scholar] [CrossRef]
- Marzbanrad, B.; Razmpoosh, M.H.; Toyserkani, E.; Jahed, H. Role of heat balance on the microstructure evolution of cold spray coated AZ31B with AA7075. J. Magnes. Alloys 2021, 9, 1458–1469. [Google Scholar] [CrossRef]
- Wang, K.D. Mechanical Properties of Friction Stir Processed Mg-AZ31 Based Composites with Al2O3 Particles and Ti Particles. Master’s Thesis, Dalian University of Technology, Dalian, China, 2009. [Google Scholar]
- Fu, J.; Du, W.; Jia, L.; Wang, Y.; Zhu, X.; Du, X. Cooling rate controlled basal precipitates and age hardening response of solid-soluted Mg–Gd–Er–Zn–Zr alloy. J. Magnes. Alloys 2021, 9, 1261–1271. [Google Scholar] [CrossRef]
- Kim, Y.J.; Lee, J.U.; Kim, Y.M.; Park, S.H. Microstructural evolution and grain growth mechanism of pre-twinned magnesium alloy during annealing. J. Magnes. Alloys 2021, 9, 1233–1245. [Google Scholar] [CrossRef]
- Zhang, M.Q. Study on Fine Grain Strengthening of Mg-Y-Sm-Zn Magnesium Alloy. Master’s Thesis, XI’AN University of Architecture and Technology, Xi’an, China, 2019. [Google Scholar]
- Li, K.; Shen, Y.; Li, D.Y.; Peng, Y.H. Phase Field Study of Second Phase Particles-Pinning on Strain Induced Grain Boundary Migration. Mater. Sci. Forum 2020, 993, 967–975. [Google Scholar] [CrossRef]
- Teng, C.Y.; Fu, Y.; Ren, Z.Y.; Li, Y.H.; Wang, Y.; Ouyang, W.L. Phase Field Simulation of Grain Growth with Particle Pinning. Key Eng. Mater. 2016, 724, 8–11. [Google Scholar] [CrossRef]
- Chakrabarti, T.; Manna, S. Zener pinning through coherent precipitate: A phase-field study. Comput. Mater. Sci. 2018, 154, 84–90. [Google Scholar] [CrossRef] [Green Version]
- Chang, K.; Feng, W.; Chen, L. Effect of second-phase particle morphology on grain growth kinetics. Acta Mater. 2009, 57, 5229–5236. [Google Scholar] [CrossRef]
- Couturier, G.; Doherty, R.; Maurice, C.; Fortunier, R. 3D finite element simulation of the inhibition of normal grain growth by particles. Acta Mater. 2005, 53, 977–989. [Google Scholar] [CrossRef]
- Vanherpe, L.; Moelans, N.; Blanpain, B.; Vandewalle, S. Pinning effect of spheroid second-phase particles on grain growth studied by three-dimensional phase-field simulations. Comput. Mater. Sci. 2010, 49, 340–350. [Google Scholar] [CrossRef]
- Frazier, W.E.; Hu, S.; Joshi, V.V. A Potts Model parameter study of particle size, Monte Carlo temperature, and “Particle-Assisted Abnormal Grain Growth”. Comput. Mater. Sci. 2020, 185, 109945. [Google Scholar] [CrossRef]
- Haghighat, S.M.H.; Taheri, A.K. Investigation of limiting grain size and microstructure homogeneity in the presence of second phase particles using the Monte Carlo method. J. Mater. Processing Technol. 2008, 195, 195–203. [Google Scholar] [CrossRef]
- He, R. Simulation of Grain Growth in AZ31 Mg Alloy Influenced by Second-Phase Particles in Different Geometric Morphology. Master’s Thesis, Northeastern University, Shenyang, China, 2014. [Google Scholar]
- Wu, Y.; Zong, Y.; Jin, J. Grain growth in a nanostructured AZ31 Mg alloy containing second phase particles studied by phase field simulations. Sci. China Mater. 2016, 59, 355–362. [Google Scholar] [CrossRef] [Green Version]
- Xian-Gang, Z.; Ya-Ping, Z.; Ming-Tao, W.; Yan, W. A physical model to express grain boundaries in grain growth simulation by phase-field method. Acta Phys. Sin. 2011, 60, 755–763. [Google Scholar] [CrossRef]
- Lai, K.W.; Shi, S.J.; Yan, Z.W.; Li, Y.S.; Jin, S.S.; Wang, D.; Maqbool, S. Phase-field simulation of re-dissolution of γ′phase in Ni–Al alloy by continuous and second-order aging treatment. Rare Met. 2021, 40, 1155–1163. [Google Scholar] [CrossRef]
- Sato, D.; Ohno, M.; Matsuura, K. Phase-Field Simulations and Analysis of Effect of Dispersed Particles on Migration of Delta to Gamma Transformation Interface. Metall. Mater. Trans. A 2015, 46, 981–988. [Google Scholar] [CrossRef]
- Song, Y.; Wang, M.; Zong, Y.; He, R.; Jin, J. Grain Refinement by Second Phase Particles under Applied Stress in ZK60 Mg Alloy with Y through Phase Field Simulation. Materials 2018, 11, 1903. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Li, Y.; Lee, C.; Kim, J. Numerical simulations of the dynamics of axisymmetric compound liquid threads with a phase-field model. Eur. J. Mech. B Fluids 2021, 89, 203–216. [Google Scholar] [CrossRef]
- Li, D.Y.; Zhang, J.; Deng, Z.C. Study on effects of reinforcement particles on microstructure in Laser Melt Casting Solidification by Phase-field Method. Hot Work. Technol. 2018, 47, 179–182. [Google Scholar]
- Zhao, Y.; Zhang, H.; Wei, H.; Zheng, Q.; Jin, T.; Sun, X. A phase field study for scaling rules of grain coarsening in polycrystalline system containing second-phase particles. Acta Metall. Sin. 2013, 49, 981–988. [Google Scholar] [CrossRef]
- Wu, Y. The Simulation and Research for a Part of Micro-Factors Influencing Recrystallization and Grain Growth in AZ31 Mg Alloy. Ph.D. Thesis, Northeastern University, Shenyang, China, 2010. [Google Scholar]
- Wu, Y. Simulation of Nanocrystalline Grain Growth and Abnormal Grain Growth for AZ31 Mg Alloy by Phase Field Methods. Master’s Thesis, Northeastern University, Shenyang, China, 2014. [Google Scholar]
- Wang, M.; Zong, B.Y.; Wang, G. Grain growth in AZ31 Mg alloy during recrystallization at different temperatures by phase field simulation. Comput. Mater. Sci. 2009, 45, 217–222. [Google Scholar] [CrossRef]
- Fan, D.; Chen, L.-Q. Computer simulation of grain growth using a continuum field model. Acta Mater. 1997, 45, 611–622. [Google Scholar] [CrossRef]
- Fan, D.; Chen, L.-Q. Computer simulation of topological Evolution in 2-D grain growth using a continuum diffuse-interface feild model. Acta Mater. 1997, 45, 1115–1126. [Google Scholar] [CrossRef]
- Liu, R.C.; Wang, L.Y.; Gu, L.G.; Huang, G.S. Study on annealing technique for wrought magnesium alloy plate and modeling research on the changing law of its grain size. Light Alloy. Fabr. Technol. 2004, 32, 22–25. [Google Scholar]
- Zhang, Y.; Brodusch, N.; Descartes, S.; Shockley, J.M.; Gauvin, R.; Chromik, R.R. The Effect of Submicron Second-Phase Particles on the Rate of Grain Refifinement in a Copper-Oxygen Alloy During Cold Spray. J. Spray Tech. 2017, 26, 1509–1516. [Google Scholar] [CrossRef]
- Zhou, G.Z.; Wang, Y.X.; Chen, Z. Phase-field method simulation of the effect of hard particles with different shapes on two-phase grain growth. Acta Metall. Sin. 2012, 48, 227–234. [Google Scholar] [CrossRef]
- Luo, Z.R.; Gao, Y.J.; Qiu, H.G. Effect of stick second-phase particles with different geometric orientations on grain growth simulated by phase field method. Chin. J. Nonferrous Met. 2010, 20, 2406–2411. [Google Scholar]
- Humphreys, F.J.; Hatherly, M. Recrystallization and Related Annealing Phenomena; Elsevier Ltd.: Amsterdam, The Netherlands, 2017; pp. 1–63. [Google Scholar]
- Li, Y.; Kim, J. Phase-field simulations of crystal growth with adaptive mesh refinement. Int. J. Heat Mass Transf. 2012, 55, 7926–7932. [Google Scholar] [CrossRef]
- Yoon, S.; Park, J.; Wang, J.; Lee, C.; Kim, J. Numerical Simulation of Dendritic Pattern Formation in an Isotropic Crystal Growth Model on Curved Surfaces. Symmetry 2020, 12, 1155. [Google Scholar] [CrossRef]
- Zhang, J.; Ludwig, W.; Zhang, Y.; Sørensen HH, B.; Rowenhorst, D.J.; Yamanaka, A.; Poulsen, H.F. Grain boundary mobilities in polycrystals. Acta Mater. 2020, 191, 211–220. [Google Scholar] [CrossRef]
- Li, J.J.; Wang, J.C.; Yang, G.C. Phase field simulations of grain growth in systems containing second-phase particles. Rare Met. Mater. Eng. 2008, 10, 1746–1750. [Google Scholar]
- Olgaard, D.L.; Evans, B. Effect of second-phase particles on grain growth in calcite. J. Am. Ceram. Soc. 1986, 69, C-272–C-277. [Google Scholar] [CrossRef]
- Longworth, H.P.; Thompson, C.V. Abnormal grain growth in aluminum alloy thin films. J. Appl. Phys. 1991, 69, 3929–3940. [Google Scholar] [CrossRef]
- Huang, Y.B.; Wang, Y.X.; Chen, Z. Phase Field Simulation of the Second Phase Particle Precipitation at Boundaries and Its Pinning Effect. Rare Met. Mater. Eng. 2012, 41, 1751–1755. [Google Scholar]
- Du, L.; Yang, S.; Zhang, P.; Du, H. Pinning effect of different shape second-phase particles on grain growth in polycrystalline: Numerical and analytical investigations. Compos. Interfaces 2018, 25, 357–368. [Google Scholar] [CrossRef]










| SPP Size, r (μm) | 0.5 | 1 | 1.5 | 2 |
|---|---|---|---|---|
| Minimal critical volume fraction, fmin | 0.20% | 0.25% | 0.30% | 0.33% |
| Maximum critical volume fraction, fmax | 11% | 20% | 35% | 40% |
| m | R2 | ||||
|---|---|---|---|---|---|
| r = 0 μm | f = 0% | 2.0 | 1.1 | 2 | 0.99 |
| r = 0.50 μm | fmin = 0.20% | 1.6 | 1.8 | 2 | 0.99 |
| r = 1.00 μm | fmin = 0.25% | 1.4 | 2.3 | 2 | 0.99 |
| r = 1.50 μm | fmin = 0.30% | 1.7 | 1.49 | 2 | 0.99 |
| r = 2.00 μm | fmin = 0.33% | 2.4 | 0.7 | 2 | 0.99 |
| SPP Volume Fraction, f | 1% | 3% | 5% | 7% |
|---|---|---|---|---|
| Maximum critical size, rmax | 3.9 μm | 6.0 μm | 6.5 μm | 7.0 μm |
| m | R2 | ||||
|---|---|---|---|---|---|
| f = 0% | r = 0 μm | 2.0 | 1.1 | 2 | 0.99 |
| f = 1.0% | rmax = 3.9 μm | 2.1 | 1.1 | 2 | 0.99 |
| f = 3.0% | rmax = 6.0 μm | 1.6 | 1.9 | 2 | 0.99 |
| f = 5.0% | rmax = 6.5 μm | 3.3 | −0.7 | 3 | 0.99 |
| f = 7.0% | rmax= 7.0 μm | 4.4 | −2.3 | 3 | 0.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Xiong, J.; Luo, Q.; Chen, J.; Zeng, R.; Wang, S. Estimation of the Critical Value of the Second-Phase Particles in the Microstructure of AZ31 Mg Alloy by Phase-Field Methods. Crystals 2022, 12, 1504. https://doi.org/10.3390/cryst12111504
Wu Y, Xiong J, Luo Q, Chen J, Zeng R, Wang S. Estimation of the Critical Value of the Second-Phase Particles in the Microstructure of AZ31 Mg Alloy by Phase-Field Methods. Crystals. 2022; 12(11):1504. https://doi.org/10.3390/cryst12111504
Chicago/Turabian StyleWu, Yan, Jinlin Xiong, Qiang Luo, Jibing Chen, Rutie Zeng, and Shuo Wang. 2022. "Estimation of the Critical Value of the Second-Phase Particles in the Microstructure of AZ31 Mg Alloy by Phase-Field Methods" Crystals 12, no. 11: 1504. https://doi.org/10.3390/cryst12111504










