The Structure of the Near-Surface Layer of the AAAC Overhead Power Line Wires after Operation and Its Effect on Their Elastic, Microplastic, and Electroresistance Properties
Abstract
:1. Introduction
2. Experimental Details
2.1. Samples
2.2. SEM, EDX, and EBSD Experimental Details
2.3. XRD Experimental Details
2.4. Details of Densitometric Measurements
2.5. Details of Acoustic Measurements
2.6. Optical Microscopy Details
2.7. Details of Electrical Resistance Measurements
3. Research Results
3.1. OM Results
3.2. SEM and EDX Results
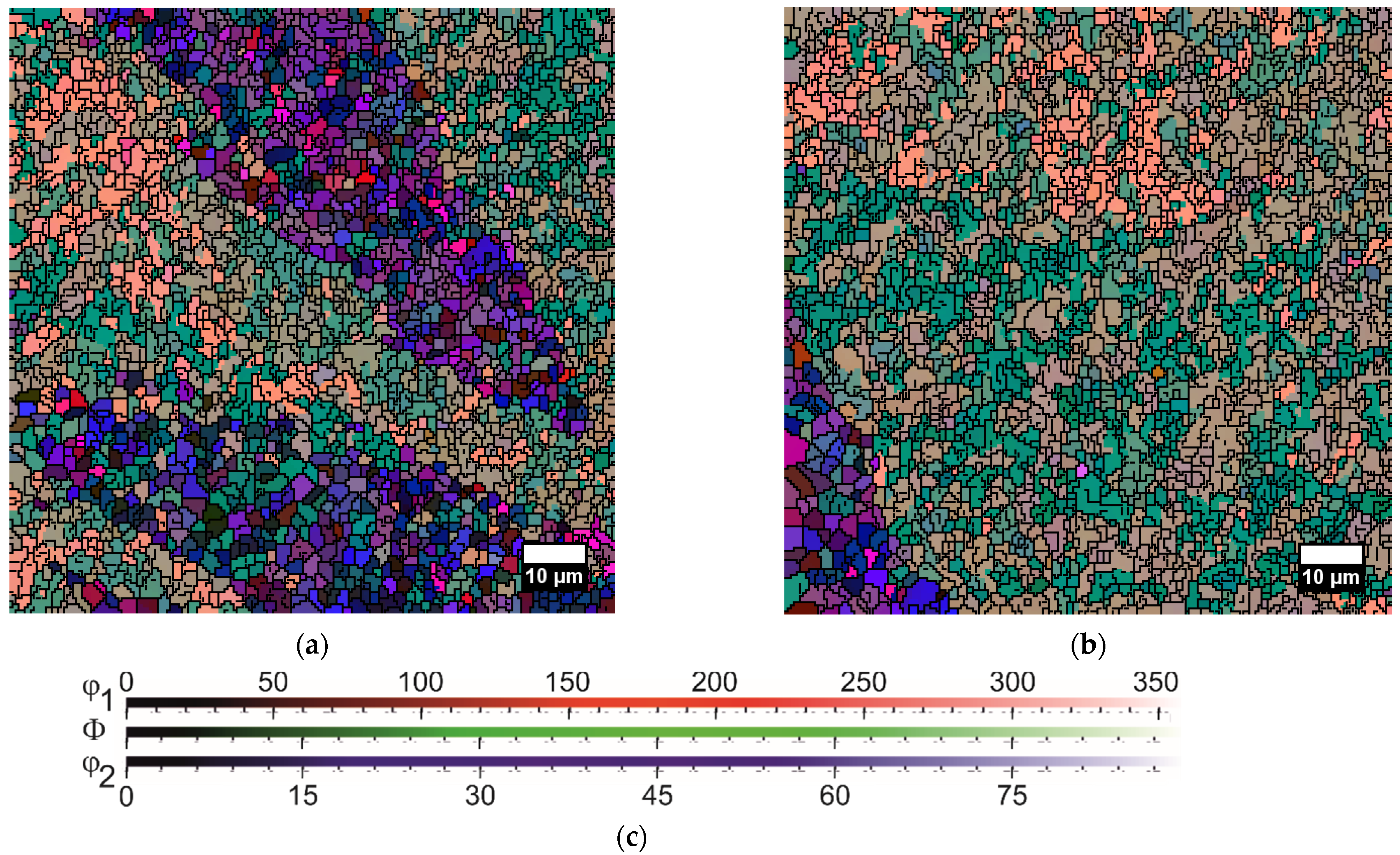
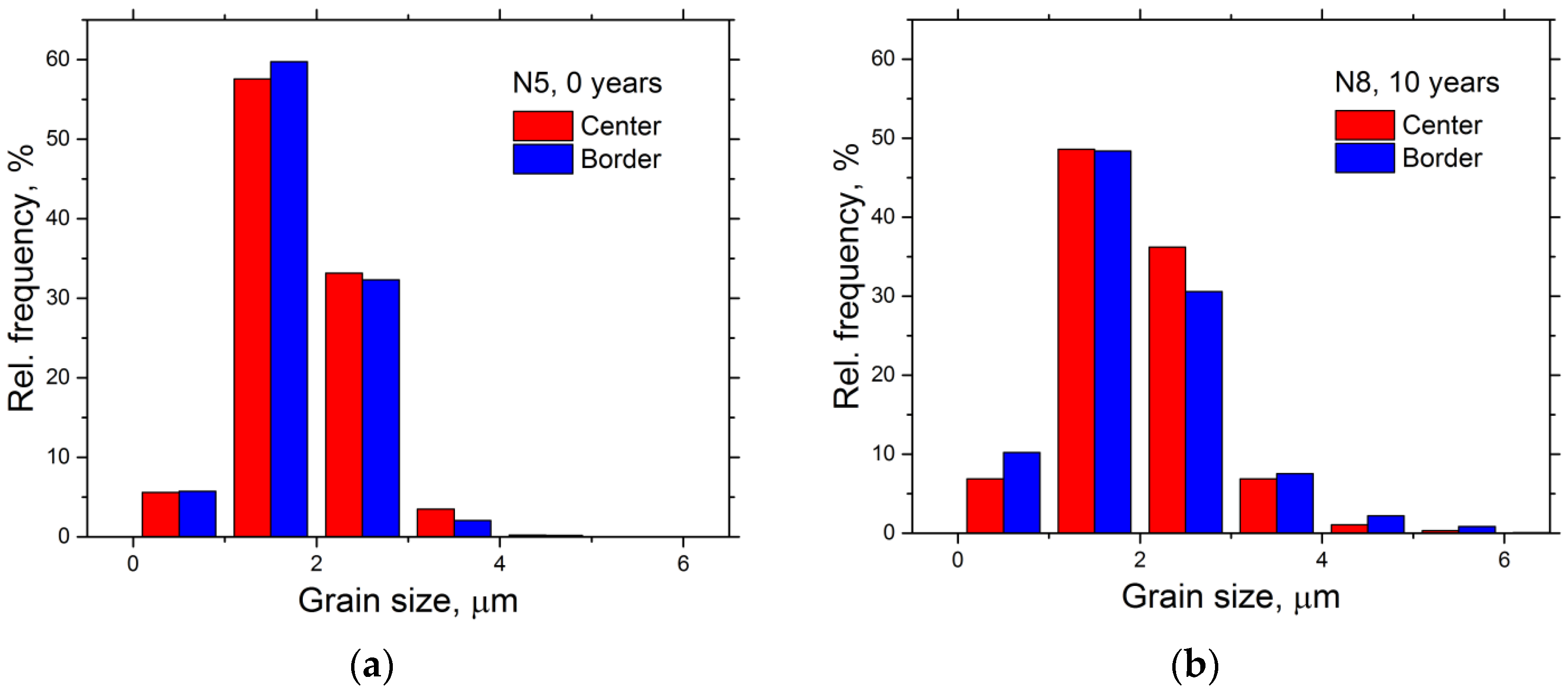
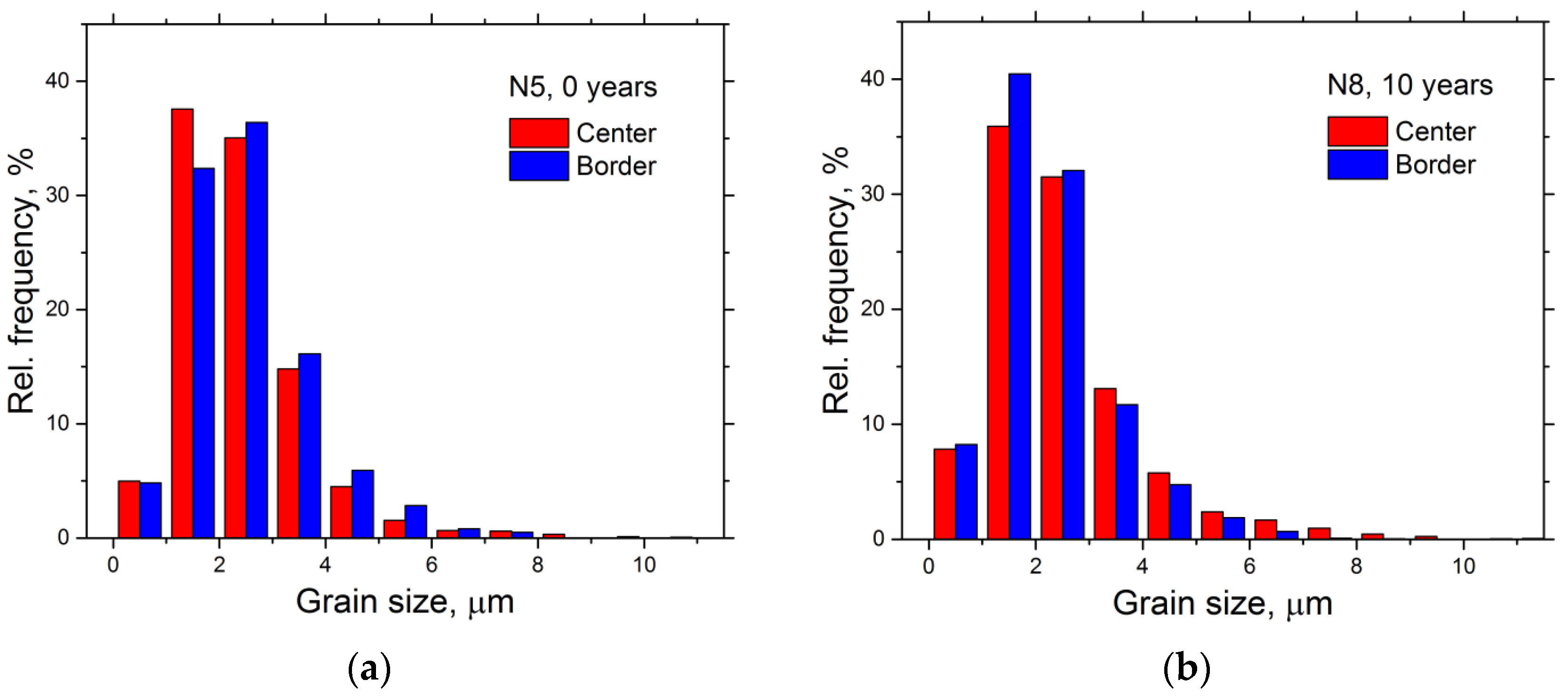
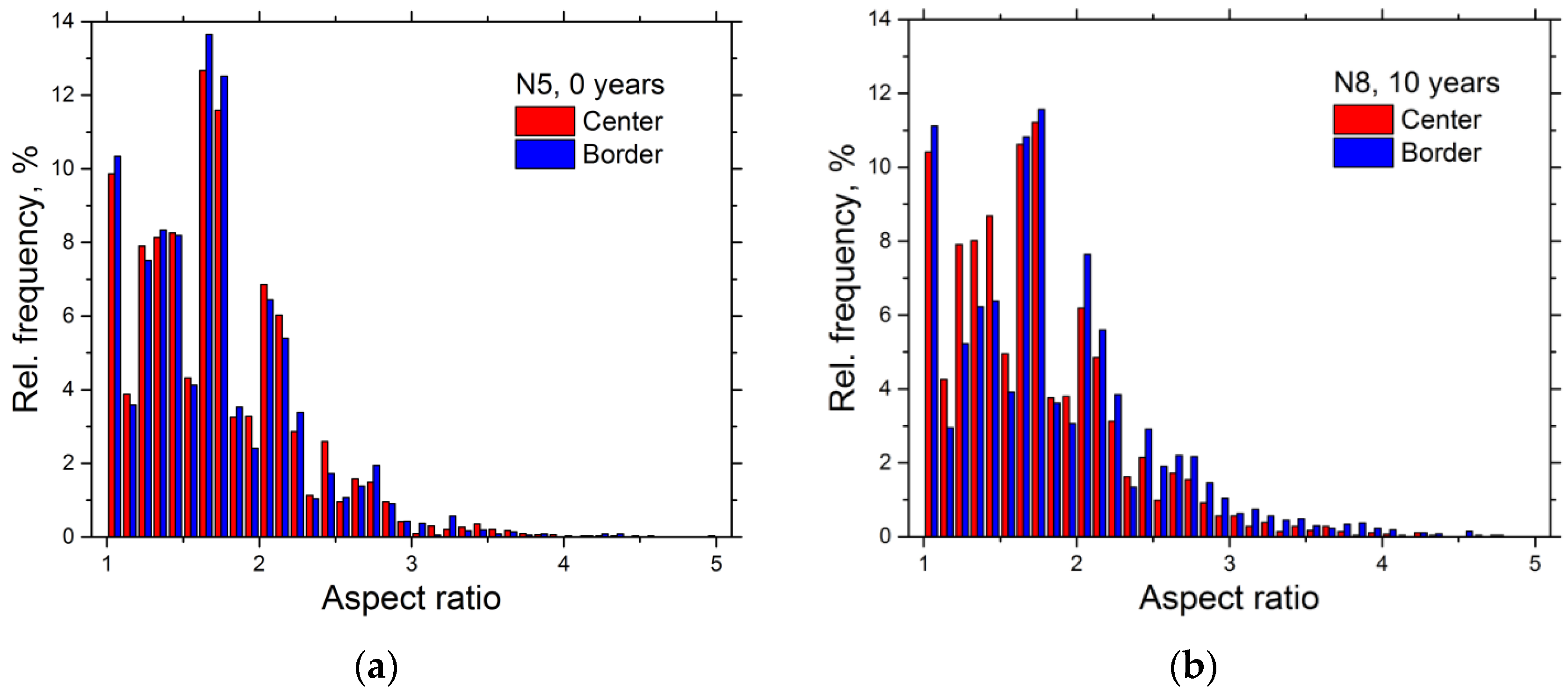
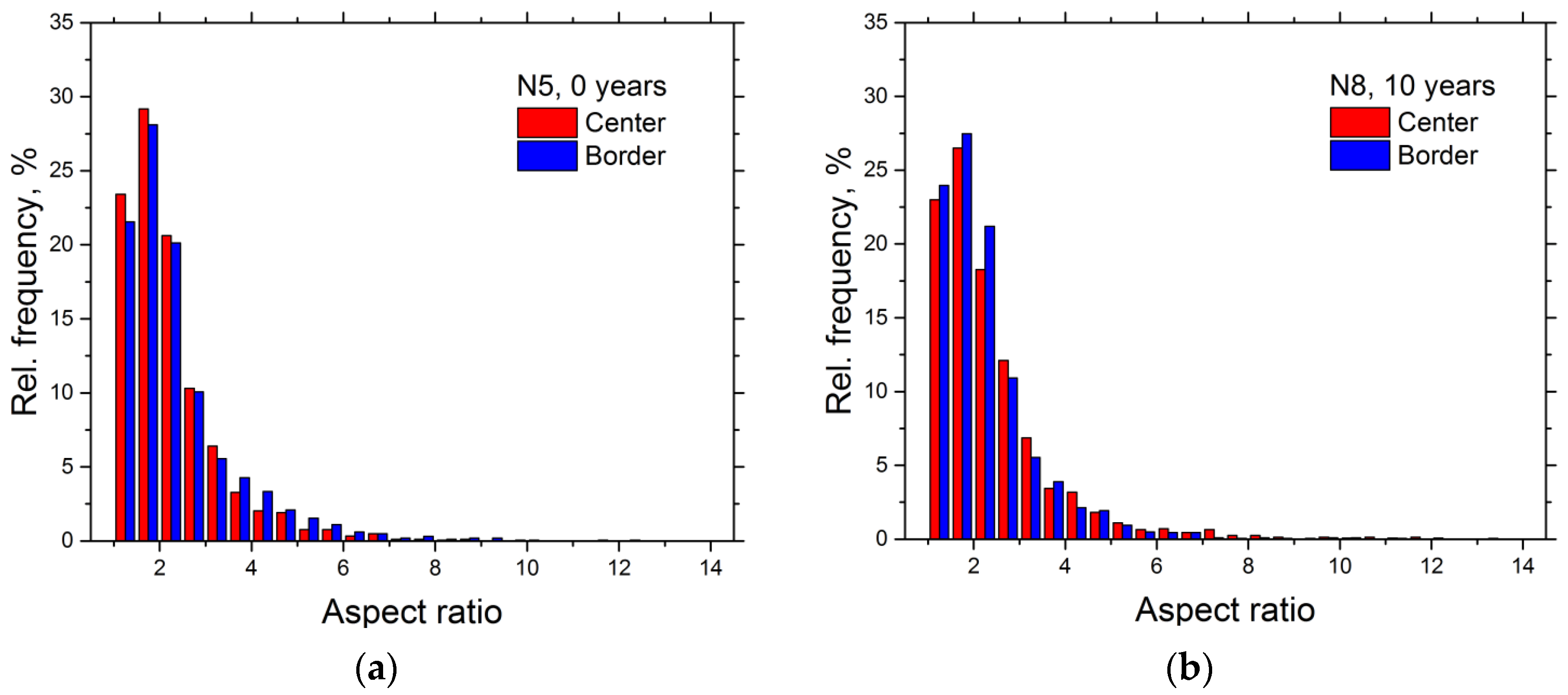
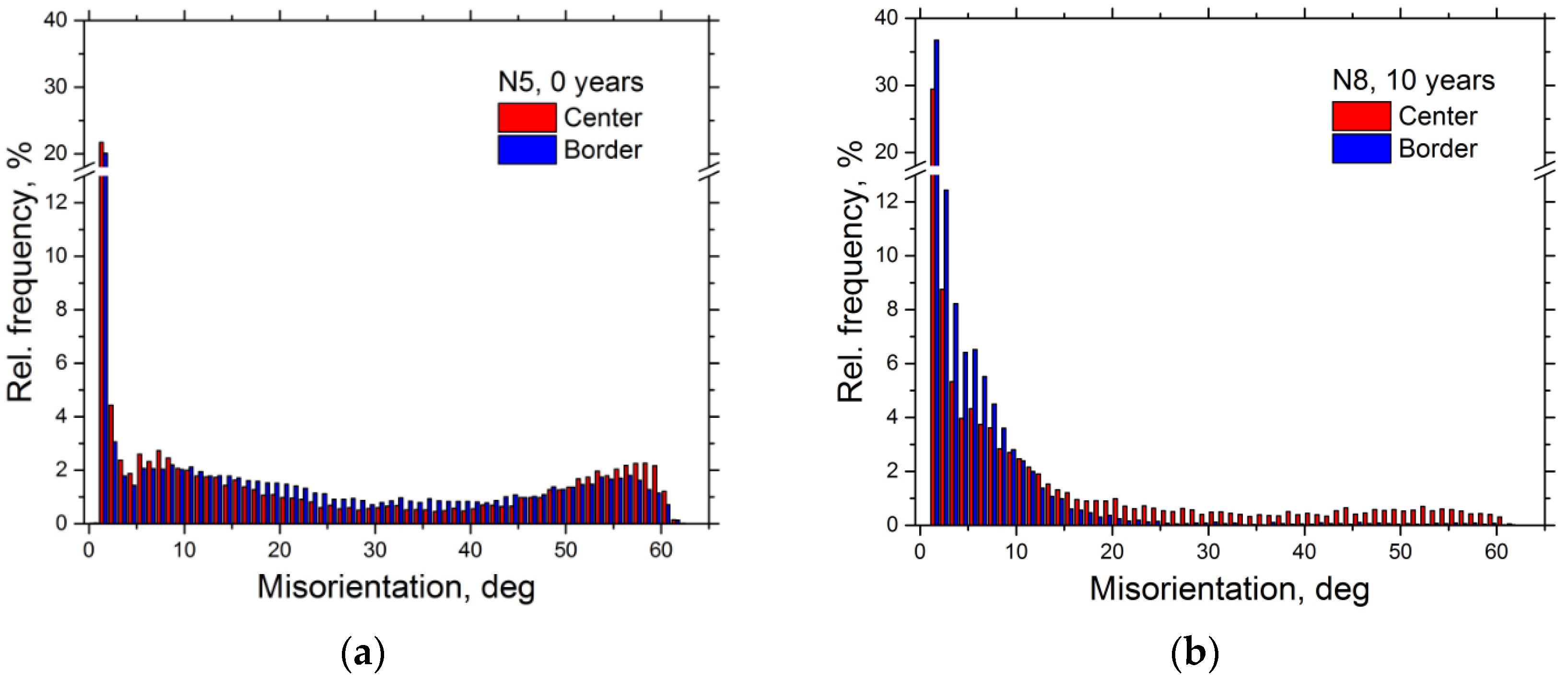
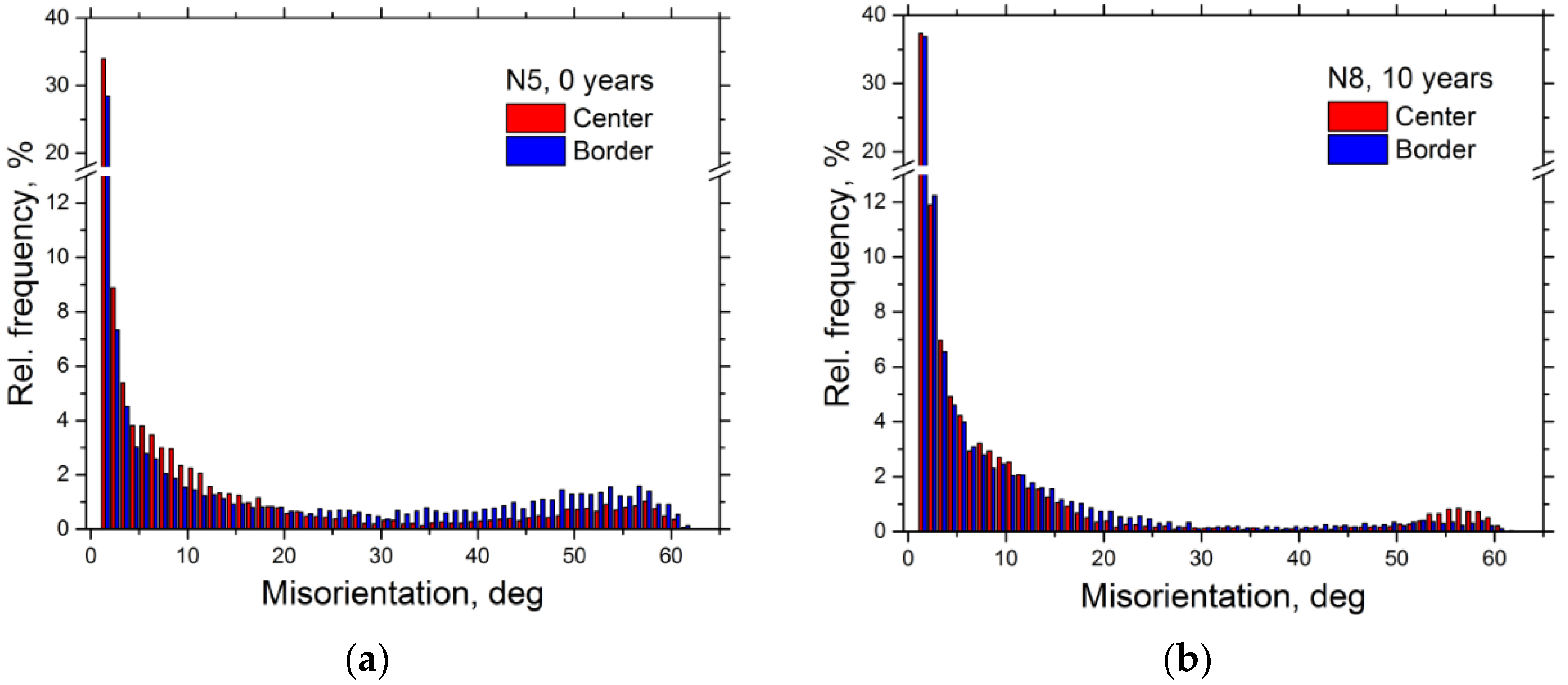
3.3. EBSD Results
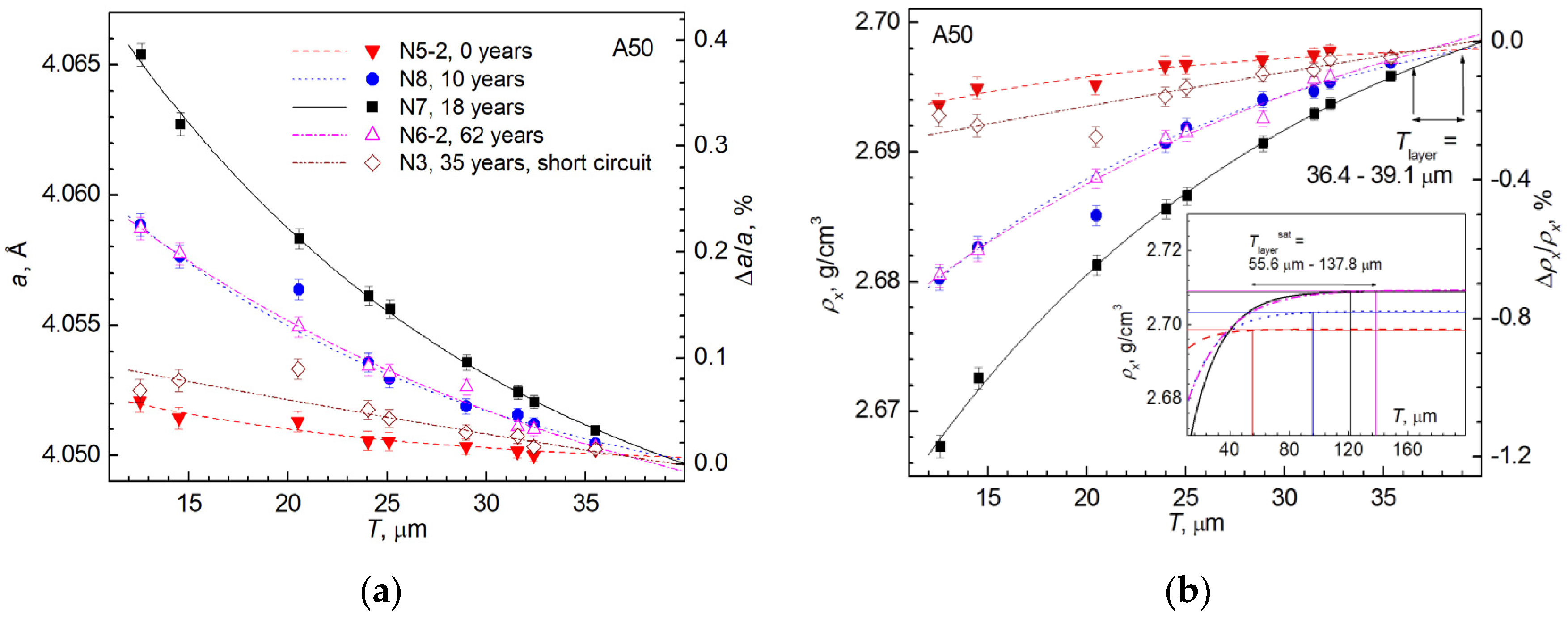
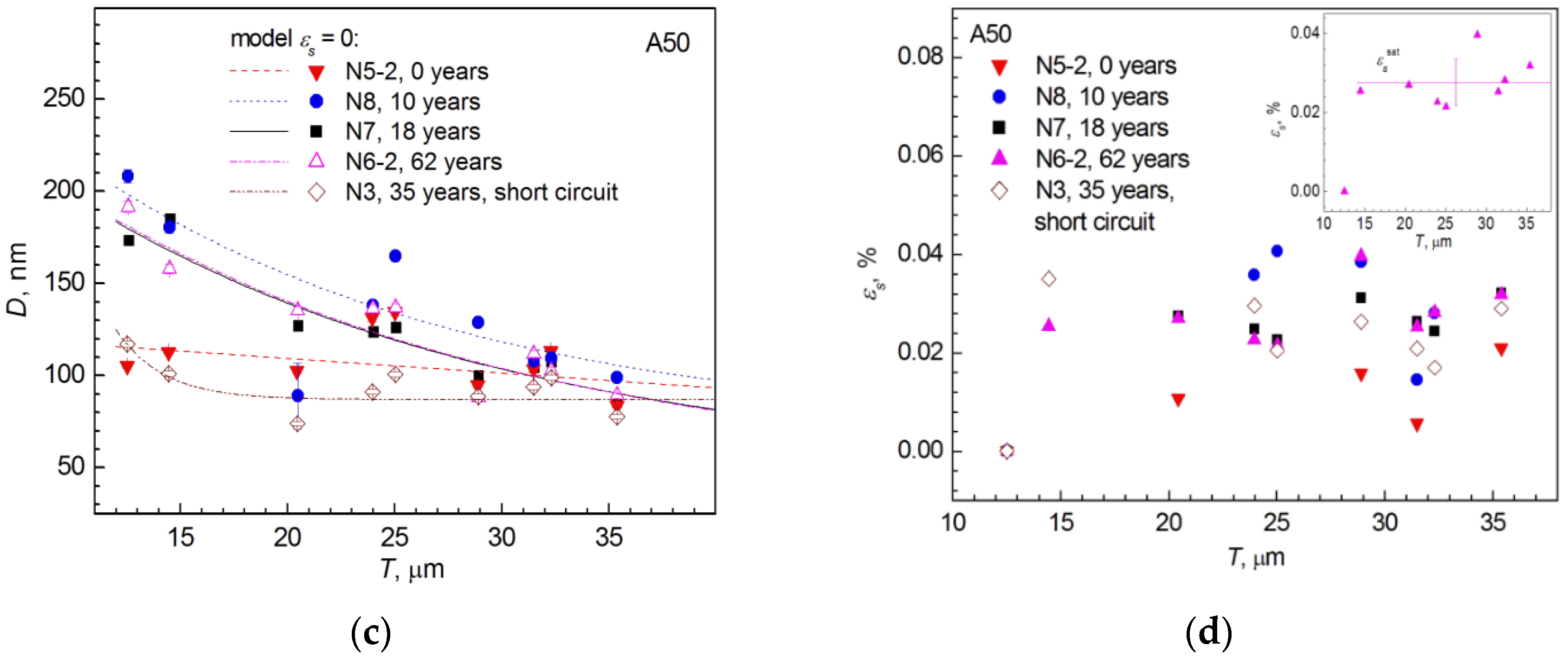
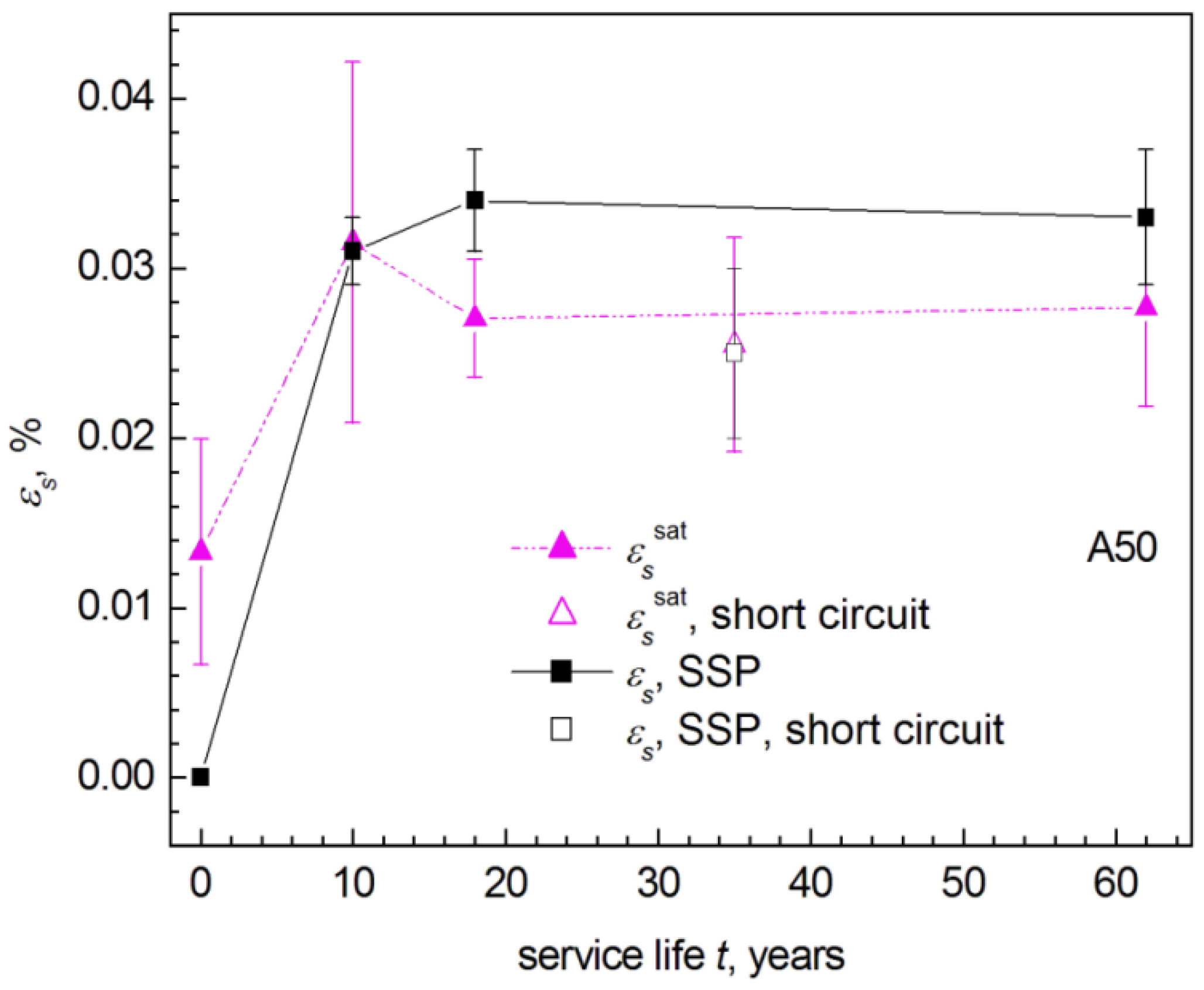
3.4. XRD Results
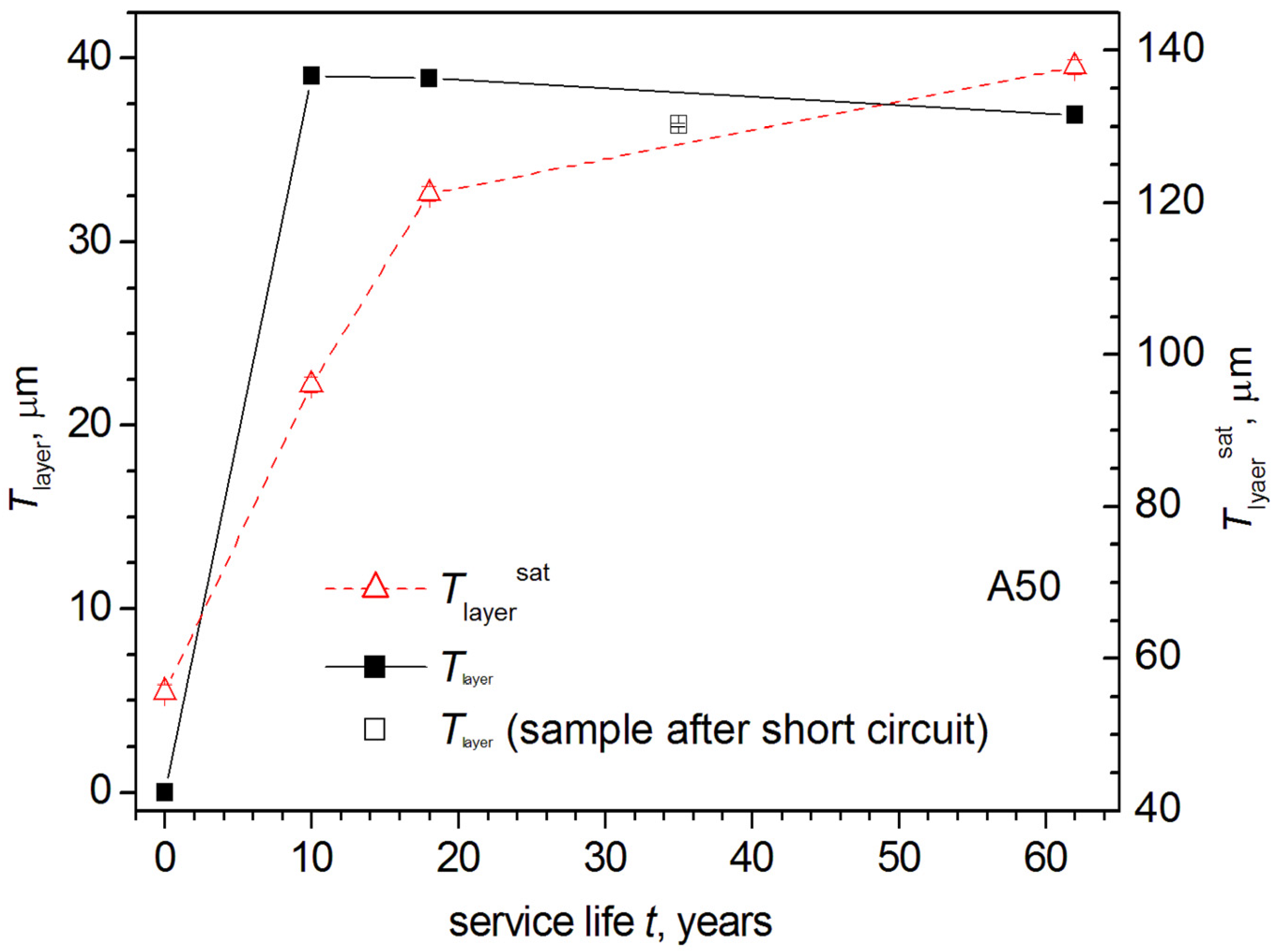
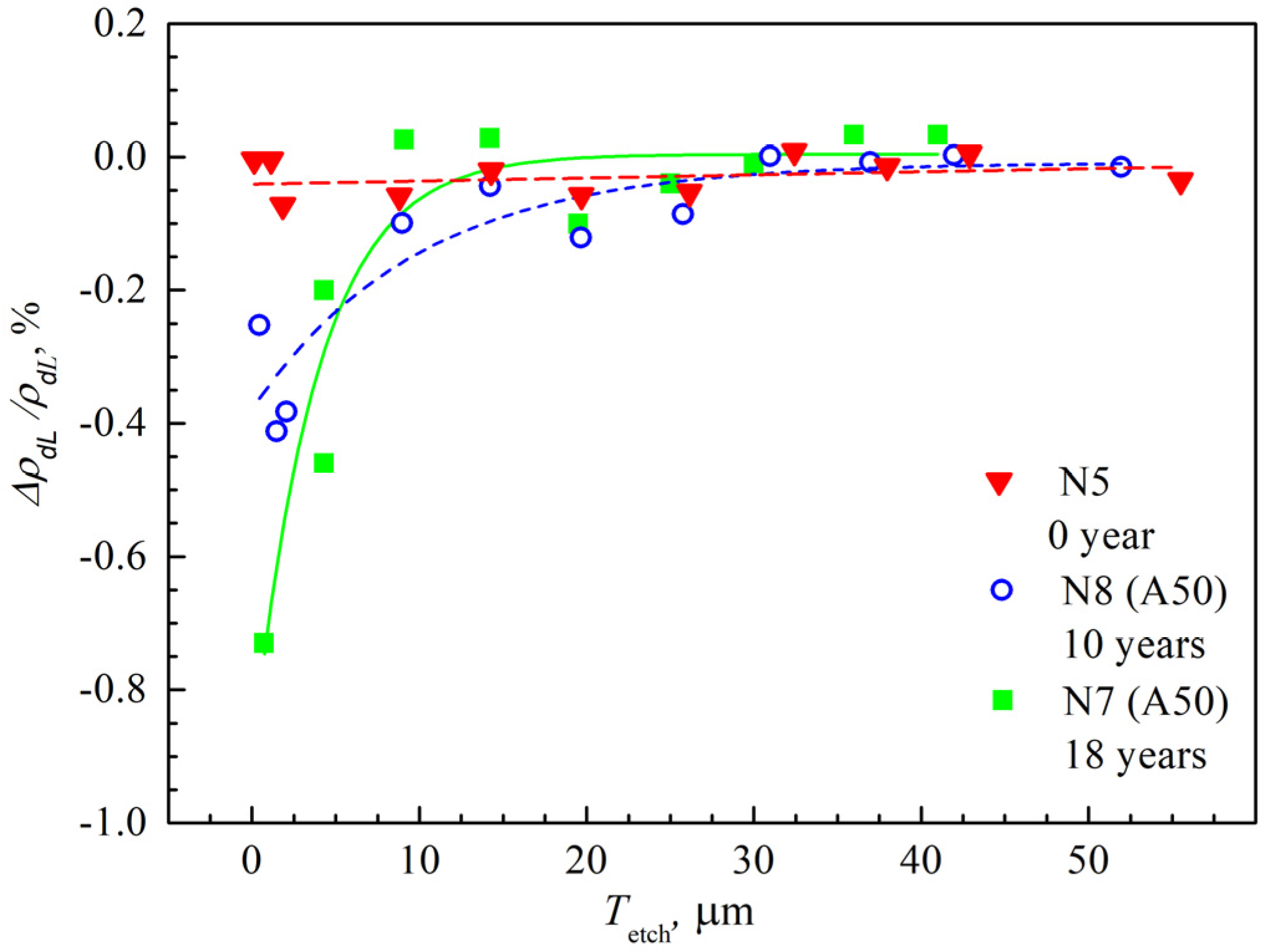
3.5. Results of Densitometric Measurements
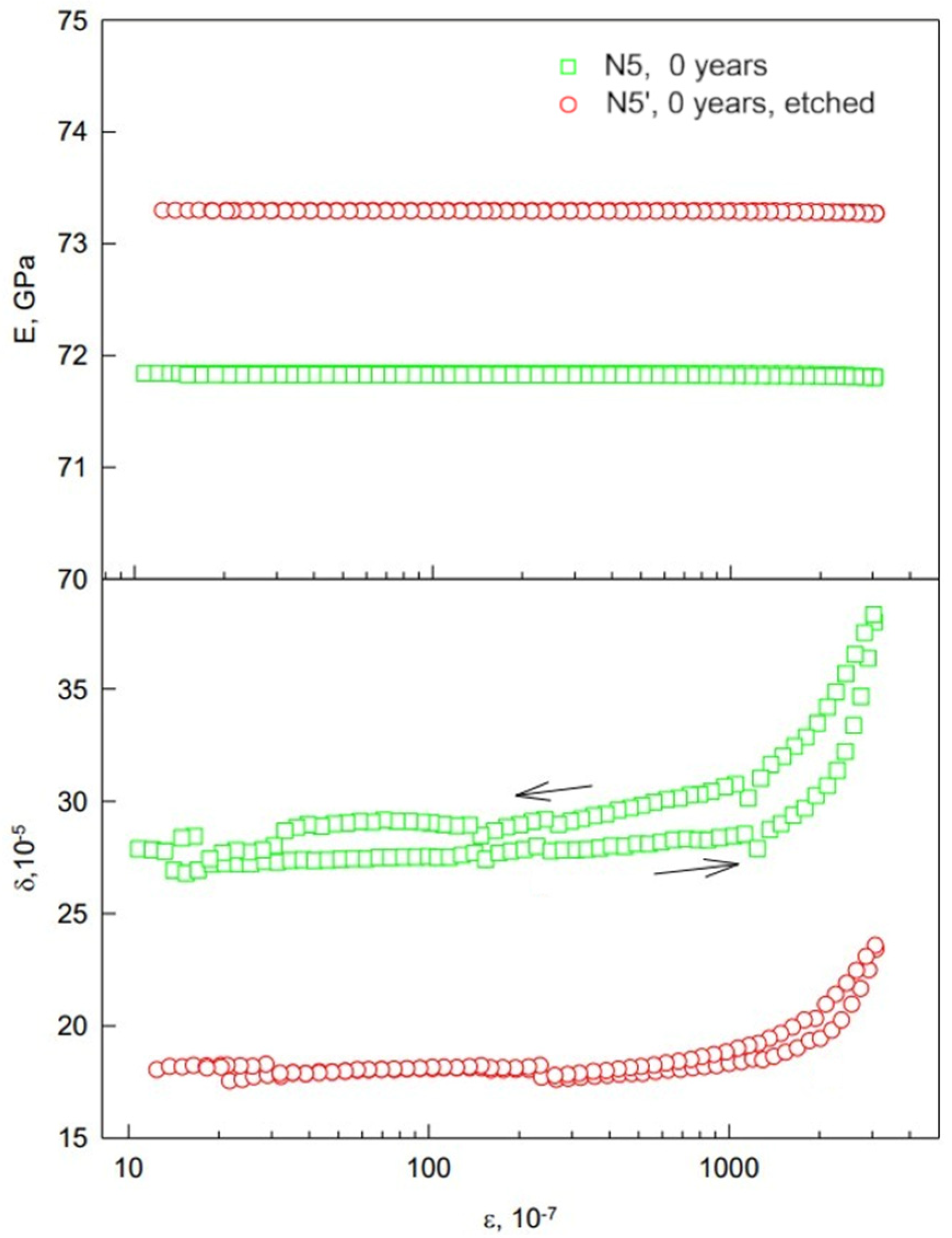
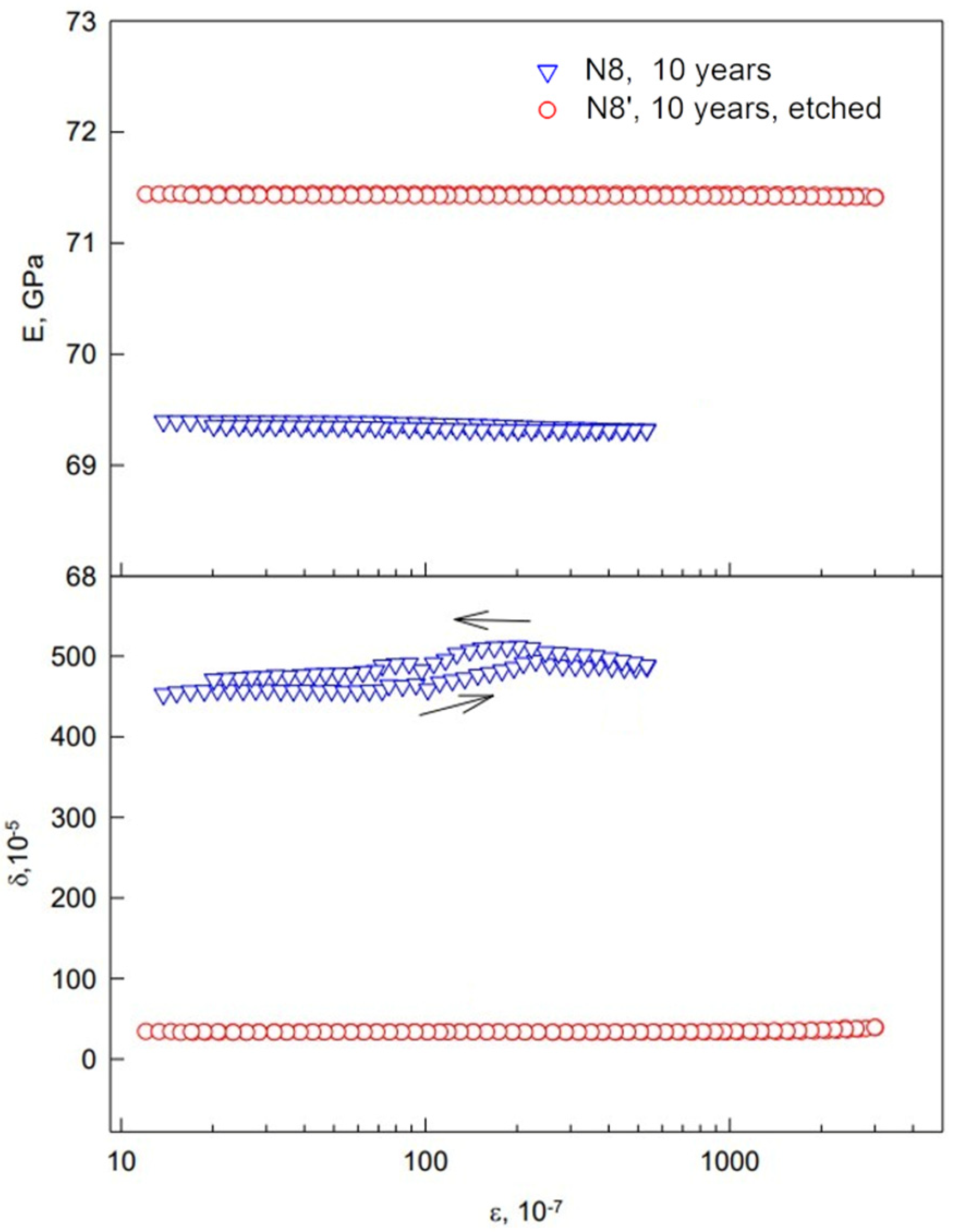
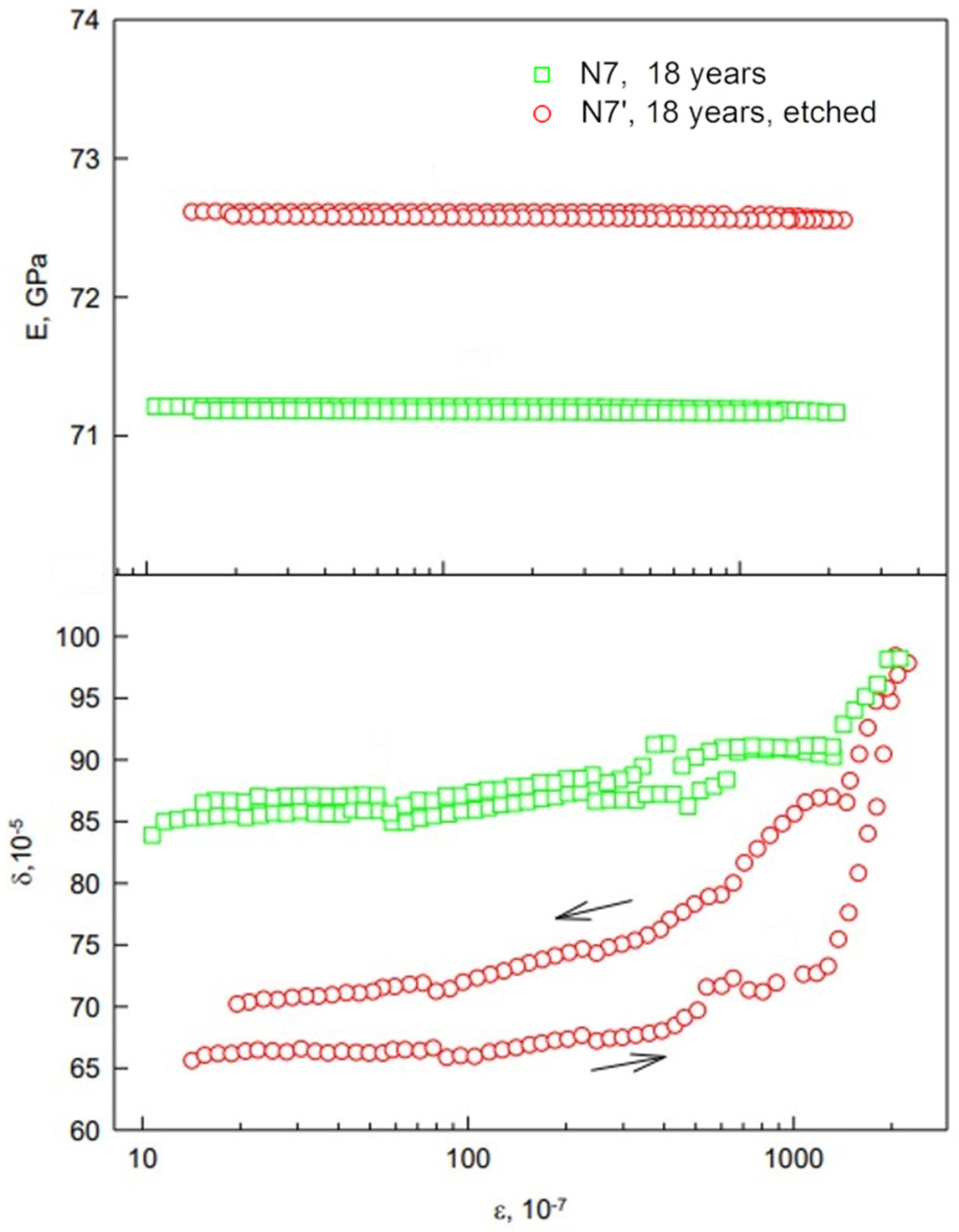
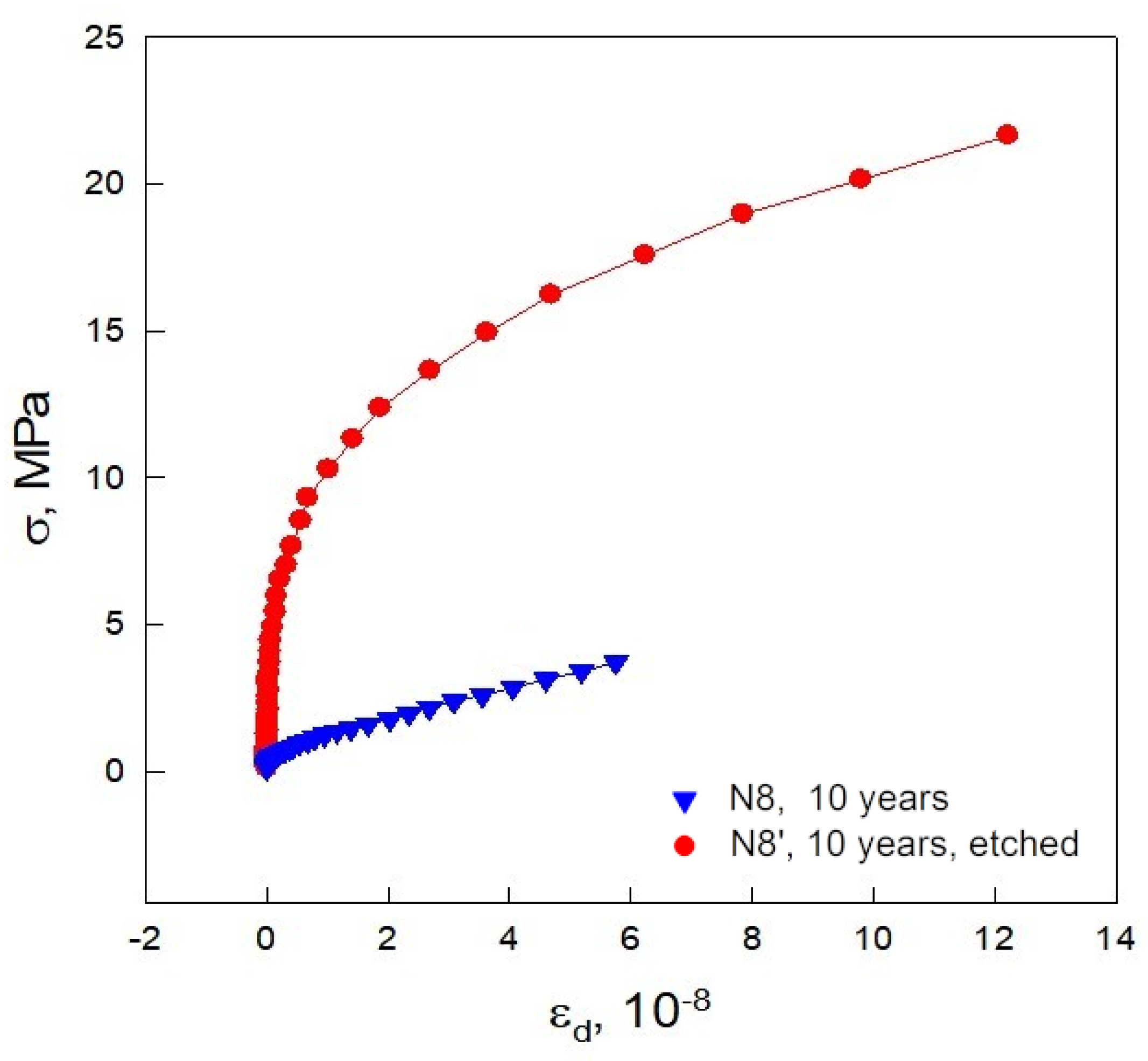
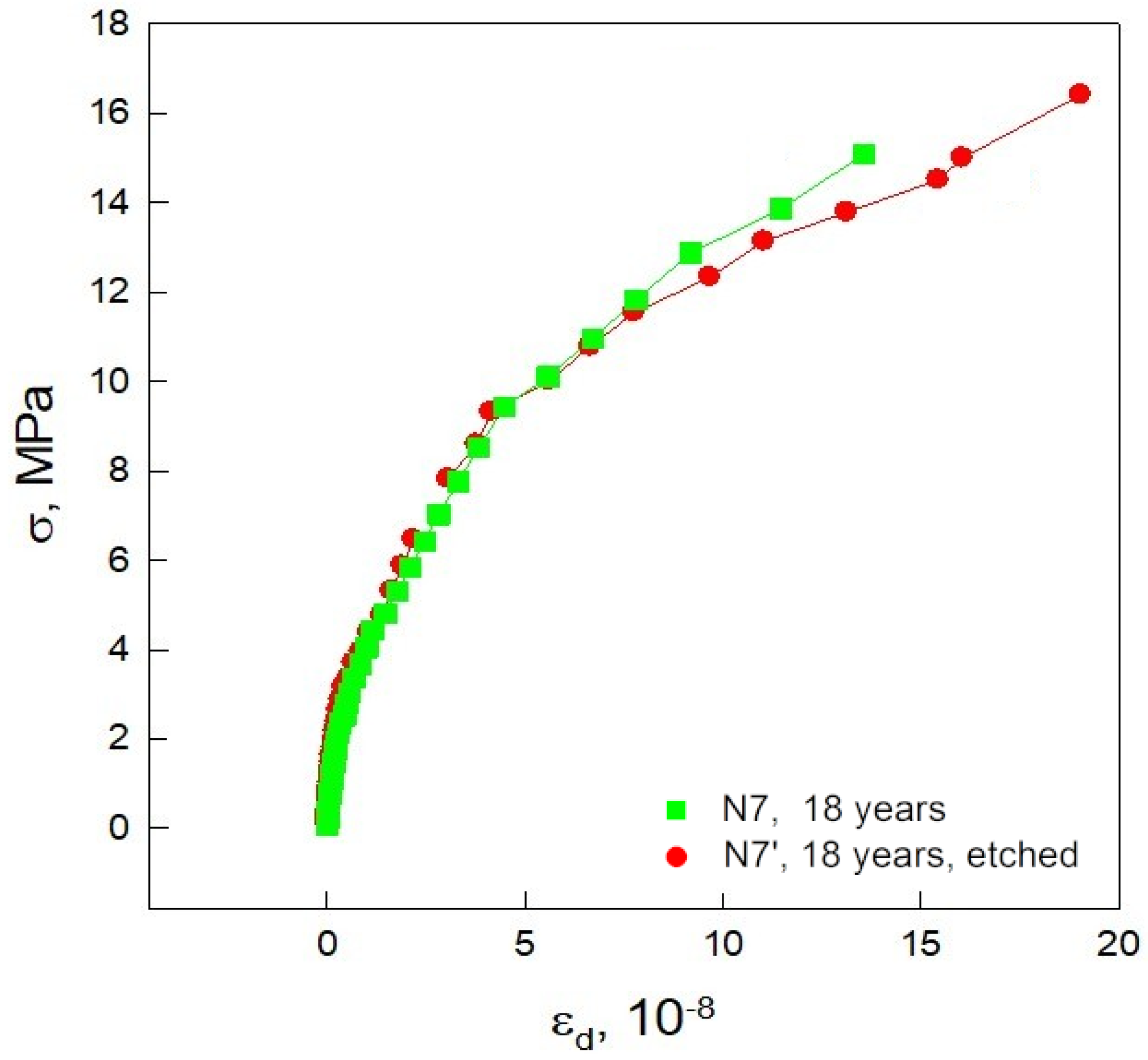
3.6. Changes of Elastic and Microplastic Properties of Wires after Etching
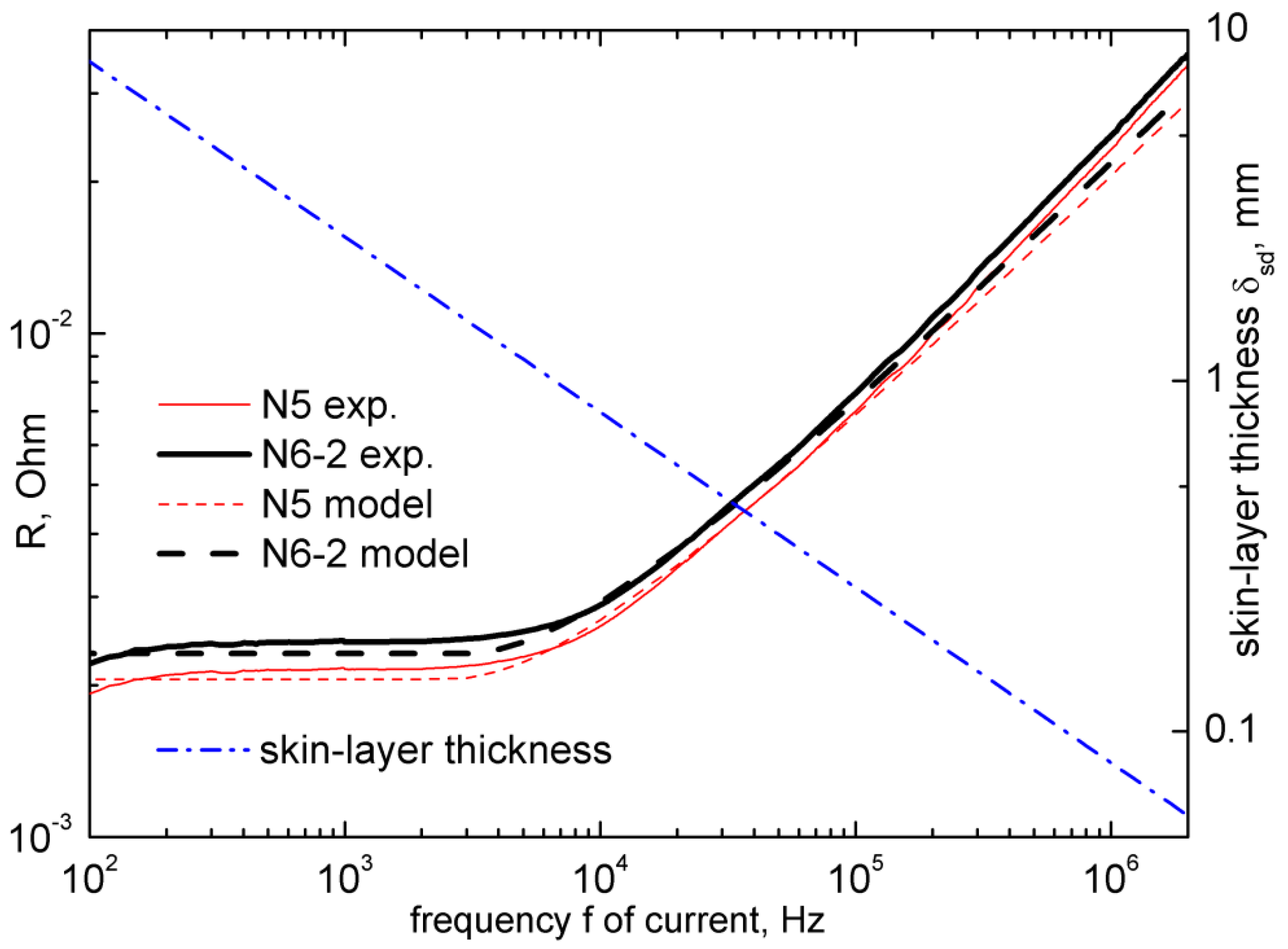
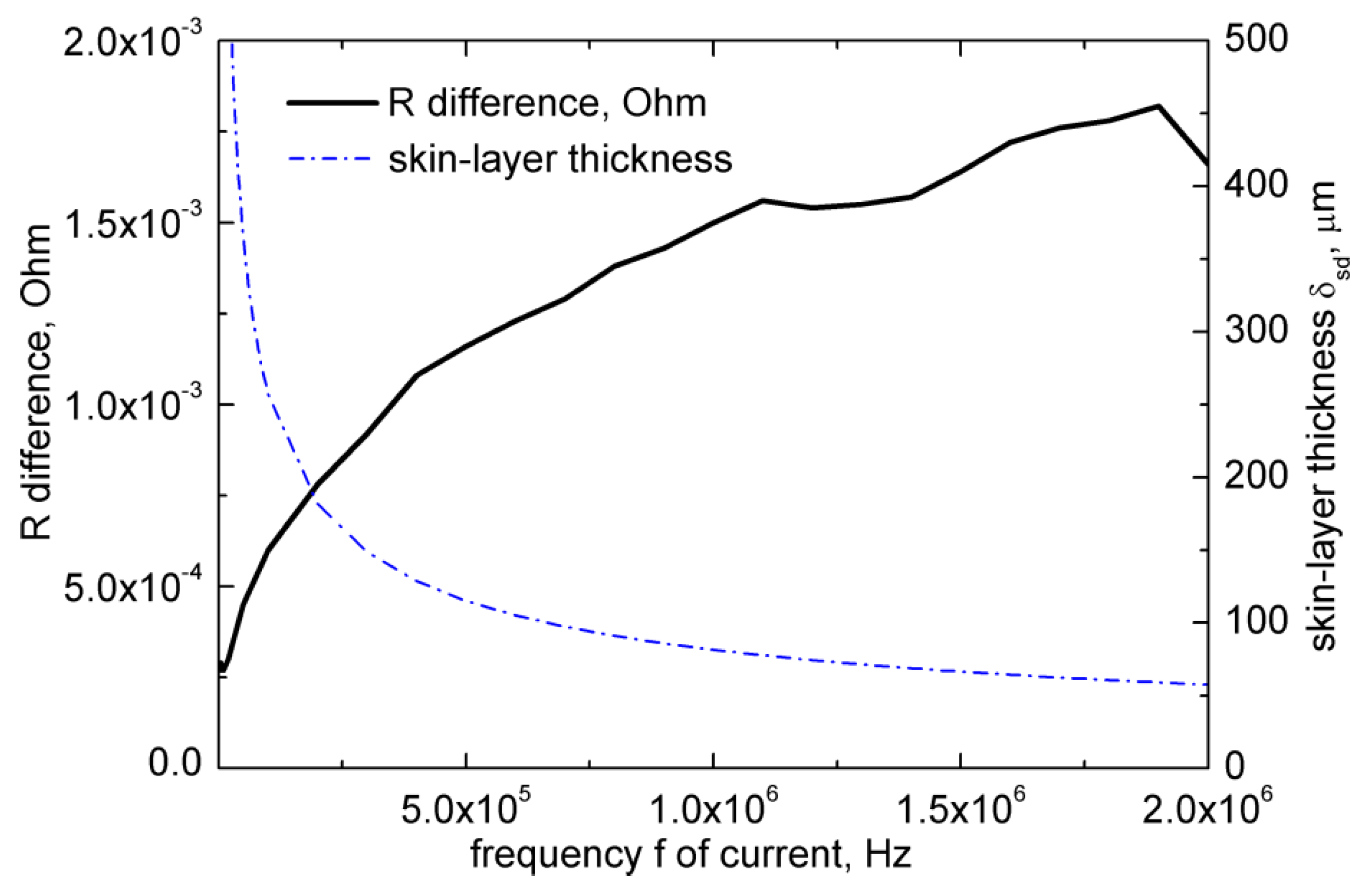
3.7. Results of Electroresistance Analysis
4. Discussion of Results
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AAAC | All Aluminum Alloy Conductor |
| ACSR | Aluminum Conductor Steel Reinforced |
| a.m.u. | atomic mass unit |
| CSAs | coherent scattering areas |
| EBSD | electron backscattering diffraction |
| EDX, EDS | energy-dispersive X-ray microanalysis |
| e.s.d., e.s.d.s. | estimated standard deviation(s) |
| FWHM | full width at half-maximum of XRD reflection |
| NSDL, NSDLs | defect near-surface layer(s) |
| OM | optical Microscopy |
| PDF-2 | Powder Diffraction File-2 |
| pV | pseudo-Voigt |
| SEM | scanning electron microscopy |
| SSP | size-strain plot |
| WHP | Williamson-Hall plot |
| XLPE | cross-linked polyethylene |
| XRD | X-ray diffraction |
| i.e., | Latin “id est” |
| etc. | Latin “et cetera” |
| cf. | Latin “confer” |
| 2θ | diffraction angle |
| 2θB | Bragg angle of XRD reflection corrected to angular corrections(zero shift and displacement) |
| 2θBobs | observed Bragg andgle of XRD reflection |
| Ar | tabular value of the atomic mass of aluminium |
| a | cubic unit cell parameter |
| a0 | parameter of the Al cubic unit cell in the bulk of a new (0 years of service) sample |
| asat | cubic-unit cell parameter of Al material at a depth of Tlayersat |
| Bint | integral width of XRD reflection |
| Ca.m.u. | conversion factor of a.m.u. into gram |
| D | average size of crystallites |
| Dεs=0 | mean crystllite size calculated in frame of zero microstrain (εs = 0) model |
| E | Young’s modulus (modulus of elasticity) |
| Ei | Young’s modulus in the amplitude-independent region |
| e | Euler’s number |
| FWHMcorr | FWHMobs corrected for the instrumental broadening |
| FWHMinstr | instrumental broadening |
| FWHMobs | observed full width at half-maximum of XRD reflection |
| FWHMsize | broadening of reflections due to the size effect of crystallites |
| FWHMstrain | broadening due to absolute value of microstrain in the crystallite |
| f | alternating-current frequency |
| hkl | Miller indices |
| KScherrer | coefficient in Scherrer equation |
| Kstrain | coefficient in Wilson-Stokes equation |
| I | moment of inertia of the sample section |
| Imax | maximum intensity of XRD reflection |
| Imin | integral intensity of XRD reflection |
| l | sample length |
| m | sample mass |
| m0 | mass of the sample before polishing (etching) |
| m1 | mass of piezoelectric quartz |
| mi | mass of the sample after polishing of the ith layer |
| n | number of harmonics of longitudinal vibrations |
| R | resistance of the conductor |
| r0, r | radius of the sample (without polishing (etching)) |
| S | sample cross-section |
| T | depth from the wire surface |
| Tetch | thickness of the layer removed by polishing (etching) |
| Tl | thickness of the modified (defect) NSL in resistance modeling |
| Tlayer | layer thickness corresponding to depth where ~70% of the decrease in the mass density ρx occurs in comparison to the ρx200μm value |
| Tlayersat | layer thickness corresponding to depth where ~99% of the decrease in the mass density ρx occurs in comparison to the ρx200μm value |
| Tosc | oscillation period |
| Tpen | penetration depth of X-ray radiation |
| penetration depth of X-ray radiation, corresponding to XRD reflection with Miller indices hkl | |
| vcor | corrosion (defect layer growth) rate |
| Z | number of formula units in the Al unit cell |
| γ | conductivity of the conductor |
| Δ2θdispl | displacement correction |
| Δ2θzero | correcting shift of the zero of the counter |
| Δa/a | defect (relative change) of the unit cell parameter |
| (ΔE/E)h | amplitude-dependent Young’s modulus defect (amplitude-dependent variation of E) |
| Δρd/ρd | defect (relative change) of the mass density ρd |
| ΔρdL/ρdL | density-defect value of the etched layer |
| Δρx/ρx | defect (relative change) of the mass density ρx |
| δ | logarithmic decrement of the sample material |
| δ1 | logarithmic decrement of the piezoelectric quartz |
| δ2 | logarithmic decrement of the piezoquartz-sample system |
| δh | amplitude-dependent part of the logarithmic decrement |
| δi | amplitude-independent part of the logarithmic decrement |
| δsd | depth of skin-layer |
| ε | vibrational strain amplitude |
| εd | non-linear inelastic strain |
| εs | absolute value of average magnitude of microstrains |
| εssat | average microstrain εssat in the NSL at depths T ≥ 15 μm, if the crystallite size is fixed and equal to the crystallite size at a depth of T~12 μm |
| θ | half a diffraction angle |
| λ | wavelength |
| μ | magnetic permeability of the conductor material |
| μ0 | magnetic permeability of physical vacuum |
| μl | the mass absorption coefficient of material |
| μr | relative magnetic permeability of the conductor material |
| μP | Poisson’s ratio of the sample material |
| ν1 | frequency of the piezoelectric quartz |
| ν2 | frequency of the piezoquartz-sample system |
| νl | individual frequency of longitudinal vibrations of the rod |
| ρ | electrical resistivity of the conductor |
| ρAl | electrical resistivity of the aluminium |
| ρd | mass density of material measured by densitometry technique |
| ρd0 | density of the sample before polishing (etching) measured by densitometry technique |
| ρdi | density of the sample after polishing (etching) of the ith layer measured by densitometry technique |
| ρdL | mass density of the etched layer obtained by densitometry technique |
| ρl | resistivity of the modified (defect) NSL |
| ρx | mass density of material calculated according to XRD structural data (XRD mass density) |
| ρx200μm | XRD mass density at depth of 200 μm from the surface estimated from the dependence ρx(T) asscording to exponetial decay law with negative multipier before exponent functiom |
| ρx500μm | same as ρx200μm but for 500 μm depth from the surface |
| ρxlayer | XRD mass density of Al material at a depth of Tlayer |
| ρxsat | XRD mass density of Al material at a depth of Tlayersat |
| ρx0 | XRD density in the bulk of the new (0 years of service) sample |
| σ | amplitude of vibrational stress |
| σs | microplastic flow stress (micro-flow stress) σs, equal to σ at inelastic strain εd = 5.0 × 10−8. |
| Φ | second Euler angle (angle of nutation) |
| φ1 | first Euler angle (angle of intrinsic rotation) |
| φ2 | third Euler angle (angle of precession) |
| ω | angular frequency of alternating current |
References
- Papailiou, K.O. (Ed.) Overhead Lines. In Handbook of Power Systems; Springer: Singapore, 2020; pp. 611–758. [Google Scholar] [CrossRef]
- Shahid, M.A.; Khan, T.M.; Zafar, Z.; Hashmi, M.F.; Imran, M. Health diagnosis scheme for in-service low voltage Aerial Bundled Cables using super-heterodyned airborne Ultrasonic testing. Electr. Power Syst. Res. 2020, 180, 106162. [Google Scholar] [CrossRef]
- Kalombo, R.B.; Martínez, J.M.G.; Ferreira, J.L.A.; da Silva, C.R.M.; Araújo, J.A. Comparative fatigue resistance of overhead conductors made of aluminium and aluminium alloy: Tests and analysis. Proc. Eng. 2015, 133, 223–232. [Google Scholar] [CrossRef] [Green Version]
- Araujo, M.M.; Manheimmer, W.A.; Serra, E. Corrosion aspects in aluminum electrical conductors. Mater. Sci. 1988, 8, 175–197. [Google Scholar] [CrossRef]
- Karabay, S.; Feyzullahoğlu, E. Determination of early failure sources and mechanisms for Al 99.7% and Al–Mg–Si alloy bare conductors used in aerial transmission lines. Eng. Fail. Anal. 2014, 38, 1–15. [Google Scholar] [CrossRef]
- Karabay, S.; Ertürk, A.T.; Zeren, M.; Yamanoğlu, R.; Karakulak, E. Failure analysis of wire-breaks in aluminum conductor production and investigation of early failure reasons for transmission lines. Eng. Fail. Anal. 2018, 83, 47–56. [Google Scholar] [CrossRef]
- Azevedo, C.R.F.; Cescon, T. Failure analysis of aluminum cable steel reinforced (ACSR) conductor of the transmission line crossing the Paraná River. Eng. Fail. Anal. 2002, 9, 645–664. [Google Scholar] [CrossRef]
- Kreislova, K.; Jaglova, M.; Turek, L.; Koukalova, A. Evaluation of corrosion of long-term exposed aluminium conductor. Koroze Ochr. Mater. 2013, 57, 25–34. [Google Scholar] [CrossRef] [Green Version]
- Levin, A.A.; Narykova, M.V.; Lihachev, A.I.; Kardashev, B.K.; Kadomtsev, A.G.; Brunkov, P.N.; Panfilov, A.G.; Prasolov, N.D.; Sultanov, M.M.; Kuryanov, V.N.; et al. Modification of the structural, microstructural, and elastoplastic properties of aluminum wires after operation. Metals 2021, 11, 1955. [Google Scholar] [CrossRef]
- Fuente, D.; Otero-Huerta, E.; Morcillo, M. Studies of long-term weathering of aluminium in the atmosphere. Corros. Sci. 2007, 49, 3134–3148. [Google Scholar] [CrossRef]
- Yamanaka, S.; Fukuda, T.; Ito, K.; Tomita, J.; Seguchi, T. Use of Residual Voltage for Diagnosis of Electric Power Cables Used in Nuclear Power Stations. Electr. Eng. Jpn. 1997, 119, 18–24. [Google Scholar] [CrossRef]
- Humpert, C. Long distance transmission systems for the future electricity supply—Analysis of possibilities and restrictions. Energy 2012, 48, 278–283. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, T. Fault location for overhead and cable hybrid transmission lines based on the difference quantities of forward propagating waves and backward propagating waves in HVDC systems. Electr. Power Syst. Res. 2022, 203, 107642. [Google Scholar] [CrossRef]
- Han, L.; Zhang, Y.; Li, X.; Jiang, L.; Chen, D. Galloping Reduction of Transmission Lines by Using Phononic Crystal. Crystals 2017, 7, 346. [Google Scholar] [CrossRef] [Green Version]
- Brettschneider, S.; Fofana, I. Evolution of Countermeasures against Atmospheric Icing of Power Lines over the Past Four Decades and Their Applications into Field Operations. Energies 2021, 14, 6291. [Google Scholar] [CrossRef]
- Lu, J.; Hu, J.; Fang, Z.; Qiao, X.; Zhang, Z. Electric Field Distribution and AC Breakdown Characteristics of Polluted Novel Lightning Protection Insulator under Icing Conditions. Energies 2021, 14, 7493. [Google Scholar] [CrossRef]
- Stracqualursi, E.; Araneo, R.; Celozzi, S. The Corona Phenomenon in Overhead Lines: Critical Overview of Most Common and Reliable Available Models. Energies 2021, 14, 6612. [Google Scholar] [CrossRef]
- Kul’kov, V.G.; Sultanov, M.M.; Kuryanov, V.N.; Norov, D.S. Electrical reliability simulation based on analysis of fatigue strength of overhead line wires. In Proceedings of the International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE), Moscow, Russia, 11–13 March 2021. [Google Scholar] [CrossRef]
- Alshwawreh, N.; Alhamarneh, B.; Altwarah, Q.; Quandour, S.; Barghout, S.; Ayasrah, O. Electrical Resistivity and Tensile Strength Relationship in Heat-Treated All Aluminum Alloy Wire Conductors. Materials 2021, 14, 5738. [Google Scholar] [CrossRef]
- Xu, X.; Yu, Z.; Li, Y.; Wang, W.; Xu, L. Microstructural Study of Arc Beads in Aluminum Alloy Wires with an Overcurrent Fault. Materials 2021, 14, 4133. [Google Scholar] [CrossRef]
- Diffrac. Suite Eva Version 5.1.0.5, Brucker AXS, Karlsruhe, Germany. 2019. Available online: https://www.bruker.com/en/products-and-solutions/diffractometers-and-scattering-systems/x-ray-diffractometers/diffrac-suite-software/diffrac-eva.html (accessed on 28 December 2021).
- Fawcett, T.G.; Kabekkodu, S.N.; Blanton, J.R.; Blanton, T.N. Chemical analysis by diffraction: The Powder Diffraction File™. Powder Diffr. 2017, 32, 63–71. [Google Scholar] [CrossRef]
- Topas Version 5, Technical reference. Brucker AXS, Karlsruhe, Germany. 2014. Available online: https://www.bruker.com/en/products-and-solutions/diffractometers-and-scattering-systems/x-ray-diffractometers/diffrac-suite-software/diffrac-topas.html (accessed on 28 December 2021).
- O’Connor, B.H.; Li, D.Y.; Hunter, B.A. The importance of the specimen displacement correction in Rietveld pattern fitting with symmetric reflection-optics diffraction data. Adv. X-ray Anal. 2001, 44, 96–102. [Google Scholar]
- Welzel, U.; Ligot, J.; Lamparter, P.; Vermeulen, A.C.; Mittemeijer, E.J. Stress analysis of polycrystalline thin films and surface regions by X-ray diffraction. J. Appl. Crystallogr. 2005, 38, 1–29. [Google Scholar] [CrossRef]
- Terlan, B.; Levin, A.A.; Börrnert, F.; Simon, F.; Oschatz, M.; Schmidt, M.; Cardoso-Gil, R.; Lorenz, T.; Baburin, I.A.; Joswig, J.-O.; et al. Effect of Surface Properties on the Microstructure, Thermal, and Colloidal Stability of VB2 Nanoparticles. Chem. Mater. 2015, 27, 5106–5115. [Google Scholar] [CrossRef]
- Terlan, B.; Levin, A.A.; Börrnert, F.; Zeisner, J.; Kataev, V.; Schmidt, M.; Eychmüller, A. A Size-Dependent Analysis of the Structural, Surface, Colloidal, and Thermal Properties of Ti1−xB2 (x = 0.03 − 0.08) Nanoparticles. Eur. J. Inorg. Chem. 2016, 2016, 3460–3468. [Google Scholar] [CrossRef]
- Langford, J.I. A Rapid Method for Analysing the Breadths of Diffraction and Spectral Lines using the Voigt Function. J. Appl. Cryst. 1978, 11, 10–14. [Google Scholar] [CrossRef]
- Scherrer, P. Bestimmung der Grösse und der inneren Struktur von Kolloidteilchen mittels Röntgenstrahlen. Nachr. Königl. Ges. Wiss. Göttingen. 1918, 26, 98–100. (In German) [Google Scholar]
- Rehani, B.R.; Joshi, P.B.; Lad, K.N.; Pratap, A. Crystallite size estimation of elemental and composite silver nano-powders using XRD principles. Indian J. Pure Appl. Phys. 2006, 44, 157–161. [Google Scholar]
- Halder, N.C.; Wagner, C.N.J. Separation of particle size and lattice strain in integral breadth measurements. Acta Cryst. 1966, 20, 312–313. [Google Scholar] [CrossRef]
- Stokes, A.R.; Wilson, A.J.C. The diffraction of X-rays by distorted crystal aggregates. Proc. Phys. Soc. 1944, 56, 174–181. [Google Scholar] [CrossRef]
- Nikanorov, S.P.; Kardashev, B.K. Elasticity and Dislocation Inelasticity of Crystals; Nauka: Moscow, Russia, 1985; p. 254. (In Russian) [Google Scholar]
- Chernov, V.M.; Kardashev, B.K.; Krjukova, L.M.; Mamaev, L.I.; Plaksin, O.A.; Rusanov, A.E.; Solonin, M.I.; Stepanov, V.A.; Votinov, S.N.; Zavialski, L.P. Internal friction and anelastic properties of vanadium and V ̶ Ti ̶ Cr alloys. J. Nucl. Mater. 1998, 257, 263–273. [Google Scholar] [CrossRef]
- Faria, J.A.M.B.; Raven, M.S. On the success of electromagnetic analytical approaches to full time-domain formulation of skin effect phenomena. Progr. Electromagn. Res. M 2013, 31, 29–43. [Google Scholar] [CrossRef] [Green Version]
- Raven, M.S. Experimental measurements of the skin effect and internal inductance at low frequencies. Acta Tech. 2015, 60, 51–69. [Google Scholar]
- Wyslouch, B.; Wecht, B.; Knuteson, B.; Katsavounidis, E.; Roland, R.; Belcher, J.; Formaggio, J.; Dourmashkin, P.; Simcoe, R. Chapter 6. Current and Resistance. In 8.02 Physics II: Electricity and Magnetism; Spring 2007; MIT Open Course Ware, Massachusetts Institute of Technology: Cambridge, MA, USA, 2007. [Google Scholar]
- Mason, J.K.; Schuh, C.A. Representation of Texture. In Electron Backscatter Diffraction in Material Science, 2nd ed.; Schwartz, A.I., Kumar, M., Adams, B.L., Field, D.P., Eds.; Springer: Boston, MA, USA, 2009; pp. 45–46. [Google Scholar] [CrossRef]
- ·Tsybulya, S.; Kryukova, G. New X-ray powder diffraction data on δ-Al2O3. Powder Diffr. 2003, 18, 309–311. [Google Scholar] [CrossRef]
- Fargeot, D.; Mercurio, D.; Dauger, A. Structural characterization of alumina metastable phases in plasma sprayed deposits. Mater. Chem. Phys. 1990, 24, 299. [Google Scholar] [CrossRef]
- Chaim, R.; Hefetz, M. Effect of grain size on elastic modulus and hardness of nanocrystalline ZrO2-3 wt.% Y2O3 ceramic. J. Mater. Sci. 2004, 39, 3057–3061. [Google Scholar] [CrossRef]
- Kardashev, B.K.; Betekhtin, V.I.; Narykova, M.V. Elastoplastic properties of micro and submicrocrystalline metals and alloys. Tech. Phys. 2015, 60, 1829–1841. [Google Scholar] [CrossRef]
- Gremaud, G. Dislocation—Point defect interactions. Mat. Sci. Forum. 2001, 366–368, 178–246. [Google Scholar] [CrossRef]
- Jurkiewicz, B.; Smyrak, B.; Zasadzińska, M.; Franczak, K.; Strzępek, P. The researches of influence of strengthening on fatigue strength of aluminium wires for OHL conductors. Arch. Civ. Mech. Eng. 2019, 19, 862–870. [Google Scholar] [CrossRef]
- Gourdet, S.; Montheillet, F. A Model of Continuous Dynamic Recrystallization. Acta Mater. 2003, 51, 2685–2699. [Google Scholar] [CrossRef]









| Sample N | Type | Service Life, Years | Damage |
|---|---|---|---|
| 5-2 | A50 | 0 | No |
| 5 | AC50 | 0 | No |
| 8 | A50 | 10 | No |
| 7 | A50 | 18 | No |
| 3 | A50 | 35 | After short circuit |
| 6-2 | A50 | 62 | No |
| Sample N | Service Life t, Years | ρd, g/cm3 | E, GPa | δi, 10−5 | σs, MPa |
|---|---|---|---|---|---|
| 5 | 0 | 2.6949 | 71.8 | 27 | 16.2 |
| 5′ | 0 | 73.2 | 17 | 17.1 | |
| 8 | 10 | 2.6906 | 69.4 | 457 | 3.3 |
| 8′ | 10 | 71.4 | 40 | 16.4 | |
| 7 | 18 | 2.6905 | 71.2 | 85 | 9.8 |
| 7′ | 18 | 72.4 | 68 | 9.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Narykova, M.V.; Levin, A.A.; Prasolov, N.D.; Lihachev, A.I.; Kardashev, B.K.; Kadomtsev, A.G.; Panfilov, A.G.; Sokolov, R.V.; Brunkov, P.N.; Sultanov, M.M.; et al. The Structure of the Near-Surface Layer of the AAAC Overhead Power Line Wires after Operation and Its Effect on Their Elastic, Microplastic, and Electroresistance Properties. Crystals 2022, 12, 166. https://doi.org/10.3390/cryst12020166
Narykova MV, Levin AA, Prasolov ND, Lihachev AI, Kardashev BK, Kadomtsev AG, Panfilov AG, Sokolov RV, Brunkov PN, Sultanov MM, et al. The Structure of the Near-Surface Layer of the AAAC Overhead Power Line Wires after Operation and Its Effect on Their Elastic, Microplastic, and Electroresistance Properties. Crystals. 2022; 12(2):166. https://doi.org/10.3390/cryst12020166
Chicago/Turabian StyleNarykova, Maria V., Aleksandr A. Levin, Nikita D. Prasolov, Alexey I. Lihachev, Boris K. Kardashev, Andrej G. Kadomtsev, Andrei G. Panfilov, Roman V. Sokolov, Pavel N. Brunkov, Makhsud M. Sultanov, and et al. 2022. "The Structure of the Near-Surface Layer of the AAAC Overhead Power Line Wires after Operation and Its Effect on Their Elastic, Microplastic, and Electroresistance Properties" Crystals 12, no. 2: 166. https://doi.org/10.3390/cryst12020166
APA StyleNarykova, M. V., Levin, A. A., Prasolov, N. D., Lihachev, A. I., Kardashev, B. K., Kadomtsev, A. G., Panfilov, A. G., Sokolov, R. V., Brunkov, P. N., Sultanov, M. M., Kuryanov, V. N., & Tyshkevich, V. N. (2022). The Structure of the Near-Surface Layer of the AAAC Overhead Power Line Wires after Operation and Its Effect on Their Elastic, Microplastic, and Electroresistance Properties. Crystals, 12(2), 166. https://doi.org/10.3390/cryst12020166








