Superplastic Deformation Behaviors and Power Dissipation Rate for Fine-Grained Ti-6Al-4V Titanium Alloy Processed by Direct Rolling

Abstract

Fine-grained Ti-6Al-4V titanium alloy plates were manufactured using a direct rolling approach, and a series of superplastic tensile tests were conducted at varying temperatures and strain rates. The maximum tensile elongation of 816% was obtained at 810 °C and 5 × 10⁻⁴ s⁻¹, and the superplastic flow behavior was dominated by a strain-induced grain boundary slip. In addition, the superplastic behaviors of the alloy were investigated, and the α-and β-phase Gibbs free energy was calculated. The vital role of phase β in the transformation was discussed from a thermodynamical perspective. A power dissipation rate model of Ti-6Al-4V during the superplastic deformation was built and used to predict the energy changing laws in the dynamic recrystallization and grain boundary sliding during the superplastic deformation.

1. Introduction

Titanium and its alloys, e.g., Ti-6Al-4V, are attractive structural materials in the aerospace, chemical, and biomedical industries due to their unique high strength–weight ratios maintained at elevated temperatures and their exceptional corrosion resistance. In recent years, Ti-6Al-4V alloys have been often selected to manufacture multilayer-structured complex-shaped components via superplastic forming or diffusional bonding [1,2,3]. For these reasons, Ti-6Al-4V alloys have been extensively studied in terms of superplastic flow behaviors and the related deformation mechanism. It is acknowledged that a stable fine-grained or nano-crystalline microstructure is preferred for the superplastic flow because the distance for the accommodation by diffusion and/or slip is shorter when a larger number of grain boundaries are involved in the sliding. Thus, the superplastic flow behavior can be more easily observed at a higher strain rate and lower deformation temperature.

Accordingly, many methods have been attempted to fabricate the fine-grained or nano-crystalline structure of the Ti-6Al-4V alloy. For example, severe plastic deformation such as high-pressure torsion was reported [4,5], and the nano-crystalline structure was achieved with a tensile elongation of >800% from 650 to 800 °C and strain rates of 10⁻⁵ to 10⁻³ s⁻¹. Ma et al. [6] proposed a novel grain refinement method for the Ti-6Al-4V alloy using stir friction welding, which demonstrated excellent superplastic behavior with tensile elongation up to 660% at 825 °C and a strain rate of 3 × 10⁻⁴ to 3 × 10⁻³ s⁻¹. HPT, FSP, and ECAP all belong to the large plastic deformation principle and are aimed at grain refinement to obtain fine and superfine grains. In terms of grain refinement, the above techniques are obviously superior to cold rolling. However, the above techniques are only applicable to the grain refinement of small-sized specimens; they cannot handle the large-sized parts in the field of engineering. A suggested effective approach for the grain refinement of the Ti-6Al-4V alloy is direct rolling, which can be conveniently extended to large-scale processing.

In all, the existing research about the superplastic behaviors of Ti-6Al-4V is concentrated on grain sizes and superplastic deformation behaviors, constitutive relation modeling and the correction of superplastic deformation, and the application of superplastic-forming technology into part and component fabrication [7,8,9,10,11]. However, grain growth and structural instability are two major phenomena during the superplastic deformation of metal materials. Though the superplastic dynamic, grain growth has been studied [12,13], though there is no thermodynamic analysis of microstructure evolution, or energy dissipation and redistribution during the superplastic deformation of Ti-6Al-4V.

In the present study, therefore, we studied the superplastic flow behavior and the underlying deformation mechanism of a two-phase Ti-6Al-4V alloy processed by direct rolling. In particular, power dissipation rate models were established for such a fine-grained Ti-6Al-4V alloy, and the microstructure evolution of superplastic deformation was predicted as well.

2. Experimental Procedures

2.1. Material and Its Preparation

The tested material was 2 mm-thick Ti-6Al-4V cold-rolled plates with a composition of 6.1 (wt.%) Al, 3.8 V, 0.18 Fe, 0.02 C, and remaining Ti. The cold rolling conditions are: the hot-rolled plates were heated to 820 °C (holding for 10 min), the reductions were 50%, 20%, 20%, and 10%, and specimen thickness was 2 mm. The specimens were annealed before cold rolling. Tensile samples were machined from the plates with gauge length of ~12 mm and width of 6 mm (Figure 1).

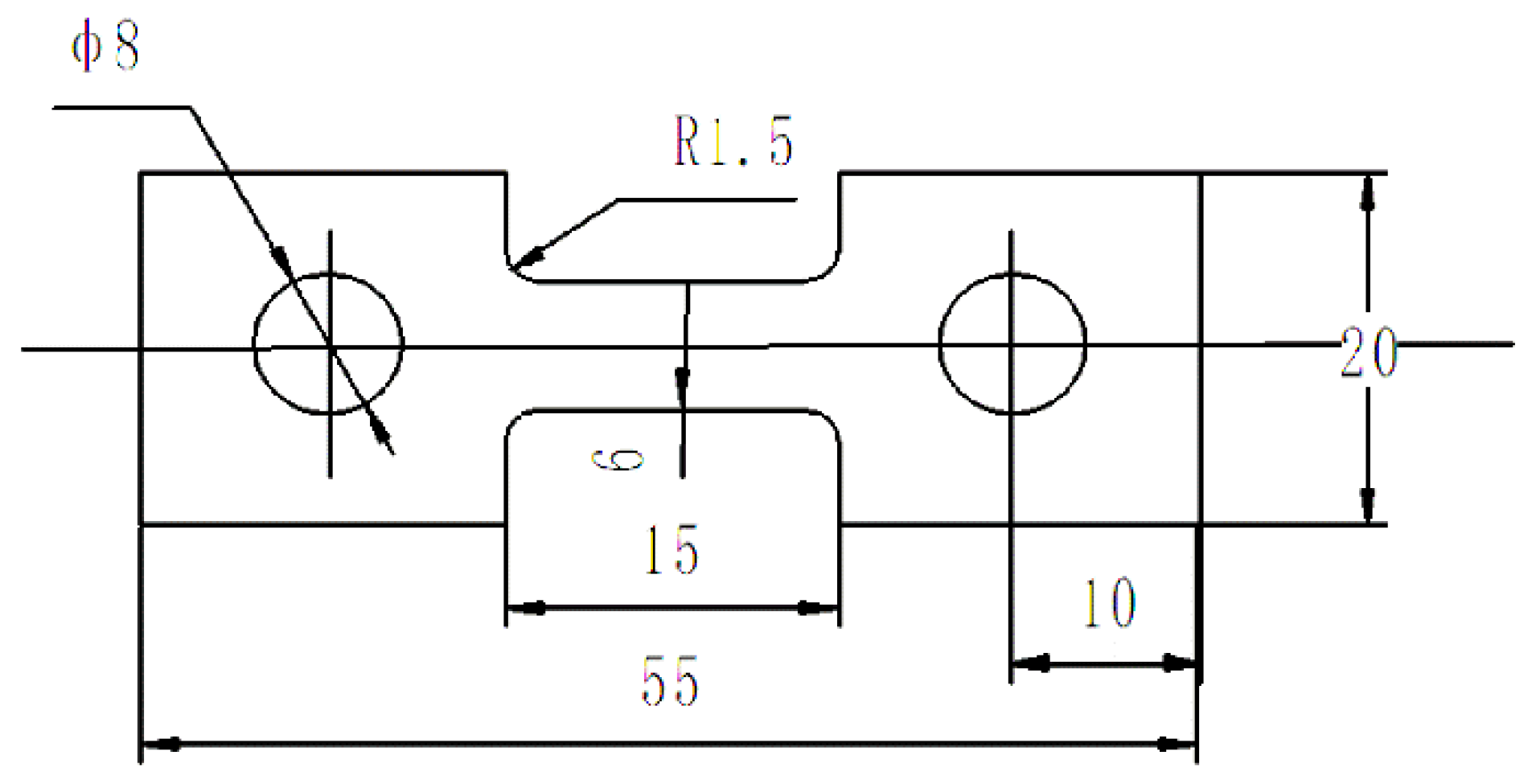
2.2. Tensile Testing

Superplastic tensile tests were conducted using an AG 250KNE electronic tensile testing machine. The tensile specimens were heated to the target temperature and preserved for 10 min to ensure uniform heating. The tensile experiments were conducted at the deformation temperature (T) of 750–810 °C with an interval of 30 °C and at an initial strain rate ($\dot{\epsilon }$) of 5 × 10⁻³, 1 × 10⁻³ and 5 × 10⁻⁴ s⁻¹. After the superplasticity, the forces of the elongation machine were loaded off, and the specimens were water-quenched to room temperature to reserve the high-temperature deformed structures for microstructural examination. All experiments were carried out in an enclosed chamber purged with high-purity argon gas.

2.3. Characterization of Microstructures

Microstructures of the specimens were analyzed by optical microcopy, transmission electron microscopy (TEM), and X-ray diffraction (XRD). The optical microstructures of the specimens after superplastic tension were observed using an OLYMPUS GX51 microscope after a 2-step etching procedure: (i) chemical etching by a reagent of 6 mL HNO₃ + 100 mL H₂O + 3 mL HF to reveal grain boundaries and (ii) differentiation of β phase using an etchant of 98 mL C₂H₂O₄·2H₂O (20 wt.%) + 1 g Fe(NO₃)₃ + 2 mL HF. The TEM foils were thinned by twin-jet electrical polishing using a solution containing 60% methanol, 34% n-butanol, and 6% perchloric acid. The electrical polishing was performed at a solution temperature of −40 to −35 °C using a voltage of 50 V and a current of 40–45 mA. The TEM specimens were observed under using a Tecnai G² 20 microscope. The phase constituents of the specimens were qualitatively analyzed using an XRD-7000 XRD device (Shimadzu, Tokyo, Japan). The microstructures in the grip and gauge sections were characterized using electron backscatter diffraction (EBSD) with a step size of 0.03 µm, where the EBSD samples were prepared by grinding with SiC papers to 3000 grit and then using argon ion beam polishing.

3. Results and Discussion

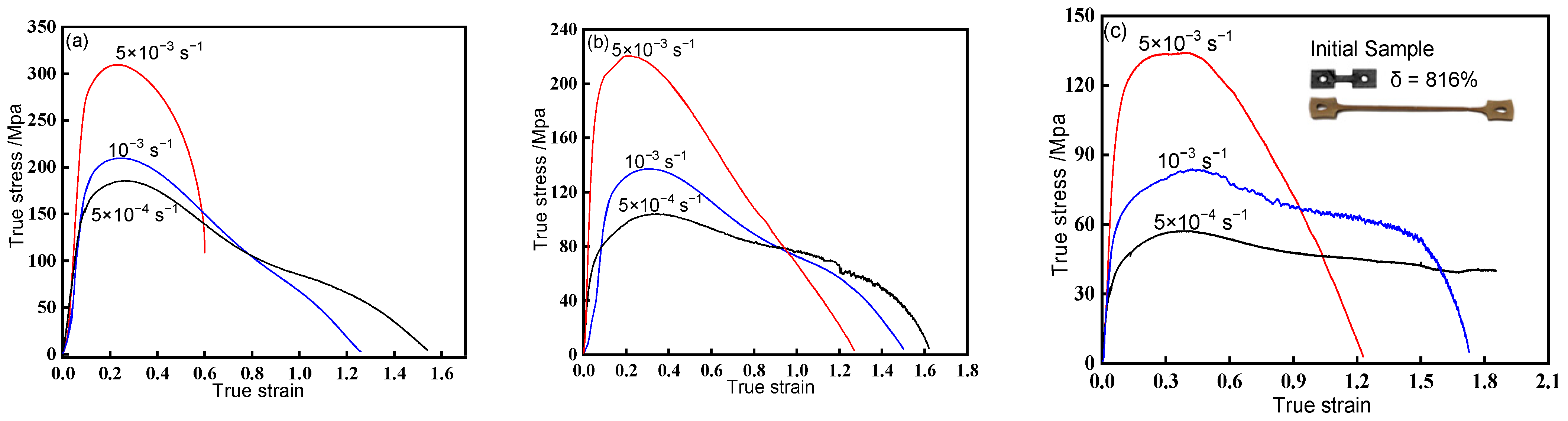
3.1. Superplastic Flow Behaviors

Figure 2 shows the true stress–strain curves of the Ti-6Al-4V alloy during the superplastic deformation. The flow stress and peak stress during the superplastic deformation both decreased with the decline of the strain rate, and dropped with the increase of the deformation temperature. At the strain rate of 5 × 10⁻³ s⁻¹, the flow stress reached a peak at the strain of ε = ~0.3 and then rapidly declined at all deformation temperatures (750–810 °C), so the steady-state interval was very narrow and no typical superplastic deformation occurred. At the strain rate of 5 × 10⁻⁴ s⁻¹, the true stress–strain curves showed very evident steady-state zones, especially at 810 °C. In brief, there was nearly an equilibrium state of work hardening and work softening, which led to high superplasticity with a maximum elongation of 816% at $\dot{\epsilon }=5$× 10⁻⁴ s⁻¹ and 810 °C (Figure 2). Thus, under the above test conditions, the superplastic-forming ability of this alloy was a function of the deformation temperature and tensile strain rate.

The strain rate sensitivity exponent m (m =$\partial \ln \sigma /\partial \ln \dot{\epsilon }$, where $\partial$ is the true stress and $\dot{\epsilon }$ is the strain rate) is a commonly used index for superplasticity, as most superplastic materials represent an m range of 0.3 to 0.7 [6]. For the ease of calculation, m can also be computed using m = ε/(2 + ε) [14], where ε is the maximum true strain (ε = ln(1 + δ)) and δ is the deformation to failure. Here, the later equation was used for all superplastic deformation conditions (

Table 1. Measured δ and calculated m values as a function of deformation temperature and strain rate.

Temperature T, °C	Initial Strain Rate $\dot{\mathit{\epsilon }}$, s−1	Strain Rate Sensitivity Exponent m	Deformation to Failure δ, %
750	5 × 10−3	0.41	301
750	10−3	0.42	327
750	5 × 10−4	0.44	390
780	5 × 10−3	0.43	367
780	10−3	0.46	448
780	5 × 10−4	0.47	500
810	5 × 10−3	0.46	434
810	10−3	0.51	692
810	5 × 10−4	0.53	816

). When the high δ of 816% was obtained at 810 and $\dot{\epsilon }$= 5 × 10⁻⁴ and 10⁻³ s⁻¹, the corresponding m was larger than 0.5. It is generally recognized that the dominant deformation mechanism is grain boundary sliding with m close to 0.5. When a relatively high strain rate of 5 × 10⁻³ s⁻¹ was used, m is within 0.41–0.42, and δ is below 440%, indicating this alloy possesses limited superplasticity and that the low δ may be due to the occurrence of energy dissipation during the microstructure evolution.

The dominant mechanisms of superplastic flow at the steady state can also be indicated by the superplastic deformation activation energy Q [15]. Q can be calculated as:

$$\mathrm{Q}=\mathrm{n}·\mathrm{R}·\frac{\partial \ln \mathsf{\sigma }}{\partial \left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{T}$}\right.\right)}| \dot{\epsilon },$$

(1)

where n is the stress index (n = 1/m), T is the absolute temperature, and R is the universal gas constant. Figure 3 shows the lnσ-1/T plot of Ti-6Al-4V for all strain rates. The Q value of this alloy under different strain rates was calculated to be 228.64–361.36 kJ/mol. As reported [16,17], the grain boundary diffusion activation energy of Ti-6Al-4V is 220.2 and 188.2 kJ/mol, which are close to our calculations, indicating that the superplastic deformation mechanism of this alloy might fit the energy dissipation conditions of grain boundary diffusion from the perspective of energy. The activation energy of the deformation increased at the strain rates of 5 × 10⁻⁴ s⁻¹ and 10⁻³ s⁻¹. This is because the changes in the proportions of phases α and β played a certain role under the above superplastic deformation conditions.

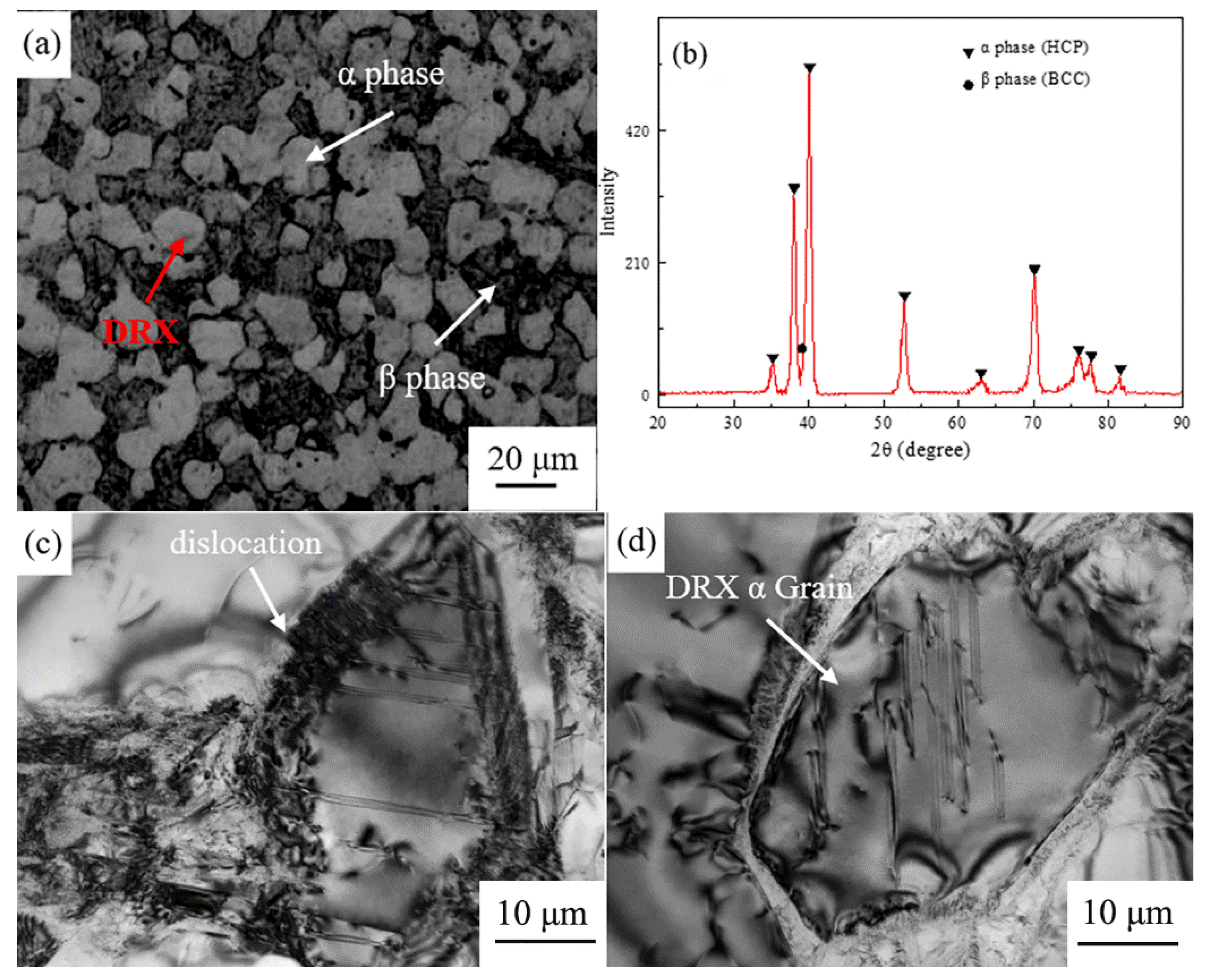
3.2. Microstructural Evolution

Figure 4 shows the initial structure of the current cold-rolled and annealed Ti-6Al-4V plates prior to deformation. The original structure of this alloy was composed of α and β phases, where equiaxed α grains were prevailing with a mean grain size of 8.3 ± 0.5 µm.

After the superplastic deformation to failure, the plate as obtained lost its starting microstructural characteristics, resulting in a deformed microstructure with different grain sizes and morphologies depending on the superplastic conditions (Figure 5a–f). Generally, the grain size increased with an increase of deformation temperature or a reduction of strain rate. This is mainly due to the time- and temperature-dependent grain growth under the deformation conditions. Equiaxed grain structure was seen in most deformed conditions except for 750 °C and 5 × 10⁻³ s⁻¹, which suggests a continuous formation of equiaxed grains through the superplastic deformation. Therefore, the tensile elongation was mainly facilitated by grain boundary sliding. Elongated grains were observed after deformation to failure at 750 °C and 5 × 10⁻³ s⁻¹. This suggests that the superplasticity is limited without the continuous formation of equiaxed grains and their GBS.

The thermal deformations of metal materials usually obey the Arrhenius constitutive model [18]: This is an example of one in an equation:

$$\dot{\epsilon }=\frac{A{D}_{0}Gb}{kT}\cdot {\left(\frac{b}{d}\right)}^p\cdot {\left(\frac{\sigma }{G}\right)}^{1/\mathrm{m}}\cdot \mathit{exp}\left(-\frac{Q}{RT}\right),$$

(2)

where d is the grain size, D₀ is the diffusion coefficient, b is the Burgers vector, G is the shear modulus, k is the Boltzmann constant, and R is the ideal gas constant. Based on the Arrhenius constitutive model, the relation curve of strain rate grain size was plotted at 810 °C (Figure 6a), where the straight-line slope stands for the grain index p, which reflects the dependence of grain size on the thermoforming conditions. The values of p of Ti-6Al-4V at different temperatures calculated with the above method are illustrated in Figure 6b.

The grain index p mainly exhibits a liner increase relationship with the deformation temperature, which is similar to that of the strain rate sensitivity index m (Figure 6b). As reported, when p is larger than 2, the material possesses high formability [19]. This corresponds well to the maximum deformation to failure of 886% at 810 °C in our study. The grain size index p can also be used to reflect the microstructure evolution during plastic deformation, especially the laws of grain growth. A high p value can be correlated to high deformation temperature and low strain rate that enable a greater extent of grain coarsening during deformation.

As for the decisive role of grain size in the superplastic elongation of Ti-6Al-4V alloy, usually fine grains or superfine grains have excellent superplasticity. Optical observation of superplastic-deformed Ti-6Al-4V revealed an α and β-phase composition in all specimens after chemical etching (Figure 7). The α/β ratio was ~65:35 at T = 810 °C and =5 × 10⁻⁴ s⁻¹. The equiaxed α grains formed through dynamical recrystallization, with slight coarsening in the course of deformation. TEM revealed that the dislocation density in the interior of the equiaxed grains was not high due to the annihilation of dislocations via continuous DRX. However, some dislocation tangles and substructures were seen inside the DRX grains, suggesting they might have experienced continuous but very minor deformations during the superplastic tension. The dislocations were consumed via the formation of subgrains, which can further develop into fresh DRX grains upon further deformation. Noticeably, the dislocation motion characteristics were obvious at the grain boundary, suggesting that dislocation motion was one of the major indications of superplastic deformation. The grain boundary in Figure 7d is very clear and the grain size is close to that of the α-phase grains undergoing DRX in Figure 7a. As for the Ti-6Al-4V two-phase titanium alloy, the β phase is a BCC structure and the α phase is an HCP structure. Because of the different structures, the two phases were the hard phase and soft phase in the superplastic deformation, and the phase ratio can moderately coordinate the superplastic elongation rate. Hence, we think the superplastic deformation of this alloy was coordinatively controlled by grain size and phase ratio. From the perspective of crystallography, the BCC structure contains more slip systems, which are favorable for the occurrence of grain boundary slip during the deformation. However, as for Ti-6Al-4V, during the superplastic deformation at 810 °C, the stability of the α and β phases is decided by the variation of its Gibbs free energy (ΔG). At ΔG > 0, the phases are stable and at ΔG < 0 the phases are unstable.

According to the ternary phase diagrams of Ti-6Al-4V, the chemical composition of the balanced phases in the α + β two-phase system is 2.1 and 16.2 V, indicating this alloy consists of α (2.1 V) and β (16.2 V). Hence, the free energy of an α-phase (HCP structure) and β phase (BCC structure) is:

$$\Delta {\mathrm{G}}^{\mathrm{S}}=\mathrm{x}\left(\mathsf{\alpha }\mathrm{Ti}\right)\Delta {\mathrm{G}}_{\mathsf{\alpha }\mathrm{Ti}}^0+\mathrm{x}\left(\mathsf{\beta }\mathrm{Ti}\right)\Delta {\mathrm{G}}_{\mathsf{\beta }\mathrm{Ti}}^0+\Delta {\mathrm{G}}_{\mathrm{mix}}^{\mathrm{xs}}-\mathrm{T}\Delta {\mathrm{S}}_{\mathrm{mix}}^{\mathrm{ideal}},$$

(3)

where x(αTi) and x(βTi) are the mole fractions of α-Ti and β-Ti, respectively; $\Delta {\mathrm{G}}_{\mathsf{\alpha }\mathrm{Ti}}^0$ and $\Delta {\mathrm{G}}_{\mathsf{\beta }\mathrm{Ti}}^0$ are the lattice stability values, $\Delta {\mathrm{G}}_{\mathsf{\alpha }\mathrm{Ti}}^0$= 7752−3.858 T, $\Delta {\mathrm{G}}_{\mathsf{\beta }\mathrm{Ti}}^0$= 2587−1.058 T [20], $\Delta {\mathrm{S}}_{\mathrm{mix}}^{\mathrm{ideal}}$ are the ideal entropy of mixing; and $\Delta {\mathrm{G}}_{\mathrm{mix}}^{\mathrm{xs}}$ is the excess Gibbs mixing free energy.

$$\Delta {\mathrm{S}}_{\mathrm{mix}}^{\mathrm{ideal}}=-\mathrm{R}\left(\left(\mathrm{x}\left(\mathsf{\alpha }\mathrm{Ti}\right)·\mathrm{lnx}\left(\mathsf{\alpha }\mathrm{Ti}\right)\right)+\left(\mathrm{x}\left(\mathsf{\beta }\mathrm{Ti}\right)·\mathrm{lnx}\left(\mathsf{\beta }\mathrm{Ti}\right)\right)\right),$$

(4)

$$\begin{gathered} \Delta {\mathrm{G}}_{\mathrm{mix}}^{\mathrm{xs}}=\mathrm{x}\left(\mathsf{\alpha }\mathrm{Ti}\right)\mathrm{x}\left(\mathsf{\beta }\mathrm{Ti}\right)\left\{{\mathrm{L}}_0+{\mathrm{L}}_1\left(\mathrm{x}\left(\mathsf{\alpha }\mathrm{Ti}\right)-\mathrm{x}\left(\mathsf{\beta }\mathrm{Ti}\right)\right)+{\mathrm{L}}_2{\left(\mathrm{x}\left(\mathsf{\alpha }\mathrm{Ti}\right)-\mathrm{x}\left(\mathsf{\beta }\mathrm{Ti}\right)\right)}^2+ \\ \cdots +{\mathrm{L}}_{\mathrm{n}}{\left[\mathrm{x}\left(\mathsf{\alpha }\mathrm{Ti}\right)-\mathrm{x}\left(\mathsf{\beta }\mathrm{Ti}\right)\right]}^{\mathrm{n}}\right\}, \end{gathered}$$

(5)

For the α phase (HCP structure), we have L₀ = −6856, L₁ = 4000, and L₂ = 4000; for the β phase (BCC structure), we have L₀ = −18,335 + 8.49 T, L₁ = 3481, L₂ = 2658−0.114 T, and T temperature/K [21].

After the above parameters were substituted into Equations (2)–(4), the free energy of α(2.1 V) and β(16.2 V) in Ti-6Al-4V at 810 °C can be calculated (

Table 2. Free energy of α(2.1 V) and β(16.2 V) at 810 °C.

Phase	x(αTi)	x(βTi)	$\Delta {\mathbf{G}}_{\mathbf{mix}}^{\mathbf{xs}} (\mathbf{J}/\mathbf{mol})$	$\Delta {\mathbf{S}}_{\mathbf{mix}}^{\mathbf{ideal}}(\mathbf{J}/\mathbf{mol})$	$\Delta {\mathbf{G}}^{\mathbf{S}}(\mathbf{J}/\mathbf{mol})$
α(2.1 V)	0.92	0.08	−49.577	2.317	665.759
β(16.2 V)	0.56	0.44	−2077.512	5.693	−5857.162

).

Clearly, the α- and β-phase free energy at 810 °C is 665.759 and −5857.162 J/mol, respectively (Table 2). According to the law of thermodynamics, the α-phase free energy of Ti-6Al-4V at 810 °C is above 0, indicating a steady-state, and the β-phase free energy is smaller than 0, indicating an unstable state, or that this alloy possessed the β-phase transformation and the slip system started to possess thermodynamic conditions. Hence, the β phase played an important regulating effect during the superplastic deformation of this alloy.

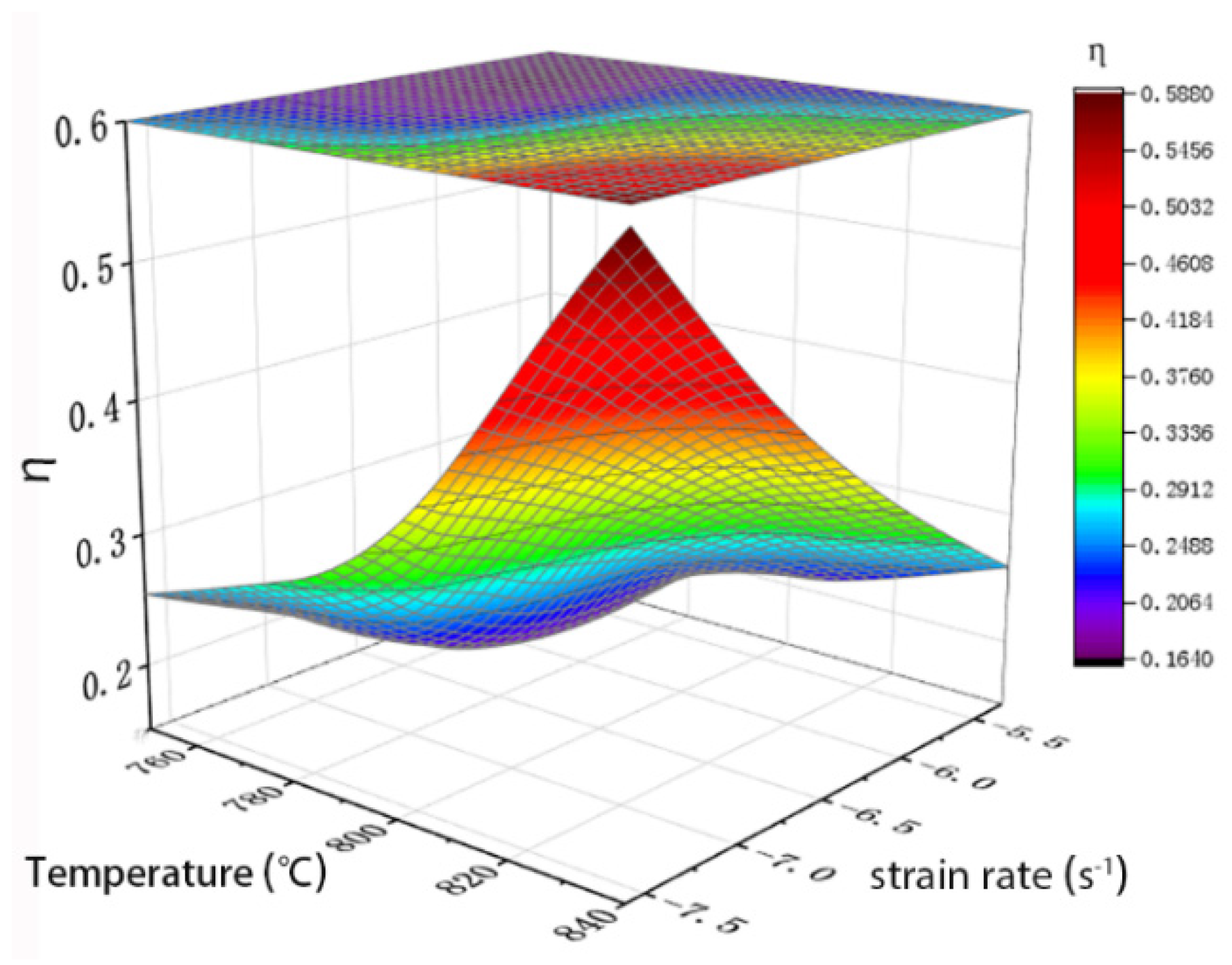
3.3. Energy Dissipation during Superplastic Deformation of Ti-6Al-4V

The thermal deformation of metal materials is a process of energy dissipation and redistribution. Prasad and Gegel established a dynamic material model according to large plastic deformation continuum mechanics, physical systems simulation, and irreversible thermodynamic theory [22]. This model is a link between structural transformation and energy conversion during the plastic deformation of metal materials. Based on the theory of dissipative structures, the input energy P into a system consists of the dissipation quantity (G) and the covariant dissipation (J) [23]:

$$P=\sigma \cdot \dot{\epsilon }=G+J={{\displaystyle \int }}_0^{\dot{\epsilon }}\sigma \cdot d\dot{\epsilon }+{{\displaystyle \int }}_0^{\sigma }\dot{\epsilon }\cdot d\sigma ,$$

(6)

where G is the energy consumed by plastic deformation (in which the majority is transformed into thermal energy, and the minority is stored in the form of crystal defect energy); J is the energy consumed by structure evolution during material deformation. The ratio of these two types of energy is decided by the strain rate sensitivity index m under certain stress:

$$\mathrm{m}=\frac{\partial J}{\partial G}=\frac{\dot{\epsilon }\partial \sigma }{\sigma \partial \dot{\epsilon }}=\frac{\partial \left(\ln \sigma \right)}{\partial \left(\ln \dot{\epsilon }\right)},$$

(7)

The physical meaning of the system energy distribution rate can be more clearly illustrated from the perspective of atomic action. The dissipation of energy is divided into two parts: potential energy and kinetic energy. The potential energy is related to the relative position between atoms, and the change in microstructures certainly will cause the variation of atomic potential energy, so potential energy corresponds to J. Moreover, kinetic energy is associated with atomic movement, or namely, dislocation is related to movement, and the kinetic energy conversion is dominated by the dissipation of thermal energy, so it corresponds to G.

J can be computed as follows [24]:

$$J={{\displaystyle \int }}_0^{\dot{\epsilon }}\sigma d\dot{\epsilon }=\frac{\mathrm{m}}{\mathrm{m}+1}\sigma \dot{\epsilon },$$

(8)

When at m = 1, the material is at the ideal linear dissipation state and J maximizes to J_max:

$$J_{\max }=\frac{\sigma \dot{\epsilon }}{2},$$

(9)

From Equations (7) and (8), a dimensionless parameter η can be determined and called the dissipation efficiency factor, and its physical meaning is the ratio of energy dissipation due to microstructure evolution to the linear energy dissipation during material formation [24]:

$$\eta =\frac{J}{J_{\max }}=\frac{2\mathrm{m}}{\mathrm{m}+1},$$

(10)

where η is a function of $\dot{\epsilon }$ and t. Based on Figure 1 and Equation (9), we can plot the contour curve of the energy dissipation rate η of Ti-6Al-4V (Figure 8).

The energy dissipation rate (red areas in Figure 8) of this alloy at 790–810 °C, and the strain rate of 5 × 10⁻⁴–10⁻³ s⁻¹, was very large and exceeded 50%. At this moment, the strain rate sensitivity index m, grain size index p, and deformation to failure δ of this alloy were all very large, which indicate the energy dissipation characteristics of this alloy during superplastic deformation. It is known from Figure 6 and Figure 7 as well as the 3D projection in the upper part of Figure 8 that the turning point on the power dissipation curve indicates the occurrence of dynamic recrystallization.

4. Conclusions

The superplastic deformation behavior and deformation mechanism of rolled Ti-6Al-4V alloy fine-grained plates were studied. The results showed that grain size and the α- to β-phase ratio both can regulate the superplastic deformation. The important role of phase β in the deformation was clarified from the perspective of thermodynamics. Furthermore, the deformation of this alloy during the superplastic deformation followed the strain-induced grain boundary sliding mechanism.

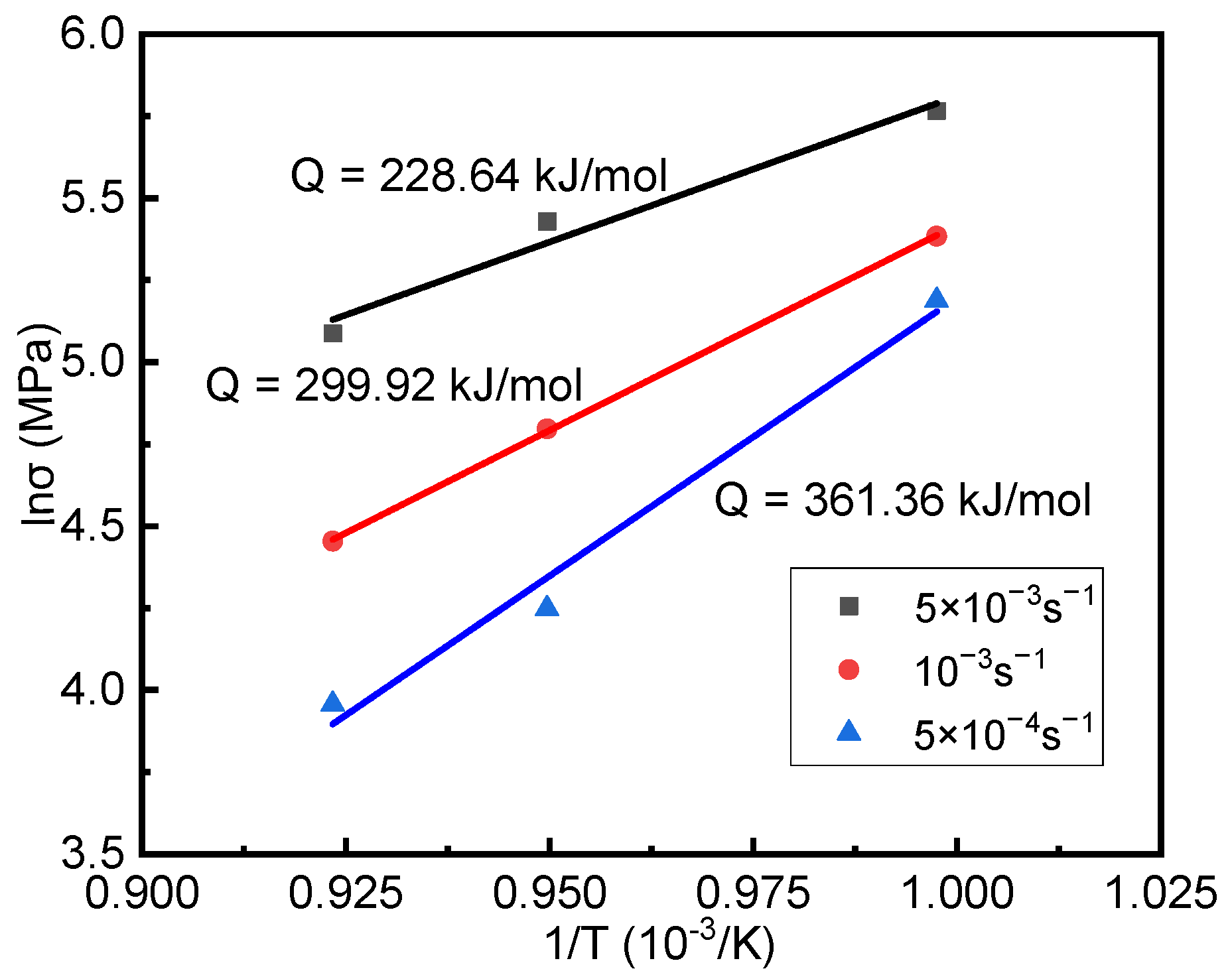
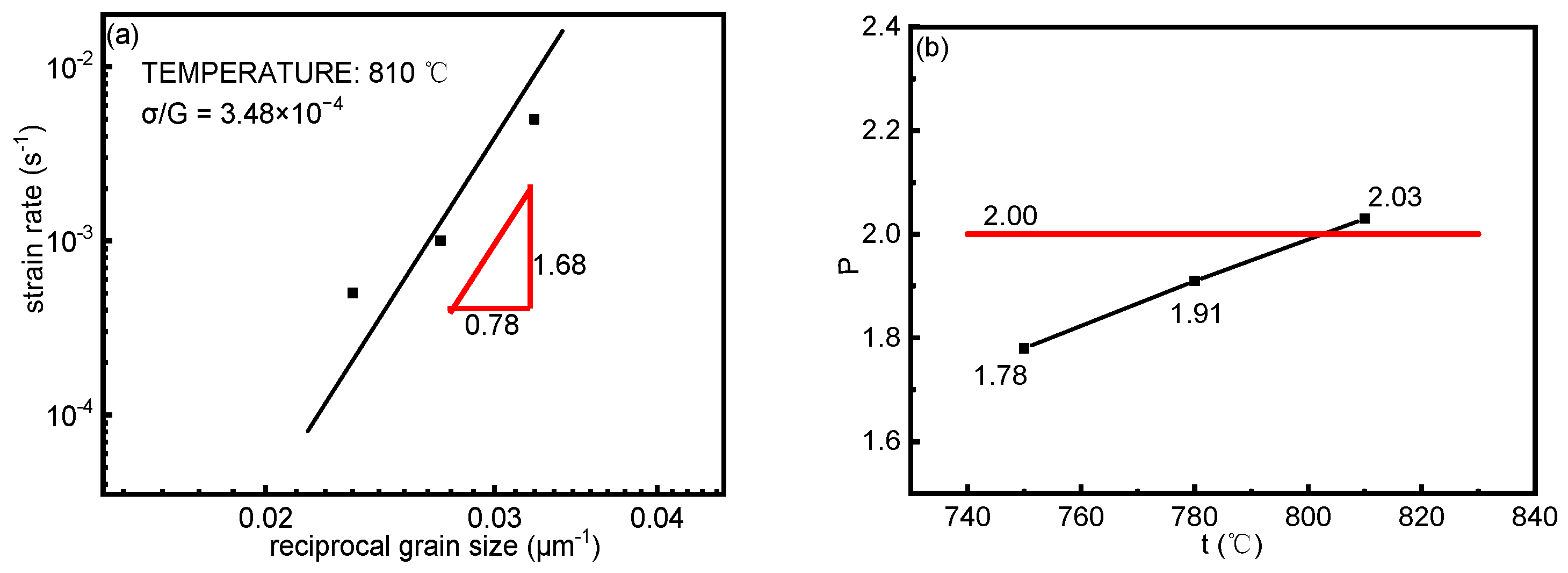
• The superplastic deformation to failure of the rolled Ti-6Al-4V alloy plates maximized to 816% at 810 °C and 5 × 10⁻⁴ s⁻¹, and at this moment, m was 0.53, Q value was 316.36 kJ/mol, and p was 2;
• The α(2.1 V)-phase and β(16.2 V)-phase Gibbs free energy of Ti-6Al-4V at 810 °C was 665.759 and −5857.162 J/mol, respectively, which thermodynamically confirmed that the β phase played an important regulating role in the superplastic deformation;
• A power dissipation rate model of Ti-6Al-4V during the superplastic deformation was built and used to predict the changing laws of energy in the dynamic recrystallization and grain boundary sliding during superplastic deformation.