Investigation of Lattice Plasmon Modes in 2D Arrays of Au Nanoantennas
Abstract
:1. Introduction
2. Experimental Section
3. Result and Discussion
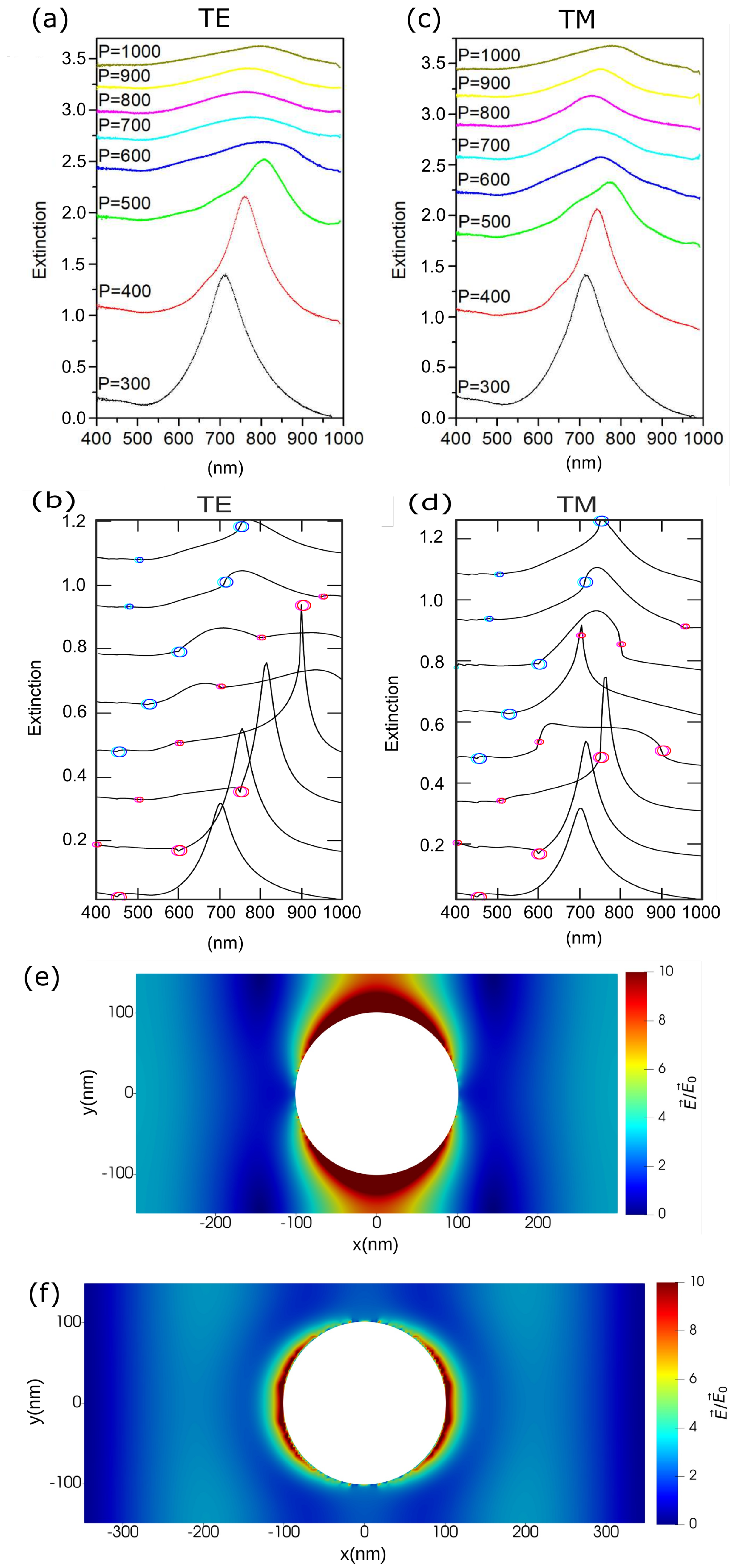
3.1. Plasmonic Response at Normal Incidence
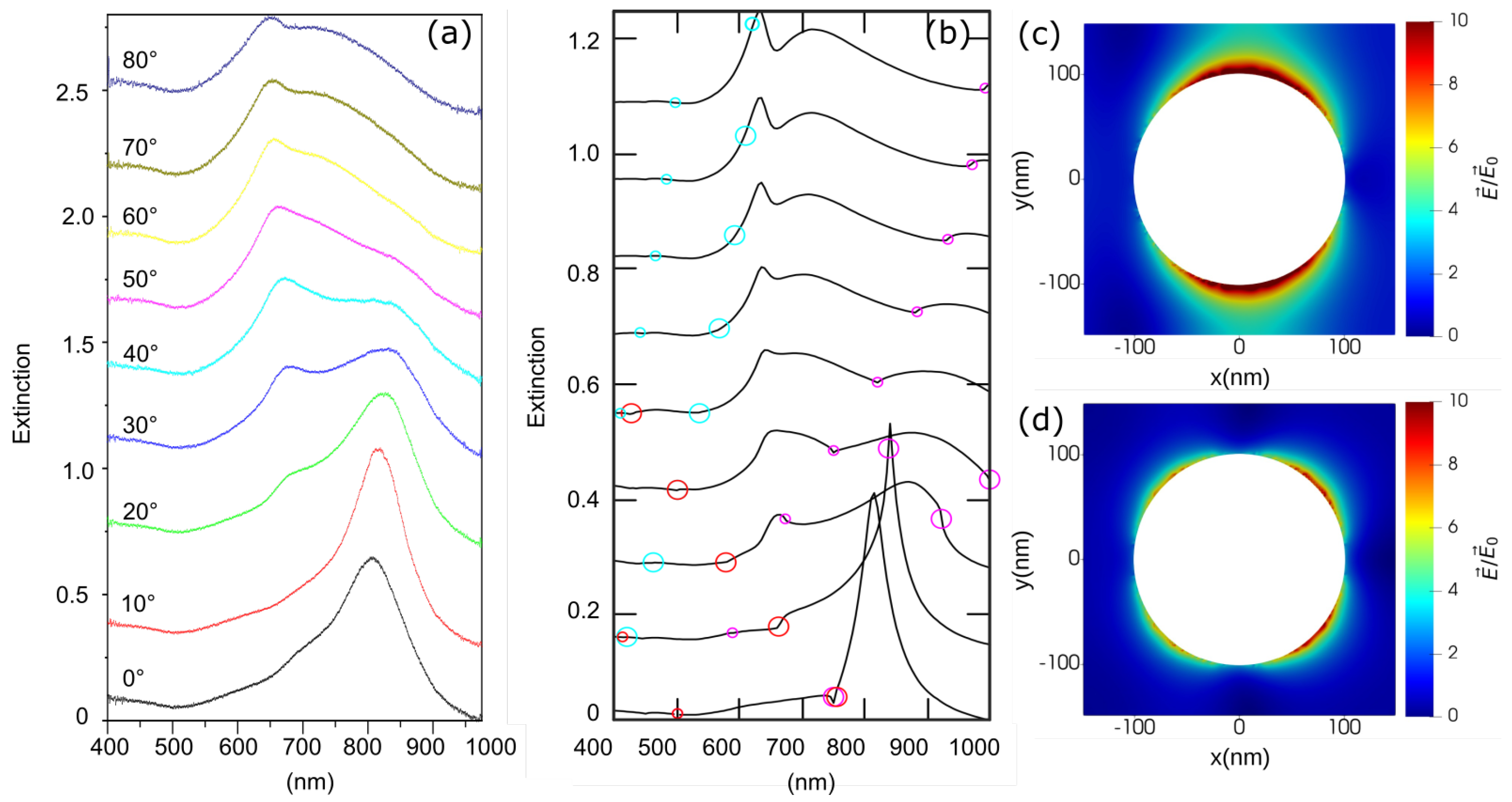
3.2. Plasmonic Response at Oblique Incidence
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lio, G.E.; Ferraro, A.; Giocondo, M.; Caputo, R.; De Luca, A. Color Gamut Behavior in Epsilon Near-Zero Nanocavities during Propagation of Gap Surface Plasmons. Adv. Opt. Mater. 2020, 8, 2000487. [Google Scholar] [CrossRef]
- Colburn, S.; Zhan, A.; Majumdar, A. Metasurface optics for full-color computational imaging. Sci. Adv. 2018, 4, eaar2114. [Google Scholar] [CrossRef] [Green Version]
- Lio, G.E.; De Luca, A.; Umeton, C.P.; Caputo, R. Opto-mechanically induced thermoplasmonic response of unclonable flexible tags with hotspot fingerprint. J. Appl. Phys. 2020, 128, 093107. [Google Scholar]
- Lio, G.E.; Ferraro, A.; Ritacco, T.; Aceti, D.M.; De Luca, A.; Giocondo, M.; Caputo, R. Leveraging on ENZ Metamaterials to Achieve 2D and 3D Hyper-Resolution in Two-Photon Direct Laser Writing. Adv. Mater. 2021, 33, 2008644. [Google Scholar] [CrossRef] [PubMed]
- Ghindani, D.; Rashed, A.R.; Habib, M.; Caglayan, H. Gate Tunable Coupling of Epsilon-Near-Zero and Plasmonic Modes. Adv. Opt. Mater. 2021, 9, 2100800. [Google Scholar] [CrossRef]
- Linic, S.; Chavez, S.; Elias, R. Flow and extraction of energy and charge carriers in hybrid plasmonic nanostructures. Nat. Mater. 2021, 20, 916–924. [Google Scholar] [CrossRef]
- Chaharsoughi, M.S.; Tordera, D.; Grimoldi, A.; Engquist, I.; Berggren, M.; Fabiano, S.; Jonsson, M.P. Hybrid Plasmonic and Pyroelectric Harvesting of Light Fluctuations. Adv. Opt. Mater. 2018, 6, 1701051. [Google Scholar] [CrossRef]
- Aieta, F.; Genevet, P.; Kats, M.A.; Yu, N.; Blanchard, R.; Gaburro, Z.; Capasso, F. Aberration-free ultrathin flat lenses and axicons at telecom wavelengths based on plasmonic metasurfaces. Nano Lett. 2012, 12, 4932–4936. [Google Scholar] [CrossRef]
- Yu, N.; Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 2014, 13, 139–150. [Google Scholar] [CrossRef]
- Ferraro, A.; Lio, G.E.; Hmina, A.; Palermo, G.; Maurer, T.; Caputo, R. Tailoring of Plasmonic Functionalized Metastructures to Enhance Local Heating Release. Nanophotonics 2021, 10, 3907–3916. [Google Scholar] [CrossRef]
- Cui, T.; Bai, B.; Sun, H.B. Tunable metasurfaces based on active materials. Adv. Funct. Mater. 2019, 29, 1806692. [Google Scholar] [CrossRef]
- Špačková, B.; Homola, J. Sensing properties of lattice resonances of 2D metal nanoparticle arrays: An analytical model. Opt. Express 2013, 21, 27490–27502. [Google Scholar] [CrossRef] [PubMed]
- Lozano, G.; Louwers, D.J.; Rodríguez, S.R.; Murai, S.; Jansen, O.T.; Verschuuren, M.A.; Rivas, J.G. Plasmonics for solid-state lighting: Enhanced excitation and directional emission of highly efficient light sources. Light. Sci. Appl. 2013, 2, e66. [Google Scholar] [CrossRef] [Green Version]
- Lozano, G.; Rodriguez, S.R.; Verschuuren, M.A.; Rivas, J.G. Metallic nanostructures for efficient LED lighting. Light. Sci. Appl. 2016, 5, e16080. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cataldi, U.; Caputo, R.; Kurylyak, Y.; Klein, G.; Chekini, M.; Umeton, C.; Bürgi, T. Growing gold nanoparticles on a flexible substrate to enable simple mechanical control of their plasmonic coupling. J. Mater. Chem. C 2014, 2, 7927–7933. [Google Scholar] [CrossRef]
- Koya, A.N.; Cunha, J.; Guerrero-Becerra, K.A.; Garoli, D.; Wang, T.; Juodkazis, S.; Proietti Zaccaria, R. Plasmomechanical Systems: Principles and Applications. Adv. Funct. Mater. 2021, 31, 2103706. [Google Scholar] [CrossRef]
- Vecchi, G.; Giannini, V.; Rivas, J.G. Surface modes in plasmonic crystals induced by diffractive coupling of nanoantennas. Phys. Rev. B 2009, 80, 201401. [Google Scholar] [CrossRef] [Green Version]
- Giannini, V.; Vecchi, G.; Rivas, J.G. Lighting up multipolar surface plasmon polaritons by collective resonances in arrays of nanoantennas. Phys. Rev. Lett. 2010, 105, 266801. [Google Scholar] [CrossRef] [Green Version]
- Giannini, V.; Fernández-Domínguez, A.I.; Heck, S.C.; Maier, S.A. Plasmonic nanoantennas: Fundamentals and their use in controlling the radiative properties of nanoemitters. Chem. Rev. 2011, 111, 3888–3912. [Google Scholar] [CrossRef]
- Humphrey, A.D.; Barnes, W.L. Plasmonic surface lattice resonances on arrays of different lattice symmetry. Phys. Rev. B 2014, 90, 075404. [Google Scholar] [CrossRef] [Green Version]
- Mahi, N.; Leveque, G.; Saison, O.; Marae-Djouda, J.; Caputo, R.; Gontier, A.; Maurer, T.; Adam, P.M.; Bouhafs, B.; Akjouj, A. In depth investigation of lattice plasmon modes in substrate-supported gratings of metal monomers and dimers. J. Phys. Chem. C 2017, 121, 2388–2401. [Google Scholar] [CrossRef]
- Li, J.F.; Li, C.Y.; Aroca, R.F. Plasmon-enhanced fluorescence spectroscopy. Chem. Soc. Rev. 2017, 46, 3962–3979. [Google Scholar] [CrossRef] [PubMed]
- Le Ru, E.; Etchegoin, P. Principles of Surface-Enhanced Raman Spectroscopy: And Related Plasmonic Effects; Elsevier: Cham, Switzerland, 2008. [Google Scholar]
- Xu, H.; Bjerneld, E.J.; Käll, M.; Börjesson, L. Spectroscopy of single hemoglobin molecules by surface enhanced Raman scattering. Phys. Rev. Lett. 1999, 83, 4357. [Google Scholar] [CrossRef] [Green Version]
- Bauch, M.; Toma, K.; Toma, M.; Zhang, Q.; Dostalek, J. Plasmon-enhanced fluorescence biosensors: A review. Plasmonics 2014, 9, 781–799. [Google Scholar] [CrossRef] [Green Version]
- Langer, J.; Jimenez de Aberasturi, D.; Aizpurua, J.; Alvarez-Puebla, R.A.; Auguié, B.; Baumberg, J.J.; Bazan, G.C.; Bell, S.E.; Boisen, A.; Brolo, A.G.; et al. Present and future of surface-enhanced Raman scattering. ACS Nano 2019, 14, 28–117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, D.; Bourgeois, M.R.; Lee, W.K.; Li, R.; Trivedi, D.; Knudson, M.P.; Wang, W.; Schatz, G.C.; Odom, T.W. Stretchable Nanolasing from Hybrid Quadrupole Plasmons. Nano Lett. 2018, 18, 4549–4555. [Google Scholar] [CrossRef]
- Thackray, B.D.; Thomas, P.A.; Auton, G.H.; Rodriguez, F.J.; Marshall, O.P.; Kravets, V.G.; Grigorenko, A.N. Super-narrow, extremely high quality collective plasmon resonances at telecom wavelengths and their application in a hybrid graphene-plasmonic modulator. Nano Lett. 2015, 15, 3519–3523. [Google Scholar] [CrossRef]
- Lio, G.E.; Madrigal, J.B.; Couteau, C.; Blaize, S.; Caputo, R. Conceptual Implementation of a Photonic–Plasmonic Transistor onto a Structured Nano-Guided Hybrid System. Phys. Status Solidi A 2020, 217, 1900911. [Google Scholar] [CrossRef]
- Maurer, T.; Marae-Djouda, J.; Cataldi, U.; Gontier, A.; Montay, G.; Madi, Y.; Panicaud, B.; Macias, D.; Adam, P.M.; Lévêque, G.; et al. The beginnings of plasmomechanics: Towards plasmonic strain sensors. Front. Mater. Sci. 2015, 9, 170–177. [Google Scholar] [CrossRef] [Green Version]
- Laible, F.; Horneber, A.; Fleischer, M. Mechanically Tunable Nanogap Antennas: Single-Structure Effects and Multi-Structure Applications. Adv. Opt. Mater. 2021, 9, 2100326. [Google Scholar] [CrossRef]
- Palermo, G.; Cataldi, U.; Condello, A.; Caputo, R.; Bürgi, T.; Umeton, C.; De Luca, A. Flexible thermo-plasmonics: An opto-mechanical control of the heat generated at the nanoscale. Nanoscale 2018, 10, 16556–16561. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Odom, T.W. Tunable subradiant lattice plasmons by out-of-plane dipolar interactions. Nat. Nanotechnol. 2011, 6, 423–427. [Google Scholar] [CrossRef] [PubMed]
- Locatelli, A.; De Angelis, C.; Modotto, D.; Boscolo, S.; Sacchetto, F.; Midrio, M.; Capobianco, A.D.; Pigozzo, F.M.; Someda, C.G. Modeling of enhanced field confinement and scattering by optical wire antennas. Opt. Express 2009, 17, 16792–16800. [Google Scholar] [CrossRef] [PubMed]
- Auguié, B.; Bendana, X.M.; Barnes, W.L.; de Abajo, F.J.G. Diffractive arrays of gold nanoparticles near an interface: Critical role of the substrate. Phys. Rev. B 2010, 82, 155447. [Google Scholar] [CrossRef] [Green Version]
- Sadeghi, S.; Wing, W.; Campbell, Q. Normal and anomalous plasmonic lattice modes of gold nanodisk arrays in inhomogeneous media. J. Appl. Phys. 2016, 119, 114307. [Google Scholar] [CrossRef] [Green Version]
- Meier, M.; Wokaun, A.; Liao, P.F. Enhanced fields on rough surfaces: Dipolar interactions among particles of sizes exceeding the Rayleigh limit. JOSA B 1985, 2, 931–949. [Google Scholar] [CrossRef]
- Auguié, B.; Barnes, W.L. Collective resonances in gold nanoparticle arrays. Phys. Rev. Lett. 2008, 101, 143902. [Google Scholar] [CrossRef] [Green Version]
- Rayleigh, L. On the dynamical theory of gratings. Proc. R. Soc. Lond. Ser. Contain. Pap. Math. Phys. Character 1907, 79, 399–416. [Google Scholar]
- Byelobrov, V.O.; Zinenko, T.L.; Kobayashi, K.; Nosich, A.I. Periodicity Matters: Grating or lattice resonances in the scattering by sparse arrays of subwavelength strips and wires. IEEE Antennas Propag. Mag. 2015, 57, 34–45. [Google Scholar] [CrossRef]
- Ferraro, A.; Zografopoulos, D.C.; Verschuuren, M.A.; de Boer, D.K.; Kong, F.; Urbach, H.P.; Beccherelli, R.; Caputo, R. Directional Emission of Fluorescent Dye-Doped Dielectric Nanogratings for Lighting Applications. ACS Appl. Mater. Interfaces 2018, 10, 24750–24757. [Google Scholar] [CrossRef]
- Kravets, V.G.; Kabashin, A.V.; Barnes, W.L.; Grigorenko, A.N. Plasmonic surface lattice resonances: A review of properties and applications. Chem. Rev. 2018, 118, 5912–5951. [Google Scholar] [CrossRef]
- Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Planar photonics with metasurfaces. Science 2013, 339, 1232009. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marae-Djouda, J.; Caputo, R.; Mahi, N.; Lévêque, G.; Akjouj, A.; Adam, P.M.; Maurer, T. Angular plasmon response of gold nanoparticles arrays: Approaching the Rayleigh limit. Nanophotonics 2017, 6, 279–288. [Google Scholar] [CrossRef]
- Chang, K.H.; Cheng, J.S.; Lu, T.W.; Lee, P.T. Engineering surface lattice resonance of elliptical gold nanodisk array for enhanced strain sensing. Opt. Express 2018, 26, 33215–33225. [Google Scholar] [CrossRef] [PubMed]
- Marae-Djouda, J.; Gontier, A.; Caputo, R.; Lévêque, G.; Bercu, B.; Madi, Y.; Montay, G.; Adam, P.M.; Molinari, M.; Stagon, S.; et al. Dense brushes of tilted metallic nanorods grown onto stretchable substrates for optical strain sensing. ACS Appl. Nano Mater. 2018, 1, 2347–2355. [Google Scholar] [CrossRef]
- Utyushev, A.D.; Zakomirnyi, V.I.; Rasskazov, I.L. Collective lattice resonances: Plasmonics and beyond. Rev. Phys. 2021, 6, 100051. [Google Scholar] [CrossRef]
- Ashraf, I.; Konrad, A.; Lokstein, H.; Skandary, S.; Metzger, M.; Djouda, J.M.; Maurer, T.; Adam, P.M.; Meixner, A.J.; Brecht, M. Temperature dependence of metal-enhanced fluorescence of photosystem I from Thermosynechococcus elongatus. Nanoscale 2017, 9, 4196–4204. [Google Scholar] [CrossRef]
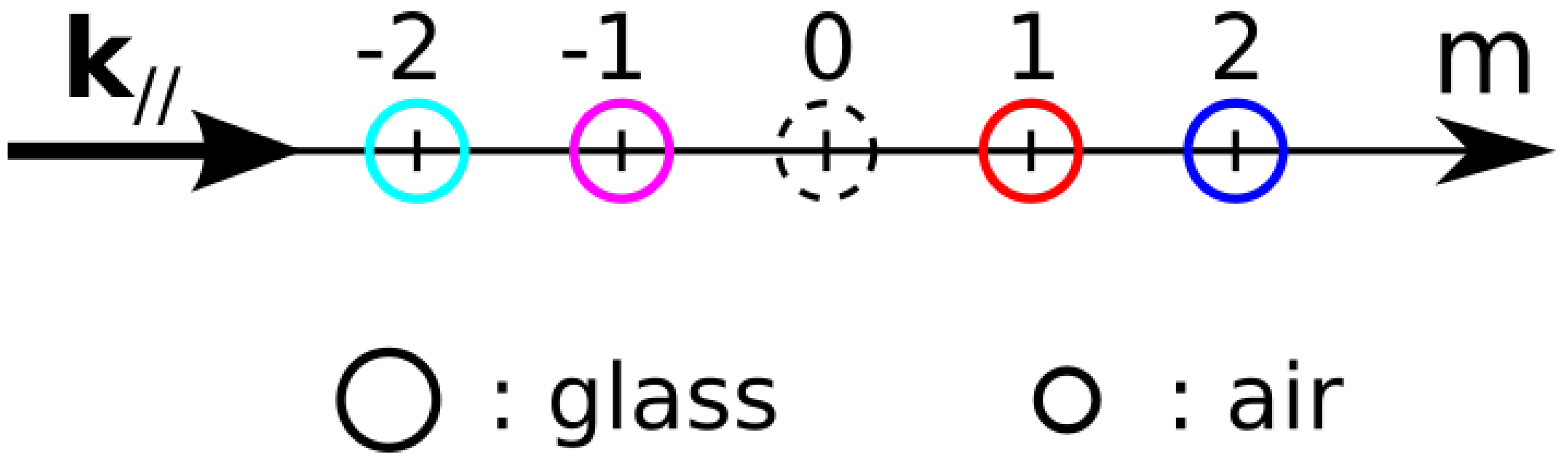

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferraro, A.; Djouda, J.M.; Lio, G.E.; Lévêque, G.; Adam, P.-M.; Umeton, C.P.; Maurer, T.; Caputo, R. Investigation of Lattice Plasmon Modes in 2D Arrays of Au Nanoantennas. Crystals 2022, 12, 336. https://doi.org/10.3390/cryst12030336
Ferraro A, Djouda JM, Lio GE, Lévêque G, Adam P-M, Umeton CP, Maurer T, Caputo R. Investigation of Lattice Plasmon Modes in 2D Arrays of Au Nanoantennas. Crystals. 2022; 12(3):336. https://doi.org/10.3390/cryst12030336
Chicago/Turabian StyleFerraro, Antonio, Joseph Marae Djouda, Giuseppe Emanuele Lio, Gaëtan Lévêque, Pierre-Michel Adam, Cesare Paolo Umeton, Thomas Maurer, and Roberto Caputo. 2022. "Investigation of Lattice Plasmon Modes in 2D Arrays of Au Nanoantennas" Crystals 12, no. 3: 336. https://doi.org/10.3390/cryst12030336
APA StyleFerraro, A., Djouda, J. M., Lio, G. E., Lévêque, G., Adam, P. -M., Umeton, C. P., Maurer, T., & Caputo, R. (2022). Investigation of Lattice Plasmon Modes in 2D Arrays of Au Nanoantennas. Crystals, 12(3), 336. https://doi.org/10.3390/cryst12030336









