High-Precision Beam Angle Expander Based on Polymeric Liquid Crystal Polarization Lenses for LiDAR Applications
Abstract
:1. Introduction
2. Working Principle
2.1. BAE Module
2.2. PB Lens
3. Experimental Results
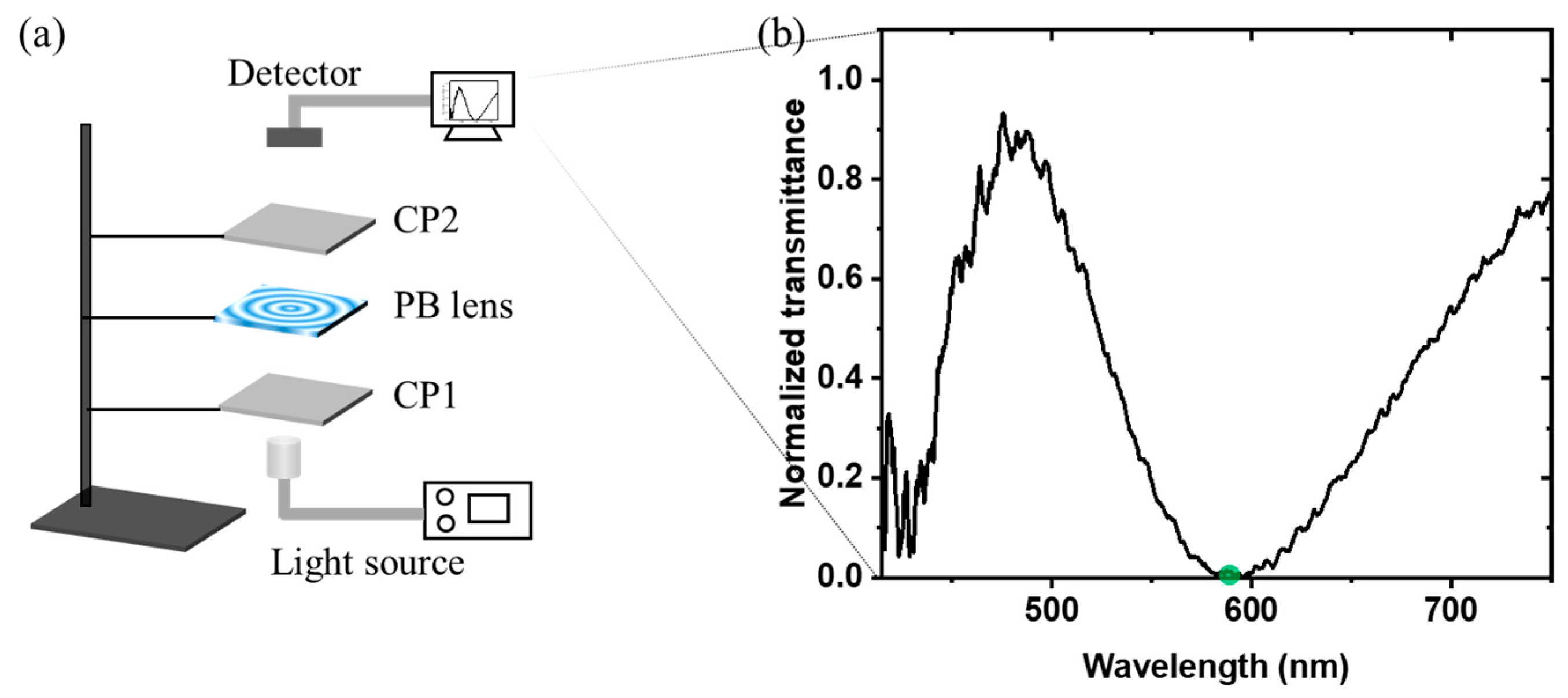
3.1. Infrared PB Lens Fabrication and Characterization
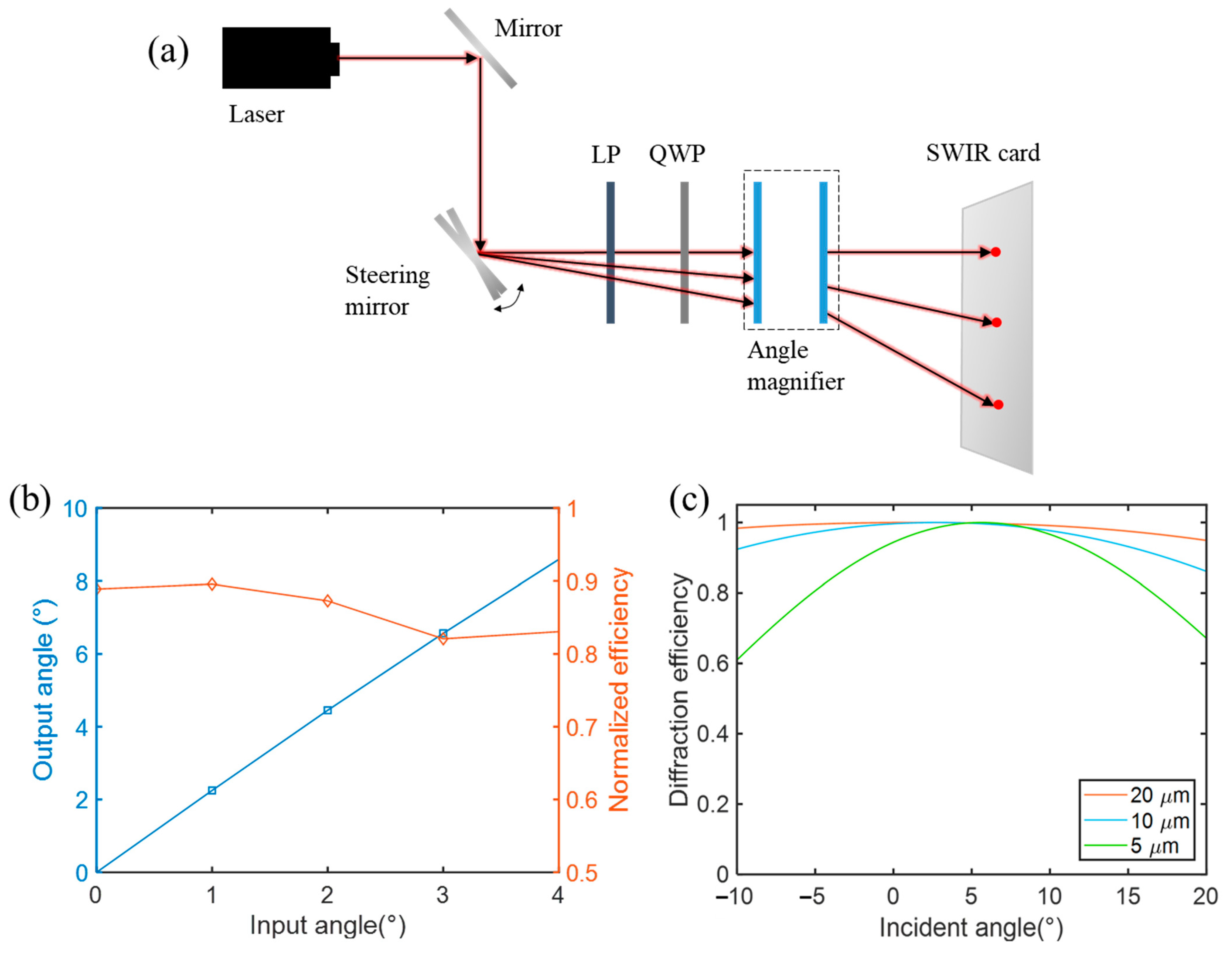
3.2. Angle Magnifier Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Resler, D.P.; Hobbs, D.S.; Sharp, R.C.; Friedman, L.J.; Dorschner, T.A. High-efficiency liquid-crystal optical phased-array beam steering. Opt. Express 1996, 21, 689–691. [Google Scholar] [CrossRef]
- McManamon, P.F.; Bos, P.J.; Escuti, M.J.; Heikenfeld, J.; Serati, S.; Xie, H.; Watson, E.A. A review of phased array steering for narrow-band electrooptical systems. Proc. IEEE 2009, 97, 1078–1096. [Google Scholar] [CrossRef]
- Takashima, Y.; Hellman, B. Review paper: Imaging lidar by digital micromirror device. Opt. Rev. 2020, 27, 400–408. [Google Scholar] [CrossRef]
- Davis, S.R.; Farca, G.; Rommel, S.D.; Johnson, S.; Anderson, M.H. Liquid crystal waveguides: New devices enabled by >1000 waves of optical phase control. Proc. SPIE 2010, 7618, 76180E. [Google Scholar]
- He, Z.; Gou, F.; Chen, R.; Yin, K.; Zhan, T.; Wu, S.T. Liquid Crystal Beam Steering Devices: Principles, Recent Advances, and Future Developments. Crystals 2019, 9, 292. [Google Scholar] [CrossRef] [Green Version]
- Hoy, C.; Stockley, J.; Shane, J.; Kluttz, K.; Mcknight, D.; Serati, S. Non-Mechanical Beam Steering with Polarization Gratings: A Review. Crystals 2021, 11, 361. [Google Scholar] [CrossRef]
- He, Z.; Wu, S.T. Compact, Fast-Response, Continuous, and Wide-Angle Laser Beam Steerers. J. Soc. Inf. Display 2021, 29, 281–287. [Google Scholar] [CrossRef]
- Liu, C.; Li, L.; Wang, Q.H. Liquid prism for beam tracking and steering. Opt. Eng. 2012, 51, 114002. [Google Scholar] [CrossRef]
- Lee, J.; Lee, J.; Won, Y.H. Achromatic doublet electrowetting prism array for beam steering device in foveated display. Opt. Express 2022, 30, 2078–2088. [Google Scholar] [CrossRef]
- Akatay, A.; Ataman, C.; Urey, H. High-resolution beam steering using microlens arrays. Opt. Lett. 2006, 31, 2861–2863. [Google Scholar] [CrossRef]
- Kim, J.; Miskiewicz, M.N.; Serati, S.; Escuti, M.J. Nonmechanical Laser Beam Steering Based on Polymer Polarization Gratings: Design Optimization and Demonstration. J. Light. Technol. 2015, 33, 2068–2077. [Google Scholar] [CrossRef]
- Gou, F.; Peng, F.; Ru, Q.; Lee, Y.H.; Chen, H.; He, Z.; Zhan, T.; Vodopyanov, K.L.; Wu, S.T. Mid-wave infrared beam steering based on high-efficiency liquid crystal diffractive waveplates. Opt. Express 2017, 25, 22404–22410. [Google Scholar] [CrossRef] [PubMed]
- Xiao, F.; Kong, L. Angular magnification method of liquid crystal optical phased array based on telescope system. Int. Soc. Opt. Photonics 2013, 8906, 89062C. [Google Scholar]
- He, Z.; Yin, K.; Wu, S.T. Miniature planar telescopes for efficient, wide-angle, high-precision beam steering. Light Sci. Appl. 2021, 10, 134. [Google Scholar] [CrossRef] [PubMed]
- Pancharatnam, S. Generalized theory of interference and its applications. Proc. Indian Acad. Sci. Sect. A 1956, 44, 398–417. [Google Scholar] [CrossRef]
- Gao, K.; Cheng, H.H.; Bhowmik, A.K.; Bos, P.J. Thin-film Pancharatnam lens with low f-number and high quality. Opt. Express 2015, 23, 26086–26094. [Google Scholar] [CrossRef]
- Li, Y.; Zhan, T.; Wu, S.T. Flat cholesteric liquid crystal polymeric lens with low f-number. Opt. Express 2020, 28, 5875–5882. [Google Scholar] [CrossRef]
- Tabiryan, N.V.; Roberts, D.E.; Liao, Z.; Hwang, J.Y.; Moran, M.; Ouskova, O.; Pshenichnyi, A.; Sigley, J.; Tabirian, A.; Vergara, R.; et al. Advances in Transparent Planar Optics: Enabling Large Aperture, Ultrathin Lenses. Adv. Opt. Mater. 2021, 9, 2001692. [Google Scholar] [CrossRef]
- Kim, J.; Li, Y.; Miskiewicz, M.N.; Oh, C.; Kudenov, M.W.; Escuti, M.J. Fabrication of ideal geometric-phase holograms with arbitrary wavefronts. Optica 2015, 2, 958–964. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Q.; Xiong, J.; Li, K.; Wu, S.T. Dual-depth augmented reality display with reflective polarization-dependent lenses. Opt. Express 2021, 29, 31478–31487. [Google Scholar] [CrossRef]
- Chigrinov, V.G.; Kozenkov, V.M.; Kwok, H.S. Photoalignment of Liquid Crystalline Materials: Physics and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Yin, K.; Xiong, J.; He, Z.; Wu, S.T. Patterning Liquid Crystal Alignment for Ultra-Thin Flat Optics. ACS Omega 2020, 5, 31485–31489. [Google Scholar] [CrossRef] [PubMed]
- Moharam, M.G.; Gaylord, T.K. Rigorous coupled-wave analysis of planar-grating diffraction. J. Opt. Soc. Am. A 1981, 71, 811818. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, W.; Yu, Y.; Wang, Q.; Mu, Q.; Li, S.; Chen, J. Twisting structures in liquid crystal polarization gratings and lenses. Crystals 2021, 11, 243. [Google Scholar] [CrossRef]


| Solute: Solvent | Coating Speed | |
|---|---|---|
| 1st LC layer | 1:4 | 1000 (30 s) |
| 2nd–8th LC layer | 1:4 | 2000 (30 s) |
| d1 (cm) | f1 (cm) | f2 (cm) | d (cm) | D1 (cm) | f1/# | D2 (cm) | f2/# | M | |
|---|---|---|---|---|---|---|---|---|---|
| 1550 nm | 1 | 1 | −0.11 | 0.88 | 0.17 | 5.71 | 0.17 | 0.64 | 8.87 |
| 2 | −0.21 | 1.78 | 0.17 | 11.43 | 0.33 | 0.64 | 9.37 | ||
| 2 | 1 | −0.12 | 0.87 | 0.35 | 2.85 | 0.19 | 0.64 | 7.87 | |
| 2 | −0.22 | 1.77 | 0.35 | 2 | 0.35 | 0.64 | 8.87 | ||
| 905 nm | 1 | 1 | −0.19 | 0.80 | 0.17 | 5.71 | 0.17 | 1.1 | 5.18 |
| 2 | −0.35 | 1.64 | 0.17 | 11.43 | 0.31 | 1.1 | 5.68 | ||
| 2 | 1 | −0.24 | 0.76 | 0.35 | 2.85 | 0.21 | 1.1 | 4.18 | |
| 2 | −0.38 | 1.61 | 0.35 | 2 | 0.35 | 1.1 | 5.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Luo, Z.; Wu, S.-T. High-Precision Beam Angle Expander Based on Polymeric Liquid Crystal Polarization Lenses for LiDAR Applications. Crystals 2022, 12, 349. https://doi.org/10.3390/cryst12030349
Li Y, Luo Z, Wu S-T. High-Precision Beam Angle Expander Based on Polymeric Liquid Crystal Polarization Lenses for LiDAR Applications. Crystals. 2022; 12(3):349. https://doi.org/10.3390/cryst12030349
Chicago/Turabian StyleLi, Yannanqi, Zhenyi Luo, and Shin-Tson Wu. 2022. "High-Precision Beam Angle Expander Based on Polymeric Liquid Crystal Polarization Lenses for LiDAR Applications" Crystals 12, no. 3: 349. https://doi.org/10.3390/cryst12030349






