Research on the Impact-Induced Deflagration Behavior by Aluminum/Teflon Projectile
Abstract
:1. Introduction
2. Experiment
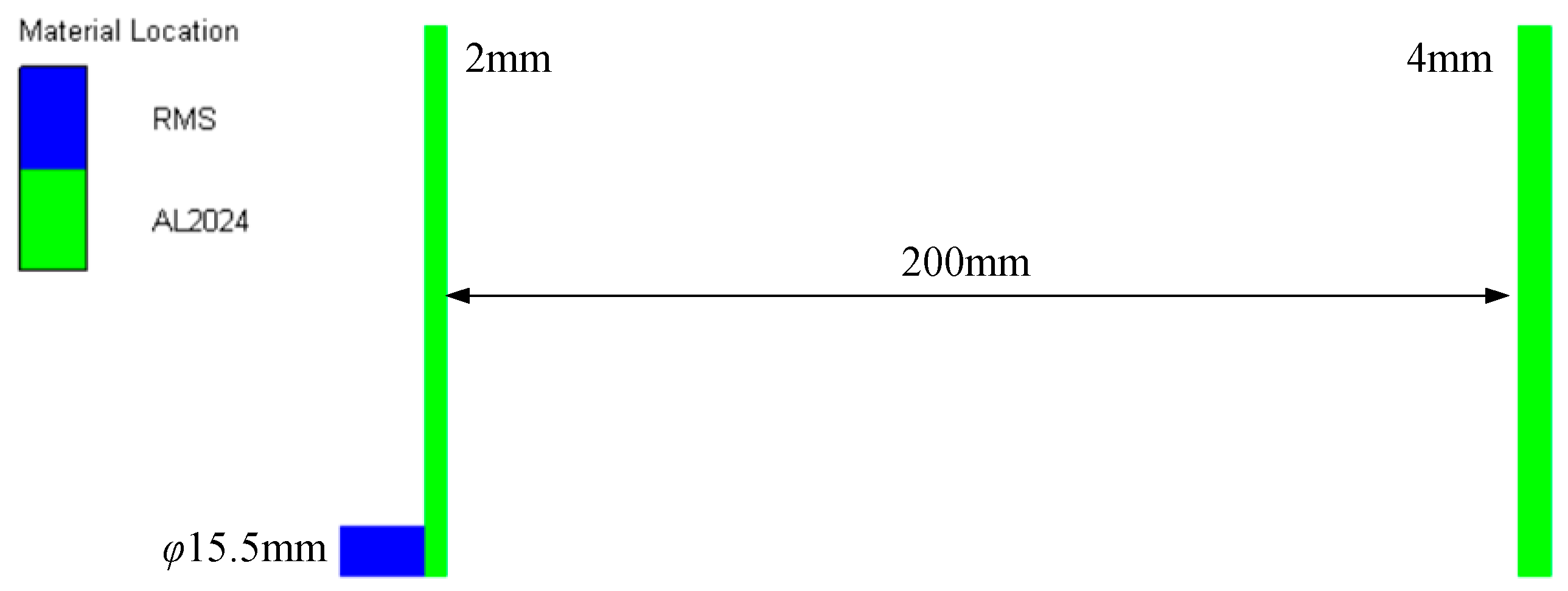
2.1. Specimen Preparation
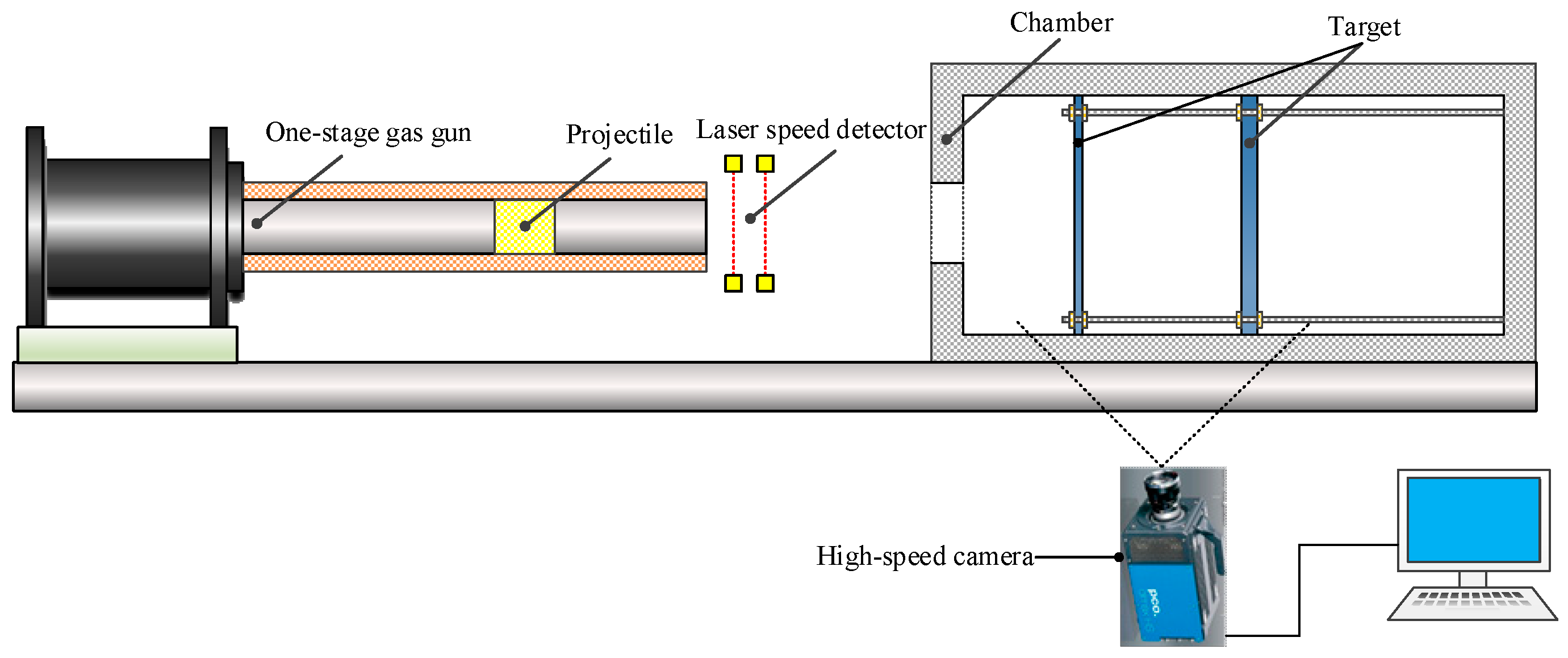
2.2. Experiment Setup
2.3. The Damage Effects of Double-Spaced Al Plates
3. Numerical Simulation
3.1. Reaction Model of Energy Release Process by RMs
3.1.1. EOS of Unreacted Reactant
3.1.2. Ignition Criterion
3.1.3. EOS of Reaction Product
3.1.4. Reaction Rate
3.1.5. Mixing Rule
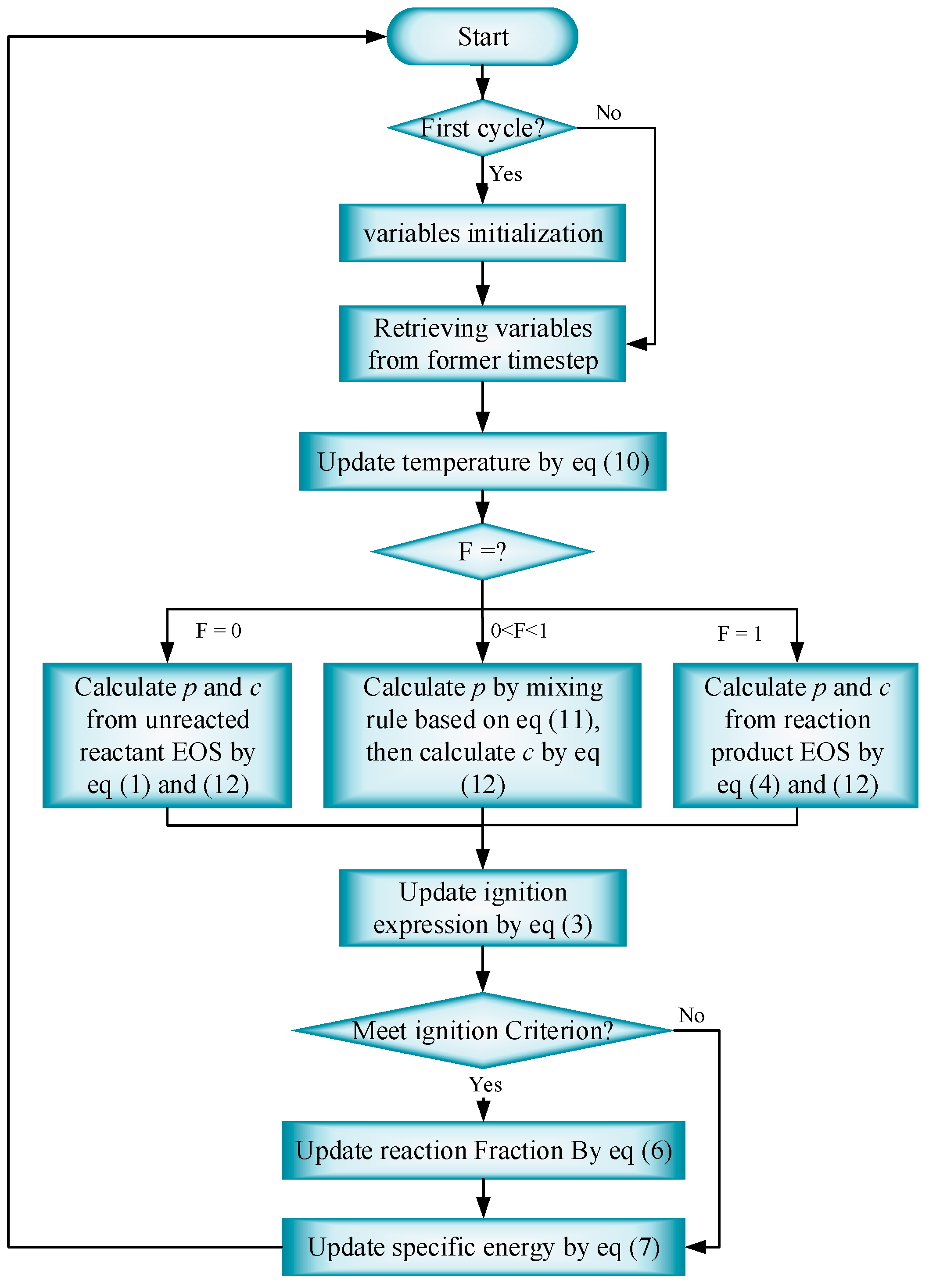
3.1.6. Program Implementation in Autodyn User’s Subroutines
3.2. Constitutive Model
3.3. Finite Element Model
4. Result and Discussion
4.1. Penetration Mechanism
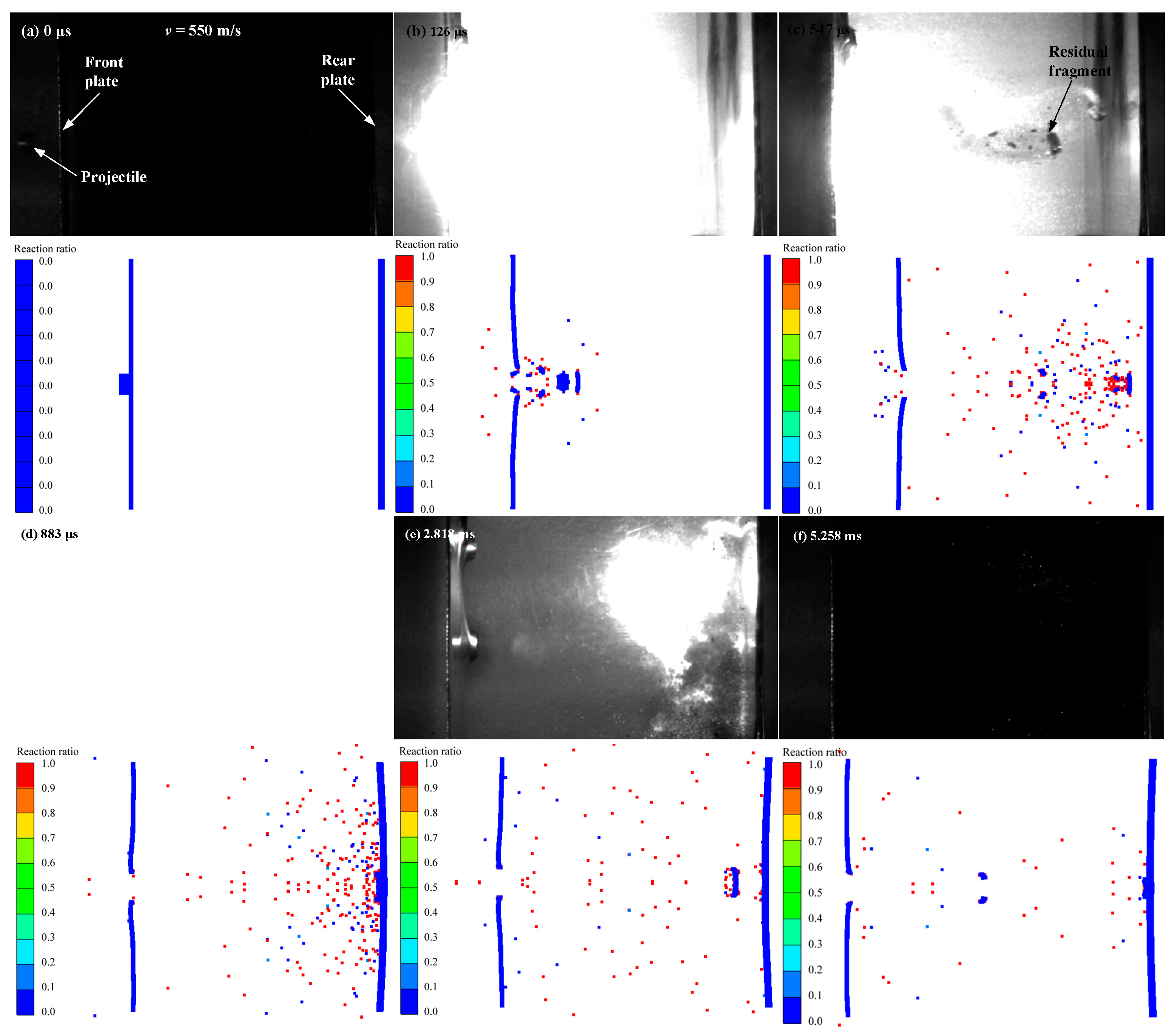
4.2. The Impact-Induced Deflagration Behavior
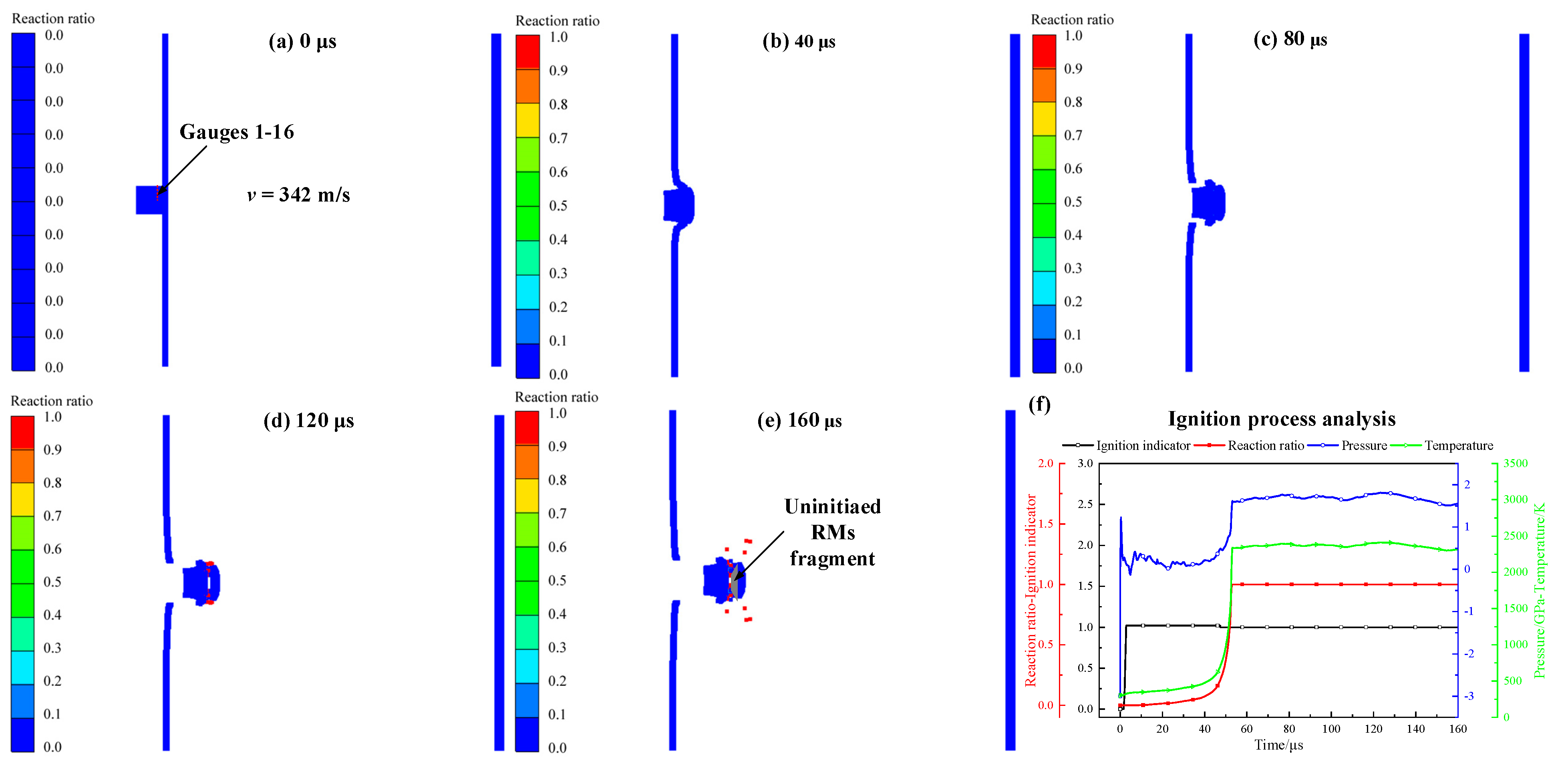
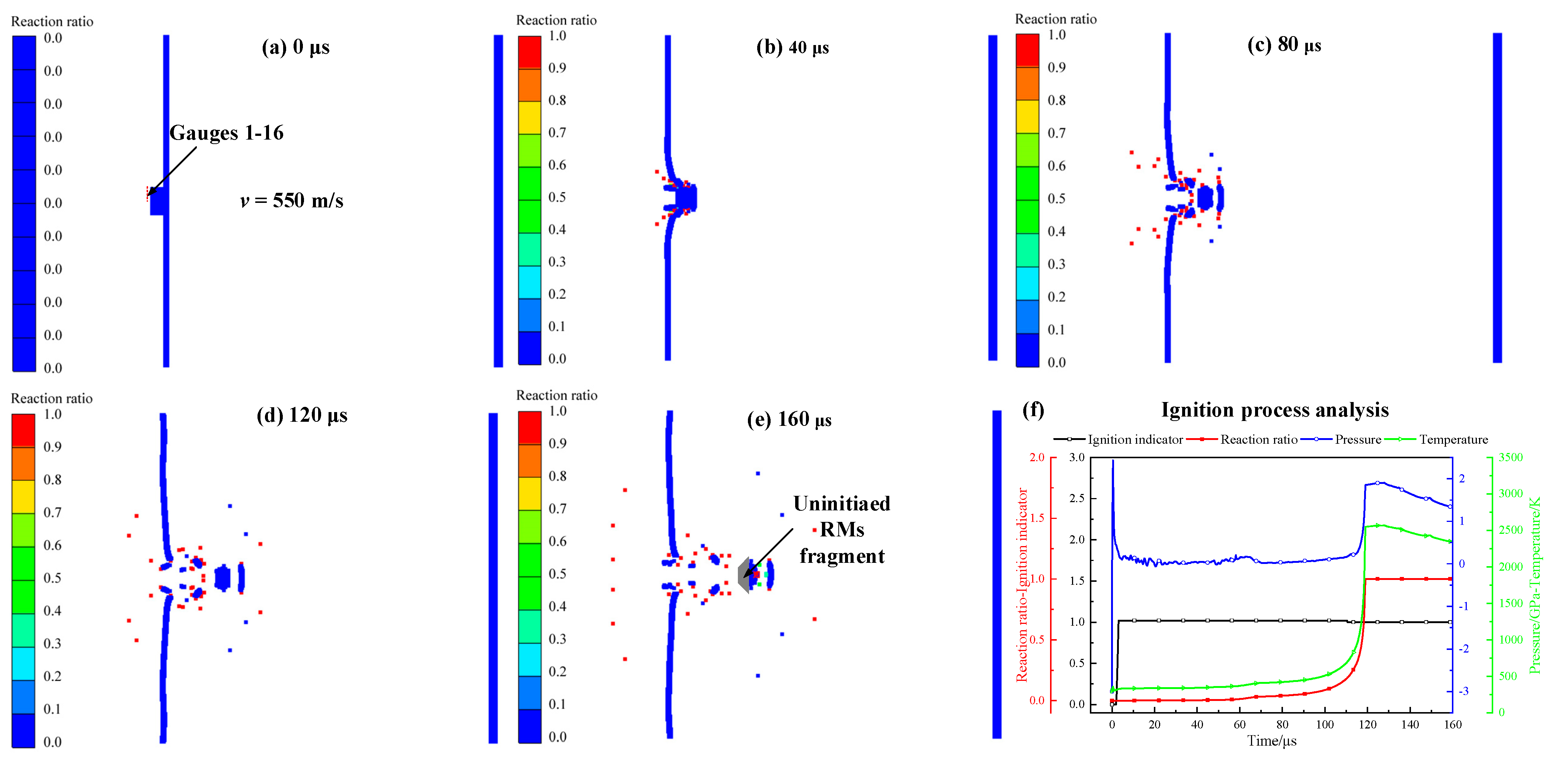
4.3. The Ignition Behavior
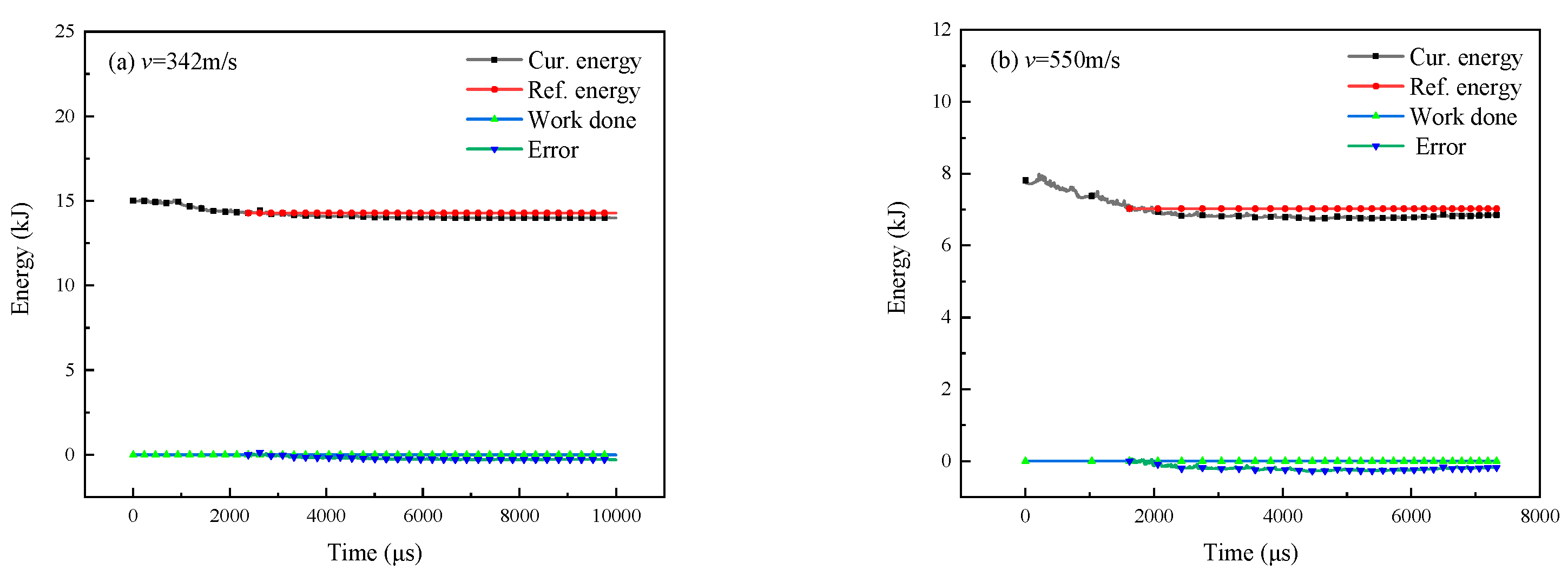
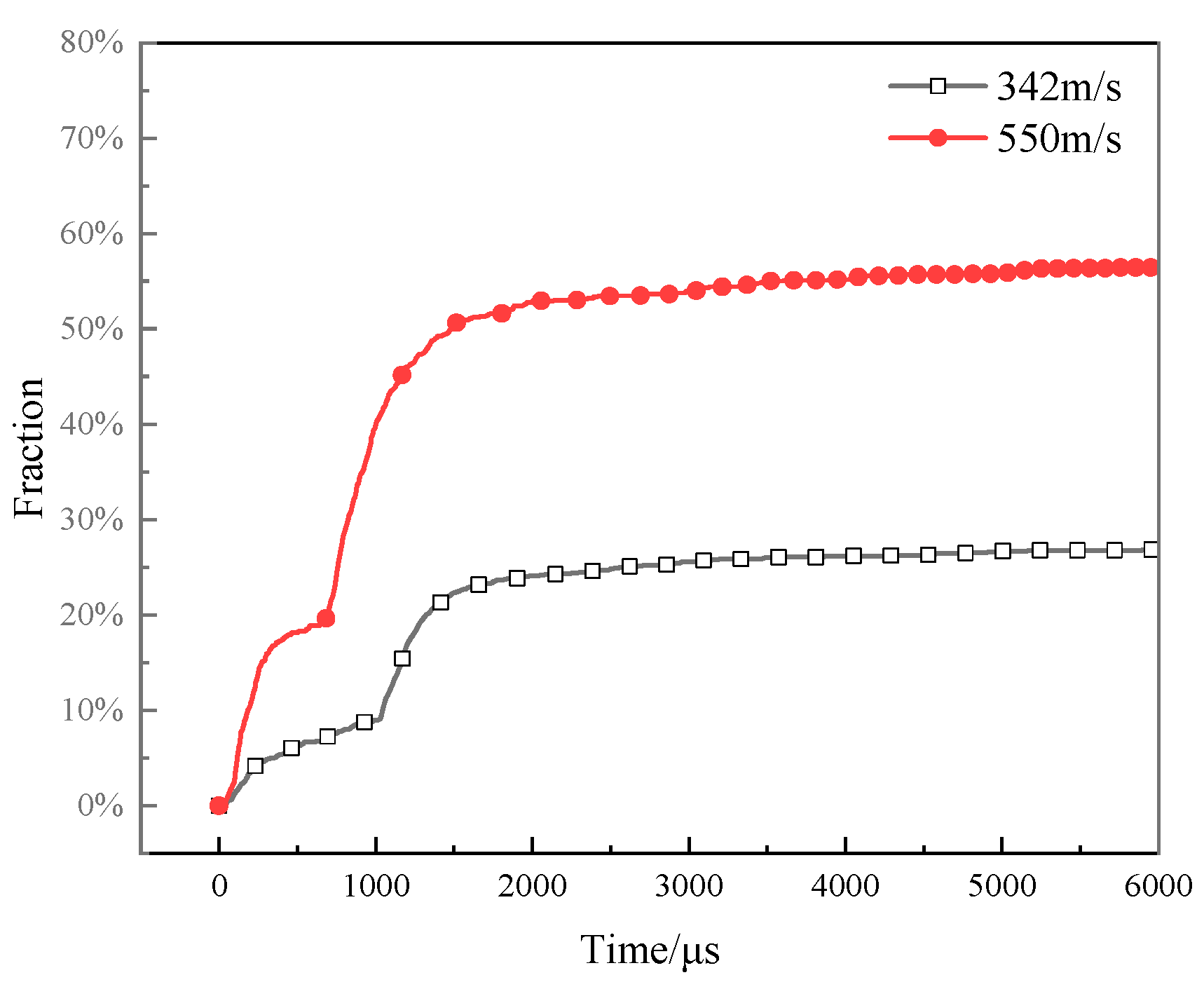
4.4. The Energy Release Behavior of RMPs
4.5. The Temperature Rise Effect
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ames, R.G. Vented chamber calorimetry for impact-initiated energetic materials. 43rd AIAA Aerosp. Sci. Meet. Exhib.-Meet. Pap. 2005, 15391–15403. [Google Scholar] [CrossRef]
- Zheng, Y.; Zheng, Z.; Lu, G.; Wang, H.; Guo, H. Mesoscale study on explosion-induced formation and thermochemical response of PTFE/Al granular jet. Def. Technol. 2022. [Google Scholar] [CrossRef]
- Rosencrantz, S.D. Characterization and Modeling Methodology of Polytetrafluoroethylene Based Reactive Materials for the Development of Parametric Models. Ph.D. Thesis, Wright State University, Dayton, OH, USA, 2007. [Google Scholar]
- Guo, H.; Zheng, Y.; Yu, Q.; Ge, C.; Wang, H. Penetration behavior of reactive liner shaped charge jet impacting thick steel plates. Int. J. Impact Eng. 2019, 126, 76–84. [Google Scholar] [CrossRef]
- Liu, S.B.; Yuan, Y.; Zheng, Y.F.; Ge, C.; Wang, H.F. Enhanced ignition behavior of reactive material projectiles impacting fuel-filled tank. Def. Technol. 2019, 15, 533–540. [Google Scholar] [CrossRef]
- Zheng, Y.; Su, C.; Guo, H.; Yu, Q.; Wang, H. Behind-Target Rupturing Effects of Sandwich-like Plates by Reactive Liner Shaped Charge Jet. Propellants Explos. Pyrotech. 2019, 44, 1400–1409. [Google Scholar] [CrossRef]
- Xiao, J.; Zhang, X.; Guo, Z.; Wang, H. Enhanced Damage Effects of Multi-Layered Concrete Target Produced by Reactive Materials Liner. Propellants Explos. Pyrotech. 2018, 43, 955–961. [Google Scholar] [CrossRef]
- Xiao, J.; Nie, Z.; Wang, Z.; Du, Y.; Tang, E. Energy release behavior of Al/PTFE reactive materials powder in a closed chamber. J. Appl. Phys. 2020, 127, 165106. [Google Scholar] [CrossRef]
- Canonsburg, T.D. Application of CFD into an automotive torque converter. Knowl. Creat. Diffus. Util. 2012, 15317, 724–746. [Google Scholar]
- Wang, H.F.; Zheng, Y.F.; Yu, Q.B.; Liu, Z.W.; Yu, W.M. Study on initiation mechanism of reactive fragment to covered explosive. Beijing Ligong Daxue Xuebao/Trans. Beijing Inst. Technol. 2012, 32, 786–823. [Google Scholar]
- Raftenberg, M.N.; Mock, W.; Kirby, G.C. Modeling the impact deformation of rods of a pressed PTFE/Al composite mixture. Int. J. Impact Eng. 2008, 35, 1735–1744. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Xu, S.-L.; Zhang, T. Preparation and Performance of PTEF/Al Reactive Materials. J. Natl. Univ. Def. Technol. 2008, 30, 39–42. [Google Scholar]
- Jiang, J.-W.; Wang, S.-Y.; Zhang, M.; Wei, Q. Modeling and simulation of JWL equation of state for reactive Al/PTFE mixture. J. Beijing Inst. Technol. 2012, 21, 150–156. [Google Scholar]
- Lee, E.L.; Tarver, C.M. Phenomenological model of shock initiation in heterogeneous explosives. Phys. Fluids 1980, 23, 2362–2372. [Google Scholar] [CrossRef]
- Mock, W.; Holt, W.H. Impact initiation of rods of pressed polytetrafluoroethylene (PTFE) and aluminum powders. AIP Conf. Proc. 2006, 845, 1097–1100. [Google Scholar]
- Mock, W.; Drotar, J.T. Effect of aluminum particle size on the impact initiation of pressed PTFE/Al composite rods. AIP Conf. Proc. 2007, 955, 971–974. [Google Scholar]
- Zhang, X.P.; Xiao, J.G.; Yu, Q.B.; Zheng, Y.F.; Wang, H.F. Demolition effect of reactive material liner shaped charge against concrete target. Beijing Ligong Daxue Xuebao/Trans. Beijing Inst. Technol. 2016, 36, 1211–1215. [Google Scholar]
- Yi, J.; Wang, Z.; Yin, J.; Zhang, Z. Simulation study on expansive jet formation characteristics of polymer liner. Materials 2019, 12, 744. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.F.; Shi, A.S.; Qiao, L.; Zhang, J.; Zhang, Y.G.; Guan, Z.W. Experimental study on impact-initiated characters of multifunctional energetic structural materials. J. Appl. Phys. 2013, 113, 083508. [Google Scholar] [CrossRef]
- Su, C.; Wang, H.; Xie, J.; Ge, C.; Zheng, Y. Penetration and Damage Effects of Reactive Material Jet against Concrete Target. Binggong Xuebao/Acta Armamentarii 2019, 40, 1829–1835. [Google Scholar]
- Zhang, Z.Y.; Tian, Z.D.; Chen, J.; Duan, Z.P. Detonation Physics; National University of Defense Technology Press: Changsha, China, 2016; p. 270. [Google Scholar]
- Lee, E.L.; Hornig, H.C.; Kury, J.W. Adiabatic Expansion of High Explosive Detonation Products; Report UCRL-50422; Lawrence Radiation Labroratory of University of California: Livermore, CA, USA, 1968. [Google Scholar]
- Xu, F.Y.; Zheng, Y.F.; Yu, Q.B.; Wang, Y.Z.; Wang, H.F. Experimental study on penetration behavior of reactive material projectile impacting aluminum plate. Int. J. Impact Eng. 2016, 95, 125–132. [Google Scholar] [CrossRef]
- Xu, F.Y.; Zheng, Y.F.; Yu, Q.B.; Zhang, X.P.; Wang, H.F. Damage effects of aluminum plate by reactive material projectile impact. Int. J. Impact Eng. 2017, 104, 38–44. [Google Scholar] [CrossRef]
- Xu, F.Y.; Yu, Q.B.; Zheng, Y.F.; Lei, M.A.; Wang, H.F. Damage effects of double-spaced aluminum plates by reactive material projectile impact. Int. J. Impact Eng. 2017, 104, 13–20. [Google Scholar] [CrossRef]
- Feng, B.; Li, Y.; Wu, S.; Wang, H.; Tao, Z.; Fang, X. A crack-induced initiation mechanism of Al-PTFE under quasi-static compression and the investigation of influencing factors. Mater. Des. 2016, 108, 411–417. [Google Scholar] [CrossRef]
- Feng, B.; Fang, X.; Li, Y.C.; Wang, H.X.; Mao, Y.M.; Wu, S.Z. An initiation phenomenon of Al-PTFE under quasi-static compression. Chem. Phys. Lett. 2015, 637, 38–41. [Google Scholar] [CrossRef]
- Sippel, T.R.; Son, S.F.; Groven, L.J. Aluminum agglomeration reduction in a composite propellant using tailored Al/PTFE particles. Combust. Flame 2014, 161, 311–321. [Google Scholar] [CrossRef]
- Osborne, D.T.; Pantoya, M.L. Effect of Al particle size on the thermal degradation of Al/Teflon mixtures. Combust. Sci. Technol. 2007, 179, 1467–1480. [Google Scholar] [CrossRef]
- Mohan, S.; Trunov, M.A.; Dreizin, E.L. Heating and ignition of metallic particles by a CO2 laser. J. Propuls. Power 2008, 24, 199–205. [Google Scholar] [CrossRef]
- Wu, Y. Study on Reaction Heat Measuring and Energy Release Characteristics of PTFE/Al Reactive Material; National University of Defense Technology: Changsha, China, 2015. [Google Scholar]
- Dolgoborodov, A.Y.; Makhov, M.N.; Kolbanev, I.V.; Streletskiǐ, A.N.; Fortov, V.E. Detonation in an aluminum-teflon mixture. JETP Lett. 2005, 81, 311–314. [Google Scholar] [CrossRef]
- Dolgoborodov, A.Y.; Makhov, M.N.; Streletskii, A.N.; Kolbanev, I.V.; Gogulya, M.F.; Brazhnikov, M.A.; Fortov, V.E. Detonation-like phenomena in non-explosive oxidizer-metal mixtures. In Proceedings of the 31st International Pyrotechnics Seminar, Fort Collins, CO, USA, 11–16 July 2004; p. 569. [Google Scholar]
- Raftenberg, M.N.; Scheidler, M.J.; Casem, D.A. A Yield Strength Model and Thoughts on an Ignition Criterion for a Reactive PTFE-Aluminum Composite; Report ARL-RP-219; Army Research Laboratory: Aberdeen Proving Ground, MD, USA, 2008. [Google Scholar]

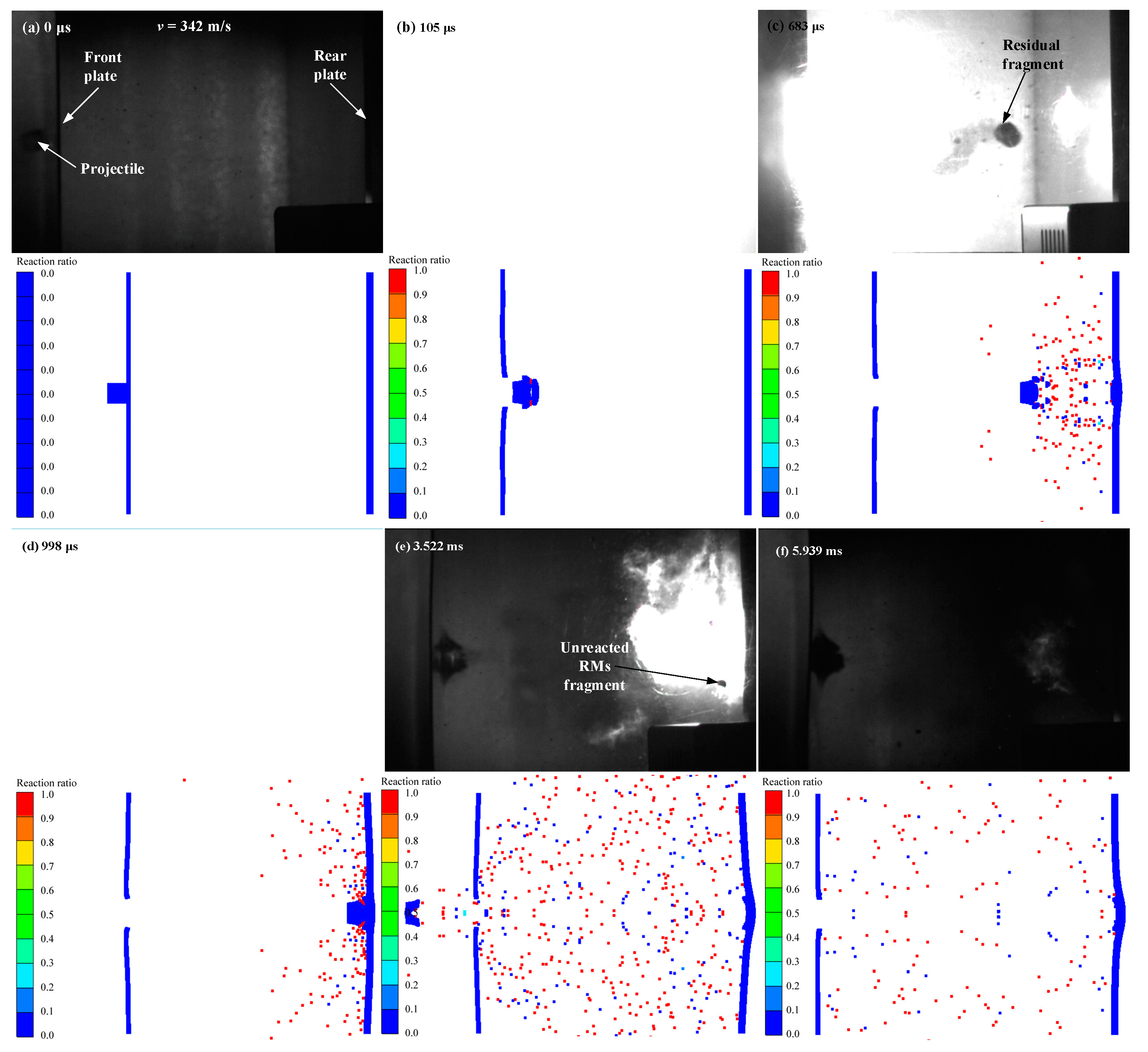

| Shot | Projectile Size (ΦD × L) (mm) | Velocity (m/s) | Penetration Hole Diameter on FP (mm) | Deflagration Time (μs) | ||
|---|---|---|---|---|---|---|
| Perforating FP | Impacting on RP | Fades Away | ||||
| 10-1 | 15.40 × 15.39 | 293 | ~15.47 | 210.24 | 210.24 | 1629.35 |
| 10-2 | 15.39 × 15.38 | 342 | ~18.01 | 420.48 | 998.63 | 5045.73 |
| 10-3 | 15.40 × 15.36 | 401 | ~24.53 | 367.92 | 2890.78 | 8672.34 |
| 10-4 | 15.41 × 15.21 | 397 | ~20.06 | 473.04 | 3521.50 | 9040.26 |
| 12-1 | 15.40 × 7.64 | 652 | 18.62 | 252.39 | 378.58 | 8539.10 |
| 12-2 | 15.50 × 7.76 | 570 | 18.73 | 294.45 | 3070.71 | 7697.81 |
| 12-3 | 15.50 × 7.80 | 550 | 17.33 | 210.32 | 252.39 | 4374.71 |
| 12-4 | 15.40 × 7.30 | 620 | 19.37 | 126.19 | 1724.65 | 8286.71 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, J.; Wang, Y.; Zhou, D.; He, C.; Li, X. Research on the Impact-Induced Deflagration Behavior by Aluminum/Teflon Projectile. Crystals 2022, 12, 471. https://doi.org/10.3390/cryst12040471
Xiao J, Wang Y, Zhou D, He C, Li X. Research on the Impact-Induced Deflagration Behavior by Aluminum/Teflon Projectile. Crystals. 2022; 12(4):471. https://doi.org/10.3390/cryst12040471
Chicago/Turabian StyleXiao, Jianguang, Yanxin Wang, Dongmo Zhou, Chenglong He, and Xiangrong Li. 2022. "Research on the Impact-Induced Deflagration Behavior by Aluminum/Teflon Projectile" Crystals 12, no. 4: 471. https://doi.org/10.3390/cryst12040471
APA StyleXiao, J., Wang, Y., Zhou, D., He, C., & Li, X. (2022). Research on the Impact-Induced Deflagration Behavior by Aluminum/Teflon Projectile. Crystals, 12(4), 471. https://doi.org/10.3390/cryst12040471






