On-State Voltage Drop Analytical Model for 4H-SiC Trench IGBTs
Abstract
:1. Introduction
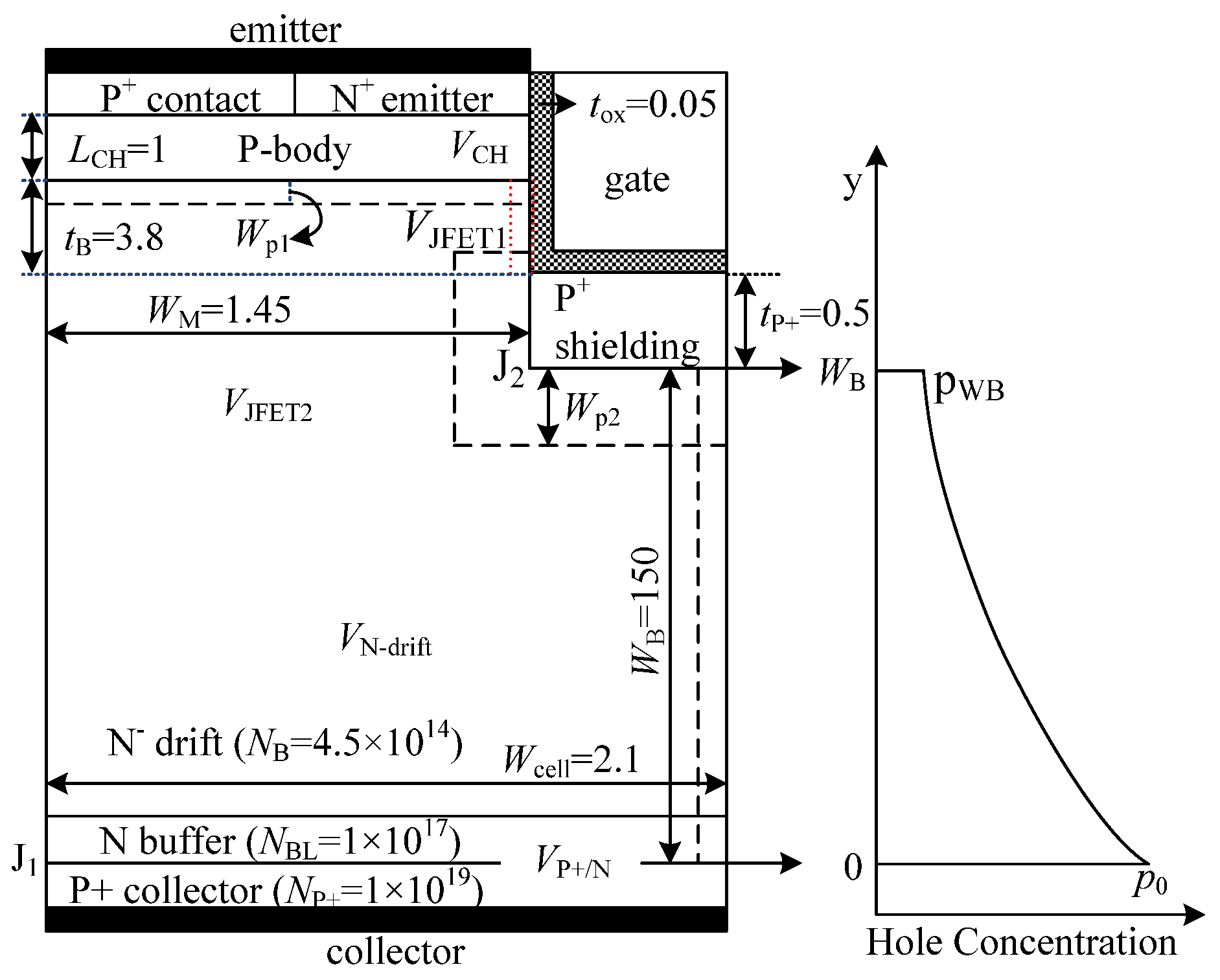
2. Forward Voltage Drop Analytical Model
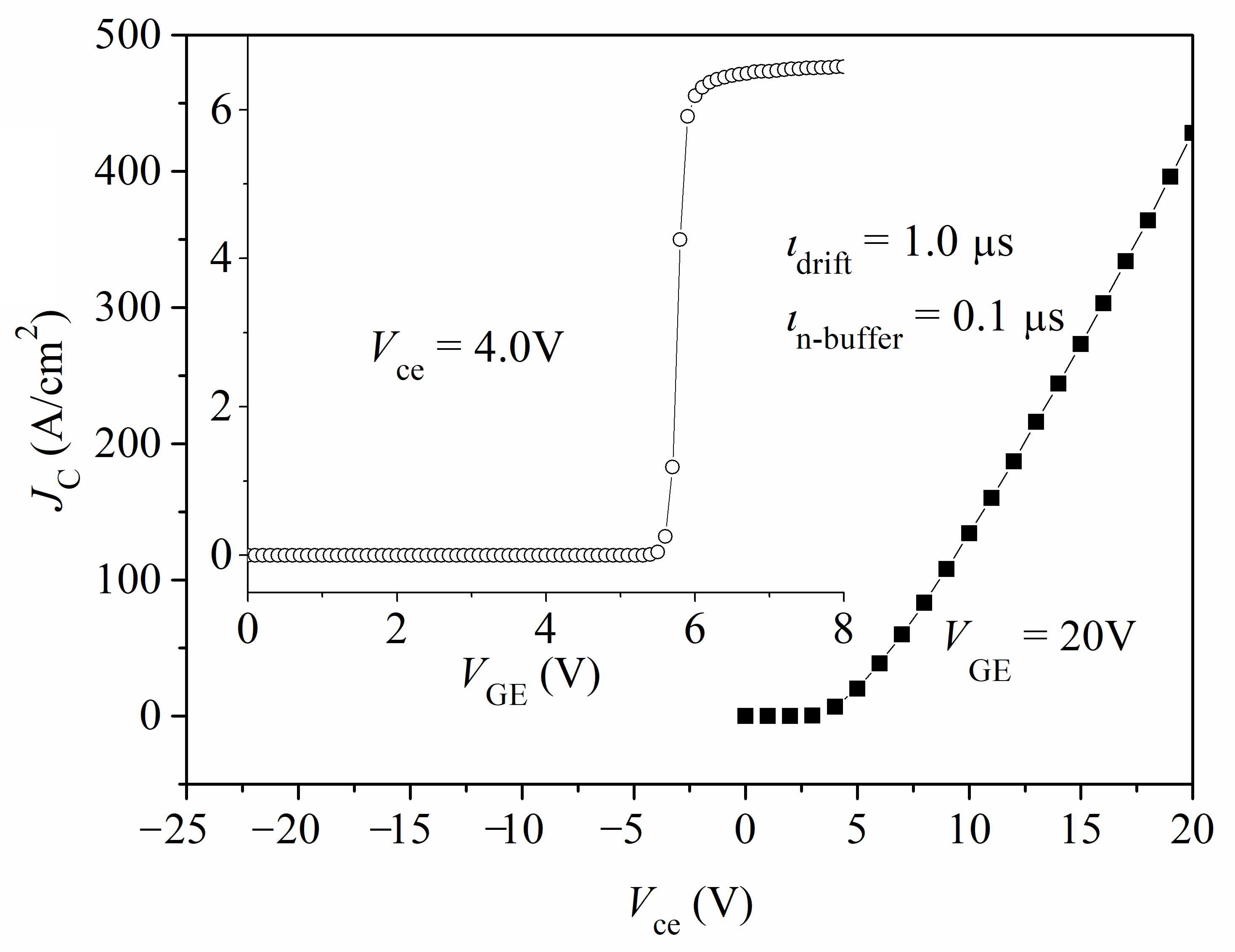
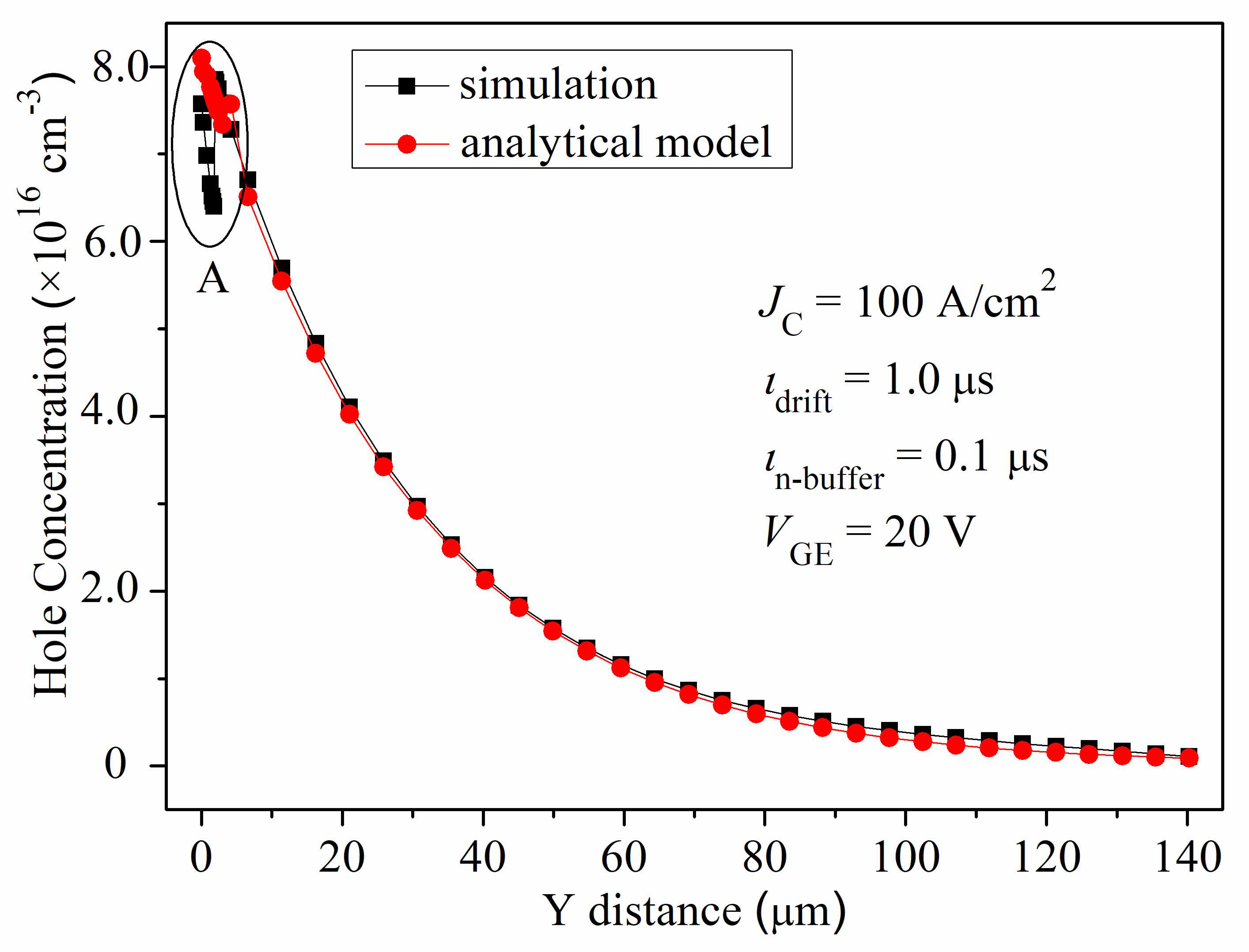
3. Simulation Results and Verification
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Roccaforte, F.; Fiorenza, P.; Greco, G.; Nigro, R.L.; Giannazzoa, F.; Iucolanob, F.; Saggiob, M. Emerging Trends in Wide Band Gap Semiconductors (SiC and GaN) Technology for Power Devices. Microelectron. Eng. 2018, 187–188, 66–77. [Google Scholar] [CrossRef]
- Nawaz, M. Predicting Potential of 4H-SiC Power Devices Over 10 kV. In Proceedings of the 2013 IEEE 10th International Conference on Power Electronics and Drive Systems (PEDS), Kitakyushu, Japan, 22–25 April 2013; pp. 1291–1296. [Google Scholar]
- Kumar, V.; Verma, J.; Maan, A.S.; Akhtar, J. Epitaxial 4H-SiC based Schottky diode temperature sensors in ultra-low current range. Vacuum 2020, 182, 109590. [Google Scholar] [CrossRef]
- Kumar, V.; Maan, A.S.; Akhtar, J. Barrier height inhomogeneities induced anomaly in thermal sensitivity of Ni/4H-SiC Schottky diode temperature sensor. J. Vac. Sci. Technol. B 2014, 32, 041203. [Google Scholar] [CrossRef]
- Tang, G.; Tang, X.; Song, Q.; Yang, S.; Zhang, Y.; Zhang, Y.; Zhang, Y. Frequency-Improved 4H-SiC IGBT with Multizone Collector Design. IEEE Trans. Electron Devices 2020, 67, 198–203. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, M.; Jiang, H.P.; Li, B.K.; Chen, K.J. Gate Structure Design of SiC Trench IGBTs for Injection-Enhancement Effect. IEEE Trans. Electron Devices 2019, 66, 3034–3039. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, C.; Mao, H.; Wu, X.; Su, F.; Li, X.; Yang, J. Low Turn-Off Loss 4H-SiC Insulated Gate Bipolar Transistor with a Trench Heterojunction Collector. IEEE J. Electron Devices Soc. 2020, 8, 1010–1015. [Google Scholar] [CrossRef]
- Yang, T.; Wang, Y.; Yue, R. SiC Trench MOSFET with Reduced Switching Loss and Increased Short-Circuit Capability. IEEE Trans. Electron Devices 2020, 67, 3685–3690. [Google Scholar] [CrossRef]
- Wen, Z.-X.; Zhang, F.; Shen, Z.-W.; Chen, J.; He, Y.-W.; Yan, G.-G.; Liu, X.-F.; Zhao, W.-S.; Wang, L.; Sun, G.-S.; et al. Design and Fabrication of 10-kV Silicon-Carbide p-channel IGBTs with Hexagonal Cells and Step Space Modulated Junction Termination Extension. Chin. Phys. B 2019, 28, 068504. [Google Scholar] [CrossRef]
- Chowdhury, S.; Hitchcock, C.; Stum, Z. 4H-SiC n-Channel Insulated Gate Bipolar Transistors on (0001) and (000-1) Oriented Free-Standing n− Substrates. IEEE Electron Device Lett. 2016, 37, 317–320. [Google Scholar] [CrossRef]
- Ryu, S.; Capell, C.; Van Brunt, E. Ultra High Voltage MOS Controlled 4H-SiC Power Switching Devices. Semicond. Sci. Technol. 2015, 30, 084001. [Google Scholar] [CrossRef]
- Menon, K.G.; Nakajima, A.; Ngwendson, L. Performance Evaluation of 10-kV SiC Trench Clustered IGBT. IEEE Electron Device Lett. 2011, 32, 1272–1274. [Google Scholar]
- Menon, K.G.; Narayanan, E.M.S. Numerical Evaluation of 10-kV Clustered Insulated Gate Bipolar Transistor in 4H-SiC. IEEE Trans. Electron Devices 2013, 60, 366–373. [Google Scholar] [CrossRef]
- Lee, M.C.; Huang, A.Q. An Injection Efficiency Model to Characterize the Injection Capability and Turn-off Speed for >10 kV 4H-SiC IGBTs. Solid-State Electron. 2014, 93, 27–39. [Google Scholar] [CrossRef]
- Wang, H.Y.; Su, M.; Sheng, K. Theoretical Performance Limit of the IGBT. IEEE Trans. Electron Devices 2017, 64, 4148–4192. [Google Scholar]
- Hohannesson, D.; Nawaz, M.; Norrga, S.; Anders, H.; Nee, H.-P. Static and Dynamic Performance Prediction of Ultrahigh-Voltage Silicon Carbide Insulated-Gate Bipolar Transistors. IEEE Trans. Power Electron. 2021, 36, 5874–5891. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Yu, C.; Fei, C. 4H-SiC Trench IGBT with Lower On-State Voltage Drop. Superlattices Microstruct. 2017, 103, 53–63. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.-J.; Wang, Y.; Hao, Y.; Yu, C.-H.; Cao, F. 4H-SiC Trench IGBT with Back-Side n-p-n Collector for Low Turn-Off Loss. IEEE Trans. Electron Devices 2017, 64, 488–493. [Google Scholar] [CrossRef]
- Liu, Y.-J.; Wang, Y.; Hao, Y.; Fang, J.P.; Shan, C.; Cao, F. A Low Turn-Off Loss 4H-SiC Trench IGBT with Schottky Contact in the Collector Side. IEEE Trans. Electron Devices 2017, 64, 4575–4580. [Google Scholar] [CrossRef]
- Silvaco Int. Two Dimensional Device Simulation Program; Silvaco Int.: Santa Clara, CA, USA, 2012. [Google Scholar]
- Jayant Baliga, B. Silicon Carbide Power Devices, 3rd ed.; 5 Toh Tuck Link; World Scientific Publishing Co., Pte. Ltd.: Singapore, 2006; pp. 343–345. [Google Scholar]
- Jayant Baliga, B. Fundamentals of Power Semiconductor Devices, 3rd ed.; 5 Toh Tuck Link; World Scientific Publishing Co., Pte. Ltd.: Singapore, 2008; pp. 208–215. [Google Scholar]
- Usman, M.; Nawaz, M. Device design assessment of 4H–SiC n-IGBT—A simulation study. Solid-State Electron. 2014, 92, 5–11. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Jia, D.; Fang, J. On-State Voltage Drop Analytical Model for 4H-SiC Trench IGBTs. Crystals 2022, 12, 582. https://doi.org/10.3390/cryst12050582
Liu Y, Jia D, Fang J. On-State Voltage Drop Analytical Model for 4H-SiC Trench IGBTs. Crystals. 2022; 12(5):582. https://doi.org/10.3390/cryst12050582
Chicago/Turabian StyleLiu, Yanjuan, Dezhen Jia, and Junpeng Fang. 2022. "On-State Voltage Drop Analytical Model for 4H-SiC Trench IGBTs" Crystals 12, no. 5: 582. https://doi.org/10.3390/cryst12050582
APA StyleLiu, Y., Jia, D., & Fang, J. (2022). On-State Voltage Drop Analytical Model for 4H-SiC Trench IGBTs. Crystals, 12(5), 582. https://doi.org/10.3390/cryst12050582




