Research Progress of Fe-Based Superelastic Alloys

Abstract

In recent years, superelastic alloys have become a current research hotspot due to the large recoverable deformation, which far exceeds the elastic recovery. This will create more possibilities in practical applications. At present, superelastic alloys are widely used in the fields of machinery, aerospace, transmission, medicine, etc., and become smart materials with great potential. Among superelastic alloys, Fe-based superelastic alloys are widely used due to the advantages of low cost, easy processing, good plasticity and toughness, and wide applicable temperature range. The research progress of Fe-based superelastic alloys are reviewed in this paper. The mechanism of thermoelastic martensitic transformation and its relation to superelasticity are summarized. The effects of the precipitate, grain size, grain orientation, and texture on the superelasticity of Fe-based superelastic alloys are discussed in detail. It is expected to provide a guide on the development and understanding of Fe-based superelastic alloys. The future development of Fe-based superelastic alloys are prospected.

1. Introduction

The essence of superelastic alloys is actually a kind of shape memory alloys, which has two characteristics of the shape memory effect and superelasticity. The superelasticity of the shape memory alloys is generally produced by temperature-induced reverse martensitic transformation to recover deformation. However, the superelastic alloy is a special type of shape memory alloy. The superelasticity in superelastic alloys relies on the thermoelastic martensitic transformation, that is, stress-induced martensitic transformation is used to recover deformation. Therefore, different with the shape memory alloys, superelastic alloys can exhibit superelasticity at a constant temperature without heating and cooling [1]. Superelasticity means that when the alloy undergoes a limited amount of plastic deformation (non-linear elastic deformation) under the action of higher than the transformation temperature and stress, the stress can be directly released to recover to its original shape. Superelastic alloys are favored by scholars due to their special mechanical behaviors, and thus have a wide range of applications in the automotive machinery, aerospace, telecommunications conduction, smart sensors, and other fields due to their extremely recoverable deformation [2,3,4,5]. Obvious stress hysteresis can be observed in the tensile curves of the superelastic alloys, which makes them possess hysteretic energy dissipation characteristics, absorbing energy, and reducing vibration [6]. This feature broadens the applications of superelastic alloys. The achievement on the hysteretic energy dissipation characteristic of superelastic alloys is expected to be applied in the fields of non-destructive testing, vibration and shock protection, biomedical imaging, and soft machinery [7,8,9,10]. In the decades of development of superelastic alloys, according to their composition classification, superelastic alloys can be divided into NiTi-based, Cu-based, and Fe-based superelastic alloys [1]. NiTi-based superelastic alloy is currently the most widely used due to the high superelastic strain of up to 8%, good mechanical properties, excellent corrosion resistance, and good biocompatibility. However, it also has some disadvantages, such as high cost and processing difficulty [11,12]. The resistivity of Cu-based superelastic alloy is relatively small, which is about an order of magnitude smaller than that of NiTi-based alloy [13]. It is not suitable for the applications of heating and charging. In addition, its low strength and high sensitivity to temperature changes further limit its application [13]. Fe-based superelastic alloy has the advantages of low cost, good ductility, high strength, easy processing, and weldability, etc., making it a substitute for NiTi-based superelastic alloy, and becoming a hot spot in current researches [14,15,16].

In this paper, the research progress of Fe-based superelastic alloys is reviewed. The effect of thermoelastic martensitic transformation on the superelasticity of Fe-based superelastic alloys is analyzed and discussed. The factors on superelasticity in Fe-based superelastic alloy are summarized. Finally, the future development directions of Fe-based superelastic alloys are prospected.

2. Superelastic Mechanisms of Fe-Based Superelastic Alloys

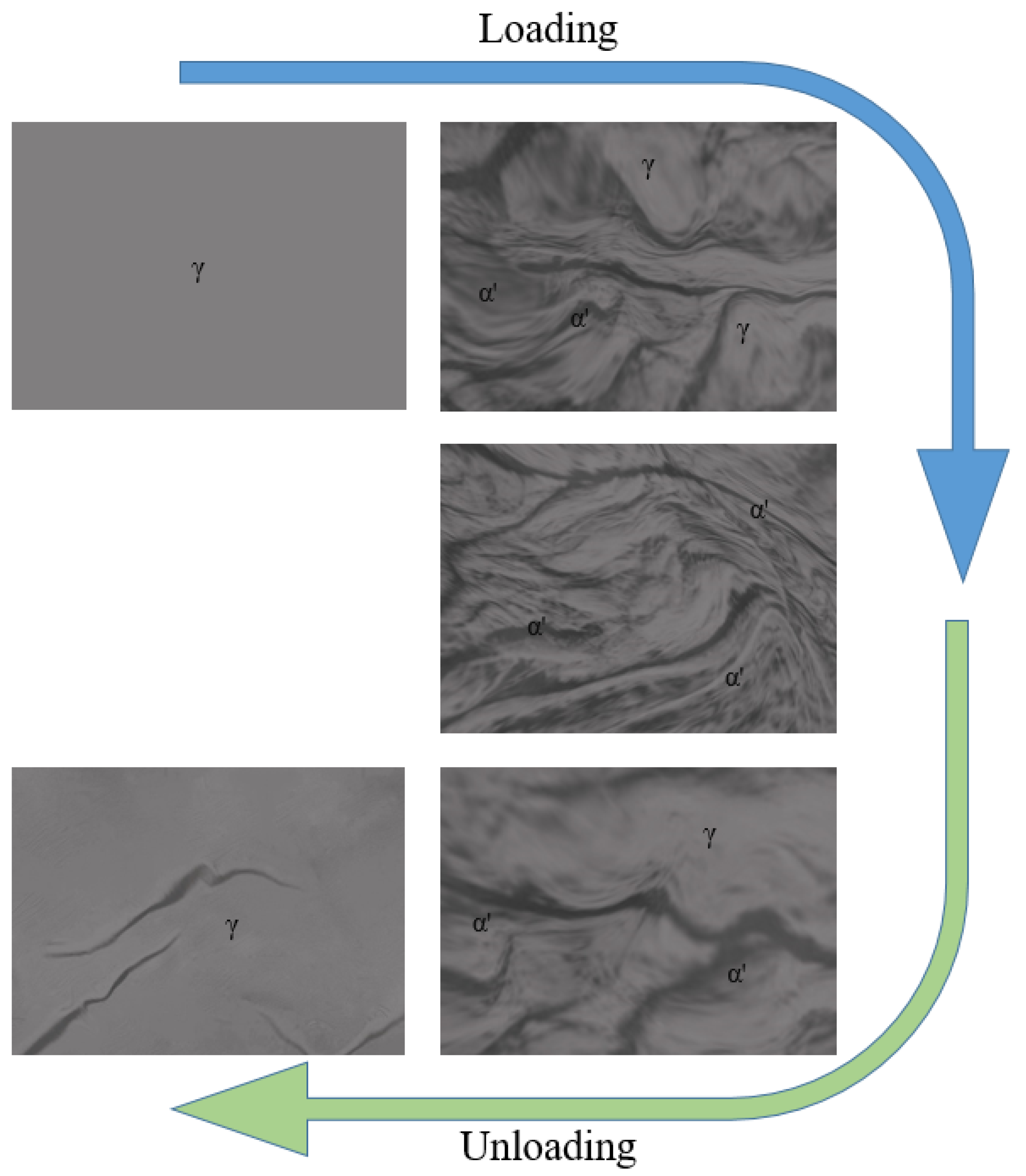
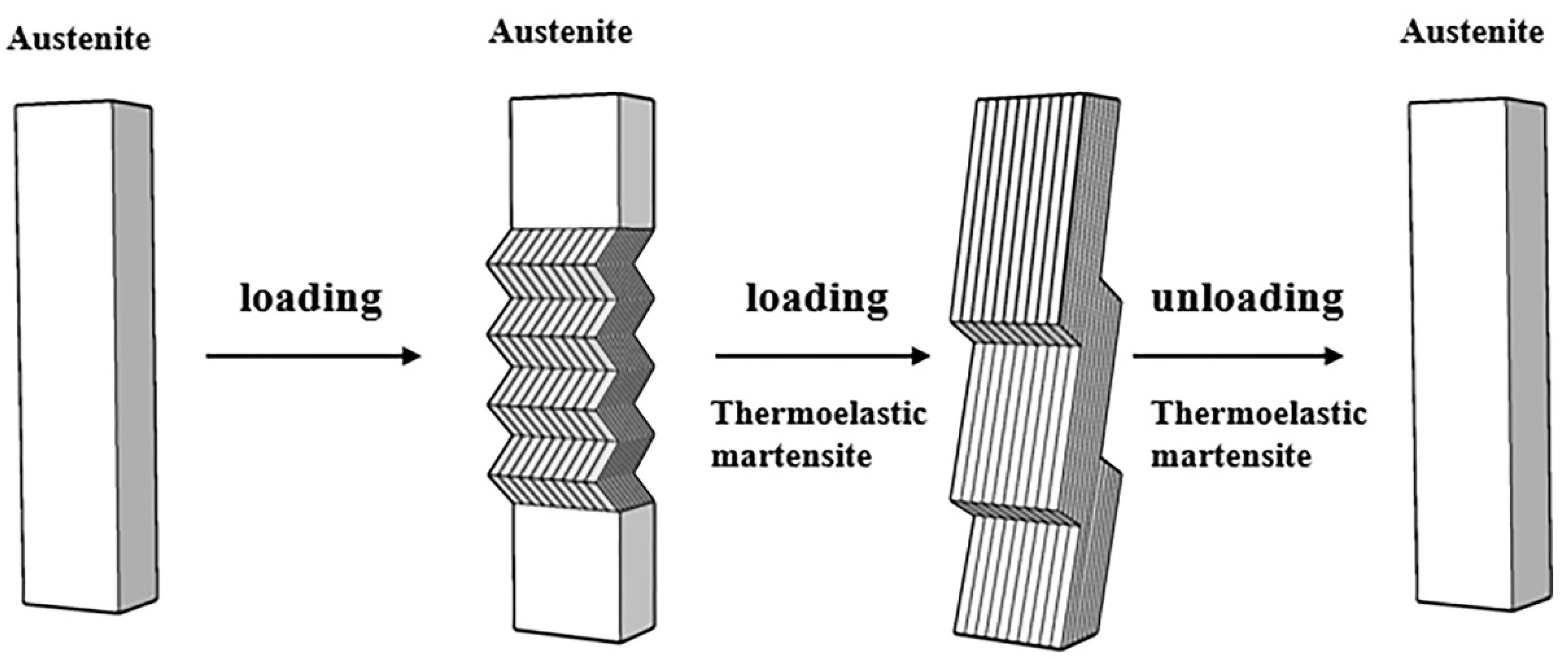
2.1. Thermoelastic Martensitic Transformation

Martensitic transformation is a very important means to strengthen the alloys [17,18,19]. In Fe-based superelastic alloys, the superelasticity is extremely dependent on the thermoelastic martensitic transformation. When quick quenching is conducted from the austenite zone, there is no time for the decomposition process of eutectoid diffusion to occur, generating martensites [20,21,22]. During the martensitic transformation, the movement of a single atom is less than the distance between two atoms [23,24]. According to the morphology, martensite can be divided into lath martensite and plate martensite. Figure 1 shows the morphologies of lath martensite and plate martensite in alloys [25]. Figure 1a shows the body centered cubic (BCC) martensite in Fe-14Mo-11.5Cr-9Ni-7Co-2Cu-0.6Ti-0.4Al (weight %) alloy austenitized at 1150 °C, and then quenched to room temperature in water. Figure 1a illustrates the lath martensite composed of clusters of laths. An austenite grain can form several lath groups with different orientations. The lath group is composed of lath bundles, which contains many slender martensite laths arranged almost in parallel. Figure 1b presents plate martensite with the body centered tetragonal (BCT) structure in Fe-0.47Cr-0.27Si-0.22Mn-1.67C (weight %) alloy, possessing needle-like or bamboo-leaf morphology [25], while the martensite plates with different sizes are not parallel to each other. In fact, the spatial morphology of plate martensite is convex lens. Lath martensite usually possesses good toughness. The dislocations are not uniformly distributed in cellular dislocation substructure, resulting in the formation of low-density dislocation areas, which provide room for dislocation motion [26]. Dislocation movement can alleviate local stress concentration, delay crack nucleation, and weaken the stress peak at the crack tip, which is beneficial to toughness [26]. The twin substructure of plate martensite will reduce the effective slip system, decreasing the toughness, but increasing the hardness and strength. With the in-depth studies of martensite and martensitic transformation by scholars, it is found that martensite and martensitic transformation are not unique in steels [27,28,29,30]. As long as certain conditions are met, the transformation can be called martensitic transformation. Xu summarized the characteristics of martensitic transformation and put forward a simple definition: martensitic transformation is a first-order and nucleation-length phase transformation characterized by invariant plane strain, in which the replacement atoms undergo non-diffusive shear displacement, resulting in shape change and surface projection [31]. The basic characteristics of martensitic transformation are: (1) non-diffusivity; (2) occur mainly through shearing with surface relief feature; (3) the martensite and matrix possess a certain orientation relationship; (4) the habit plane of martensite does not produce distortion, and does not rotate during the process of phase transformation [32,33,34,35,36]. All phase transformations that meet these characteristics can be called martensitic transformation.

Most Fe-based shape memory alloys undergo non-thermoelastic martensitic transformation, and thus do not exhibit superelasticity [37,38,39]. The martensitic transformation in Fe-based superelastic alloy must be thermoelastic so that the alloy can possess superelasticity. The thermoelastic martensitic transformation is a sufficient and necessary condition for the alloy to possess superelasticity [40]. When the shape change of martensitic transformation is coordinated with elastic deformation, this transformation is called thermoelastic martensitic transformation. During the cooling process, the thermoelastic martensite will expand; when the temperature increases, the thermoelastic martensite will shrink. In Fe-based superelastic alloys, stress can also induce thermoelastic martensitic transformation [41]. A schematic diagram of stress-induced martensitic transformation is shown in Figure 2. During loading, the martensitic transformation occurs. After unloading, the martensite undergoes a reverse phase transformation and transforms into the parent phase, recovering the strain. In case of thermoelastic martensitic transformation, the driving force of thermoelastic martensite is mechanical, and comes from the interaction between the applied stress field and the transformation strain. In the thermoelastic martensitic transformation, the volume change is small, because the deformation caused by the transformation is basically elastic. In addition, during the reverse phase transformation of thermoelastic martensite, the thermal hysteresis is relatively small. According to the characteristics of thermoelastic martensitic transformation, Xu et al. gave the judgment basis for thermoelastic martensitic transformation: (1) Both the critical driving force of phase transformation, and the thermal hysteresis during the phase transformation are small; (2) Phase interface can move with the phase transformation or reverse transformation; (3) The strain produced by the phase transformation is elastic, and the elastic strain energy stored in the martensite is the driving force for the reverse phase transformation [42,43]. Studies have shown that the driving force for superelastic martensite transformation in Fe-Mn-Al-Ni superelastic alloy is only 32 J/mol, while the driving force for martensite phase transformation in Fe-based non-superelastic alloy is as high as 1000 J/mol [44]. It can be seen that the driving force for the transformation of non-thermoelastic martensite is about 10 times more than that of thermoelastic martensite.

The superelasticity of Fe-based alloys relies on the occurrence of thermoelastic martensitic transformation, and its reverse transformation to recover deformation [42]. In Fe-Mn-Al-Ni superelastic alloy, martensitic transformation occurs from the BCC matrix to face center cubic (FCC) martensite phase, while the transformation is from the FCC matrix to BCT martensite phase in Fe-Ni-Co-Al and Fe-Ni-Co-Ti superelastic alloys. Here, α refers to the austenite phase and γ refers to the martensite phase. When the thermoelastic martensitic transformation occurs, temperature varies. At high temperature, the α austenite phase has greater entropy, so the Gibbs free energy of α austenite phase is larger than that of the γ martensite phase. Thus, the α phase is more stable than γ phase at high temperature, which leads to γ→α phase transformation at high temperature [44]. The α phase is ferromagnetic, and its entropy can be reduced by magnetic ordering. The low temperature will make the magnetic ordering, thereby reducing the entropy, causing the ferromagnetic α phase to possess a lower entropy than the γ phase, leading to the α→γ phase transformation at low temperature [44]. These two transformations can change back and forth with the difference in temperature to recover the strain, thus possessing superelasticity.

2.2. Clausius–Clapeyron Equation

The critical stress (σ_cr) for stress-induced martensitic transformation tends to change with temperature. Clausius–Clapeyron equation can quantitatively represent the critical stress as a function of temperature [45,46]. Clausius–Clapeyron equation is shown as follows [45,46]:

$$\frac{d{\sigma }_{cr}}{dT}=-\frac{\Delta S}{V_m\epsilon }=-\frac{\Delta H}{{\epsilon }_0{T}_0}$$

(1)

where T is the temperature, ΔS and ΔH are the transformation entropy and transformation enthalpy, V_m is the molar volume, ε is the critical strain, ε₀ is the orientation-dependent lattice deformation, and T₀ is the chemical equilibrium temperature [45,46]. The martensitic transformation temperature can be obtained from Equation (2) [47]:

$$M_s\left({\sigma }_d\right)=T_0^d\left({\sigma }_d\right)-\Delta T$$

(2)

where M_s(σ_d) is the martensitic transformation temperature when the stress reaches σ_d, T₀^d(σ_d) is the phase equilibrium temperature of the parent phase and martensite when the stress is σ_d, ΔT is the degree of subcooling required for phase transformation [47]. Equation (3) can be obtained from Equation (2). Substituting Equation (3) into Equation (1) yields Equation (4). The relationship between stress and start temperature of martensitic transformation can be obtained from Equation (4). Based on the Clausius–Clapeyron equation, the temperature sensitivity of the critical stress for the martensitic transformation can be identified. According to Equation (4), one can know the effect of stress on the start temperature of martensitic transformation.

$$\frac{d{T}_0^{\sigma }}{d{\sigma }_d}=\frac{d{M}_s}{d{\sigma }_d}$$

(3)

$$\frac{d{\sigma }_d}{d{M}_s}=-\frac{\Delta H}{{\epsilon }_0{T}_0}$$

(4)

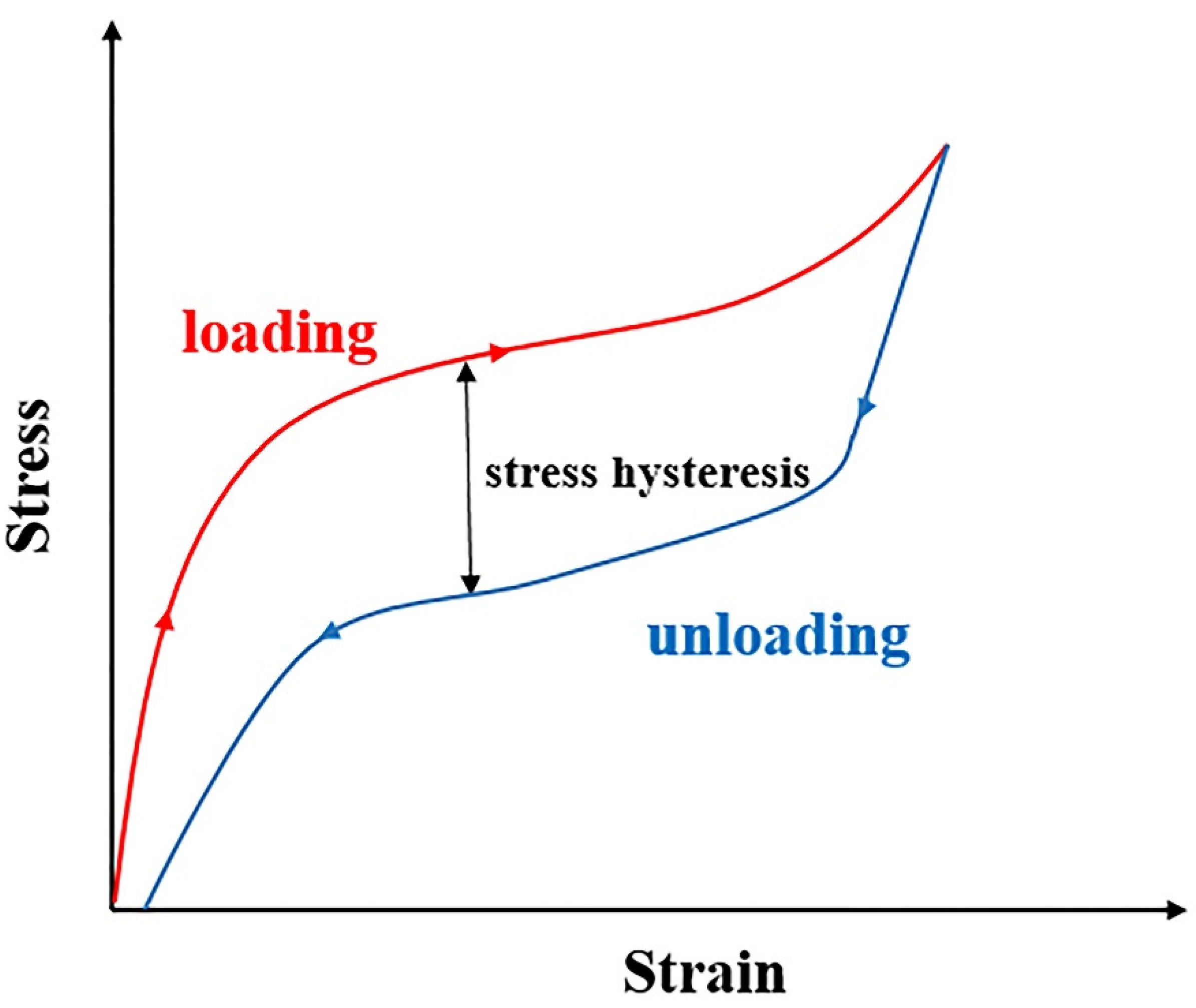
2.3. Superelasticity

Superelasticity is achieved by the dynamic changes of martensite and austenite at low temperatures. Temperature and stress can induce martensitic transformation and its recovery. Superelasticity is a dynamic combination of these two stages, and caused by martensitic transformation [48]. When loading temperature is above the austenite transformation temperature, the austenite will undergo martensitic transformation accompanied by a transformation strain. Subsequent to the isothermal unloading, the martensite reverse transformation will occur. In the martensite reverse transformation, the transformation strain generated during the martensitic transformation can be eliminated, exhibiting a hysteresis phenomenon at the same time. The schematic diagram of the thermoelastic martensitic transformation is shown in Figure 3. Above the A_f temperature (end temperature of austenite transformation), the material is in austenite state. After loading, the stress induces martensitic transformation, resulting in the formation of martensite variants with different orientations. At this time, the material undergoes macroscopic deformation, and then changes from austenite to martensite with continuous loading. After unloading, the martensite is reversely transformed into austenite, recovering deformation. The superelasticity caused by martensite reorientation is attributed to the reorientation of martensite variants caused by stress. However, the reoriented martensite variant can be recovered to its original direction by recovery force, which will also cause hysteresis [49,50]. Figure 4 shows the stress–strain curve of Fe-based superelastic alloy during loading and unloading. It can be seen that in the initial stretching stage, the stress–strain curve is a straight line, which belongs to the elastic deformation stage. When the stress continues to increase, the stress–strain curve deviates from the straight line. In this case, martensitic transformation occurs. The stress value at the deviated point, ε_Ms, is the critical stress value of martensitic transformation. At this time, there will be a stress plateau. When the curve breaks away from the stress plateau, it marks the end of the martensitic transformation. During unloading, the reverse martensitic transformation will occur, thereby eliminating the existing strain, and recovering to the original state.

Although superelastic alloy belongs to shape memory alloy, it is different from shape memory alloys that recover deformation through temperature change. Superelastic alloy can recover deformation at a constant temperature. Both superelasticity and shape memory effect are closely related to temperature, exhibiting various macroscopic mechanical properties at different temperatures [51]. Figure 5 shows the mechanical behaviors of the alloys at different temperatures. In Figure 5, M_d is the critical temperature of stress-induced martensitic transformation, A_s is the start temperature of austenite transformation, A_f is the end temperature of austenite transformation, and M_f is the end temperature of martensitic transformation. When T > M_d, the critical stress required to form martensite is very large, so the material undergoes plastic deformation before the occurrence of stress-induced martensitic transformation. Fracture may occur before the occurrence of martensitic transformation. When A_f < T < M_d, the alloy is composed of austenite, and stress-induced martensitic transformation occurs in this stage. If the martensitic transformation at this time is thermoelastic, the material possesses superelasticity. When T < M_f, after stretching and unloading, only a part of the elastic deformation can be recovered. Residual strain still exists. Only by heating the alloy above the A_s temperature can make the material recover to its original shape, as shown by the red dashed line in Figure 5.

Superelasticity significantly depends on the thermoelastic martensitic transformation. Only the occurrence of phase transformation and reverse phase transformation from thermoelastic martensite can achieve superelasticity. The reason why thermoelastic martensite can undergo a reverse transformation is that the driving force for the phase transformation is the difference in chemical-free energy between the two phases. The driving force of the phase transformation and elastic energy are in a dynamic equilibrium state [52]. When the thermoelastic martensitic transformation occurs, the driving force causes the phase transformation to occur. The material deforms to store up the elastic energy. The reverse phase transformation of thermoelastic martensite occurs during unloading. Then, the stored elastic energy is released. The thermoelastic balance of these two opposite energy terms makes the alloy stretch or shrink according to the change of external stress [53]. At the same time, because the energy barrier of lattice shear in the process of thermoelastic martensitic transformation is higher than that of non-thermoelastic martensitic transformation, it is difficult for plastic deformation to occur, so that the deformation can be recovered [54,55,56].

To sum up, in order to obtain good superelasticity, it is necessary to control the phase transformation to be thermoelastic martensitic phase transformation, that is, controlling the thermal balance between the elastic energy and driving force. Among Fe-based superelastic alloys, including Fe-Mn-Al-Ni system, Fe-Ni-Co-Al system, and Fe-Ni-Co-Ti system alloys, the most effective method is to introduce coherent precipitates to change non-thermoelastic martensitic transformation into thermoelastic martensitic transformation [57,58]. On the one hand, the coherent precipitates are dispersedly distributed in the matrix, which can strengthen the matrix, and make the matrix better adapt to the deformation caused by external stress. On the other hand, the disperse distribution of coherent precipitates can also suppress the slip of dislocations. In this case, critical stress of martensitic transformation can be reached before plastic deformation of the dislocation slips. The occurrence of martensitic transformation inhibits plastic deformation. In addition, the existence of the coherent precipitates also provides elastic energy, which can achieve the mutual transformation between the elastic energy and driving force of the phase transformation. All the above three points should be satisfied to ensure the occurrence of thermoelastic martensitic transformation, making the alloy obtain excellent superelasticity [40,59,60]. For example, Fe-Mn-Al-Ni superelastic alloy can obtain superelasticity by strengthening the parent phase and controlling the grain size to obtain the bamboo structure [61]. The superelasticity in Fe-Ni-Co-Al superelastic alloy is limited due to the precipitation of brittle phases at the grain boundary. It is found that the addition of B element can control the precipitation of grain boundaries together with large cold-rolling deformation amount to possess small-angle grain boundaries, obtaining good superelasticity [41]. In Fe-Ni-Co-Ti superelastic alloy, the precipitation of brittle phases at grain boundaries can be suppressed by adding B element or Cu element to reduce thermal hysteresis to obtain superelasticity [62,63].

3. Effects of Precipitates on Superelasticity

3.1. Effects of Coherent Precipitates on Superelasticity

The superelasticity of Fe-based alloys depends on thermoelastic martensitic transformation. The martensitic transformation of many systems is usually non-thermoelastic or semi-thermoelastic, such as Fe-Mn-Al, Fe-Mn-Si, Fe-C, Fe-Mn-C alloys, etc. [64,65,66,67]. Ando et al. studied the martensitic transformation of Fe-Mn-Al alloy [64], whose martensitic lath contains high-density twins, resulting in high thermal hysteresis of phase transformation. This leads to the occurrence of the incomplete martensitic reverse transformation, and incomplete restoration of martensitic to original phase. According to the thermoelastic martensitic transformation criterion described above, the martensitic transformation of Fe-Mn-Al alloy is semi-thermoelastic. There is no equilibrium between the thermal driving force and elastic energy in the non-thermoelastic or semi-thermoelastic martensitic transformation. Adjusting the equilibrium between the thermal driving force and elastic energy can make the martensitic transformation become thermoelastic. The introduction of coherent precipitates is the most common method to achieve this goal. Thermoelastic martensitic transformation can be achieved by introducing coherent precipitates in Fe-based alloys, which can be obtained by adding alloying elements or heat treatment [41,61,68,69,70].

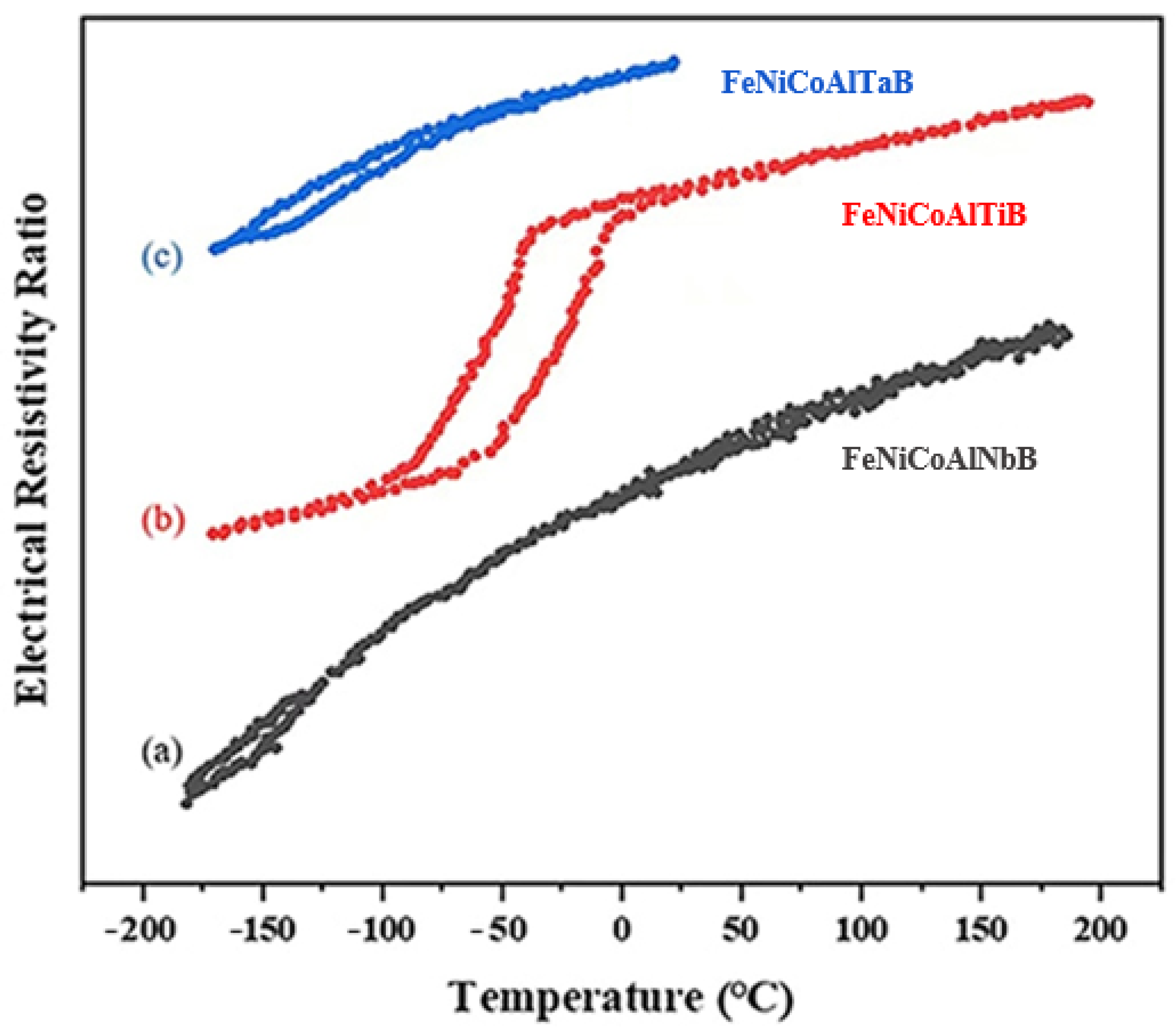
3.1.1. Effects of Coherent Precipitates on Martensitic Transformation

In Fe-based superelastic alloys, thermoelastic martensitic transformation can be achieved by introducing coherent precipitates in order to obtain superelasticity. The types of coherent precipitates are different in different alloy systems. For example, the coherent precipitates in Fe-Mn-Al-Ni superelastic alloys are B2 phase, and L1₂-γ′ phase in Fe-Ni-Co-Al and Fe-Ni-Co-Ti superelastic alloys.

The effect of coherent precipitates on the martensitic transformation can be directly reflected by M_s point. The effect of precipitation on M_s point can be attributed to the following three aspects: (1) the content of Ni in matrix decreases with the precipitation, which leads to the increase of thermodynamic equilibrium temperature; (2) the precipitates possess strengthening effect, increasing the energy barrier of martensitic transformation; (3) the stress field energy is different between the parent phase/precipitate and the martensite/precipitate [70]. To a certain extent, the decrease of M_s point will reduce the thermal hysteresis. The most obvious characteristic of thermoelastic martensitic transformation is the small thermal hysteresis (generally <100 K) [42].

In Fe-Mn-Al-Ni superelastic alloys, the precipitation of B2 phase makes the martensitic transformation become thermoelastic, because B2 precipitate is coherent with parent phase and martensitic phase [61]. B2 phase can contribute elastic energy, which is conducive to reverse transformation, and makes the phase transformation into thermoelastic, thus obtaining superelasticity [71,72].

The γ′ phase in Fe-Ni-Co-Al and Fe-Ni-Co-Ti superelastic alloys can change the deformation mechanism from slip to twinning [51,73]. The critical shear stress required by twinning is larger than slip, and thus the energy required to start the plastic deformation mechanism is higher. This makes it easier for the alloy to satisfy the criterion that the critical stress of thermoelastic martensitic transformation is less than the yield stress. The thermoelastic martensitic transformation occurs before the initiation of plastic deformation mechanism, and superelasticity is obtained. The emergence of precipitate can effectively avoid dislocation slip during martensitic transformation. The precipitate improves the tetragonal degree of martensite, and is conducive to the interface compatibility between parent phase and martensite phase [41]. In addition, the precipitate also reduces the elastic strain energy during martensitic transformation and makes martensitic transformation into thermoelastic [74].

3.1.2. Effects of Alloying on Coherent Precipitates

In both Fe-Mn-Al-Ni and Fe-Ni-Co-Al systems, coherent precipitates are obtained by adding alloying elements. Omori et al. added Ni element into Fe-Mn-Al alloy, making the martensitic transformation become thermoelastic, forming Fe-Mn-Al-Ni superelastic alloy [61]. Tanaka et al. added strong γ′ phase elements into Fe-Ni-Co-Al alloy to introduce γ′ phase, occurring thermoelastic martensitic transformation and exhibiting superelasticity [41,68,69].

The predecessor of Fe-Mn-Al-Ni superelastic alloy is Fe-Mn-Al alloy. In NiTi-based superelastic alloy, some studies show that introducing precipitate can improve the matrix order degree, strengthen the matrix to make plastic deformation difficult to occur, and further improve the superelasticity [75]. For Fe-Mn-Al alloy, it can be considered to introduce the precipitate to realize the thermoelastic martensitic transformation, and obtain superelasticity. Omori et al. first added Ni element to Fe-Mn-Al alloy to investigate the effect of Ni element on phase transformation [61]. There is no mismatch at the interface between the parent phase and β phase, indicating that the β phase and parent phase are coherent, which is beneficial to the occurrence of thermoelastic martensitic transformation [61]. The internal stress generated by β phase precipitation is regulated by nano-twin, which does not change the interatomic fit, and does not affect the thermal balance of thermoelastic martensitic transformation. However, Omori et al. only stated that the β phase precipitation after the addition of Ni could make the martensitic transformation into thermoelastic, without further explaining the reason [61]. Roca et al. further investigated how the β phase affected the martensitic transformation [71,72], and found that B2 precipitates could store elastic energy. On the one hand, the elastic energy acts as the driving force to carry out the reverse transformation. On the other hand, it is beneficial to maintain the thermoelastic equilibrium, thus producing the thermoelastic martensitic transformation. At the same time, the B2 phase also increases the hardness, thus inhibiting the occurrence of irreversible deformation [71]. In addition, Walnsch et al. developed a thermodynamic model to further illustrate the contribution of B2 phase to the generation of thermoelastic martensitic transformation [72]. The dispersed B2 phase stabilizes the austenite matrix, and transforms into the elastic L1₀ phase after martensitic transformation, which can store the energy released during the reverse transformation from martensite to austenite [72].

The thermoelastic martensitic transformation of Fe-Ni-Co-Al system’s superelastic alloy is from FCC-γ parent phase to body centered tetragonal (BCT)-α′ martensite phase. Thermoelastic martensitic transformation does not occur in Fe-Ni-Co-Al alloys. However, with the addition of strong γ′ elements such as Nb, Ti, and Ta, the alloy is superelastic with the occurrence of thermoelastic martensitic transformation [41,68,69]. After adding strong γ′ phase elements, the solid-solution temperature of γ′ phase increases. More γ′ phase will be precipitated after heat treatment [41]. These γ′ phases will increase the hardness and the tetragonality of martensite. After adding Nb, Ti, and Ta, the alloys obtained superelasticity of 5%, 4.2%, and 13.5%, respectively [41,68,69].

In addition, Vallejos et al. found that the addition of Al significantly affected the martensitic transformation temperature, and the formation of B2 phase in Fe-Mn-Al-Ni alloy [76]. The martensitic transformation temperature of 17Al is lower than −250 °C, while that of 15Al is about −10 °C [76]. However, calculation shows that the martensitic transformation temperature of the Fe-34Mn-15Al-7.5Ni alloy is 900 °C, which is far higher than the results reported by Vallejos et al. [77]. The reason for this significant difference is due to the thermodynamic contribution of β phase to the formation of martensite. As high Al content makes the parent phase stable, a larger degree of undercooling is needed to provide enough energy for phase transformation, leading to a lower M_s point of 17Al. When the parent phase is stable, the temperature where the two-phase miscibility gap starts will increase. If the two-phase miscibility gap is reached at a higher temperature, the driving force of precipitation will increase, resulting in a large amount of B2 phase precipitation after quenching, with a superelasticity of about 8.4% [76]. Some studies have shown that Al element has a significant effect on obtaining a wide range of single α phase region or γ phase region in the phase diagram [78]. Heat treatment in the region of single phase or uniform solid solution is beneficial to obtain B2 phase [78]. In Fe-Mn-Al-Ni alloy, the addition amount of Al element is limited. The addition of 5 at. % Al requires the compensation of a large amount of Mn and Ni elements [78]. However, in terms of manufacturing, both Mn and Ni elements cannot be added in large amounts. Mn has strong volatility, which will cause the chemical composition of the alloy to be unstable, and also cause the negative influence to production [79]. Although Ni element will not cause production problems, the addition of a large amount of Ni requires extremely high cost [80]. Starting from increasing the single-phase region in the high temperature range, Kaputkina et al. proposed to increase the amount of Al by adding C element [78]. After the addition of C element, a single-phase region of phase diagram appears in the range of 1000 °C to 1200 °C, and thus, the content of Al element is allowed to increase [78].

3.1.3. Effects of Heat Treatments on Coherent Precipitates

In some alloy systems, coherent precipitates can be obtained only by heat treatment without alloying elements. In addition, although the alloy system with alloying elements can precipitate coherent precipitates, their sizes can be further optimized to obtain better superelasticity. Studies have shown that the size of coherent precipitate is too small or too large to ensure its coherence with parent phase, and cannot play a role in strengthening parent phase to obtain good superelasticity [81]. At this time, the size of coherent precipitate needs to be controlled by heat treatment.

The addition of Ni or strong γ’ elements can make the martensitic transformation of Fe-Mn-Al-Ni alloy and Fe-Ni-Co-Al alloy into thermoelastic. However, in order to obtain better superelasticity, coherent precipitates can be regulated by heat treatment (controlling the aging temperature and time), as shown in Figure 6a [81]. Tseng et al. studied the effects of aging temperatures (200 °C and 300 °C) and time on the compression superelastic response of <100> orientation FeMnAlNi single crystal, and found that the size of B2 phase increased with the increase of aging time [81]. The same results were obtained in Fe-Ni-Co-Al superelastic and Fe-Ni-Co-Ti superelastic alloys [82,83]. Evirgen et al. found that the γ’ phase size is 3–4 nm at 700 °C aging and 5 nm at 600 °C in FeNiCoAlTa single crystal [82]. Figure 6b shows the relationship between aging time and superelasticity in FeMnAlNi alloy [81]. When aging at 200 °C for 1–3 h, the superelasticity increases with the increase of aging time, and reaches a peak value of 7.2% at 3 h [81]. FeNiCoAlTa single crystal obtained 4.3% superelasticity after 90 h aging at 600 °C [82]. The longer aging time increases the size and volume fraction of B2 phase, but decreases the number density. This indicates that the precipitate is still growing during the aging process, but the nucleation has ended. As the aging time continues to increase, the superelasticity gradually decreases. When the aging time is not long enough, the B2 phase is too small and insufficient to strengthen the austenite matrix to resist plastic deformation, and thus the superelasticity is poor [81]. When the aging time is too long, the precipitate and the parent phase lose the coherence. The effect of precipitation strengthening is reduced, weakening the superelasticity. The best superelasticity can be obtained for 200 °C/3 h in FeMnAlNi alloy. At this time, the size of the B2 phase is 6–10 nm, which achieves the balance of precipitation strengthening and strong coherence, showing a 7.2% superelasticity [81]. Titenko et al. also used this method to obtain the optimum superelasticity of 4.5% in Fe-Ni-Co-Ti alloy aged at 650 °C for 10 min [84]. With the increase of aging time, the composition of precipitate changes, which will affect the martensitic transformation. In Fe-Mn-Al-Ni superelastic alloy, the content of Al and Ni elements decreases in the matrix, while the content of Fe element increases with the increasing aging time [81]. In Fe-Ni-Co-Al superelastic alloy, the aging process also changes the composition of the coherent γ′ phase [85]. The matrix is rich in Fe and Co elements, while the precipitates are rich in Ni, Al, and Ta after short-time aging [85]. As the aging time increases, the content of Ni, Al, and Ta in the matrix gradually decreases. The shape of the precipitate also changes from plate to granular [85]. The change of the composition of coherent precipitates also affects the composition of the matrix, which affects the transformation temperature. The temperature of martensitic transformation is very sensitive to the Ni content. The decrease of Ni content in matrix leads to the increase of martensitic transformation temperature [86]. At the same time, the Co element has the effect of increasing hardness of the austenite matrix, promoting the formation of the thin-plate martensite phase, and reducing the phase volume change caused by the Invar effect [41,87]. Increasing the critical slip stress can enable the occurrence of martensitic transformation before plastic deformation. In addition, the increase of the martensitic transformation temperature also reduces the thermal hysteresis. At the same time, element changes in the matrix promotes the occurrence of martensitic transformation [87]. These above three factors make the martensitic transformation into thermoelastic.

An interesting phenomenon was discovered by Ozcan et al. [88]. At room temperature, the FeMnAlNi alloy has a natural aging phenomenon [88]. No matter after solution treatment, or in samples that have been aged at 200 °C for 3 h, natural aging can occur at room temperature, and the B2 phase can be precipitated. The FeMnAlNi alloy presents no superelasticity after solution treatment. After the precipitation of B2 phase by natural aging, the alloy acquires superelasticity. After 30 days of natural aging, the alloy achieved 5% superelasticity, and the size of the B2 phase also increased from 5 nm to 7 nm [88]. However, the author did not explain the essence of room temperature aging, which requires further investigations. Natural aging is a double-edged sword. If it is well controlled, superelasticity can be improved without additional heat treatment. Otherwise, superelasticity will be unstable and affect the applications.

3.2. Effects of Grain Boundary Precipitates on Superelasticity

Not all precipitates in Fe-based superelastic alloys are conducive to superelasticity. In addition to coherent precipitates, other precipitates may also be generated during thermo-mechanical treatment. These precipitates tend to adhere to grain boundaries, and have harmful effects on the superelasticity, such as γ phase in Fe-Mn-Al-Ni alloy, B2 phase in Fe-Ni-Co-Al alloy, and η-Ni3Ti phase (D0₂₄ structure) in Fe-Ni-Co-Ti alloy, etc. [60,63,89].

These precipitates are apt to precipitate at grain boundaries. In general, B2 phase in Fe-Ni-Co-Al alloy and η-Ni3Ti phase (D0₂₄ structure) in Fe-Ni-Co-Ti alloy are brittle, causing the alloy to fracture before exhibiting superelasticity [60,63]. For example, the superelasticity of Fe-28.9Ni-18.2Co-8.3Ti alloy possesses only 0.7% superelasticity due to the precipitation of η phase at grain boundaries [90]. In Fe-Ni-Co-Al superelastic alloy, it is also found that the B2 phase at grain boundary is not conducive to the superelasticity [60]. γ phase in Fe-Mn-Al-Ni alloy will form the serrated interface, which is not conducive to thermoelastic martensitic transformation [89]. The most serious problems are: (1) the precipitate at grain boundaries leads to stress concentration and fracture during deformation; (2) the precipitate pins martensite/matrix interface, hindering reverse martensitic transformation [60,89].

To solve the above problems, alloying elements were added to inhibit the precipitates at grain boundaries. For example, in Fe-Ni-Co-Al and Fe-Ni-Co-Ti superelastic alloys, the addition of B element can inhibit the precipitation of brittle phases at grain boundaries [60,63]. In Fe-Mn-Al-Ni superelastic alloy, Ti element is used to reduce the γ phase precipitation in non-rapid cooling [89]. Some studies have shown that B element can strengthen grain boundary, and reduce the precipitation of brittle phase at grain boundary in Ni-based and Fe-based superalloys [91]. It can be seen clearly in Figure 7 that after the addition of B element inhibits the precipitation at grain boundary [60,63,68]. The addition of B element reduces the grain boundary energy, making the nucleation at grain boundary more difficult, so the precipitation of brittle phase at grain boundary is inhibited [60].

Quenching in cold water will lead to crack formation along the grain boundaries in the Fe-Mn-Al-Ni alloy [89]. In this case, superelasticity cannot be obtained. At present, studies have shown that grain boundary cracking can be effectively prevented by controlling the cooling rate during quenching, that is, quenching in hot water to reduce the cooling rate [92]. In the case of non-rapid cooling, the second phase generates the serrated interface at the grain boundaries, as shown in Figure 8 [89]. This structure is very unfavorable to the superelasticity. As γ phase is not the phase that can occur in phase transformation, it will produce plastic deformation, and dissipate part of the elastic strain energy when martensitic transformation occurs [89]. Moreover, the serrations of the interface also increase the constraint of the reverse martensitic transformation. Studies have shown that the thin-layer γ phase at the grain boundary can prevent intergranular cracking during quenching, but does not significantly affect the superelasticity [92]. However, in the Fe-Mn-Al-Ni alloy, obtaining a thin-layer γ phase requires a fast cooling rate. When the material has a large cross-section, it is difficult to obtain a fast cooling rate, limiting the practical applications of Fe-Mn-Al-Ni alloy. In order to solve this problem, Vollmer et al. added Ti element into Fe-Mn-Al-Ni alloy to control the quenching sensitivity [89]. After the addition of 1.5 at. % Ti element, the volume fraction of precipitates at the grain boundary was significantly reduced. A thin-layer γ phase appeared at the grain boundary, as shown in the inset of Figure 8b [89]. Ti can stabilize the matrix α phase, thus inhibiting the formation of large amounts of γ phase by inhibiting the short-range diffusion of Mn and Al across the boundary of α/γ phase [89]. In a single crystal sample with nearly <102> orientation, the alloy almost completely recovered its deformation under the compression test from −150 °C to 20 °C and 1.5% strain [89]. In tensile test, the superelasticity at 20 °C to 10.5% strain reaches 4.5% [89].

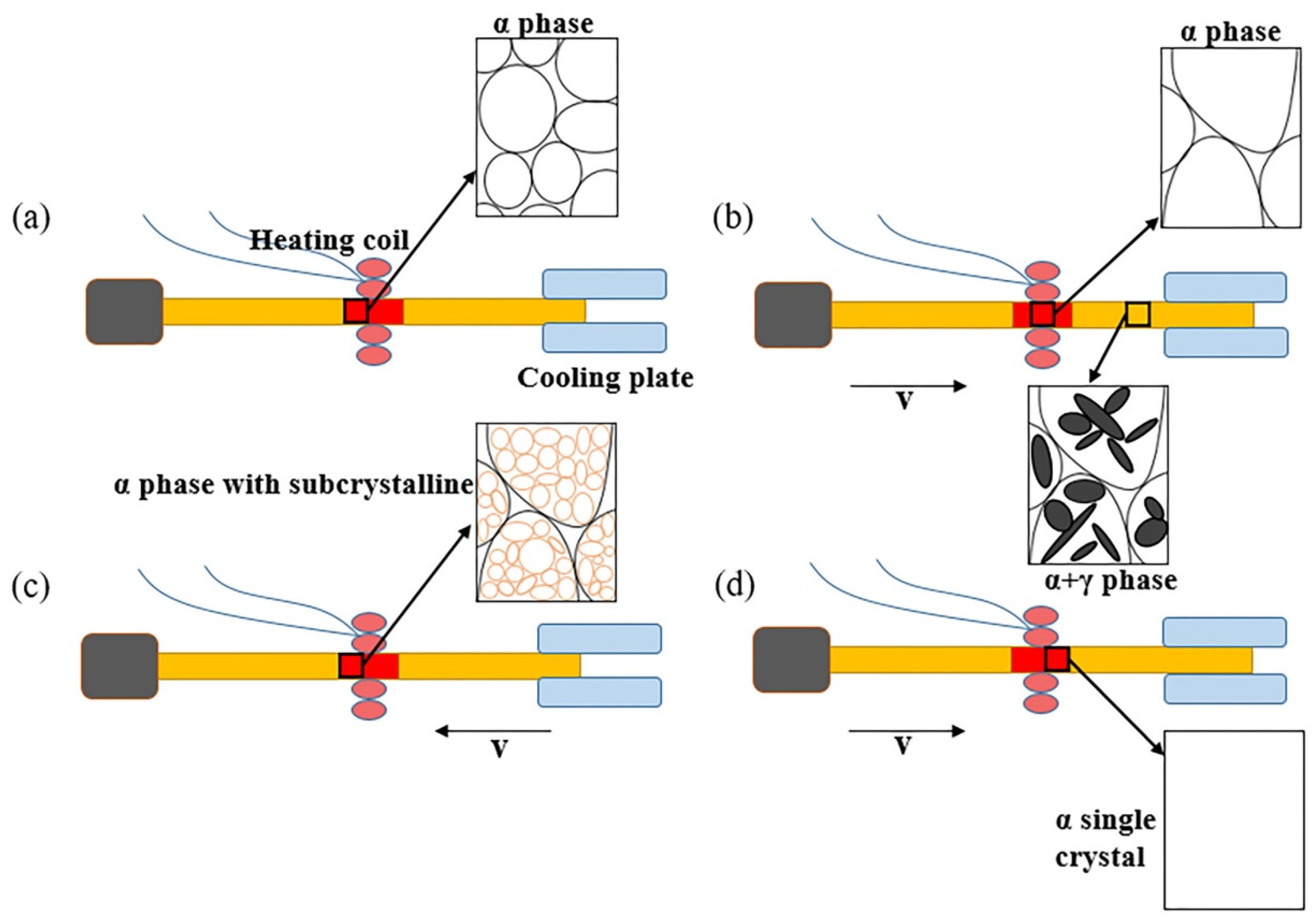
4. Effects of Grain Size on Superelasticity

Grain size is a very important factor affecting superelasticity for the practical applications in many materials [93,94,95,96]. In Cu-based superelastic alloys, superelasticity is affected by the grain size due to the phase transformation and the anisotropy of grains [97,98,99]. The grain boundaries have a restrictive effect on the deformation. In NiTi-based superelastic alloys, the effect of grain size on superelasticity is not significant. There are 24 kinds of martensite variants in NiTi-based superelastic alloys, in which 12 kinds of martensite variants can be activated to coordinate deformation when the alloy undergoes the phase transformation from B2 to B19’ [100]. In Fe-based alloys, there are 12 kinds of martensite variants for Nishiyama orientation and 24 for Kurdjumov–Sachs (K–S) orientation relationships [101]. However, only three kinds of martensite variants are related to the martensitic transformation of Fe-based superelastic alloys [102]. When the number of martensite variants related to the martensitic transformation is small, the phase interface reciprocal migration is difficult [102]. This is not conducive to the occurrence of thermoelastic martensitic transformation. The grain boundaries can be regarded as the phase interface during phase transformation, and the grain size affects the volume fraction of the grain boundary, which further affects the phase interface during phase transformation. Inferred from this, the grain size also has an effect on the superelasticity in Fe-based superelastic alloys. Omori et al. made the alloy into wire to investigate the effect of grain size on the superelasticity [103]. They used d/D to measure the grain size, where d is the average grain size and D is the diameter of the wire. Two models, Taylor and Sachs, are used to calculate the critical stress value and recoverable strain value of martensitic transformation [104,105]. It is found that as the d/D value increases, the recoverable strain value becomes larger, while the critical stress becomes smaller. When d/D > 1, the Fe-Mn-Al-Ni wire with bamboo structure possesses ~5% superelasticity due to the decrease of grain constraint effect [103]. When d/D > 1, almost every grain can be transformed into martensite independently. The resistance is relatively small during martensitic transformation and recover transformation, which is extremely beneficial to superelasticity [103]. Tseng et al. also proved that the increase in grain size can enhance the plasticity, reduce the critical transformation stress, and increase the recoverable strain [106]. When d/t (t is the width of the sample) is 0.67, the superelasticity is 1.5%; when the d/t is 1.67, the superelasticity is 3% [106]. This is because the increase in grain size reduces the amount of grain boundaries. During the deformation of polycrystalline alloys, the presence of grain boundaries restricts the deformation of the grains, thereby affecting the superelasticity. At present, the effect of grain size on the superelasticity of Fe-Ni-Co-Al and Fe-Ni-Co-Ti superelastic alloys is rarely studied, needing further investigations.

The larger the grain size, the better the superelasticity. Therefore, the method of obtaining large-size grains is particularly important. The principle of obtaining large-size grains is to provide energy for grain growth, which can be divided into normal grain growth and abnormal grain growth. Omori et al. used the normal grain growth method to prepare large α-phase grains [103]. Solid solution at 1200 °C was conducted for different times, so that the grains can obtain enough energy to grow. In fact, the grain size obtained by normal grain growth is not particularly large and thus, abnormal grain growth is usually used to prepare large-size grains. Studies have shown that the presence of texture pinning is a key factor in determining abnormal grain growth [107]. If there is texture pinning after the precipitate is dissolved, abnormal growth of columnar crystals will occur; if there is no texture pinning, only normal growth will occur, limiting the grain size [107]. Cyclic heat treatment is the most commonly used method for abnormal grain growth. Omori et al. first proposed the use of cyclic heat treatment in 2016 to prepare 10 times larger grains than the normal grains [108]. They carried out cyclic heat treatment between the α single-phase zone (1200 °C) and the α + γ dual-phase zone (600–1100 °C). When the α single-phase zone is cooled to the α+γ dual-phase zone, the γ phase precipitates out. When the α + γ dual-phase region is heated to the α single-phase region, the γ phase transforms into the α phase and sub-grains are formed. The grains grow by the gradual annexation of the sub-grains, producing large-sized grains [108]. The cyclic heat treatment method used by Tseng et al. is different from that by Omori et al. They heat-treated the sample at 1200 °C for 0.5 h, and then air-cooled to room temperature, which was used as a cycle for multiple cycles [108]. After 5 cycles, they produced large-sized grains of more than 5 mm. Vollmer et al. investigated the effect of Ti and Cr elements on abnormal grain growth of Fe-Mn-Al-Ni alloy by cyclic heat treatment in single-phase and dual-phase regions [109]. The results show that Ti can promote the abnormal grain growth, while Cr can inhibit the abnormal grain growth. As shown in Figure 9, the grain size of Fe-Mn-Al-Ni-Ti is larger than that of Fe-Mn-Al-Ni in the micrograph after a single- cycle heat treatment [109]. However, the existence of triple junctions can still be seen in Figure 9a,c, which is very unfavorable to superelasticity [109]. After a single-cyclic heat treatment, the average grain size of Fe-Mn-Al-Ni is 2.3 mm, the average grain size of Fe-Mn-Al-Ni-Ti is 7.2 mm, and the average grain size of Fe-Mn-Al-Ni-Cr is 0.66 mm (no difference from the average grain size of the non-cyclic heat treatment) [109]. The addition of Ti element promotes the grain boundary mobility, accelerating the grain growth. The grain boundary mobility of Fe-Mn-Al-Ni-Ti was determined to be 1.84 × 10⁻⁵ m/s, which is more than 7 times higher than that of Fe-Mn-Al-Ni (2.5 × 10⁻⁶ m/s) [109]. The increase of grain boundary mobility is due to the decrease of the sub-grain size. The small size of sub-grain increases the driving force of abnormal grain growth, and makes the grain grow larger [109]. The reason why Cr element inhibits the abnormal growth of grains is that the part enclosed by the red dashed line in Figure 10 has no sub-crystals near the grain boundaries, while there are a large number of sub-grains in the center area, resulting in the formation of low-density area of sub-grains [109]. The premise of making the grain abnormal growth is that the sub-crystalline low-density region needs to be overcome by the normal growth of grains at large angular grain boundaries, otherwise the abnormal growth of grains will not arise. The abnormal growth of the grains occurs when the grain first contacts the sub-grain. In Figure 10, the large-angle grain boundaries and sub-grains are clearly separated by the low-density region, so the abnormal growth of grains is strongly suppressed [109]. In this study, Vollmer et al. prepared 220 mm long Fe-Mn-Al-Ni-Ti single crystal rod, obtaining a good superelasticity in tensile test under 8% applied strain [109].

The use of cyclic heat treatment makes it possible to prepare large-sized grains, but this method has a fatal problem, that is, it takes an extremely long time. For cyclic heat treatment, it takes 48.2 h to prepare a 60 mm single crystal [110]. Vallejos et al. pioneered the combination of directional annealing and cyclic heat treatment, which solved the long time-consuming problem [110]. The principle of cyclic directional annealing is a combination of directional annealing to produce strong thermal gradients to cause grain growth and cyclic heat treatment to cause abnormal grain growth. The schematic diagram of cyclic directional annealing is shown in Figure 11. At the beginning of heating, the grains in the hot zone grow equiaxed, as shown in Figure 11a. The grains outside the region cannot grow due to the insufficient energy provided by the temperature to migrate the grain boundaries. When the sample rod moves, the grains that have grown up just after the heating move, passing through the ungrown grains. The difference in grain size provides the driving force, which continuously promotes the migration of grain boundaries and the grain growth, as shown in Figure 11b. α sub-grains will be produced during the thermal cycling, as shown in Figure 11c. These sub-grains can continuously provide driving force, which makes the grain boundaries continue to migrate. The grains grow larger and larger, even becoming single crystals, as shown in Figure 11d. In directional annealing or cyclic heat treatment, the driving force will be dissipated as the grains grow, which hinders the migration of grain boundaries. This is also the reason for the long time-consuming cycle of heat treatment. However, cyclic directional annealing also has some disadvantages. The size of the grains is limited by the hot zone size, but this process also provides a method for preparing large grains in a short time.

5. Effects of Grain Orientation and Texture on Superelasticity

Studies have shown that the superelasticity strongly depends on the grain orientation in NiTi-based superelastic alloys [111]. The orientation of the grains can affect the martensitic variation to adjust the strain in NiTi-based superelastic alloys. It is speculated that grain orientation affects the superelasticity of Fe-based superelastic alloys by affecting the martensite variation. Large-sized grains or single crystals can be obtained by abnormal grain growth by cyclic heat treatment in Fe-Mn-Al-Ni superelastic alloys. Therefore, it is obvious that grain orientation significantly affects the superelasticity of Fe-Mn-Al-Ni superelastic alloys. For polycrystalline alloys, grains are arranged in order along certain directions to produce texture. However, Fe-Ni-Co-Al and Fe-Ni-Co-Ti superelastic alloys are extremely difficult to prepare large grains or single crystals due to the low mobility of grain boundary. In the case of polycrystalline alloys, texture has a significant effect on the superelasticity.

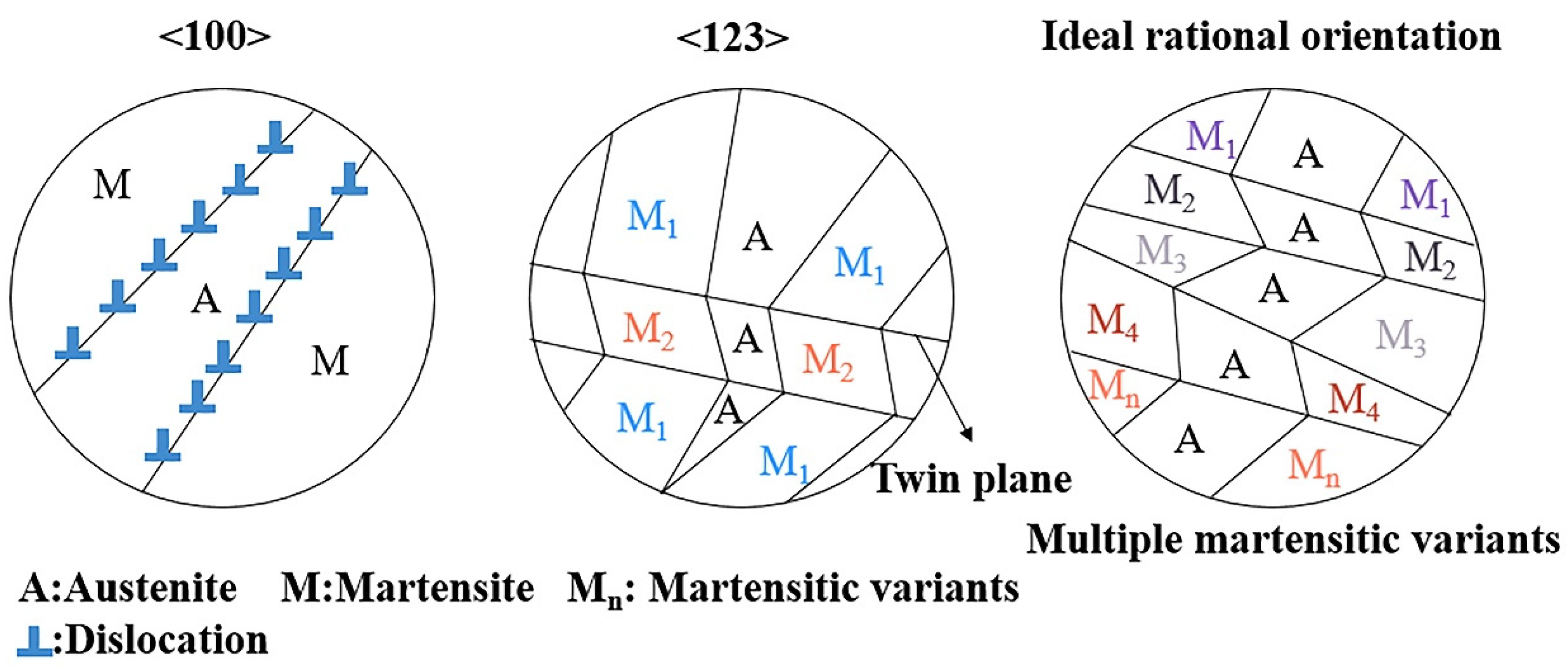
5.1. Effects of Grain Orientation on Superelasticity

Grain orientation has a significant effect on the superelasticity [102]. Tseng et al. calculated the superelasticity of <100> and <123> orientations as 10.5% and 9%, respectively, according to the energy minimization theory and lattice deformation theory in Fe-Mn-Al-Ni superelastic alloy [102,112,113]. In the tensile experiment, the superelasticity of <123> orientation is ~7.8%, which is similar to 9% calculated by the theoretical model. However, the superelasticity of the <100> orientation is only 3.5%, which is quite different from the calculation result [102]. Figure 12a shows the TEM bright field image of Fe-Mn-Al-Ni single crystal in <100> orientation. It can be seen that there is a large amount of parallelism dislocations and hairpin dislocations at the austenite–martensite interface and austenite matrix [102]. These dislocations pin the martensite phase, and suppress the occurrence of the reverse martensitic transformation, resulting in a low recovery strain. Figure 12b shows that high-density dislocations are not observed in <123> orientation, but two martensite variants are found, making it possible for martensite to easily form twins to accommodate the lattice strains, and reducing the likelihood of dislocation formation [102]. Only one martensite variant is available to accommodate tensile strain along the <100> orientation. This makes it difficult to accommodate lattice mismatch between the austenite and martensite, and thus results in the creation of dislocations that pin the martensite [102]. The austenite–martensite phase interface has a higher mobility, and can adapt to the transformation of thermoelastic martensite, thereby obtaining good superelasticity [102]. It is worth mentioning that the phenomenon of different orientation and different superelasticity was also observed in the compression experiment. The superelasticity of the <100>, <111>, and <123> oriented samples are 7.2%, 5.7%, and 1%, respectively [114].

The mechanism diagram of grain orientation on superelasticity is summarized in Figure 13. There are different kinds of martensite variants in different orientations. If the type of martensite variants is less than 2, a large number of dislocation is easily generated at the interface between austenite and martensite, and the dislocation is deposited at the interface. When martensitic transformation occurs, the phase interface is difficult to reciprocate, which prevents the occurrence of thermoelastic martensitic transformation, making it difficult to obtain superelasticity. The more the martensite variants, the easier the reciprocating migration of phase interface, which is beneficial for the occurrence of thermoelastic martensitic transformation. According to the above mechanism, good superelasticity can be achieved by obtaining more martensite variants in a reasonable orientation to reduce dislocation density, facilitate phase interface migration, and promote the occurrence of thermoelastic martensitic transformation.

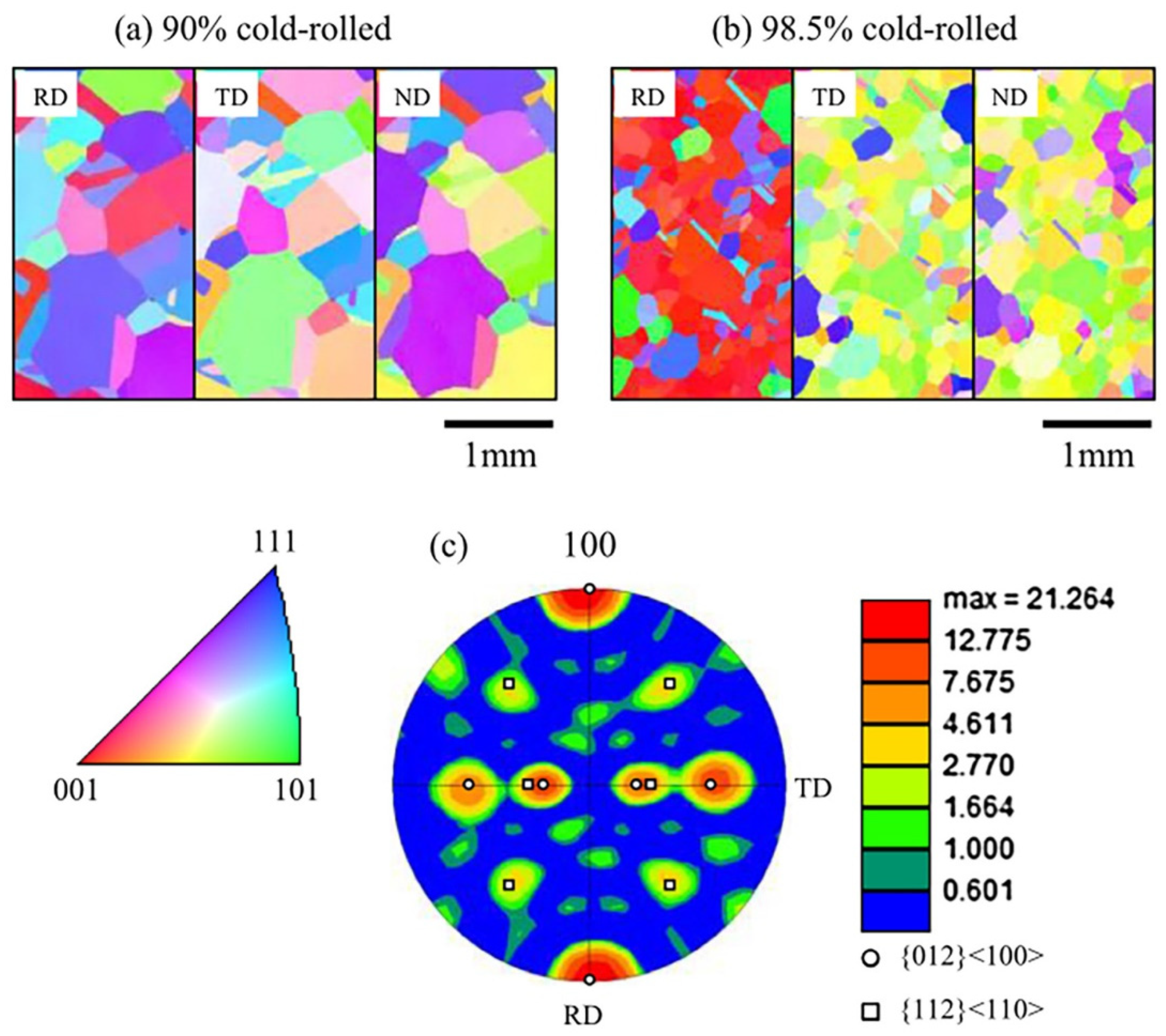
5.2. Effects of Texture on Superelasticity

In Fe-Ni-Co-Al superelastic alloy, if there is no strong texture, it will fracture before showing superelasticity during deformation [41]. Even if thermoelastic martensitic transformation is obtained by the precipitation of the γ′ phase, the sample breaks before the phase transformation occurs. Figure 14 shows that the FeNiCoAlTiB alloy specimen with random grain orientation breaks under 90% cold-rolling deformation without exhibiting superelasticity, as shown in Figure 15a [69]. After 98.5% large cold-rolling deformation, most of the grains are <100> orientation along the rolling direction, as shown in Figure 15b. In Figure 15c, it can be seen that the sample has a strong {012}<100> texture and relatively weak {112}<110> texture, showing 4.2% superelasticity, as shown in Figure 14 [69]. FeNiCoAlNbB alloy also has two kinds of textures of {111}<110> and {112}<110> after 98.5% large deformation cold-rolling, showing 5% superelasticity [68]. FeNiCoAlTaB alloy has a {035}<100> texture after 98.5% cold-rolling, and exhibits 13.5% superelasticity [41], while no superelasticity is presented in the case without strong textures. Although the addition of B element inhibits the precipitation of the B2 phase at the grain boundary, there are still a certain amount of B2 phases observed at the grain boundary without strong textures. In the alloy samples with strong textures, the B2 phases are precipitated only at specific types of grain boundaries [69,115]. The selective precipitation of B2 phase improves the mechanical properties of the alloy and contributes to the excellent superelasticity. The existence of strong textures affects the characters of grain boundaries. In the samples without texture, there are a large number of large-angle grain boundaries, which possess high energy. B2 phase is easy to nucleate and grow up at large-angle grain boundaries, weakening the grain boundaries. Due to the presence of strong texture, many small-angle grain boundaries and coincidence site lattice boundaries appear. The energy of these grain boundaries is extremely small, which inhibits the precipitation of B2 phase [69,115]. In addition, the small-angle grain boundary and coincidence site lattice boundaries also reduce the constraint of the grain boundary during deformation. These factors provide sufficient conditions for obtaining superelasticity.

6. Other Influencing Factors on Superelasticity

The thermal hysteresis also has a significant effect on the thermoelastic martensitic transformation. Reducing thermal hysteresis is beneficial to superelasticity. Reducing the shear modulus of austenite is an effective method to reduce the thermal hysteresis of martensitic transformation in Fe-Ni-Co-Ti alloy, while this will lead to a reduction in the elastic properties of the martensite grown together with austenite [116]. In Fe-Ni alloys, Cu alloying can reduce the elastic modulus of austenite [117]. Kokorin et al. added Cu element into Fe-Ni-Co-Ti alloy to investigate the martensitic transformation characteristics [62]. After the addition of Cu, a relatively small thermal hysteresis of about 60 K is obtained [62]. This is firstly due to the transformation of thermoelastic martensite. Secondly, the alloying of Cu reduces the elastic modulus of austenite, which reduces the elastic energy of growing martensite grains. In the cyclic tensile unloading experiment, the Fe-Ni-Co-Ti-Cu alloy exhibited a superelasticity of 4.5% [118]. This is much higher than the 0.7% superelasticity obtained by Kokorin et al. in the Fe-Ni-Co-Ti alloy, which is the same as obtained by Titenko et al. in the Fe-Ni-Co-Ti alloy through heat treatment [84,90]. The Fe-Ni-Co-Al superelastic alloy with strong γ′ phase element also possesses low thermal hysteresis, as shown in Figure 16. The resistivity curves of FeNiCoAlNbB, FeNiCoAlTiB, and FeNiCoAlTaB alloys are closed with small thermal hysteresis of 20 K, 31 K, and 24 K, respectively, corresponding to 5%, 4.2%, and 13.5% superelasticity [41,68,69].

After the addition of alloying elements, the properties of the alloys will change. As mentioned in the former, the addition of alloying elements (Ni, C, Ti, Nb, Ta, B, Cu) can affect the formation of precipitates and grain sizes, and further affect superelasticity. Although the addition of Cr inhibits the abnormal growth of grains, Fe-Mn-Al-Ni-Cr alloy can show excellent superelasticity in an extremely wide temperature window through proper heat treatment [119]. The relation between the critical stress and temperature of Fe-Mn-Al-Ni-Cr alloy is almost zero, indicating that the temperature has no effect on the critical stress [119]. This kind of alloy with a wide range of applications and small critical stress changes is expected to become a candidate for aerospace parts.

7. Conclusion and Outlook

Fe-based superelastic alloys are favored by virtue of their good superelasticity, large superelastic temperature range, low temperature dependence, low price and easy processing, possessing significant development prospects. The thermoelastic martensitic transformation of Fe-based superelastic alloy is affected by factors such as structure and grain. Therefore, factors such as precipitate size, grain size, grain orientation, and grain boundary characteristic may all affect the superelasticity. Obtaining good superelasticity requires that both the precipitates and grains have appropriate sizes; more martensite variants can be activated during deformation; a good grain boundary state, etc. Grains with appropriate size can reduce the constraints of grain boundaries during phase transformation. Precipitates with appropriate size can coherently strengthen the parent phase. Activating more martensite variants can make martensitic transformation and its recovery to easily occur, reducing the formation of dislocations at the phase interface, and thereby reduce the pinning effect of dislocations on martensite. A good grain boundary characteristic can ensure that the material does not break before exhibiting superelasticity. Although the research of Fe-based superelastic alloy has made some progress, there are still some problems that have not been solved. The properties are difficult to meet the requirements of practical applications. The relevant basic theoretical researches are still needed and mainly as follows:

(1)

The superelasticity of Fe-based superelastic alloy depends on the thermoelastic martensitic transformation, which can be induced by two factors (temperature and stress). Although there are some studies on the thermodynamics and kinetics of temperature-induced Fe-based thermoelastic martensitic transformation, stress-induced martensitic transformation has not been studied in depth. However, the thermodynamic and kinetic mechanism of thermoelastic martensitic transformation induced by stress is rarely reported.

(2)

The low-energy grain boundary can inhibit the precipitation of brittle phases at the grain boundary, and ensure that the alloy obtains good superelasticity. At present, the only way to suppress the precipitation of brittle phases at grain boundaries is the addition of B element combined with cold-rolling with large deformation to obtain strong texture. However, some brittle phases will still precipitate and weaken the grain boundaries. In addition, cold-rolling with large deformation amount is generally difficult to achieve. Therefore, it is urgent to find a simple and practical method to obtain low-energy grain boundaries.

(3)

It is necessary to further investigate the influence of composition and thermomechanical treatment on the superelasticity, since microstructure is determined by the composition and thermomechanical treatment.

(4)

The current precipitation strengthening is to make the martensitic transformation into thermoelastic by precipitating single coherent ordered phases. It is theoretically feasible to study and design two or multiple coherent ordered precipitates to synergistically strengthen the alloy to obtain good superelasticity.