Influence Mechanism of a New-Style Resonator on Band Gap of Locally Resonant Phononic Crystal Double Panel Structure
Abstract
:1. Introduction
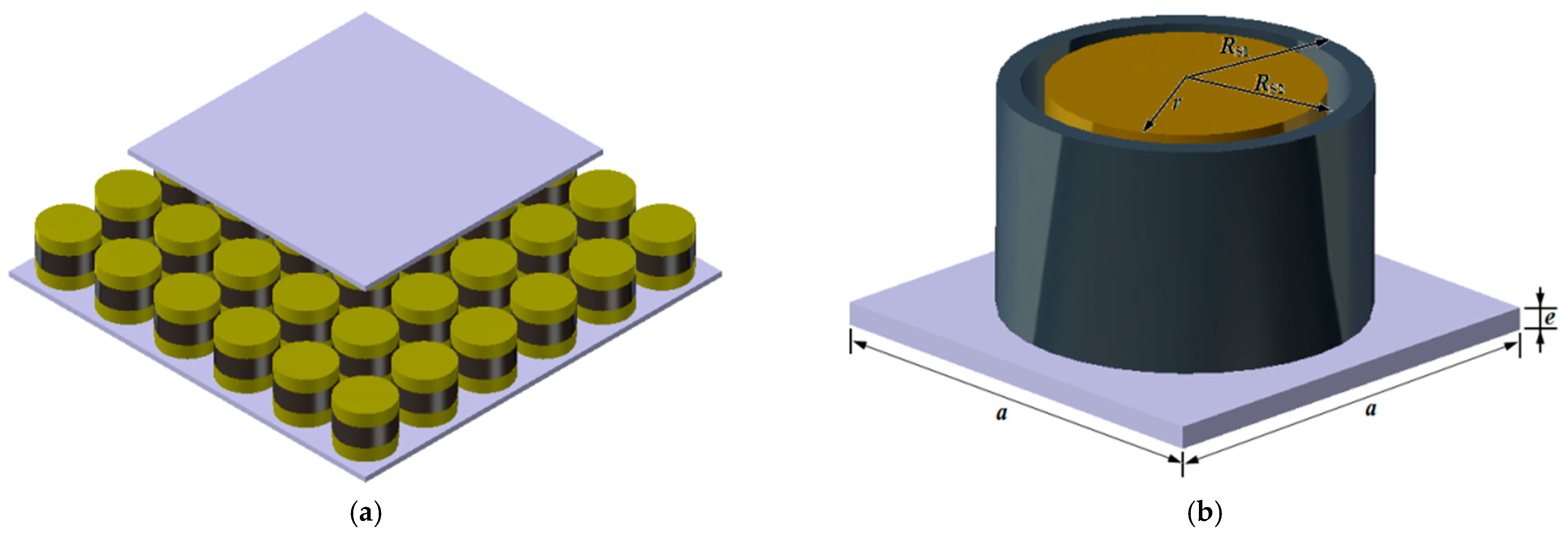
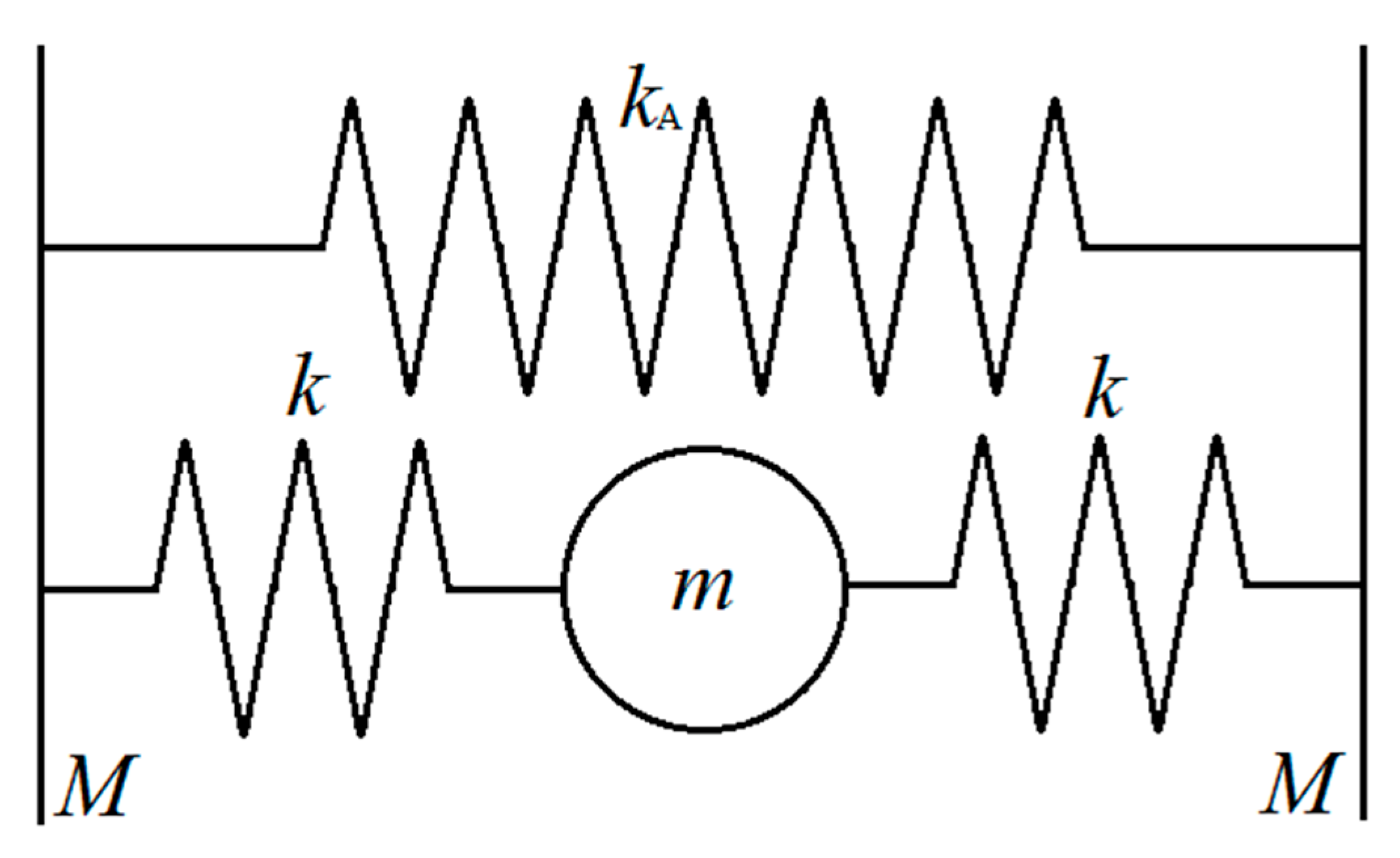
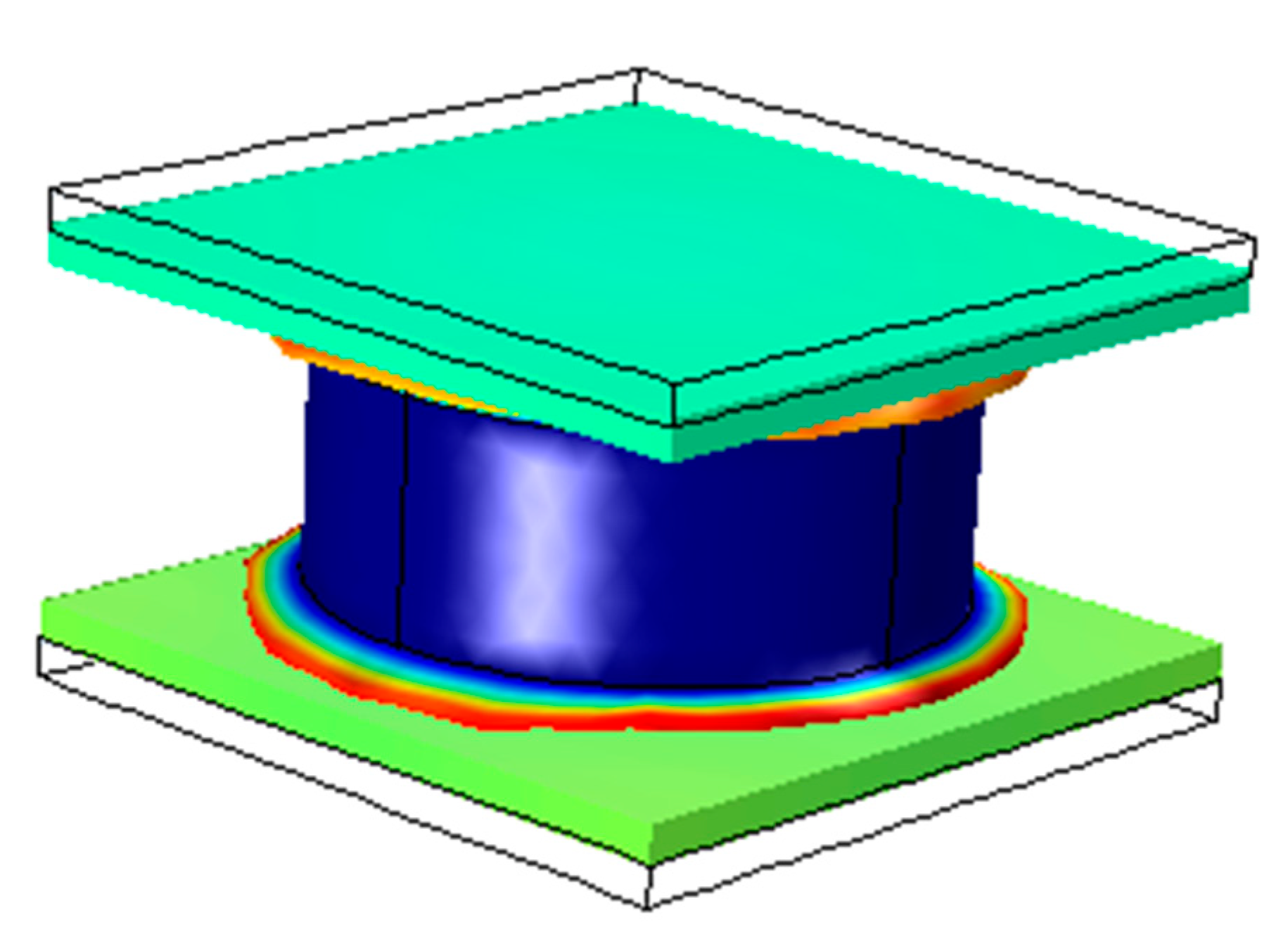
2. Model and Method
3. Numerical Results and Analyses
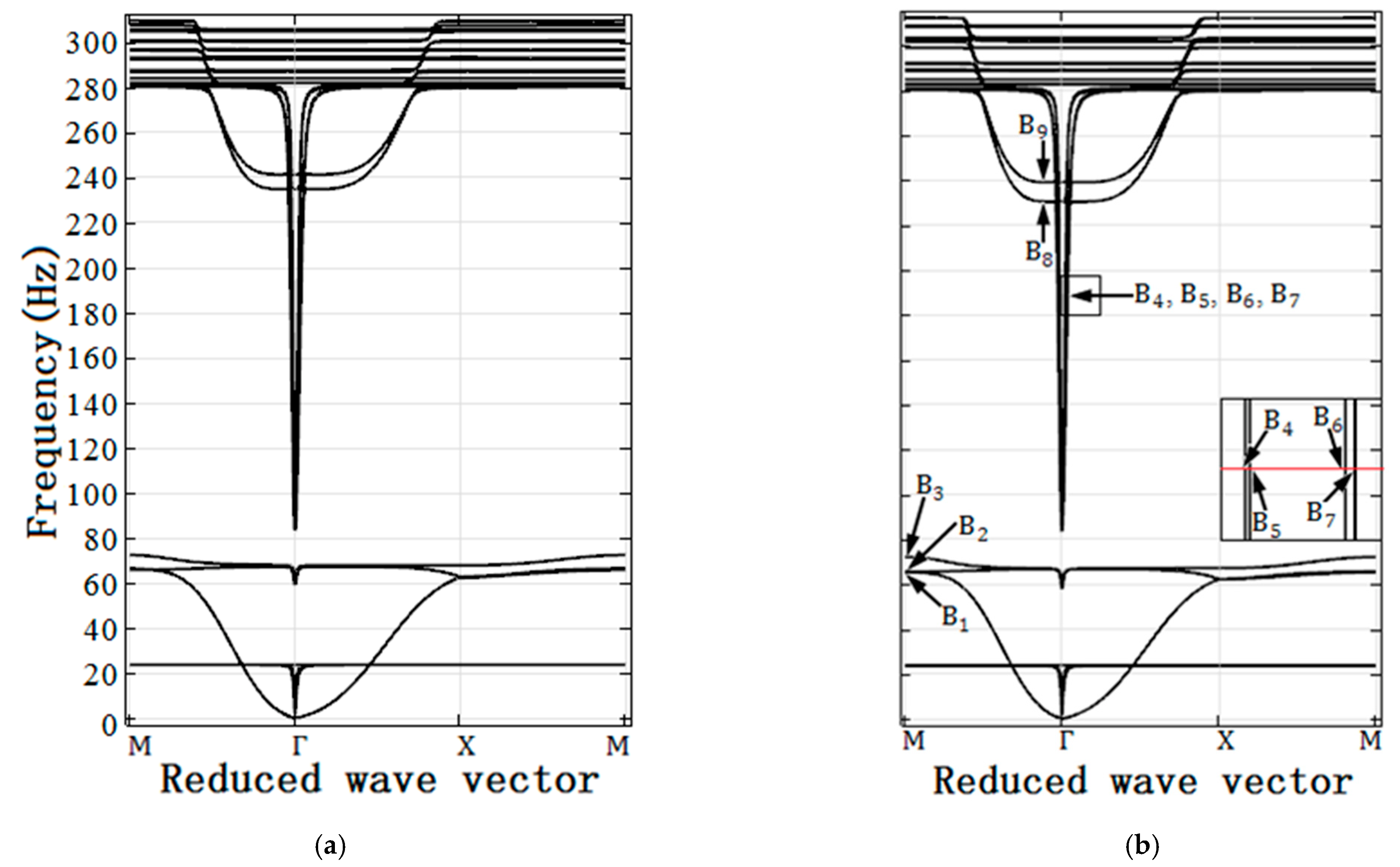
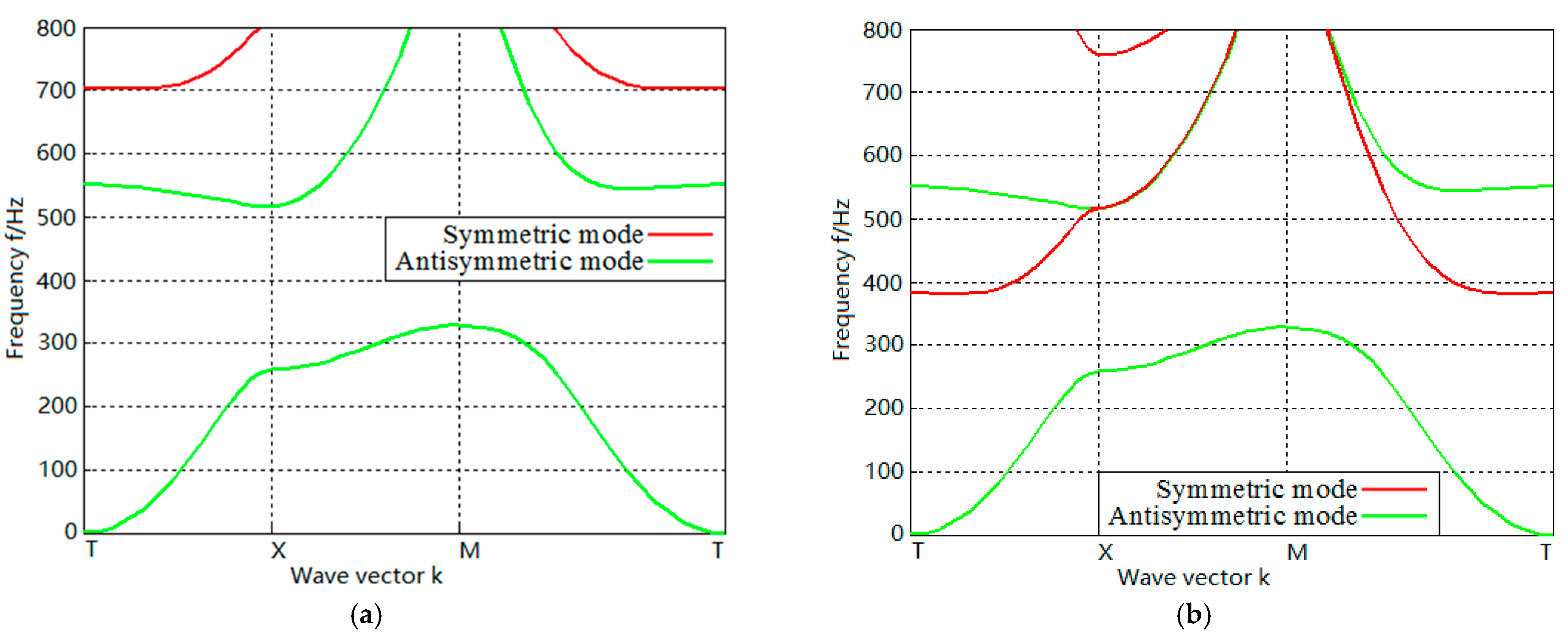
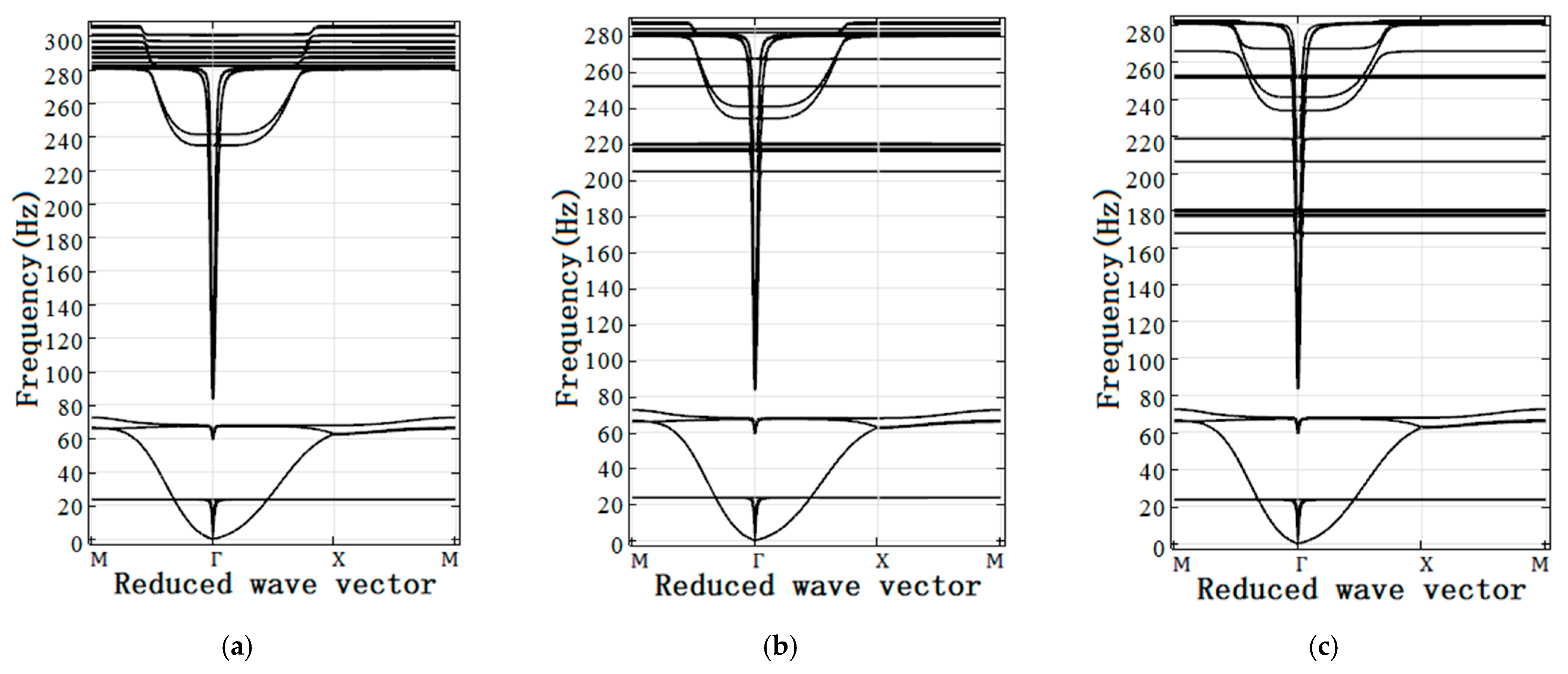
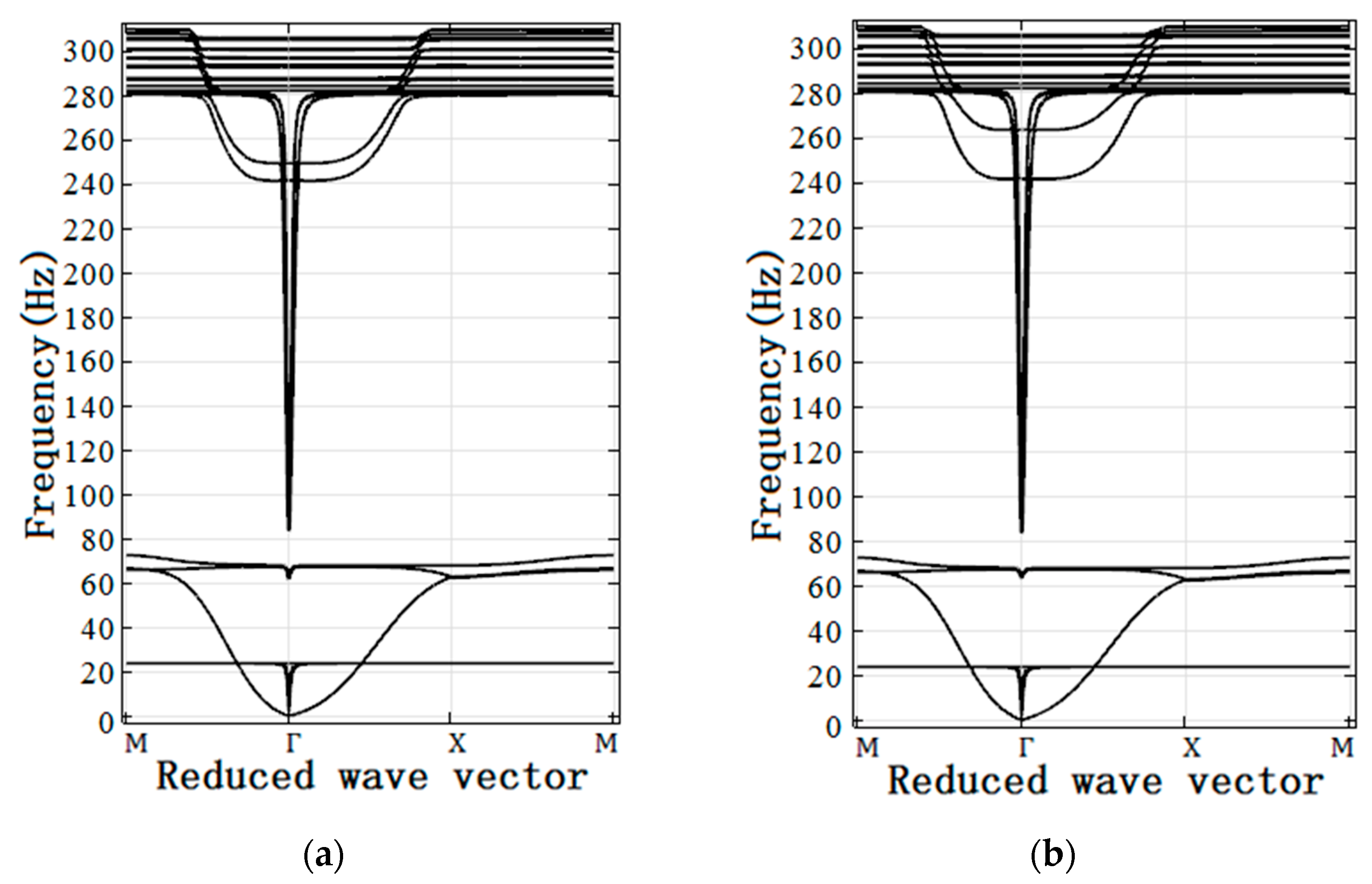
3.1. Band Structures of LRPC DPSs with and without Surrounded Soft Shell
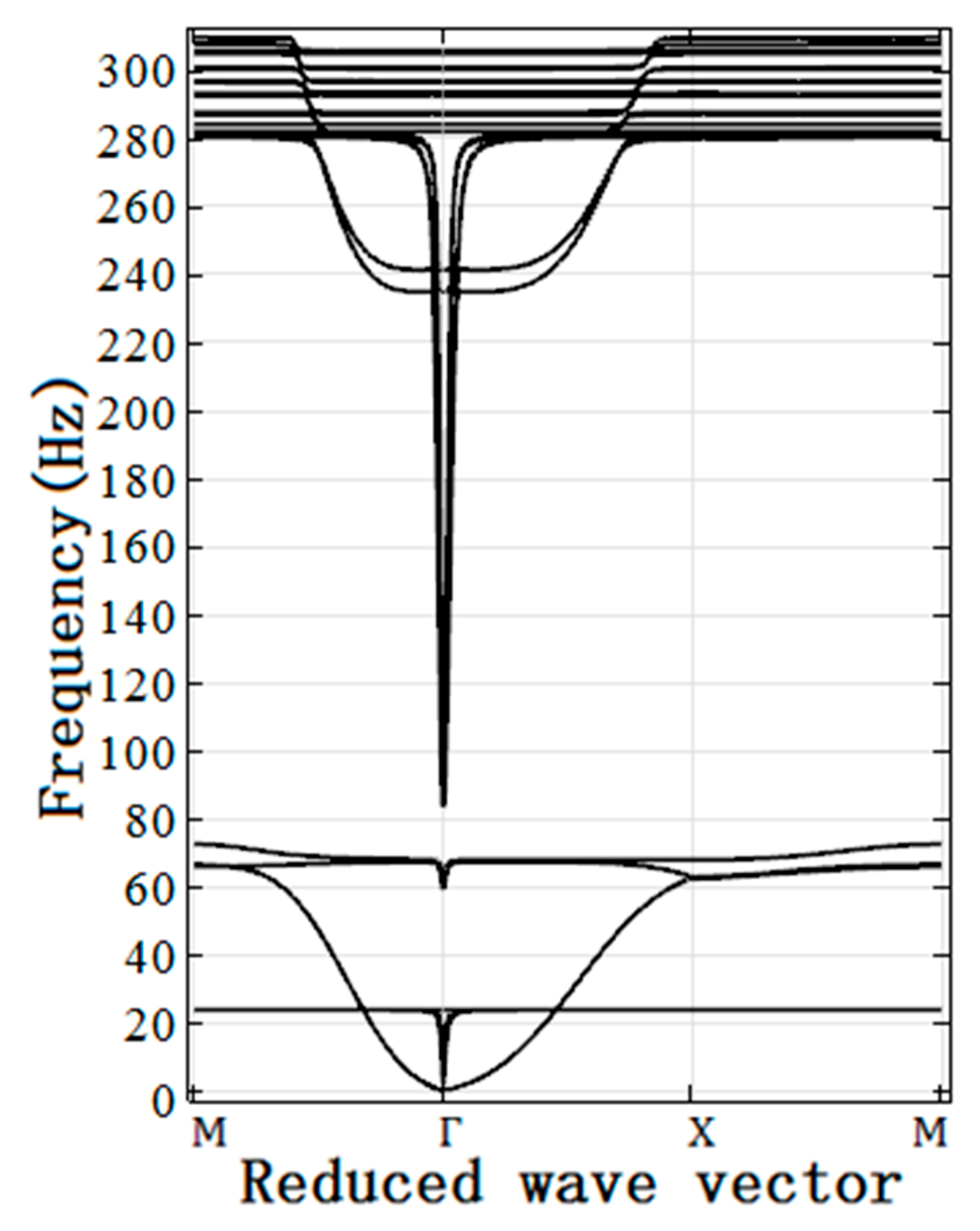
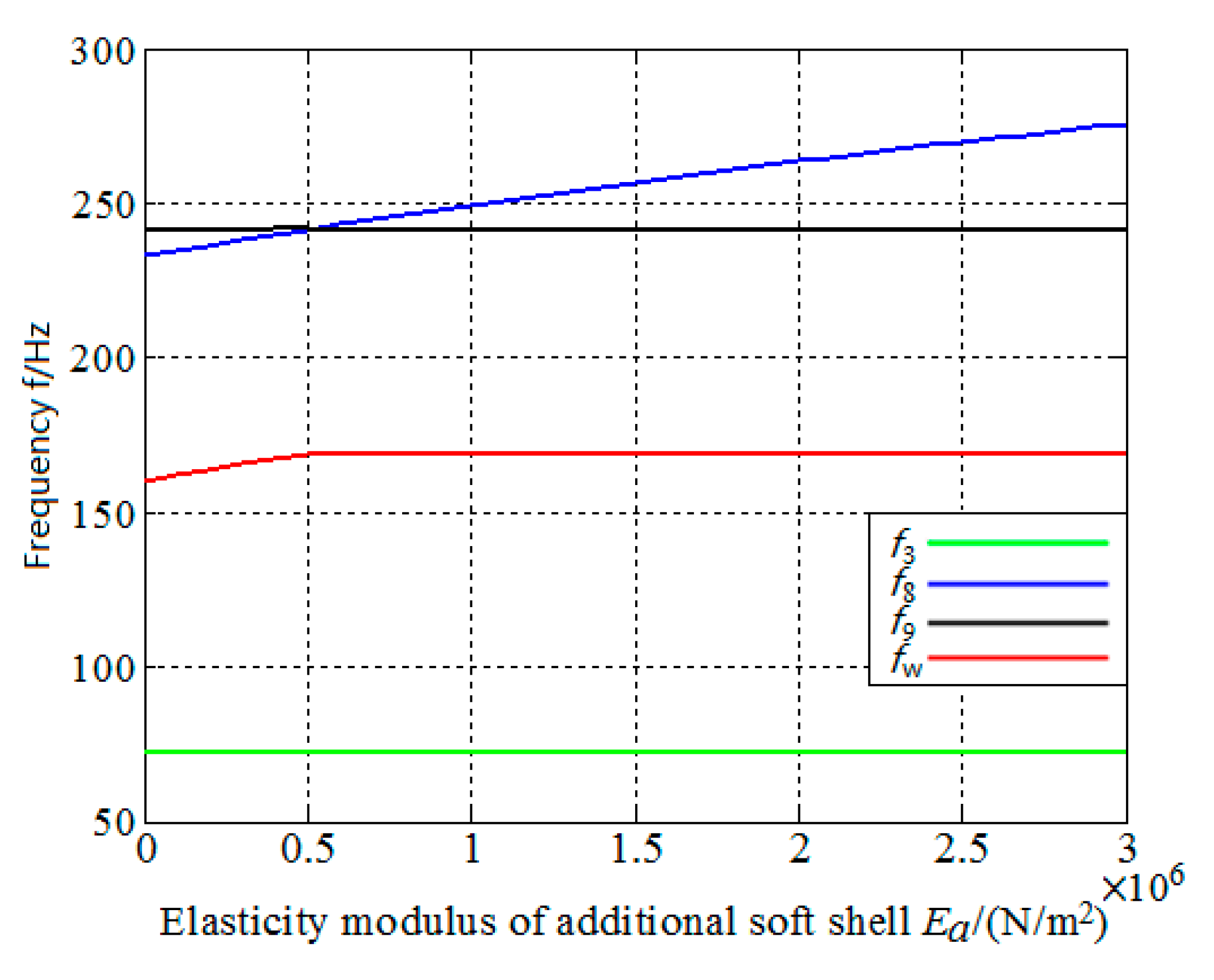
3.2. Influences of Soft Shell Parameters on Band Gap
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Heo, J.W.; Chung, J.; Choi, K. Dynamic time responses of a flexible spinning disk misaligned with the axis of rotation. J. Sound Vib. 2003, 262, 25–44. [Google Scholar] [CrossRef]
- Rossetti, D.J.; Norris, M.A. A comparison of actuation and sensing techniques for aircraft cabin noise control. Noise Control Eng. J. 1996, 44, 53–58. [Google Scholar] [CrossRef]
- Valoor, M.T.; Chandrashekhara, K.; Agarwal, S. Self-adaptive vibration control of smart composite beams using recurrent neural architecture. Int. J. Solids Struct. 2001, 38, 7857–7874. [Google Scholar] [CrossRef]
- Jung, J.-W.; Lee, S.-H.; Lee, G.-H.; Hong, J.-P.; Lee, D.-H.; Kim, K.-N. Reduction Design of Vibration and Noise in IPMSM Type Integrated Starter and Generator for HEV. IEEE Trans. Magn. 2010, 46, 2454–2457. [Google Scholar] [CrossRef]
- Pietrzko, S.J.; Mao, Q. New results in active and passive control of sound transmission through double wall structures. Aerosp. Sci. Technol. 2008, 12, 42–53. [Google Scholar] [CrossRef]
- Thongchom, C.; Saffari, P.R.; Refahati, N.; Saffari, P.R.; Pourbashash, H.; Sirimontree, S.; Keawsawasvong, S. An analytical study of sound transmission loss of functionally graded sandwich cylindrical nanoshell integrated with piezoelectric layers. Sci. Rep. 2022, 12, 3048. [Google Scholar] [CrossRef]
- Thongchom, C.; Jearsiripongkul, T.; Refahati, N.; Saffari, P.R.; Saffari, P.R.; Sirimontree, S.; Keawsawasvong, S. Sound Transmission Loss of a Honeycomb Sandwich Cylindrical Shell with Functionally Graded Porous Layers. Buildings 2022, 12, 151. [Google Scholar] [CrossRef]
- Sigalas, M.M.; Economou, E.N. Elastic and acoustic wave band structure. J. Sound Vib. 1992, 158, 377–382. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally Resonant Sonic Materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Z.; Liu, Y. Elastic wave band gaps for three-dimensional phononic crystals with two structural units. Phys. Lett. A 2003, 313, 455–460. [Google Scholar] [CrossRef]
- Ho, K.M.; Cheng, C.K.; Yang, Z.; Zhang, X.X.; Sheng, P. Broadband locally resonant sonic shields. Appl. Phys. Lett. 2003, 83, 5566–5568. [Google Scholar] [CrossRef]
- Oudich, M.; Li, Y.; Assouar, B.; Hou, Z. A sonic band gap based on the locally resonant phononic plates with stubs. New J. Phys. 2010, 12. [Google Scholar] [CrossRef]
- Badreddine Assouar, M.; Oudich, M. Enlargement of a locally resonant sonic band gap by using double-sides stubbed phononic plates. Appl. Phys. Lett. 2012, 100, 123506. [Google Scholar] [CrossRef]
- Hsu, J.C. Local resonances-induced low-frequency band gaps in two-dimensional phononic crystal slabs with periodic stepped resonators. J. Phys. D Appl. Phys. 2011, 44, 055401. [Google Scholar] [CrossRef]
- Xiao, Y.; Wen, J.; Wen, X. Flexural wave band gaps in locally resonant thin plates with periodically attached spring-mass resonators. J. Phys. D Appl. Phys. 2012, 45, 195401. [Google Scholar] [CrossRef]
- Ruan, Y.; Liang, X.; Hua, X.; Zhang, C.; Xia, H.; Li, C. Isolating low-frequency vibration from power systems on a ship using spiral phononic crystals. Ocean Eng. 2021, 225, 108804. [Google Scholar] [CrossRef]
- Xiao, W.; Zeng, G.W.; Cheng, Y.S. Flexural vibration band gaps in a thin plate containing a periodic array of hemmed discs. Appl. Acoust. 2008, 69, 255–261. [Google Scholar] [CrossRef]
- Qian, D.; Shi, Z. Bandgap properties in locally resonant phononic crystal double panel structures with periodically attached pillars. J. Theor. Appl. Mech. 2017, 55, 1167–1179. [Google Scholar] [CrossRef] [Green Version]
- Qian, D.; Shi, Z. Bandgap properties in locally resonant phononic crystal double panel structures with periodically attached spring-mass resonators. Phys. Lett. A 2016, 380, 3319–3325. [Google Scholar] [CrossRef]
- Wang, Y.F.; Wang, Y.S.; Su, X.X. Large bandgaps of two-dimensional phononic crystals with cross-like holes. J. Appl. Phys. 2011, 110, 2059. [Google Scholar] [CrossRef]
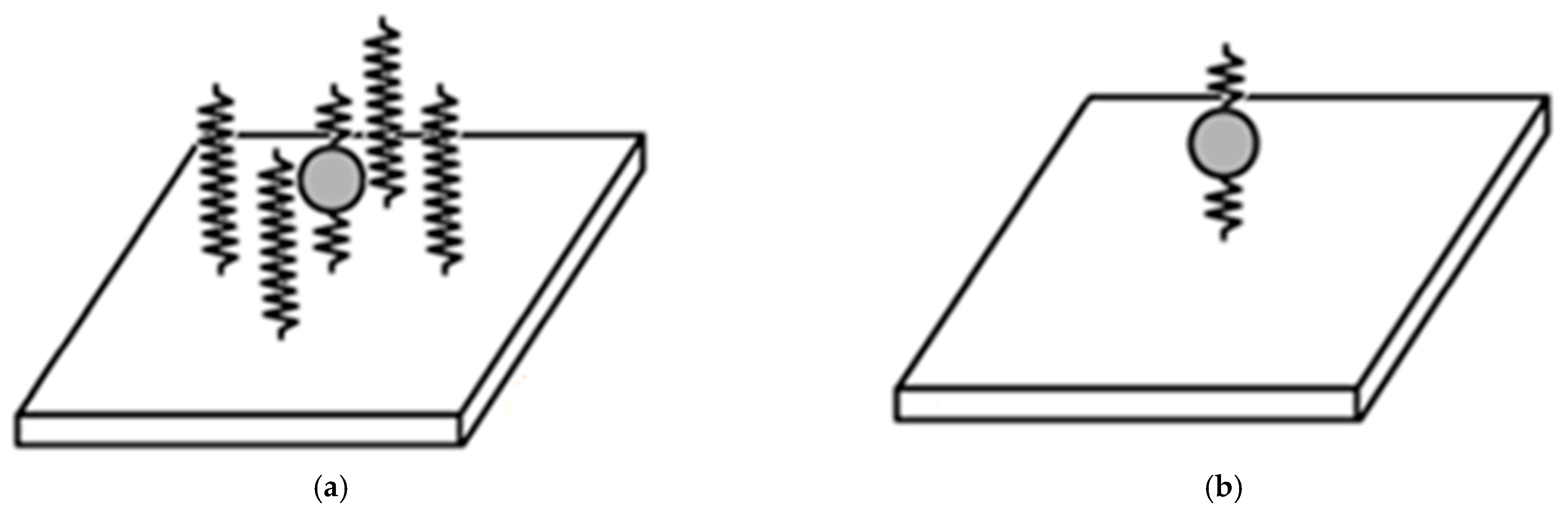
| Material | Mass Density | Young’s Modulus | Poission’s Ratio |
|---|---|---|---|
| Epoxy | 1180 | 0.435 | 0.368 |
| Rubber | 1300 | 1.175 × 10−5 | 0.469 |
| Pb | 11,600 | 4.08 | 0.37 |
| 0.1 | 0.005 | 0.04 | 0.01 | 0.03 | 0.046 | 0.043 |
| 77.6 | 0.35 | 2730 | 0.1 |
| 0.002 | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, Y.; Chen, M.; Qian, D.; Shi, Z. Influence Mechanism of a New-Style Resonator on Band Gap of Locally Resonant Phononic Crystal Double Panel Structure. Crystals 2022, 12, 609. https://doi.org/10.3390/cryst12050609
Xiang Y, Chen M, Qian D, Shi Z. Influence Mechanism of a New-Style Resonator on Band Gap of Locally Resonant Phononic Crystal Double Panel Structure. Crystals. 2022; 12(5):609. https://doi.org/10.3390/cryst12050609
Chicago/Turabian StyleXiang, Yujia, Molin Chen, Denghui Qian, and Zhiyu Shi. 2022. "Influence Mechanism of a New-Style Resonator on Band Gap of Locally Resonant Phononic Crystal Double Panel Structure" Crystals 12, no. 5: 609. https://doi.org/10.3390/cryst12050609
APA StyleXiang, Y., Chen, M., Qian, D., & Shi, Z. (2022). Influence Mechanism of a New-Style Resonator on Band Gap of Locally Resonant Phononic Crystal Double Panel Structure. Crystals, 12(5), 609. https://doi.org/10.3390/cryst12050609





