Fast, Accurate and Full Extraction of Coupling-of-Modes Parameters by Finite Element Method
Abstract
:1. Introduction
2. Theory to Extract COM Parameters
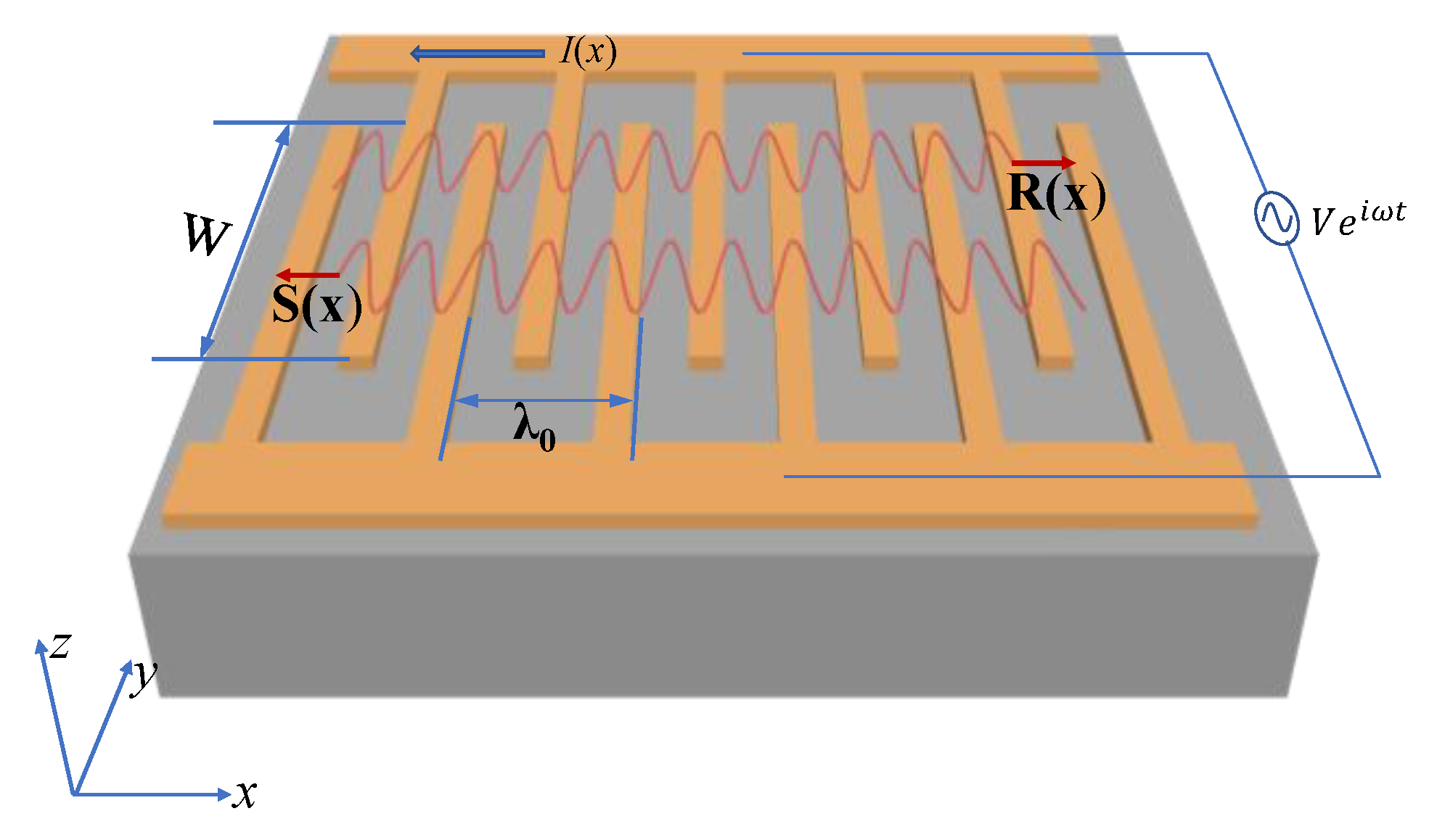
2.1. COM Model
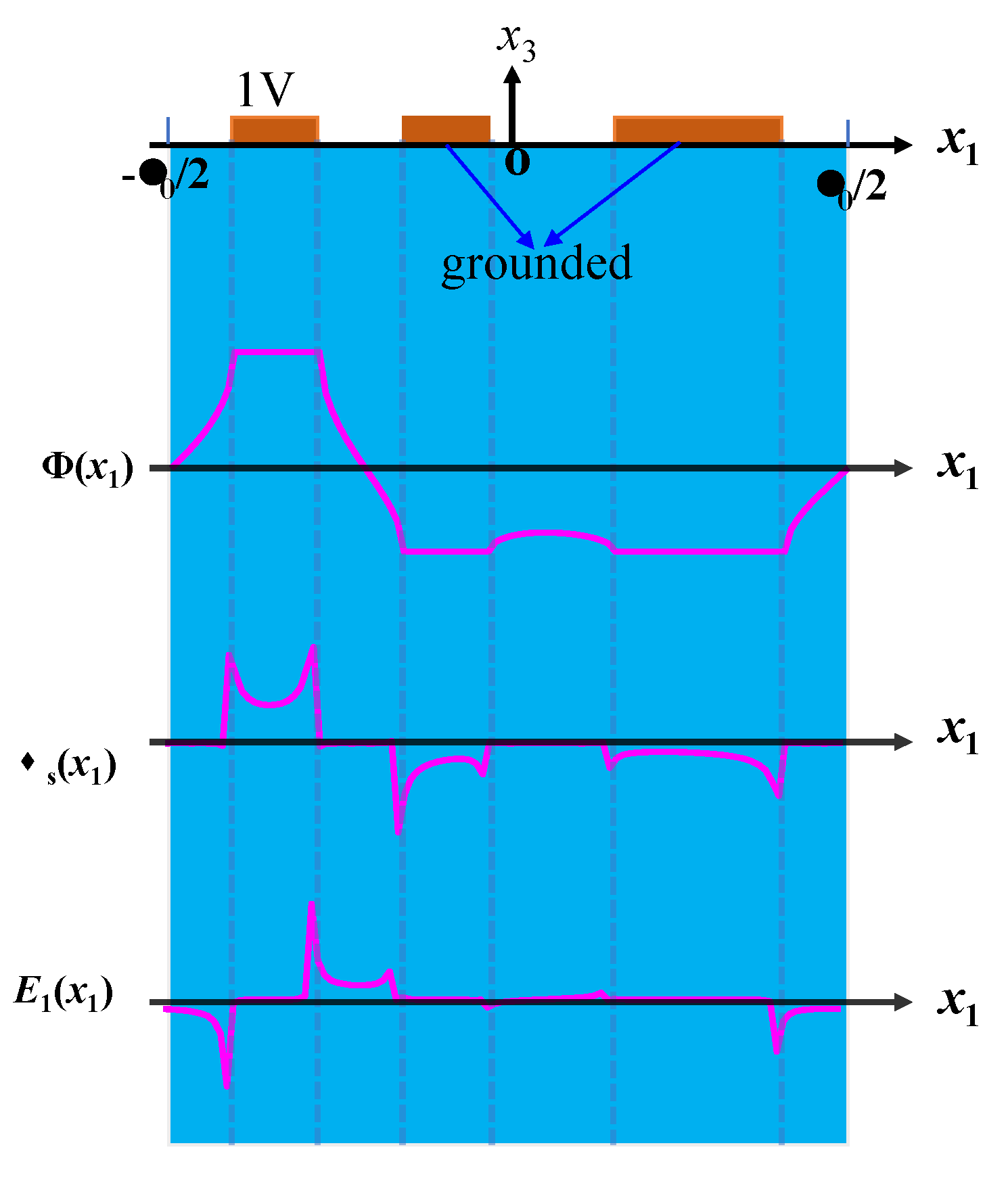
2.2. Extraction Technique of COM Parameters
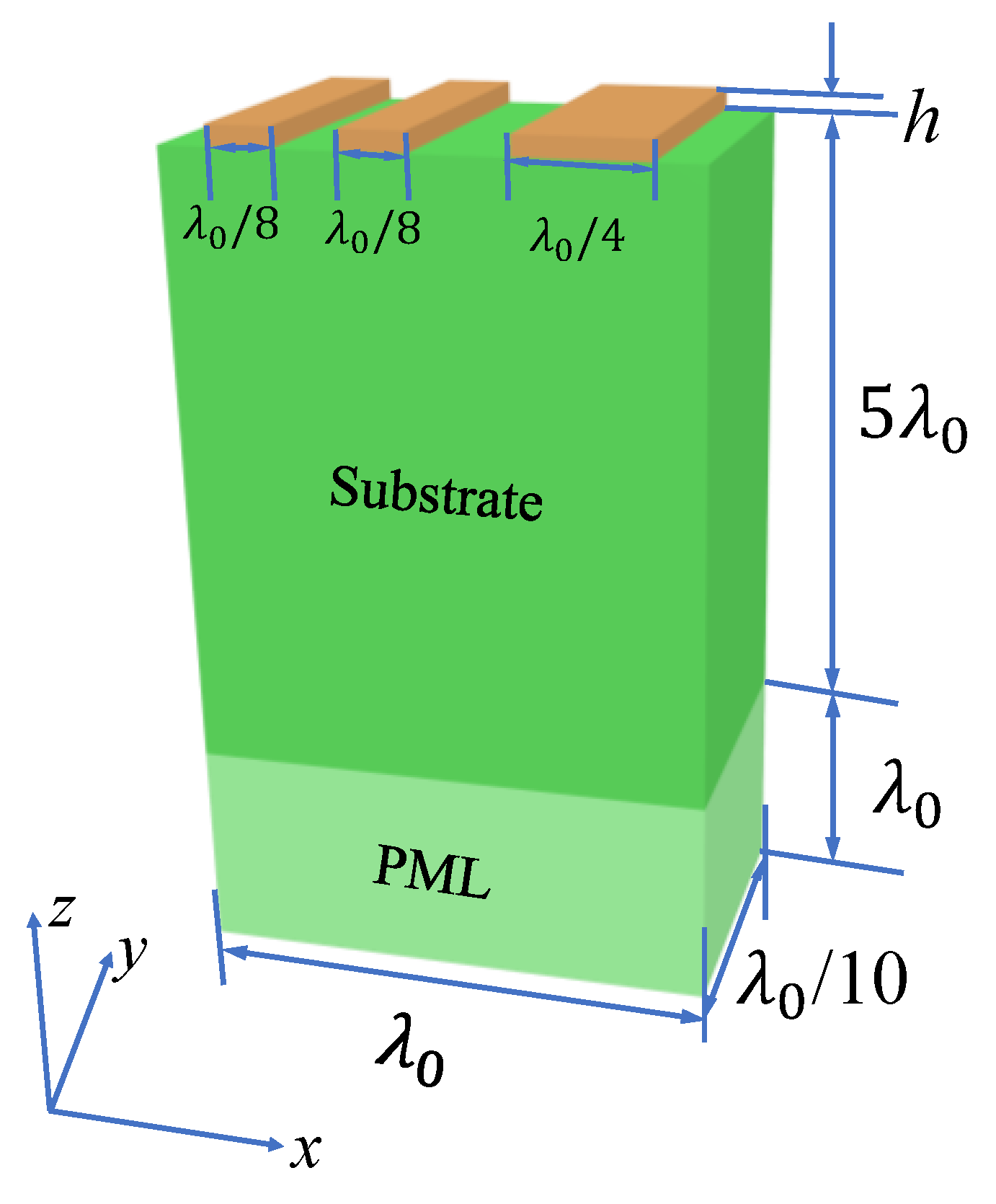
2.3. FEM Model Description and Simulation
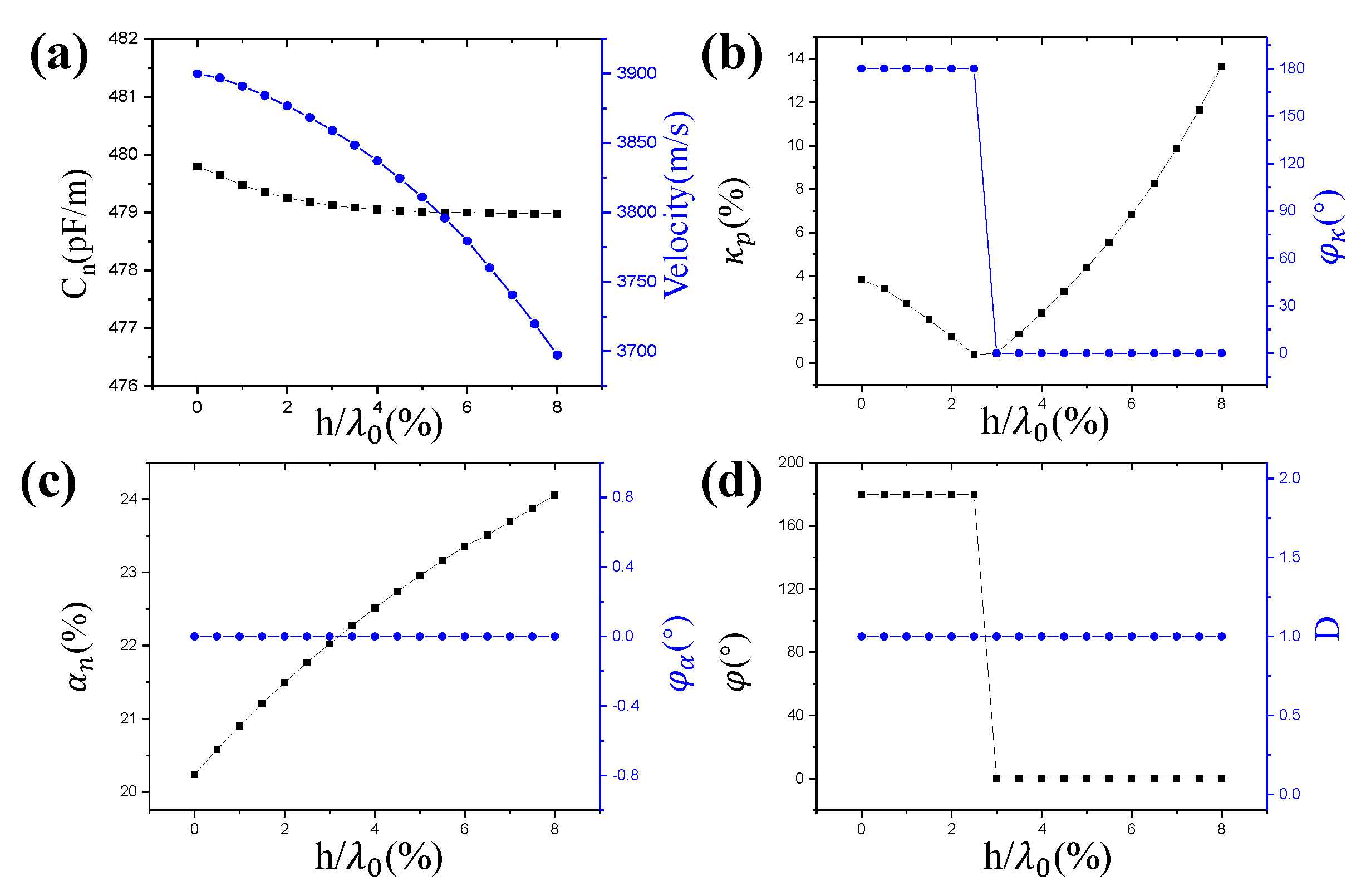
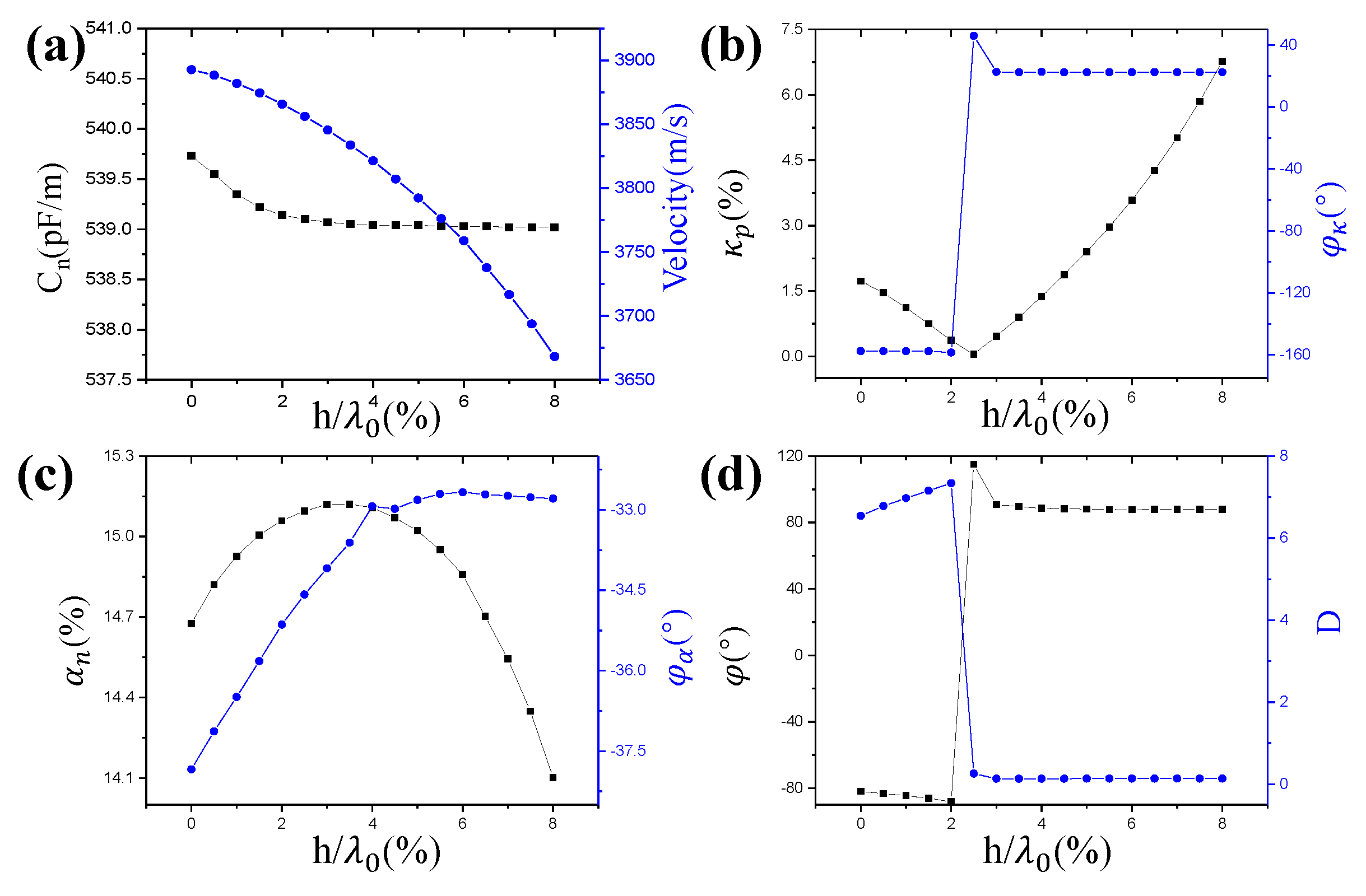
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Belyankova, T.; Vorovich, E.; Kalinchuk, V.; Tukodova, O. Specific features of SH-waves propagation in structures with prestressed inhomogeneous coating made of piezoceramics based on LiNbO 3. J. Adv. Dielectr. 2021, 11, 2160007. [Google Scholar] [CrossRef]
- Belyankova, T.; Vorovich, E.; Kalinchuk, V.; Tukodova, O. Peculiarities of surface acoustic waves, propagation in structures with functionally graded piezoelectric materials, coating from different ceramics on the basis of PZT. J. Adv. Dielectr. 2020, 10, 2060017. [Google Scholar] [CrossRef]
- Hofer, M.; Finger, N.; Kovacs, G.; Schoberl, J.; Zaglmayr, S.; Langer, U.; Lerch, R. Finite-element simulation of wave propagation in periodic piezoelectric SAW structures. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2006, 53, 1192–1201. [Google Scholar] [CrossRef] [PubMed]
- Koskela, J.; Plessky, V.; Willemsen, B.; Turner, P.; Hammond, B.; Fenzi, N. Hierarchical cascading algorithm for 2-D FEM simulation of finite SAW devices. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2018, 65, 1933–1942. [Google Scholar] [CrossRef] [PubMed]
- Willemsen, B.; Plesski, V.; Koskela, J. Fast, Highly Accurate, Full-Fem Surface Acoustic Wave Simulation. U.S. Patent 11,296,677, 5 April 2022. [Google Scholar]
- Li, X.; Bao, J.; Huang, Y.; Zhang, B.; Omori, T.; Hashimoto, K.-Y. Use of Hierarchical Cascading Technique for FEM Analysis of Transverse-Mode Behaviors in Surface Acoustic-Wave Devices. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2019, 66, 1920–1926. [Google Scholar] [CrossRef]
- Li, X.; Bao, J.; Qiu, L.; Matsuoka, N.; Omori, T.; Hashimoto, K.-Y. 3D FEM simulation of SAW resonators using hierarchical cascading technique and general purpose graphic processing unit. Jpn. J. Appl. Phys. 2019, 58, SGGC05. [Google Scholar] [CrossRef]
- Fernandez-Afonso, Y.; García-Zaldívar, O.; Calderón-Piñar, F. Equivalent circuit for the characterization of the resonance mode in piezoelectric systems. J. Adv. Dielectr. 2015, 5, 1550032. [Google Scholar] [CrossRef] [Green Version]
- Plessky, V.; Koskela, J. Coupling-of-modes analysis of SAW devices. Int. J. High Speed Electron. Syst. 2000, 10, 867–947. [Google Scholar] [CrossRef]
- Hartmann, C.; Abbott, B. Experimentally determining the transduction magnitude and phase and the reflection magnitude and phase of SAW SPUDT structures. In Proceedings of the IEEE Symposium on Ultrasonics, Honolulu, HI, USA, 4–7 December 1990; pp. 37–42. [Google Scholar]
- Kondratiev, S.; Thorvaldsson, T.; Sakharov, S.; Buzanov, O.; Medvedev, A. Extraction of COM parameters on langasite substrates and the application to design of a SAW filter. In Proceedings of the 2001 IEEE Ultrasonics Symposium. Proceedings. An International Symposium (Cat. No. 01CH37263), Atlanta, GA, USA, 7–10 October 2001; pp. 53–56. [Google Scholar]
- Ventura, P.; Hodé, J.; Solal, M.; Desbois, J.; Ribbe, J. Numerical methods for SAW propagation characterization. In Proceedings of the 1998 IEEE Ultrasonics Symposium. Proceedings (Cat. No. 98CH36102), Sendai, Japan, 5–8 October 1998; pp. 175–186. [Google Scholar]
- Dufilie, P.; Ventura, P.; Hecht, F. COM parameters for thick metal and partially buried electrodes extracted from a mixed FEM/BEM numerical model. In Proceedings of the 2012 IEEE International Ultrasonics Symposium, Dresden, Germany, 7–10 October 2012; pp. 807–810. [Google Scholar]
- Shaposhnikov, K.; Kaltenbacher, M.; Nicolay, P. Fast full-FEM computation of COM parameters. Application to multilayered SAW structures. In Proceedings of the 2014 IEEE International Ultrasonics Symposium, Chicago, IL, USA, 3–6 September 2014; pp. 1501–1504. [Google Scholar]
- Hashimoto, K.-Y.; Zheng, G.Q.; Yamaguchi, M. Fast analysis of SAW propagation under multi-electrode-type gratings with finite thickness. In Proceedings of the 1997 IEEE Ultrasonics Symposium Proceedings. An International Symposium (Cat. No. 97CH36118), Toronto, ON, Canada, 5–8 October 1997; pp. 279–284. [Google Scholar]
- Hashimoto, K.-Y.; Koskela, J.; Salomaa, M.M. Fast determination of coupling-of-modes parameters based on strip admittance approach. In Proceedings of the 1999 IEEE Ultrasonics Symposium. Proceedings. International Symposium (Cat. No. 99CH37027), Tahoe, NV, USA, 17–20 October 1999; pp. 93–96. [Google Scholar]
- Hartmann, C.; Wright, P.; Kansy, R.; Garber, E. An analysis of SAW interdigital transducers with internal reflections and the application to the design of single-phase unidirectional transducers. In Proceedings of the 1982 Ultrasonics Symposium, San Diego, CA, USA, 27–29 October 1982; pp. 40–45. [Google Scholar]
- Hashimoto, K.-y.; Hashimoto, K.-Y. Surface Acoustic Wave Devices in Telecommunications; Springer: Berlin/Heidelberg, Germany, 2000; Volume 116. [Google Scholar]
- Ruppel, C.C.; Fjeldly, T.A. Advances in Surface Acoustic Wave Technology, Systems and Applications; World Scientific: Singapore, 2001; Volume 20. [Google Scholar]
- Lin, J.; Wang, N.; Chen, H.; Shui, Y. Fast, precise, and full extraction of the COM parameters for multielectrode-type gratings by periodic Green’s function method. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2002, 49, 1735–1738. [Google Scholar]
- Chen, D.-P.; Haus, H.A. Analysis of metal-strip SAW gratings and transducers. IEEE Trans. Sonics Ultrason. 1985, 32, 395–408. [Google Scholar] [CrossRef]
- Hashimoto, K.-y.; Omori, T.; Ahn, C.-J. Extension of scalar potential formalism for transverse mode analysis of surface acoustic wave resonators. In Proceedings of the 2011 IEEE International Ultrasonics Symposium, Orlando, FL, USA, 18–21 October 2011; pp. 333–336. [Google Scholar]
- Huang, Y.; Bao, J.; Li, X.; Zhang, B.; Omori, T.; Hashimoto, K.-Y. Parameter extraction of coupling-of-modes equations including coupling between two surface acoustic waves on SiO2/Cu/LiNbO3 structures. Jpn. J. Appl. Phys. 2018, 57, 07LD13. [Google Scholar] [CrossRef]
- Abbott, B.P. A Coupling-of-Modes Model for SAW Transducers with Arbitrary Reflectivity Weighting; University of Central Florida: Orlando, FL, USA, 1989. [Google Scholar]
- Wu, T.-T.; Wang, S.-M.; Chen, Y.-Y.; Wu, T.-Y.; Chang, P.-Z.; Huang, L.-S.; Wang, C.-L.; Wu, C.-W.; Lee, C.-K. Inverse determination of coupling of modes parameters of surface acoustic wave resonators. Jpn. J. Appl. Phys. 2002, 41, 6610. [Google Scholar] [CrossRef]
- Chen, Y.-Y.; Wu, T.-T.; Chou, T.-T. Analysis of the frequency response of a dispersive IDT/ZnO/sapphire SAW filter using effective permittivity and the coupling of modes model. J. Phys. D Appl. Phys. 2003, 37, 120. [Google Scholar] [CrossRef]
- Alyakna, Y.Y.; Gulyaev, Y.V.; Kozlov, A.; PLESSKII, V. Infulence of modulation of the grrove depth of a Bragg reflective grating on the Rayleigh-wave reflection coefficient. Sov. Phys. Acoust.-USSR 1984, 30, 346–348. [Google Scholar]
- Sun, X.; Liu, W.; Ge, S.; Zhou, S.; Li, X.; Lin, D. Achieving both high electromechanical response and stable temperature behavior in Si/SiO2/Al/LiTaO3 sandwich structure. AIP Adv. 2019, 9, 035145. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.-m.; Jin, J.; Li, H.-l.; Hu, H.-p. A novel method to extract COM parameters for SAW based on FEM. In Proceedings of the 2019 13th Symposium on Piezoelectrcity, Acoustic Waves and Device Applications (SPAWDA), Harbin, China, 11–14 January 2019; pp. 1–5. [Google Scholar]
- Dühring, M.B.; Laude, V.; Khelif, A. Energy storage and dispersion of surface acoustic waves trapped in a periodic array of mechanical resonators. J. Appl. Phys. 2009, 105, 093504. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.; Zhou, S.; Cheng, J.; Lin, D.; Liu, W. Full extraction of the COM parameters for Rayleigh type surface acoustic wave. AIP Adv. 2022, 12, 025007. [Google Scholar] [CrossRef]
- Koskela, J.; Plessky, V.P.; Salomaa, M.M. SAW/LSAW COM parameter extraction from computer experiments with harmonic admittance of a periodic array of electrodes. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1999, 46, 806–816. [Google Scholar] [CrossRef]
- Lin, J.; Wu, H.; Wang, N.; Qiu, H.; Shui, Y.A. Precise and full extraction of the coupling-of-mode parameters with periodic Green’s function. Sci. China Ser. F Inf. Sci. 2003, 46, 298–308. [Google Scholar] [CrossRef]
- Kovacs, G.; Anhorn, M.; Engan, H.; Visintini, G.; Ruppel, C. Improved material constants for LiNbO/sub 3/and LiTaO/sub 3. In Proceedings of the IEEE symposium on ultrasonics, Honolulu, HI, USA, 4–7 December 1990; pp. 435–438. [Google Scholar]
- He, S.; Chen, D.; Wang, C. The Structures of SAW Single-electrode IDT without Internal Reflection and the Analysis on Their Properties. Piezoelectr. Acoustoopt. 1992, 14, 55–59. (In Chinese) [Google Scholar]
- Sun, X.; Liu, W.; Shao, X.; Zhou, S.; Wang, W.; Lin, D. Surface acoustic wave gyroscopic effect in an interdigital transducer. Sensors 2018, 19, 106. [Google Scholar] [CrossRef] [PubMed] [Green Version]



| Parameters | Symbol | Dimension (SI) |
|---|---|---|
| Velocity in short-circuited grating | ν | m/s |
| Reflection coefficient | κp = κλ0 | % |
| Transduction coefficient | αp = αλ0 | |
| Normalized transduction coefficient | % | |
| Capacitance | Cp = Cλ0 | F |
| Normalized capacitance | Cn= Cp/W | F/m |
| Parameters | Values |
|---|---|
| Normalized capacitance (pF/m) | 546.33 |
| Velocity in short-circuited grating (m/s) | 3892.7 |
| Reflection coefficient |κp| (%) | 1.73 |
| Phase of reflection coefficient | −157.56° |
| Normalized transduction coefficient (%) | 14.68 |
| Phase of transduction coefficient | −37.84° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Ma, R.; Zhou, S.; Shao, X.; Cheng, J.; Lin, D.; Wang, W.; Liu, W. Fast, Accurate and Full Extraction of Coupling-of-Modes Parameters by Finite Element Method. Crystals 2022, 12, 706. https://doi.org/10.3390/cryst12050706
Sun X, Ma R, Zhou S, Shao X, Cheng J, Lin D, Wang W, Liu W. Fast, Accurate and Full Extraction of Coupling-of-Modes Parameters by Finite Element Method. Crystals. 2022; 12(5):706. https://doi.org/10.3390/cryst12050706
Chicago/Turabian StyleSun, Xueping, Rui Ma, Shun Zhou, Xiuting Shao, Jin Cheng, Dabin Lin, Wen Wang, and Weiguo Liu. 2022. "Fast, Accurate and Full Extraction of Coupling-of-Modes Parameters by Finite Element Method" Crystals 12, no. 5: 706. https://doi.org/10.3390/cryst12050706
APA StyleSun, X., Ma, R., Zhou, S., Shao, X., Cheng, J., Lin, D., Wang, W., & Liu, W. (2022). Fast, Accurate and Full Extraction of Coupling-of-Modes Parameters by Finite Element Method. Crystals, 12(5), 706. https://doi.org/10.3390/cryst12050706








