Effect of Forced Melt Flow on Al–Si Eutectic-Alloy Microstructures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Experiments
- Step 1: Unidirectional solidification without magnetic stirring for up to 55 mm length.
- Step 2: Unidirectional solidification using 150 mT magnetic induction at the end of the sample.
2.2. Complex Characterisation of the Irregular Eutectic Structure
- P0: average perimeter of the Si lamella in the investigated light-microscopy images (μm); it can be measured using image analysis software.
- N: number of eutectic lamellae.
- Ap: area of the micrograph (μm2).
- Af: area fraction of eutectic lamellae in the eutectic structure.
3. Results and Discussion
3.1. Mesostructure and Macro-Segregation
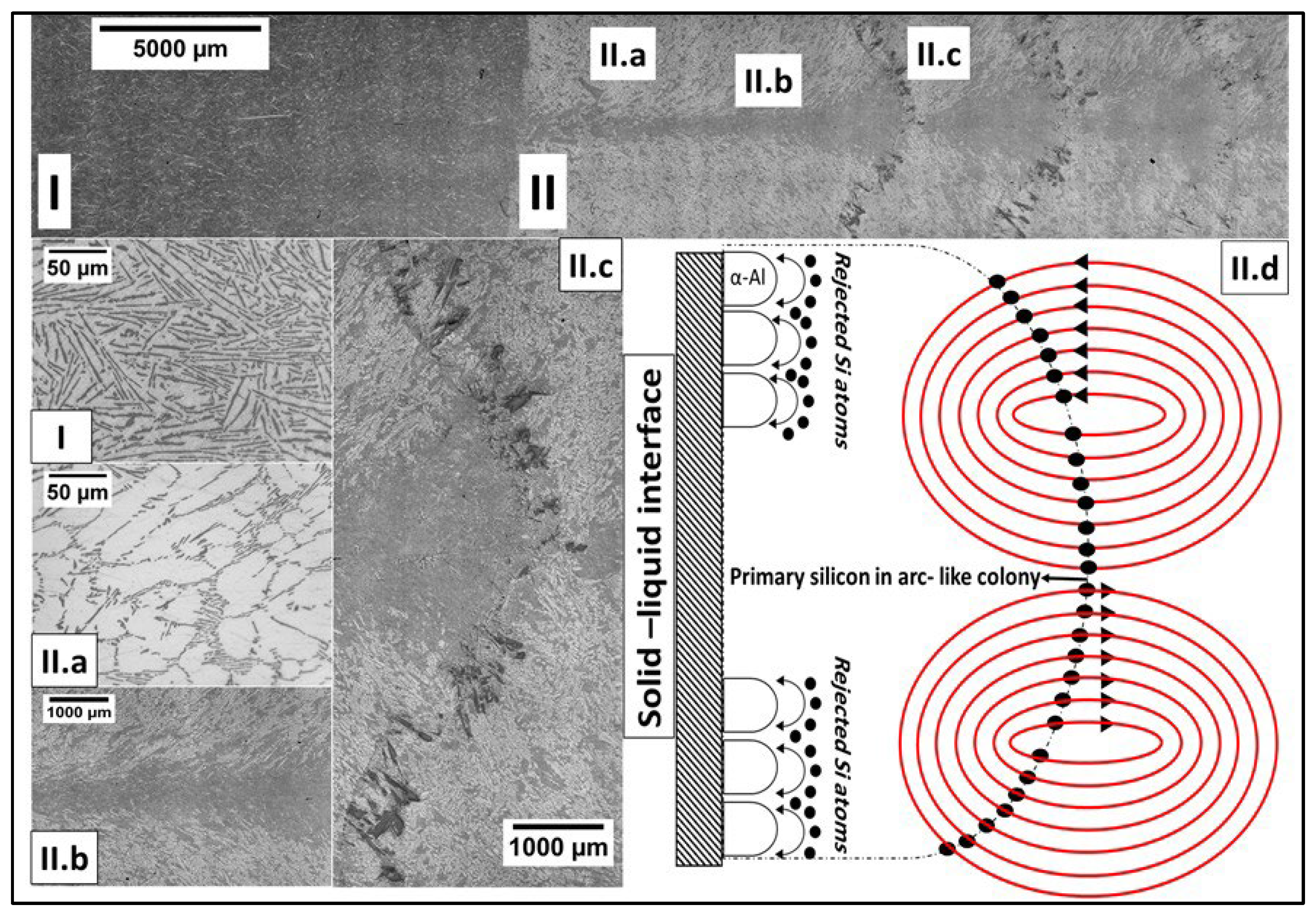
- Owing to the spiral flow, the solute is transferred from the edges to the centre-axis channel. Consequently, the primary Al solidifies at the edges (Figure 3II.a), whereas the eutectic structure solidifies at the centre area.
- In the case of low magnetic induction, laminar flow occurs, in which a fluid flows in parallel layers without any disruption between the layers. However, when a high magnetic intensity is applied, the laminar flow loses its stability and converts to turbulent flow. The turbulent flow is characterised by the random appearance of Taylor and Gortler (T–G) vortices along the sidewall of the cylindrical sample. The T–G vortices transport the rejected solute in both directions between the mushy zone and molten liquid. Willer reported a significant amplification in the radial flow when the T–G vortex impinges the mushy zone, signifying that, in the radial flow, the solute transport is enhanced momentarily along the mushy zone [27]. Local re-melting occurs at the spots where a high Si concentration exists near the axis. As a result, the interface changes to a wavy shape, and the eutectic structure solidifies in the form of a side-arm freckle around the axis of the sample. This segregation pattern is referred to as Christmas-tree-like (CTL) segregation (see Figure 3II.b).
- When super-high magnetic induction is applied, the velocity of the flows transporting the solute is very high. Thus, a large amount of solute is transferred. The CTL segregation pattern reduces the amount and concentration of the solute by solidifying as a eutectic structure in the side-arm freckle around the axis; however, the amount of solute remains high. This is described by another segregation pattern, which manifests as periodic arc-like colonies along the sample (Figure 3II.c). Two scenarios are proposed to explain arc-like colony solidification. (i) The Taylor and Gortler vortices transport the solute from the liquid to the mushy zone. Owing to the high magnetic intensity, the impingements of the T–G vortices on the mushy zone cause a large radial flow. This flow has the form of complete radial waves towards the liquid and transports a high concentration of Si. Local re-melting occurs in spots with high Si concentrations, causing solidification of the primary Si phase in arc-like colonies ahead of the solid–liquid interface. (ii) The secondary flow results in the formation of arc-like primary Si colonies. The secondary meridional flow transports the rejected Si atoms from the mushy zone to the liquid and from the liquid to the mushy zone during recurring inversion. This leads to the accumulation of the transported Si in the flow paths. The flow paths near the axis experience a momentary reduction in the Si concentration owing to the solidification of the eutectic side-arm freckles. This indicates that the axis area requires much time to attain the Si concentration required to form primary Si. The case is different for the flow paths near the edges because no concentration reduction occurs therein; therefore, the primary Si forms earlier in the edges than at the axis. The time required to attain the primary-Si concentration varies with the flow path. The flow paths near the sample axis require more time, whereas those near the edges of the sample require less time. As a result, the primary Si gradually solidifies into an arc-like colony (Figure 3II.d).
- After the first Si arc-colony solidification, the overall concentration returns to the original value, that is, the eutectic concentration. However, magnetic stirring continues; therefore, the previous mechanism periodically repeats until the RMF is switched off.
3.2. Eutectic Lamellae’s Distances (λ)
3.3. Eutectic Lamellar Lengths
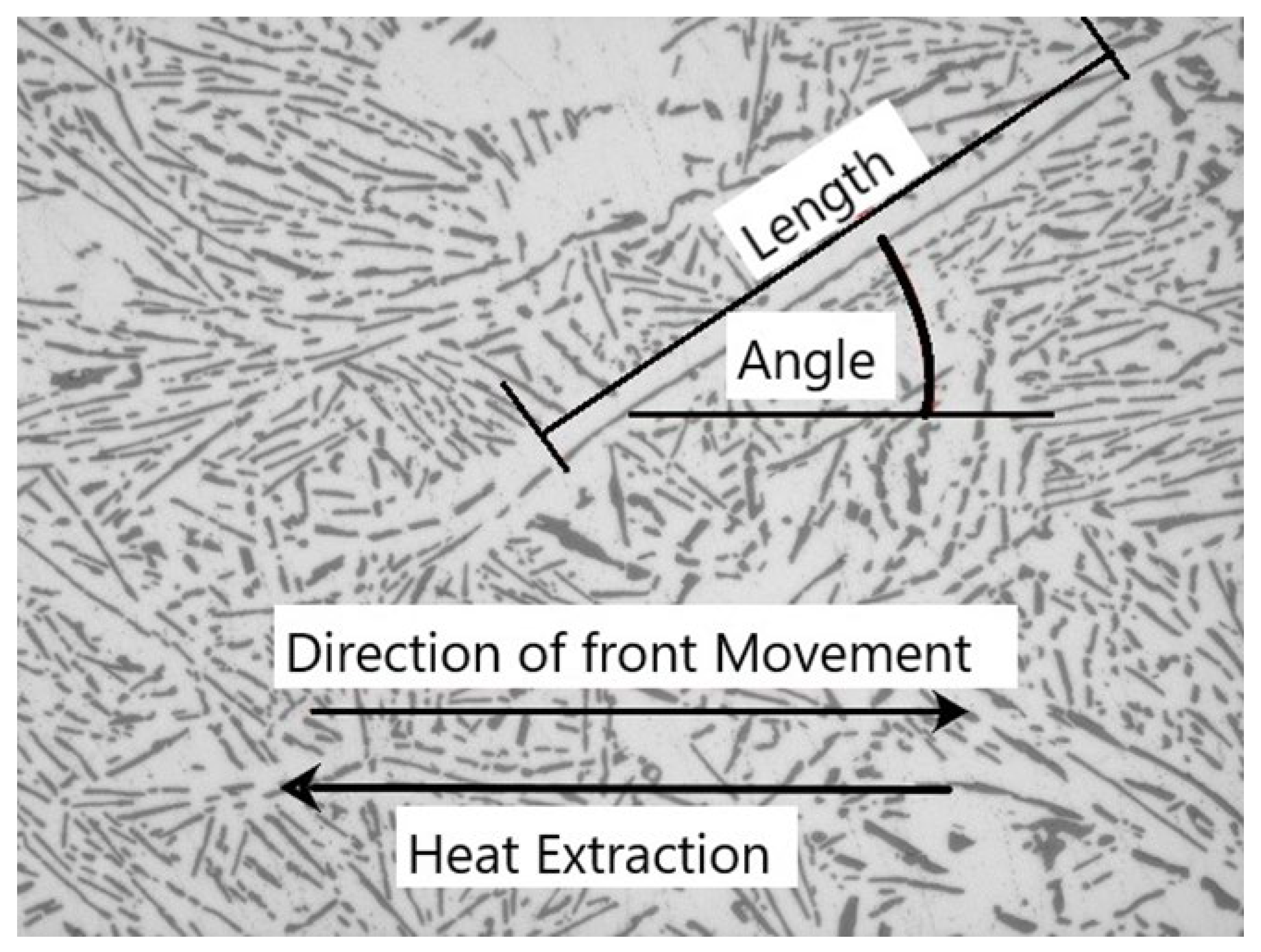
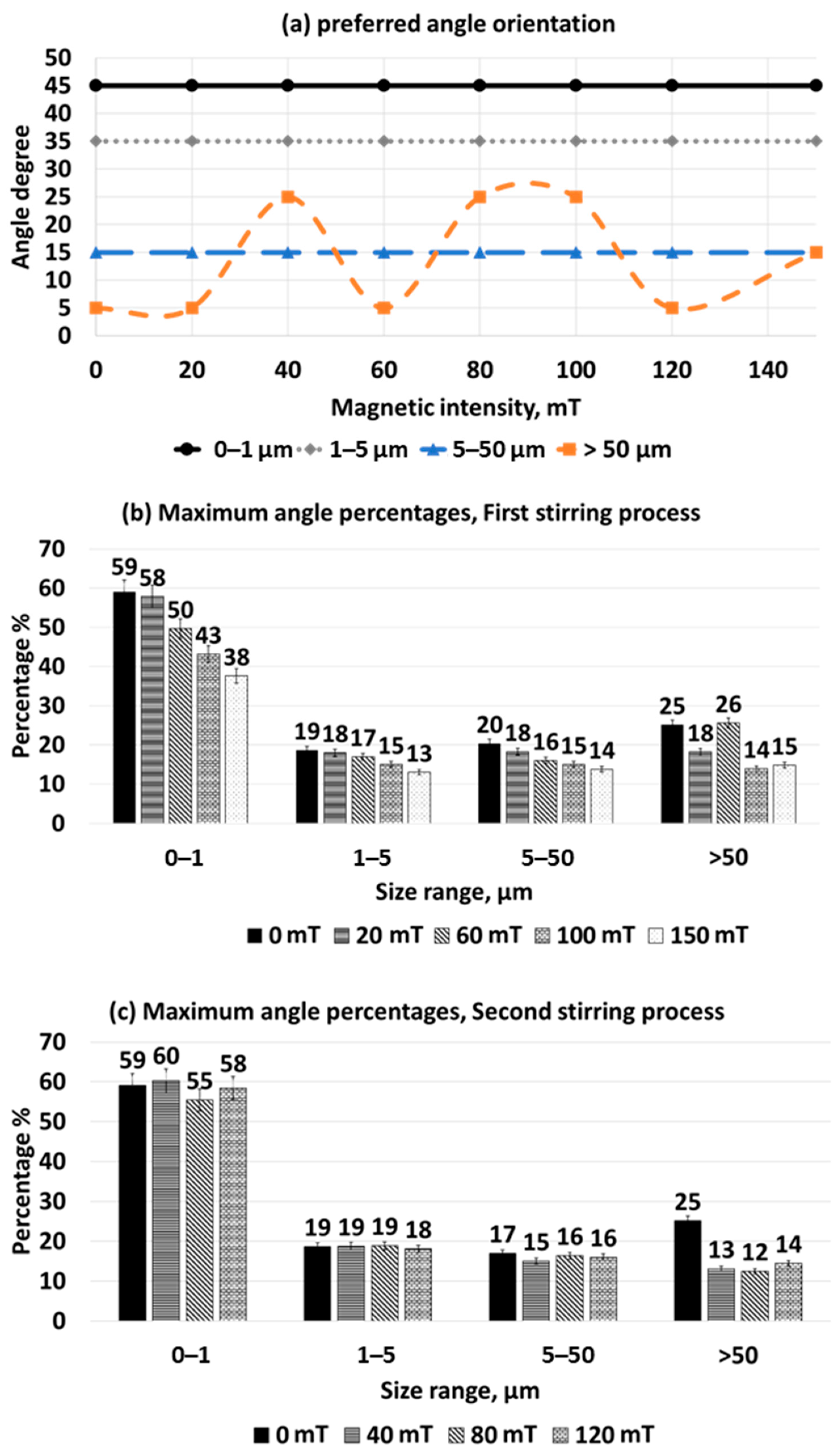
3.4. Eutectic Lamellar Angles
4. Conclusions
- Applying an RMF during solidification promotes two types of flow inside the molten liquid: primary flow, which transports the melt around the axis of the sample, and secondary flow, which transports the alloying element from the mushy zone to the pure liquid. Owing to this complex flow, thermo-solute redistribution occurs, and new segregation patterns are observed.
- In general, the flow enriches the centre area with the alloying element (Si), which results in solidification of the eutectic structure in the centre area and primary Al at the edges of the sample. A Christmas-tree-like (CTL) segregation pattern is observed owing to turbulent flow. In the case of super-high magnetic induction, the primary Si solidifies as periodic arc-like colonies, along with the sample.
- A new method was used to measure inter-lamellar distance (λ)—Specific Perimeter Method (SPM). The average inter-lamellar distance (λ) was calculated on the basis of the area fraction of the eutectic Si plates, area of the micrograph, number of eutectic Si plates, and average perimeter of the Si plates.
- SPM measurements reveal a distinct effect of the RMF on the inter-lamellar distance (λ). The first stirring process decreases the inter-lamellar distance. In contrast, increasing the intensity of the second stirring process leads to an increase in the inter-lamellar distance.
- In the stirred parts, the eutectic structure exhibits three growth morphologies depending on the surrounding phase: a fine eutectic structure near the α Al-solid solution, a coarse eutectic structure near the primary Si phase, and a prominent eutectic structure at the centre of the sample.
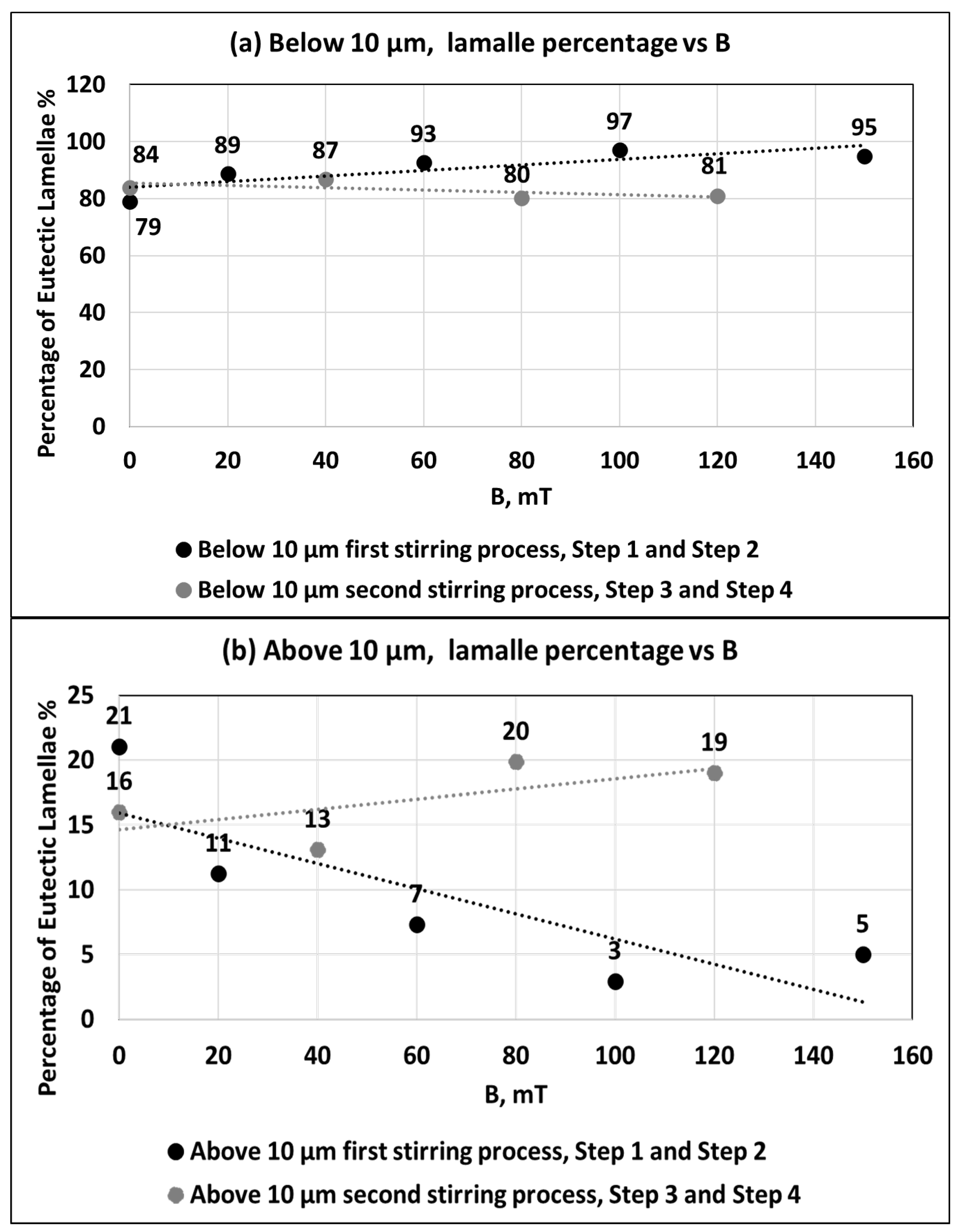
- The RMF causes size refinement, increases the percentage of fine eutectic Si lamellae (<10 μm), and decreases the percentage of coarse eutectic structures (>10 μm). Increasing the stirring intensity increases the percentage of fine eutectic lamellae.
- The angle orientation of the eutectic Si lamellae was measured using ImageJ processing software. Lamellar angle is defined as the degree of inclination between the axis of projection of the eutectic Si lamellae and the direction of solidification movement.
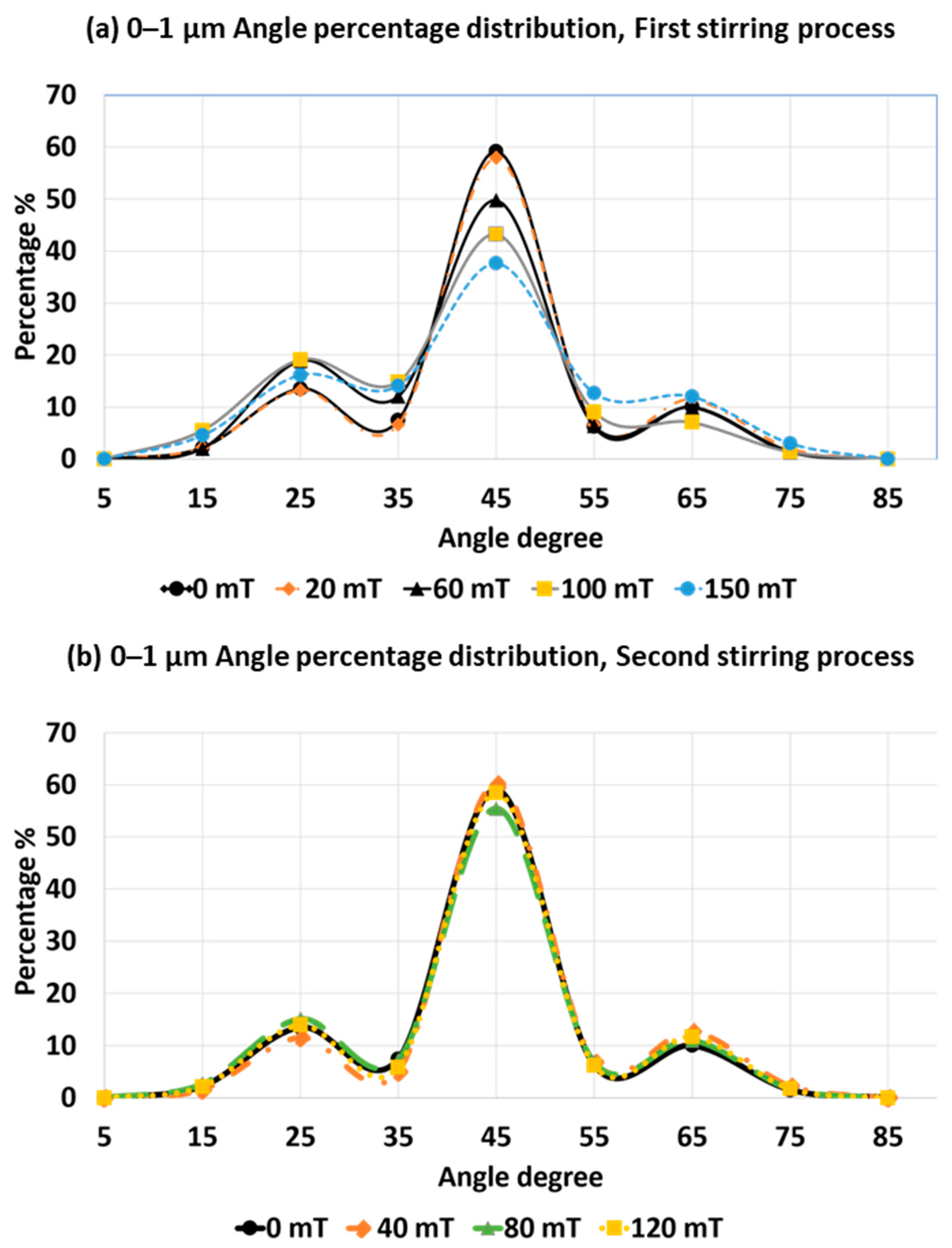
- The angle measurements show that fine eutectic Si lamellae prefer orienting in the angle range of 40–50°. However, larger eutectic lamellae have a more parallel growth direction with the solidification movement.
- RMF increases the diversity of the angles of Si lamellae.
- Increasing the RMF intensity results in highly diverse orientations of the eutectic Si lamellae.
- When the microstructure is stirred twice in a row, the second stirring process has a negligible effect on the size and growth direction of the eutectic Si lamellae.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fredriksson, H.; Åkerlind, U. Solidification and Crystallization Processing in Metals and Alloys; John Wiley & Son: Chichester, UK, 2012. [Google Scholar]
- Stefanescu, D. Science and Engineering of Casting Solidification; Kluwer Academic/Plenum Publishers: New York, NY, USA, 2002. [Google Scholar]
- Jackson, K.; Hunt, J. Lamellar and Rod Eutectic Growth. Trans. Metall. Soc. AIME 1966, 236, 1129. [Google Scholar]
- Fisher, D.; Kurz, W. A theory of branching limited growth of irregular eutectics. Acta Metall. 1980, 28, 777–794. [Google Scholar] [CrossRef]
- Magnin, P.; Mason, J.; Trivedi, R. Growth of irregular eutectics and the AlSi system. Acta Metall. Et Mater. 1991, 39, 469–480. [Google Scholar] [CrossRef]
- Magnin, P.; Kurz, W. An analytical model of irregular eutectic growth and its application to Fe-C. Acta Metall. 1987, 35, 1119–1128. [Google Scholar] [CrossRef]
- Steen, H.A.H.; Hellawell, A. The growth of eutectic silicon-contribution to undercooling. Acta Metall. 1975, 23, 529–535. [Google Scholar] [CrossRef]
- Akamatsu, S.; Bottin-Rousseau, S.; Faivre, G. Determination of the Jackson–Hunt constants of the In–In2Bi eutectic alloy based on in situ observation of its solidification dynamics. Acta Mater. 2011, 59, 7586–7591. [Google Scholar] [CrossRef]
- Timpel, M.; Wanderka, N.; Kumar, G.V.; Banhart, J. Microstructural investigation of Sr-modified Al-15wt%Si alloys in the range from micrometer to atomic scale. Ultramicroscopy 2011, 111, 695–700. [Google Scholar] [CrossRef]
- Gündüz, M.; Kaya, H.; Çadırlı, E.; Özmen, A. Interflake spacings and undercoolings in Al-Si irregular eutectic alloy. Mater. Sci. Eng. 2004, 369, 215–229. [Google Scholar] [CrossRef]
- Clapham, L.; Smith, R. Partial modification in unidirectionally solidified Al-Si eutectic alloys. Acta Metall. 1989, 37, 303–311. [Google Scholar] [CrossRef]
- Kaya, H.; Çadırh, E.; Gündüz, M.; Ülgen, A. Effect of the Temperature Gradient, Growth Rate, and the Interflake Spacing on the Microhardness in the Directionally Solidified Al-Si Eutectic Alloy. J. Mater. Eng. Perform. JMEPEG 2003, 12, 544–551. [Google Scholar] [CrossRef]
- Zimmermann, G.; Weiss, A.; Mbaya, Z. Effect of forced melt flow on microstructure evolution in AlSi7Mg0.6 alloy during directional solidification. Mater. Sci. Eng. A 2005, 413–414, 236–242. [Google Scholar] [CrossRef]
- Fragoso, B.; Santos, H. Aluminum a grain refinement in A354 by rotating magnetic field (RMF). Int. J. Cast Met. Res. 2013, 26, 193–200. [Google Scholar] [CrossRef]
- Yasuda, H.; Nakatsuka, N.; Nagira, T.; Sugiyama, A.; Yoshiya, M.; Uesugi, K.; Umetani, K. X-ray imaging study on grain refinement due to dendrite fragmentation. In Proceedings of the 6th International Conference on Electromagnetic Processing of Materials EPM 2009, Dresden, Germany, 19 October 2009. [Google Scholar]
- Sugiura, K.; Iwai, K. Refining mechanism of solidified structure of alloy by electromagnetic refining process. ISIJ Int. 2005, 45, 962–966. [Google Scholar] [CrossRef] [Green Version]
- Jie, D.; Jianzhong, C.; Wenjiang, D. Theoretical discussion of the effect of a low-frequency electromagnetic vibrating field on the as-cast microstructures of DC Al–Zn–Mg–Cu–Zr ingots. J. Cryst. Growth 2006, 2, 179–187. [Google Scholar] [CrossRef]
- Hernández, F.R.; Sokolowski, J. Comparison among chemical and electromagnetic stirring and vibration melt treatments for Al–Si hypereutectic alloys. J. Alloys Compd. 2006, 426, 205–212. [Google Scholar] [CrossRef]
- Quenisset, J.; Naslain, R. Effect of forced convection on eutectic growth. J. Cryst. Growth 1981, 54, 465–474. [Google Scholar] [CrossRef]
- Li, X.; Fautrelle, Y.; Gagnoud, A.; Ren, Z.; Moreau, R. EBSD Study of the Influence of a High Magnetic Field on the Microstructure and Orientation of the Al-Si Eutectic During Directional Solidification. Metall. Mater. Trans. A 2016, 47, 2952–2963. [Google Scholar] [CrossRef]
- Li, X.; Gagnoud, A.; Fautrelle, Y.; Ren, Z.; Moreau, R. Influence of thermoelectric effects on the morphology of Al–Si eutectic during directional solidification under an axial strong magnetic field. J. Cryst. Growth 2013, 367, 94–103. [Google Scholar] [CrossRef]
- Botton, V.; Lehmann, P.; Bolcato, R.; Moreau, R.; Haettel, R. Measurement of solute diffusivities. Part II. Experimental measurements in a convection-controlled shear cell. Interest of a uniform magnetic field. Int. J. Heat Mass Transf. 2001, 44, 3345–3357. [Google Scholar] [CrossRef]
- Rónaföldi, A.; Kovács, J.; Roósz, A. Solidification Facility Equipped With A Magnetohydrodynamic Stirrer; University of Miskolc (UOM): Miskolc, Hungary, 2006. [Google Scholar]
- Al-Omari, K.; Ronafoldi, A.; Veres, Z. Complex Characterization of Irregular Eutectic Structure. Mater. Sci. Eng. 2020, 45, 171–181. [Google Scholar]
- Wang, X.; Fautrelle, Y.; Etay, J.; Moreau, R. A Periodically Reversed Flow Driven by a Modulated Traveling Magnetic Field: Part I. Experiments with GaInSn. Metall. Mater. Trans. B 2009, 40, 82–90. [Google Scholar] [CrossRef]
- Wang, X.; Moreau, R.; Etay, J.; Fautrelle, Y. A Periodically Reversed Flow Driven by a Modulated Traveling Magnetic Field: Part II. Theoretical Model. Metall. Mater. Trans. B 2009, 40, 104–113. [Google Scholar] [CrossRef]
- Willers, B.; Eckert, S.; Nikrityuk, P.A.; Räbiger, D.; Dong, J.; Eckert, K.; Gerbeth, G. Efficient Melt Stirring Using Pulse Sequences of a Rotating Magnetic Field: Part II. Application to Solidification of Al-Si Alloys. Metall. Mater. Trans. B 2008, 39, 304–316. [Google Scholar] [CrossRef]
- Hellawell, A.; Liu, S.; Lu, S.Z. Dendrite fragmentation and the effects of fluid flow in castings. JOM 1997, 49, 18–20. [Google Scholar] [CrossRef]
- Genders, R. The Interpretation of the Macrostructure of Cast Metals. J. Inst. Met. 1926, 35, 259. [Google Scholar]
- Pilling, J.; Hellawell, A. Mechanical deformation of dendrites by fluid flow. Metall. Mater. Trans. A 1996, 27, 229–232. [Google Scholar] [CrossRef]
- Jackson, K.A.; Hunt, J.; Uhlmann, D.; Seward, T. On origin of equiaxed zone in castings. Trans. Metall. Soc. AIME 1966, 236, 149. [Google Scholar]
- Ananiev, S.; Nikrityuk, P.; Eckert, K. Dendrite fragmentation by catastrophic elastic remelting. Acta Mater. 2009, 57, 657–665. [Google Scholar] [CrossRef]



| Sample | B (mT) | ||||
|---|---|---|---|---|---|
| Step 1 | Step 2 | Step 3 | Step 4 | Step 5 | |
| AlSi20 | 0 | 20 | 0 | 40 | 0 |
| AlSi60 | 0 | 60 | 0 | 80 | 0 |
| AlSi100 | 0 | 100 | 0 | 120 | 0 |
| AlSi150 * | 0 | 150 | N/A | N/A | N/A |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Omari, K.; Roósz, A.; Rónaföldi, A.; Veres, Z. Effect of Forced Melt Flow on Al–Si Eutectic-Alloy Microstructures. Crystals 2022, 12, 731. https://doi.org/10.3390/cryst12050731
Al-Omari K, Roósz A, Rónaföldi A, Veres Z. Effect of Forced Melt Flow on Al–Si Eutectic-Alloy Microstructures. Crystals. 2022; 12(5):731. https://doi.org/10.3390/cryst12050731
Chicago/Turabian StyleAl-Omari, Kassab, András Roósz, Arnold Rónaföldi, and Zsolt Veres. 2022. "Effect of Forced Melt Flow on Al–Si Eutectic-Alloy Microstructures" Crystals 12, no. 5: 731. https://doi.org/10.3390/cryst12050731
APA StyleAl-Omari, K., Roósz, A., Rónaföldi, A., & Veres, Z. (2022). Effect of Forced Melt Flow on Al–Si Eutectic-Alloy Microstructures. Crystals, 12(5), 731. https://doi.org/10.3390/cryst12050731





