Twist Angle-Dependent Interlayer Exciton in MoS2 Bilayers Revealed by Room-Temperature Reflectance
Abstract
:1. Introduction
2. Experimental Method
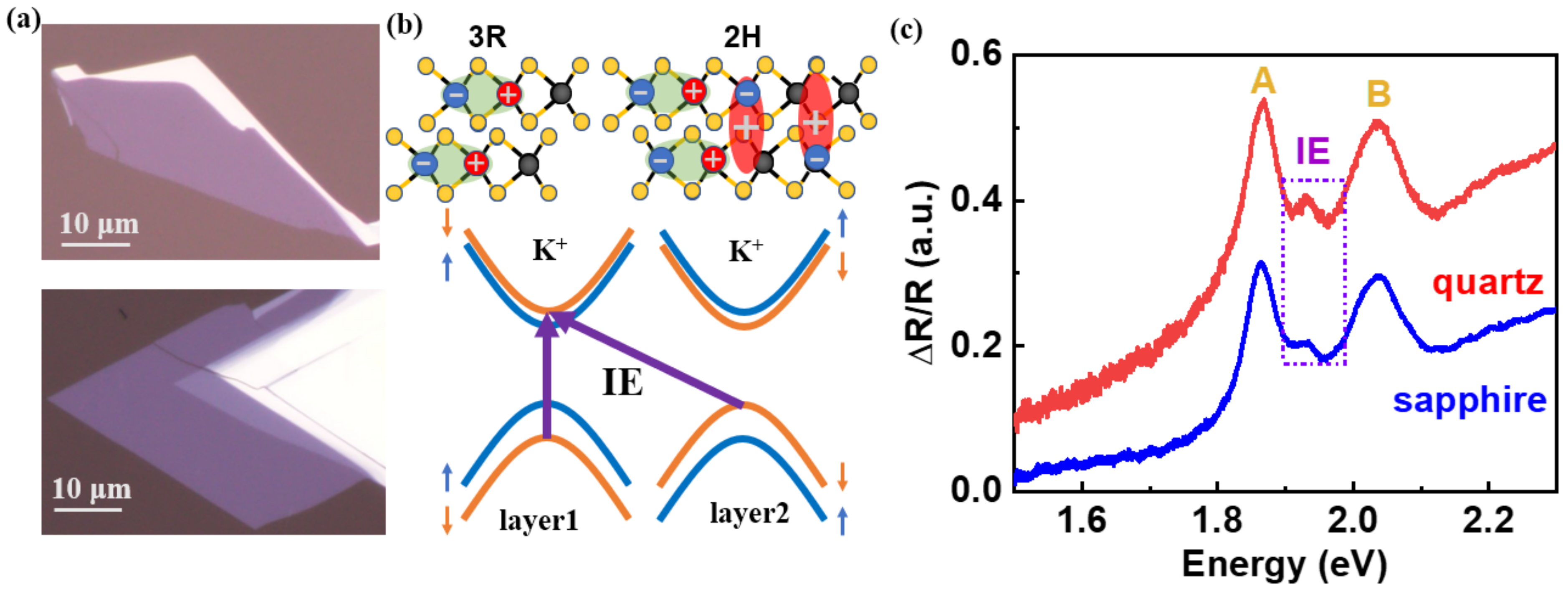
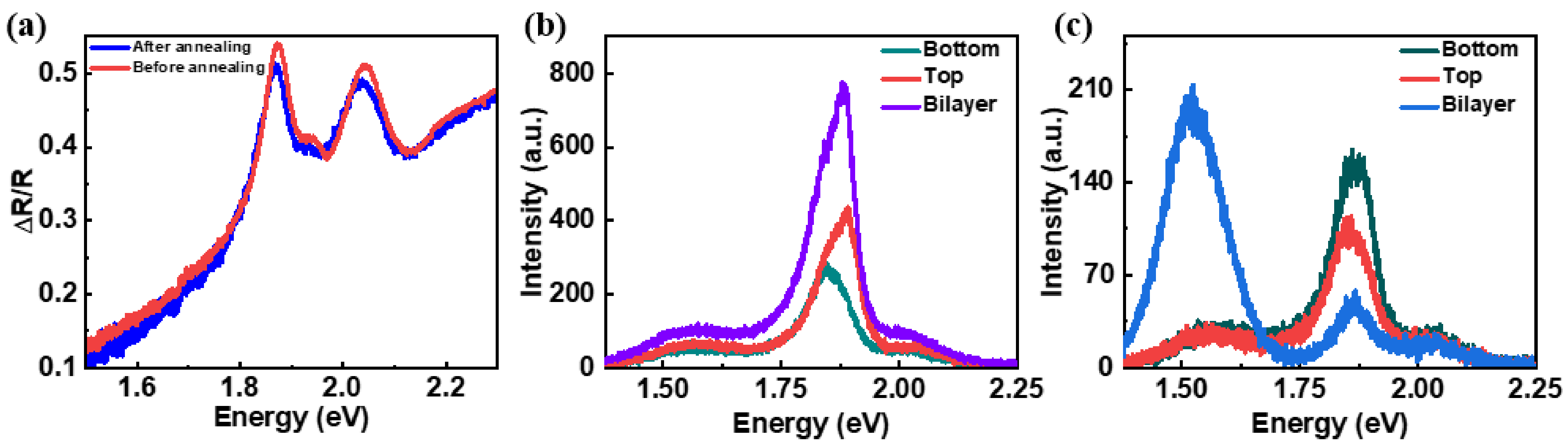
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gong, Y.; Lin, J.; Wang, X.; Shi, G.; Lei, S.; Lin, Z.; Zou, X.; Ye, G.; Vajtai, R.; Yakobson, B.I.; et al. Vertical and in-Plane Heterostructures from WS2/MoS2 Monolayers. Nat. Mater. 2014, 13, 1135–1142. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Plechinger, G.; Nagler, P.; Kraus, J.; Paradiso, N.; Strunk, C.; Schüller, C.; Korn, T. Identification of Excitons, Trions and Biexcitons in Single-Layer WS2. Phys. Status Solidi R 2015, 9, 457–461. [Google Scholar] [CrossRef] [Green Version]
- Withers, F.; Bointon, T.H.; Hudson, D.C.; Craciun, M.F.; Russo, S. Electron Transport of WS2 Transistors in a Hexagonal Boron Nitride Dielectric Environment. Sci. Rep. 2014, 4, 4967. [Google Scholar] [CrossRef] [Green Version]
- Sorkin, V.; Pan, H.; Shi, H.; Quek, S.Y.; Zhang, Y.W. Nanoscale Transition Metal Dichalcogenides: Structures, Properties, and Applications. Crit. Rev. Solid State 2014, 39, 319–367. [Google Scholar] [CrossRef]
- Komsa, H.P.; Kotakoski, J.; Kurasch, S.; Lehtinen, O.; Kaiser, U.; Krasheninnikov, A.V. Two-Dimensional Transition Metal Dichalcogenides under Electron Irradiation: Defect Production and Doping. Phys. Rev. Lett. 2012, 109, 035503. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J.N.; Strano, M.S. Electronics and Optoelectronics of Two-Dimensional Transition Metal Dichalcogenides. Nat. Nanotechnol. 2012, 7, 699–712. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Dai, Y.; Guo, M.; Niu, C.; Lu, J.; Huang, B. Electronic and Magnetic Properties of Perfect, Vacancy-Doped, and Nonmetal Adsorbed MoSe2, MoTe2 and WS2 Monolayers. Phys. Chem. Chem. Phys. 2011, 13, 15546–15553. [Google Scholar] [CrossRef]
- Gong, Z.; Liu, G.B.; Yu, H.; Xiao, D.; Cui, X.; Xu, X.; Yao, W. Magnetoelectric Effects and Valley-Controlled Spin Quantum Gates in Transition Metal Dichalcogenide Bilayers. Nat. Commun. 2013, 4, 2053. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.; Florian, M.; Steinhoff, A.; Erben, D.; Tran, K.; Kim, D.S.; Sun, L.; Quan, J.; Claassen, R.; Majumder, S.; et al. Twist angle-dependent interlayer exciton lifetimes in van der Waals heterostructures. Phys. Rev. Lett. 2021, 126, 047401. [Google Scholar] [CrossRef]
- Rivera, P.; Schaibley, J.R.; Jones, A.M.; Ross, J.S.; Wu, S.; Aivazian, G.; Klement, P.; Seyler, K.; Clark, G.; Ghimire, N.J.; et al. Observation of long-lived interlayer excitons in monolayer MoSe2–WSe2 heterostructures. Nat. Commun. 2015, 6, 6242. [Google Scholar] [CrossRef] [Green Version]
- Nagler, P.; Plechinger, G.; Ballottin, M.V.; Mitioglu, A.; Meier, S.; Paradiso, N.; Strunk, C.; Chernikov, A.; Christianen, P.C.M.; Schüller, C.; et al. Interlayer exciton dynamics in a dichalcogenide monolayer heterostructure. 2D Mater. 2017, 4, 025112. [Google Scholar] [CrossRef]
- Scuri, G.; Andersen, T.I.; Zhou, Y.; Wild, D.S.; Sung, J.; Gelly, R.J.; Bérubé, D.; Heo, H.; Shao, L.; Joe, A.Y.; et al. Electrically Tunable Valley Dynamics in Twisted WSe2 Bilayers. Phys. Rev. Lett. 2020, 124, 217403. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.; Hsu, W.T.; Lu, L.S.; Sun, L.; Cheng, H.Y.; Lee, M.H.; Quan, J.; Tran, K.; Wang, C.Y.; Staab, M.; et al. Moiré Potential Impedes In-terlayer Exciton Diffusion in Van Der Waals Heterostructures. Sci. Adv. 2020, 39, 8866. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Shi, Q.; Shih, E.M.; Zhou, L.; Wu, W.; Bai, Y.; Rhodes, D.; Barmak, K.; Hone, J.; Dean, C.R.; et al. Dif-fusivity Reveals Three Distinct Phases of Interlayer Excitons in MoSe2/WSe2 Heterobilayers. Phys. Rev. Lett. 2021, 126, 106804. [Google Scholar] [CrossRef] [PubMed]
- Yuan, L.; Zheng, B.; Kunstmann, J.; Brumme, T.; Kuc, A.B.; Ma, C.; Deng, S.; Blach, D.; Pan, A.; Huang, L. Twist-Angle-Dependent Interlayer Exciton Diffusion in WS2-WSe2 Heterobilayers. Nat. Mater. 2020, 19, 617–623. [Google Scholar] [CrossRef] [PubMed]
- Ciarrocchi, A.; Unuchek, D.; Avsar, A.; Watanabe, K.; Taniguchi, T.; Kis, A. Polarization switching and electrical control of interlayer excitons in two-dimensional van der Waals heterostructures. Nat. Photonics 2019, 13, 131–136. [Google Scholar] [CrossRef]
- Slobodeniuk, A.O.; Koperski, M.; Molas, M.R.; Kossacki, P.; Nogajewski, K.; Bartos, M.; Watanabe, K.; Taniguchi, T.; Faugeras, C.; Potemski, M. Fine structure of K-excitons in multilayers of transition metal dichalcogenides. 2D Mater. 2019, 6, 025026. [Google Scholar] [CrossRef]
- Horng, J.; Stroucken, T.; Zhang, L.; Paik, E.Y.; Deng, H.; Koch, S.W. Observation of interlayer excitons in MoSe2 single crystals. Phy. Rev. B 2018, 97, 241404. [Google Scholar] [CrossRef] [Green Version]
- Gerber, I.C.; Courtade, E.; Shree, S.; Robert, C.; Taniguchi, T.; Watanabe, K.; Balocchi, A.; Renucci, P.; Lagarde, D.; Marie, X.; et al. Interlayer Excitons in Bilayer MoS2 with Strong Oscillator Strength up to Room Temperature. Phys. Rev. B 2019, 99, 035443. [Google Scholar] [CrossRef] [Green Version]
- Liu, K.; Zhang, L.; Cao, T.; Jin, C.; Qiu, D.; Zhou, Q.; Zettl, A.; Yang, P.; Louie, S.G.; Wang, F. Evolution of Interlayer Coupling in Twisted Molybdenum Disulfide Bilayers. Nat. Commun. 2014, 5, 4966. [Google Scholar] [CrossRef]
- Huang, S.; Ling, X.; Liang, L.; Kong, J.; Terrones, H.; Meunier, V.; Dresselhaus, M.S. Probing the Interlayer Coupling of Twisted Bilayer MoS2 Using Photoluminescence Spectroscopy. Nano Lett. 2014, 14, 5500–5508. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Chuu, C.P.; Ren, X.; Li, M.Y.; Li, L.J.; Jin, C.; Chou, M.Y.; Shih, C.K. Interlayer Couplings, Moiré Patterns, and 2d Electronic Superlattices in MoS2/WSe2 Hetero-Bilayers. Sci. Adv. 2017, 3, 1601459. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Z.; Förste, J.; Watanabe, K.; Taniguchi, T.; Urbaszek, B.; Baimuratov, A.S.; Gerber, I.C.; Högele, A.; Bilgin, I. Stacking-Dependent Exciton Multiplicity in WSe2 Bilayers. arXiv 2021, arXiv:2112.08994. [Google Scholar]
- Grzeszczyk, M.; Szpakowski, J.; Slobodeniuk, A.O.; Kazimierczuk, T.; Bhatnagar, M.; Taniguchi, T.; Watanabe, K.; Kossacki, P.; Potemski, M.; Babiński, A.; et al. The optical response of artificially twisted MoS2 bilayers. Sci. Rep. 2021, 11, 17037. [Google Scholar] [CrossRef] [PubMed]
- Hsu, W.T.; Zhao, Z.A.; Li, L.J.; Chen, C.H.; Chiu, M.H.; Chang, P.S.; Chou, Y.C.; Chang, W.H. Second harmonic generation from artificially stacked transition metal dichalcogenide twisted bilayers. ACS Nano 2014, 8, 2951–2958. [Google Scholar] [CrossRef]
- Tong, Q.; Yu, H.; Zhu, Q.; Wang, Y.; Xu, X.; Yao, W. Topological Mosaics in Moiré Superlattices of Van der Waals Heterobilayers. Nat. Phys. 2017, 13, 356–362. [Google Scholar] [CrossRef]
- Mak, K.F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T.F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [Google Scholar] [CrossRef] [Green Version]
- Hsu, W.T.; Lin, B.H.; Lu, L.S.; Lee, M.H.; Chu, M.W.; Li, L.J.; Yao, W.; Chang, W.H.; Shih, C.K. Tailoring Excitonic States of Van Der Waals Bilayers through Stacking Configuration, Band Alignment, and Valley Spin. Sci. Adv. 2019, 5, 7407. [Google Scholar] [CrossRef] [Green Version]
- Dou, X.; Ding, K.; Jiang, D.; Fan, X.; Sun, B. Probing spin–orbit coupling and interlayer coupling in atomically thin molybdenum disulfide using hydrostatic pressure. ACS Nano 2016, 10, 1619–1624. [Google Scholar] [CrossRef]
- Hsu, W.T.; Quan, J.; Pan, C.R.; Chen, P.J.; Chou, M.Y.; Chang, W.H.; MacDonald, A.H.; Li, X.; Lin, J.F.; Shih, C.K. Quantitative determination of interlayer electronic coupling at various critical points in bilayer MoS2. arXiv 2022, arXiv:2203.16189. [Google Scholar]
- Qiao, W.; Sun, H.; Fan, X.; Jin, M.; Liu, H.; Tang, T.; Xiong, L.; Niu, B.; Wang, G. Interlayer Coupling and Pressure Engineering in Bilayer MoS2. Crystals 2022, 12, 693. [Google Scholar] [CrossRef]
- Paradisanos, I.; Shree, S.; George, A.; Leisgang, N.; Robert, C.; Watanabe, K.; Taniguchi, T.; Warburton, R.J.; Turchanin, A.; Marie, X.; et al. Controlling Interlayer Excitons in MoS2 Layers Grown by Chemical Vapor Deposition. Nat. Commun. 2020, 11, 2391. [Google Scholar] [CrossRef] [PubMed]
- Alexeev, E.M.; Catanzaro, A.; Skrypka, O.V.; Nayak, P.K.; Ahn, S.; Pak, S.; Lee, J.; Sohn, J.I.; Novoselov, K.S.; Shin, H.S.; et al. Imaging of Interlayer Coupling in Van Der Waals Heterostructures Using a Bright-Field Optical Microscope. Nano Lett. 2017, 17, 5342–5349. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, L.; Tang, T.; Fan, X.; Liu, H.; Zhu, P.; Zhang, X.; Qiao, W.; Wang, Q.; Wang, Z.; Niu, B.; et al. Twist Angle-Dependent Interlayer Exciton in MoS2 Bilayers Revealed by Room-Temperature Reflectance. Crystals 2022, 12, 761. https://doi.org/10.3390/cryst12060761
Xiong L, Tang T, Fan X, Liu H, Zhu P, Zhang X, Qiao W, Wang Q, Wang Z, Niu B, et al. Twist Angle-Dependent Interlayer Exciton in MoS2 Bilayers Revealed by Room-Temperature Reflectance. Crystals. 2022; 12(6):761. https://doi.org/10.3390/cryst12060761
Chicago/Turabian StyleXiong, Lei, Tianhong Tang, Xiaoyue Fan, Haiyang Liu, Peng Zhu, Xiaolan Zhang, Wei Qiao, Qinsheng Wang, Zhiwei Wang, Binghui Niu, and et al. 2022. "Twist Angle-Dependent Interlayer Exciton in MoS2 Bilayers Revealed by Room-Temperature Reflectance" Crystals 12, no. 6: 761. https://doi.org/10.3390/cryst12060761
APA StyleXiong, L., Tang, T., Fan, X., Liu, H., Zhu, P., Zhang, X., Qiao, W., Wang, Q., Wang, Z., Niu, B., & Wang, G. (2022). Twist Angle-Dependent Interlayer Exciton in MoS2 Bilayers Revealed by Room-Temperature Reflectance. Crystals, 12(6), 761. https://doi.org/10.3390/cryst12060761






