Simulation of a New CZTS Solar Cell Model with ZnO/CdS Core-Shell Nanowires for High Efficiency
Abstract
:1. Introduction
2. Materials and Methods
3. Meshing Geometric Models
4. Results and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mahbub, R.; Islam, M.S.; Anwar, F.; Satter, S.S.; Ullah, S.M. Simulation of CZTS thin-film solar cell for different buffer layers for high-efficiency performance. South Asian J. Eng. Tech. 2016, 2, 1–10. [Google Scholar]
- Benami, A. Effect of CZTS Parameters on Photovoltaic Solar Cell from Numerical Simulation. J. Energy Power Eng. Sci. 2019, 13, 32–36. [Google Scholar]
- Gupta, G.K.; Dixit, A. Simulation Studies of CZT(S,Se) Single and Tandem Junction Solar Cells Towards Possibilities for Higher Efficiencies up to 22%. arXiv 2018, arXiv:1801.08498. Available online: https://arxiv.org/ftp/arxiv/papers/1801/1801.08498.pdf (accessed on 28 March 2022).
- Jimbo, K.; Kimura, R.; Kamimura, T.; Yamada, S.; Maw, W.S.; Araki, H.; Oishi, K.; Katagiri, H. Cu2ZnSnS4-type Thin-film Solar Cells Using Abundant Materials. Thin Solid Film 2007, 515, 5997–5999. [Google Scholar] [CrossRef]
- Wang, J.; Xin, X.; Lin, Z. Cu2ZnSnS4 nanocrystals and graphene quantum dots for photovoltaics. Nanoscale 2011, 3, 3040–3048. [Google Scholar] [CrossRef]
- Bakr, N.A.; Khodair, Z.T.; Mahdi, H.I. Influence of Thiourea Concentration on Some Physical Properties of Chemically Sprayed Cu2ZnSnS4 Thin Films. Int. J. Mater. Sci. 2016, 5, 261–270. [Google Scholar]
- Swati, S.I.; Matin, R.; Bashar, S.; Mahmood, Z.H. Experimental study of the optical properties of Cu2ZnSnS4 thin-film absorber layer for solar cell application. J. Phys. Conf. Ser. 2018, 1086, 012010. [Google Scholar] [CrossRef]
- Katagiri, H.; Jimbo, K.; Yamada, S.; Kamimura, T.; Maw, W.S.; Fukano, T.; Ito, T.; Motohiro, T. Enhanced Conversion Efficiencies of Cu2ZnSnS4-Based Thin-film Solar Cells by Using Preferential Etching Technique. Appl. Phys. Express 2008, 1, 041201. [Google Scholar] [CrossRef]
- Sethi, V.K.; Pandey, M.; Shukla, P. Use of Nanotechnology in Solar PV Cell. Int. J. Chem. Eng. Appl. 2011, 2, 2. Available online: http://www.ijcea.org/papers/79-A555.pdf (accessed on 28 March 2022). [CrossRef] [Green Version]
- Michallon, J.; Bucci, D.; Morand, A.; Zanuccoli, M.; Consonni, V.; Cachopo, A.K. Light trapping in ZnO nanowires arrays covered with an absorbing shell for solar cells. Opt. Express 2014, 22, A1174–A1189. [Google Scholar] [CrossRef] [Green Version]
- Anwar, F. Simulation and Performance Study of Nanowires CdS/CdTe Solar Cell. Int. J. Renew. Energy Res. 2016, 7, 885–893. [Google Scholar] [CrossRef]
- Malek, M.F.; Sahdan, M.Z.; Mamat, M.H.; Musa, M.Z.; Khusaimi, Z.; Husairi, S.S.; Sin, N.D.; Rusop, M. A novel fabrication of MEH-PPV/Al:ZnO nanorod arrays based ordered bulk heterojunction hybrid solar cells. Appl. Surf. Sci. 2013, 275, 75–83. [Google Scholar] [CrossRef]
- Saurdi, I.; Mamat, M.H.; Malek, M.F.; Rusop, M. Preparation of Aligned ZnO Nanorod Arrays on Sn-Doped ZnO Thin Films by Sonicated Sol-Gel Immersion Fabricated for Dye-Sensitized Solar Cell. Adv. Mater. Sci. Eng. 2014, 2014, 636725. [Google Scholar] [CrossRef] [Green Version]
- Rouhi, J.; Mamat, M.H.; Raymond, O.C.H.; Mahmud, S.; Mahmood, M.R. Based on Morphology-Controllable Synthesis of ZnO–ZnS Heterostructure Nanocone Photoanodes. PLoS ONE 2015, 10, e0123433. [Google Scholar] [CrossRef] [Green Version]
- Ding, M.; Yao, N.; Wang, C.; Huang, J.; Shao, M.; Zhang, S.; Li, P.; Deng, X.; Xu, X. ZnO@CdS Core-Shell Heterostructures: Fabrication, Enhanced Photocatalytic, and Photoelectrochemical Performance. Nanoscale Res. Lett. 2016, 11, 205. [Google Scholar] [CrossRef] [Green Version]
- Kumar, K.; Pattanaik, S.; Dash, S.K. Modeling of the Nanowires CdS-CdTe Device Design for Enhanced Quantum Efficiency in Window Absorber Type Solar Cells. Int. J. Sci. Res. Rev. 2019, 7, 2279–2543. [Google Scholar]
- Rokade, A.; Rondiya, S.; Date, A.; Sharma, V.; Prasad, M.; Pathan, H.; Jadkar, S. Electrochemical synthesis of core-shell ZnO/CdS nanostructure for photocatalytic water splitting application. In Proceedings of the 1st International Conference on Electronics Packaging, Power Energy, ICEP2016, RMIT University, Melbourne, Australia, 14–16 December 2016. [Google Scholar]
- Yur, K.; Zolotkov, A.; Unit Convertor. Convert Terahertz [THz] to Wavelength in Meters. December. 2021. Available online: https://www.translatorscafe.com/unit-converter/en-US/frequency-wavelength/4-27/terahertz-wavelength%20in%20metres/ (accessed on 28 March 2022).
- Liu, Q.; Sandgren, E.; Barnhart, M.; Zhu, R.; Huang, G. Photonic Nanostructures Design and Optimization for Solar Cell Application. Photonics 2015, 2, 893–905. [Google Scholar] [CrossRef]
- Björkman, C.P.; Barreau, N.; Choubrac, M.B.L.; Grenet, L.; Heo, J.; Kubart, T.; Mittiga, A.; Sanchez, Y.; Scragg, J.; Sinha, S.; et al. Back and front contacts in kesterite solar cells: State-of-the-art and open questions. J. Phys. Energy 2019, 1, 044005. [Google Scholar] [CrossRef]
- Sun, W.; Brozak, M.; Armstrong, J.C.; Cui, J. Solar Cell Structures Based on ZnO/CdS core-shell nanowires Arrays Embedded in Cu2ZnSnS4 Light Absorber. In Proceedings of the IEEE Photovoltaic Specialists Conference (PVSC), 39th PVSC, Tampa, FL, USA, 16–21 June 2013; pp. 2042–2046. [Google Scholar]
- Çetinkaya, S. Study of electrical effect of transition-metal dichalcogenide-MoS2 layer on the performance characteristic of Cu2ZnSnS4 based solar cells using wxAMPS. Optik 2019, 181, 627–638. [Google Scholar] [CrossRef]
- Liu, X. Molybdenum Back Contact Treatment for Cu2ZnSnS4 Solar Cells. UNSW August 2015 Open ACCESS. Available online: http://unsworks.unsw.edu.au/fapi/datastream/unsworks:41049/SOURCE02?view=true (accessed on 28 March 2022).
- Vishwakarma, M.; Thota, N.; Karakulina, O.; Habermann, J.; Mehta, B.R. Role of graphene interlayer on the formation of the MoS2-CZTS interface during growth. AIP 2018, 1953, 100064. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Falko, V.I.; Colombo, L.; Gellert, P.R.; Schwab, M.G.; Kim, K. A roadmap for graphene. Nature 2012, 490, 192–200. [Google Scholar] [CrossRef]
- Hu, Y.H.; Wang, H.; Hu, B. Thinnest Two-Dimensional Nanomaterial-Graphene for Solar Energy. ChemSusChem 2010, 3, 782–796. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Skachko, I.; Barker, A.; Andrei, E.Y. Approaching ballistic transport in suspended graphene. Nat. Nano 2008, 3, 491–495. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, B.; Hu, Y.H. MoS2 as a co-catalyst for photocatalytic hydrogen production from water. Energy Sci. Eng. 2016, 128, 285–304. [Google Scholar] [CrossRef] [Green Version]
- Jaramillo, T.F.; Jorgensen, K.P.; Bonde, J.; Nielsen, J.H.; Horch, S.; Chorkendorff, I. Identification of Active Edge Sites for Electrochemical H2 Evolution from MoS2 Nanocatalysts. Science 2007, 317, 100–102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, K.; Kim, J.K.; Ma, M.; Yim, S.Y.; Lee, C.L.; Shin, H.; Park, J.H. Delocalized Electron Accumulation at Nanorod Tips: Origin of Efficient H2 Generation. Adv. Funct. Mater. 2016, 26, 4527–4534. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-Dimensional Gas of Massless Dirac Fermions in Graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K. Graphene: Status and Prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Murali, S.; Cai, W.; Li, X.; Suk, J.W.; Potts, J.R.; Ruoff, R.S. Graphene and graphene oxide: Synthesis, properties, and applications. Adv. Mater. 2010, 22, 3906–3924. [Google Scholar] [CrossRef]
- Britnell, L.; Ribeiro, R.M.; Eckmann, A.; Jalil, R.; Belle, B.D.; Mishchenko, A.; Kim, Y.J.; Gorbachev, R.V.; Georgiou, T.; Morozov, S.V.; et al. Strong Light-Matter Interactions in Heterostructures of Atomically Thin Films. Science 2013, 340, 1311–1314. [Google Scholar] [CrossRef] [Green Version]
- Jiang, J.W. Graphene versus MoS2: A short review. Front. Phys. 2015, 10, 287–302. [Google Scholar] [CrossRef] [Green Version]
- Seo, D.B.; Trung, T.N.; Bae, S.S.; Kim, E.T. Improved Photoelectrochemical Performance of MoS2 through Morphology-Controlled Chemical Vapor Deposition Growth on Graphene. Nanomaterials 2021, 11, 1585. [Google Scholar] [CrossRef]
- Dong, H.; Li, J.; Chen, M.; Wang, H.; Jiang, X.; Xiao, Y.; Tian, B.; Zhang, X. High-throughput Production of ZnO-MoS2 Graphene Heterostructures for Highly Efficient PhotocatalyticHydrogen Evolution. Materials 2019, 12, 2233. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Drame, B.; Niare, L.; Yuegang, F. Optimization of the Shell Thickness of the ZnO/CdS Core-Shell Nanowire Arrays in a CZTS Absorber. Int. J. Opt. 2022, 2022, 5301790. [Google Scholar] [CrossRef]
- Kim, H.U.; Kim, M.; Jin, Y.; Hyeon, Y.; Kim, K.S.; Anb, B.S.; Yangb, C.W.; Kanade, V.; Moonc, J.Y.; Yeom, G.Y.; et al. Low-temperature wafer-scale growth of MoS2-graphene heterostructures. Appl. Surf. Sci. 2019, 470, 129–134. [Google Scholar] [CrossRef]
- Liu, X.; Balla, I.; Bergeron, H.; Campbell, G.P.; Bedzyk, M.J.; Hersam, M.C. Rotationally Commensurate Growth of MoS2 on Epitaxial Graphene. ACS Nano 2016, 10, 1067–1075. [Google Scholar] [CrossRef] [Green Version]
- Anttu, N.; Xu, H.Q. Coupling of light into nanowire arrays and subsequent absorption. J. Nanosci. Nanotechnol. 2010, 10, 7183–7187. [Google Scholar] [CrossRef]
- Wen, L.; Zhao, Z.; Li, X.; Shen, Y.; Guo, H.; Wang, Y. Theoretical analysis and modeling of light trapping in high-efficiency GaAs nanowire array solar cells. Appl. Phys. Lett. 2011, 99, 143116. [Google Scholar] [CrossRef]
- Kupec, J.; Stoop, R.L.; Witzigmann, B. Light absorption and emission in nanowire array solar cells. Opt. Express 2010, 18, 27589–27605. [Google Scholar] [CrossRef]
- Gu, Z.; Prete, P.; Lovergine, N.; Nabet, B. On optical properties of GaAs and GaAs/AlGaAs core-shell periodic nanowire arrays. J. Appl. Phys. 2011, 109, 064314–064316. [Google Scholar] [CrossRef]
- Huang, N.; Lin, C.; Povinelli, M.L. Broadband absorption of semiconductor nanowire arrays for photovoltaic applications. J. Opt. 2012, 14, 024004. [Google Scholar] [CrossRef] [Green Version]
- Hu, L.; Chen, G. Analysis of optical absorption in silicon nanowire arrays for photovoltaic applications. Nano Lett. 2007, 7, 3249–3252. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Povinelli, M.L. Optical absorption enhancement in silicon nanowire arrays with a large lattice constant for photovoltaic applications. Opt. Express 2009, 17, 19371–19381. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Yu, H.; Wong, S.M.; Li, X.; Zhang, G.; Lo, P.G.Q.; Kwong, D.L. Design guidelines of periodic Si nanowire arrays for solar cell application. Appl. Phys. Lett. 2009, 95, 243113. [Google Scholar] [CrossRef]
- Li, J.; Yu, H.; Li, Y. Solar energy harnessing in hexagonally arranged Si nanowire arrays and effects of array symmetry on optical characteristics. Nanotechnology 2012, 23, 194010. [Google Scholar] [CrossRef] [PubMed]
- Anttu, N.; Xu, H.Q. Efficient light management in vertical nanowire arrays for photovoltaics. Opt. Express 2013, 21, A558–A575. [Google Scholar] [CrossRef] [PubMed]
- Dalapati, G.K.; Zhuk, S.; Panah, S.M.; Kushwaha, A.; Seng, H.L.; Chellappan, V.; Suresh, V.; Su, Z.; Batabyal, S.K.; Tan, C.C.; et al. Impact of molybdenum out-diffusion and interface quality on the performance of sputter grown CZTS based solar cells. Sci. Rep. 2017, 2, 1350. [Google Scholar] [CrossRef] [PubMed]
- Jhuma, F.A.; Shaily, M.Z.; Rashid, M.J. Towards High-Efficiency CZTS Solar Cell through Buffer Layer Optimization Mater. Renew. Sustain. Energy 2019, 8, 6. Available online: https://link.springer.com/article/10.1007/s40243-019-0144-1 (accessed on 28 March 2022). [CrossRef] [Green Version]
- Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres, N.M.R.; Geim, A.K. Fine structure constant defines visual transparency of graphene. Science 2008, 320, 1308. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Zhang, X. Ultrasensitive optical absorption in graphene-based on bound states in the continuum. Sci. Rep. 2015, 5, 8266. [Google Scholar] [CrossRef]
- Wang, Q.; Ouyang, Z.; Lin, M.; Zheng, Y. High-Quality Graphene-Based Tunable Absorber Based on Double-Side Coupled-Cavity Effect. Nanomaterials 2021, 11, 2824. [Google Scholar] [CrossRef]
- Shin, D.M.; Tsege, E.L.; Kang, S.H.; Seung, W.; Kim, S.W.; Kim, H.K.; Hong, S.W.; Hwang, Y.H. Freestanding ZnO nanorod/graphene/ZnO nanorod epitaxial double-heterostructure for improved piezoelectric nanogenerators. Nano Energy 2015, 12, 268–277. [Google Scholar] [CrossRef]
- Introduction to Comsol Multiphysics 5.3, 1998–2017. pp. 6–153. Available online: https://doc.comsol.com/5.3a/doc/com.comsol.help.comsol/IntroductionToCOMSOLMultiphysics.pdf (accessed on 20 February 2020).
- Semiconductor Module User’s Guide—Comsol Multiphysics 5.4, 1998–2018. pp. 11–264. Available online: https://doc.comsol.com/5.4/doc/com.comsol.help.semicond/SemiconductorModuleUsersGuide.pdf (accessed on 20 February 2020).
- RF Module User’s Guide-Comsol Multiphysics 5.3, 1998–2017. Available online: https://doc.comsol.com/5.4/doc/com.comsol.help.rf/RFModuleUsersGuide.pdf (accessed on 12 December 2020).
- Kavakl, I.G.; Kantarli, K. Single and Double-Layer Antireflection Coatings on Silicon. Turk. J. Phys. 2002, 26, 349–354. [Google Scholar]
- Kosoboutskyy, P.; Karkulovska, M.; Morgulis, A. The Principle of Multilayer Plane-Parallel Structure Antireflection. Opt. Appl. 2010, XL, 4. Available online: https://www.dbc.wroc.pl/dlibra/publication/98216/edition/58485/content?ref=struct (accessed on 28 March 2022).
- Guo, H.; Wen, L.; Li, X.; Zhao, Z.; Wang, Y. Analysis of Optical Absorption in GaAs Nanowires Arrays. Nano Res. Lett. 2011, 6, 617. Available online: http://www.nanoscalereslett.com/content/6/1/617 (accessed on 28 March 2022). [CrossRef] [Green Version]
- Wilson, D.P.; Lapierre, R.R. Simulation of optical absorption in conical nanowires. Opt. Express 2021, 29, 9544–9552. [Google Scholar] [CrossRef]
- Oriel Product Training—On Solar Simulation. Available online: https://www.semanticscholar.org/paper/ORIEL-PRODUCT-TRAINING-Solar-Simulation/9dcad5adc1e65f9f3099d4e5e74a2e6c9d76069a (accessed on 25 November 2021).
- Aghaeipour, M.; Pettersson, H. Enhanced broadband absorption in nanowire arrays with integrated Bragg reflectors. Nanophotonics 2018, 7, 819–825. [Google Scholar] [CrossRef] [Green Version]
- Byrnes, S.J. Multilayer Optical Calculations. arXiv 2021, arXiv:1603.02720. Available online: https://arxiv.org/pdf/1603.02720.pdf (accessed on 3 January 2022).
- Refractive Index Database of Materials. Available online: https://refractiveindex.info/ (accessed on 20 November 2020).
- Rohatgi, A. WebPlotDigitizer User Manual, Version 4.3, July 2020. Available online: https://automeris.io/WebPlotDigitizer/userManual.pdf (accessed on 4 January 2022).
- Sturmberg, B.C.P.; Dossou, K.B.; Botten, L.C.; Asatryan, A.A.; Poulton, C.G.; Sterke, C.M.; McPhedran, R.C. Modal analysis of enhanced absorption in silicon nanowire arrays. Opt. Express 2011, 19, A1067–A1081. [Google Scholar] [CrossRef] [Green Version]
- Tivanov, M.; Moskalev, A.; Kaputskaya, I.; Żukowski, P. Calculation of the Ultimate Efficiency of p-n-Junction Solar Cells Taking into Account the Semiconductor Absorption Coefficient. Prz. Elektrotech. 2016, 92, 85–87. Available online: https://sigma-not.pl/publikacja-99983-2016-8.html (accessed on 28 March 2022). [CrossRef]
- Wang, W.; Winkler, M.T.; Gunawan, O.; Gokmen, T.; Todorov, T.K.; Zhu, Y.; Mitzi, D.B. Device characteristics of CZTSSe thin-film solar cells with 12.6% efficiency. Adv. Energy Mater. 2014, 4, 1301465. [Google Scholar] [CrossRef]
- Guo, S.D. Phonon Transport in Janus monolayer MoSSe: A first-principles study. Phys. Chem. Chem. Phys. 2018, 20, 7236–7242. [Google Scholar] [CrossRef] [Green Version]
- Peng, B.; Zhang, H.; Shao, H.; Xu, Y.; Zhang, X.; Zhu, H. Thermal conductivity of monolayer MoS2, MoSe2, and WS2: Interplay of mass effect, interatomic bonding, and anharmonicity. RSC Adv. 2016, 6, 5767. [Google Scholar] [CrossRef] [Green Version]
- Cozza, D.; Ruiz, C.M.; Duché, D.; Giraldo, S.; Saucedo, E.; Simon, J.J.; Escoubas, L. Optical modeling and optimizations of Cu2ZnSnSe4 solar cells using the modified transfer matrix method. Opt. Express 2016, 24, A1201–A1209. [Google Scholar] [CrossRef]
- Song, N.; Green, M.A.; Huang, J.; Hu, Y.; Hao, X. Study of sputtered Cu2ZnSnS4 thin films on Si. Appl. Surf. Sci. 2018, 459, 700–706. [Google Scholar] [CrossRef]
- Reya, G.; Larramonab, G.; Bourdaisb, S.; Chońeb, C.; Delatoucheb, B.; Jacobb, A.; Dennlerb, G.; Siebentritta, S. On the origin of band-tails in kesterite. Sol. Energy Mater. Sol. Cells 2018, 179, 142–151. [Google Scholar] [CrossRef]
- Cozza, D.; Ruiz, C.; Duché, M.; Simon, J.J.; Escoubas, L. Modeling the back contact of Cu2ZnSnS4 solar cells. IEEE J. Photovolt. 2016, 6, 1292–1297. [Google Scholar] [CrossRef]
- Zhang, Z.; Cui, T.; Lv, R.; Zhu, H.; Wang, K.; Wu, D.; Kang, F. Improved efficiency of graphene/Si heterojunction solar cells by optimizing hydrocarbon feed rate. J. Nanomater. 2014, 2014, 359305. [Google Scholar] [CrossRef]
- Miao, X.; Tongay, S.; Petterson, M.K.; Berke, K.; Rinzler, A.G.; Appleton, B.R.; Hebard, A.F. High-efficiency graphene solar cells by chemical doping. Nano Lett. 2012, 12, 2745–2750. [Google Scholar] [CrossRef] [Green Version]
- Zhong, S.; Hua, X.; Shen, W.; Hua, X. Simulation of high-efficiency crystalline silicon solar cells with homo–heterojunctions. IEEE Trans. Electron. Devices 2013, 60, 2104–2110. [Google Scholar] [CrossRef]
- Gangopadhyay, U.; Roy, S.; Garain, S.; Jana, S.; Das, S. Comparative simulation study between n-type and p-type silicon solar cells and the variation of efficiency of n-type solar cell by the application of passivation improvement layer with different thickness using AFORS HET and PC1D. IOSR J. Eng. 2012, 2, 41–48. [Google Scholar] [CrossRef]
- Patel, K.; Tyagi, P.K. Multilayer graphene as a transparent conducting electrode in silicon heterojunction solar cells. AIP Adv. 2015, 5, 077165. [Google Scholar] [CrossRef] [Green Version]
- Zandi, S.; Saxena, P.; Razaghi, M.; Gorjic, N.E. Simulation of CZTSSe thin-film solar cells in COMSOL: 3D coupled optical, electrical, and thermal model. IEEE J. Photovolt. 2020, 10, 1503–1507. [Google Scholar] [CrossRef]
- Huang, P.; Riccardi, E.; Messelot, S.; Graef, H.; Valmorra, F.; Tignon, J.; Taniguchi, T.; Watanabe, K.; Dhillon, S.; Plaçais, B.; et al. Ultra-long carrier lifetime in neutral graphene-hBN van der Waals heterostructures under mid-infrared illumination. Nat. Commun. 2020, 11, 863. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cismaru, A.; Dragoman, M.; Dinescu, A.; Dragoman, D.; Stavrinidis, G.; Konstantinidis, G. Microwave and millimeter-wave electrical permittivity of graphene monolayer. arXiv 2013, arXiv:1309.0990. [Google Scholar]
- Pop, E.; Varshney, V.; Roy, A.K. Thermal properties of graphene: Fundamentals and applications. Mater. Res. Soc. Symp. Proc. 2012, 37, 1273–1281. [Google Scholar] [CrossRef] [Green Version]
- Jahan, F.; Islam, M.H.; Smith, B.E. Bandgap and refractive index determination of Mo-black coatings using several techniques. Sol. Energy Mater. Sol. Cells 1995, 37, 283–293. [Google Scholar] [CrossRef]
- Latrous, A.R.; Mahamdi, R.; Touafek, N.; Pasquinelli, M. Performance Enhancement in CZTS Solar Cells by SCAPS-1D. Int. J. Thin. Fil. Sci. Techol. 2021, 10, 75–81. [Google Scholar]
- Jhuma, F.A.; Rashid, M.J. Simulation study to find suitable dopants of CdS buffer layer for CZTS solar cell. J. Theor. Appl. Phys. 2020, 14, 75–84. [Google Scholar] [CrossRef] [Green Version]
- Jabeen, M.; Haxha, S. High rear reflectance and light trapping in textured graphene-based silicon thin-film solar cells with back dielectric-metal reflectors. OSA Contin. 2019, 2, 1807–1821. [Google Scholar] [CrossRef]
- Nakamura, R.; Tanaka, K.; HisaoUchikiHisao, H.; Nakamura, R.; Jimbo, K.; Washio, T.; Katagiri, H. Cu2ZnSnS4 thin film deposited by sputtering with Cu 2 ZnSnS 4 compound target. Jpn. J. Appl. Phys. 2014, 53, 02BC10. [Google Scholar] [CrossRef]
- Hanson, G.W. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys. 2008, 103, 064302. [Google Scholar] [CrossRef] [Green Version]
- Zhong, H.; Liu, Z.; Liu, X.; Fu, G.; Liu, G.; Chen, J.; Tang, C. Ultra-high quality graphene perfect absorbers for high performance switching manipulation. Opt. Express 2020, 28, 37294–37306. [Google Scholar] [CrossRef]
- Wang, D.W.; Zhao, W.S.; Gu, X.Q.; Chen, W.; Fellow, W.Y.Y. Wideband Modeling of Graphene-Based Structures at Different Temperatures Using Hybrid FDTD Method. IEEE Trans. Nanotechnol. 2015, 14, 250–258. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, L.; Wang, B.; Ruoff, R.S. Chemical vapor deposition of graphene on thin-metal films. Cell Rep. Phys. Sci. 2021, 24, 100372. [Google Scholar] [CrossRef]
- Hodes, G. Semiconductor and ceramic nanoparticle films deposited by chemical bath deposition. Phys. Chem. Chem. Phys. 2007, 9, 2181–2196. [Google Scholar]
- Hamel, A.; Chibani, A. Characterization of texture surface for solar cells. J. Appl. Sci. 2010, 10, 231–234. [Google Scholar] [CrossRef]
- Shockley, V.; Read, W.T. Statistics of the recombination of holes and electrons. Phys. Rev. 1952, 87, 835–842. [Google Scholar] [CrossRef]
- Hall, R.N. Electron-hole recombination in germanium. Phys. Rev. 1952, 87, 387. [Google Scholar] [CrossRef]
- Hingerl, J. Data Analysis for Nanomaterials: Effective Medium Approximation, Its Limits and ImplementationsK. Ellipsometry at the Nanoscale March 2013. pp. 145–177. Available online: http://old.ceitec.eu/2-data-analysis/f33667 (accessed on 2 February 2020).
- Permittivity, Maxwell’s Equations. 2012. Available online: https://maxwells-equations.com/materials/permittivity.php (accessed on 1 December 2020).
- ElsayedGhitas, A. Studying the effect of spectral variations intensity of the incident solar radiation on the Si solar cells performance. NRIAG J. Astron. Geophys. 2012, 1, 165–171. [Google Scholar]
- Nair, K.K.; Jose, J.; Ravindran, A. Analysis of temperature-dependent parameters on solar cell efficiency using MATLAB. Int. J. Eng. Dev. Res. 2016, 4, 2321–9939. [Google Scholar]
- Honsberg, C.; Bowden, S. Diffusion Length. PV Education. Available online: https://www.pveducation.org/pvcdrom/pn-junctions/diffusion-length (accessed on 10 December 2020).
- Al-Jumaili, M.H.; Abdalkafor, A.S.; Taha, M.Q. Analysis of the hard and soft shading impact on photovoltaic module performance using solar module tester. Int. J. Eng. Dev. Res. 2019, 10, 1014–1021. [Google Scholar] [CrossRef]
- Su, R.R.; Yu, Y.X.; Xiao, Y.H.; Yang, X.F.; Zhang, W.D. Earth-abundant ZnO/CdS/CuSbS2 core-shell nanowire arrays as highly efficient photoanode for hydrogen evolution. Int. J. Hydrog. Energy 2018, 43, 6040–6048. [Google Scholar] [CrossRef]
- Tak, Y.; Hong, S.J.; Leeb, J.S.; Yong, K. Fabrication of ZnO/CdS core/shell nanowire arrays for efficient solar energy conversion. J. Mater. Chem. 2009, 19, 5945–5951. [Google Scholar] [CrossRef] [Green Version]
- Salazar, R.; Delamoreanub, A.; Clémentc, C.L.; Ivanova, V. ZnO/CdTe and ZnO/CdS core-shell nanowire arrays for extremely thin absorber solar cells. Energy Procedia 2011, 10, 122–127. [Google Scholar] [CrossRef] [Green Version]
- Van Dam, D.; Van Hoof, N.J.; Cui, Y.; Van Veldhoven, P.J.; Bakkers, E.P.; Gómez Rivas, J.; Haverkort, J.E. High-efficiency nanowire solar cells with omnidirectionally enhanced absorption due to self-aligned indium-tin-oxide Mie scatterers. ACS Nano 2016, 10, 11414–11419. [Google Scholar] [CrossRef]
- Khvol’son, O.D. Course of Physics; Gosizdat RSFSR: Berlin, Germany, 1923; Volume 2. [Google Scholar]
- Shockley, W.; Queisser, H.J. Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]
- Lee, K.S.; Chung, Y.D.; Park, N.M.; Cho, D.H.; Kim, K.H.; Kim, J. Analysis of the Current-voltage Curves of a Cu(In,Ga)Se2 Thin-film Solar Cell Measured at Different Irradiation Conditions. J. Opt. Soc. Korea 2010, 14, 321–325. [Google Scholar] [CrossRef] [Green Version]
- Varshni, Y.P. Temperature dependence of the energy gap in semiconductors. Physica 1967, 34, 149–154. [Google Scholar] [CrossRef]
- Han, J.Z.; Chen, R.S. Tunable broadband terahertz absorber based on a single-layer graphene metasurface. Opt. Express 2020, 28, 30289. [Google Scholar] [CrossRef] [PubMed]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media. Section 9, 2nd ed.Pergamon Press: Oxford, UK, 1984. [Google Scholar]
- Looyenga, H. Dielectric Constants of Heterogeneous Mixtures. Physica 1965, 31, 401. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics; Wiley: New York, NY, USA, 1962. [Google Scholar]
- Fowler, M. Maxwell’s Equations and Electromagnetic Waves. Physics Department, UVa. Available online: http://galileo.phys.virginia.edu/classes/109N/more_stuff/Maxwell_Eq.html (accessed on 22 April 2022).
- Sinton, R.A.; Cuevas, A. Contactless determination of current-voltage characteristics and minority-carrier lifetimes in semiconductors from quasi-steady-state photoconductance data. Appl. Phys. Lett. 1996, 69, 2510–2512. [Google Scholar] [CrossRef]
- Sabbar, E.H.; Saleh, M.H.; Salih, S.M.; Salih, S.H. Deposition of SeTe/Si Thin Film via Thermal Evaporation. Am. J. Condens. Matter Phys. 2013, 3, 119–122. [Google Scholar]

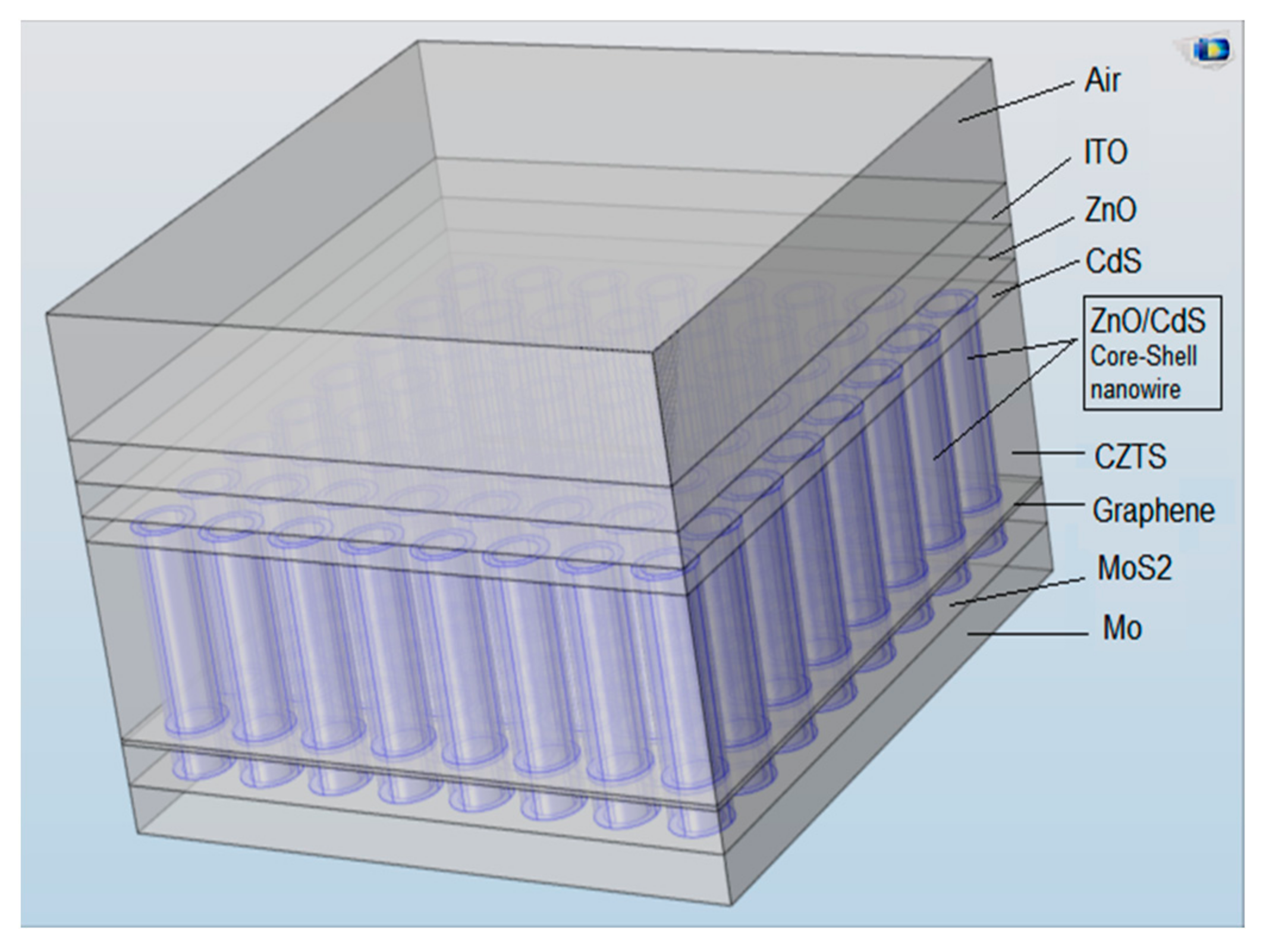

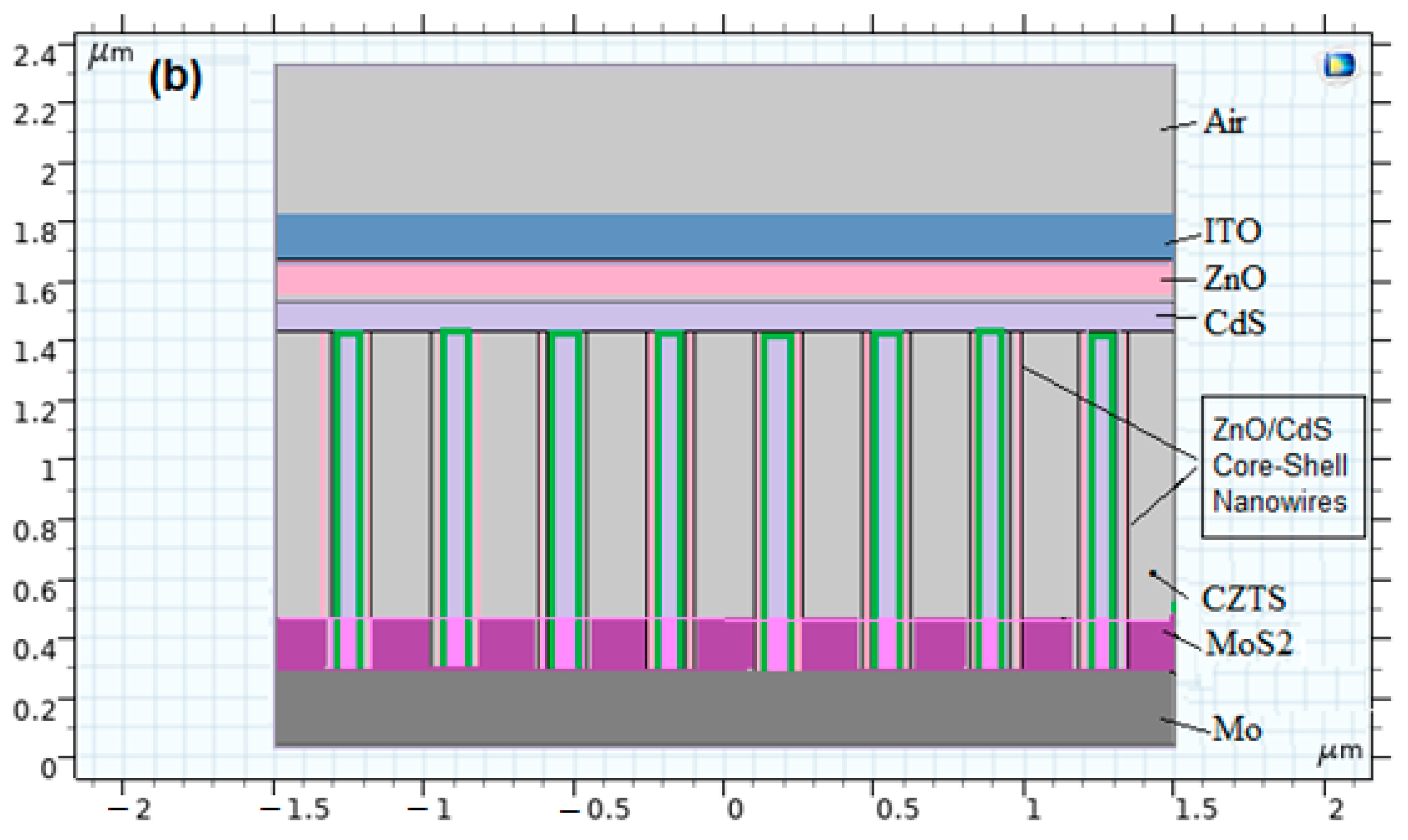
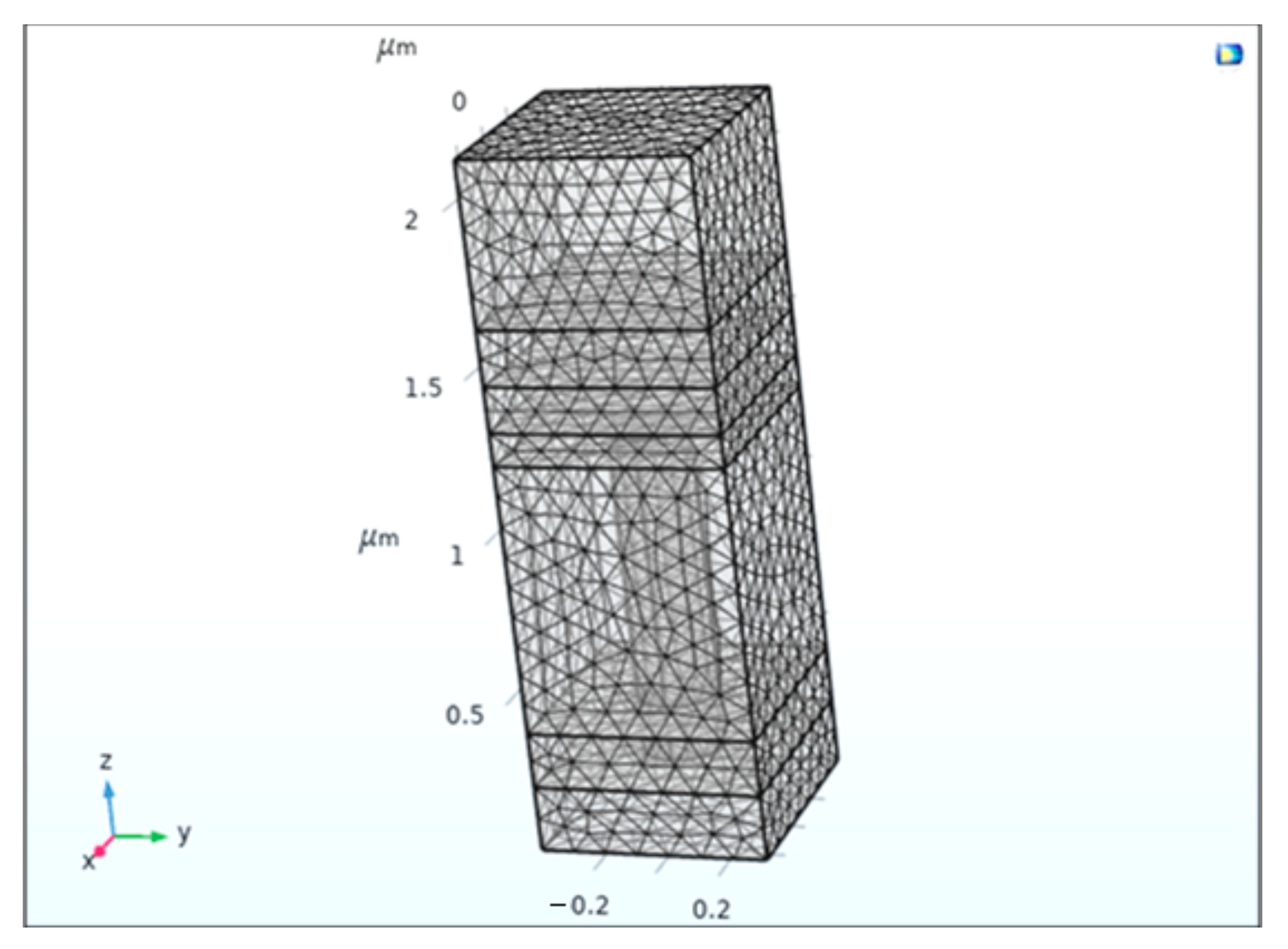
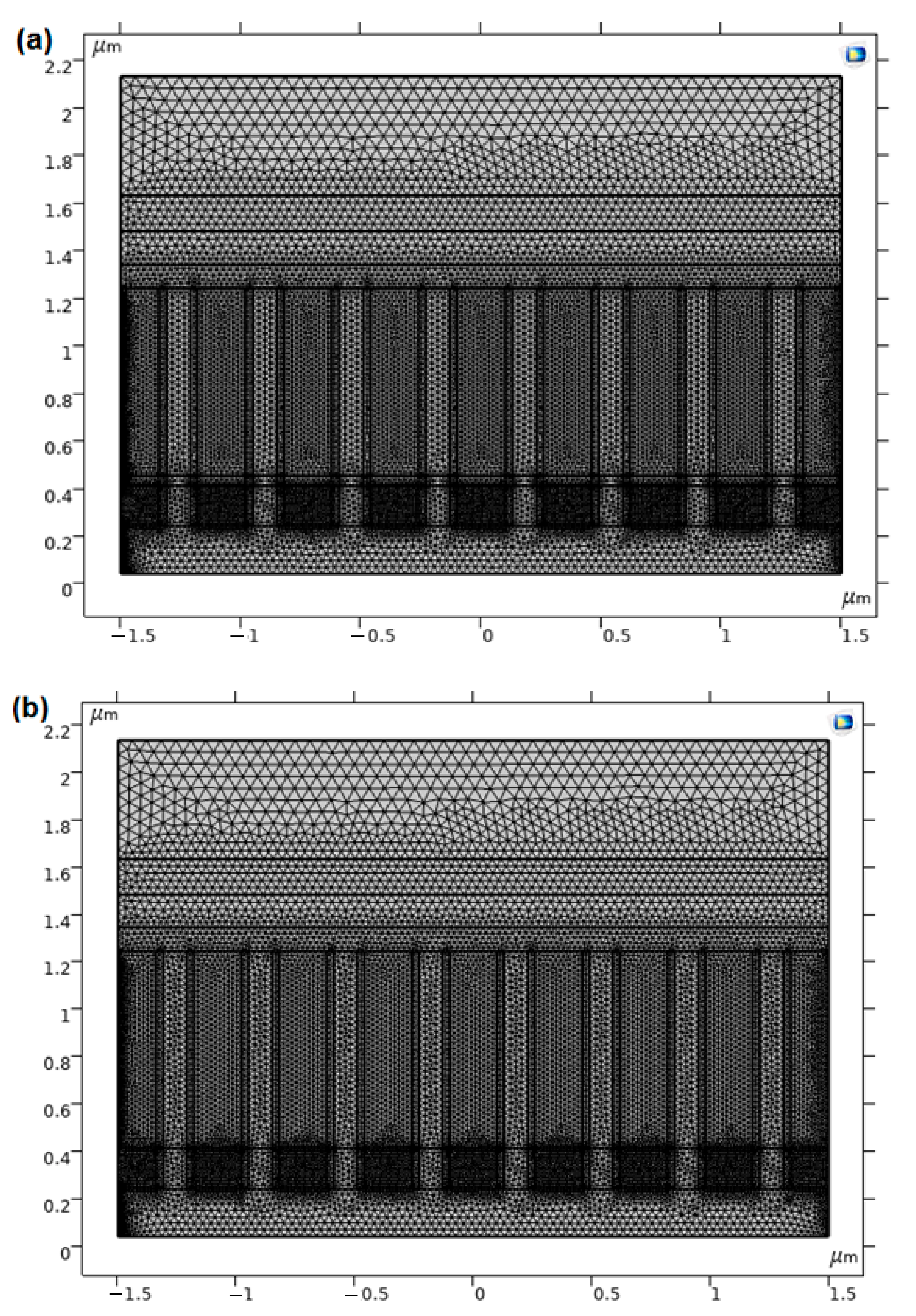



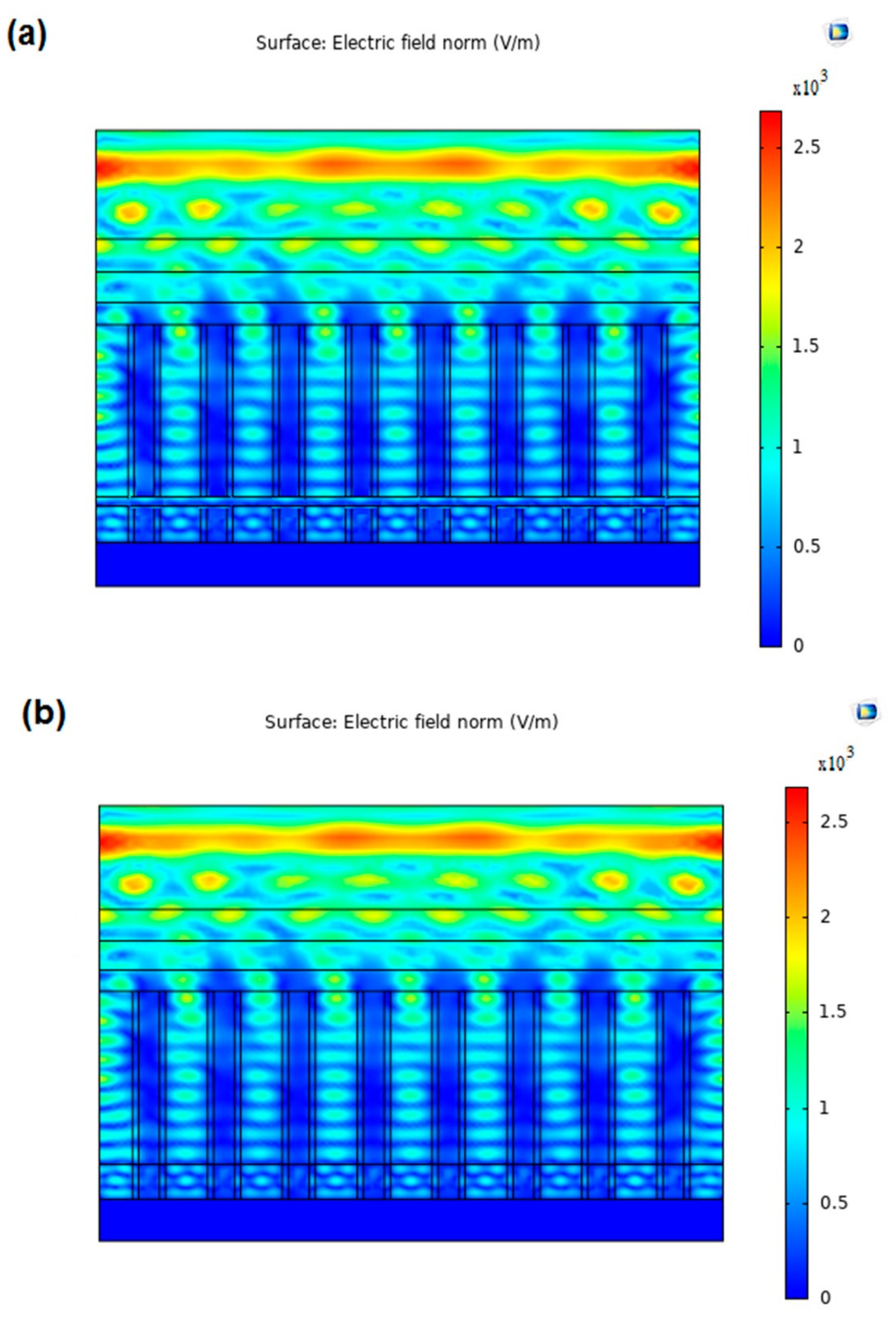
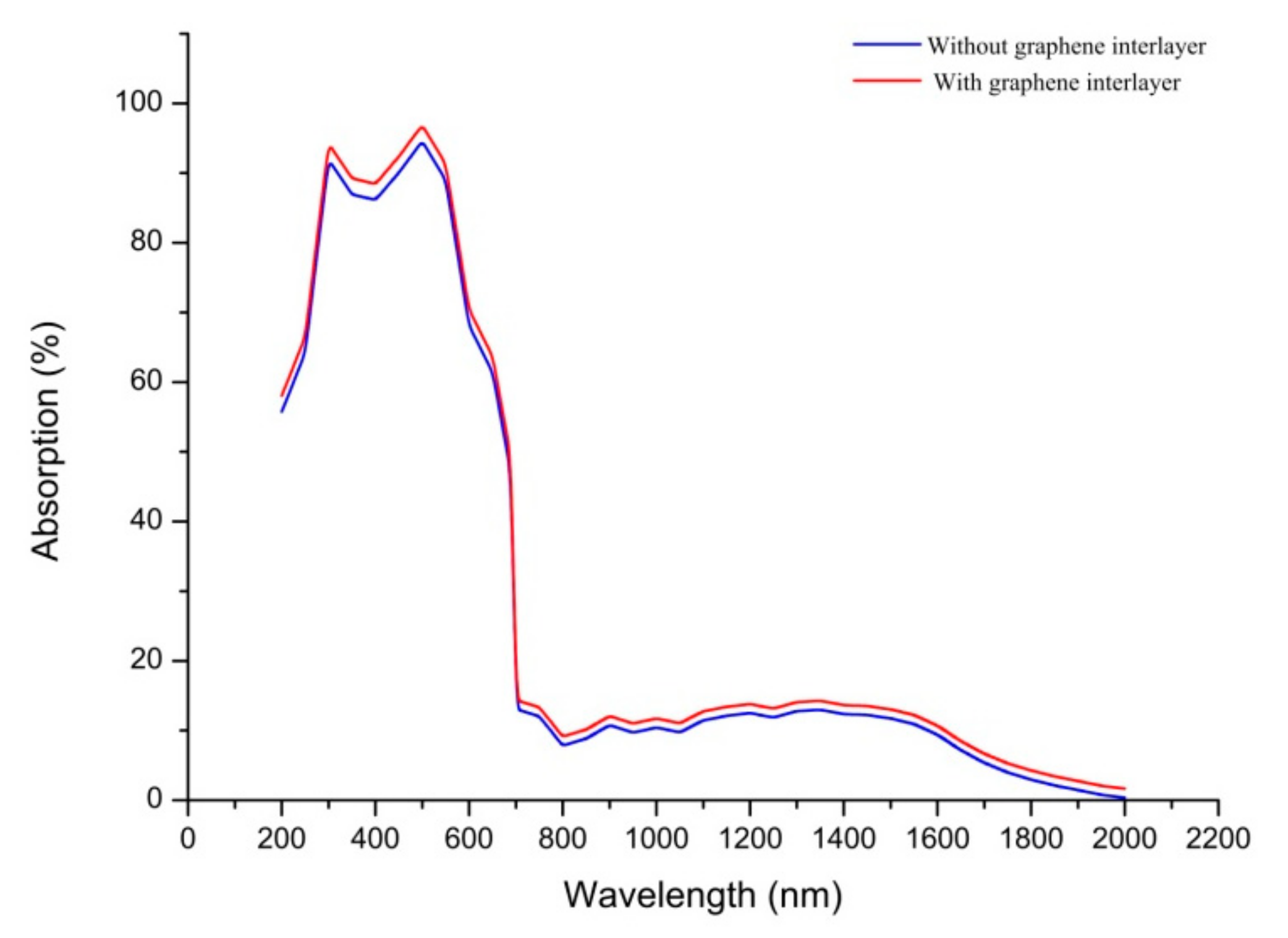
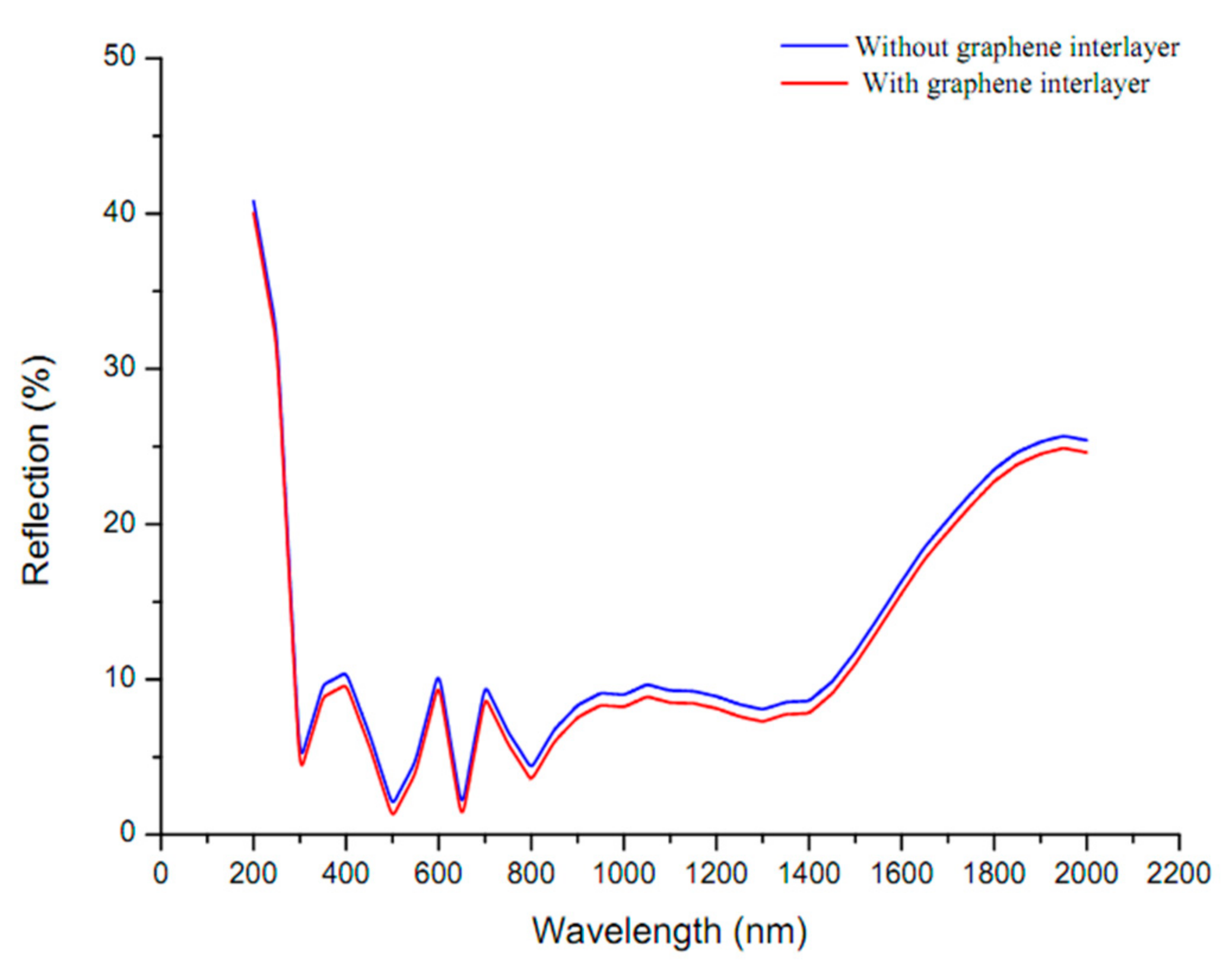

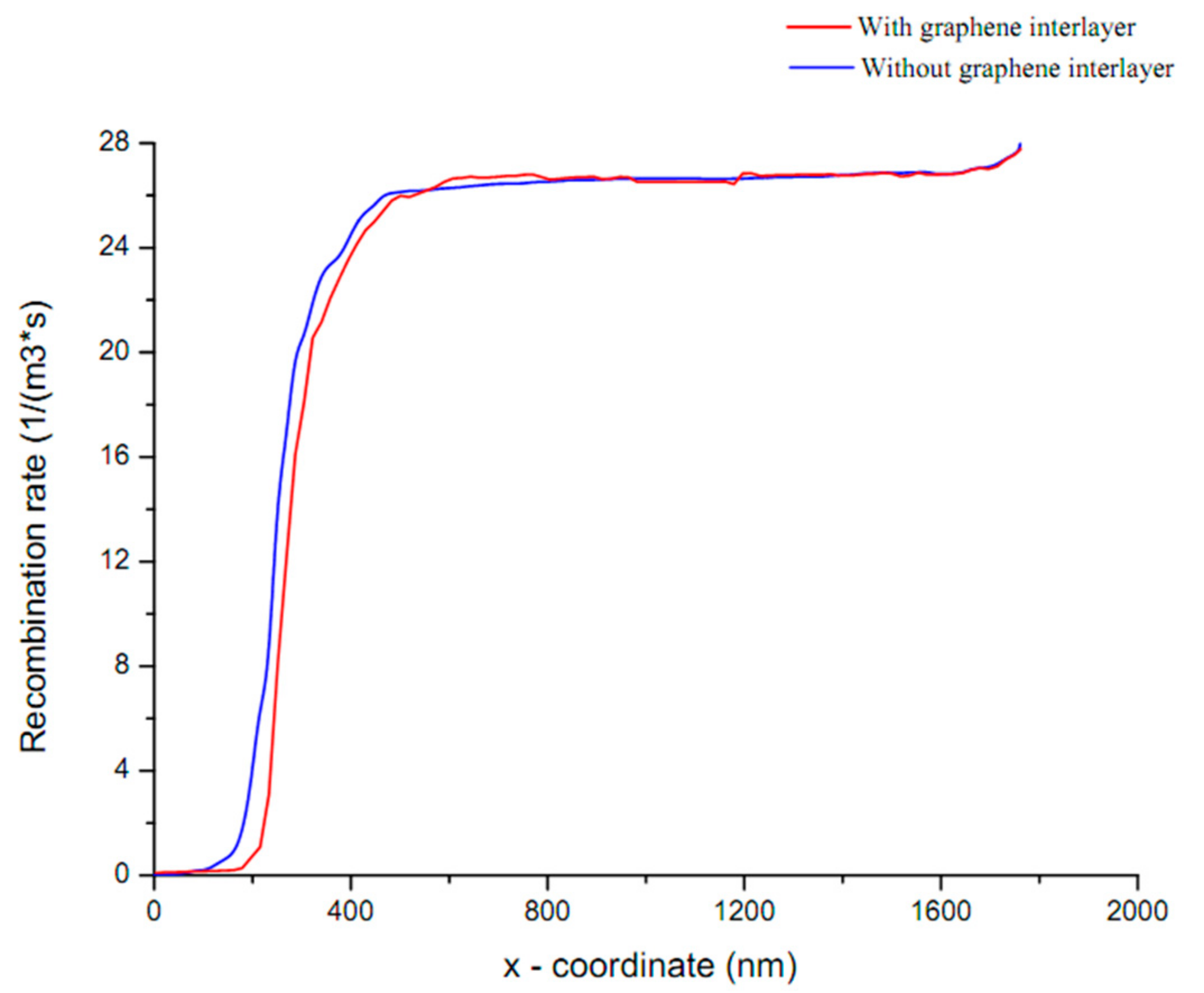

| Parameters | Mo | Graphene | MoS2 | CZTS | CdS | ZnO | ITO |
|---|---|---|---|---|---|---|---|
| W (nm) | 200 | 1 | 170 | 1000 | 100 | 140 | 150 |
| εr | - | 3.3 | 10 | 13.6 | 9 | 9 | 9 |
| Nc (cm−3) | - | 1 × 1018 | 0.7 × 1018 | 2.2 × 1018 | 2.2 × 1018 | 2.2 × 1018 | 2.2 × 1018 |
| Nv (cm−3) | - | 1 × 1019 | 0.3 × 1019 | 1.8 × 1019 | 1.8 × 1019 | 1.8 × 1019 | 1.8 × 1019 |
| μn (cm2/V·s) | - | 1 × 109 | 100 | 100 | 30 | 100 | 100 |
| χ (eV) | - | 3.5 | 4.14 | 4.2 | 4.2 | 4.4 | 3.6 |
| Eg (eV) | 1.96 | 0–0.25 | 1.1 | 1.45 | 2.4 | 3.3 | 3.6 |
| CB (cm−3) | 2.2 × 1018 | 3 × 109–3 × 1022 | 2.2 × 1018 | 2.2 × 1018 | 2.2 × 1019 | 2.2 × 1019 | 4 × 1019 |
| VB (cm−3) | 1.8 × 1019 | 3 × 109–3 × 1022 | 1.8 × 1019 | 1.8 × 1019 | 1.8 × 1018 | 1.8 × 1019 | 1 × 1019 |
| NA (cm−3) | - | - | 1 × 1015 | 1 × 1016 | 1 × 1013 | 1 × 1013 | 1 × 1013 |
| ND (cm−3) | - | 1 × 1019 | 5 × 1013 | 5 × 1013 | 5 × 1017 | 5 × 1018 | 1 × 1019 |
| CB (cm−3) | 2.2 × 1018 | 1 × 1022 | 2.2 × 1018 | 2.2 × 1018 | 2.2 × 1019 | 2.2 × 1019 | 2.2 × 1019 |
| VB (cm−3) | 1.8 × 1019 | 1 × 1022 | 1.8 × 1019 | 1.8 × 1019 | 1.8 × 1018 | 1.8 × 1019 | 1.8 × 1019 |
| Tvn (cms−1) | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 |
| Tvp (cms−1) | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 |
| D (g·cm−1) | 4.69 | 2.328 | 6.9 | 4.56 | 4.82 | 5.61 | 7.12 |
| K (W/m·K) | 138 | 140 | 103 | 2.95 | 6.2 | 23.4 | 10 |
| Cp (Jg–1 K–1) | 0.277 | 0.7 | 0.12 | 0.41 | 0.21 | 0.404 | 0.36 |
| τn/τp (ns) | - | 0.03/0.03 | 2.4/2.4 | 5.4/5.4 | 0.005/0.005 | 0.003/0.003 | 0.003/0.003 |
| h (W/m2K) | 363 × 106 | 30 × 102 | 605 × 106 | 14 × 104 | 124 × 104 | 468 × 106 | 33 × 106 |
| h (W/m2K) | 363 × 106 | 30 × 102 | 605 × 106 | 14 × 104 | 124 × 104 | 468 × 106 | 33 × 106 |
| Cn (cm6 s−1) | 0 | 0 | 0 | 1 × 10−29 | 1 × 10−29 | 1 × 10−29 | 1 × 10−29 |
| Cp (cm6 s−1) | 0 | 0 | 0 | 1 × 10−29 | 1 × 10−29 | 1 × 10−29 | 1 × 10−29 |
| C (cm3 s−1) | 0 | 0 | 0 | 5 × 10−9 | 5 × 10−9 | 5 × 10−9 | 5 × 10−9 |
| Single Nanowire Model-(Core Diameter/Shell Thickness) | Maximum ElectricField in the Nanowire (V/m) | Maximum Absorption in the Nanowire | Maximum Reflection in the Nanowire |
|---|---|---|---|
| 70 nm/45 nm | 1000 | 89% at 390 nm | 64% at 1820 nm |
| 100 nm/30 nm | 1300 | 96% at 500 nm | 43% at 1800 nm |
| 120 nm/20 nm | 1200 | 94% at 420 nm | 62% at 1810 nm |
| Model of Solar Cell | Voc (V) | Jsc (mA/cm2) | FF (%) | EFF (%) |
|---|---|---|---|---|
| With graphene interlayer | 0.63 | 6.2 | 81.7 | 16.6 |
| Without graphene interlayer | 0.6 | 6.1 | 79.2 | 15.07 |
| Physical Model of | Voc (V) | Jsc (mA/cm2) | FF (%) | EFF (%) | Max Absoption (nm) | Wavelength (nm) |
|---|---|---|---|---|---|---|
| W. Sun et al. [21] | 0.17 | 0.7 | 29.41 | 0.035 | - | 500 |
| R. Su et al. [56] | - | 6.48 | - | 52 | - | 480 |
| Y. Tak et al. [57] | 1.55 | 7.23 | 64.51 | 3.53 | - | 500 |
| C. Wang et al. [38] | 0.63 | 6.39 | 41.2 | 16.8 | 97% | 500 |
| M. Malek et al. [12] | 0.195 | 5.32 | 27.71 | 0.287 | ||
| I. Saurdi et al. [13] | 0.552 | 2.840 | 0.381 | 0,599 | ||
| J. Rouhi et al. [14] | 0.68 | 12.2 | 0.49 | 4.07 | ||
| Our study | 0.63 | 6.2 | 81.7 | 16.6 | 97.8 | 500 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Drame, B.; Niare, L.; Yuegang, F. Simulation of a New CZTS Solar Cell Model with ZnO/CdS Core-Shell Nanowires for High Efficiency. Crystals 2022, 12, 772. https://doi.org/10.3390/cryst12060772
Wang C, Drame B, Niare L, Yuegang F. Simulation of a New CZTS Solar Cell Model with ZnO/CdS Core-Shell Nanowires for High Efficiency. Crystals. 2022; 12(6):772. https://doi.org/10.3390/cryst12060772
Chicago/Turabian StyleWang, Chonge, Boubacar Drame, Lucien Niare, and Fu Yuegang. 2022. "Simulation of a New CZTS Solar Cell Model with ZnO/CdS Core-Shell Nanowires for High Efficiency" Crystals 12, no. 6: 772. https://doi.org/10.3390/cryst12060772
APA StyleWang, C., Drame, B., Niare, L., & Yuegang, F. (2022). Simulation of a New CZTS Solar Cell Model with ZnO/CdS Core-Shell Nanowires for High Efficiency. Crystals, 12(6), 772. https://doi.org/10.3390/cryst12060772






