Next Article in Journal
Laser-Induced Exothermic Bonding of SiCp/Al Composites with Nanostructured Al/Ni Energetic Interlayer
Next Article in Special Issue
Computational Studies on the Interaction of Organophosphorus Pesticides with Acetylcholinesterase and Butyrylcholinesterase: Quantum Chemical Cluster Model and HSAB Approaches
Previous Article in Journal
Optical Terahertz Sources Based on Difference Frequency Generation in Nonlinear Crystals
Previous Article in Special Issue
Hydrogen Bonds in Precursor Solution: The Origin of the Anomalous J–V Curves in Perovskite Solar Cells
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 12
Issue 7
10.3390/cryst12070937
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Bifurcated Halogen Bond-Driven Supramolecular Double Helices from 1,2-Dihalotetrafluorobenzene and 2,2′-Bi(1,8-naphthyridine)

by
Ziyu Wang
SDU-ANU Joint Science College, Shandong University, Weihai 264209, China
Crystals 2022, 12(7), 937; https://doi.org/10.3390/cryst12070937
Submission received: 20 June 2022 / Revised: 30 June 2022 / Accepted: 30 June 2022 / Published: 2 July 2022
(This article belongs to the Special Issue Theoretical Investigation on Non-covalent Interactions)
Browse Figures
Review Reports Versions Notes

Abstract

:
The unique enantiomeric pairs of double helices have been found in the structure of the cocrystal between 1,2-diiodotetrafluorobenzene and 2,2′-bi(1,8-naphthyridine). The formation of the supramolecular double helices is driven by the strong bifurcated iodine bonds which can force the herringbone packing arrangement of the molecules 2,2′-bi(1,8-naphthyridine) into a face-to-face π···π stacking pattern. In contrast, the cocrystal between 1,2-dibromotetrafluorobenzene (or 1,2-dichlorotetrafluorobenzene) and 2,2′-bi(1,8-naphthyridine) was not obtained under the same conditions. The interaction energies of the bifurcated halogen bonds and π···π stacking interactions were computed with the reliable dispersion-corrected density functional theory. The computational results show that the bifurcated iodine bond is much stronger than the bifurcated bromine bond and bifurcated chlorine bond, and it is the much stronger bifurcated iodine bond that makes the cocrystal of 1,2-diiodotetrafluorobenzene and 2,2′-bi(1,8-naphthyridine) much easier to be synthesized.

1. Introduction

Besides the well-known hydrogen bond, the halogen bond and π···π stacking interaction are the other two important types of noncovalent interactions. In recent years, much of the focus of attention in the field of noncovalent interaction has been on the theoretical and experimental studies of the halogen bond, one of the subsets of the σ-hole bonds [1,2,3,4,5,6,7,8,9,10,11,12,13]. The perfluorinated halobenzenes are commonly used halogen atom donors in the crystal engineering involving the halogen bonds. In contrast to the 1,4-dihalotetrafluorobenzene, 1,3-dihalotetrafluorobenzene and 1,3,5-trihalotrifluorobenzene, the 1,2-dihalotetrafluorobenzene is relatively seldom studied because of its two crowded halogen atoms [1,2,3]. Besides the monocentric halogen bonds, there are also many bifurcated halogen bonds although in most cases the bifurcated halogen bonds are energetically inferior to the monocentric halogen bonds [14]. The bifurcated halogen bonds are frequently seen in the halogen bond-directed cocrystals in which the 1,2-dihalotetrafluorobenzene molecules act as the halogen atom donors [15,16,17,18]. There are mainly two kinds of bifurcated halogen bonds: one is the bifurcated halogen bonds with bifurcated halogen atom acceptors [15,16]; the other is the bifurcated halogen bonds with bifurcated halogen atom donors [17,18]. Jin and coworkers reported the structure and optical properties of the cocrystal between 1,2-diiodotetrafluorobenzene and 1,10-phenanthroline driven by the C–I···(N,N) asymmetrical bifurcated halogen bond [18]. The N···N interatomic distance in 1,10-phenanthroline in this cocrystal structure is 2.720 Å. An interesting question is what will happen to the bifurcated halogen bond if the N···N interatomic distance becomes shorter. In this study, we select the 1,2-dichlorotetrafluorobenzene (C6F4Cl2), 1,2-dibromotetrafluorobenzene (C6F4Br2), 1,2-diiodotetrafluorobenzene (C6F4I2) and 2,2′-bi(1,8-naphthyridine) (C16H10N4) as models to address this question. The molecular structures of C6F4Cl2, C6F4Br2, C6F4I2 and C16H10N4 are shown in Figure 1. The crystal structure of C16H10N4 has been reported in 2015 [19]. The distance between two adjacent N atoms in the crystal structure of C16H10N4 is 2.311 Å, which is obviously smaller than the N···N interatomic distance in 1,10-phenanthroline. Hence, the molecule C16H10N4 is a very good model for addressing above-mentioned issue.
Figure 2 demonstrates the molecular electrostatic potential maps of C6F4Cl2, C6F4Br2, C6F4I2 and C16H10N4 along with some selected local minima or maxima of the surface electrostatic potentials. The computational details for the molecular electrostatic potentials can be found in Section 2.3. The halogen bond has different subsets such as the chlorine bond, bromine bond and iodine bond [20]. The bifurcated chlorine bond can be formed between C6F4Cl2 and C16H10N4; the bifurcated bromine bond can be formed between C6F4Br2 and C16H10N4; the bifurcated iodine bond can be formed between C6F4I2 and C16H10N4. Theoretically, one C16H10N4 molecule can form two bifurcated halogen bonds with two 1,2-dihalotetrafluorobenzene molecules. As shown in Figure 2, the most positive electrostatic potential on I is larger than that on Br, and the most positive electrostatic potential on Cl is the smallest one. Considering that the strong halogen bond is an electrostatically driven noncovalent interaction [21], it is reasonable to assume the halogen bond strength order of bifurcated iodine bond > bifurcated bromine bond > bifurcated chlorine bond. However, such a strength order may be affected by the π···π stacking interactions between the halogen atom acceptors C16H10N4. C16H10N4 is a relatively large aromatic molecule. The π···π stacking interactions between the aromatic molecules C16H10N4 should be strong enough to compete with the bifurcated halogen bonds. The second purpose of this study is thus to explore the strengths of the bifurcated halogen bonds and π···π stacking interactions and their mutual effects.

2. Materials and Methods

2.1. Cocrystal Synthesis

The reactants C6F4Br2 (liquid, purity ≥ 98%), C6F4I2 (solid, 98%) and C16H10N4 (solid, purity ≥ 98%) were purchased from J&K Scientific Ltd., Beijing, China and C6F4Cl2 (liquid, purity ≥ 98%) was purchased from Alfa Chemical Co., Ltd., Zhengzhou, China. The solvent chloroform (analytical grade) was obtained commercially from local company in Zhengzhou, China. All the chemicals and solvent were used as received.
A series of binary mixtures of C16H10N4 with C6F4Cl2, C6F4Br2, and C6F4I2, respectively, in different molar ratios (2:1, 1:1 and 1:2) were dissolved in chloroform in glass vials. Each vial was sealed with parafilm having several pinholes for slow solvent evaporation. After the nine glass vials were kept at room temperature for about five days, the colorless single crystals suitable for X-ray diffraction analyses were obtained. However, the X-ray crystal structure resolution performed on these single crystals showed that only the 1:1 cocrystal between C6F4I2 and C16H10N4 was successfully synthesized, and all the other single crystals are the crystals of C16H10N4. The desirable cocrystals between C6F4Cl2 and C16H10N4 and between C6F4Br2 and C16H10N4 were not obtained.

2.2. X-ray Crystallography

The crystallographic data of the cocrystal between C6F4I2 and C16H10N4 were collected on the Rigaku Oxford SuperNova diffractometer (Rigaku, Tokyo, Japan) with the Mo-Kα radiation (λ = 0.71073 Å) at a temperature of 289 K. The CrysAlisPro software was used for data processing [22]. The cocrystal structure was solved and refined by using the SHELX-2014 and Olex2.0 programs [23,24,25]. The crystallographic data of the cocrystal between C6F4I2 and C16H10N4 have been deposited in the Cambridge Crystallographic Data Centre (CCDC), and the deposition number is CCDC 2168308. At the same time, the crystallographic information file of the cocrystal between C6F4I2 and C16H10N4 was also provided as the Supplementary Material.

2.3. Computational Details

The geometries of the monomers C6F4Cl2, C6F4Br2, C6F4I2 and C16H10N4 were fully optimized at the PBE0-D3(BJ)/def2-TZVPP theory level [26,27,28,29]. The PBE0-D3(BJ)/def2-TZVPP electrostatic potentials of these monomers were calculated on the outer 0.001 a.u. contours of the molecules’ electronic densities [21]. Unless otherwise stated, the geometries of the dimers in the crystal structure were not optimized and are extracted directly from the crystal structure. The geometries of the trimers in the gas phase were fully optimized at the PBE0-D3(BJ)/def2-TZVPP level of theory. The PBE0-D3(BJ)/def2-TZVPP interaction energies of the dimers and trimers were calculated using the supermolecule method and the basis set superposition error corrections to the interaction energies were carried out with the counterpoise method [30]. Previous studies have proved that PBE0-D3 is an excellent functional for the study of π-stacked complexes [31,32]. All the calculations were performed with the GAUSSIAN 09 suite of programs [33].

3. Results and Discussion

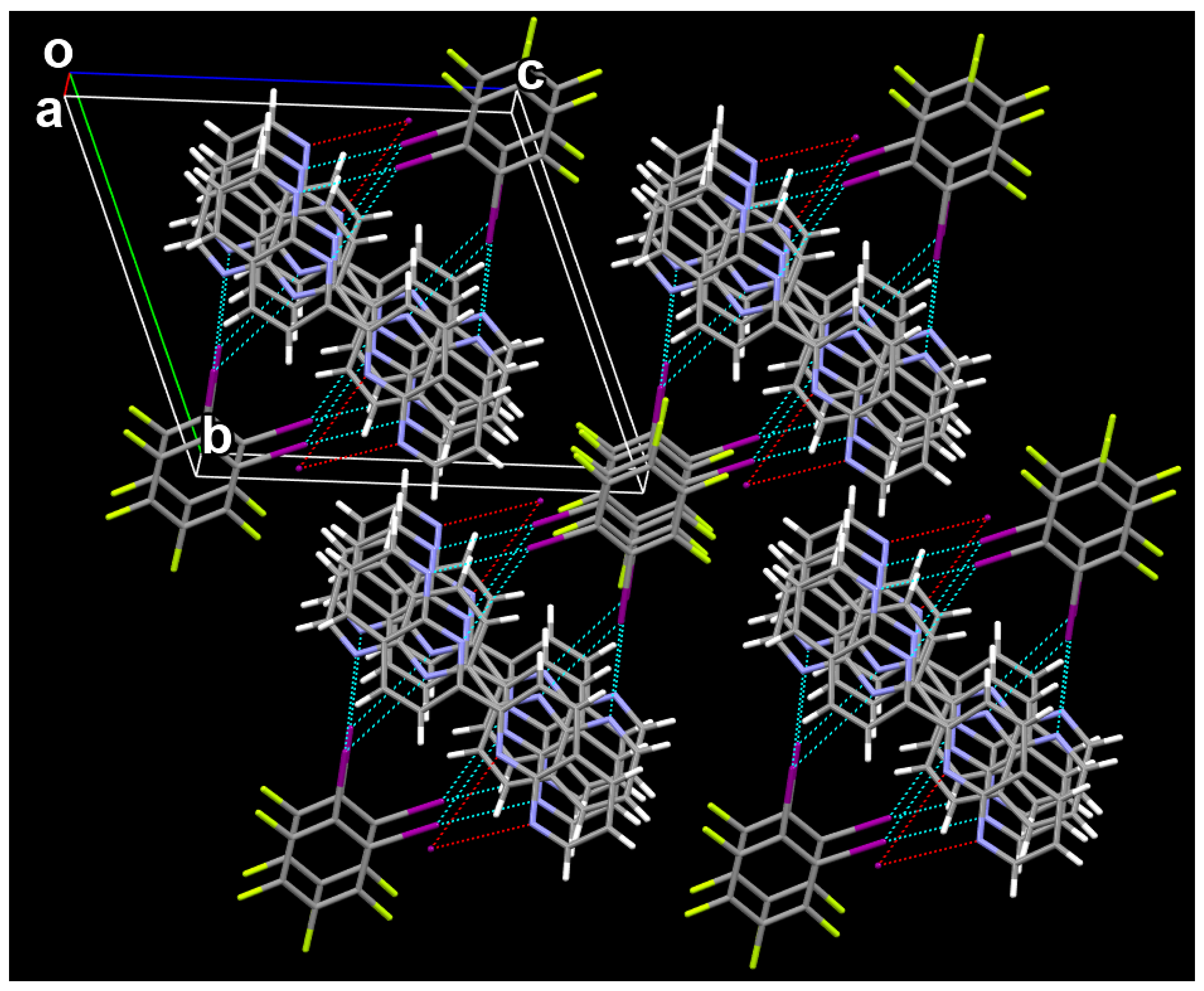
3.1. The Cocrystal Structure

Figure 3 shows the 2 × 2 × 2 unit cell of the 1:1 cocrystal between C6F4I2 and C16H10N4 viewed along the a axis. It can be clearly seen from Figure 3 that there exist the bifurcated iodine bonds between C6F4I2 and C16H10N4, π···π stacking interactions between molecules C6F4I2 and π···π stacking interactions between molecules C16H10N4 in the cocrystal structure. For clarity, the weak C–H···F hydrogen bonds in the cocrystal structure are not shown in Figure 3. There are two different C–I···(N,N) bifurcated iodine bonds in the cocrystal structure, and both of them are asymmetrical. The I···N interatomic distances are 2.952(3) and 3.485(2) Å in one C–I···(N,N) bifurcated iodine bond, and are 3.102(4) and 3.473(3) Å in the other C–I···(N,N) bifurcated iodine bond. Firstly, the 2D structure is formed via the bifurcated iodine bonds between C6F4I2 and C16H10N4, π···π stacking interactions between molecules C6F4I2 and π···π stacking interactions between molecules C16H10N4. Then, different 2D structures are connected together by the weak C–H···F hydrogen bonds to form the 3D structure of the cocrystal. The crystallographic data for the cocrystal (M = 660.14 g/mol) are summarized as follows: triclinic, space group P 1 ¯ (no. 2), a = 7.3663(3) Å, b = 11.9334(7) Å, c = 13.3466(6) Å, α = 68.924(5)°, β = 84.768(4)°, γ = 85.522(4)°, V = 1088.89(10) Å3, Z = 2, T = 289 K, μ(CuKα) = 2.939 mm−1, Dcalc = 2.013 g/cm3, 15893 reflections measured (6.508° ≤ 2Θ ≤ 56.856°), 4720 unique (Rint = 0.0499, Rsigma = 0.0489), which were used in all calculations. The final R1 was 0.0355 (I > 2σ(I)) and wR2 was 0.0846 (all data).
Close inspection of the cocrystal structure reveals that a pair of enantiomeric (P and M) supramolecular double helices are assembled by the bifurcated iodine bonds between C6F4I2 and C16H10N4 and π···π stacking interactions between molecules C16H10N4. Different pairs of P and M supramolecular double helices are assembled together by the π···π stacking interactions between molecules C6F4I2 to form the 2D structure of the cocrystal. In fact, in recent years the halogen bond-driven supramolecular double helices have been reported in many studies [34,35,36,37,38]. In this work, the P supramolecular helix and M supramolecular helix share the same π-stacked C16H10N4 molecules to assemble the enantiomeric pair of double helices. This case is very similar to the supramolecular double helices assembled by the hydrogen-bonded 3-mer arylamide foldamer and 1,4-diiodotetrafluorobenzene, in which the P supramolecular helix and M supramolecular helix also have the overlapping region [36].
The PBE0-D3(BJ)/def2-TZVPP interaction energies of the bifurcated iodine bonds and π···π stacking interactions can be seen in Figure 4. The interaction energy of the π···π stacking interaction between two C16H10N4 molecules is –16.47 kcal/mol. In contrast, the interaction energy of the parallel-displaced benzene dimer is only –2.70 kcal/mol [39]. This means that the π···π stacking interaction between two C16H10N4 molecules is rather strong. There are two different π···π stacking interactions between C6F4I2 molecules, the interaction energies of which are –7.16 and –7.37 kcal/mol, respectively. There are also two different bifurcated iodine bonds in the cocrystal structure, the interaction energies of which are –10.09 and –10.67 kcal/mol, respectively. The PBE0-D3(BJ)/def2-TZVPP interaction energy of the bifurcated iodine bond in the cocrystal between 1,2-diiodotetrafluorobenzene and 1,10-phenanthroline is –9.91 kcal/mol [18]. The interaction energy difference between the bifurcated iodine bonds in the two different cocrystals is very small, which indicates that the strength of the C–I···(N,N) bifurcated iodine bond is not dependent on the N···N interatomic distance. It is well-known that the H atom positions cannot be precisely determined by the single-crystal X-ray diffraction. For the dimers between C6F4I2 and C16H10N4 (see Figure 4), we evaluated their interaction energies with and without the optimizations of the H atom positions, and found that the differences are negligible. On the other hand, such a result also reflects that the C–H···I interactions in these dimers are very weak. Throughout this study, we did not discuss the effects of adjacent C–H···I interactions on the bifurcated iodine bonds.
The crystal structure of C16H10N4 can be viewed and retrieved from the Cambridge Structural Database (refcode: QETZIB) [40]. Figure 5 demonstrates different stacking patterns of the two C16H10N4 molecules in the C16H10N4 crystal and in the cocrystal between C6F4I2 and C16H10N4. In the π-stacked C16H10N4 dimer in the C16H10N4 crystal, the N atoms of the two C16H10N4 molecules are in the eclipsed arrangement, whereas in the π-stacked C16H10N4 dimer in the cocrystal between C6F4I2 and C16H10N4, the N atoms of the two C16H10N4 molecules are in the opposed arrangement. The interaction energy of the former dimer is –11.22 kcal/mol, and the interaction energy of the latter dimer is –16.47 kcal/mol. Although the π···π stacking interaction of the C16H10N4 dimer in Figure 5b is much stronger than the π···π stacking interaction of the C16H10N4 dimer in Figure 5a, there is no C16H10N4 dimer in Figure 5b found in the crystal structure of C16H10N4. In the crystal structure of C16H10N4, the C16H10N4 molecules are assembled in a herringbone pattern which is more stable because of the dense packing [41]. That is to say, the 1D columnar stacking structure of the C16H10N4 molecules in the cocrystal between C6F4I2 and C16H10N4 is unfavorable in enthalpic gain for the cocrystal formation. However, the introduction of the strong bifurcated iodine bonds offsets the enthalpic loss and promotes the cocrystal formation. It can be concluded here that the bifurcated iodine bond changes the stacking pattern of the C16H10N4 molecules and the cocrystal formation is driven by the bifurcated iodine bond.

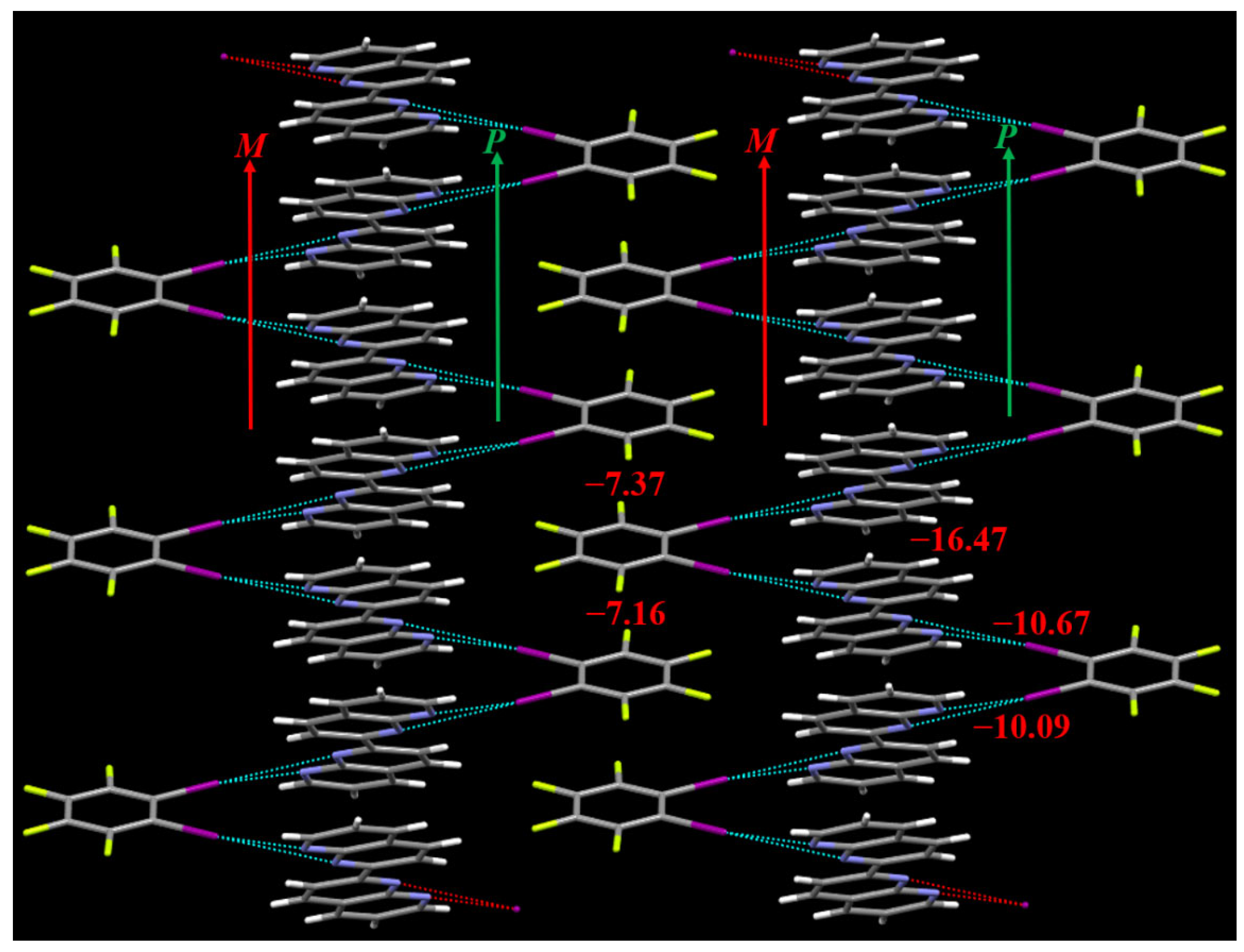
3.2. The Noncovalent Interactions in the Gas Phase

Under the same conditions, synthesis of the cocrystal between C6F4I2 and C16H10N4 succeeded, but syntheses of the cocrystal between C6F4Br2 and C16H10N4 and cocrystal between C6F4Cl2 and C16H10N4 failed. In order to uncover the underlying cause of the experimental discrepancies, we have investigated computationally the bifurcated halogen bonds between C6F4X2 (X = Cl, Br or I) and C16H10N4 and the π···π stacking interactions between the C16H10N4 molecules in the gas phase. The geometries of the dimer C16H10N4···C16H10N4 and trimers C6F4X2···(C16H10N4)2 shown in Figure 6 were fully optimized at the PBE0-D3(BJ)/def2-TZVPP level of theory. Finally, it was found that all the optimized structures in Figure 6 have approximate C2 symmetry. This means that the two bifurcated halogen bonds in each trimer are identical to each other. In fact, as can be seen in Figure 4, the interaction energy difference between the two bifurcated iodine bonds is only 0.58 kcal/mol, and two bifurcated iodine bonds in the cocrystal structure are also almost the same.
Figure 6 summarizes the X···N interatomic distances and interaction energies of the bifurcated halogen bonds and π···π stacking interactions in the four optimized complexes. The two X···N distances in each bifurcated halogen bond are obviously different, which shows that all the bifurcated halogen bonds are asymmetrical. The I···N distance of 2.999 Å is shorter than the Br···N distance of 3.086 Å and Cl···N distance of 3.189 Å, although the order of atomic radii is I > Br > Cl. Such an order of X···N interatomic distances reflects the strength order of the bifurcated halogen bonds, and indicates that the bifurcated iodine bond is much stronger than the bifurcated bromine bond and weakest bifurcated chlorine bond. There are two methods to calculate the interaction energies of the bifurcated halogen bonds and π···π stacking interactions in the three trimers in Figure 6. One method is to consider the mutual effects of the bifurcated halogen bonds and the π···π stacking interactions in the trimers, and the other method is not to consider these mutual effects. The interaction energies of the π-stacked C16H10N4 dimers in C6F4Cl2···(C16H10N4)2, C6F4Br2···(C16H10N4)2 and C6F4I2···(C16H10N4)2 are –16.35, –16.27 and –16.19 kcal/mol, respectively, without considering the effects of adjacent bifurcated halogen bonds. If we consider the effects of adjacent two bifurcated halogen bonds, the interaction energy of the π-stacked C16H10N4 dimer can be calculated as the difference between the total interaction energy of the trimer and the total interaction energy of two identical bifurcated halogen bonds. Note that, as shown in Figure 6, the total interaction energy of two identical bifurcated halogen bonds in each trimer can be easily obtained if we treat the π-stacked C16H10N4 dimer as one entity. Employing such a computational method, the interaction energies of the π-stacked C16H10N4 dimers in C6F4Cl2···(C16H10N4)2, C6F4Br2···(C16H10N4)2 and C6F4I2···(C16H10N4)2 are calculated to be –16.32, –16.24 and –16.16 kcal/mol, respectively. The differences between the interaction energies calculated from two different methods are quite small, which means that the mutual effects of the bifurcated halogen bonds and the π···π stacking interactions in the trimers can be neglected.
The interaction energy of the π-stacked C16H10N4 dimer in the gas phase is –16.41 kcal/mol (Figure 6). Upon the trimer formation, it slightly decreases to –16.35, –16.27 and –16.19 kcal/mol, respectively. In the cocrystal structure, the interaction energy of the π-stacked C16H10N4 dimer is –16.47 kcal/mol (Figure 4). These similar values of interaction energy support that the π···π stacking interactions between the C16H10N4 molecules are strong enough to be kept rigid in the solid and gas phases. The interaction energies of the bifurcated chlorine bond, bifurcated bromine bond and bifurcated iodine bond are –4.53, –6.42 and –9.75 kcal/mol, respectively. This strength order is consistent with the one predicted by the X···N interatomic distances. The interaction energy of the bifurcated iodine bond in the gas phase is also close to the corresponding ones shown in Figure 4. The binding energies of the monocentric C–I···N iodine bonds are less than 7.00 kcal/mol [42]. In contrast to the C–I···N monocentric iodine bonds, the C–I···(N,N) bifurcated iodine bonds are much stronger and much more rigid.
One C16H10N4 molecule can form two bifurcated halogen bonds with two C6F4X2 molecules. To explain why the C16H10N4 crystal not the expected cocrystal between C6F4Cl2 and C16H10N4 or the expected cocrystal between C6F4Br2 and C16H10N4 was formed in the synthesis experiments, it is significant to compare the interaction energy of the π-stacked C16H10N4 dimer in the C16H10N4 crystal with the sum of the interaction energies of the two identical bifurcated halogen bonds. As can be seen in Figure 6, the values of the sum of the two interaction energies are –9.06, –12.84 and –19.50 kcal/mol for the bifurcated chlorine bond, bifurcated bromine bond and bifurcated iodine bond, respectively. Figure 5 shows that the interaction energy of the π-stacked C16H10N4 dimer in the C16H10N4 crystal is 11.22 kcal/mol. From the energetic point of view, only two bifurcated iodine bonds are strong enough to prevent the formation of the C16H10N4 crystal. This explains why only the cocrystal between C6F4I2 and C16H10N4 was obtained in the synthesis experiments.

4. Conclusions

The unique enantiomeric pairs of double helices in the structure of the cocrystal between C6F4I2 and C16H10N4 have been reported in the present study. It was found that the formation of the cocrystal is driven by the strong bifurcated iodine bonds because they change the eclipsed arrangement of the π-stacked C16H10N4 dimer in the C16H10N4 crystal into the opposed arrangement in the cocrystal between C6F4I2 and C16H10N4. The C–I···(N,N) bifurcated iodine bond is much stronger than the C–I···N monocentric iodine bond. On the other hand, the strength of the C–I···(N,N) bifurcated iodine bond is not dependent on the N···N interatomic distance in the iodine atom acceptor.
In contrast to the cocrystal between C6F4I2 and C16H10N4, the cocrystal between C6F4Br2 and C16H10N4 and the cocrystal between C6F4Cl2 and C16H10N4 are difficult to be synthesized under the same conditions. To explain the underlying reasons for these differences, the interaction energies of the bifurcated halogen bonds and π···π stacking interactions in the gas phase have been calculated at the PBE0-D3(BJ)/def2-TZVPP level of theory. The absolute values of the interaction energies for the opposed configurations of the π-stacked C16H10N4 dimers are all larger than 16.00 kcal/mol, which makes these π-stacked C16H10N4 dimers hard to be affected by the adjacent bifurcated halogen bonds including the strongest bifurcated iodine bond with an interaction energy of –9.75 kcal/mol. The interaction energies of the bifurcated chlorine bond and bifurcated bromine bond are –4.53 and –6.42 kcal/mol, respectively. It is the much stronger bifurcated iodine bond that makes the cocrystal of C6F4I2 and C16H10N4 much easier to be synthesized.
In this study, the results clearly show that the stacking pattern of large aromatic molecules containing the N atoms can be changed by the halogen bond. Such a strategy may be useful in the design and synthesis of the organic optoelectronic materials.

Supplementary Materials

The following is available online at https://www.mdpi.com/article/10.3390/cryst12070937/s1, cif file of the cocrystal 2168308.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data is contained within the article.

Acknowledgments

Z.W. acknowledges Luoyang Normal University for the chance to carry out the experiments during the outbreak of COVID-19 in 2020, and thanks the anonymous reviewers for their helpful comments and suggestions.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The Halogen Bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  2. Wang, H.; Wang, W.; Jin, W.J. σ-Hole Bond vs π-Hole Bond: A Comparison Based on Halogen Bond. Chem. Rev. 2016, 116, 5072–5104. [Google Scholar] [CrossRef] [PubMed]
  3. Wang, W.; Zhang, Y.; Jin, W.J. Halogen Bonding in Room-Temperature Phosphorescent Materials. Coord. Chem. Rev. 2020, 404, 213107. [Google Scholar] [CrossRef]
  4. Alkorta, I.; Elguero, J.; Frontera, A. Not Only Hydrogen Bonds: Other Noncovalent Interactions. Crystals 2020, 10, 180. [Google Scholar] [CrossRef] [Green Version]
  5. Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen Bonding: The σ-Hole. J. Mol. Model. 2007, 13, 291–296. [Google Scholar] [CrossRef]
  6. Bulatova, M.; Ivanov, D.M.; Haukka, M. Classics Meet Classics: Theoretical and Experimental Studies of Halogen Bonding in Adducts of Platinum(II) 1,5-Cyclooctadiene Halide Complexes with Diiodine, Iodoform, and 1,4-Diiodotetrafluorobenzene. Cryst. Growth Des. 2021, 21, 974–987. [Google Scholar] [CrossRef]
  7. Rajakumar, K.; Sharutin, V.V.; Adonin, S.A.; Zherebtsov, D.A.; Sakhapov, I.F.; Islamov, D.R.; Prabunatan, P.; Vershinin, M.A.; Naifert, S.A.; Polozov, M.A. Di- and Tetraiodoxylenes: Structure and Features of Non-Covalent Interaction in a Solid State. J. Struct. Chem. 2022, 63, 620–625. [Google Scholar] [CrossRef]
  8. Kryukova, M.A.; Sapegin, A.V.; Novikov, A.S.; Krasavin, M.; Ivanov, D.M. New Crystal Forms for Biologically Active Compounds. Part 2: Anastrozole as N-Substituted 1,2,4-Triazole in Halogen Bonding and Lp-π Interactions with 1,4-Diiodotetrafluorobenzene. Crystals 2020, 10, 371. [Google Scholar] [CrossRef]
  9. Eliseeva, A.A.; Ivanov, D.M.; Novikov, A.S.; Kukushkin, V.Y. Recognition of the π-Hole Donor Ability of Iodopentafluorobenzene—a Conventional σ-Hole Donor for Crystal Engineering Involving Halogen Bonding. CrystEngComm 2019, 21, 616–628. [Google Scholar] [CrossRef]
  10. Ragusa, A.C.; Peloquin, A.J.; McMillen, C.D.; Pennington, W.T. 2,5-Diiodothiophene: A Versatile Halogen Bonding Synthon for Crystal Engineering. Cryst. Growth Des. 2022, 22, 1906–1913. [Google Scholar] [CrossRef]
  11. Bondarenko, M.A.; Abramov, P.A.; Novikov, A.S.; Sokolov, M.N.; Adonin, S.A. Cu(II) Pentaiodobenzoate Complexes: “Super Heavy Carboxylates” Featuring Strong Halogen Bonding. Polyhedron 2022, 214, 115644. [Google Scholar] [CrossRef]
  12. Posavec, L.; Nemec, V.; Stilinović, V.; Cinčić, D. Halogen and Hydrogen Bond Motifs in Ionic Cocrystals Derived from 3-Halopyridinium Halogenides and Perfluorinated Iodobenzenes. Cryst. Growth Des. 2021, 21, 6044–6050. [Google Scholar] [CrossRef] [PubMed]
  13. Zheng, S.; Han, J.; Jin, X.; Ye, Q.; Zhou, J.; Duan, P.; Liu, M. Halogen Bonded Chiral Emitters: Generation of Chiral Fractal Architecture with Amplified Circularly Polarized Luminescence. Angew. Chem. Int. Ed. 2021, 60, 22711–22716. [Google Scholar] [CrossRef] [PubMed]
  14. Scheiner, S. Comparison of Bifurcated Halogen with Hydrogen Bonds. Molecules 2021, 26, 350. [Google Scholar] [CrossRef]
  15. Cinčić, D.; Friščić, T.; Jones, W. Experimental and Database Studies of Three-Centered Halogen Bonds with Bifurcated Acceptors Present in Molecular Crystals, Cocrystals and Salts. CrystEngComm 2011, 13, 3224–3231. [Google Scholar] [CrossRef]
  16. Aakeröy, C.B.; Wijethunga, T.K.; Desper, J. Constructing Molecular Polygons Using Halogen Bonding and Bifurcated N-Oxides. CrystEngComm 2014, 16, 28–31. [Google Scholar] [CrossRef] [Green Version]
  17. Efimenko, Z.M.; Eliseeva, A.A.; Ivanov, D.M.; Galmés, B.; Frontera, A.; Bokach, N.A.; Kukushkin, V.Y. Bifurcated μ2-I···(N,O) Halogen Bonding: The Case of (Nitrosoguanidinate)NiII Cocrystals with Iodine(I)-Based σ-Hole Donors. Cryst. Growth Des. 2021, 21, 588–596. [Google Scholar] [CrossRef]
  18. Gao, Y.J.; Li, C.; Liu, R.; Jin, W.J. Phosphorescence of Several Cocrystals Assembled by Diiodotetrafluorobenzene and Three Ring Angular Diazaphenanthrenes via C–I···N Halogen Bond. Spectrochim. Acta Part A 2017, 173, 792–799. [Google Scholar] [CrossRef]
  19. Sadhukhan, N.; Saha, S.; Bera, J.K. Multinuclear Complexes Derived from Bi-1, 8-naphthyridine Ligands. J. Indian Chem. Soc. 2015, 92, 1957–1964. [Google Scholar]
  20. Cavallo, G.; Metrangolo, P.; Pilati, T.; Resnati, G.; Terraneo, G. Naming Interactions from the Electrophilic Site. Cryst. Growth Des. 2014, 14, 2697–2702. [Google Scholar] [CrossRef]
  21. Politzer, P.; Murray, J.S.; Clark, T. Halogen Bonding: An Electrostatically-Driven Highly Directional Noncovalent Interaction. Phys. Chem. Chem. Phys. 2010, 12, 7748–7757. [Google Scholar] [CrossRef] [PubMed]
  22. CrysAlisPro, Rigaku Oxford Diffraction, version 1.171.39.46; Oxford Diffraction Ltd.: Yarnton, UK, 2018.
  23. Sheldrick, G.M. SHELXT–Integrated Space-Group and Crystal-Structure Determination. Acta Crystallogr. Sect. A 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  24. Sheldrick, G.M. Crystal Structure Refinement with SHELXL. Acta Crystallogr. Sect. C 2015, 71, 3–8. [Google Scholar] [CrossRef]
  25. Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A Complete Structure Solution, Refinement and Analysis Program. J. Appl. Cryst. 2009, 42, 339–341. [Google Scholar] [CrossRef]
  26. Adamo, C.; Barone, V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6169. [Google Scholar] [CrossRef]
  27. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  28. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
  29. Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
  30. Boys, S.F.; Bernardi, F. The Calculation of Small Molecular Interactions by the Difference of Separate Total Energies. Some Procedures with Reduced Errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
  31. Wang, W.; Sun, T.; Zhang, Y.; Wang, Y.B. The Benzene···Naphthalene Complex: A more Challenging System than the Benzene Dimer for newly Developed Computational Methods. J. Chem. Phys. 2015, 143, 114312. [Google Scholar] [CrossRef]
  32. Wang, W.; Zhang, Y.; Wang, Y.B. Highly Accurate Benchmark Calculations of the Interaction Energies in the Complexes C6H6···C6X6 (X = F, Cl, Br, and I). Int. J. Quantum Chem. 2017, 117, e25345. [Google Scholar] [CrossRef]
  33. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2010. [Google Scholar]
  34. Ng, C.-F.; Chow, H.-F.; Mak, T.C.W. Halogen-Bond-Mediated Assembly of a Single-Component Supramolecular Triangle and an Enantiomeric Pair of Double Helices from 2-(Iodoethynyl)pyridine Derivatives. Angew. Chem. Int. Ed. 2018, 57, 4986–4990. [Google Scholar] [CrossRef] [PubMed]
  35. Liu, C.-Z.; Koppireddi, S.; Wang, H.; Zhang, D.-W.; Li, Z.-T. Halogen Bonding Directed Supramolecular Quadruple and Double Helices from Hydrogen-Bonded Arylamide Foldamers. Angew. Chem. Int. Ed. 2019, 58, 226–230. [Google Scholar] [CrossRef] [PubMed]
  36. Koppireddi, S.; Liu, C.-Z.; Wang, H.; Zhang, D.-W.; Li, Z.-T. Halogen and Hydrogen Bonding-Driven Self-Assembly of Supramolecular Macrocycles and Double Helices from Hydrogen-Bonded Arylamide Foldamers. CrystEngComm 2019, 21, 2626–2630. [Google Scholar] [CrossRef]
  37. Liu, C.-Z.; Koppireddi, S.; Wang, H.; Zhang, D.-W.; Li, Z.-T. Halogen Bonding-Driven Formation of Supramolecular Macrocycles and Double Helix. Chin. Chem. Lett. 2019, 30, 953–956. [Google Scholar] [CrossRef]
  38. Xu, Y.; Hao, A.; Xing, P. X···X Halogen Bond-Induced Supramolecular Helices. Angew. Chem. Int. Ed. 2022, 61, e202113786. [Google Scholar]
  39. Pitoňák, M.; Neogrády, P.; Řezáč, J.; Jurečka, P.; Urban, M.; Hobza, P. Benzene Dimer: High-Level Wave Function and Density Functional Theory Calculations. J. Chem. Theory Comput. 2008, 4, 1829–1834. [Google Scholar] [CrossRef]
  40. Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Crystallogr. Sect. B 2016, 72, 171–179. [Google Scholar] [CrossRef] [PubMed]
  41. Gierschner, J.; Lüer, L.; Milián-Medina, B.; Oelkrug, D.; Egelhaaf, H.-J. Highly Emissive H-Aggregates or Aggregation-Induced Emission Quenching? The Photophysics of All-Trans para-Distyrylbenzene. J. Phys. Chem. Lett. 2013, 4, 2686–2697. [Google Scholar] [CrossRef]
  42. Wang, W.; Zhang, Y.; Wang, Y.-B. The π···π Stacking Interactions between Homogeneous Dimers of C6FxI(6-x) (x = 0, 1, 2, 3, 4, and 5): A Comparative Study with the Halogen Bond. J. Phys. Chem. A 2012, 116, 12486–12491. [Google Scholar] [CrossRef]
Crystals 12 00937 g001 550
Figure 1. The molecular structures of C6F4Cl2, C6F4Br2, C6F4I2 and C16H10N4.
Figure 1. The molecular structures of C6F4Cl2, C6F4Br2, C6F4I2 and C16H10N4.
Crystals 12 00937 g001
Crystals 12 00937 g002 550
Figure 2. The electrostatic potential maps of the molecules C6F4Cl2, C6F4Br2, C6F4I2 and C16H10N4. The numbers are the local minima or maxima of the surface electrostatic potentials (in kcal/mol).
Figure 2. The electrostatic potential maps of the molecules C6F4Cl2, C6F4Br2, C6F4I2 and C16H10N4. The numbers are the local minima or maxima of the surface electrostatic potentials (in kcal/mol).
Crystals 12 00937 g002
Crystals 12 00937 g003 550
Figure 3. The 2 × 2 × 2 unit cell of the cocrystal viewed along the a axis.
Figure 3. The 2 × 2 × 2 unit cell of the cocrystal viewed along the a axis.
Crystals 12 00937 g003
Crystals 12 00937 g004 550
Figure 4. The enantiomeric pair of double helices in the cocrystal structure. The red numbers are the interaction energies (kcal/mol) of the bifurcated iodine bonds and π···π stacking interactions.
Figure 4. The enantiomeric pair of double helices in the cocrystal structure. The red numbers are the interaction energies (kcal/mol) of the bifurcated iodine bonds and π···π stacking interactions.
Crystals 12 00937 g004
Crystals 12 00937 g005 550
Figure 5. The interaction energies (kcal/mol) of the π-stacked C16H10N4 dimers in the C16H10N4 crystal (a) and in the cocrystal between C6F4I2 and C16H10N4 (b).
Figure 5. The interaction energies (kcal/mol) of the π-stacked C16H10N4 dimers in the C16H10N4 crystal (a) and in the cocrystal between C6F4I2 and C16H10N4 (b).
Crystals 12 00937 g005
Crystals 12 00937 g006 550
Figure 6. The PBE0-D3(BJ)/def2-TZVPP interatomic distances (blue numbers in Å) and interaction energies (red numbers in kcal/mol) for the complexes in the gas phase.
Figure 6. The PBE0-D3(BJ)/def2-TZVPP interatomic distances (blue numbers in Å) and interaction energies (red numbers in kcal/mol) for the complexes in the gas phase.
Crystals 12 00937 g006
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Wang, Z. Bifurcated Halogen Bond-Driven Supramolecular Double Helices from 1,2-Dihalotetrafluorobenzene and 2,2′-Bi(1,8-naphthyridine). Crystals 2022, 12, 937. https://doi.org/10.3390/cryst12070937

AMA Style

Wang Z. Bifurcated Halogen Bond-Driven Supramolecular Double Helices from 1,2-Dihalotetrafluorobenzene and 2,2′-Bi(1,8-naphthyridine). Crystals. 2022; 12(7):937. https://doi.org/10.3390/cryst12070937

Chicago/Turabian Style

Wang, Ziyu. 2022. "Bifurcated Halogen Bond-Driven Supramolecular Double Helices from 1,2-Dihalotetrafluorobenzene and 2,2′-Bi(1,8-naphthyridine)" Crystals 12, no. 7: 937. https://doi.org/10.3390/cryst12070937

APA Style

Wang, Z. (2022). Bifurcated Halogen Bond-Driven Supramolecular Double Helices from 1,2-Dihalotetrafluorobenzene and 2,2′-Bi(1,8-naphthyridine). Crystals, 12(7), 937. https://doi.org/10.3390/cryst12070937

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop