Parametrical Study on the Capillary Flowing Characteristics of the Parallel Microchannel Array
Abstract
:1. Introduction
2. Experimental Description and Numerical Method
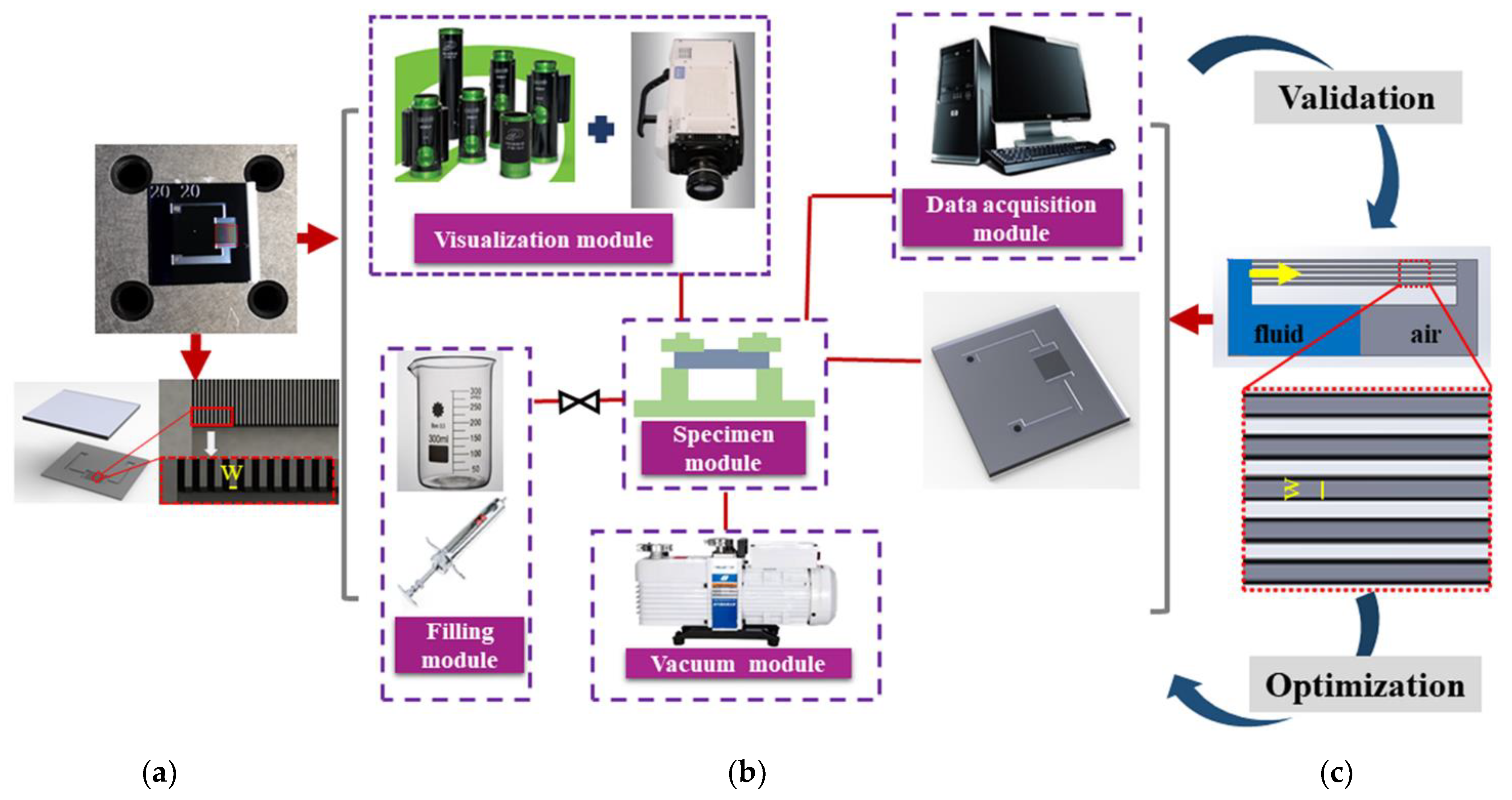
2.1. Experimental Description
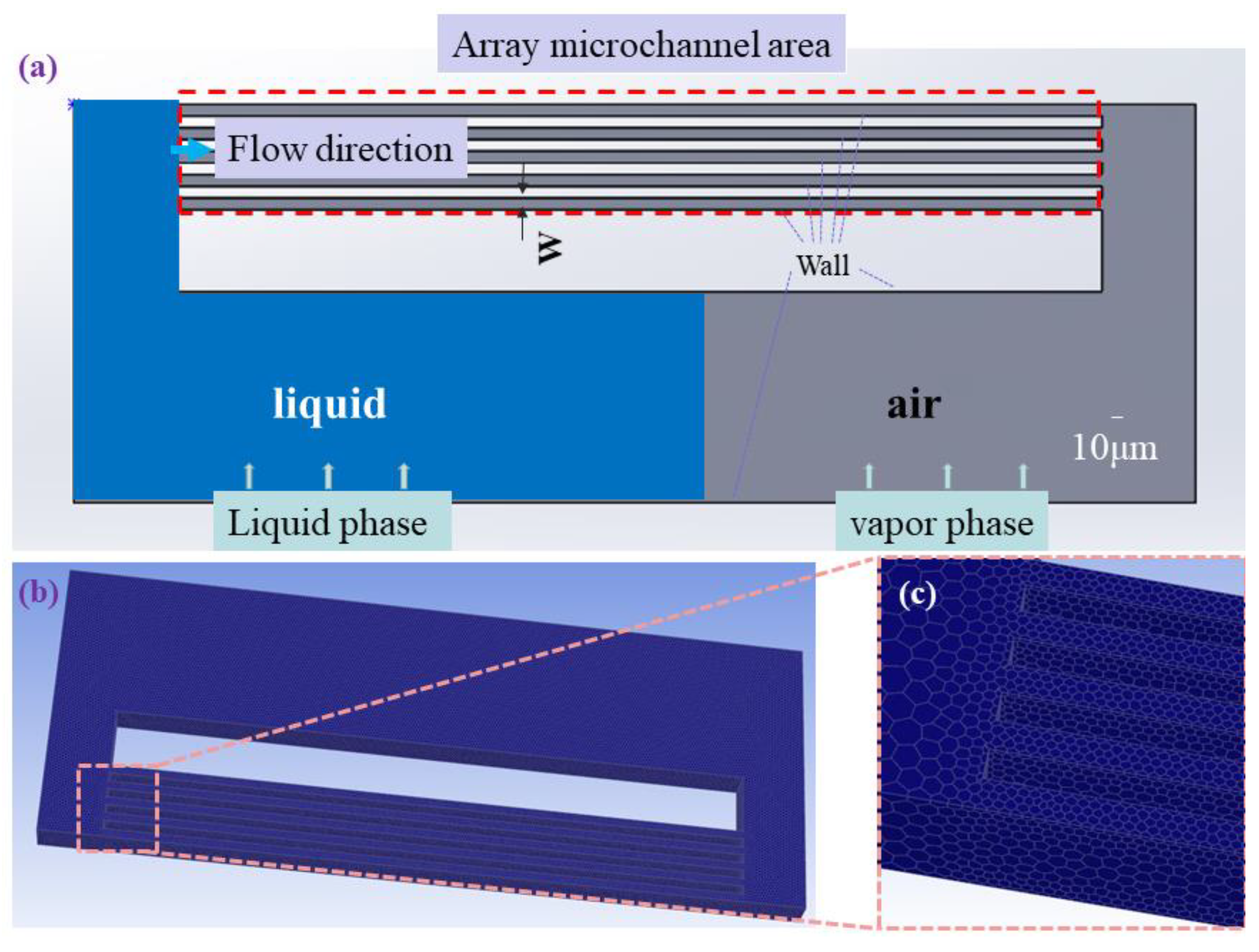
2.1.1. Model and Fabrication of Microchannels
2.1.2. Experimental Device
2.2. Numerical Method
3. Results and Discussion
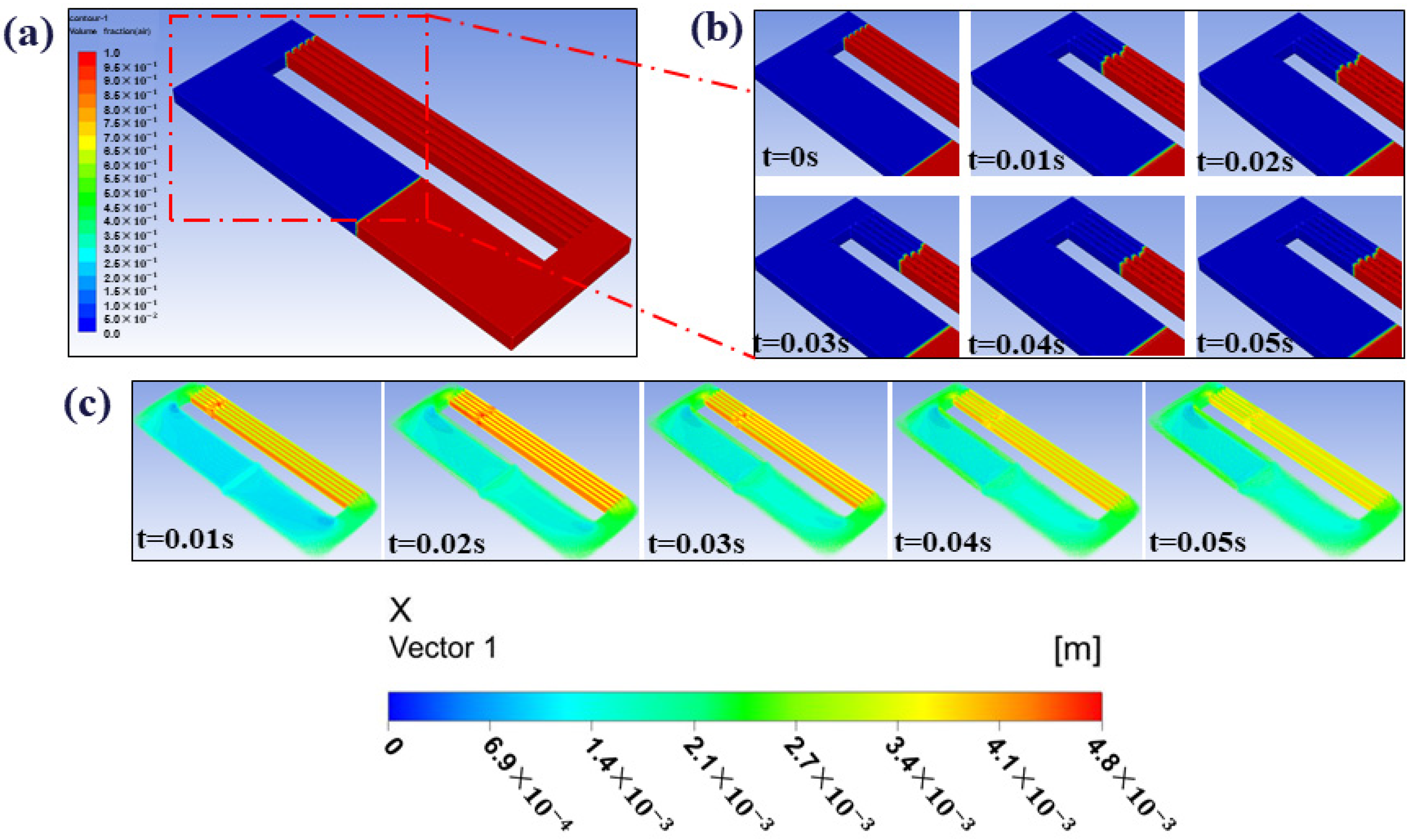
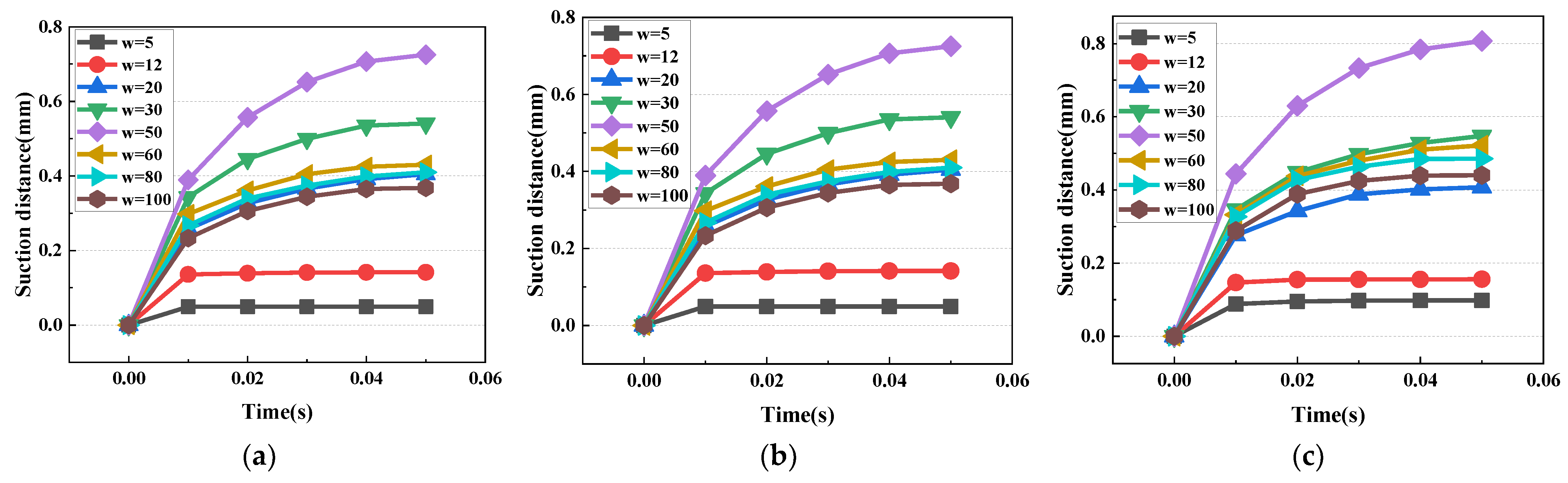
3.1. Experimental Capillary Suction Results
3.2. Simulation and Model Validation
3.3. Optimization of Microchannel Structure
4. Conclusions
- A visual research experimental platform was built to visualize the capillary flow inside the silicon-based microchannels of three sizes. The general law of the flow process changing with time was found, and with the change of the microchannel width, the flow distance was prolonged, and the capillary performance was enhanced.
- Three microchannel models were established, and the variation law of the flow distance inside each microchannel model with time was simulated based on the CFD-FVM technique. The maximum deviation between the experimental and numerical suction distance is 38.3% and the average value is 24.3%, while the deviation can be attributed to the inertial force and surface roughness of the microchannels.
- To find the microchannel AR for optimal suction performance, a parametric analysis of the geometrical characteristics of the microchannels was conducted. It was found that an AR between 3 and 4 had the best pumping performance in the investigated microchannel depth range (depth between 150 μm and 200 μm), enabling a suction distance of 0.8 mm.
- Based on the conclusions of this manuscript, the effect of heat transfer and the phase transition process on the capillary mechanism is required to be further explored.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chakraborty, S.; Kapoorm, H. Towards Controlling Chip Temperature by Dynamic Cache Reconfiguration in Multiprocessors. In Proceedings of the 30th International Conference on VLSI Design and 16th International Conference on Embedded Systems (VLSID), Hyderabad, India, 7–11 January 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 75–80. [Google Scholar]
- Ghasemi, S.; Ranjbar, A.; Hosseini, M. Experimental evaluation of cooling performance of circular heat sinks for heat dissipation from electronic chips using nanofluid. Mech. Res. Commun. 2017, 84, 85–89. [Google Scholar] [CrossRef]
- Zhao, J.; Du, M.; Zhang, Z.; Ling, X. Thermal management strategy for electronic chips based on combination of a flat-plate heat pipe and spray cooling. Int. J. Heat Mass Transf. 2021, 181, 121894. [Google Scholar] [CrossRef]
- Zheng, R.; Wu, Y.; Li, Y.; Wang, G.; Ding, G.; Sun, Y. Development of a hierarchical microchannel heat sink with flow field reconstruction and low thermal resistance for high heat flux dissipation. Int. J. Heat Mass Transf. 2022, 182, 121925. [Google Scholar] [CrossRef]
- Qu, J.; Wu, H.Y. Flow visualization of silicon-based micro pulsating heat pipes. Sci. China Technol. Sci. 2010, 53, 984–990. [Google Scholar] [CrossRef]
- Dixit, P.; Lin, N.; Miao, J.; Wong, W.K.; Choon, T.K. Silicon nanopillars based 3D stacked microchannel heat sinks concept for enhanced heat dissipation applications in MEMS packaging. Sens. Actuators A Phys. 2008, 141, 685–694. [Google Scholar] [CrossRef]
- Kuddusi, L. First and second law analysis of fully developed gaseous slip flow in trapezoidal silicon microchannels considering viscous dissipation effect. Int. J. Heat Mass Transf. 2011, 54, 52–64. [Google Scholar] [CrossRef]
- Qu, W.; Mala, G.M.; Li, D. Pressure-driven water flows in trapezoidal silicon microchannels. Int. J. Heat Mass Transf. 2000, 43, 353–364. [Google Scholar] [CrossRef]
- Fb, M.; Chen, G.M.; Tso, C.P. Viscous dissipation effect on CuO-Water nanofluid-cooled microchannel heat sinks. Case Stud. Therm. Eng. 2021, 26, 101159. [Google Scholar] [CrossRef]
- Zhao, Q.; Qiu, J.; Zhou, J.; Lu, M.; Li, Q.; Chen, X. Visualization study of flow boiling characteristics in open microchannels with different wettability. Int. J. Heat Mass Transf. 2021, 180, 121808. [Google Scholar] [CrossRef]
- Soleimani, A.; Sattari, A.; Hanafizadeh, P. Thermal analysis of a microchannel heat sink cooled by two-phase flow boiling of Al2O3 HFE-7100 nanofluid. Therm. Sci. Eng. Prog. 2020, 20, 100693. [Google Scholar] [CrossRef]
- Chen, H.; Tong, R.; Yang, G.; Zhou, J.; Yi, Z.; Zhang, L.; Lei, J. Ultrafast water harvesting and transport in hierarchical microchannels. Nat. Mater. 2021, 17, 935–942. [Google Scholar] [CrossRef] [PubMed]
- Estelle, P.; Cabaleiro, D.; Zyla, G.; Lugo, L.; Murshed, S. Current trends in surface tension and wetting behavior of nanofluids. Renew. Sustain. Energy Rev. 2018, 94, 931–944. [Google Scholar] [CrossRef]
- Khezerloo, M.; Djenidi, L.; Tardu, S. Combined effect of roughness and suction on heat transfer in a laminar channel flow. Int. Commun. Heat Mass Transf. 2021, 126, 105377. [Google Scholar] [CrossRef]
- Cheng, X.; Wu, H. Improved flow boiling performance in high-aspect-ratio interconnected microchannels. Int. J. Heat Mass Transf. 2021, 165, 120627. [Google Scholar] [CrossRef]
- Zeng, J.; Zhang, S.; Chen, G.; Lin, L.; Sun, Y.; Chuai, L.; Yuan, W. Experimental investigation on thermal performance of aluminum vapor chamber using micro-grooved wick with reentrant cavity array. Appl. Therm. Eng. 2017, 130, 185–194. [Google Scholar] [CrossRef]
- Hung, T.C.; Yan, W.M.; Li, W.P. Analysis of heat transfer characteristics of double-layered microchannel heat sink—ScienceDirect. Int. J. Heat Mass Transf. 2012, 55, 3090–3099. [Google Scholar] [CrossRef]
- Fu, B.R.; Lee, C.Y.; Pan, C. The effect of aspect ratio on flow boiling heat transfer of HFE-7100 in a microchannel heat sink. Int. J. Heat Mass Transf. 2013, 58, 53–61. [Google Scholar] [CrossRef]
- Pan, Y.H.; Zhao, R.; Fan, X.H.; Nian, Y.L.; Cheng, W.L. Study on the effect of varying channel aspect ratio on heat transfer performance of manifold microchannel heat sink. Int. J. Heat Mass Transf. 2020, 163, 120461. [Google Scholar] [CrossRef]
- Al-Zaidi, A.H.; Mahmoud, M.M.; Karayiannis, T.G. Effect of aspect ratio on flow boiling characteristics in microchannels. Int. J. Heat Mass Transf. 2021, 164, 120587. [Google Scholar] [CrossRef]
- Cheng, X.; Wu, H. Enhanced flow boiling performance in high-aspect-ratio groove-wall microchannels. Int. J. Heat Mass Transf. 2021, 164, 120468. [Google Scholar] [CrossRef]
- Yan, Z.; Liu, J.; Zhu, K. Research of Fluid Flow Characteristics for Surface Morphology of Solid. J. Phys. Conf. Ser. 2021, 1846, 012032. [Google Scholar] [CrossRef]
- Di, Y.; Qiu, J.; Wang, G.; Wang, H.; Zheng, B. Exploring Contact Angle Hysteresis Behavior of Droplets on the Surface Microstructure. Langmuir 2021, 37, 7078–7086. [Google Scholar] [CrossRef] [PubMed]
- Ronshin, F.; Chinnov, E. Experimental characterization of two-phase flow patterns in a slit microchannel. Exp. Therm. Fluid Sci. 2019, 103, 262–273. [Google Scholar] [CrossRef]
- Jong, W.R.; Kuo, T.H.; Ho, S.W.; Chiu, H.H.; Peng, S.H. Flows in rectangular microchannels driven by capillary force and gravity. Int. Commun. Heat Mass Transf. 2007, 34, 186–196. [Google Scholar] [CrossRef]
- Xue, Y.; Guo, C.; Gu, X.; Xu, Y.; Xue, L.; Lin, H. Study on Flow Characteristics of Working Medium in Microchannel Simulated by Porous Media Model. Micromachines 2020, 12, 18. [Google Scholar] [CrossRef]
- Cheng, Z.D.; He, Y.L.; Cui, F.Q. Numerical investigations on coupled heat transfer and synthetical performance of a pressurized volumetric receiver with MCRT–FVM method. Appl. Therm. Eng. 2013, 50, 1044–1054. [Google Scholar] [CrossRef]
- Lee, P.S.; Garimella, S.V. Saturated flow boiling heat transfer and pressure drop in silicon microchannel arrays. Int. J. Heat Mass Transf. 2008, 51, 789–806. [Google Scholar] [CrossRef] [Green Version]
- Jiang, T.S.; Soo-Gun, O.H.; Slattery, J.C. Correlation for dynamic contact angle. J. Colloid Interface Sci. 1979, 69, 74–77. [Google Scholar] [CrossRef]
- Gai, D.; Liu, Z.; Liu, W.; Yang, J. Characteristics of temperature oscillation in miniature loop heat pipe with flat evaporator. J. Chem. Ind. Eng. Soc. China 2009, 60, 1390–1397. Available online: http://en.cnki.com.cn/Article_en/CJFDTOTAL-HGSZ200906010.htm. (accessed on 20 May 2022).
- Lucas, R. Ueber das Zeitgesetz des kapillaren Aufstiegs von Flüssigkeiten. Kolloid-Z. 1918, 23, 15–22. [Google Scholar] [CrossRef]
- Washburn, E.W. The dynamics of capillary flow. Phys. Rev. 1921, 17, 273–283. [Google Scholar] [CrossRef]



| Grid Cells (Million) | Maximum Suction Distance |
|---|---|
| 0.5 | 1.152 |
| 1.2 | 0.958 |
| 2.1 | 0.817 |
| 2.9 | 0.802 |
| 3.7 | 0.790 |
| Sample | 12 μm | 20 μm | 30 μm |
|---|---|---|---|
| 1 | 0.545 | 0.452 | 0.352 |
| 2 | 0.532 | 0.457 | 0.340 |
| 3 | 0.537 | 0.451 | 0.357 |
| Average | 0.538 | 0.453 | 0.350 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, L.; Guo, C.; Zhang, Y.; Xu, Y.; Li, B. Parametrical Study on the Capillary Flowing Characteristics of the Parallel Microchannel Array. Crystals 2022, 12, 950. https://doi.org/10.3390/cryst12070950
Xue L, Guo C, Zhang Y, Xu Y, Li B. Parametrical Study on the Capillary Flowing Characteristics of the Parallel Microchannel Array. Crystals. 2022; 12(7):950. https://doi.org/10.3390/cryst12070950
Chicago/Turabian StyleXue, Lihong, Chunsheng Guo, Yuankun Zhang, Yanfeng Xu, and Baorui Li. 2022. "Parametrical Study on the Capillary Flowing Characteristics of the Parallel Microchannel Array" Crystals 12, no. 7: 950. https://doi.org/10.3390/cryst12070950
APA StyleXue, L., Guo, C., Zhang, Y., Xu, Y., & Li, B. (2022). Parametrical Study on the Capillary Flowing Characteristics of the Parallel Microchannel Array. Crystals, 12(7), 950. https://doi.org/10.3390/cryst12070950







