Effect of Cooling Rate on the Crystal Quality and Crystallization Rate of SiC during Rapid Solidification Based on the Solid–Liquid Model
Abstract
:1. Introduction
2. Simulation Conditions and Methods
3. Results and Discussion
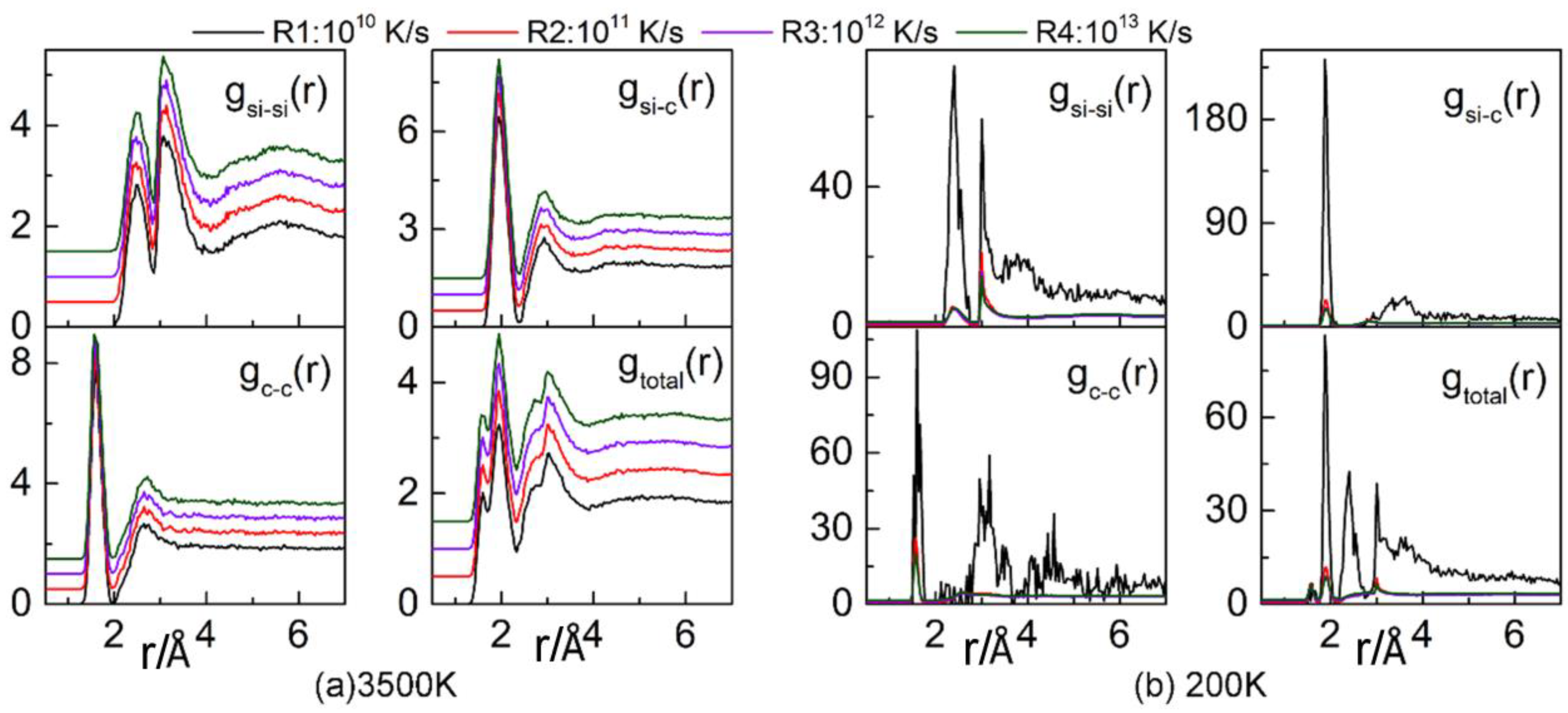
3.1. Radial Distribution Function
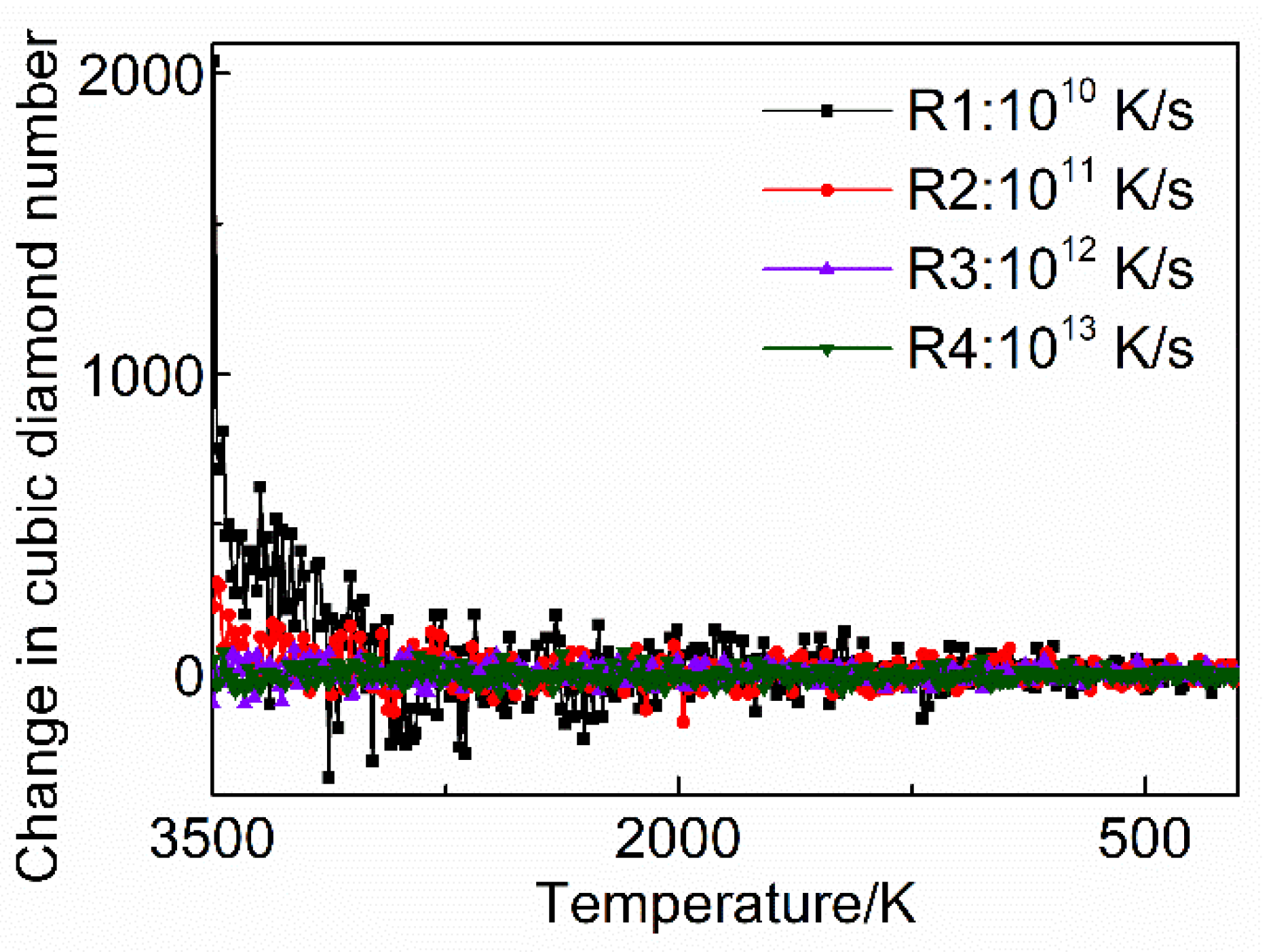
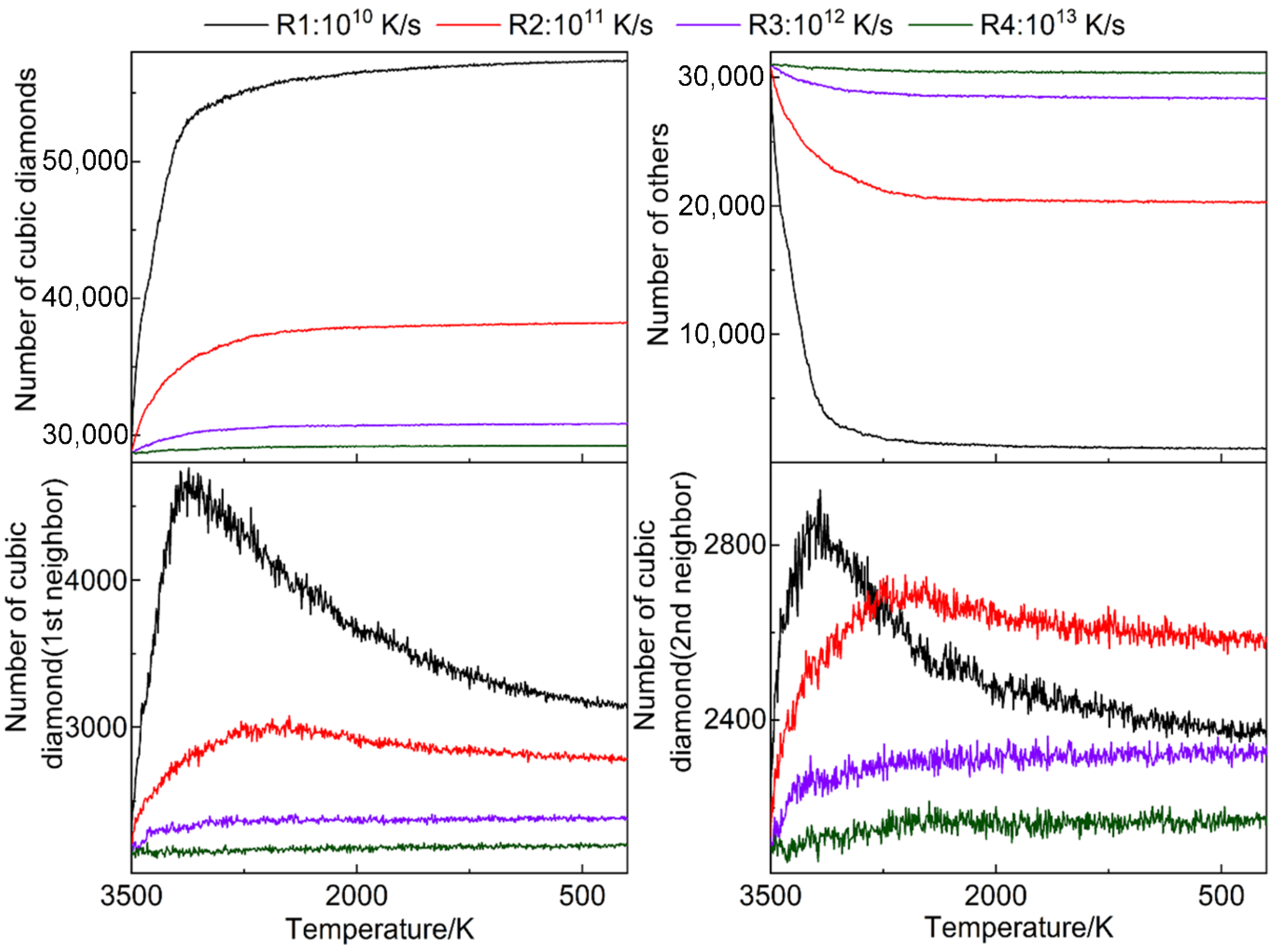
3.2. Crystallization Rate
3.3. Bond Angle Analysis
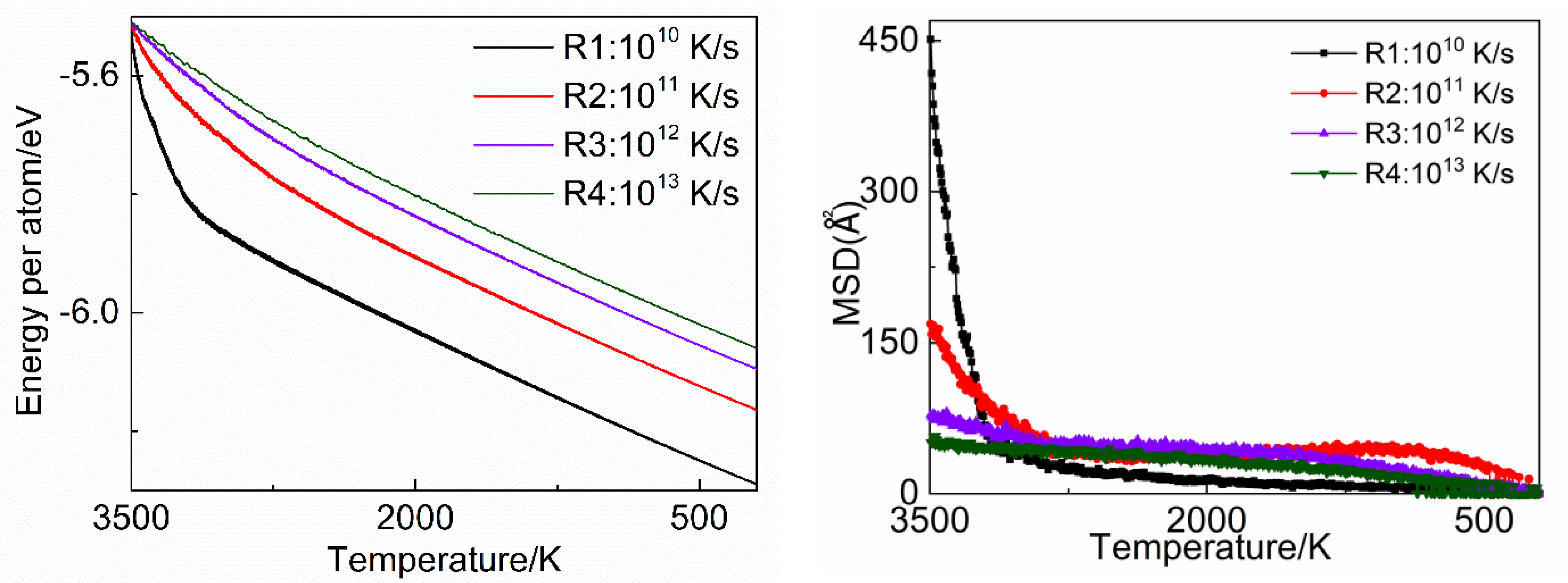
3.4. Energy and Mean Square Displacement (MSD) Analysis
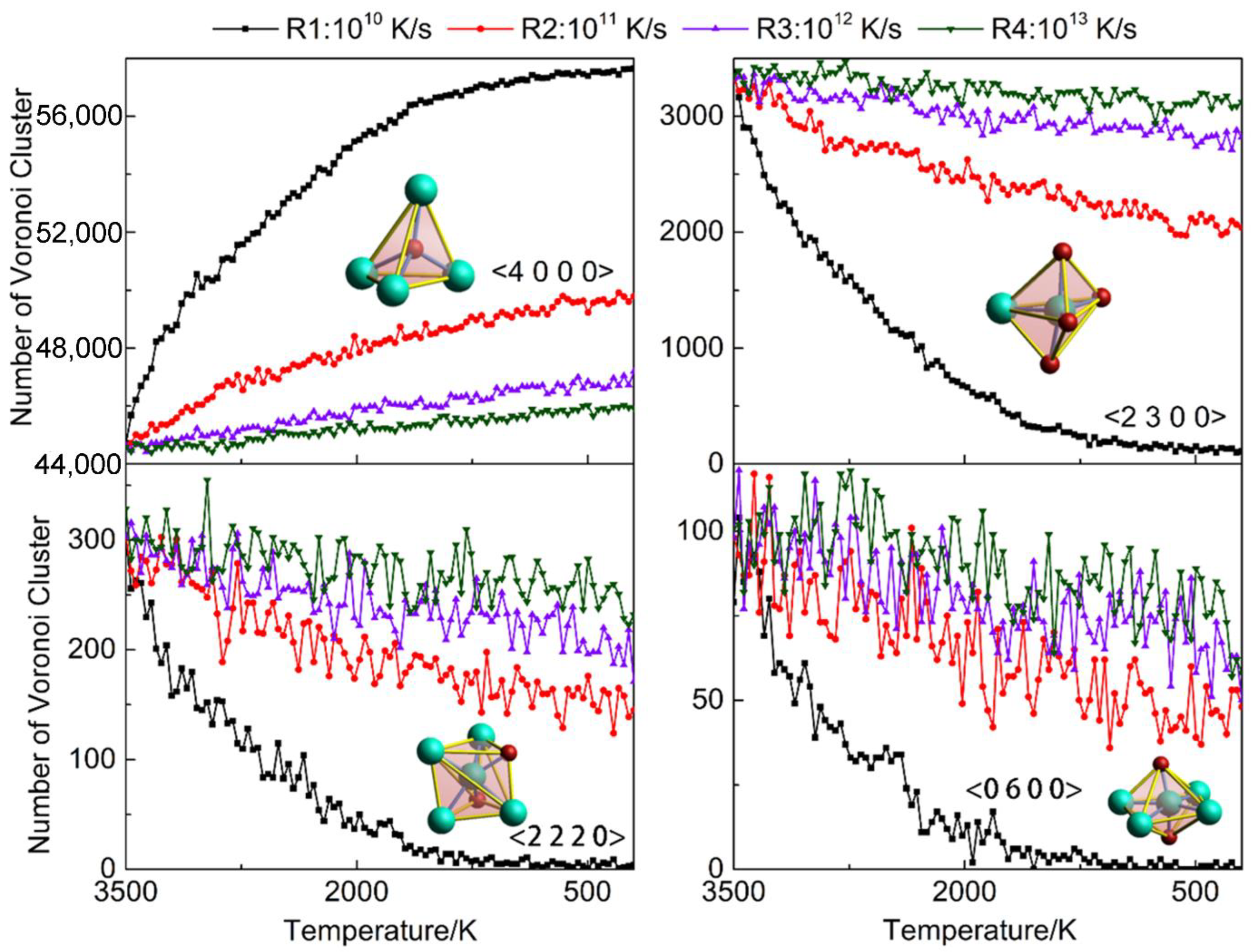
3.5. Voronoi Analysis
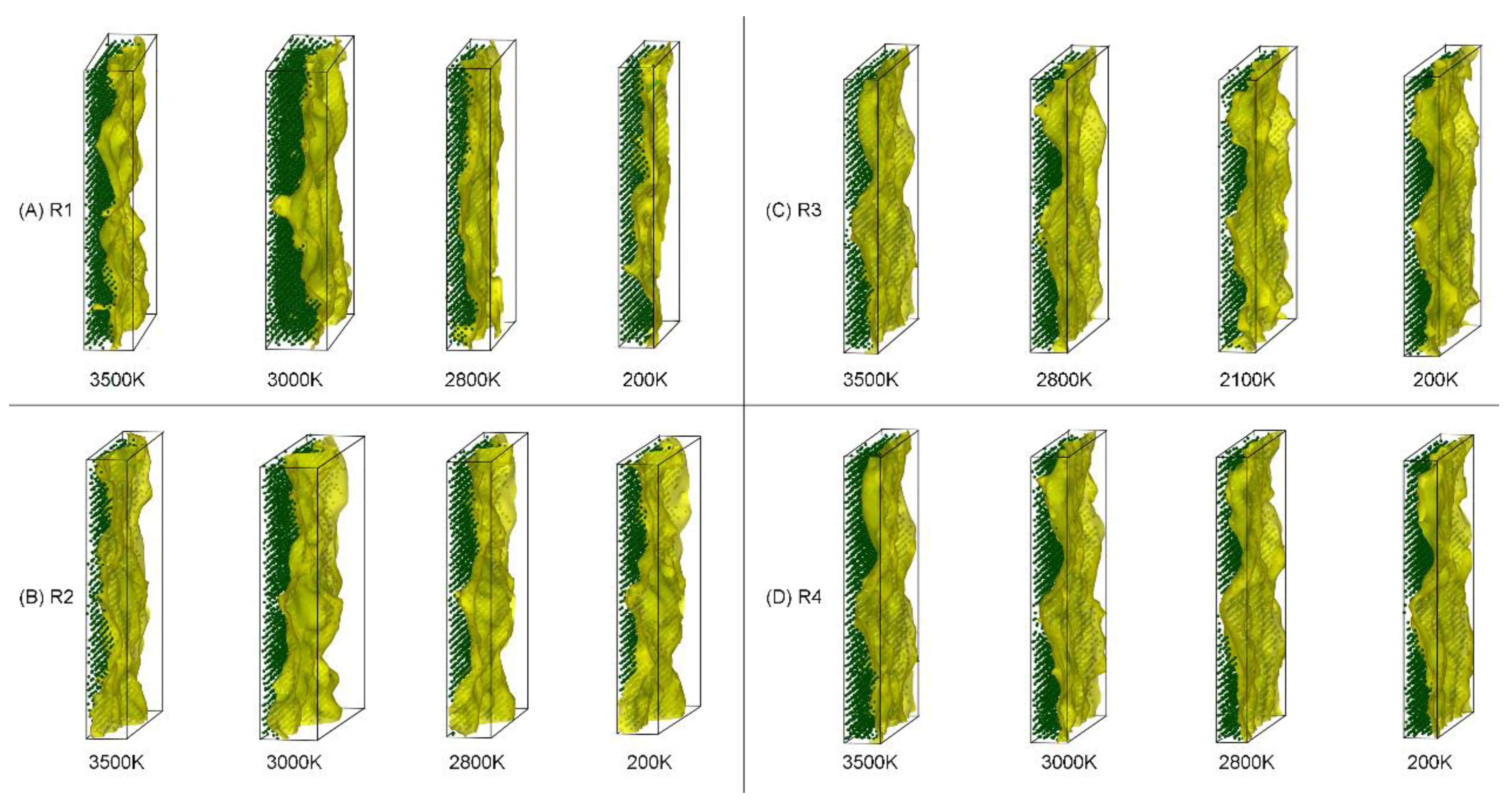
3.6. Visualization
3.7. Defect Statistics
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.T.; Ekinci, K.L.; Huang, X.M.H.; Schiavone, L.M.; Roukes, M.L. Monocrystalline silicon carbide nanoelectromechanical systems. App. Phy. Lett. 2001, 78, 162. [Google Scholar] [CrossRef] [Green Version]
- Shur, M.; Rumyantsev, S.; Levinshtein, M. SiC Materials and Devices; World Scientific: Singapore, 2006. [Google Scholar]
- Ikeda, M.; Matsunami, H.; Tanaka, T. Site effect on the impurity levels in 4 H, 6 H, and 1 5 R SiC. Phys. Rev. B. 1980, 22, 2842. [Google Scholar] [CrossRef]
- Lin, L.; Yao, L.; Yu, W.; Zhu, L.; Huang, J.; Zhang, Z. Electronic structures and magnetic properties of (Cr, Fe) co-doped 3C-SiC. Mater. Res. Exp. 2019, 10, 6. [Google Scholar] [CrossRef]
- Bossuyt, S. Microstructure and crystallization behavior in bulk glass forming alloys. Diss. Abstr. Int. 2001, 62, 2449. [Google Scholar]
- Conrad, H. Influence of an electric or magnetic field on the liquid-solid transformation in materials and on the microstructure of the solid. Mater. Sci. Eng. A 2000, 287, 205. [Google Scholar] [CrossRef]
- Lee, B.S.; Burr, G.W.; Shelby, R.M.; Raoux, S.; Rettner, C.T.; Bogle, S.N.; Darmawikarta, K.; Bishop, S.G.; Abelson, J.R. Observation of the Role of Subcritical Nuclei in Crystallization of a Glassy Solid. Science 2009, 326, 980. [Google Scholar] [CrossRef]
- Lorenzzi, J.; Souliere, V.; Carole, D.; Jegenyes, N.; Kim-Hak, O.; Cauwet, F.; Ferro, G. Effect of nitrogen impurity on the stabilization of 3C–SiC polytype during heteroepitaxial growth by vapor–liquid–solid mechanism on 6H–SiC substrates. Diam. Relat. Mater. 2011, 20, 808. [Google Scholar] [CrossRef]
- Alizadeh, M.; Paydar, M.H.; Terada, D.; Tsuji, N. Effect of SiC particles on the microstructure evolution and mechanical properties of aluminum during ARB process. Mater. Sci. Eng. A 2012, 540, 13. [Google Scholar] [CrossRef]
- Zhou, L.L.; Liu, R.S.; Hou, Z.Y.; Tian, Z.A.; Lin, Y.; Liu, Q.H. Simulation study of effects of cooling rate on evolution of micro-cluster structures during solidification of liquid Pb. Acta Phys. Sin. 2008, 57, 3653. [Google Scholar] [CrossRef]
- Ren, L.; Gao, T.H.; Ma, R.; Xie, Q.; Tian, Z.A.; Chen, Q.; Liang, C.H.Y.; Hu, X.C.H. The connection of icosahedral and defective icosahedral clusters in medium-range order structures of CuZrAl alloy. J. Non-Cryst. Solids 2019, 521, 119475. [Google Scholar] [CrossRef]
- Luo, J.; Gao, T.H.; Ren, L.; Xie, Q.; Tian, Z.A.; Chen, Q.; Liang, Y.C.H. Segregation phenomena of As in GaAs at different cooling rates during solidification. Mat. Sci. Semicon. Proc. 2019, 104, 104680. [Google Scholar] [CrossRef]
- Perova, T.S.; Wasyluk, J.; Kukushkin, S.A. Micro-Raman Mapping of 3C-SiC Thin Films Grown by Solid–Gas Phase Epitaxy on Si (111). Nanoscale Res. Lett. 2010, 5, 1507. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Dong, S.; Li, X. Synthesis, properties, and multifarious applications of SiC nanoparticles: A review. Ceram Inter. 2022, 7, 8882–8913. [Google Scholar] [CrossRef]
- Yamada, T.; Araki, F.; Ishihara, J. Fabrication of silicon carbide nanoparticles using picosecond pulsed laser ablation in acetone with characterizations from TEM and XRD. AIP Adv. 2019, 10, 105011. [Google Scholar] [CrossRef] [Green Version]
- Castelletto, S.; Almutairi, A.F.M.; Thalassinos, G. Fluorescent color centers in laser ablated 4H-SiC nanoparticles. Opt Lett. 2017, 7, 1297–1300. [Google Scholar] [CrossRef]
- Tersoff, J. Chemical order in amorphous silicon carbide. Phys. Rev. B 1994, 49, 16349. [Google Scholar] [CrossRef]
- Kelires, P.C. Short-range order and energetics of disordered silicon-carbon alloys. Phys. Rev. B Condens. Matt. 1992, 46, 10048. [Google Scholar] [CrossRef]
- Zhou, N.G.; Hong, T.; Zhou, L. A comparative study between MEAM and Tersoff potentials on the characteristics of melting and solidification of carborundum. Acta Phys. Sin. 2012, 61, 028101. [Google Scholar] [CrossRef]
- Bao, J.; Norimatsu, W.; Iwata, H.; Matsuda, K.; Ito, T.; Kusunoki, M. Synthesis of Freestanding Graphene on SiC by a Rapid-Cooling Technique. Phys. Rev. Lett. 2016, 117, 205501. [Google Scholar] [CrossRef] [Green Version]
- Tersoff, J. Modeling solid-state chemistry: Interatomic potentials for multicomponent systems. Phys. Rev. B Condens. Matter. 1989, 39, 5566. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1. [Google Scholar] [CrossRef] [Green Version]
- Yoo, S.; Zeng, X.C.; Morris, J.R. The melting lines of model silicon calculated from coexisting solid–liquid phases. J. Chem. Phys. 2004, 120, 1654. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, W. Simulation and Calculation of Microstructures and Properties of Semiconductor Material (SiC); Guizhou University: Guiyang, China, 2014; p. 48. [Google Scholar]
- Ortega-Liébana, M.C.; Hueso, J.L.; Arenal, R.; Lahoz, R.; Fuente, G.F.; Santamaria, J. Continuous-Mode Laser Ablation at the Solid–Liquid Interface of Pelletized Low-Cost Materials for the Production of Luminescent Silicon Carbide Nanocrystals. J. Phys. Chem. C 2015, 119, 2158. [Google Scholar] [CrossRef] [Green Version]
- Galli, G.; Martin, R.M.; Car, R.; Parrinello, M. Parrinello 1990 Ab initio calculation of properties of carbon in the amorphous andliquid states. Phys. Rev. B 1990, 42, 7470. [Google Scholar] [CrossRef] [PubMed]
- Gao, T.H.; Yan, W.J.; Guo, X.T.; Qing, Y.X.; Xie, Q. Strutural properties in liquid Si during rapid cooling processes. Phys. B Condens. Matter. 2013, 10, 1016. [Google Scholar]
- Chun, S.Y.; Bang, I.C.; Choo, Y.J.; Song, C.H. Heat transfer characteristics of Si and SiC nanofluids during a rapid quenching and nanoparticles deposition effects. Inter. J. Heat. Mass. Trans. 2011, 54, 1217. [Google Scholar] [CrossRef]
- Finney, J.L. Random Packings and the Structure of Simple Liquids. I. The Geometry of Random Close Packing. Series A Mat. Phys. Sci. 1970, 319, 479. [Google Scholar]
- Gao, T.; Hu, X.; Li, Y.; Tian, Z.; Xie, Q.; Chen, Q.; Liang, Y.; Luo, X.; Ren, L.; Luo, J. Microstructural properties and evolution of nanoclusters in liquid Si during rapid cooling process. Jetp Lett. 2017, 106, 667. [Google Scholar] [CrossRef]
- Ziebert, C.; Ye, J.; Ulrich, S.; Prskalo, A.P.; Schmauder, S. Sputter deposition of nanocrystalline beta-SiC films and molecular dynamics simulations of the sputter process. J. Nano sci. Nanotechnol. 2010, 10, 1120. [Google Scholar] [CrossRef] [Green Version]
- Brancato, G.; Barone, V. Molecular dynamics simulations in a NpT ensemble using non-periodic boundary conditions. Chem. Phys. Lett. 2009, 483, 177. [Google Scholar] [CrossRef]
- Levine, B.G.; Stone, J.E.; Kohlmeyer, A. Fast analysis of molecular dynamics trajectories with graphics processing units—Radial distribution function histogramming. J. Comput. Phys. 2011, 230, 3556. [Google Scholar] [CrossRef] [Green Version]
- Stukowski, A.; Bulatov, V.V.; Arsenlis, A. Automated identification and indexing of dislocations in crystal interfaces. Model. Simul. Mater. Sc. 2012, 20, 085007. [Google Scholar] [CrossRef]
- Ueno, K.; Shibuta, Y. Composition dependence of solid-liquid interfacial energy of Fe-Cr binary alloy from molecular dynamics simulations. Comp. Mater. Sci. 2019, 167, 1. [Google Scholar] [CrossRef]
- Qi, C.; Xu, B.; Kong, L.T.; Li, J.F. Solid-liquid interfacial free energy and its anisotropy in the Cu-Ni binary system investigated by molecular dynamics simulations. J. Alloys Compd. 2017, 708, 1073. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Gao, Y.; Meng, Z.; Gao, T. Effect of Cooling Rate on the Crystal Quality and Crystallization Rate of SiC during Rapid Solidification Based on the Solid–Liquid Model. Crystals 2022, 12, 1019. https://doi.org/10.3390/cryst12081019
Guo X, Gao Y, Meng Z, Gao T. Effect of Cooling Rate on the Crystal Quality and Crystallization Rate of SiC during Rapid Solidification Based on the Solid–Liquid Model. Crystals. 2022; 12(8):1019. https://doi.org/10.3390/cryst12081019
Chicago/Turabian StyleGuo, Xiaotian, Yue Gao, Zihao Meng, and Tinghong Gao. 2022. "Effect of Cooling Rate on the Crystal Quality and Crystallization Rate of SiC during Rapid Solidification Based on the Solid–Liquid Model" Crystals 12, no. 8: 1019. https://doi.org/10.3390/cryst12081019
APA StyleGuo, X., Gao, Y., Meng, Z., & Gao, T. (2022). Effect of Cooling Rate on the Crystal Quality and Crystallization Rate of SiC during Rapid Solidification Based on the Solid–Liquid Model. Crystals, 12(8), 1019. https://doi.org/10.3390/cryst12081019





