Abstract
The electric-field gradient (EFG) at nuclei in solids is a sensitive probe of the charge distribution. Experimental data, which previously only existed in insulators, have been available for metals with the development of nuclear measuring techniques since about 1970. An early, systematic investigation of the temperature dependence of the EFG in metals, originally based on results for Cd, but then also extended to various other systems, has suggested a proportionality to T3/2. However, later measurements in the structurally and electronically similar material Zn, which demonstrated much more complex behavior, were largely ignored at the time. The present experimental effort has confirmed the reliability of this unexpected behavior, which was previously unexplained.
1. Introduction
The study of the interaction of nuclear quadrupole moments (Q) with the charges of the surrounding can give detailed insight into the electronic distribution that creates bonding in solids. Since the discovery of nuclear quadrupole resonance (NQR) in the middle of the last century [1], as well as the qualitative understanding of the temperature effects involved [2], an abundant number of experimental and theoretical studies of molecular and ionic solids have been performed. Electric field gradients (EFG), the second derivative of the charge density Vzz at the nuclear site, which determine the quadrupole interaction constant νQ = eQVzz/h, were thus understood quite early for such materials in a semiquantitative manner.
For metallic solids, on the other hand, the applications of a radiofrequency technique like NQR are severely limited, and therefore, only very few systems could be investigated earlier. With the introduction of perturbed angular correlation (PAC) [3] and perturbed angular distribution (PAD) [4] spectroscopy in the early 1970s, these limitations disappeared. In addition, such nuclear methods also allow the study of impurities, even at extreme dilutions. Thus, since about 50 years ago, an abundant amount of experimental information on nuclear quadrupole interactions in metals has quickly evolved. It has become evident, however, that the electronic structure theory techniques available at the time were not appropriate for a quantitative calculation of the EFG—even in simple sp-metals. Thus, for the interpretation of the experimental results, including those regarding EFG temperature dependence, recourse to semiquantitative approximations had to be accepted.
A large-scale, systematic study of the EFG (here for simplicity called q) temperature dependence [5], however, generated a uniform description of a suggested “law” as {q(T)-q(0)}/q(0), very closely proportional to T3/2. This dependence apparently had so much appeal that it was later used in practically all cases, thus implying that lattice vibrations were the only effective sources. Other early attempts to account for EFG temperature dependence have tried to incorporate the structural and vibration changes [6,7] in their approaches. These calculations, using screened pseudopotentials, however, could at best only qualitatively account for the experimental data as quantitative electronic structure calculation for EFG was not possible at the time.
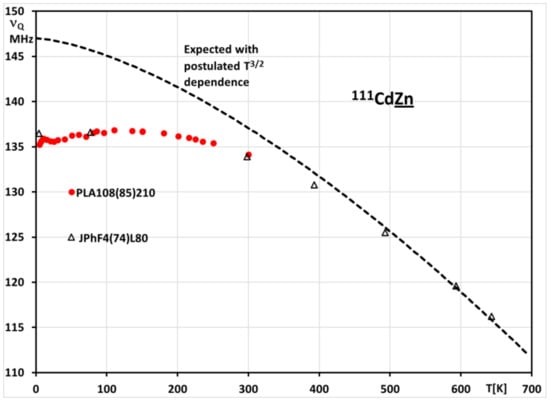
The situation changed dramatically with the availability of reliable density functional calculations for metals [8,9]. Such techniques were actually used in two recent theoretical attempts to account for EFG in Cd and Zn as function of temperature [10,11]. These calculations, however, largely concentrated on the effect of lattice vibrations, which were apparently stimulated by the T3/2 “law”. Unfortunately, these works, as well as all previous discussions, ignored the fact that experimental data for EFG temperature dependence in Zn, which contradicted the proposed universal law, have been available for quite some time via Mössbauer spectroscopy [12], nuclear magnetic resonance [13] and, in particular, perturbed angular correlation measurements [14,15]. Figure 1 demonstrates the dramatic failure of the T3/2 law in accounting for the PAC results for 111Cd (5/2+) in Zn. The present investigation was initiated with the purpose of testing the correctness of these early PAC measurements and to add new data points. That seems especially important as such data have been the basis for a recent quantitative explanation of the EFG temperature dependence of Zn and Cd [16].
2. Materials and Methods
In the present measurements, two different samples were employed. For the initial experiment series up to 540 K, a commercially obtained single crystal of Zn, with a thickness of 0.5 mm and dimensions of 4 by 5 mm (MaTecK GmbH, Jülich, Germany), was surface-cleaned, first by polishing and then by sputtering with an Ar beam. For the later measurements (closer to the Zn melting point of 419.5 °C (592.7 K)), a 0.1 mm thick, rolled foil (Goodfellow Cambridge Limited, Huntingdon, England) was scratched using a scalpel immediately prior to implantation so as to create a clean surface.
For the initial PAC experiments, the necessary 111In activity was commercially obtained and implanted at room temperature with an energy of 80 keV and an incidence angle of 10° (from the surface normal) at the Bonn Radioisotope Separator and Implanter (BONIS) facility in Bonn, Germany [17,18]. Monte Carlo simulations, using SRIM (Stopping and range of ions in matter) software with TRIM (Transport of ions in matter) [19], provided an average implantation depth of the order of 30 nm. The latter-used foil sample was doped with 111In at a 30 keV implantation energy produced by the high-energy proton irradiation of uranium-carbide at the ISOLDE-CERN [20] online isotope separator.
Before the measurements, an annealing in the Ar atmosphere at 473 K was performed on both samples, as the originally implanted, single crystal showed, in agreement with [14], only a distribution of EFG values, presumably due to the lattice defects created by the implantation process.
PAC measurements were carried out at the ISOLDE-CERN [21] solid-state facilities, with the initial single-crystal runs employing an analogue 4-detector system with an angle of 90° between the detectors and BaF2 scintillator crystals coupled to photomultiplier tubes [22]. The hardware selected signals using the photopeaks of the start and stop γ-rays in the cascade in 111Cd following the EC decay of 111In. Their time-differences were used to record the 12 (4 for 180° spectra and 8 for 90° spectra) possible coincidence time-spectra using the DOS-based software UNCPAC [23]. For data acquisition and storage, the Ortec Model 918 ADCAM Multichannel Buffer (MCB) was used and controlled via a dedicated dual-port memory interface on a computer. In all measurements, the surface normal of the single crystal, the crystal c-axis, was oriented in the detector plane at 45° between the detectors as well as was possible.
The measurements with the polycrystalline foil sample, concentrating in the higher temperature region, were made using the KATAME digital spectrometer [24], with an array of 6 lanthanum–bromide scintillation detectors.
For the experiments carried out below room temperature, the sample, contained in a glass tube under N2 gas, was measured in a Dewar filled with liquid nitrogen or an acetone-solid CO2 slush. Higher temperatures were obtained in an insulated glass tube heated with resistive wire under slight gas flow, controlled by a thermocouple.
For the 12, respectively 30, time-spectra recorded the normalized and background-corrected W(θ,t). The conventional ratio function given by Equation (1) was fitted to the corresponding theoretical perturbation function, appropriate to the crystal orientation, to obtain the quadrupole interaction frequencies νQ.
3. Results
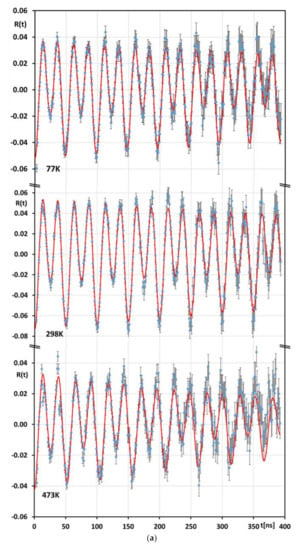
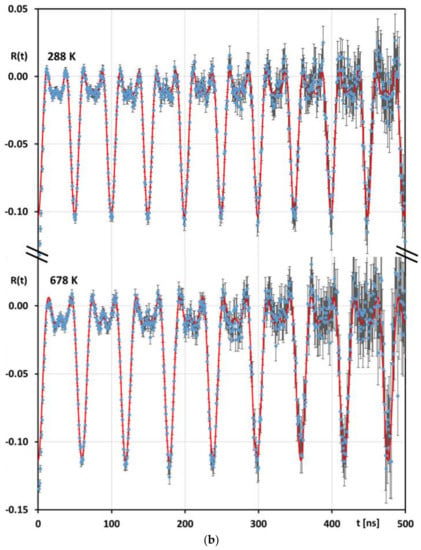
Selected PAC spectra are shown in Figure 2a,b. The results for the effective nuclear quadrupole coupling constant obtained at the various temperatures are summarized in Table 1.
Figure 2.
(a) Examples for observed PAC spectra taken with the single-crystal sample. The red, solid curves show the least-squares fits that give the quadrupole interaction parameters presented in Table 1. The clear difference between the EFGs is visualized by comparing the spectra obtained at 77 K or 298 K with the spectrum taken at 473 K, and analogous in Figure 2b. (b) Examples for observed PAC spectra taken with the polycrystalline sample. The pattern seen is characteristic of a random EFG orientation.
Table 1.
Nuclear quadrupole coupling constant νQ measured for 111Cd (5/2+) in a Zn single crystal as function of temperature. The lower four rows present data from the experiments with polycrystalline Zn.
Please note that the tubular furnace used for high-temperature measurements has an uncertainty of ±5–10 °C.
4. Discussion
Measurements with the earlier, standard PAC technique, including our single-crystal data, must be adjusted according to the uncertainty of the time-calibration. Correcting for the at-most 0.3 MHz different frequencies at 77 K of the various experiments, our results agree very well with the earlier data in the low-temperature range of [15] and also with the datapoint at room temperature reported by [14]. Our second series of measurements, using digital frequency measurement and improved temperature control, was triggered by the fact that the frequencies at 473 K and 543 K appeared to deviate from the data in [14] by more than the combined temperature and frequency uncertainty. In addition, in their pioneering study of EFG temperature dependence for Cd in Cd [25], the authors of reference [14] made a serious temperature error, later corrected in [4]. Our new, precise data, however, fully agree with their results for Cd in Zn.
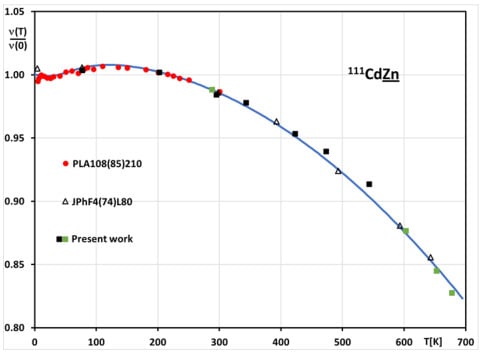
All frequencies, properly corrected, are presented in Figure 3 relative to the νQ determined as 135.32(10) MHz for T = 0. This result is considerably smaller than the frequency of 136.5(14) MHz at 4.2 K reported in [14], although it is still within the (very liberally) quoted error. It evidently agrees with the results of [15] of around 4.2 K, taking as error 0.3 MHz. A new, precise measurement at 4.2 K could, however, be extremely worthwhile as, in [15], the data around 4 K appear to show a yet-inexplicable scatter.
Figure 3.
Normalized temperature dependence of EFG for Cd in Zn, including the present data; the green squares denote the results using the polycrystalline sample. The blue curve shows the one-parameter fit described in the text. References: JPhF4(74)L80 [14], PLA108(85)210 [15].
The now well-confirmed trend is in good agreement with the recently proposed functional temperature dependence for EFG [16], making use of reanalyzed structural data for the calculation of EFG for the static lattice with the now-standard density functional technique. For determining the vibrational dependence of EFG, the proportionality with the average Debye–Waller factor as function of temperature, as obtained via a new analysis of experimental vibrational data, was employed, multiplied by one fitted parameter.
Figure 3 demonstrates reasonably well the extent to which this treatment can explain all of the now-available experimental data. Obviously, the quite minor discrepancies still existing could warrant a series of considerably more precise PAC measurements using the time precision that is now possible with fully digital electronics. This project will, of course, also require temperature control that is much more precise than the one used to date. Only with these precision data could the actual functional dependence through the vibrational motion be checked in detail. The reliability of the final accuracy obtainable in this way would, unfortunately, still be limited by the dependence on the precision of the experimental thermal displacement amplitudes presently obtainable from X-ray analysis, with Zn actually being the non-cubic metal from which the best such data are available.
5. Conclusions
The present study used the PAC spectroscopy method to probe the temperature dependence of the nuclear quadrupole coupling constant νQ in Zn crystals implanted with the nuclear probe 111In(111Cd). Our results agree well with previous data [14,15] and demonstrate the complex temperature dependence of the electric field gradient, which is extremely different from that which was previously expected due to the T3/2 law. The fact that the corresponding data for νQ in Cd ([4,5,25] and others) quite closely follow this simple tendency must thus be fortuitous.
Author Contributions
Conceptualization, H.H.; methodology, H.H., D.Z. and J.S.; formal analysis, H.H. and D.Z.; investigation, H.H., D.Z., J.S., T.T.D., I.C.J.Y., I.M., D.G., A.M.G., C.N. and R.B.; resources, J.S., C.N. and R.B.; data curation, H.H. and D.Z.; writing—original draft preparation, H.H.; writing—review and editing, H.H. and J.S.; visualization, H.H.; supervision, H.H. and J.S.; project administration, J.S.; funding acquisition, J.S. and R.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Federal Ministry of Education and Research (BMBF) through grant No. 05K16PGA and by the ISOLDE collaboration.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are available from the corresponding author upon reasonable request.
Acknowledgments
We acknowledge the financial support received from the Federal Ministry of Education and Research (BMBF) through grant No. 05K16PGA and the support from the ISOLDE collaboration.
Conflicts of Interest
The authors declare no conflict of interest.
References and Note
- Dehmelt, H.G.; Krueger, H. Quadrupol-Resonanzfrequenzen von Cl- und Br-Kernen in kristallinem Dichloraethylen und Methylbromid. Z. Phys. 1951, 129, 401–415. [Google Scholar] [CrossRef]
- Bayer, H. Zur Theorie der Spin-Gitterrelaxation in Molekülkristallen. Z. Phys. 1951, 130, 227–238. [Google Scholar] [CrossRef]
- Raghavan, P.; Raghavan, R.S. Nuclear quadrupole interaction in cadmium metal. Phys. Rev. Lett. 1971, 27, 724. [Google Scholar] [CrossRef]
- Bleck, J.; Butt, R.; Haas, H.; Ribbe, W.; Zeitz, W. In-beam measurements of the nuclear quadrupole interaction in cadmium metal. Phys. Rev. Lett. 1972, 29, 1371. [Google Scholar] [CrossRef]
- Christiansen, J.; Heubes, P.; Keitel, R.; Klinger, W.; Loeffler, W.; Sandner, W.; Witthuhn, W. Temperature dependence of the electric field gradient in noncubic metals. Z. Phys. B Cond. Matt. 1976, 24, 177–187. [Google Scholar] [CrossRef]
- Nishiyama, K.; Dimmling, F.; Kornrumpf, T.; Riegel, D. Theory of the temperature dependence of the electric field gradient in noncubic metals. Phys. Rev. Lett. 1976, 37, 357. [Google Scholar] [CrossRef]
- Nishiyama, K.; Riegel, D. Recent developments in the analysis of electric field gradients in metals. Hyperfine Interact. 1978, 4, 490–508. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Dederichs, P.H. First-principles calculation of the electric-field gradient in hcp metals. Phys. Rev. B 1988, 37, 2792. [Google Scholar] [CrossRef]
- Blaha, P.; Dufek, P.; Schwarz, K.; Haas, H. Calculation of electric hyperfine interaction parameters in solids. Hyperfine Interact. 1996, 97, 1–10. [Google Scholar] [CrossRef]
- Torumba, D.; Parlinski, K.; Rots, M.; Cottenier, S. Temperature dependence of the electric-field gradient in hcp-Cd from first principles. Phys. Rev. B 2006, 74, 144304. [Google Scholar] [CrossRef]
- Nikolaev, A.V.; Chtchelkatchev, N.M.; Salamatin, D.A.; Tsvyashchenko, A.V. Towards an ab initio theory for the temperature dependence of electric field gradients in solids: Application to hexagonal lattices of Zn and Cd. Phys. Rev. B 2020, 101, 064310. [Google Scholar] [CrossRef] [Green Version]
- Potzel, W.; Adlassnig, W.; Närger, U.; Obenhuber, T.; Riski, K.; Kalvius, G.M. Temperature dependence of hyperfine interactions and anisotropy of recoil-free fraction: A Mössbauer study of the 93.3 keV resonance of 67Zn in single crystals of zinc metal. Phys. Rev. B 1984, 30, 4980. [Google Scholar] [CrossRef]
- Bastow, T.J. 67Zn NMR in zinc metal. J. Phys. Condens. Matter. 1996, 8, 11309. [Google Scholar] [CrossRef]
- Raghavan, P.; Raghavan, R.S.; Kaufmann, E.N.; Krien, K.; Naumann, R.A. Nuclear quadrupole interaction of 111Cd in zinc (by PAC). J. Phys. F Met. Phys. 1974, 4, L80. [Google Scholar] [CrossRef]
- Hermans, L.; van Cauteren, J.; Rots, M. Anomalous low temperature behaviour of the electric field gradient at 111Cd in cadmium and zinc. Phys. Lett. A 1985, 108, 210–214. [Google Scholar] [CrossRef]
- Haas, H. Temperature Dependence of Electric-Field Gradient in Zn and Cd: Ending the T3/2 “Myth”. Manuscript to Be Submitted to Physical Review B. Available online: https://indico.cern.ch/event/1182057/ (accessed on 3 July 2022).
- Freitag, K. A facility for ion implantation in samples colder than 0.5 K. Radiat. Eff. 1979, 44, 185. [Google Scholar] [CrossRef]
- Schell, J.; Lupascu, D.C.; Carbonari, A.W.; Mansano, R.D.; Junior, I.S.R.; Dang, T.T.; Anusca, I.; Trivedi, H.; Johnston, K.; Vianden, R. Ion implantation in titanium dioxide thin films studied by perturbed angular correlations. J. Appl. Phys. 2017, 121, 145302. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Ziegler, M.D.; Biersack, J. SRIM—The Stopping and Range of Ions. Matter. Nucl. Instr. Meth. 2010, B268, 1818–1823. [Google Scholar] [CrossRef] [Green Version]
- Catherall, R.; Andreazza, W.; Breitenfeldt, M.; Dorsival, A.; Focker, G.J.; Gharsa, T.P.; Giles, T.J.; Grenard, J.-L.; Locci, F.; Martins, P.; et al. The ISOLDE facility. J. Phys. G Nucl. Part. Phys. 2017, 44, 094002. [Google Scholar] [CrossRef] [Green Version]
- Johnston, K.; Schell, J.; Correia, J.G.; Deicher, M.; Gunnlaugsson, H.P.; Fenta, A.S.; David-Bosne, E.; Costa, A.R.G.; Lupascu, D.C. The solid state physics programme at ISOLDE: Recent developments and perspectives. J. Phys. G Nucl. Part. Phys. 2017, 44, 104001. [Google Scholar] [CrossRef]
- Schell, J.; Schaaf, P.; Lupascu, D.C. Perturbed angular correlations at ISOLDE: A 40 years young technique. AIP Adv. 2017, 7, 105017. [Google Scholar] [CrossRef] [Green Version]
- Hofsaess, H.; Deicher, M. Perturbed γ-γ-Angular Correlation Program. Version 5.25 of 20-jan-2002. The UNCPAC software has been mostly developed by H. Hofsäss based on a first version called PAC written by H. Hofsäss and M. Deicher in 1988.
- Nagl, M.; Vetter, U.; Uhrmacher, M.; Hofsäss, H. A new all-digital time differential γ-γ angular correlation spectrometer. Rev. Sci. Instrum. 2010, 81, 073501. [Google Scholar] [CrossRef]
- Raghavan, R.S.; Raghavan, P. Anomalous temperature dependence of the quadrupole interaction in cadmium. Phys. Lett. A 1971, 36, 313. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).