Boundary Effect and Critical Temperature of Two-Band Superconducting FeSe Films
Abstract
1. Introduction
2. Theoretical Scheme
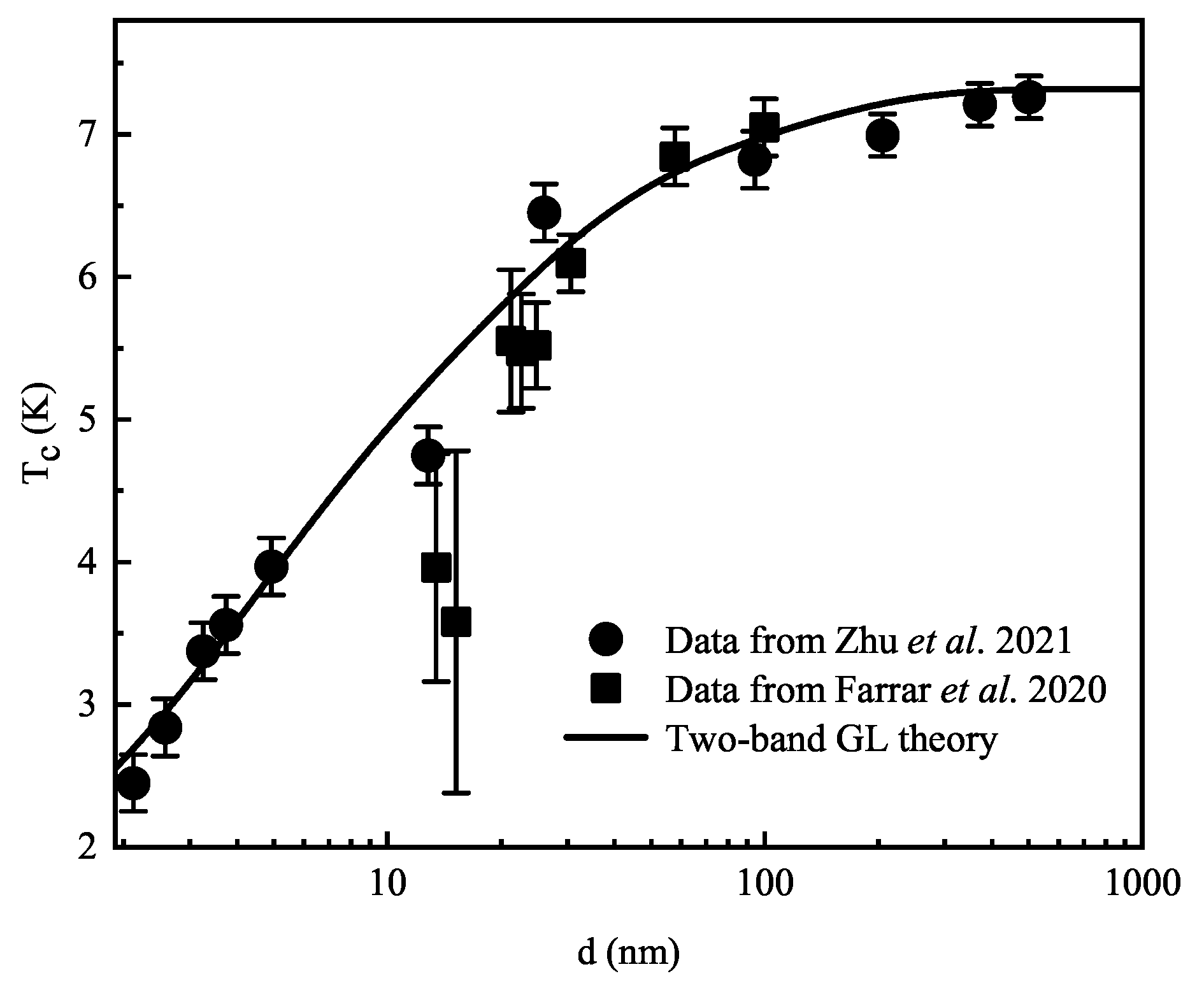
3. Critical Temperature of FeSe Films in Ginzburg–Landau Theory
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kamihara, Y.; Watanabe, T.; Hirano, M.; Hosono, H. Iron-Based layered superconductor La[O1−xFx]FeAs (x=0.05−0.12) with Tc = 26 K. J. Am. Chem. Soc. 2008, 130, 3296–3297. [Google Scholar] [CrossRef] [PubMed]
- Hsu, F.C.; Luo, J.Y.; Yeh, K.W.; Chen, T.K.; Huang, T.W.; Wu, P.M.; Lee, Y.C.; Huang, Y.L.; Chu, Y.Y.; Yan, D.C.; et al. Superconductivity in the PbO-type structure α-FeSe. Proc. Natl. Acad. Sci. USA 2008, 105, 14262. [Google Scholar] [CrossRef] [PubMed]
- Schneider, R.; Zaitsev, A.G.; Fuchs, D.; Löhneysen, H.V. Excess conductivity and Berezinskii-Kosterlitz-Thouless transition in superconducting FeSe thin films. J. Phys. Condens. Matter 2014, 26, 455701. [Google Scholar] [CrossRef] [PubMed]
- Terashima, T.; Kikugawa, N.; Kiswandhi, A.; Choi, E.S.; Brooks, J.S.; Kasahara, S.; Watashige, T.; Ikeda, H.; Shibauchi, T.; Matsuda, Y.; et al. Anomalous Fermi surface in FeSe seen by Shubnikov-de Haas oscillation measurements. Phys. Rev. B 2014, 90, 144517. [Google Scholar] [CrossRef]
- McQueen, T.M.; Williams, A.J.; Stephens, P.W.; Tao, J.; Zhu, Y.; Ksenofontov, V.; Casper, F.; Felser, C.; Cava, R.J. Tetragonal-to-orthorhombic structural phase transition at 90 K in the superconductor Fe1.01Se. Phys. Rev. Lett. 2009, 103, 057002. [Google Scholar] [CrossRef]
- McQueen, T.M.; Huang, Q.; Ksenofontov, V.; Felser, C.; Xu, Q.; Zandbergen, H.; Hor, Y.S.; Allred, J.; Williams, A.J.; Qu, D.; et al. Extreme sensitivity of superconductivity to stoichiometry in Fe1+δSe. Phys. Rev. B 2009, 79, 014522. [Google Scholar] [CrossRef]
- Watson, M.D.; Kim, T.K.; Haghighirad, A.A.; Davies, N.R.; McCollam, A.; Narayanan, A.; Blake, S.F.; Chen, Y.L.; Ghannadzadeh, S.; Schofield, A.J.; et al. Emergence of the nematic electronic state in FeSe. Phys. Rev. B 2015, 91, 155106. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Li, Z.; Zhang, W.H.; Zhang, Z.C.; Zhang, J.S.; Li, W.; Ding, H.; Ou, Y.B.; Deng, P.; Chang, K.; et al. Interface-induced high-temperature superconductivity in single unit-cell FeSe films on SrTiO3. Chin. Phys. Lett. 2012, 29, 037402. [Google Scholar] [CrossRef]
- Chareev, D.; Osadchii, E.; Kuzmicheva, T.; Lin, J.Y.; Kuzmichev, S.; Volkova, O.; Vasiliev, A. Single crystal growth and characterization of tetragonal FeSe1−x superconductors. Cryst. Eng. Commun. 2013, 15, 1989. [Google Scholar] [CrossRef]
- Lin, J.Y.; Hsieh, Y.S.; Chareev, D.A.; Vasiliev, A.N.; Parsons, Y.; Yang, H.D. Coexistence of isotropic and extended s-wave order parameters in FeSe as revealed by low-temperature specific heat. Phys. Rev. B 2011, 84, 220507(R). [Google Scholar] [CrossRef]
- Schneider, R.; Zaitsev, A.G.; Fuchs, D.; Hott, R. Anisotropic field dependence of the electronic transport in superconducting FeSe thin films. Supercond. Sci. Technol. 2020, 33, 075011. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, W.H.; Xing, Y.; Li, F.S.; Zhao, Y.F.; Xia, Z.C.; Wang, L.L.; Ma, X.C.; Xue, Q.K.; Wang, J. High temperature superconducting FeSe films on SrTiO3 substrates. Sci. Rep. 2014, 4, 6040. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.K.; Luo, J.Y.; Ke, C.T.; Chang, H.H.; Huang, T.W.; Yeh, K.W.; Chang, C.C.; Hsu, P.C.; Wu, C.T.; Wang, M.J.; et al. Low-temperature fabrication of superconducting FeSe thin films by pulsed laser deposition. Thin Solid Films 2010, 519, 1540. [Google Scholar] [CrossRef]
- Tan, S.Y.; Zhang, Y.; Xia, M.; Ye, Z.Y.; Chen, F.; Xie, X.; Peng, R.; Xu, D.F.; Fan, Q.; Xu, H.C.; et al. Interface-induced superconductivity and strain-dependent spin density waves in FeSe/SrTiO3 thin films. Nat. Mater. 2013, 12, 634. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.Y.; Zhang, W.H.; Zhang, Z.C.; Sun, Y.; Xing, Y.; Wang, Y.Y.; Wang, L.L.; Ma, X.C.; Xue, Q.K.; Wang, J. Thickness dependence of superconductivity and superconductor-insulator transition in ultrathin FeSe films on SrTiO3 (001) substrate. 2D Mater. 2015, 2, 044012. [Google Scholar] [CrossRef]
- Nabeshima, F.; Imai, Y.; Hanawa, M.; Tsukada, I.; Maeda, A. Enhancement of the superconducting transition temperature in FeSe epitaxial thin films by anisotropic compression. Appl. Phys. Lett. 2013, 103, 172602. [Google Scholar] [CrossRef]
- Schneider, R.; Zaitsev, A.G.; Fuchs, D.; Löhneysen, H.V. Superconductor-insulator quantum phase transition in disordered FeSe thin films. Phys. Rev. Lett. 2012, 108, 257003. [Google Scholar] [CrossRef]
- Zhu, C.S.; Lei, B.; Sun, Z.L.; Cui, J.H.; Shi, M.Z.; Zhuo, W.Z.; Luo, X.G.; Chen, X.H. Evolution of transport properties in FeSe thin flakes with thickness approaching the two-dimensional limit. Phys. Rev. B 2021, 104, 024509. [Google Scholar] [CrossRef]
- Farrar, L.S.; Bristow, M.; Haghighirad, A.A.; McCollam, A.; Bending, S.J.; Coldea, A.I. Suppression of superconductivity and enhanced critical field anisotropy in thin flakes of FeSe. NPJ Quantum Mater. 2020, 5, 29. [Google Scholar] [CrossRef]
- Böhmer, A.E.; Taufour, V.; Straszheim, W.E.; Wolf, T.; Canfield, P.C. Variation of transition temperatures and residual resistivity ratio in vapor-grown FeSe. Phys. Rev. B 2016, 94, 024526. [Google Scholar]
- Phan, G.N.; Nakayama, K.; Sugawara, K.; Sato, T.; Urata, T.; Tanabe, Y.; Tanigaki, K.; Nabeshima, F.; Imai, Y.; Maeda, A.; et al. Effects of strain on the electronic structure, superconductivity, and nematicity in FeSe studied by angle-resolved photoemission spectroscopy. Phys. Rev. B 2017, 95, 224507. [Google Scholar] [CrossRef]
- Suhl, H.; Matthias, B.T.; Walker, L.R. Bardeen-Cooper-Schrieffer theory of superconductivity in the case of overlapping bands. Phys. Rev. Lett. 1959, 3, 552–554. [Google Scholar] [CrossRef]
- Moskalenko, V.A. Superconductivity in metals with overlapping energy bands. Fiz. Metal. Metalloved 1959, 8, 2518–2520. [Google Scholar]
- Tilley, D.R. The Ginzburg-Landau equations for pure two band superconductors. Proc. Phys. Soc. 1964, 84, 573. [Google Scholar] [CrossRef]
- Tilley, D.R. The Ginsburg-Landau equations for anisotropic alloys. Proc. Phys. Soc. 1965, 86, 289. [Google Scholar] [CrossRef]
- Gurevich, A. Enhancement of the upper critical field by nonmagnetic impurities in dirty two-gap superconductors. Phys. Rev. B 2003, 67, 184515. [Google Scholar] [CrossRef]
- Zhitomirsky, M.E.; Dao, V.H. Ginzburg-Landau theory of vortices in a multigap superconductor. Phys. Rev. B 2004, 69, 054508. [Google Scholar] [CrossRef]
- Dao, V.H.; Zhitomirsky, M.E. Anisotropy of the upper critical field in MgB2: The two-gap Ginzburg-Landau theory. Eur. Phys. J. B 2005, 44, 183. [Google Scholar] [CrossRef]
- Gurevich, A. Limits of the upper critical field in dirty two-gap superconductors. Physica C 2007, 456, 160. [Google Scholar] [CrossRef]
- Silaev, M.; Babaev, E. Microscopic theory of type-1.5 superconductivity in multiband systems. Phys. Rev. B 2011, 84, 094515. [Google Scholar] [CrossRef]
- Silaev, M.; Babaev, E. Microscopic derivation of two-component Ginzburg-Landau model and conditions of its applicability in two-band systems. Phys. Rev. B 2012, 85, 134514. [Google Scholar] [CrossRef]
- Zhang, L.F.; Covaci, L.; Milošević, M.V.; Berdiyorov, G.R.; Peeters, F.M. Unconventional vortex states in nanoscale superconductors due to shape-induced resonances in the inhomogeneous cooper-pair condensate. Phys. Rev. Lett. 2012, 109, 107001. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.F.; Covaci, L.; Milošević, M.V.; Berdiyorov, G.R.; Peeters, F.M. Vortex states in nanoscale superconducting squares: The influence of quantum confinement. Phys. Rev. B 2013, 88, 144501. [Google Scholar] [CrossRef]
- Zhang, L.F.; Becerra, V.F.; Covaci, L.; Milošević, M.V. Electronic properties of emergent topological defects in chiral p-wave superconductivity. Phys. Rev. B 2016, 94, 024520. [Google Scholar] [CrossRef]
- Zhang, L.F.; Covaci, L.; Milošević, M.V. Topological phase transitions in small mesoscopic chiral p-wave superconductors. Phys. Rev. B 2017, 96, 224512. [Google Scholar] [CrossRef]
- de Gennes, P.G. Superconductivity of Metals and Alloys; Westview Press: New York, NY, USA, 1966. [Google Scholar]
- Benfenati, A.; Samoilenka, A.; Babaev, E. Boundary effects in two-band superconductors. Phys. Rev. B 2021, 103, 144512. [Google Scholar] [CrossRef]
- Gonçalves, W.C.; Sardella, E.; Becerra, V.F.; Milošević, M.V.; Peeters, F.M. Numerical solution of the time dependent Ginzburg-Landau equations for mixed (d+s)-wave superconductors. J. Math. Phys. 2014, 55, 041501. [Google Scholar] [CrossRef]
- Aguirre, C.; Martins, Q.D.; Barba-Ortega, J. Vortices in a superconducting two-band disk: Role of the Josephson and bi-quadratic coupling. Physica C 2021, 581, 1353818. [Google Scholar] [CrossRef]
- Aguirre, C.; de Arruda, A.; Faúndez, J.; Barba-Ortega, J. ZFC process in 2+1 and 3+1 multi-band superconductor. Physica B 2021, 615, 413032. [Google Scholar] [CrossRef]
- Ketterson, J.B.; Song, S.N. Superconductivity; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Subedi, A.; Zhang, L.J.; Singh, D.J.; Du, M.H. Density functional study of FeS, FeSe, and FeTe: Electronic structure, magnetism, phonons, and superconductivity. Phys. Rev. B 2008, 78, 134514. [Google Scholar] [CrossRef]
- Chen, Y.J.; Zhu, H.P.; Shanenko, A.A. Interplay of Fermi velocities and healing lengths in two-band superconductors. Phys. Rev. B 2020, 101, 214510. [Google Scholar] [CrossRef]
- Tamai, A.; Ganin, A.Y.; Rozbicki, E.; Bacsa, J.; Meevasana, W.; King, P.D.C.; Caffio, M.; Schaub, R.; Margadonna, S.; Prassides, K.; et al. Strong electron correlations in the normal state of the iron-based FeSe0.42Te0.58 superconductor observed by angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 2010, 104, 097002. [Google Scholar] [CrossRef] [PubMed]
- Ilin, K.S.; Vitusevich, S.A.; Jin, B.B.; Gubin, A.I.; Klein, N.; Siegel, M. Peculiarities of the thickness dependence of the superconducting properties of thin Nb films. Physica C 2004, 408–410, 700. [Google Scholar] [CrossRef]
- Gubin, A.I.; Ilin, K.S.; Vitusevich, S.A.; Siegel, M.; Klein, N. Dependence of magnetic penetration depth on the thickness of superconducting Nb thin films. Phys. Rev. B 2005, 72, 064503. [Google Scholar] [CrossRef]
- Chen, L.Z.; Wang, X.C.; Wen, Y.H.; Zhu, Z.Z. Jahn-Teller effect in Nb planar atomic sheet. Acta Phys. Sin. 2007, 56, 2920. [Google Scholar] [CrossRef]
- Li, C.Z.; Li, C.; Wang, L.X.; Wang, S.; Liao, Z.M.; Brinkman, A.; Yu, D.P. Bulk and surface states carried supercurrent in ballistic Nb-Dirac semimetal Cd3As2 nanowire-Nb junctions. Phys. Rev. B 2018, 97, 115446. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, C.; Che, J.; Huang, H. Boundary Effect and Critical Temperature of Two-Band Superconducting FeSe Films. Crystals 2023, 13, 18. https://doi.org/10.3390/cryst13010018
Ye C, Che J, Huang H. Boundary Effect and Critical Temperature of Two-Band Superconducting FeSe Films. Crystals. 2023; 13(1):18. https://doi.org/10.3390/cryst13010018
Chicago/Turabian StyleYe, Chenxiao, Jiantao Che, and Hai Huang. 2023. "Boundary Effect and Critical Temperature of Two-Band Superconducting FeSe Films" Crystals 13, no. 1: 18. https://doi.org/10.3390/cryst13010018
APA StyleYe, C., Che, J., & Huang, H. (2023). Boundary Effect and Critical Temperature of Two-Band Superconducting FeSe Films. Crystals, 13(1), 18. https://doi.org/10.3390/cryst13010018