Diameter Prediction of Silicon Ingots in the Czochralski Process Based on a Hybrid Deep Learning Model
Abstract
1. Introduction
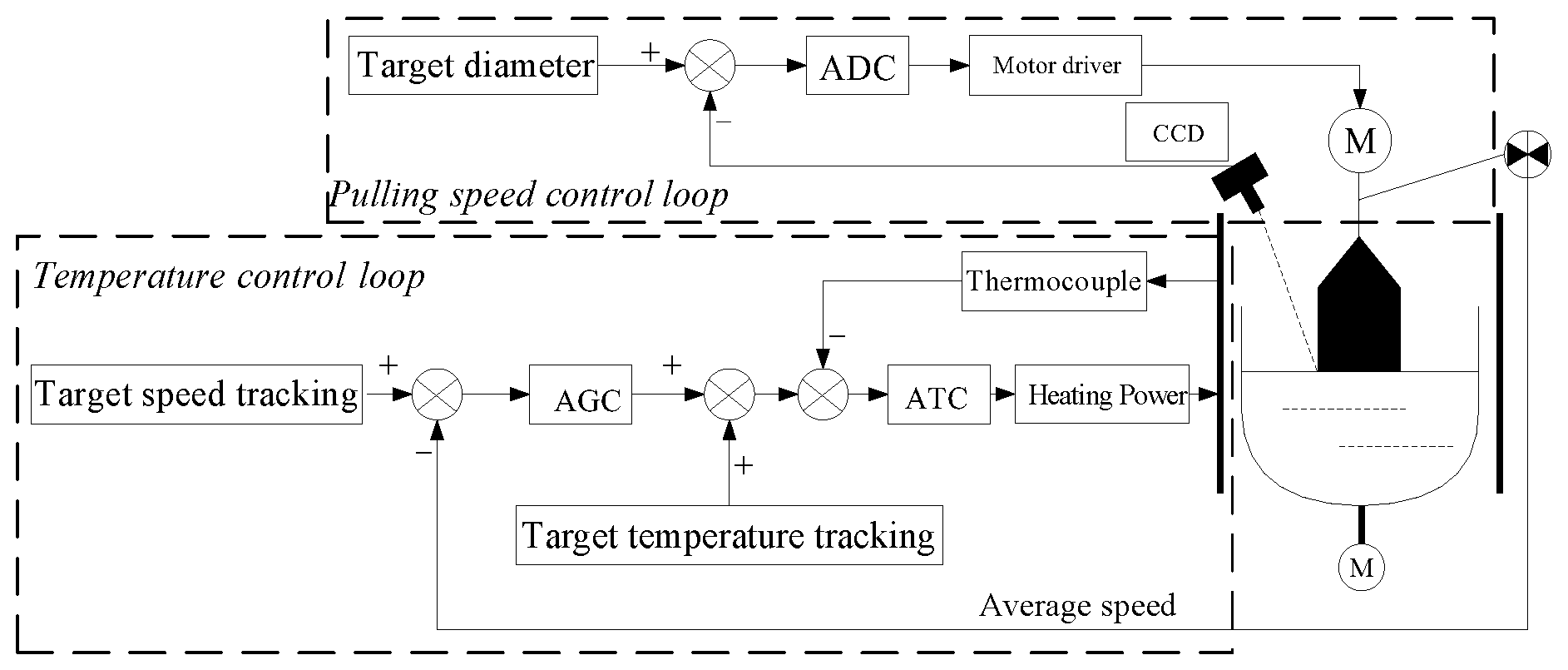
2. Description of the Object
3. Research Methodology
3.1. CRBM-DBN
3.2. Support Vector Regression
3.3. Ant Lion Optimizer (ALO)
- (1)
- Random Walk of Ants
- (2)
- Entrapping ants
- (3)
- Building Trap
- (4)
- The ant gliding to the antlion
- (5)
- Capturing prey and rebuilding the trap
- (6)
- Elitism
4. Diameter Prediction Model Based on CRBM-DBN-ALO-SVR
5. Results
5.1. Data Source and Evaluation Indices
5.2. Diameter Prediction of Silicon Ingots
5.3. Comparison of Different Prediction Methods
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Czochralski, J. Ein neues Verfahren zur Messung des Kristallisationsgeschwindigkeit der Metalle. Z. Phys. Chem. 1918, 92, 219–221. [Google Scholar] [CrossRef]
- Hurle, D.J.T.; Joyce, G.C.; Ghassempoory, M.; Crowley, A.B.; Stern, E.J. The dynamics of czochralski growth. J. Cryst. Growth 1990, 100, 11–25. [Google Scholar] [CrossRef]
- Neubert, M.; Rudolph, P. Growth of semi-insulating GaAs crystals in low temperature gradients by using the Vapour Pressure Controlled Czochralski Method (VCz). Prog. Cryst. Growth Charact. Mater. 2001, 43, 119–185. [Google Scholar] [CrossRef]
- Motakef, S.; Kelly, K.; Koai, K. Comparison of calculated and measured dislocation density in LEC-grown GaAs crystals. J. Cryst. Growth 1991, 113, 279–288. [Google Scholar] [CrossRef]
- Jordan, A.S.; Caruso, R.; VonNeida, A.R.; Nielsen, J.W. A comparative study of thermal stress induced dislocation generation in pulled GaAs, InP, and Si crystals. J. Appl. Phys. 1981, 52, 3331–3336. [Google Scholar] [CrossRef]
- Hurle, D.T.J. Control of diameter in Czochralski and related crystal growth techniques. J. Cryst. Growth 1977, 42, 473–482. [Google Scholar] [CrossRef]
- Duffar, T. Crystal Growth Processes Based on Capillarity: Czochralski, Floating Zone, Shaping and Crucible Techniques; John and Wiley and Sons: New York, NY, USA, 2010. [Google Scholar]
- Winkler, J.; Neubert, M.; Rudolph, J. Nonlinear model-based control of the Czochralski process I: Motivation, modeling and feedback controller design. J. Cryst. Growth 2010, 312, 1005–1018. [Google Scholar] [CrossRef]
- Dropka, N.; Holena, M. Application of Artificial Neural Networks in Crystal Growth of Electronic and Opto-Electronic Materials. Crystals 2020, 10, 663. [Google Scholar] [CrossRef]
- Asadian, M.; Seyedein, S.; Aboutalebi, M.; Maroosi, A. Optimization of the parameters affecting the shape and position of crystal–melt interface in YAG single crystal growth. J. Cryst. Growth 2009, 311, 342–348. [Google Scholar] [CrossRef]
- Kumar, K.V. Neural Network Prediction of Interfacial Tension at Crystal/Solution Interface. Ind. Eng. Chem. Res. 2009, 48, 4160–4164. [Google Scholar] [CrossRef]
- Sun, X.; Tang, X. Prediction of the Crystal’s Growth Rate Based on BPNN and Rough Sets. In Proceedings of the Second International Conference on Computational Intelligence and Natural Computing (CINC), Wuhan, China, 13–14 September 2010. [Google Scholar]
- Tsunooka, Y.; Kokubo, N.; Hatasa, G.; Harada, S.; Tagawa, M.; Ujihara, T. High-speed prediction of computational fluid dynamics simulation in crystal growth. CrystEngComm 2018, 20, 6546–6550. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, Q.; Liu, D. Research Into the LSTM Neural Network-Based Crystal Growth Process Model Identification. IEEE Trans. Semicond. Manuf. 2019, 32, 220–225. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, N.; Jiang, L.; Zhao, X.G.; Duan, W.F. Nonlinear Generalized Predictive Control of the Crystal Diameter in CZ-Si Crystal Growth Process Based on Stacked Sparse Autoencoder. IEEE Trans. Control. Syst. Technol. 2019, 28, 1132–1139. [Google Scholar] [CrossRef]
- Boucetta, A.; Kutsukake, K.; Kojima, T.; Kudo, H.; Matsumoto, T.; Usami, N. Application of artifificial neural network to optimize sensor positions for accurate monitoring: An example with thermocouples in a crystal growth furnace. Appl. Phys. Express 2019, 12, 125503. [Google Scholar] [CrossRef]
- Wang, C.-N.; Yang, F.-C.; Nguyen, V.T.T.; Vo, N.T.M. CFD Analysis and Optimum Design for a Centrifugal Pump Using an Effectively Artificial Intelligent Algorithm. Micromachines 2022, 13, 1208. [Google Scholar] [CrossRef] [PubMed]
- Billings, S.A. Nonlinear System Identification: NARMAX Methods in the Time, Frequency, and Spatio-Temporal Domains; John and Wiley and Sons: West Sussex, UK, 2013. [Google Scholar]
- He, X.; Asada, H. A new method for identifying orders of input-output models for nonlinear dynamic systems. In Proceedings of the American Control Conference (ACC), San Francisco, CA, USA, 2–4 June 1993. [Google Scholar]
- Liang, Y.M. Data-Driven Based Growth Control for Silicon Single Crystal. Ph.D. Thesis, Xi’an University of Technology, Xi’an, China, 2014. [Google Scholar]
- Mohammed, L.B.; Hamdan, M.A.; Abdelhafez, E.A.; Shaheen, W. Hourly solar radiation prediction based on nonlinear autoregressive exogenous (NARX) neural network. Jordan J. Mech. Ind. Eng. 2013, 7, 11–18. [Google Scholar]
- Arel, I.; Rose, D.C.; Karnowski, T.P. Deep machine learning-a new frontier in artificial intelligence research. IEEE Comput. Intell. Mag. 2010, 5, 13–18. [Google Scholar] [CrossRef]
- Nguyen, T.V.T.; Huynh, N.-T.; Vu, N.-C.; Kieu, V.N.D.; Huang, S.-C. Optimizing compliant gripper mechanism design by employing an effective bi-algorithm: Fuzzy logic and ANFIS. Microsyst. Technol. 2021, 27, 3389–3412. [Google Scholar] [CrossRef]
- Grigorescu, S.; Trasnea, B.; Cocias, T.; Macesanu, G. A survey of deep learning techniques for autonomous driving. J. Field Robot. 2020, 37, 362–386. [Google Scholar] [CrossRef]
- Arellano-Espitia, F.; Delgado-Prieto, M.; Martinez-Viol, V.; Saucedo-Dorantes, J.J.; Osornio-Rios, R.A. Deep-Learning-Based Methodology for Fault Diagnosis in Electromechanical Systems. Sensors 2020, 20, 3949. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Yang, C.; Gao, Z.; Yao, Y. Ensemble deep kernel learning with application to quality prediction in industrial polymerization processes. Chemom. Intell. Lab. Syst. 2018, 174, 15–21. [Google Scholar] [CrossRef]
- Hinton, G.E. A practical guide to training restricted Boltzmann machines. In Neural Networks: Tricks of the Trade; Montavon, G., Orr, G.B., Müller, K.R., Eds.; Springer: Berlin, Germany, 2012; pp. 599–619. [Google Scholar]
- Hinton, G.E.; Deng, L.; Yu, D.; Dahl, G.E.; Mohamed, A.R.; Jaitly, N.; Kingsbury, B. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Proc. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Tran, V.T.; AlThobiani, F.; Ball, A. An approach to fault diagnosis of reciprocating compressor valves using Teager–Kaiser energy operator and deep belief networks. Expert Syst. Appl. 2014, 41, 4113–4122. [Google Scholar] [CrossRef]
- Tamilselvan, P.; Wang, P. Failure diagnosis using deep belief learning based health state classification. Reliab. Eng. Syst. Saf. 2013, 115, 124–135. [Google Scholar] [CrossRef]
- Schmidt, E.M.; Kim, Y.E. Learning emotion-based acoustic features with deep belief networks. In Proceedings of the 2011 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 16–19 October 2011. [Google Scholar]
- Chen, H.; Murray, A.F. Continuous restricted Boltzmann machine with an implementable training algorithm. IEE Proc. Vis. Image Signal Process 2003, 150, 153–158. [Google Scholar] [CrossRef]
- Chen, H.; Murray, A.F. A continuous restricted Boltzmann machine with a hardware-amenable learning algorithm. In Proceedings of the 12th International Conference on Artificial Neural Networks (ICANN), Madrid, Spain, 28–30 August 2002. [Google Scholar]
- Vapnik, V.N. Statistical Learning Theory; John and Wiley and Sons: New York, NY, USA, 1998. [Google Scholar]
- Wu, F.; Zhou, H.; Ren, T.; Zheng, L.; Cen, K. Combining support vector regression and cellular genetic algorithm for multi-objective optimization of coal-fired utility boilers. Fuel 2009, 88, 1864–1870. [Google Scholar] [CrossRef]
- Smola, A. Regression Estimation with Support Vector Learning Machines. Master’s Thesis, Technical University of Munich, Munich, Germany, 1996. [Google Scholar]
- Heckman, N. The theory and application of penalized methods or Reproducing Kernel Hilbert Spaces made easy. Statist. Surv. 2012, 6, 113–141. [Google Scholar] [CrossRef]
- Smola, A.J.; Scholkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Hsieh, H.I.; Lee, T.P.; Lee, T.S. A hybrid particle swarm optimization and support vector regression model for financial time series forecasting. Int. J. Bus. Adm. 2011, 2, 48–56. [Google Scholar]
- Mirjalili, S. The Ant Lion Optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Zhao, X.G.; Liu, D.; Jing, K.L. Identification of Nonlinear System with Noise Based on Improved Ant Lion Optimization and T-S Fuzzy Model. Control. Decis. 2019, 34, 759–766. [Google Scholar]
- Zhao, X.G.; Jing, K.L.; Liu, D.; Yan, X.M. Improved Ant Lion Optimizer and its application in modeling of Czochralski crystal growth. In Proceedings of the IEEE 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018. [Google Scholar]










| Software and Hardware | Configuration |
|---|---|
| Operation System | Windows 10 Professional |
| CPU | i5-4590, 3.7 GHz |
| RAM | 8 GB |
| Matlab | R2016b |
| RMSE | MAE | |
|---|---|---|
| SVR | 0.0269 | 0.0965 |
| BPNN | 1.3259 × 10−4 | 0.0106 |
| CRBM-DBN-SVR | 5.2152 × 10−5 | 0.0067 |
| CRBM-DBN-ALO-SVR | 1.9632 × 10−7 | 3.4235 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Liu, D.; Yan, X. Diameter Prediction of Silicon Ingots in the Czochralski Process Based on a Hybrid Deep Learning Model. Crystals 2023, 13, 36. https://doi.org/10.3390/cryst13010036
Zhao X, Liu D, Yan X. Diameter Prediction of Silicon Ingots in the Czochralski Process Based on a Hybrid Deep Learning Model. Crystals. 2023; 13(1):36. https://doi.org/10.3390/cryst13010036
Chicago/Turabian StyleZhao, Xiaoguo, Ding Liu, and Xiaomei Yan. 2023. "Diameter Prediction of Silicon Ingots in the Czochralski Process Based on a Hybrid Deep Learning Model" Crystals 13, no. 1: 36. https://doi.org/10.3390/cryst13010036
APA StyleZhao, X., Liu, D., & Yan, X. (2023). Diameter Prediction of Silicon Ingots in the Czochralski Process Based on a Hybrid Deep Learning Model. Crystals, 13(1), 36. https://doi.org/10.3390/cryst13010036






