The Indentation Size Effect (ISE) of Ag–Cu Alloys
Abstract
:1. Introduction
2. Characteristics of the Use of Ag–Cu Alloys in Practice
2.1. Ag–Cu Alloys Intended for Practical Use, Especially for the Production of Jewelry, Utensils, Table Decorations and Coins
2.2. Ag–Cu Alloys Intended for Industrial Use, Primarily in Electronics
- The internal properties of the tested material, for example work hardening during indentation or penetration into the sample, indentation elastic recovery, the load needed to initiate plastic deformation, and the elastic resistance of the materials are possible sources in the work of Sangwal [28].
- The sample preparation method (grinding, polishing) and the resulting roughness [29].
3. Materials and Methods
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pačaiová, H.; Sinay, J.; Turisová, R.; Hajduová, Z.; Markulik, Š. Measuring the Qualitative Factors on Copper Wire Surface. Measurement 2017, 109, 359–365. [Google Scholar] [CrossRef]
- Markulik, S.; Nagyova, A.; Turisova, R.; Villinsky, T. Improving Quality in the Process of Hot Rolling of Steel Sheets. Appl. Sci. 2021, 11, 5451. [Google Scholar] [CrossRef]
- Markulik, Š.; Cehlár, M.; Kozel, R. Process Approach in the Mining Conditions. Acta Montan. Slovaca 2018, 23, 7. [Google Scholar]
- Silver and Silver Alloys. Available online: https://www.totalmateria.com/page.aspx?ID=CheckArticle&site=ktn&NM=239 (accessed on 27 October 2022).
- Zliatiny Neželezných Kovov. Available online: http://kmi2.uniza.sk/wp-content/uploads/2020/01/5_Zliatiny-nezelezn%C3%BDch-kovov.pdf (accessed on 27 October 2022).
- Zhu, X.; Xiao, Z.; An, J.; Jiang, H.; Jiang, Y.; Li, Z. Microstructure and Properties of Cu-Ag Alloy Prepared by Continuously Directional Solidification. J. Alloy. Compd. 2021, 883, 160769. [Google Scholar] [CrossRef]
- Benefits of Alloying Ag with Copper Alloys. Available online: https://www.belmontmetals.com/benefits-of-alloying-ag-with-copper-alloys/ (accessed on 27 October 2022).
- What Is Silver Alloy? Available online: https://sciencing.com/silver-alloy-7239734.html (accessed on 27 October 2022).
- Tian, Y.Z.; Li, J.J.; Zhang, P.; Wu, S.D.; Zhang, Z.F.; Kawasaki, M.; Langdon, T.G. Microstructures, Strengthening Mechanisms and Fracture Behavior of Cu–Ag Alloys Processed by High-Pressure Torsion. Acta Mater. 2012, 60, 269–281. [Google Scholar] [CrossRef]
- Silver Processing—The Metal and Its Alloy. Available online: https://www.britannica.com/technology/silver-processing/The-metal-and-its-alloys (accessed on 27 October 2022).
- Feng, G.; Liu, M.; Liu, Y.; Jin, Z.; Wang, Y.; Deng, D. Wetting Behavior of the Ag-5CuO Brazing Alloy on ZTA Composite Ceramic with/without CuO Coating in Air. Crystals 2021, 11, 609. [Google Scholar] [CrossRef]
- Tian, Y.Z.; Han, W.Z.; Yang, H.J.; Li, S.X.; Wu, S.D.; Zhang, Z.F. Shear Banding Observations in Cu–16wt.% Ag Alloy Subjected to One-Pass Equal Channel Angular Pressing. Scr. Mater. 2010, 62, 183–186. [Google Scholar] [CrossRef]
- Raabe, D.; Mattissen, D. Microstructure and Mechanical Properties of a Cast and Wire-Drawn Ternary Cu–Ag–Nb in Situ Composite. Acta Mater. 1998, 46, 5973–5984. [Google Scholar] [CrossRef]
- Bao, G.; Xu, Y.; Huang, L.; Lu, X.; Zhang, L.; Fang, Y.; Meng, L.; Liu, J. Strengthening Effect of Ag Precipitates in Cu–Ag Alloys: A Quantitative Approach. Mater. Res. Lett. 2016, 4, 37–42. [Google Scholar] [CrossRef] [Green Version]
- Sengul, S.; Guder, V. Key Factors of Deformation Mechanism of Cu-Ag Alloy. J. Non-Cryst. Solids 2022, 576, 121270. [Google Scholar] [CrossRef]
- Chang, T.-L.; Zhou, X.; Liang, J. Synthesis and Characterization of Ag-Cu Alloy Nanoparticles for Antimicrobial Applications: A Polydopamine Chemistry Application. Mater. Sci. Eng. C 2019, 98, 675–684. [Google Scholar] [CrossRef] [PubMed]
- Ciacotich, N.; Kvich, L.; Sanford, N.; Wolcott, J.; Bjarnsholt, T.; Gram, L. Copper-Silver Alloy Coated Door Handles as a Potential Antibacterial Strategy in Clinical Settings. Coatings 2020, 10, 790. [Google Scholar] [CrossRef]
- Abdul Salam, A.; Singaravelan, R.; Vasanthi, P.; Bangarusudarsan Alwar, S. Electrochemical Fabrication of Ag–Cu Nano Alloy and Its Characterization: An Investigation. J. Nanostruct. Chem. 2015, 5, 383–392. [Google Scholar] [CrossRef] [Green Version]
- Qi, Y.; Dai, X.; Wei, L.; Luo, H.; Liu, Y.; Dong, X.; Yang, D.; Li, Y. Nano-AgCu Alloy on Wood Surface for Mold Resistance. Nanomaterials 2022, 12, 1192. [Google Scholar] [CrossRef] [PubMed]
- Petrík, J.; Blaško, P.; Markulík, Š.; Šolc, M.; Palfy, P. The Indentation Size Effect (ISE) of Metals. Crystals 2022, 12, 795. [Google Scholar] [CrossRef]
- Westbrook, H.; Conrad, H. The Science of Hardness Testing and Its Research Application; Metals Park American Society for Metals: Russell Township, OH, USA, 1973. [Google Scholar]
- ISO 6507-1; Metallic Materials—Vickers Hardness Test Part 1—Test Method. International Organization for Standardization ISO: Geneva, Switzerland, 2018.
- ISO 14577-1; Metallic Materials—Instrumented Indentation Test for Hardness and Materials Parameters Part 1—Test Method. International Organization for Standardization ISO: Geneva, Switzerland, 2015.
- Gong, J.; Wu, J.; Guan, Z. Examination of the Indentation Size Effect in Low-Load Vickers Hardness Testing of Ceramics. J. Eur. Ceram. Soc. 1999, 19, 2625–2631. [Google Scholar] [CrossRef]
- Sangwal, K.; Surowska, B.; Błaziak, P. Analysis of the Indentation Size Effect in the Microhardness Measurement of Some Cobalt-Based Alloys. Mater. Chem. Phys. 2003, 77, 511–520. [Google Scholar] [CrossRef]
- Ren, X.J.; Hooper, R.M.; Griffiths, C.; Henshall, J.L. Indentation Size Effect in Ceramics: Correlation with H/E. J. Mater. Sci. Lett. 2003, 22, 1105–1106. [Google Scholar] [CrossRef]
- Petrík, J.; Blaško, P.; Domovcová, L.; Sedlák, R.; Guzanová, A.; Ťavodová, M.; Pribulová, A.; Futaš, P. Influence of Testers on the ISE Effect. Mater. Test. 2022, 64, 550–562. [Google Scholar] [CrossRef]
- Sangwal, K. On the Reverse Indentation Size Effect and Microhardness Measurement of Solids. Mater. Chem. Phys. 2000, 63, 145–152. [Google Scholar] [CrossRef]
- Kim, J.-Y.; Kang, S.-K.; Lee, J.-J.; Jang, J.; Lee, Y.-H.; Kwon, D. Influence of Surface-Roughness on Indentation Size Effect. Acta Mater. 2007, 55, 3555–3562. [Google Scholar] [CrossRef]
- Navrátil, V.; Novotná, J. Some problems of microhardness of metals. J. Appl. Math. 2009, 2, 241–244. [Google Scholar]
- Blaško, P.; Kupková, M.; Petrík, J.; Futaš, P.; Vasilňaková, A. The Indentation Size Effect of Sintered Fe/3.3 wt-%Cu + Cn Hm Measured by Vickers Scale. Mater. Sci. Technol. 2020, 36, 403–408. [Google Scholar] [CrossRef]
- Chicot, D.; Puchi-Cabrera, E.S.; Iost, A.; Staia, M.H.; Decoopman, X.; Roudet, F.; Louis, G. Analysis of Indentation Size Effect in Copper and Its Alloys. Mater. Sci. Technol. 2013, 29, 868–876. [Google Scholar] [CrossRef] [Green Version]
- Jönsson, B.; Hogmark, S. Hardness Measurements of Thin Films. Thin Solid Film. 1984, 114, 257–269. [Google Scholar] [CrossRef]
- Korsunsky, A.M.; McGurk, M.R.; Bull, S.J.; Page, T.F. On the Hardness of Coated Systems. Surf. Coat. Technol. 1998, 99, 171–183. [Google Scholar] [CrossRef]
- Kaya, H.; Çadırlı, E.; Böyük, U.; Maraşlı, N. Variation of Microindentation Hardness with Solidification and Microstructure Parameters in the Al Based Alloys. Appl. Surf. Sci. 2008, 255, 3071–3078. [Google Scholar] [CrossRef]
- ISO 6507-2; Metallic Materials—Vickers Hardness Test Part 2—Verification and Calibration of Testing Machines. International Organization for Standardization ISO: Geneva, Switzerland, 2005.
- Petrík, J.; Palfy, P.; Blaško, P.; Girmanová, L.; Havlík, M. The Indentation Size Effect (ISE) and the Speed of the Indenter Penetration into Test Piece. Manuf. Technol. 2016, 16, 771–777. [Google Scholar] [CrossRef]
- Li, H.; Bradt, R.C. The Microhardness Indentation Load/Size Effect in Rutile and Cassiterite Single Crystals. J. Mater. Sci. 1993, 28, 917–926. [Google Scholar] [CrossRef]
- Michels, B.D.; Frischat, G.H. Microhardness of Chalcogenide Glasses of the System Se-Ge-As. J. Mater. Sci. 1982, 17, 329–334. [Google Scholar] [CrossRef]
- Kim, H.; Kim, T. Measurement of Hardness on Traditional Ceramics. J. Eur. Ceram. Soc. 2002, 22, 1437–1445. [Google Scholar] [CrossRef]
- Petrík, J. On the Load Dependence of Micro-Hardness Measurements: Analysis of Data by Different Models and Evaluation of Measurement Errors. Arch. Metall. Mater. 2016, 61, 1819–1824. [Google Scholar] [CrossRef]
- Sargent, P.M. Indentation Size Effect and Strain-Hardening. J. Mater. Sci. Lett. 1989, 8, 1139–1140. [Google Scholar] [CrossRef]
- Tabor, D. The Hardness of Metals; Oxford Classic Texts in the Physical Sciences; Clarendon Press; Oxford University Press: Oxford, NY, USA, 2000; ISBN 978-0-19-850776-5. [Google Scholar]
- Elmustafa, A.A.; Eastman, J.A.; Rittner, M.N.; Weertman, J.R.; Stone, D.S. Indentation Size Effect: Large Grained Aluminum versus Nanocrystalline Aluminum-Zirconium Alloys. Scr. Mater. 2000, 43, 951–955. [Google Scholar] [CrossRef]
- Elmustafa, A.A.; Stone, D.S. Indentation Size Effect in Polycrystalline F.C.C. Metals. Acta Mater. 2002, 50, 3641–3650. [Google Scholar] [CrossRef]
- Atkinson, M. Calculation of Characteristic Macro-Hardness from Low-Load Indentation Tests. Mater. Sci. Eng. A 1995, 197, 165–169. [Google Scholar] [CrossRef]
- Tošenovský, J.; Tošenovský, F. Possibilities of Using Graphical and Numerical Tools in the Exposition of Process Capability Assessment Techniques. QIP J. 2019, 23, 13. [Google Scholar] [CrossRef]
- Klaput, P.; Vykydal, D.; Tošenovský, F.; Halfarová, P.; Plura, J. Problems of Application of Measurement System Analysis (MSA) in Metallurgical Production. Metalurgija 2016, 55, 535–537. Available online: https://www.researchgate.net/publication/298850843_Problems_of_application_of_measurement_system_analysis_MSA_in_metallurgical_production (accessed on 30 October 2022).
- Petrík, J.; Palfy, P. The Influence of the Load on the Hardness. Metrol. Meas. Syst. 2011, 18, 223–234. [Google Scholar] [CrossRef] [Green Version]
- Petrík, J. The Micro-Hardness of Heat Treated Carbon Steel. Mater. Sci. 2014, 20, 21–24. [Google Scholar] [CrossRef] [Green Version]
- Northover, P.; Northover, S.; Wilson, A. Microstructures of Ancient and Historic Silver. Metal 2013, 16–25, 253–260. [Google Scholar]
- Greil, S.; Edtmaier, C.; Haubner, R.; Lauter, L. Metallographic Investigations of Silver Alloys Used for Minting. MSF 2017, 891, 89–94. [Google Scholar] [CrossRef]
- Northover, S.M.; Northover, J.P. Microstructures of Ancient and Modern Cast Silver–Copper Alloys. Mater. Charact. 2014, 90, 173–184. [Google Scholar] [CrossRef]
- Aakre, A. Statistical Functions and Tools in Microsoft Excel; Trondheim, Norway, 2004. Microsoft Silver Application Development Partner. Available online: http://trafikk.info/evu_tt_oslo_2007/litteratur/excel_all_statistical_functions_and_tools_a5.pdf (accessed on 30 November 2022).
- McDonald, J.H. Handbook of Biological Statistics (3rd ed.); Sparky House Publishing: Baltimore, MD, USA, 2014; Available online: http://www.biostathandbook.com/multipleregression.html (accessed on 28 November 2022).


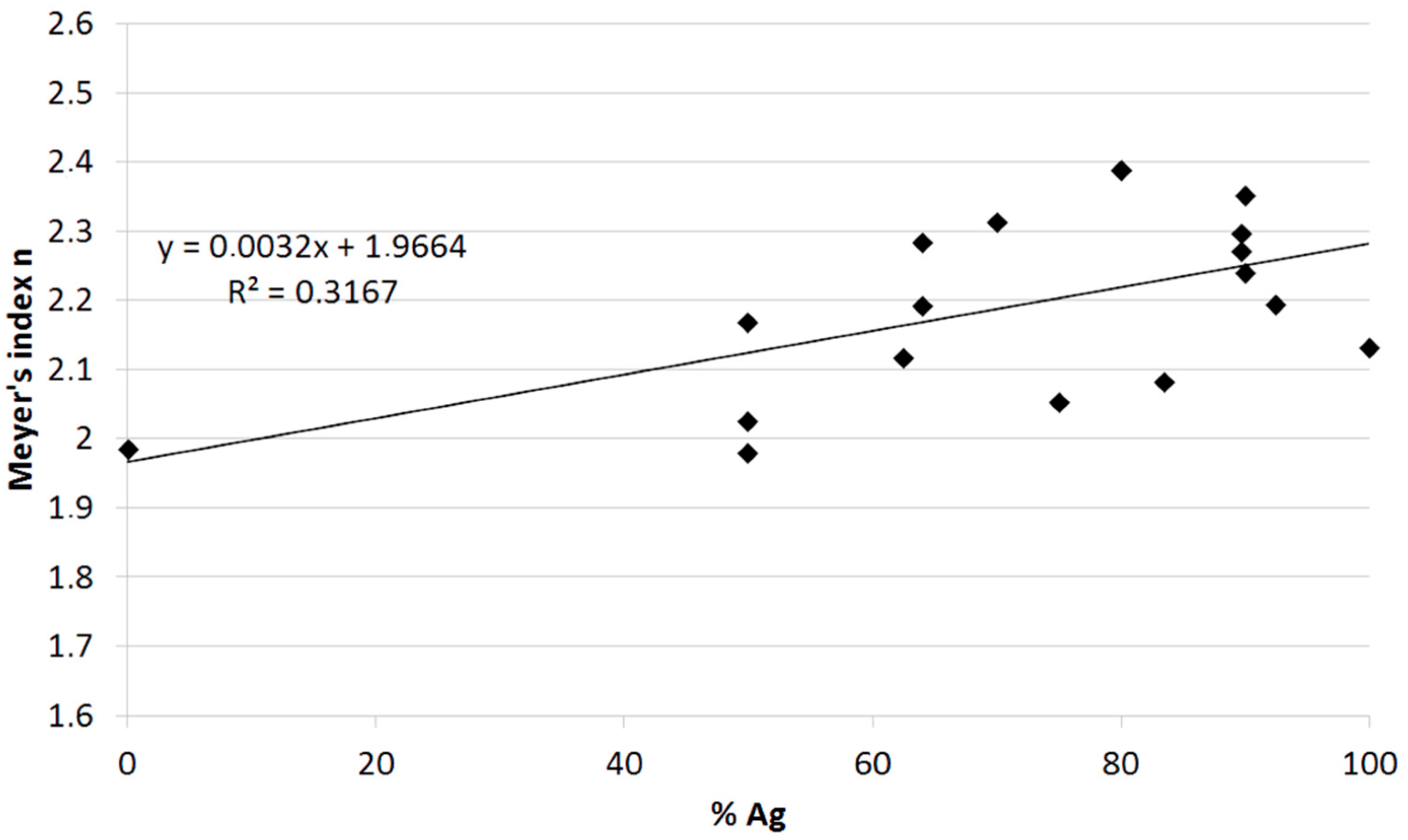

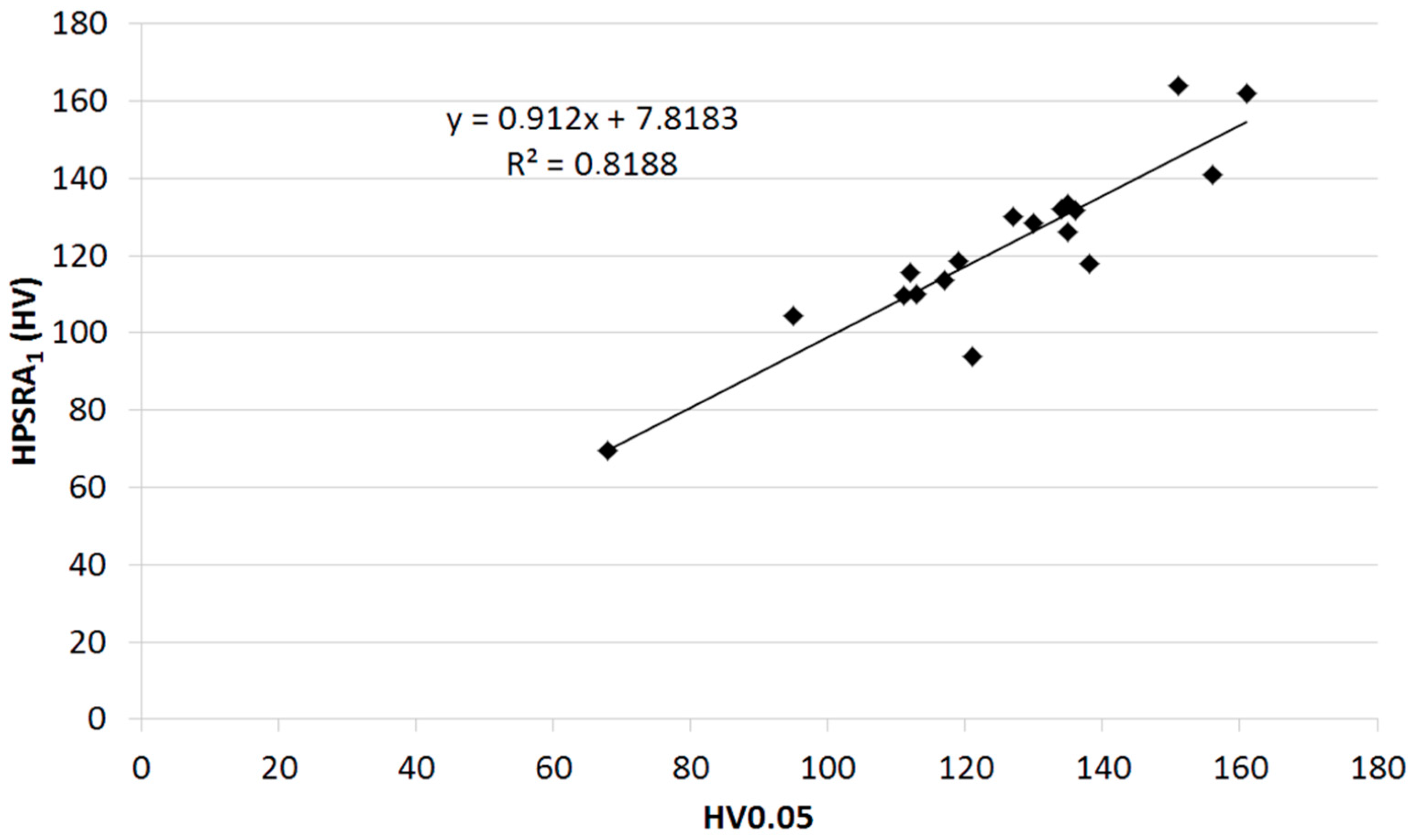

| Sample No. | Origin | Age (Years) | Silver Content (%wt.) | HV0.01 | HV0.025 | HV0.05 | HV0.1 | Indentator Speed (µm s−1) |
|---|---|---|---|---|---|---|---|---|
| 1 | Slovakia | 7 | 0.05 | 116 | 128 | 138 | 114 | 1.367 |
| 2 | Germany | 1 | 99.99 | 65 | 70 | 75 | 69 | 1.5 |
| 3 | Slovakia | 22 | 92.5 | 96 | 111 | 124 | 124 | 0.9 |
| 4 | Germany | 114 | 90 | 78 | 100 | 119 | 113 | 0.89 |
| 5 | Germany | 114 | 90 | 83 | 102 | 113 | 106 | 1.038 |
| 6 | Slovakia | 22 | 89.75 | 94 | 110 | 122 | 124 | 0.851 |
| 7 | Slovakia | 22 | 89.75 | 99 | 109 | 134 | 140 | 0.89 |
| 8 | Austria–Hungary | 129 | 83.5 | 101 | 116 | 127 | 128 | 0.864 |
| 9 | Austria–Hungary | 122 | 80 | 86 | 119 | 125 | 127 | 0.934 |
| 10 | Austria–Hungary | 122 | 80 | 101 | 121 | 131 | 139 | 0.856 |
| 11 | Slovakia | 21 | 75 | 106 | 125 | 138 | 119 | 0.86 |
| 12 | Czechoslovakia | 90 | 70 | 92 | 105 | 119 | 111 | 1.131 |
| 13 | Hungary | 85 | 64 | 95 | 110 | 121 | 102 | 1.875 |
| 14 | Hungary | 85 | 64 | 98 | 110 | 135 | 131 | 1.35 |
| 15 | Poland | 48 | 62.5 | 97 | 111 | 122 | 108 | 0.874 |
| 16 | Czechoslovakia | 87 | 50 | 105 | 115 | 125 | 105 | 1.21 |
| 17 | Czechoslovakia | 87 | 50 | 110 | 124 | 136 | 129 | 1.19 |
| 18 | Slovakia | 81 | 50 | 105 | 125 | 138 | 138 | 0.942 |
| Sample No. | n | Aln | c0 | c1 | c2 | W | A1 | c1/c2 | HPSR A1 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.9847 | 6.4802 | −0.0306 | 3.441 | 537.13 | 0.0095 | 599.95 | 0.00641 | 113.4505 |
| 2 | 2.1312 | 6.1450 | −0.0471 | 2.412 | 333.66 | −0.0095 | 367.24 | 0.007230 | 69.4451 |
| 3 | 2.1928 | 7.3783 | −0.1946 | 16.473 | 361.54 | −0.0012 | 666.66 | 0.04556 | 126.0654 |
| 4 | 2.2399 | 7.7507 | −0.221 | 14.316 | 379.43 | −0.0369 | 626.85 | 0.03773 | 118.5400 |
| 5 | 2.3501 | 7.1725 | −0.2632 | 18.354 | 273.48 | −0.0223 | 582.34 | 0.06711 | 110.1205 |
| 6 | 2.2960 | 7.4393 | −0.1540 | 10.570 | 485.30 | −0.0270 | 678.70 | 0.02178 | 128.3422 |
| 7 | 2.2698 | 8.4805 | −0.0326 | −0.024 | 866.67 | −0.0329 | 866.17 | −2.8E−05 | 163.7927 |
| 8 | 2.0802 | 7.3272 | −0.0060 | −0.472 | 696.50 | −0.0120 | 687.40 | −0.00068 | 129.9873 |
| 9 | 2.3881 | 7.7988 | −0.2766 | 20.500 | 322.60 | −0.0281 | 697.57 | 0.06355 | 131.9105 |
| 10 | 2.3808 | 8.1287 | −0.2080 | 15.690 | 538.00 | −0.0360 | 855.70 | 0.02916 | 161.8129 |
| 11 | 2.0513 | 6.9040 | −0.2098 | 20.425 | 247.76 | 0.0272 | 623.56 | 0.08244 | 117.9152 |
| 12 | 2.3120 | 7.0618 | −0.1030 | 5.293 | 519.30 | −0.0360 | 611.00 | 0.01019 | 115.5401 |
| 13 | 2.1910 | 6.3104 | −0.4490 | 35.370 | −70.17 | 0.0280 | 495.70 | −0.50406 | 93.7369 |
| 14 | 2.2821 | 7.6449 | −0.2302 | 18.735 | 353.30 | −0.0111 | 704.83 | 0.05303 | 133.2834 |
| 15 | 2.1159 | 6.7737 | −0.0523 | 3.2906 | 523.18 | −0.0115 | 580.67 | 0.00629 | 109.8047 |
| 16 | 1.9779 | 6.4455 | 0.1171 | −10.744 | 741.50 | −0.0134 | 552.57 | −0.01449 | 104.4910 |
| 17 | 2.1679 | 7.1045 | −0.1144 | 9.1285 | 523.18 | −0.0097 | 696.70 | 0.01745 | 131.7460 |
| 18 | 2.0240 | 8.0925 | 0.0110 | −2.130 | 788.60 | −0.0110 | 745.80 | −0.00207 | 141.0308 |
| Sample No. | Grain Diameter (µm) | Diagonal of the Indentation (µm) | |||
|---|---|---|---|---|---|
| HV0.01 | HV0.025 | HV0.05 | HV0.1 | ||
| 6 | 0.7–3.0 | 14.06 | 20.53 | 27.57 | 38.67 |
| 9 | 1.0–6.0 | 14.70 | 19.74 | 27.24 | 38.21 |
| 16 | 2.0–10.0 | 13.29 | 20.08 | 27.24 | 42.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šolc, M.; Blaško, P.; Petrík, J.; Palfy, P.; Girmanová, L. The Indentation Size Effect (ISE) of Ag–Cu Alloys. Crystals 2023, 13, 91. https://doi.org/10.3390/cryst13010091
Šolc M, Blaško P, Petrík J, Palfy P, Girmanová L. The Indentation Size Effect (ISE) of Ag–Cu Alloys. Crystals. 2023; 13(1):91. https://doi.org/10.3390/cryst13010091
Chicago/Turabian StyleŠolc, Marek, Peter Blaško, Jozef Petrík, Pavol Palfy, and Lenka Girmanová. 2023. "The Indentation Size Effect (ISE) of Ag–Cu Alloys" Crystals 13, no. 1: 91. https://doi.org/10.3390/cryst13010091
APA StyleŠolc, M., Blaško, P., Petrík, J., Palfy, P., & Girmanová, L. (2023). The Indentation Size Effect (ISE) of Ag–Cu Alloys. Crystals, 13(1), 91. https://doi.org/10.3390/cryst13010091









