Vibrational Properties of the Potassium Titanyl Phosphate Crystal Family

Abstract

The crystal family of potassium titanyl phosphate (KTiOPO${}_4$) is a promising material group for applications in quantum and nonlinear optics. The fabrication of low-loss optical waveguides, as well as high-grade periodically poled ferroelectric domain structures, requires a profound understanding of the material properties and crystal structure. In this regard, Raman spectroscopy offers the possibility to study and visualize domain structures, strain, defects, and the local stoichiometry, which are all factors impacting device performance. However, the accurate interpretation of Raman spectra and their changes with respect to extrinsic and intrinsic defects requires a thorough assignment of the Raman modes to their respective crystal features, which to date is only partly conducted based on phenomenological modelling. To address this issue, we calculated the phonon spectra of potassium titanyl phosphate and the related compounds rubidium titanyl phosphate (RbTiOPO${}_4$) and potassium titanyl arsenate (KTiOAsO${}_4$) based on density functional theory and compared them with experimental data. Overall, this allows us to assign various spectral features to eigenmodes of lattice substructures with improved detail compared to previous assignments. Nevertheless, the analysis also shows that not all features of the spectra can unambigiously be explained yet. A possible explanation might be that defects or long range fields not included in the modeling play a crucial rule for the resulting Raman spectrum. In conclusion, this work provides an improved foundation into the vibrational properties in the KTiOPO${}_4$ material family.

1. Introduction

Highly efficient single photon sources and optical frequency converters based on nonlinear optical effects are key components for quantum communication. In this regard, the ferroelectric potassium titanyl phosphate (KTiOPO${}_4$, KTP) and related compounds, such as rubidium titanyl phospate (RbTiOPO${}_4$, RTP) or potassium titanyl arsenate (KTiOAsO${}_4$, KTA), are strong candidates for applications due to their inherent large second-order optical nonlinearities, wide transparency windows (320 nm up to 4000 nm) and large damage thresholds [1,2,3,4,5,6]. The unique dispersion properties allow for decorrelated quantum light sources in the telecom band [7].

The central elements of any nonlinear, integrated photonic device are low-loss optical waveguides and the possibility to achieve phase matching between the interacting waves. In KTP, for example, low-loss, strongly guiding waveguides can be realized by exchanging the highly mobile alkali ion, e.g., K${}^{+}$, for another substituent, e.g., Rb${}^{+}$ or Cs${}^{+}$, by a simple diffusion process effectively creating mixed crystals, e.g., Rb${}_{1-x}$K${}_x$TiOPO${}_4$ [3,8,9,10,11,12]. Other options include direct laser-writing, i.e., locally modifying the crystal via an intense, focused laser beam [13]; He-implatation [14]; or diamond-blade diced ridged waveguides [15].

Phase matching between interacting waves in any ferroelectric crystal can be realized independently of waveguide design by employing the quasi-phase matching scheme within periodically poled domain structures [15,16,17]. Periodically inverted domain structures can be fabricated by electric field poling via (lithographically) structured electrodes. The large asymmetry in directional domain propagation speed and other intrinsic properties allow for the fabrication of ultra-short domain periods in the KTiOPO${}_4$-family members [18,19], which in other materials such as lithium niobate (LiNbO${}_3$) are so far very challenging to realize [4]. Ultra-short domain periods in the micrometer and sub-micrometer are required for various quantum-optical and nonlinear-optical applications such as the efficient coupling of UV-quantum memories with fiber-optical communication networks in the telecom band [15], mirrorless optical parametric oscillators [20] or counter-propagating parametric down conversion, which enables bright and narrow-band single-photon generation [21,22], in most of which applications have been readily demonstrated in the KTiOPO${}_4$-family.

The fabrication and optimization of homogeneous domain structures and low-loss waveguides both require a thorough analysis of the generated structures and a profound knowledge of the underlying physical mechanisms. For example, during the fabrication of diffused waveguides, it was noticed that the diffusion depth depends on the width of the waveguide, making the fabrication of homogeneous waveguides challenging [3]. Here, it is suspected that strains may play an important role in the phenomenon. While the stoichiometry profile of these diffused waveguides can be analyzed by energy dispersive X-ray spectroscopy (EDX), only limited insight into the strain, local defects or other properties can be inferred from this method. Similarly, for the analysis and imaging of ferroelectric domain structures, a multitude of methods are available. Among the most common are selective chemical etching, piezo-response force microscopy and second-harmonic microscopy [23,24,25,26,27]. While all these methods provide in-depth insight into the domain structure, they only provide limited—if any—insight into the local stoichiometry, strain of the diffused or other waveguide types. In this regard, (confocal) $\mu$-Raman spectroscopy provides an ideal tool to study and visualize (local) strain, stoichiometry, defects and domain structures, as well as their interactions, which can act as a mediator between the various established techniques [3,25,28,29,30,31].

Raman spectroscopy is based on the inelastic scattering of photons with phonons. As the phonon frequencies, their selection rules and scattering cross-section are influenced by the presence of domain walls, strains, defects or the stoichiometry [3,25,28,29,30,31]; a detailed analysis of the spectrum may provide in-depth insight into the local material properties. However, any in-depth interpretation of spectral changes is challenging because the Raman spectra of the KTiOPO${}_4$ family are very complex and only partly understood. The unit cell of the (stoichiometric) material contains 8 formular units, i.e., 64 atoms. This results in 189 vibrational degrees of freedom. Due to the low symmetry in the system, all 189 optical modes are non-degenerate and all are Raman- active. Based on group theory, the phonons can be further differentiated into four symmetry groups of 48 phonons of $A_1$, 47 of $A_2$, 47 of $B_1$, and 47 of $B_2$ types [32].

Up to now, no full theoretical prediction of the vibrational properties and the Raman spectra based on first-principles exists for any member of the KTiOPO${}_4$-family. So far, the main spectral features—providing the basis for interpretation of spectroscopic data—have been assigned in terms of the vibrational eigenmodes of idealized substructures of the crystal, most prominently the TiO${}_6$ octahedron and the PO${}_4$ or AsO${}_4$ tetrahedron [32,33,34]. Here, the eigenfrequencies and selection rules of these substructures have been calculated. This approach allows for understanding that the high-wavenumber phonons in the >800 cm${}^{-1}$ range are mostly governed by eigenmodes of the PO${}_4$ tetrahedron, while many dominating peaks in the lower wavenumber range are associated with eigenmodes of the TiO${}_6$ octahedron. However, any further predictions based on this approach are limited, as the actual structures of the octahedra and tetrahedra within the real crystal structure differ from their ideal counterparts, which leads to the lifted degeneracy of modes or altered selection rules compared to the idealized structure [32,33]. Furthermore, this model disregards the influence of the alkali ions completely, as well as vibrations involving larger crystallographic substructures, e.g., the low wavenumber vibrations of complete parts of the sublattice.

Therefore, in this work, we calculate the Raman spectra and phonon properties for KTiOPO${}_4$, RbTiOPO${}_4$ and KTiOAsO${}_4$ from first principles based on density functional theory (DFT), and systematically compare the results with polarized Raman spectroscopy. In the past, this approach was successfully applied to lithium niobate, lithium tantalate (LiTaO${}_3$) and strained crystals, as well as mixed crystals (LiTa${}_{1-x}$Nb${}_x$O${}_3$), where it provided much improved insight and unambiguous phonon assignment [29,35,36], which we aim to extend to the KTP family.

2. Methods

2.1. Computational Method

The ground-state properties of KTP, RTP and KTA are determined using DFT routines, as implemented in the Quantum Espresso software package [37]. The Perdew-Zunger (PZ) parametrization of the local density approximation (LDA) is thereby used to account for electronic exchange and correlation [38]. Norm-conserving pseudopotentials within the PZ formulation are used to model the electron-ion interaction. In addition to all open shells, atomic orbitals P${}_{3\mathrm{s}}$, O${}_{2\mathrm{s}}$ and As${}_{4\mathrm{s}}$ have been treated as valence states. In the case of Ti, a modified electron configuration was assumed, with the 3d and 4s shell being occupied by 3 and 1 electrons, respectively. Electronic wave functions were expanded into plane waves up to a cutoff energy of 100 Ry, ensuring a convergence of Raman spectra regarding peak positions and heights. Integration over the Brillouin zone was carried out using a regular 2 × 4 × 2 k-point mesh.

Since Raman spectra are known to be very sensitive to lattice distortions, lattice constants of all three materials are kept constant at their respective experimental values [39] instead of the LDA ones (overestimations of the calculated values of up to 2% are observed).

For all three materials, the structural relaxation via a quasi-Newtonian algorithm was performed until residual forces and total energy changes fell below threshold values of 10${}^{-4}$ Ry/bohr and 10${}^{-8}$ Ry, respectively. The subsequent calculation of the phonon modes and Raman cross sections are carried out using density-functional perturbation theory (DFPT) routines. For further details regarding the DFPT implementation in the Quantum Espresso package, the reader is referred to Refs. [40,41]. We restrict this study on the investigation of transverse optical (TO) phonons by evaluating the third-order Raman tensor at the $\Gamma$ point only, neglecting the influence of long-range electric fields. The assignment of individual modes in the Raman spectra remains unaffected by this approach, because no mixing between longitudinal optical (LO) and TO phonon branches occurs within the space group $Pna{2}_1$.

2.2. Raman Spectroscopy

The Raman experiments were performed on a home-built Raman setup with a linear polarized cw-laser (532 nm; 50 mW; frequency-doubled Nd:YAG) as the excitation source. For the experiment, the focused laser spot was placed approximately 10 $\mathsf{\mu }$m below the surface of the crystal via an objective lens with a numerical aperture of 0.7. The scattered light is collected in back scattering via the same objective and spectrally separated from the elastically scattered light via a dichroic beam splitter and a Notch filter allowing one to detect phonons down to 100 cm${}^{-1}$ of the Raman shift. For the polarized measurements, a half wave plate and analyzer are placed in the excitation and detection path, respectively. The spectral analysis is performed via a spectrometer with an attached CCD-camera allowing for a spectral resolution of approximately 2.3 cm${}^{-1}$. More details on the experimental setup can also be found in references [29,31,42]. The crystals were flux-grown crystal platelets of a z-cut orientation obtained from Raicol Crystals Ltd. (Rosh Haayin, Israel). For the polarized experiments incidentally from the x- and y-directions, pieces were cut along the main crystallographic axes and polished on the respective faces. In order to denote a particular Raman-scattering geometry, the Porto notation ${\overrightarrow{k}}_i({\overrightarrow{e}}_i,{\overrightarrow{e}}_s){\overrightarrow{k}}_s$ is used. For the incident beam, the direction of propagation and polarization is thereby indicated by ${\overrightarrow{k}}_i$ and ${\overrightarrow{e}}_i$, respectively. Similarly, the scattered light beam is characterized by ${\overrightarrow{k}}_s$ and ${\overrightarrow{e}}_s$. A backscattering geometry therefore implies ${\overrightarrow{k}}_i\Vert {\overrightarrow{k}}_s$. Directions of propagation and polarization are always chosen along the three Cartesian axes x, y and z. In the case of theoretical Raman spectra, the directions of the propagation are not explicitly considered and therefore are omitted in the notation.

3. Results and Discussion

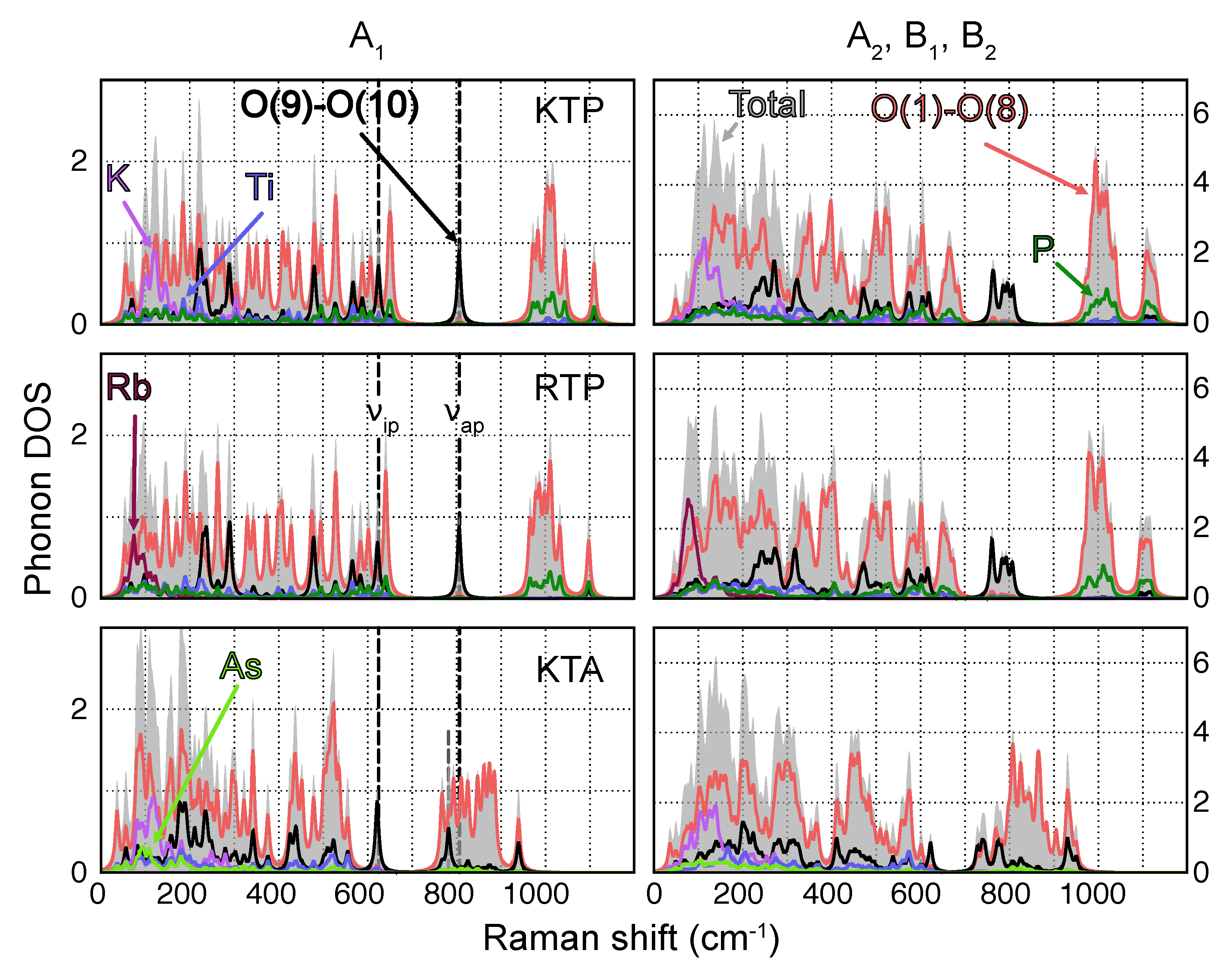
3.1. Phonon Modes

In the first step, the distribution of phonon wavenumbers and displacement patterns of all three materials are analyzed by evaluating the atomically resolved phononic density of stats (DOS). To this end, the displacement patterns of all respective 189 phonon modes are first projected onto each of the 64 atoms within the unit cell. For a given mode, the contributions of individual Ti, P [As] and K [Rb] atoms are summed up to acquire the entire contribution of the atomic species to the phonon mode. In the case of Oxygen (O), contributions of P−Ti coordinated O(1)−O(8) and Ti−Ti coordinated O(9)−O(10) ions are analyzed individually, as these have previously been identified to be connected to the emergence of the ferroelectric properties [1,2]. The phononic DOS is then modeled by Lorentzian functions with an arbitrary line width of 10 cm${}^{-1}$, which are centered at the individual phonon frequencies $\omega$ and whose heights correspond to each respective atomic species contribution.

In Figure 1, the atomically resolved phononic DOS of KTP, RTP and KTA are shown. Since the main diagonal components (x,x), (y,y) and (z,z) only feature phonons of $A_1$ symmetry (see

Table 1. Raman selection rules for crystals of space group $Pna{2}_1$ in backscattering geometry. In addition, experimental and calculated intensities of the respective phonon branches in KTP, normalized to $A_2$-TO, are displayed.

Scattering	Observable	Relative Intensity	Relative Intensity
Geometry	Phonon Branch	(Experimental)	(Calculated)
$y(x,x)\overline{y}$	$A_1$-TO	4.2	8.1
$z(x,x)\overline{z}$	$A_1$-LO	1.8	-
$x(y,y)\overline{x}$	$A_1$-TO	11.2	12.7
$z(y,y)\overline{z}$	$A_1$-LO	9.0	-
$x(z,z)\overline{x}$	$A_1$-TO	26.3	31.9
$y(z,z)\overline{y}$	$A_1$-TO	26.3	31.9
$z(x,y)\overline{z}$	$A_2$-TO	1.0	1.0
$y(x,z)\overline{y}$	$B_1$-TO	1.9	2.2
$x(y,z)\overline{x}$	$B_2$-TO	10.2	9.3

), $A_1$ phonons are displayed separately. A number of common features can be made out in the phononic DOS of all three materials. For one, each spectrum can be roughly subdivided into the following intervals, where specific atomic contributions dominate:

• Vibrations featuring displacements of the heavy alkali atoms K [Rb] with respect to the surrounding PO${}_4$ (AsO${}_4$) and TiO${}_6$ polyhedra are found predominantly in the low wavenumber regime (<300 cm${}^{-1}$);
• Owing to their relatively large force constants due to higher bond strength and overall lower masses, P−O-type vibrations are localized essentially at wavenumbers upwards of 950 cm${}^{-1}$;
• Since As has a much higher mass compared to P, As−O-type vibrations posses much lower force constants and are thus localized at frequencies close to the K and Rb regime;
• Vibrations involving Ti are found in a broad wavenumber range below around 650 cm${}^{-1}$.

Additionally, in the case of KTP and RTP, a broad gap between 650 cm${}^{-1}$ and 950 cm${}^{-1}$ is observed in the phononic DOS, occupied exclusively by phonons of O(9) and O(10)-type character. The sublattice of O(9) and O(10)-type atoms takes a special role in the phononic DOS, since its chemical environment is identical in KTP, RTP and KTA. Vibrations of predominantly O(9) and O(10) characters should therefore be found at virtually equal frequencies for all three materials. This observation holds especially for phonons in the middle of the gap region, at around 800 cm${}^{-1}$. Even in the phononic DOS of KTA, in which the gap region is superimposed by high wavenumber vibrations of O(1)−O(8)-type, phonons of O(9) and O(10)-type experience only a relatively small wavenumber shift compared to KTP and RTP. Out of those phonons, only a single one (in the following labeled ${\nu }_{\mathrm{ap}}$) is of $A_1$ symmetry, located at 806 cm${}^{-1}$ (KTP and RTP) and 782 cm${}^{-1}$ (KTA). Its displacement pattern in the case of KTP is displayed in Figure 2, with the respective displacement patterns in RTP and KTA being nearly identical.

The induced distortion of the TiO${}_6$ octahedra is found to depend on their orientation, i.e., if neighboring octahedra are linked in a cis or trans manner. In the case of octahedra oriented along the x direction (trans-type linking), ${\nu }_{\mathrm{ap}}$ induces an anti-phase stretch/compression along the [011] and [01$\overline{1}$] directions, while octahedra oriented along y (cis-type linking) experience predominantly an anti-phase stretch/compression of a single octahedron edge along [001]. In addition to ${\nu }_{\mathrm{ap}}$, the O(9)−O(10)-type mode ${\nu }_{\mathrm{ip}}$ located at 622 cm${}^{-1}$ is expected to play an important role in the interpretation of the Raman spectra of all three materials, since both modes are easily separated from the remaining phonon bands. Unlike ${\nu }_{\mathrm{ap}}$, the displacement pattern of ${\nu }_{\mathrm{ip}}$ thereby features an in-phase distortion of the TiO${}_6$ octahedra; see Figure 2.

In their pioneering work, Kugel et al. mapped the entire phonon spectrum of KTP, obtained by infrared and Raman spectroscopy, onto the vibrational eigenmodes of the PO${}_4$ and TiO${}_6$ substructures [32]. A comparison between the spectra of KTP and RTP thereby indicated the existence of external lattice modes (involving the displacement of K and Rb) below 200 cm${}^{-1}$. Additionally, based on calculated frequencies of the internal vibrations in PO${}_4$, Raman bands in the high-wavenumber regime could be mapped to two triply degenerate PO${}_4$ vibrational modes in the range between 950 cm${}^{-1}$ and 1100 cm${}^{-1}$. In the present study, these two mappings are essentially confirmed. In order to complete the internal mode analysis in KTP, the remaining Raman bands have been assigned to (i) internal TiO${}_6$ modes and (ii) collective modes involving displacements of the entire TiO${}_6$ substructure with respect to the rest of the crystal as well as individual components of a breathing mode within TiO${}_6$. This assignment thereby stands on a phenomenological footing and is based on similarities regarding mode distributions in KTP, RTP and other materials with TiO${}_6$ octahedra, such as the archetypal perovskite barium titanate (BaTiO${}_3$). It ultimately leads to the conclusion that Raman bands of the highest intensity are related to anti-phase vibrations involving the long and short Ti−O bonds in TiO${}_6$. For KTP, vibrations of this character can be identified in the present phonon spectrum as an amalgamation of modes with various symmetries around ${\nu }_{\mathrm{ap}}$ and ${\nu }_{\mathrm{ip}}$. For this reason, the hypothesis by Kugel et al. may be extended: Phonon modes of O(9) and O(10) characters in general should be responsible for the most prominent Raman peaks. Regarding $A_1$-type phonons, observable within the main diagonal components $(x,x)$, $(y,y)$ and $(z,z)$, this further underlines the important role of the modes ${\nu }_{\mathrm{ap}}$ and ${\nu }_{\mathrm{ip}}$.

Within the KTP-family unit cell, the alkali atom can occupy two distinct lattice sites K(1) and K(2) [Rb(1) and Rb(2)] [39]. These are particularly relevant, as apart from the alternating length of the Ti−O chains, the K [Rb] atoms at these sites play another role in the ferroelectricity and have therefore been of particular interest. Figure 3 shows the phononic DOS for A${}_1$-type phonons in RTP (left) and KTP (right) resolved for the two lattice sites Rb(1) and Rb(2) [(K(1) and K(2)] in the low wavenumber region. Based on the calculated DOS, certain phonons can be distinctively associated with one or the other of these lattice sites, e.g., in RTP, a peak at 75 cm${}^{-1}$ is dominated by the displacement of the Rb atom at the Rb(2) site, while a peak slightly larger at 90 cm${}^{-1}$ can be associated with the Rb(1) site. This indicates that Raman spectroscopy may be used to study the occupancy of those two lattice sites, as well.

3.2. Raman Spectra

In the next step, this presumed prominent role of O(9) and O(10) modes is further analyzed by calculating the Raman cross sections of all modes for all three materials. Calculated spectra are obtained by introducing an artificial Lorentzian broadening of 10 cm${}^{-1}$ around the respective phonon wavenumber. As shown in previous examples, this yields reasonable spectra to compare with experimental results [35].

As a benchmark test, the tensor elements $|{\overrightarrow{e}}_i·R^{\nu }·{\overrightarrow{e}}_s{|}^2$ of phonons $\nu$ with the highest calculated Raman cross section per polarization configuration (s,i) are compared with experimental data. Since all three materials are members of the same space group and relative intensities of tensor elements should therefore be similar, we restrict this analysis to KTP only. According to Table 1, $A_2$-TO phonons in (x,y) and $A_1$-TO phonons in (z,z) polarization show the lowest and highest intensities, respectively, separated by a factor of about 26. With respect to (z,z), $A_1$-TO phonons within the other two main diagonal components (x,x) and (y,y) show weaker intensities, at around 16 and 43%, respectively. Similar observations have been made by Kugel et al. [32]. This can be expected, as the largest change in polarizability occurs along z as the direction of internal polarization [2]. The experimental trends regarding relative intensities within different scattering geometries are generally well reproduced by the present calculations. As the only exception, the Raman scattering within (x,x) polarization is predicted at about twice the intensity with respect to the experimental data. This might be a consequence of the calculated Raman spectrum of KTP in (x,x) polarization being essentially governed by a single high intensity peak at 530 cm${}^{-1}$, related to a PO${}_4$-type vibration; see Figure 1 and Figure 4. An uncertainty in the peak height of this mode would therefore predominantly affect the relative intensity in (x,x). In fact, if the mode of the second-highest intensity was chosen as a reference, the relative intensity would drop to 4.57, which is much closer to the experimental value.

Next, experimental and calculated Raman spectra of all three materials are directly compared. To this end, the spectra of all polarization configurations and materials are normalized to the highest intensity. The comparison of main- and off-diagonal components is depicted in Figure 4 and Figure 5, respectively.

While the wavenumber range, in which Raman-active modes are detected in the experiment, agrees qualitatively and in the overall shape reproduced by the present theoretical spectra, the overall agreement regarding mode position and peak height is rather unsatisfying for a number of reasons. For one, unlike within the experimental spectra, most high intensity peaks are found in the low-wavenumber regime around and below 200 cm${}^{-1}$, involving K- and Rb-type vibrations. In particular, the modes of the highest intensity for nearly all off-diagonal and the (z,z) component fall into this wavenumber range. A noticeable difference between the spectra of KTP/KTA and RTP is thereby observed, as related to the admixture of K and Rb into the modes in the low-wavenumber regime. For this reason, in the case of RTP, the influence of the utilized pseudopotential on the overall shape of the spectra is analyzed by testing a modified pseudopotential including the Rb${}_{4\mathrm{p}}$ orbitals as valence states. However, apart from a very tiny blueshift of all modes involving oxygen, no significant difference in the Raman intensity of the low wavenumber part of the RTP spectrum is observed.

In comparison, the high wavenumber regime around and above 1000 cm${}^{-1}$, involving vibrations of PO${}_4$ and AsO${}_4$, shows an overall much better agreement with the experimental spectra. Especially for the main diagonal components, peak positions and relative intensities are reproduced favorably. This discrepancy in agreement with the experiment is a consequence of the fact that modes involving PO${}_4$/AsO${}_4$ are nearly decoupled from the remaining lattice, as stated by Kugel et al. [32].

The biggest discrepancy between calculated and experimental spectra is observed in the mid-wavenumber regime, in particular regarding the experimentally detected mode of the highest Raman intensity. Using the notation of Kugel et al., this mode shall be labeled ${\nu }_1$ and is found at 692 cm${}^{-1}$ (KTP), 690 cm${}^{-1}$ (RTP) and 670 cm${}^{-1}$ (KTA) for the $A_1$-TO phonon branch for all three possible polarization configurations. However, all three frequencies fall into the before-mentioned gap region within the phononic DOS; thus, no direct assignment to calculated phonon modes based on the wavenumber and peak height can be made. This mode is particularly dominant in the experimental spectra and was observed by all previous works on Raman spectroscopy in KTP and related compounds; thus, it can be ruled out to be specific to our investigated crystal only [31,32,33,34,43,44,45,46]. According to Kugel et al., the strong modes in these regions can be assigned to the Ti−O vibrations somewhat similar to the ${\nu }_{\mathrm{ip}}$ and ${\nu }_{\mathrm{ap}}$ introduced in this study. The assignment by Kugel et al. also seems plausible, because the asymmetry in the Ti−O links is associated strongly with the ferroelectricity and polar nature of the crystal. This fits well with the observation that these intense modes in different scattering configurations appear to be reacting strongly to the presence of a domain wall [30,31], as well as showing a strong directional dispersion, i.e., change in intensity and frequency at oblique propagation angles [30].

In the vicinity of the gap region in the calculated phonon DOS, only a few modes with nonzero Raman intensity within any polarization configuration are observed, the previously discussed modes ${\nu }_{\mathrm{ip}}$ and ${\nu }_{\mathrm{ap}}$, in particular. Since LDA is known to overestimate vibrational frequencies, an assignment to ${\nu }_{\mathrm{ap}}$ appears to be more likely, albeit a difference in the wavenumber of around 100 cm${}^{-1}$. This difference is partially explainable by the utilized pseudopotential and lattice constants, as the wavenumber of ${\nu }_{\mathrm{ap}}$ in KTP is found to decrease by around 20 cm${}^{-1}$ if the phonon spectrum is calculated using PBEsol and relaxed lattice constants. Further evidence for ${\nu }_1$ being associated with ${\nu }_{\mathrm{ap}}$ is the wavenumber difference between its value in KTP/RTP and KTA, as the experimentally detected difference of 20 cm${}^{-1}$ is identical to the one observed for ${\nu }_{\mathrm{ap}}$.

This mode assignment, however, is not supported by the calculated Raman intensity of ${\nu }_{\mathrm{ap}}$. Unlike the highest-intensity peak in the experimental spectra, the peak height of ${\nu }_{\mathrm{ap}}$ is found to be highly anisotropic: For all three materials, it is largest for (y,y) polarization and almost zero for (x,x); see Figure 4. A similar observation can be made for ${\nu }_{\mathrm{it}}$, with the highest and lowest intensity for (z,z) and (x,x) polarizations, respectively. The origin of this dissimilarity between experimental and calculated spectra is not fully clear. In order to rule out a strong link between the observed dissimilarity and the utilized DFPT methodology, Raman spectra of all three materials are calculated again within the Vienna Ab initio Simulation Package (VASP) [47], using finite-difference routines [35] and the same computational settings/atomic geometries, as described previously. As expected, all spectra experience a blueshift of up to 40 cm${}^{-1}$ due to the changes in lattice constants and pseudopotentials. The general trend regarding the mid-wavenumber regime, however, does not change. For one, the modes ${\nu }_{\mathrm{ip}}$ and ${\nu }_{\mathrm{ap}}$ are found below and above ${\nu }_1$, respectively. In addition, the Raman intensity of both modes is nearly zero for (x,x) polarization, with the intensity of modes ${\nu }_{\mathrm{ip}}$ and ${\nu }_{\mathrm{ap}}$ being the highest for (z,z) and (y,y), respectively. The discrepancy between experimental and calculated spectra is therefore not mainly related to the used methodology.

It should be noted that dissimilarities in peak heights within the low- and mid-wavenumber regime are not independent, as a reduction in relative intensity for the low-wavenumber part would naturally lead to an increase in the mid-wavenumber part and vice versa. As it is widely known from the literature, all three materials are prone to K and Rb deficiencies, which are expected to influence the low-wavenumber regime of the respective spectra, as observed by a number of experimental Raman studies [32,33,45,48,49].

Exemplarily, this is illustrated for the x(y,y)$\overline{x}$ polarization of KTP in Figure 6.

The three experimental spectra from Voronko et al. [49], Kugel et al. [32] and ours were thereby obtained under room temperature conditions. Above 350 cm${}^{-1}$, the amount of detected peaks as well as relative intensities does not change between the three spectra. In the low-wavenumber part, however, the spectra differ noticeably. In particular, the intensity of a prominent peak at 265 cm${}^{-1}$ shows a considerable spread, being either much stronger or weaker compared to ${\nu }_1$. For this reason, the nonstoichiometry of the utilized crystals in general and alkali-atom deficiency in particular are expected to at least partially explain the observed discrepancies between experimental and calculated spectra.

4. Summary and Conclusions

Calculations of phonon spectra and Raman cross sections of KTP, RTP and KTA were performed using DFPT routines. The phonon spectra were thereby found to be subdivided into a number of regions with varying vibrational characters, overall confirming the prior phenomenologically footed mapping by Kugel et al. [32] and others. Exemplarily, we have shown that the calculation of an improved assignment of phonons could be used to investigate the crystals to a more detailed level, such as when determining the occupancy of different lattice sites. While the relative intensities of the highest peaks within most of the spectral ranges and different polarization configurations are well-reproduced in theory, no conclusive matching between experimental and DFT-calculated high-intensity peaks could be made. In particular, the experimental $A_1$-type mode ${\nu }_1$-type of the highest intensity for all three materials is located directly within a calculated gap region, preventing a direct, wavenumber-based mode assignment. Additionally, all calculated modes in the vicinity of the gap region (modes ${\nu }_{\mathrm{ip}}$ and ${\nu }_{\mathrm{ap}}$, in particular) are found to feature a pronounced modulation of the peak height with respect to the polarization configuration, which is not observed in the experiment. Nonetheless, a number of arguments can be made for an assignment between ${\nu }_1$ and ${\nu }_{\mathrm{ap}}$. (i) The blueshift of ${\nu }_{\mathrm{ap}}$ with respect to ${\nu }_1$ is partially explainable by the use of the PZ-LDA functional; (ii) both modes feature the same redshift of about 20 cm${}^{-1}$ between materials KTP/RTP and KTA; (iii) the relative peak heights between ${\nu }_1$ and low-wavenumber modes are known to be affected significantly by the density of K vacancies, partially explaining the dissimilarities regarding experimental and calculated peak heights. In order to verify this mapping, however, argument (iii) should be further quantified by analyzing the experimental and theoretical Raman signatures of nonstoichiometric KTP, RTP and KTA and external defects, as well as including long-range effects such as LO-TO coupling. Nevertheless, our work demonstrates that, based on first-principles calculations, a more in-depth understanding of the spectra is possible and can be applied in the study, optimizing novel devices within the KTP crystal family.