Studies on Optoelectronic and Transport Properties of XSnBr3 (X = Rb/Cs): A DFT Insight
Abstract
:1. Introduction
2. Computational Method
3. Results and Discussion
3.1. Structural Properties
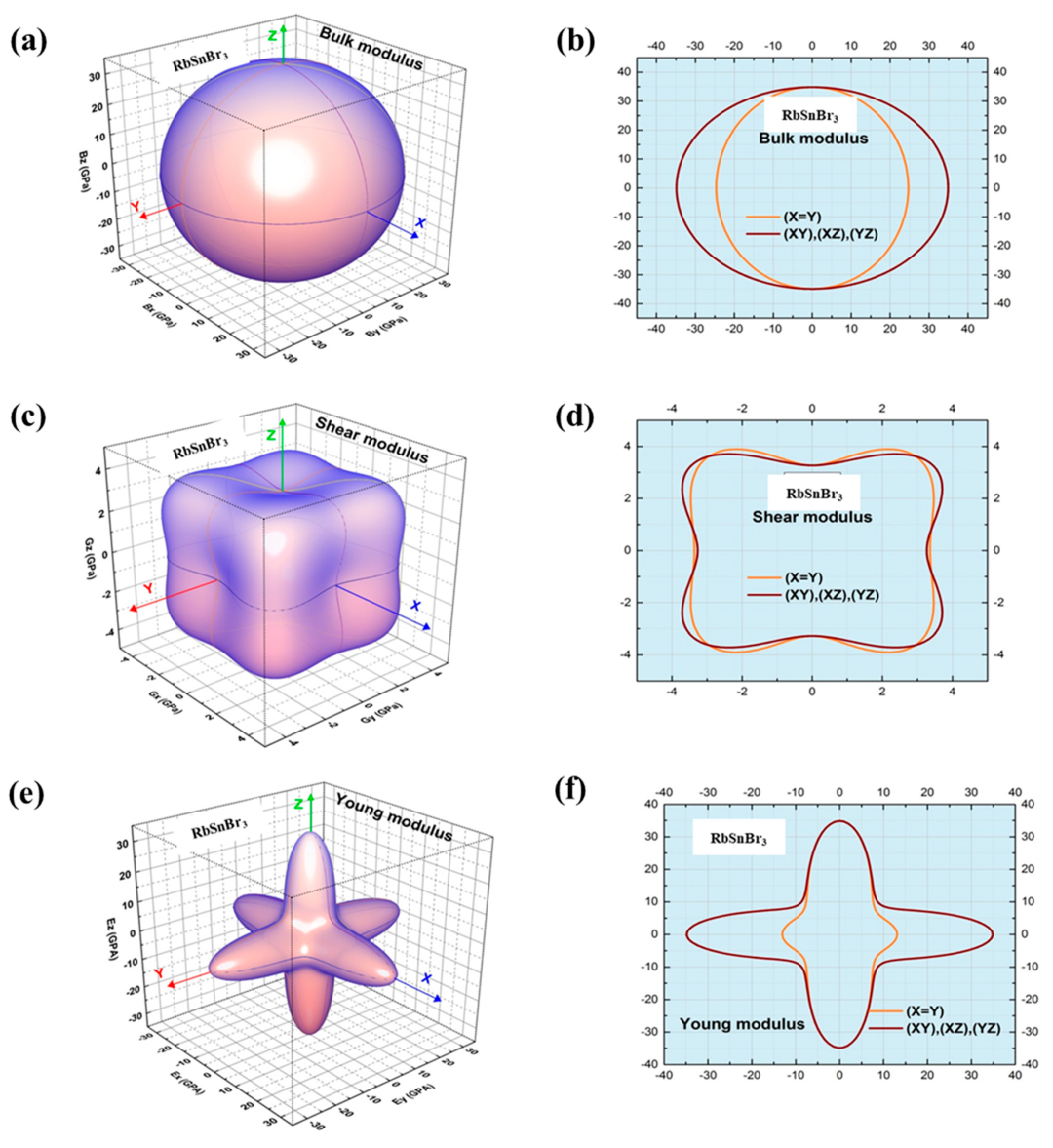
3.2. Elastic Characteristics
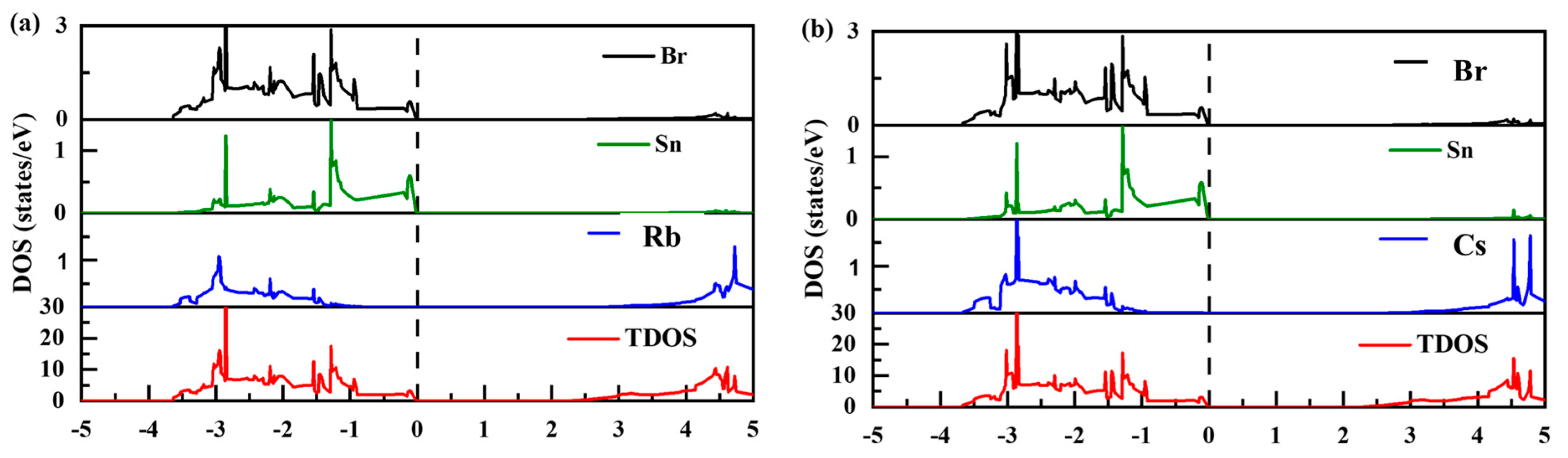
3.3. Electronic Properties
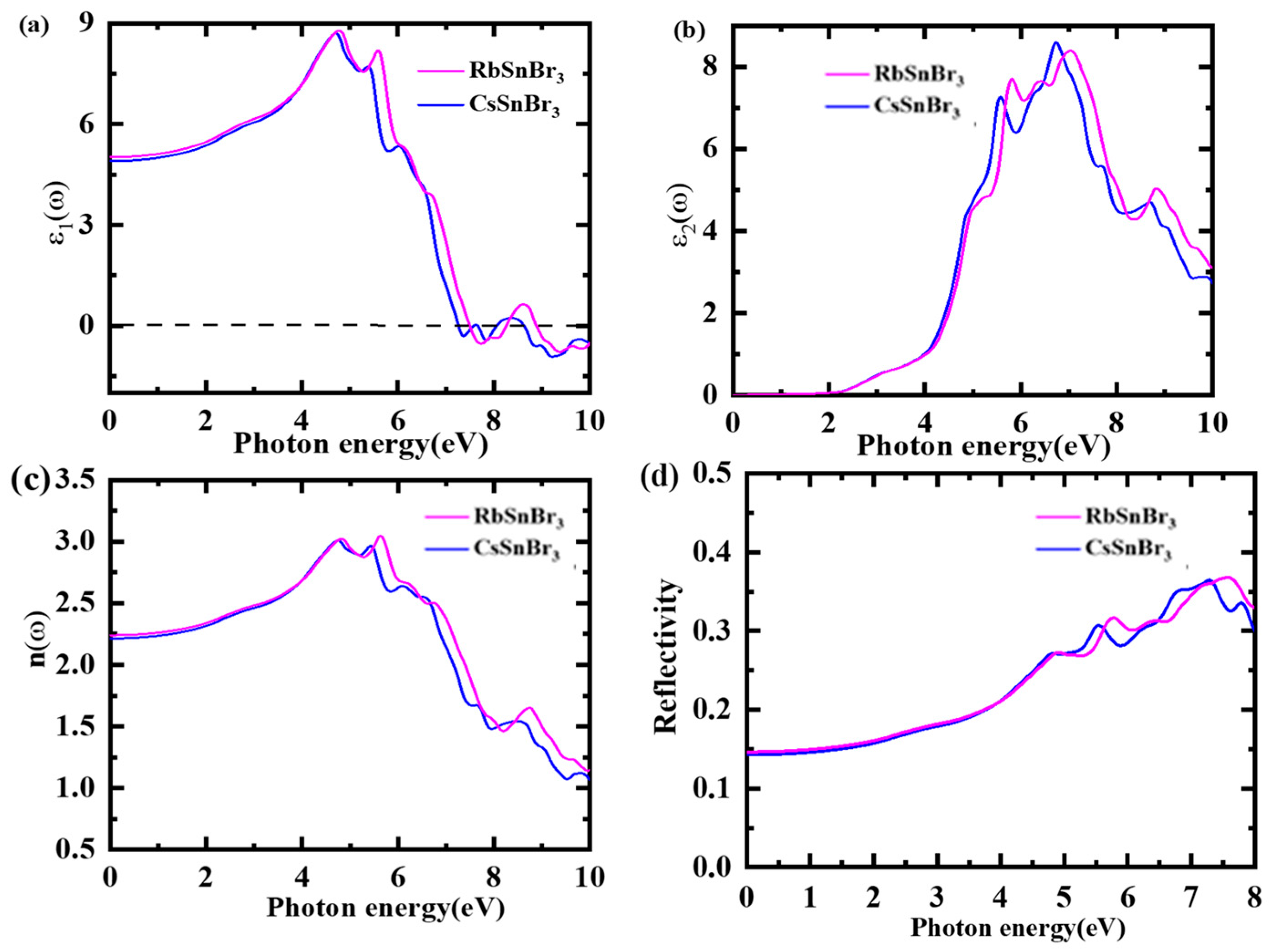
3.4. Optical Properties
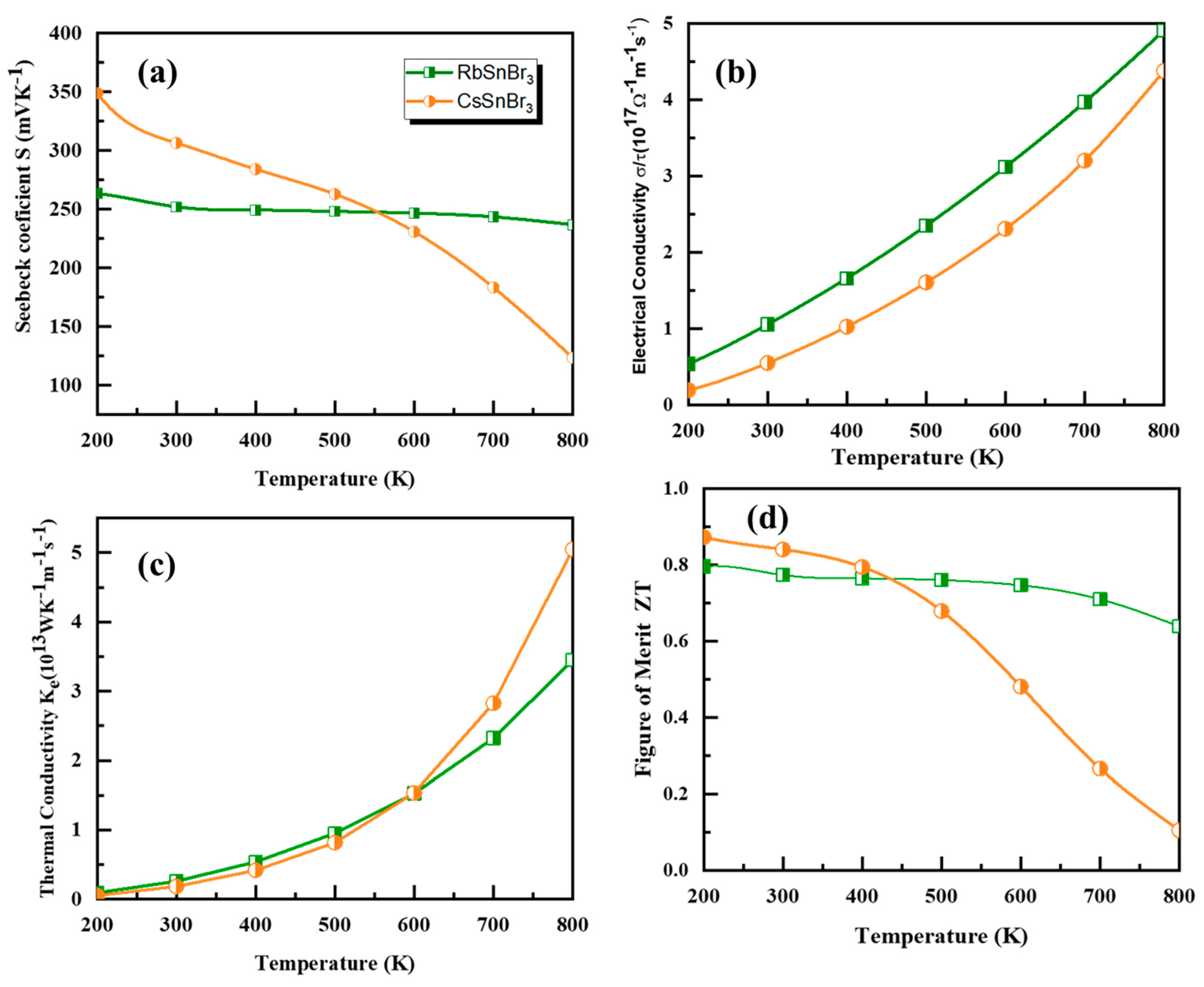
3.5. Thermoelectricity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jarman, J.T.; Khalil, E.E.; Khalaf, E. Energy Analyses of Thermoelectric Renewable Energy Sources. Open J. Energy Effic. 2013, 2013, 143–153. [Google Scholar] [CrossRef]
- Haq, B.U.; Ahmed, R.; AlFaify, S.; Butt, F.K.; Shaari, A.; Laref, A. Exploring Thermoelectric Materials for Renewable Energy Applications: The Case of Highly Mismatched Alloys Based on AlBi1-XSbx and InBi1-XSbx. Intermetallics 2018, 93, 235–243. [Google Scholar] [CrossRef]
- Goldsmid, H.J. Introduction to Thermoelectricity; Springer: Berlin/Heidelberg, Germany, 2010; Volume 121, ISBN 3642007570. [Google Scholar]
- Behera, D.; Al-Qaisi, S.; Manzoor, M.; Sharma, R.; Srivastava, V.; mana Al-Anazy, M.; El Shiekh, E.; Mukherjee, S.K. First Principles Studies on Optoelectronics and Transport Properties of KSrY (Y= Sb, Bi) for Renewable Energy Application. Mater. Sci. Eng. B 2023, 297, 116765. [Google Scholar] [CrossRef]
- Dixit, A.; Saxena, A.; Sharma, R.; Behera, D.; Mukherjee, S. Solar Photovoltaic Principles; Ismail, B.I., Ed.; IntechOpen: Rijeka, Croatia, 2023; p. Ch. 1. ISBN 978-1-83768-677-3. [Google Scholar]
- Goldsmid, H.J. Improving the Thermoelectric Figure of Merit. Sci. Technol. Adv. Mater. 2021, 22, 280–284. [Google Scholar] [CrossRef] [PubMed]
- Behera, D.; Sharma, R.; Ullah, H.; Waheed, H.S.; Mukherjee, S.K. Electronic, Optical, and Thermoelectric Investigations of Zintl Phase AAg2Se2 (A= Sr, Ba) Compounds: A First First-Principles Approach. J. Solid State Chem. 2022, 312, 123259. [Google Scholar] [CrossRef]
- Nemir, D.; Beck, J. On the Significance of the Thermoelectric Figure of Merit Z. J. Electron. Mater. 2010, 39, 1897–1901. [Google Scholar] [CrossRef]
- Kharlamov, V.F. Thermoelectric Figure of Merit of a Material Consisting of Semiconductor or Metal Particles. J. Exp. Theor. Phys. 2013, 117, 83–88. [Google Scholar] [CrossRef]
- Wu, T.; Gao, P. Development of Perovskite-Type Materials for Thermoelectric Application. Materials 2018, 11, 999. [Google Scholar] [CrossRef]
- Haque, M.A.; Kee, S.; Villalva, D.R.; Ong, W.; Baran, D. Halide Perovskites: Thermal Transport and Prospects for Thermoelectricity. Adv. Sci. 2020, 7, 1903389. [Google Scholar] [CrossRef]
- Manzoor, M.; Behera, D.; Sharma, R.; Iqbal, M.W.; Mukherjee, S.K.; Khenata, R.; Bin-Omran, S.; Alshahrani, T.; El Shiekh, E.; Ouahrani, T. Structural, Electronic, Optical, and Thermoelectric Studies on Zintl SrCd2Pn2 (Pn= P/As) Compounds for Solar Cell Applications: A First Principle Approach. J. Solid State Chem. 2023, 326, 124188. [Google Scholar] [CrossRef]
- Kumavat, S.R.; Sonvane, Y.; Singh, D.; Gupta, S.K. Two-Dimensional CH3NH3PBI3 with High Efficiency and Superior Carrier Mobility: A Theoretical Study. J. Phys. Chem. C 2019, 123, 5231–5239. [Google Scholar] [CrossRef]
- Andrianov, A.V.; Aleshin, A.N.; Matyushkin, L.B. Terahertz Vibrational Modes in CH3NH3PBI3 and CsPbI3 Perovskite Films. JETP Lett. 2019, 109, 28–32. [Google Scholar] [CrossRef]
- Afsari, M.; Boochani, A.; Shirdel, F. Electronic and Optical Properties of Two Propounded Compound in Photovoltaic Applications, CsPbI3 and CH3NH3PbI3: By DFT. Optik 2019, 199, 163360. [Google Scholar] [CrossRef]
- Roknuzzaman, M.; Ostrikov, K.; Wang, H.; Du, A.; Tesfamichael, T. Towards Lead-Free Perovskite Photovoltaics and Optoelectronics by Ab-Initio Simulations. Sci. Rep. 2017, 7, 14025. [Google Scholar] [CrossRef]
- Wu, Y.; Li, X.; Zeng, H. Lead-free Halide Double Perovskites: Structure, Luminescence, and Applications. Small Struct. 2021, 2, 2000071. [Google Scholar] [CrossRef]
- Mukhtar, M.W.; Ramzan, M.; Rashid, M.; Hussain, A.; Naz, G.; Ciftci, Y.O.; Dahshan, A.; Znaidia, S. Systematic Study of Optoelectronic and Thermoelectric Properties of New Lead-Free Halide Double Perovskites A2KGaI6 (A= Cs, Rb) for Solar Cell Applications via Ab-Initio Calculations. Mater. Sci. Eng. B 2022, 285, 115957. [Google Scholar] [CrossRef]
- Zhao, X.-G.; Yang, J.-H.; Fu, Y.; Yang, D.; Xu, Q.; Yu, L.; Wei, S.-H.; Zhang, L. Design of Lead-Free Inorganic Halide Perovskites for Solar Cells via Cation-Transmutation. J. Am. Chem. Soc. 2017, 139, 2630–2638. [Google Scholar] [CrossRef]
- Xiao, Z.; Yan, Y. Progress in Theoretical Study of Metal Halide Perovskite Solar Cell Materials. Adv. Energy Mater. 2017, 7, 1701136. [Google Scholar] [CrossRef]
- Li, C.; Lu, X.; Ding, W.; Feng, L.; Gao, Y.; Guo, Z. Formability of Abx3 (X= f, Cl, Br, i) Halide Perovskites. Acta Crystallogr. Sect. B: Struct. Sci. 2008, 64, 702–707. [Google Scholar] [CrossRef]
- Sun, J.; Singh, D.J. Thermoelectric Properties of N-Type SrTiO3. APL Mater. 2016, 4, 104803. [Google Scholar] [CrossRef]
- Aboub, Z.; Seddik, T.; Daoudi, B.; Boukraa, A.; Behera, D.; Batouche, M.; Mukherjee, S.K. Impact of La, Ni-Doping on Structural and Electronic Properties of SrTiO3 for Photocatalytic Water Splitting. Inorg. Chem. Commun. 2023, 153, 110871. [Google Scholar] [CrossRef]
- Asmara, T.C.; Annadi, A.; Santoso, I.; Gogoi, P.K.; Kotlov, A.; Omer, H.M.; Motapothula, M.; Breese, M.B.H.; Rübhausen, M.; Venkatesan, T. Mechanisms of Charge Transfer and Redistribution in LaAlO3/SrTiO3 Revealed by High-Energy Optical Conductivity. Nat. Commun. 2014, 5, 3663. [Google Scholar] [CrossRef] [PubMed]
- Bouadjemi, B.; Bentata, S.; Abbad, A.; Benstaali, W. Ab-Initio Study of Optoelectronic and Magnetic Properties of the Orthorhombic NdMnO3 Perovskite. Solid State Commun. 2015, 207, 9–15. [Google Scholar] [CrossRef]
- Murtaza, G.; Ahmad, I.; Amin, B.; Afaq, A.; Maqbool, M.; Maqssod, J.; Khan, I.; Zahid, M. Investigation of Structural and Optoelectronic Properties of BaThO3. Opt. Mater. 2011, 33, 553–557. [Google Scholar] [CrossRef]
- Noor, N.A.; Hassan, M.; Rashid, M.; Alay-e-Abbas, S.M.; Laref, A. Systematic Study of Elastic, Electronic, Optical and Thermoelectric Properties of Cubic BiBO3 and BiAlO3 Compounds at Different Pressure by Using Ab-Initio Calculations. Mater. Res. Bull. 2018, 97, 436–443. [Google Scholar] [CrossRef]
- Aktary, M.; Kamruzzaman, M.; Afrose, R. A Comparative Study of the Mechanical Stability, Electronic, Optical and Photocatalytic Properties of CsPbX 3 (X= Cl, Br, I) by DFT Calculations for Optoelectronic Applications. RSC Adv. 2022, 12, 23704–23717. [Google Scholar] [CrossRef]
- Sabir, B.; Murtaza, G.; Khalil, R.M.A.; Mahmood, Q. First Principle Study of Electronic, Mechanical, Optical and Thermoelectric Properties of CsMO3 (M= Ta, Nb) Compounds for Optoelectronic Devices. J. Mol. Graph. Model. 2019, 86, 19–26. [Google Scholar] [CrossRef]
- Ilyas, A.; Khan, S.A.; Liaqat, K.; Usman, T. Investigation of the Structural, Electronic, Magnetic, and Optical Properties of CsXO3 (X= Ge, Sn, Pb) Perovskites: A First-Principles Calculations. Optik 2021, 244, 167536. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Sorantin, P.; Trickey, S.B. Full-Potential, Linearized Augmented Plane Wave Programs for Crystalline Systems. Comput. Phys. Commun. 1990, 59, 399–415. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Madsen, G.K.H.; Kvasnicka, D.; Luitz, J. Wien2k. Augment. Plane Wave+ Local Orbitals Program Calc. Cryst. Prop. 2001, 60, 1. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Koller, D.; Tran, F.; Blaha, P. Merits and Limits of the Modified Becke-Johnson Exchange Potential. Phys. Rev. B 2011, 83, 195134. [Google Scholar] [CrossRef]
- Behera, D.; Manzoor, M.; Maharana, M.; Iqbal, M.W.; Zahid, T.; Lakra, S.; Mukherjee, S.K.; Alarfaji, S.S. Structural, Electronic, Optical, and Thermoelectric Response of Zintl Phase AAg2S2 (A= Sr/Ba) Compounds for Renewable Energy Applications. Phys. B Condens. Matter 2023, 649, 414446. [Google Scholar] [CrossRef]
- Madsen, G.K.H.; Singh, D.J. BoltzTraP. A Code for Calculating Band-Structure Dependent Quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef]
- Sharma, R.; Dey, A.; Dar, S.A.; Srivastava, V. A DFT Investigation of CsMgX3 (X= Cl, Br) Halide Perovskites: Electronic, Thermoelectric and Optical Properties. Comput. Theor. Chem. 2021, 1204, 113415. [Google Scholar] [CrossRef]
- Katsura, T.; Tange, Y. A Simple Derivation of the Birch–Murnaghan Equations of State (EOSs) and Comparison with EOSs Derived from Other Definitions of Finite Strain. Minerals 2019, 9, 745. [Google Scholar] [CrossRef]
- Fedorovskiy, A.E.; Drigo, N.A.; Nazeeruddin, M.K. The Role of Goldschmidt’s Tolerance Factor in the Formation of A2BX6 Double Halide Perovskites and Its Optimal Range. Small Methods 2020, 4, 1900426. [Google Scholar] [CrossRef]
- Emery, A.A.; Wolverton, C. High-Throughput DFT Calculations of Formation Energy, Stability and Oxygen Vacancy Formation Energy of ABO3 Perovskites. Sci. Data 2017, 4, 170153. [Google Scholar] [CrossRef]
- Behera, D.; Mukherjee, S.K. Optoelectronics and Transport Phenomena in Rb2InBiX6 (X= Cl, Br) Compounds for Renewable Energy Applications: A DFT Insight. Chemistry 2022, 4, 1044–1059. [Google Scholar] [CrossRef]
- Mahmood, Q.; Yaseen, M.; Hassan, M.; Rashid, M.S.; Tlili, I.; Laref, A. The First-Principle Study of Mechanical, Optoelectronic and Thermoelectric Properties of CsGeBr3 and CsSnBr3 Perovskites. Mater. Res. Express 2019, 6, 45901. [Google Scholar] [CrossRef]
- Anderson, O.; Schreiber, E.; Soga, N. Elastic Constants and Their Measurements; McGraw-Hill Companies, Inc.: New York, NY, USA, 1973. [Google Scholar]
- Mouhat, F.; Coudert, F.-X. Necessary and Sufficient Elastic Stability Conditions in Various Crystal Systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
- Behera, D.; Mukherjee, S.K. Theoretical Investigation of the Lead-Free K2InBiX6 (X= Cl, Br) Double Perovskite Compounds Using First Principle Calculation. JETP Lett. 2022, 116, 537–546. [Google Scholar] [CrossRef]
- Behera, D.; Dixit, A.; Nahak, B.; Srivastava, A.; Dubey, S.; Sharma, R.; Mishra, A.K.; Mukherjee, S.K. Structural, Electronic, Elastic, Vibrational and Thermodynamic Properties of Antiperovskites Mg3NX (X= Ge, Sn): A DFT Study. Phys. Lett. A 2022, 453, 128478. [Google Scholar] [CrossRef]
- Al-Qaisi, S.; Rached, H.; Alrebdi, T.A.; Bouzgarrou, S.; Behera, D.; Mukherjee, S.K.; Khuili, M.; Adam, M.; Verma, A.S.; Ezzeldien, M. Study of Mechanical, Optical, and Thermoelectric Characteristics of Ba2XMoO6 (X= Zn, Cd) Double Perovskite for Energy Harvesting. J. Comput. Chem. 2023. [Google Scholar] [CrossRef]
- Kube, C.M. Elastic Anisotropy of Crystals. AIP Adv. 2016, 6, 95209. [Google Scholar] [CrossRef]
- Chung, D.H.; Buessem, W.R. The Elastic Anisotropy of Crystals. J. Appl. Phys. 1967, 38, 2010–2012. [Google Scholar] [CrossRef]
- Pugh, S.F. XCII. Relations between the Elastic Moduli and the Plastic Properties of Polycrystalline Pure Metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Dixit, A.; Behera, D.; Tripathi, S.K.; Srivastava, A.; Sharma, R.; Khenata, R.; Albalawi, H.; Mahmoud, Z.; Mukherjee, S.K. Vibrational, Mechanical, Electronic and Thermodynamic Properties of Rhenium-Based Perovskites XReO3 (X= Li, Be) by an Ab-Initio Computation. Mater. Sci. Eng. B 2023, 294, 116545. [Google Scholar] [CrossRef]
- Behera, D.; Manzoor, M.; Iqbal, M.W.; Lakra, S.; Mukherjee, S.K. Revealing Excellent Electronic, Optical, and Thermoelectric Behavior of EU Based Euag2y2 (Y= S/Se): For Solar Cell Applications. Comput. Condens. Matter 2022, 32, e00723. [Google Scholar] [CrossRef]
- Cohen, M.H.; Ham, F.S. Electron Effective Mass in Solids—A Generalization of Bardeen’s Formula. J. Phys. Chem. Solids 1960, 16, 177–183. [Google Scholar] [CrossRef]
- Savin, A.; Nesper, R.; Wengert, S.; Fässler, T.F. ELF: The Electron Localization Function. Angew. Chem. Int. Ed. Engl. 1997, 36, 1808–1832. [Google Scholar] [CrossRef]
- Watcharatharapong, T.; Minakshi Sundaram, M.; Chakraborty, S.; Li, D.; Shafiullah, G.M.; Aughterson, R.D.; Ahuja, R. Effect of Transition Metal Cations on Stability Enhancement for Molybdate-Based Hybrid Supercapacitor. ACS Appl. Mater. Interfaces 2017, 9, 17977–17991. [Google Scholar] [CrossRef] [PubMed]
- Abt, R.; Ambrosch-Draxl, C.; Knoll, P. Optical Response of High Temperature Superconductors by Full Potential LAPW Band Structure Calculations. Phys. B: Condens. Matter 1994, 194, 1451–1452. [Google Scholar] [CrossRef]
- Penn, D.R. Wave-Number-Dependent Dielectric Function of Semiconductors. Phys. Rev. 1962, 128, 2093. [Google Scholar] [CrossRef]
- Cai, J.; Mahan, G.D. Effective Seebeck Coefficient for Semiconductors. Phys. Rev. B 2006, 74, 75201. [Google Scholar] [CrossRef]
- Behera, D.; Mohammed, B.; Taieb, S.; Mokhtar, B.; Al-Qaisi, S.; Mukherjee, S.K. First-Principle Investigations on Optoelectronics and Thermoelectric Properties of Lead-Free Rb2InSbX6 (X= Cl, Br) Double Perovskites: For Renewable Energy Applications. Eur. Phys. J. Plus 2023, 138, 520. [Google Scholar] [CrossRef]
- Haque, E.; Hossain, M.A. Origin of Ultra-Low Lattice Thermal Conductivity in Cs2BiAgX6 (X= Cl, Br) and Its Impact on Thermoelectric Performance. J. Alloys Compd. 2018, 748, 63–72. [Google Scholar] [CrossRef]
- Shaheen, M.A.M.; Hasanien, H.M.; Turky, R.A.; Ćalasan, M.; Zobaa, A.F.; Abdel Aleem, S.H.E. OPF of Modern Power Systems Comprising Renewable Energy Sources Using Improved CHGS Optimization Algorithm. Energies 2021, 14, 6962. [Google Scholar] [CrossRef]
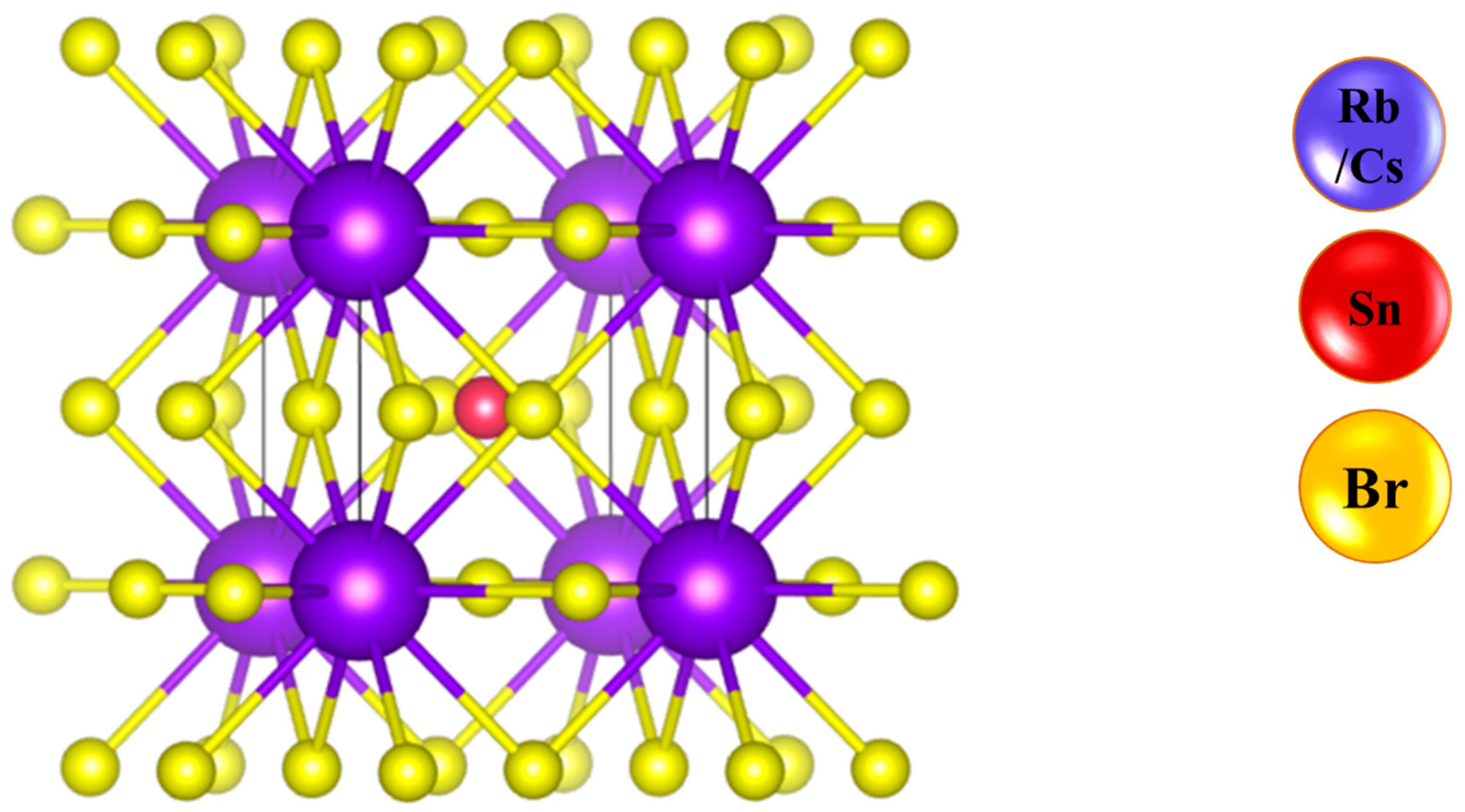
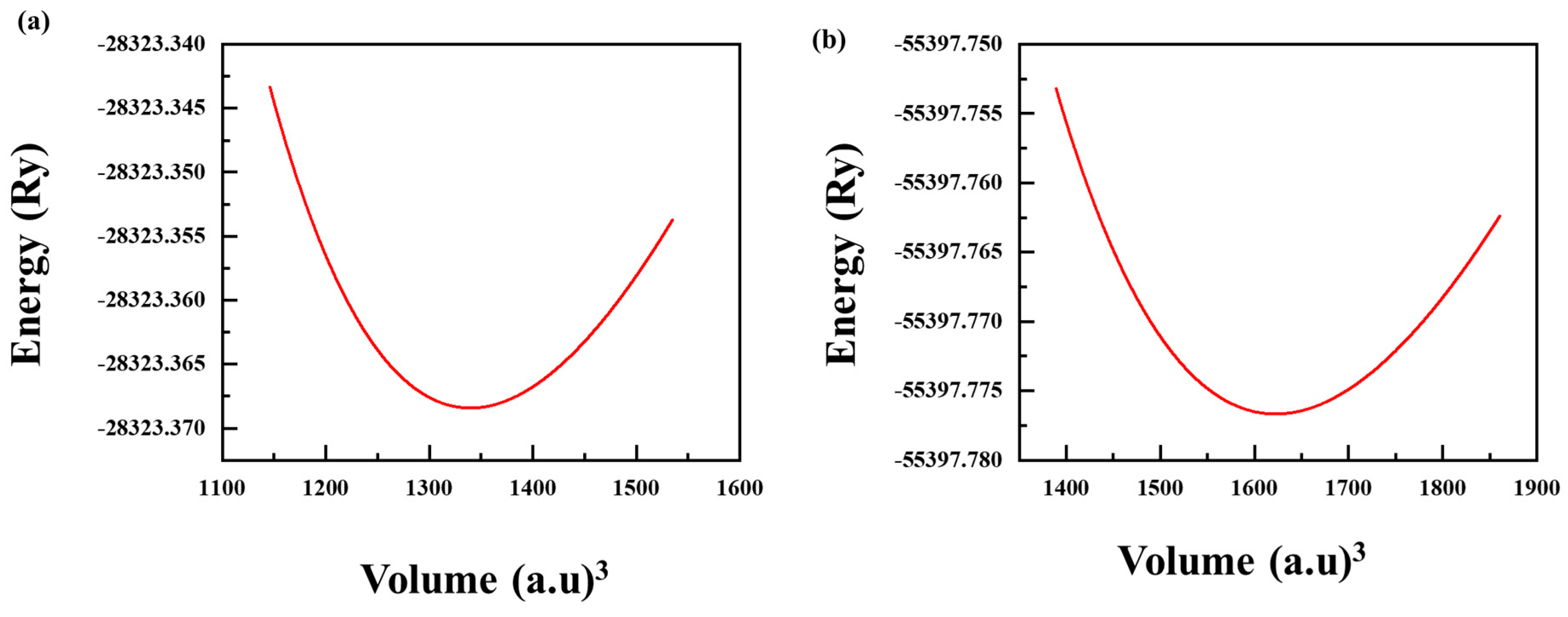



| HH | a (Å) | V (a.u.)3 | B | Bp | Etot (Ry) | τ | Ef (eV/atom) |
|---|---|---|---|---|---|---|---|
| RbSnBr3 | 5.61 | 545.005 | 43.869 | 3.935 | −7676.422 | 0.97 | −1.662 |
| CsSnBr3 | 5.82 | 651.515 | 35.041 | 4.014 | −19,454.663 | 0.96 | −1.690 |
| Other Studies [42] | 5.46 |
| Material Property | RbSnBr3 | CsSnBr3 | Other Studies [42] |
|---|---|---|---|
| C11 (GPa) | 61.93 | 63.88 | 58.18 |
| C12 (GPa) | 10.83 | 12.32 | 11.70 |
| C44 (GPa) | 7.62 | 7.14 | 9.27 |
| S11 (GPa−1) | 0.01710179 | 0.01669554 | |
| S12 (GPa−1) | −0.00246767 | −0.00269933 | |
| S44 (GPa−1) | 0.13123359 | 0.14005602 | |
| Bulk modulus, B (GPa) | 27.87 | 29.51 | 27.00 |
| Shear modulus, G (GPa) | 14.79 | 14.59 | 13.53 |
| Young modulus, E (GPa) | 37.70 | 37.58 | 34.83 |
| Poisson ratio, σ (GPa) | 0.27 | 0.28 | |
| Pugh ratio, B/G (GPa) | 1.88 | 2.02 | 2.01 |
| Cauchy pressure CP (GPa) | 3.21 | 5.18 | |
| Anisotropy factor (A) | 0.29 | 0.27 | |
| Transverse sound velocity (m/s) | 1706 | 16,585 | |
| Longitudinal sound velocity(m/s) | 3204 | 3254 | |
| Average sound velocity (m/s) | 1906 | 1886 | |
| Temperature ΘD (K) | 199 | 196.6 | |
| Melting temperature (K) | 783.7 | 768 |
| HHs | GGA | mBJ | Effective Mass | Bader Charge |
|---|---|---|---|---|
| RbSnBr3 | 2.02 | 2.15 | me* = 0.27 mh* = 0.29 | Rb = 0.85 Sn = 1.06 Br = −1.52 |
| CsSnBr3 | 2.07 | 2.14 | me* = 0.26 mh* = 0.28 | Cs = 0.87 Sn = 1.12 Br = −1.62 |
| Other Studies [42] | 2.20 |
| Material Property | RbSnBr3 | CsSnBr3 | Other Study [42] | |
|---|---|---|---|---|
| Optical properties | ε1(0) | 5.03 | 4.88 | 5.92 |
| n(0) | 2.24 | 3.08 | 2.43 | |
| Transport properties (300 K) | S(µVK) | 249 | 298 | |
| σ/τ(Ωms)−1(1017) | 0.61 | 1.1 | ||
| k/τ (W/mKs)(1013) | 0.21 | 0.20 | ||
| ZT | 0.79 | 0.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behera, D.; Akila, B.; Mukherjee, S.K.; Geleta, T.A.; Shaker, A.; Salah, M.M. Studies on Optoelectronic and Transport Properties of XSnBr3 (X = Rb/Cs): A DFT Insight. Crystals 2023, 13, 1437. https://doi.org/10.3390/cryst13101437
Behera D, Akila B, Mukherjee SK, Geleta TA, Shaker A, Salah MM. Studies on Optoelectronic and Transport Properties of XSnBr3 (X = Rb/Cs): A DFT Insight. Crystals. 2023; 13(10):1437. https://doi.org/10.3390/cryst13101437
Chicago/Turabian StyleBehera, Debidatta, Boumaza Akila, Sanat Kumar Mukherjee, Tesfaye Abebe Geleta, Ahmed Shaker, and Mostafa M. Salah. 2023. "Studies on Optoelectronic and Transport Properties of XSnBr3 (X = Rb/Cs): A DFT Insight" Crystals 13, no. 10: 1437. https://doi.org/10.3390/cryst13101437
APA StyleBehera, D., Akila, B., Mukherjee, S. K., Geleta, T. A., Shaker, A., & Salah, M. M. (2023). Studies on Optoelectronic and Transport Properties of XSnBr3 (X = Rb/Cs): A DFT Insight. Crystals, 13(10), 1437. https://doi.org/10.3390/cryst13101437








