The Renaissance and Golden Age of Epitaxial Dry Germanene

Abstract

Germanene, as an artificial graphene-like near room temperature topological insulator, compatible with ubiquitous silicon technology, is potentially the most promising artificial Xene for ultra-scale nanoelectronics. Here, we follow its emergence and development when prepared in situ under ultra-high vacuum in clean and controlled conditions by dry epitaxy on prominent metal surfaces (e.g., aluminum, silver, gold). We describe its predicted electronic properties and its birth in 2014, even if it was just a renaissance, as it was only understood after 51 years after an undeciphered birth certificate lost in oblivion. We emphasize the lifting of germanene flakes from an aluminum template with the tip of a scanning tunneling microscope, and their repositioning to form bilayer germanene with Bernal stacking. Finally, we discuss the growth of monolayer germanene in a single phase harboring Dirac fermions, following a bottom-up synthesis strategy by segregation on a gold thin film in epitaxy on a germanium support.

1. Introduction

Germanene is an artificial two-dimensional (2D) graphene-like germanium allotrope belonging to the class of so-called Xenes materials. It was synthesized in 2014, exactly ten years after the isolation of graphene [1], and just two years after the synthesis of silicene, the first Xene ever synthesized [2,3]. The tenth anniversary of silicene, the birth of germanene and the advent of its successors, from borophene to tellurene, have been highlighted in a recently published collective book [4].

At the origin of all Xenes is the seminal paper of Takeda and Shiraishi [5], who predicted in 1994 the ‘Theoretical possibility of stage corrugation in Si and Ge analogs of graphite’, in other words, the stability of freestanding silicene and germanene in a so-called low-buckled honeycomb geometry, in contrast with graphene, which is nominally flat.

In 2014, three groups announced independently, just within a few weeks, the successful synthesis of germanene. The first article described the in situ deposition of Ge onto a Pt(111) substrate [6], but the paper was rapidly questioned because of the likely formation of Ge₃Pt germanide clusters arranged in a 2D lattice, instead of the claimed germanene sheet [7]. The second article, the most cited experimental paper on germanene (according to Web of Science database in 2023), described the top-down synthesis on a Au(111) template [8]. The third one, immediately after, showed, instead, the bottom-up formation of germanene by segregation on top of preformed Ge₂Pt clusters, where their sizes were, clearly, a limitation [9]. These articles illustrate the two methods of choice, top-down and bottom-up, for the dry synthesis of germanene (and other Xenes).

Our aim in this concise review is not a comprehensive overview on germanene. Instead, we intend to highlight the most striking findings obtained on Al(111), Ag(111), and Au(111) substrates, the prominent templates for the obtention of pure, extended, germanene phases necessary for future applications in the electronics sector, where most significant advances are expected and desired. We will not omit the controversies, which have inevitably arisen, and will address the issues at stake. Of note is that aluminum, silver, and gold are all fcc metals (Al a simple metal, Ag and Au noble metals) with nearly identical lattice parameters: a_Al = 4.05 Å, a_Ag = 4.09 Å, and a_Au = 4.08 Å. We will begin with a brief description on the predicted fascinating properties of standalone germanene, typically as a 2D topological insulator. Indeed, these properties were the main motivation for the quest for germanene after that for silicene. Obviously, once silicene had been synthesized, the general belief that such quests were a foolish mission suddenly crumbled (see Chapter 2 by H. J. W. Zandvliet in [4]), opening the door to the creation of germanene, and, further, all its other Xene successors.

2. Standalone Germanene

As mentioned above, at the origin, in 1994, was Takeda and Shiraishi’s theoretical article [5] ten years before the isolation of graphene [1]. In this iconoclastic paper, through density functional theory (DFT) calculations, the authors demonstrated that a free-standing atom-thin sheet of Si or Ge atoms in a honeycomb lattice could be energetically viable, but, in contrast with graphene, which is purely sp² hybridized and atomically flat, in a buckled configuration, as shown in Figure 1a. However, the paper remained practically uncited for eighteen years, until the birth of silicene in 2012 when its number of citations jumped up dramatically. Since Si and Ge exist in nature only in diamond form, i.e., purely sp³ hybridized, in contrast with carbon, whose most stable form is sp² hybridized-layered graphite, obviously until 2012 nobody believed in the possibility of graphene-like silicon or germanium [10].

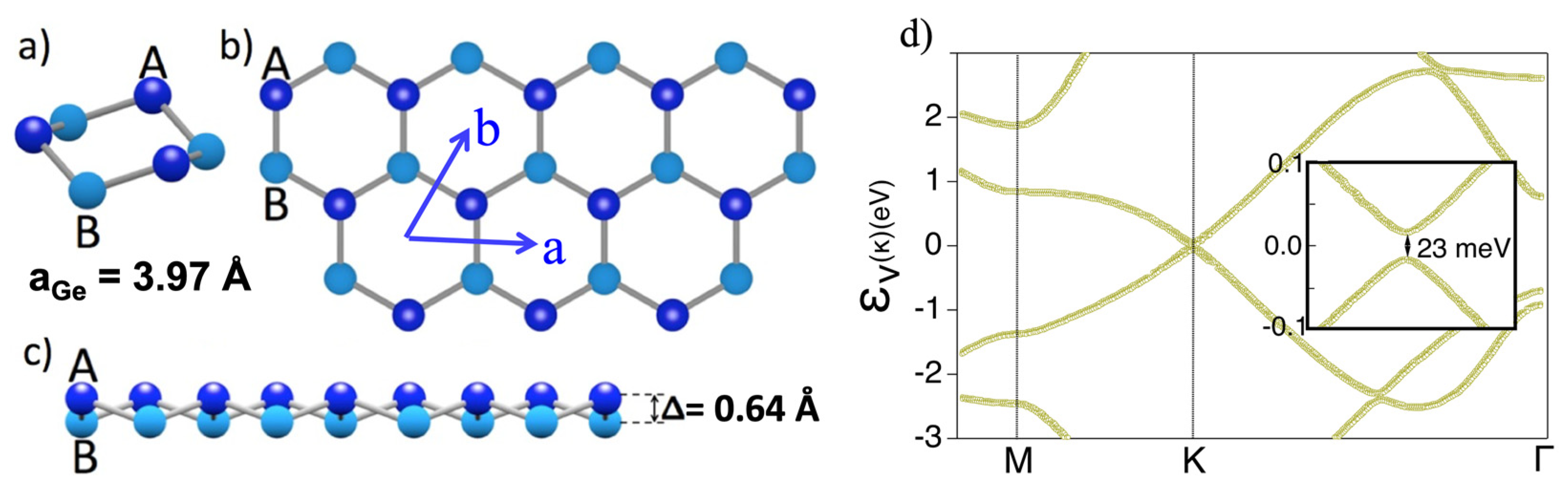
The buckling in germanene is Δ = 0.64 Å, but, still, the characteristic Dirac-like electronic band structure of graphene is preserved [11], albeit with the opening of a 23 meV gap at the K and K’ points of the surface Brillouin zone associated with a synergetic combination of spin–orbit coupling and buckling, as seen in Figure 1d [12]. This gap (compared to just 8 μeV in graphene and 1.55 meV in silicene [12]) leads to the tantalizing possibility a 2D topological insulator hosting the quantum spin Hall effect at nearly room temperature (RT). Furthermore, this gap can be tuned by a perpendicular electric field, which could also help control topological phase transitions. Typically, switching from such states as quantum spin Hall, quantum valley Hall or quantum anomalous Hall insulators to a normal insulator state in germanene nanoribbons might be achieved [13].

Very high intrinsic mobilities, even beating those of graphene both for electrons and holes, have been predicted, indicating that germanene should be of extremely high relevance to ultra-scale nanoelectronics, since germanium fits nicely with the conventional silicon semiconductor industry [14].

Last but not least, unconventional triplet superconductivity or topological superconductivity, might emerge, e.g., by interaction with a substrate or by photo-irradiation and proximity coupling with an s-wave superconductor [15,16].

Figure 1. Atomic geometry and quasiparticle band structure of standalone germanene in its stable low-buckled configuration. (a) Perspective, (b) top, and (c) side views, (d) Dirac-like electronic structure. The inset zooms in at the Dirac point. (a–c) from Figure 37.1 of Salomon et al. [10], (d) derived from Matthes et al. [12].

Figure 1. Atomic geometry and quasiparticle band structure of standalone germanene in its stable low-buckled configuration. (a) Perspective, (b) top, and (c) side views, (d) Dirac-like electronic structure. The inset zooms in at the Dirac point. (a–c) from Figure 37.1 of Salomon et al. [10], (d) derived from Matthes et al. [12].

3. Germanene on Al(111) Substrates: Synthesis, Controversies, Fundamental Issues

The success of the synthesis of silicene launched a gold-rush for the realization of germanene. In this respect, Al(111) has been a favored substrate, where a sharp (3 × 3) pattern and an extended Al(111)-(3 × 3) lattice were first observed by low-energy electron diffraction (LEED) and scanning tunneling microscopy (STM) upon in situ Ge deposition at about 87 °C [17]. The initial interpretation was in terms of a (2 × 2) reconstructed honeycomb germanene single layer, matching a (3 × 3) Al(111) supercell. Next, upon deposition of Ge at somewhat higher temperatures (about 200 °C), a new periodicity co-existing with the (3 × 3) one was discovered [18]. This new periodicity is a (√7 × √7) R ± 19.1° superstructure with respect to bare Al(111)-(1 × 1), assigned also to a strongly buckled 2 × 2 germanene adlayer in rotated domains [18]. In both (3 × 3) and (√7 × √7) R ± 19.1° cases, the appearance of the STM images is hexagonal, as seen in Figure 2a,b. Sharp Ge 3d core-level (CL) spectra obtained from a surface on which the (3 × 3) reconstruction was dominating could be fitted with four spin–orbit split components related to different local atomic geometries of the four Ge sites of the (2 × 2) germanene reconstruction (Figure 2c).

A (√7 × √7) R ± 19.1° superstructure has also been formed at near RT. It was studied by STM/STS and DFT calculations, and the atomic structure of this surface was predicted to be a (√3 × √3) R(30°) reconstructed germanene adlayer in which one Ge atom per unit cell markedly protrudes into the vacuum side [19]. The (3 × 3) structure was re-investigated by means of coaxial impact collision ion scattering spectroscopy (CAICISS), which is one of the most surface-sensitive structural analysis techniques. In contrast with the previously reported (2 × 2) honeycomb germanene lattices, it was concluded that the supercell was composed of 10 Ge atoms in a “kagome-like” arrangement [20], as in the case of silicon adsorbed on Al(111) [21]. The calculated band structure nicely reproduced the main bands measured by ARPES (Figure 2d,e).

Figure 2. Atomically resolved filled state STM images (~19 × 19 nm2) recorded at RT. (a) single hexagonal structure with (3 × 3) periodicity. (b) two rotated hexagonal structures with (√7 × √7) periodicity. (c) Ge 3d core-level spectra obtained at a photon energy of 135 eV in normal emission for a surface on which the (3 × 3) reconstruction was dominating. Dots: experimental data; solid curves: sum of the SC1 to SC4 components. The relative weight of each component is indicated. (d) Measured ARPES intensity distribution and (e) calculated band structure for the (3 × 3) reconstruction. (a,b) Figure 2 and (c) Figure 4 of Wang and Uhrberg [18], (d,e) Figures 4 and 5 of Kubo et al. [20].

Figure 2. Atomically resolved filled state STM images (~19 × 19 nm2) recorded at RT. (a) single hexagonal structure with (3 × 3) periodicity. (b) two rotated hexagonal structures with (√7 × √7) periodicity. (c) Ge 3d core-level spectra obtained at a photon energy of 135 eV in normal emission for a surface on which the (3 × 3) reconstruction was dominating. Dots: experimental data; solid curves: sum of the SC1 to SC4 components. The relative weight of each component is indicated. (d) Measured ARPES intensity distribution and (e) calculated band structure for the (3 × 3) reconstruction. (a,b) Figure 2 and (c) Figure 4 of Wang and Uhrberg [18], (d,e) Figures 4 and 5 of Kubo et al. [20].

The different interpretations in terms of germanene adlayers have been quickly questioned. Controversies soon appeared with interpretations, instead, in terms of surface alloys. Especially, using ion-scattering techniques combined with direct recoils and time-of-flight measurements (TOF-DRS) in conjunction with more standard surface science tools and DFT calculations to investigate the Al(111)-(3 × 3) structure, an alloyed surface phase was retained with a 5:3 Ge/Al ratio, instead of a pure germanene adlayer [22]. This contradicts the CAICISS results just mentioned, but we note that the heavy projectiles used in TOF-DRS (Ne⁺, Ar⁺, and Kr⁺ in the energy range of 4 to 10 keV) are likely to affect the structure resolution much more than the 2.0 keV helium ions (He+) impinging on the sample in the CAICISS experiments.

Furthermore, a SXRD study of the same structure along with DFT calculations pointed to a two-layered surface alloy, i.e., a mixed Ge–Al honeycomb layer on top of an alloyed interfacial layer, namely Ge₄Al₄/Ge₂Al₇ [23]. Just recently, the same group, using the same tools and methodology, has shown that the (√7 × √7) R ± 19.1° superstructure reconstruction obtained after RT deposition is a mixed Ge–Al honeycomb layer on top of an Al(111) plane (Ge₃Al₃/Al(111) (√7 × √7)), and not a pure germanene layer [24].

In addition, the theoretical STM image corresponding to the Ge₃Al₃/Al₇ model has been computed and appears to be in good agreement with the corresponding experimental high-resolution STM images of Muzychenko et al. (Figure 3) [25].

However, these last authors emphasized that they had presented clear evidence for the growth of intrinsic germanene phases. They revealed salient new characteristics of the germanene adlayers, supported by a combined study relying on DFT-based calculations and STM experiments. Advanced extra-high-resolution STM measurements with true atomic-scale vertical and lateral resolutions provided unique insights into the atomic arrangement for (2 × 2) germanene on Al(111)-(3 × 3), as well as for both (2 × 2) and (√3 × √3) R30° germanene phases on Al(111)-(√7 × √7), confirming their 2D honeycomb basic structures, as seen in Figure 3. The corresponding first principle calculations suggested atomic models with strongly buckled (2 × 2) and (√3 × √3) R30° germanene phases with one out of eight and one out of six Ge atoms protruding upward, respectively.

Noteworthy, is that the evolution of the formation energy as a function of the chemical potential Δμ_Ge, i.e., the deviation of μ_Ge with respect to E_Ge bulk, for both the (3 × 3) and the (√7 × √7) models was calculated by Zhang et al. [24]. This evolution is shown in Figure 4a, where the lowest curve for Δμ_Ge = 0 corresponds to Ge₃Al₃. As Δμ_Ge increases, alloyed (3 × 3) models become favored, but not germanene layers. Clearly, these calculations are in total opposition with the pure germanene phases obtained by Muzychenko et al. [25].

Up till now all the experimental results presented in this section were obtained following Ge deposition onto Al(111) substrates. Instead, Yuhara et al. adopted a bottom-up approach and obtained a single phase, namely, (2 × 2) hexagonal germanene on Al(111)-(3 × 3), by atomic segregation epitaxy upon annealing, at 430 °C, an Al(111) thin film originally grown on a Ge(111) template, as shown in Figure 4b [26]. It turns out that the high-resolution Ge 3d CL is nearly identical to that in Figure 2c, comprising four easily identifiable components (with spin–orbit split), which can be associated with the four different Ge sites with labels 1 to 4 in Figure 4c. Accordingly, the sharp Al 2p CL, shown in Figure 4d in very surface sensitive conditions, is fitted with only two components (with spin–orbit split), assigned to the bulk component and the top-most aluminum layer below the (2 × 2) germanene sheet, i.e., a sole interfacial component. This excludes the formation of a surface alloy that would present at least another distinct component, as is the case for the Sn 4d CL for stanene grown on Pd(111) past the formation of an Pd₂Sn surface alloy [27], or the Pb 5d core level for plumbene synthesized on a Pd_1-xPb_x surface alloy [28].

The simulated STM image (according to the optimized DFT model shown in Figure 4c)) nicely reproduces the measured hexagonal ones. Hence, this single phase is essentially the same as the (2 × 2) hexagonal germanene on Al(111)-(3 × 3) that was obtained by the top-down approach by Wang and Uhrberg [18]. It is obviously the most stable phase since it is obtained by segregation upon annealing at high temperature (430 °C). Instead, upon annealing at lower temperatures, multi-phase regions comprise twisted germanene domains in correspondence with an Al(111)(√7 × √7) R ± 19° superstructure, as obtained in the previous studies mentioned above.

Here, it is worth citing a recent theoretical paper, where the authors explore systematically explored the structures of the surface of Ge deposition onto the Al(111) surface by sophisticated theoretical calculations combined with available STM and LEED data [29]. Using ab initio evolutionary simulations and high-level random-phase approximation (RPA) calculations, they showed that the formation of germanene on Al(111) is energetically unfavorable. The two experimental phases are identified as honeycomb alloys Al₃Ge₃/Al(111)(√7 × √7) R(±19°) and Al₃Ge₄/Al(111)(3 × 3) with a vacancy left in the substrate, respectively. They further claim that their results clarify the structural controversy of the Ge/Al(111) system and indicate that the fabrication of germanene on Al(111) remains challenging.

There are many conflicting conclusions, often in regard to strong contradictory assertions, are extremely confusing and raise fundamental questions. In general, similar DFT calculations are always called in support of the interpretations of the different experimental results acquired.

Firstly, let us stress that in our opinion, that despite the use of sophisticated van der Waals functionals, the calculations restricted to a four Al layer slab as used by Yan et al. [29] may not lead to more convincing conclusions than any other standard calculations. In this respect, we note that in the work of Yuhara et al. [26], the simulated surface was modeled with a symmetric slab with 18 layers in which the central eight layers were fixed, while in the band calculation of Kubo et al. [20], the number of Al layers was set at 20.

Secondly, while the Ge growth is performed at 300 K or above, DFT calculations are carried out at 0 K, and, in general, no molecular dynamics studies follow. Hence, the normal thermal expansion of the substrate, and the anomalous, negative one of germanene, as well as the significant stress–strain involved are totally ignored [30].

As for the comparison of the thermodynamic stabilities of the different models, its relevance is not clear. As discussed by Zhang et al. [24], and shown in Figure 4a, the reference to E_Ge bulk, corresponding to the energy of one Ge atom within a germanium crystal, although a common assumption, appears questionable, simply because germanene does not exist in nature.

Returning to the work by Muzychenko et al. [25], we finally report the important new findings which merit to be highlighted. The authors showed that germanene flakes can be easily torn from the aluminum substrate and attached onto the STM tip, retaining the stable 2D configuration (no rumpling). Furthermore, they were able to create in situ Bernal AB-stacked bilayer germanene by the re-deposition of germanene flakes picked up by the STM tip on top of single layer germanene. Undoubtedly, this is a very important step toward the fabrication of germanene-based nanoscale devices.

4. Germanene on a Silver Plate: Ag(111) Substrates

A first indication of germanene synthesis by germanium adsorption on a silver (111) substrate at RT and further annealing at 415 K was given in 2014 [31]. A (9√3 × 9√3) R30° LEED pattern was observed, while a honeycomb lattice with moiré structure was imaged in STM. First principle calculations by Wang et al. further confirmed that the honeycomb structure of germanene was retained on Ag, Au, Cu, and Pt surfaces, and that its Dirac cone was nearly preserved on Ag and Au substrates [32].

New developments while depositing Ge on Ag(111) revealed dual germanene phases in a low-buckled honeycomb lattice, supported by a detailed combined study of STM, ARPES, LEED, and ab initio theory [33]. While at a lower Ge coverage, a partially commensurate striped phase (SP) was formed, very interestingly, at a higher Ge coverage, a fully incommensurate quasi-freestanding phase (QP) developed.

Yuhara et al., used the segregation method through pre-formed epitaxial Ag(111) thin films grown on Ge(111) and annealed at 480 °C [34]. They found a large area adlayer confirmed by measurements of the Ge 3d CL, assigned to a germanene superstructure of (3√21 × 3√21) R10.9° matching a Ag(111) (7√7 × 7√7) R19.1° supercell, as shown in Figure 5a–c. Further, using the segregation method, Suzuki et al. demonstrated the growth of h-BN-capped germanene on Ag(111) by ex situ Raman spectroscopy (Figure 5d) [35]. This is clearly a very promising development for the fabrication of future germanene-based nanoelectronic devices.

In contrast with these results, upon following real-time STM the evolution of the successive structures formed on Ag(111) upon Ge deposition in the 380–430 K temperature range, Zhang et al. concluded that Ge atoms easily exchange with Ag atoms to form various Ag–Ge surface alloys, including a disordered hexagonal phase, and, hence, no structure was found compatible with a germanene layer within the explored experimental conditions [36].

Nevertheless, Deng et al. demonstrated that monolayer germanene could be successfully fabricated on an Ag₂Ge surface alloy. Scanning tunneling spectroscopy revealed a linear energy dispersion relationship, supported by DFT calculations [37].

Finally, a recent investigation of the structural evolution of epitaxially grown germanene on Ag(111) is encouraging [38]. Using powerful surface analysis tools, such as LEED, X-ray photoelectron spectroscopy (XPS), and X-ray photoelectron diffraction (XPD) with synchrotron radiation, this study provided a survey of germanium formations at different layer thicknesses right up to quasi-freestanding germanene. High-resolution CL spectroscopy of the Ge 3d and the Ag 3d orbitals was performed, revealing that the germanene phase was chemically decoupled from the substrate resulting in a freestanding layer. Moreover, the optimum structure derived from an XPD analysis recovered a surprisingly low-buckled honeycomb structure, that was very comparable to the germanene phase which was grown by Yuhara et al. via segregation through Ag(111) [34].

To summarize, there is little doubt that Ag(111) is an excellent substrate to produce in the right conditions for quasi-freestanding germanene, that can be encapsulated in situ and preserved in air for device fabrication.

5. The Golden Age of Germanene

The very first article on the synthesis of germanene, a synthetic graphene-like germanium allotrope not occurring in nature, considered as a hallmark, was accepted for publication in 2014, eight years ago [8]. The creation of germanene took place in Marseille on a Au(111) substrate, following a top-down procedure. The choice was historical: at the beginning of the 1970s, gold had been the very first noble metal deposited onto a clean germanium (111) surface to monitor the growth, at various temperatures of deposition or annealing [39].

For the synthesis of germanene an atom-thin, ordered, two-dimensional film was grown in situ the other way around by germanium molecular beam epitaxy on a Au(111) substrate. A multi-phase film was obtained, but one of the phases, forming large domains as observed in STM, displayed a clear, nearly flat honeycomb structure. Thanks to high-resolution CL measurements and advanced DFT calculations it was identified as a (√3 × √3) R30° germanene layer in conjunction with a (√7 × √7) R19.1° Au(111) supercell.

A few layer of germanene, displaying Dirac cones was also obtained on a gold template two years later [40].

At the beginning of the 1970s, using a (111)-oriented germanium rod cleaved in situ to yield a sharp Ge(111)-(2 × 1) clean reconstruction, a curious LEED pattern was discovered after gold deposition and annealing. In addition to strong (1/3, 1/3) spots stemming from a Ge(111)-(√3 × √3) R30°-Au reconstruction, it showed 24 sharp spots distributed in pairs on a ring, as seen in Figure 6a. Having no Rosetta stone, this undecipherable LEED pattern remained buried in a 1971 thesis and was never published. However, we recently resurrected it during a progressive annealing up to about 260 °C of an initially flat epitaxial Au(111) film, (about 10 nm thick, as confirmed by ex situ ellipsometry) deposited in situ at RT onto a sputtered and annealed piece of Ge(111) wafer, showing initially the clean c(2 × 8) reconstruction. Note that such a thin Au(111) film grown on Ge(111) at RT was extracted and observed in transmission electron microscopy and transmission electron diffraction (TEM/TED) [39,41]. Instead, after annealing, large epitaxial 3D Au(111) crystallites were observed in the same way, a characteristic example of the Stranski–Krastanov growth mode, where, here, a 2D Ge(111)-(√3 × √3) R30°-Au layer initially formed, followed by the growth of 3D Au(111) crystallites in epitaxy [39,41].

After growth of the Au(111) thin film no LEED pattern was observed at RT, indicating disorder at the surface. However, at about 200 °C, besides the spots of the 2D Ge(111)-(√3 × √3) R30°-Au layer, a ring structure started to appear that developed at 260 °C into numerous sharp spots, with 24 spots on a ring (Figure 6b,c), first observed more than 51 years ago. Ex situ scanning electron microscopy (SEM) images showed islands (Figure 6d), with typical sizes of several tens of nanometers, on top of irregular flat gold patches, revealing the dewetting process of the Au film in the course of the evolution to the Stranski–Krastanov mode. In backscattered electron imaging these islands appear darker than the gold surrounding, indicating that they are germanium islands formed by segregation. The scenario is clear: Ge atoms randomly segregate on top of the epitaxial Au(111) film at RT, where they form a disordered phase and/or just 2D islands smaller than the coherence length of the electron beam in LEED. Upon heating, 2D Ge islands developed in size but with rotational azimuthal disorder; they displayed the initial ring structure in LEED patterns. At 260 °C, these islands became fully epitaxially oriented and gave sharp spots because the typical size of the islands was larger than the coherence length of the electron beam in LEED.

The complex LEED patterns could be interpreted with a symmetry-breaking supercell with respect to Au(111), (5 0/0 8) in matrix notation (in short (5 × 8)) existing in six equivalent rotational domains. Of note here, is that upon deposition of about one monolayer (ML) of Ge onto a Au(111) surface, Wang and Uhrberg obtained a structure which they assigned to (5 0/8 -14) in matrix notation [42], probably a not drastically different one.

STM images that unfortunately could not be resolved at atomic scale, confirmed the (5 × 8) supercell (described by the orange rhombus in Figure 6e) and a rather flat top surface (maximum corrugation of ~7 pm). Round and Z-like protrusions were observed but gave no information on the internal atomic arrangements. High-resolution CL spectroscopy revealed a very narrow single component Ge 3d CL (spin–orbit split, only 0.3 eV full width at half maximum) together with also very narrow Au 4f CLs in just two-components. The strongest one was assigned to the bulk Au(111) film, the second one at a higher binding energy was attributed to the Au atoms below the Ge islands. These are the signatures of long range order and of the absence of alloying, as discussed above for germanene on Al(111) substrates, or the formation of Ge multilayers, which proves that a single layer of Ge atoms segregated through the epitaxial gold film and that it is a self-limiting process [8,13]. Therefore, most probably, a certain germanene layer is formed by this bottom-up process.

A simple tentative atomic model for the (5 × 8) supercell consists of germanene islands with armchair edges along one dense [1,2,3,4,5,6,7,8,9,10] direction, the ×8 direction, of a bulk-terminated Au(111) surface, and also armchair edges along the ×5 direction at 120°. The strain would be rather small since corresponding Ge–Ge in-plane distances (assuming a bulk-terminated Au(111) film), would be 0.257 and 0.241 nm, respectively, compared to the 0.255 nm one determined in [8], and the calculated value of 0.238 nm for free-standing germanene [11]. However, we cannot exclude a complex interfacial gold reconstruction, which could explain the weird aspect of the STM images: one remembers that the clean bare Au(111) surface itself hosts a large symmetry-breaking (22 × √3) reconstruction, denser than a bulk Au(111) plane.

The ARPES data (Figure 6h) along M−Γ−M of the (1 × 1) surface Brillouin zone of the Au(111) surface reveal linear dispersions in a V-shape band at the zone center Γ, pointing to Dirac fermions with a Fermi velocity of ~0.75 ± 0.15 10⁶ ms⁻¹, quite close to that of graphene. Because of the large (5×8) reconstruction, extended DFT calculations could not be conducted, but, still, test calculations confirmed that alloying is not favorable in accordance with the results mentioned above by Dávila et al. and Wang et al. [8,30]. Furthermore, detailed CL, LEED and ARPES studies of ultra-thin Ge films grown on Au(111), with nominal thicknesses between 1.0 Å and 7.2 Å essentially confirmed the existence of Dirac fermions [43]. The ARPES spectra revealed the emergence of Dirac-like dispersions at the ML limit, which persists for thicker films up to 7.2 Å. These bands were related to the folding of the Dirac cones of germanene due to the presence of an (8×8) surface superstructure, which could prevent their hybridization with the substrate bands, in accordance with the initial results of Dávila et al. [8,41]. This was a remarkable finding since from first principles the interaction of germanene with Au(111) had been considered to preclude the existence of Dirac fermions [44]. In view of all this, both top-down and bottom-up strategies would lead to the formation of germanene on Au(111) surfaces, but in slightly different 2D phases. However, there are still different opinions.

On the one hand, Muzychenko et al. studied the initial stage of the adsorption of Ge on a Au(111) surface for coverages ≤1 monolayer in a range from RT to about 500 K by STM at 78 K and DFT analysis [45]. They concluded that the formation of a Au–Ge alloy, at least in the first two surface layers, with an ordered (4 × 14) structure with respect to Au(111)-(1 × 1) observed by Ge deposition or annealing at ~500 K. We note that this situation most probably corresponds to a metastable transient one, since to the best of our knowledge, it has not been reproduced by other groups.

On the other hand, Cantero et al. [46] monitored the growth of Ge on Au(111) by TOF-DRS, in a similar fashion as mentioned above for an Al(111) substrate [22], using 4.2 keV Ar⁺ ions. They found the coexistence of Ge and Au atoms at the top-most layer for all stages of growth, even for their thicker layers, in a ratio of about 2:1, where the STM images were consistent with a commensurate (5 × 8) arrangement.

Conversely, Zhuang et al. [47] investigated the superstructures of Ge layers grown on a Au(111) substrate by STM and in situ Raman spectroscopy at 77 K. Combined with DFT calculations, a bilayer germanium nanosheet with a honeycomb arrangement of Ge atoms on a Au(111) surface was derived, where the lattice constant for the (4 × 2√3) unit cell of Au(111) matched that of the (√7 × √7) reconstructed germanene. The honeycomb arrangement of (1 × 1) germanene was directly revealed with atomic resolution. Furthermore, Raman spectroscopy identified the distinctive phonon mode and electron phonon coupling in the (√7 × √7) germanene superstructure, attributed to its buckled geometry.

Since this hardly appears disputable, we suggest that the conflicting results of Muzychenko et al. [45] and Cantero et al. [46] may stem from their top-down preparations, kinetic paths, and/or special investigation tools. Instead, bottom-up approaches by segregation are likely to lead to more stable and reproducible germanene phases.

6. Summary and Outlook

We have focused this concise review on the dry synthesis of germanene on the three most-relevant metal surfaces and have highlighted the most exciting findings reported by different international groups. The growth of germanene has been obtained successfully both by top-down and bottom-up strategies.

The lifting of germanene flakes and their repositioning to form bilayer Bernal stacks is a fantastic achievement. It proves that free-standing germanene does exist, in contradiction with common beliefs.

In 2014, a renaissance after more than half a century of oblivion, only two years after silicene, the eldest of the Xenes’ siblings, germanene is still in its infancy. Yet, as a near to RT 2D topological insulator expected to be easily incorporated into the existing silicon-based industry, its advent will surely lead to the development of a totally new class of low-energy consumption nanoelectronic devices.

Even if the properties and potential applications of this emerging 2D material are far from being fully elucidated, the prospects for ultra-scale nanoelectronics, spintronics and quantum computing undoubtedly appear highly promising. This is the golden age of germanene.