Next Article in Journal
Evaluation of the Minority-Carrier Lifetime of IMM3J Solar Cells under Proton Irradiation Based on Electroluminescence
Next Article in Special Issue
Relative Stability of Pyrazinamide Polymorphs Revisited: A Computational Study of Bending and Brittle Forms Phase Transitions in a Broad Temperature Range
Previous Article in Journal
A Brief Review of Sodium Bismuth Titanate-Based Lead-Free Materials for Energy Storage: Solid Solution Modification, Metal/metallic Oxide Doping, Defect Engineering and Process Optimizing
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 13
Issue 2
10.3390/cryst13020296
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Two Crystal Forms of 4′-Methyl-2,4-dinitrodiphenylamine: Polymorphism Governed by Conformational Flexibility of a Supramolecular Synthon

by
Ivan V. Fedyanin
1,2,* and
Aida I. Samigullina
2
1
A. N. Nesmeyanov Institute of Organoelement Compounds, Russian Academy of Sciences, Vavilova St. 28, 119991 Moscow, Russia
2
N. D. Zelinsky Institute of Organic Chemistry, Russian Academy of Sciences, 47 Leninsky Prospect, 119991 Moscow, Russia
*
Author to whom correspondence should be addressed.
Crystals 2023, 13(2), 296; https://doi.org/10.3390/cryst13020296
Submission received: 2 December 2022 / Revised: 3 February 2023 / Accepted: 7 February 2023 / Published: 10 February 2023
(This article belongs to the Special Issue Crystalline Materials: Polymorphism)
Browse Figures
Versions Notes

Abstract

:
Single crystals of two polymorphic forms of 4′-methyl-2,4-dinitrodiphenylamine were obtained by crystallization and characterized by X-ray diffraction analysis. One of the forms is non-centrosymmetric (space group P21212), while the second is centrosymmetric (space group P¯1) and contains two crystallographically independent molecules in the asymmetric unit. In both forms, the same supramolecular synthon, a dimer linked by bonding N-H···O, O···O, and C-H···O interactions were found. Despite nearly the same connectivity of the bonding interactions, the conformation of the supramolecular synthon is different, including its unavoidably different symmetry in two polymorphs. The comparison of the crystal packing of the orthorhombic polymorph with that of the related 2,4-dinitrodiphenylamine (space group P21/n) shows the quasi-isostructurality of the fragments, infinite π-stacks joined by weak non-directional intermolecular interactions. However, the fragments are linked by the supramolecular synthons via either a two-fold axis or an inversion center, which lead to only the partial isostructurality of the crystals.

1. Introduction

The polymorphism of molecular crystals [1] is a well-known phenomenon in the field of materials science and is of great importance not only from theoretical, but also from a practical point of view. Indeed, while many physical properties of a material are governed mainly by the chemical structure of the compound, crystal packing can also play a significant role [2]. The polarization of the electron density caused by strong intermolecular interactions such as hydrogen or halogen bonds, the stabilization of certain molecular conformations, intra- and intermolecular charge transfers can lead to notable differences in the physical properties of polymorphic forms of biologically active compounds used as active pharmaceutical ingredients (APIs) [3], energetic compounds [4], etc. In some cases, only the polymorph that crystallizes in a space group belonging to a specific point group reveals the desired physical property: a well-known example is non-centrosymmetric crystals exhibiting non-linear optical (NLO) properties [5].
Despite considerable research efforts, there is no simple approach to predict the formation of polymorphs, let alone a practical recipe to obtain a real-world polymorphic form of an arbitrary compound [6,7]. However, certain properties of a molecule can lead to an increased likelihood of its polymorphic behavior. For instance, conformationally flexible molecules appear in different conformations in different crystal forms that lead to so-called conformational polymorphism [8].
Another important factor responsible for the enhanced probability of polymorphism is the presence in a crystal of so-called supramolecular synthons. A supramolecular synthon is defined as “a structural unit within supermolecules which can be formed and/or assembled by known or conceivable synthetic operations involving intermolecular interactions” [9]. It is usually suggested that the formation of different supramolecular synthons by the same functional groups of the molecule increases the probability of polymorphism due to the competition between different intermolecular interactions. Indeed, such competition (e.g., dimers vs. chains) automatically leads to different crystal packing, and thus, to different polymorphic forms [10].
However, the formation of the same supramolecular synthon can lead to polymorphic behaviors as well due to the conformational lability of the resulting supramolecular associate. Indeed, the most common supramolecular synthons in crystals are usually built by relatively weak hydrogen [11] or halogen bonds [12] that have a pronounced, but not always strong, directionality. This permits significant conformational flexibility of the synthon without the loss of the bonding pattern.
In this paper, we report two polymorphic forms of the title compound, 4′-methyl-2,4-dinitrodiphenylamine 1 (Scheme 1). This molecule contains both the formally electron donor and electron acceptor fragments, which assumes the possibility of intramolecular charge transfer in the π-conjugated system. Although compound 1 has been known of for many years and was tested for a potential application as antibacterial agent [13] and for non-linear optical properties [14], its crystal structure is not yet reported. However, as the powder sample of compound 1 is known to exhibit second-harmonic generation [15,16], it has been expected to be non-centrosymmetric. Recently, a crystal structure of the closely related phenyl-substituted compound 2,4-dinitrodiphenylamine (2) was reported [17], and while it has the same color and morphology as a bulk sample of compound 1, it crystallizes in the centrosymmetric space group P21/n. It turns out that compound 1 crystallizes at least in two polymorphic forms, which were established by single-crystal X-ray diffraction analysis. The supramolecular synthons in the polymorphs were thoroughly studied using DFT calculations and a topological analysis of the theoretical electron density distribution.

2. Materials and Methods

2.1. Crystallization of Polymorphic Forms

Compound 1 was synthesized by a known procedure [18] via nucleophilic aromatic substitution on 1-chloro-2,4-dinitrobenzene by 4-methylaniline. The crystals of the orthorhombic form I were obtained by recrystallization from ethanol at room temperature, a number of other solvents and their mixtures were also tested, which lead to the same form, including acetone, acetonitrile, and water. The phase purity of the bulk sample of form I was confirmed by powder X-ray diffraction (see Supporting Information Figure S3).
A few single crystals of the apparently metastable triclinic form II were obtained together with the red form by recrystallization from a very diluted cold acetone solution. Unfortunately, all of our attempts to obtain the form II in pure bulk form, either by selection of the solvent or by seeding, failed.

2.2. Single-Crystal X-ray Crystallography

Data collection for both of the samples was performed using a Bruker Smart APEX II CCD diffractometer (graphite-monochromated MoKα radiation, λ = 0.71073 Å, ω-scans). Frames were integrated using the Bruker SAINT software package [19] by a narrow-frame algorithm. A semi-empirical absorption correction was applied with the SADABS [20] program using the intensity data of the equivalent reflections. The structures were solved by the dual-space method with the SHELXT program [21] and refined by the full-matrix least-squares technique on F2 in the anisotropic approximation for all of the non-hydrogen atoms using the SHELXL [22] software package. The positions of the hydrogen atoms of NH groups were found using difference Fourier syntheses, while the positions of all of the other hydrogen atoms were calculated. The hydrogen atoms of NH groups were refined in the isotropic approximation, and those connected to carbon atoms were refined in the riding model, with Uiso(Hm) = 1.5Ueq(Cm) for the methyl groups and Uiso(Hi) = 1.2Ueq(Ci) for the phenyl groups. Detailed crystallographic information is given in Table 1. Structural data were deposited to the Cambridge Structural Database, CCDC 1434708 and 1434709, containing the supplementary crystallographic data in this paper. These data can be obtained free of charge via https://www.ccdc.cam.ac.uk/structures/ (accessed on 1 January 2023).

2.3. Computational Details

Ab initio calculations of the crystal structures, isolated molecules, and dimers were performed with the CRYSTAL17 software package [23]. In all of the calculations, the dispersion-corrected PBE0-D3 function [24,25] was used with the POB-TZVP basis set [26], which was parameterized for periodic solid state calculations. The use of shrinking factor 4 4 4 for the Monkhorst-Pack grid yielded 27 and 36 k-points in the irreducible Brillouin zone for forms I and II, respectively. For the crystal structures, the atomic positions were optimized using experimental unit cell parameters and symmetry. For all of the optimized models, the harmonic frequencies were calculated (at the Γ-point for the crystal structures) using a numerical algorithm, with two atomic displacements in each Cartesian direction. For the calculation of the lattice energy, the wavefunctions of the isolated molecules in the crystal geometry were also computed. The basis set superposition error (BSSE) was corrected by the counterpoise approach [27] by using special algorithms implemented in CRYSTAL17 (the keywords were MOLEBSSE for the crystals and GHOSTS for the isolated dimers).
A topological analysis of the electron density distribution ρ(r) in terms of Bader’s Quantum Theory of Atoms in Molecules (QTAIM) [28] was performed with the TOPOND program [29] integrated in CRYSTAL17. The results of the topological analysis were visualized with the AIMStudio program from the AIMAll [30] software package, the output files of the TOPOND were converted to the sumviz format using an in-house utility topond2sumviz. To compare the energy of individual interatomic bonding interactions the empirical Espinosa–Molins–Lecomte (EML) correlation [31] was used: EEML = −0.5a03v(r), where EEML is interaction energy, a0 is Bohr radius, and v(r) is potential energy density in a bond critical point. Although this approximation was criticized for its empirical nature and unreliability [32], its theoretical justification and its possible limitations have been proposed [33], and it was successfully applied for studying different close-shell interactions [34]. As the approximation is the only way to estimate the contribution of an individual bonding contact into the interaction energy, we used the EML correlation in this work, but only for a semi-qualitative comparison of the order of the interaction energy.

3. Results and Discussion

3.1. Molecular Geometry

Form I, Figure 1a, is non-centrosymmetric (space group P21212), while form II is centrosymmetric (space group P¯1) and contains two crystallographically independent molecules in the asymmetric unit (further denoted as A and B). The bond lengths and angles of the molecules in both forms are very similar and are comparable to typical values for the comparable molecular fragments, as indicated by a Mogul geometry check [35].
Note that the bonds of the central amino atom N3 with the carbon atom C1 of the electronic acceptor dinitrobenzene fragment are shorter (1.341(4) Å in form I and 1.351(2) and 1.353(2) Å in form II) than they are with the carbon atom C7 of the toluene moiety (1.426(4), and 1.425(2) and 1.424(2) Å), which suggests more effective conjugation of the lone electron pair of the nitrogen atom with the aromatic system of the acceptor benzene ring. The specific orientation of the lone pair is determined by the intramolecular H-bond with S(6) graph set [36] that closes a highly favorable [37] six-membered H-bonded ring. The geometric parameters of this H-bond are very similar for the molecules in both of the polymorphs (Table 2). Note that in both of the structures, the intramolecular H-bond is the major component of a bifurcated bond (see below), and the variation of its strength can reflect different strength of the weaker secondary bond. The intramolecular H-bond clearly fixes the orientation of the nitro group N1 O1 O2, while the second nitro group is conformationally labile, however, both of the nitro groups in both of the polymorphs are nearly co-planar to the benzene ring, with the angles between the mean planes falling in the range from 3.00(17) to 9.06(19)°.
As a result of the bonding pattern and intramolecular non-covalent interactions, the molecular conformations are very similar in both of the polymorphic forms, with almost identical dihedral angles between the mean planes of the phenyl rings (51.65(8) in I, and 50.19(4) and 49.17(4)° in II). The conformation also resembles the conformation of the related molecule 2 (Figure 2). Considering the small differences between the molecular geometries, the structures of forms I and II cannot be considered as “conformational polymorphs”, and their polymorphic behavior is defined by intermolecular interactions.
It should be mentioned that the molecular geometry, including the conformation and geometric parameters of the intramolecular H-bond, is well reproduced by the DFT geometry optimization of the experimental structures. Thus, the results of the DFT calculations are considered to be adequate for the further analysis of the intermolecular interactions.

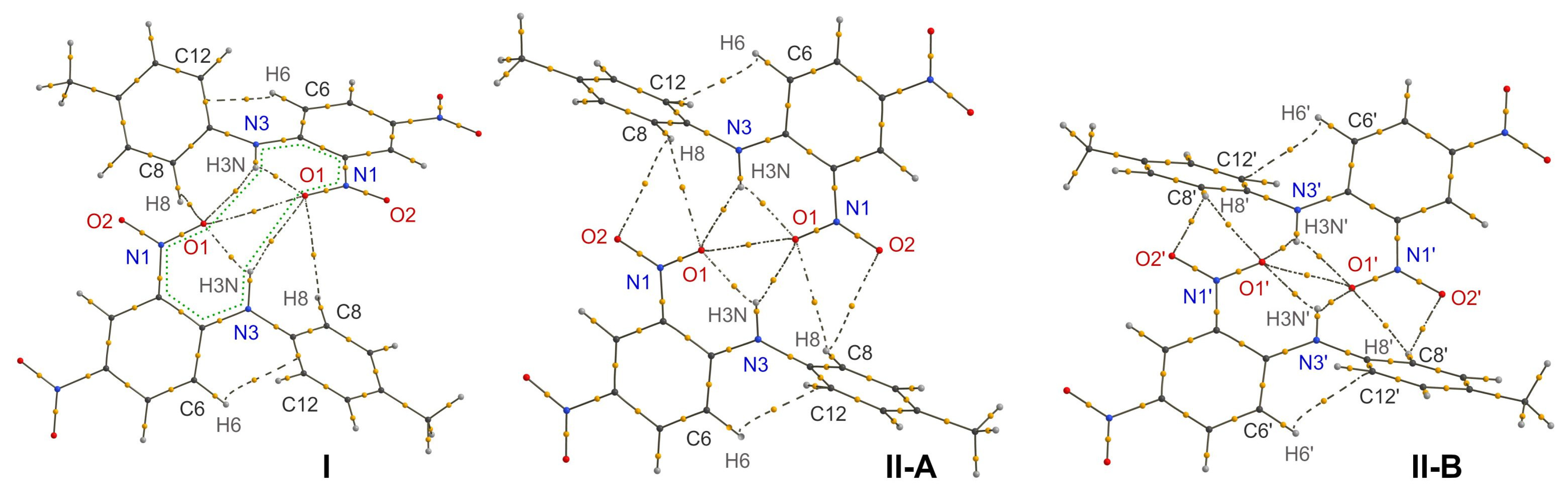
3.2. Intermolecular H-Bonds

As mentioned above, the H-bond formed by the hydrogen atom H3N is bifurcated, and the weaker intermolecular bonds (Figure 2) connect the molecules into R22(12) dimer (Figure 2). It is interesting that the acceptor atom O1 of the secondary H-bond is the same as that of the intramolecular bond. Based on geometric parameters (Table 2), the secondary bond is quite weak and could have been considered as unimportant for crystal packing. However, this bond is observed in both of the polymorphic forms of 1 (albeit of different geometry), as well as in the crystal of the closely related compound 2. Therefore, the resulting dimer can indeed be considered as a supramolecular synthon.
The same supramolecular synthon with intramolecular S(6) and intramolecular R22(12) H-bonded patterns was previously found by some of us [38] for 2,4,6-trinitroaniline (TNA), and it was also observed for a significant number of crystal structures of o-nitroanilines (ca. 15%) in the Cambridge Structural Database [39]. The specific interesting feature of the synthon is the relatively short distance between the two acceptor atoms of the H-bond, which are often much shorter than the doubled van der Waals radius of the oxygen atom. This short contact corresponds to a bonding interaction in terms of the QTAIM theory, as it is energetically favorable, and additionally, stabilizes the resulting dimeric system with the overall binding energy of 6.6 kcal/mol calculated for TNA at the B3LYP-D3/def2-TZVP level of theory.
While in most structures the synthon is located about an inversion center, it was also observed for some structures in non-centrosymmetric space groups. In polymorph I, the molecules in the dimer are related by a two-fold axis, and while intermolecular H-bonds are very weak, the experimentally determined O···O distance of 2.699(3) Å is unexpectedly short. However, such geometry is not reproduced well by the DFT calculation of the crystal structure, as both the N-H···O and O···O distances in the optimized structure are notably longer. Such an inconsistency between the experimental and the theoretical data is most probably due to slight dynamic disorder of the nitro group that cannot be resolved by a conventional X-ray diffraction experiment. Indeed, even a slight deviation of the N-O bonds from the co-linearity increases the O···O distance and also disrupts the geometry of the intermolecular H-bond.
In polymorphic form II, the molecules in the dimer are related by an inversion center, thus the synthon is formed between the symmetry independent molecules. For molecule A, the geometry of the dimer with nearly co-planar interacting six-membered H-bonded rings resembles those in TNA, molecule 2, and many of the related structures. On the other hand, in the synthon formed by molecule B, the interacting six-membered H-bonded rings, though they are nearly parallel, are shifted in the perpendicular direction by ca. 1.7 Å. Such an orientation notably increases the length of the O···O contact and the H-bonds. However, the formal criteria of the presence of these weak interactions are still satisfied. Note that in the case of form II, the DFT optimization of the crystal structure leads to much smaller changes in the geometry of the dimer, as compared to those of form I, with only a slight increase of the O···O and O···H distances.
In order to identify the bonding interactions in the synthons and rationalize the differences between the polymorphic forms, we have performed a topological analysis of the theoretical electron density ρ(r) in the optimized crystal structures with reference to the QTAIM theory. The resulting topological graphs for the supramolecular synthons are presented in Figure 2, and the quantitative data are provided in Table 2.
As expected, all of the bond critical points (3,-1) (BCPs) and gradient paths corresponding to covalent and strong intramolecular hydrogen bonds were found. In addition, BCPs corresponding to an intramolecular C6-H6···C12(π) interaction were found for both of the polymorphs, which is also mentioned for compound 2 from the B3LYP/6-31++G(d,p) single-point electron density analysis [17] of the isolated associate.
As for intermolecular interactions, all of the BCPs and bond paths characteristic of the discussed supramolecular synthon were located, despite there being significant differences in the relative orientation of the component molecules. In the dimers of Ci symmetry in form II, two additional weak C-H···O contacts with the H atom of the tolyl fragment are observed, which additionally stabilize the synthon, whereas in form I, only one of these bonds remains due to there being a significantly greater distance between the atoms in the dimer of C2 symmetry. The energy of all of the non-covalent bonding interactions was estimated from the EML approximation (Table 2). Note again that this empirical approach allows only the semi-qualitative comparison of the interaction energy. It turns out that the energy of intramolecular H-bonds is very close, and the bond in form I is the strongest one. As expected from geometric parameters, the intermolecular H-bonds are weaker by an order of magnitude, and the bonds in form II-A are the strongest ones due to the most favorable orientation of interacting atoms. Interestingly, the energy of O···O interaction is nearly three times higher than one of the intermolecular H-bonds, which makes the contribution of these two interaction types into stabilization of the synthon almost equal.
Thus, except for the weakest C-H···O interaction, the connectivity of the topological graph for the dimers in polymorphs I and II is the same. However, the symmetry of the dimers is different, and the relative orientation of the molecular fragments is responsible for the synthon formation. This allows us to consider these distinct geometries as different conformations of the supramolecular synthon.
The same observation was recently reported by some of us for crystal structures of 8-hydroxyquinoline (8HQ) and its derivatives [40]. As for the polymorphs of form 1, in different crystal forms of 8HQ the molecules are linked into H-bonded dimers, either centrosymmetric (space groups P21/n and P¯1) or located about a two-fold axis (space group Fdd2). In contrast to 8HQ, where the supramolecular synthon of C2 point group is an energy minimum and the centrosymmetric dimer is a transition state, for form 1, both the C2 and Ci symmetries are found to be energy minima, with a very small energy difference of 0.22 kcal/mol. However, the lowest calculated vibration frequencies of 8.5 and 11.2 cm−1, respectively, indicate the flatness of the potential energy surface for molecular libration. The resulting conformation lability allows the synthon to adjust to different crystal surroundings.
The pair interaction energy was calculated by PBE0-D3/POB-TZVP method for isolated H-bonded dimers in the optimized crystal geometry. It turns out that the binding energy of the dimer observed in form I (4.4 kcal/mol) is the lowest one when it is compared to those of forms II-A (8.6 kcal/mol) and II-B (9.2 kcal/mol). The main reason for the much greater stability of the H-bonded dimers in polymorph II seems to be its additional stabilization by the C-H···O interactions.

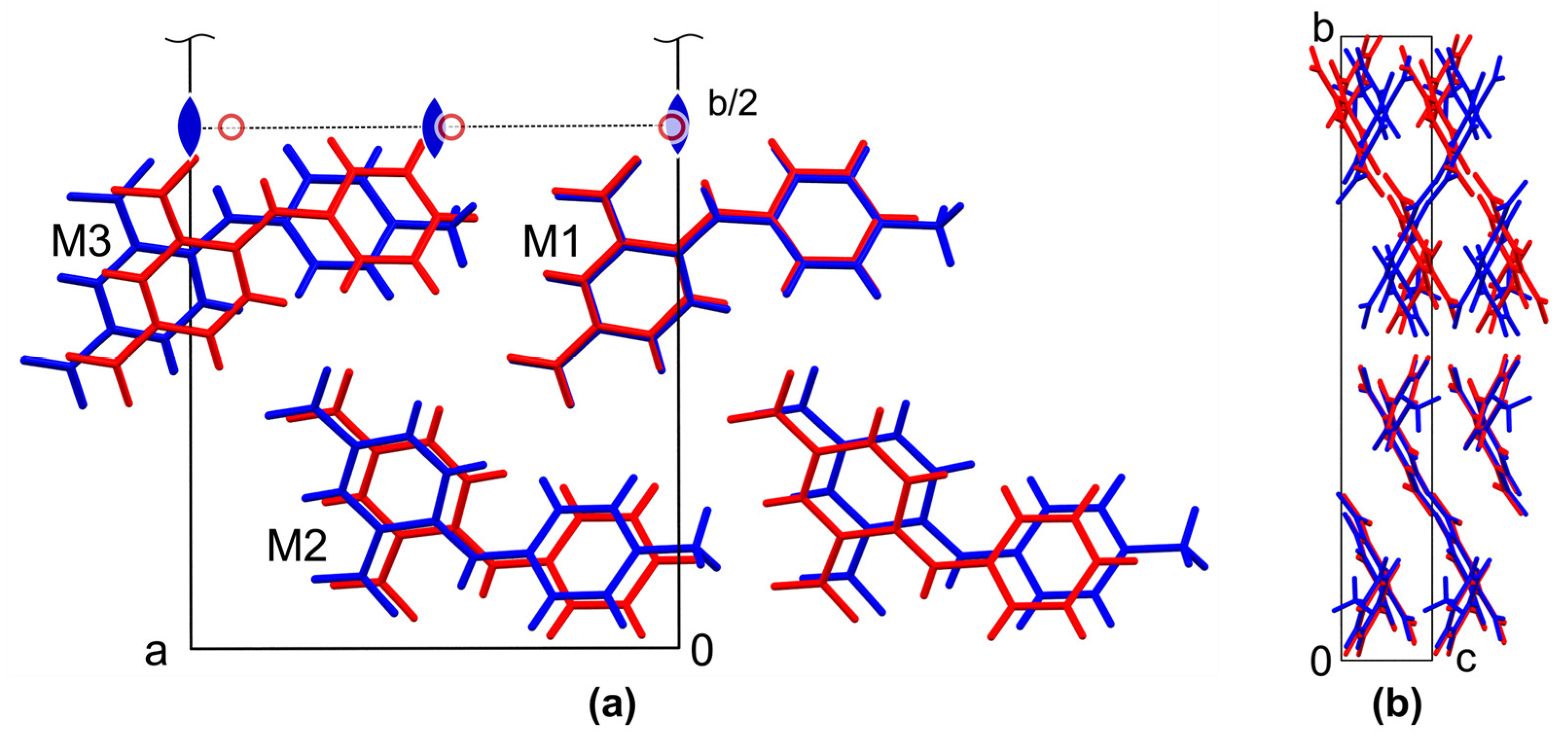
3.3. Other Intermolecular Interactions and Crystal Packing

In addition to the intermolecular interactions in the supramolecular synthon discussed above, all of the intermolecular bonding interactions were found as BCPs in the intermolecular space. A full list of the BCPs is provided in Supporting Information (Tables S2 and S4). The list for polymorph I contains N-H···O, C-H···O, O···O, O···C, C···C, and H···H interactions; note that in this form, there are no direct interactions between the atoms of nitro groups, except for those in the H-bonded dimer, in accordance with the packing pattern (Figure S1 in Supporting Information). It is interesting that the infinite π-stacks in form I are built by partially overlapping benzene rings of the same type and not by alternating electron-rich and electron-deficient cycles, which are more typical for this type of compound. On the other hand, the list of the intermolecular BCPs for polymorph II includes interactions of nearly all of the possible types: N-H···O, C-H···O, C-H···N, O···O, O···C, N···C, C···C, and H···H. In the case of this polymorph, the structure contains dimer-like aggregates built by π-stacking interactions between partially overlapping donor and acceptor cycles.
The lattice energy of the polymorphs was calculated by the PBE0-D3/POB-TZVP method as the difference between the full energy of an optimized crystal structure and a molecule in the crystal geometry. The values of 32.4 and 34.1 kcal/mol for forms I and II, respectively, suggest more effective crystal packing for the triclinic form, and this is in line with its slightly higher density at 100 K. The cohesive energies were calculated to be 31.2 and 32.9 kcal/mol, respectively; the same difference between the forms implies the negligible energy difference between the molecular conformations, and thus, the same deformation energy of ca. 1.2 kcal/mol for molecules I, II-A, and II-B. It should be mentioned that the lattice energy, the cohesion energy, and the crystal density are higher for the triclinic form, while it is less likely to be obtained by crystallization at ambient conditions. Unfortunately, due to the lack of pure bulk sample of the form II, we cannot perform the experimental comparison of the stability of the polymorphs. However, the differential scanning calorimetry measurements of the bulk form I shows the absence of phase transitions up to the melting temperature (see Supporting Information Figure S4), and form I is the polymorph that crystallizes from the melt.
It should be emphasized that based on the ρ(r) and/or EEML values, there are multiple intermolecular interactions that are comparable in energy with those that were found in the supramolecular synthon. In fact, the contribution of the dimerization energy into the total lattice energy is quite small (8.0, 12.6, and 13.5% for I, II-A, and II-B, respectively). However, the supramolecular synthon is formed in both of the polymorphic forms, in structure 2, and in a significant number of o-nitro diphenylamines. Thus, the formation of the synthon can be considered as an important factor for crystal packing and/or for seeding and crystal growth processes.
Interestingly, the comparison of the unit cell parameters of the form I with the data for 2,4-dinitrodiphenylamine 2 shows a strong similarity with regard to the different order of axes. In fact, the smallest dimension nearly coincides, while two others differ only by ca. 0.7 and 1.2 Å. Moreover, the monoclinic angle in form 2 is close to 90°, which leads to pseudo-merohedral twinning of the structure. To reveal the possible similarity of the crystal structures, a ‘Crystal Packing Similarity’ tool implemented to the Mercury 2022.2.0 package [41] was used, as described previously [42]. The clusters of 15 closest molecules in polymorph I was compared with the cluster in polymorph 2. The results of the comparison are depicted in Figure 3.
It turns out that both of the structures contain the same packing fragment, a stack along the crystallographic c axis in form I (or along the a direction in 2) formed by molecules M1 in Figure 3a. These fragments fit perfectly, with an RMS deviation of the common atoms of only 0.062 Å. In the next stack M2, which is related to M1 by a two-fold screw axis, the molecules of form 2 are slightly shifted, and in the stack M3, which is related to M1 by a translation, the shift relative to form I reaches the above-mentioned difference of ca. 1.2 Å of the corresponding unit cell parameter. The latter shift is approximately equal to the linear size difference of the H and Me substituents. Thus, taking into account the difference in the size of the substituents, we can consider the fragment depicted in Figure 3a as quasi-isostructural ones. On the other hand, these fragments are related to each other in the whole unit cell by a proper two-fold rotation axis in form I, but by an inversion center in form 2, which leads to the observed difference in crystal symmetry (Figure 3b). It should be noted that partial isotructurality is a known phenomenon, and the structures of 1 and 2 are a perfect illustration to its relationship with polymorphism [43].
Note that sometimes it is desirable to fix the symmetry relation of fragments, e.g., stacks, by choosing a highly directional supramolecular synthon to exclude, for example, the possibility of inversion and predictably obtain a non-centrosymmetric crystal structure [44]. However, in other cases conformation flexibility of a supramolecular synthon can help it to switch from a centrosymmetric to a non-centrosymmetric structure by variation of the substituent peripheral to the synthon, as in the case of polymorph I and 2. Clearly, the variation in the crystal packing in the structures discussed in this paper results from the interplay between the conformation of the supramolecular synthon and the differences in the overall molecular shape, size, and weak intermolecular interactions, as the conformation of the synthon is not directly affected by the substituents.

4. Conclusions

To summarize, two polymorphic modifications of 4′-methyl-2,4-dinitrodiphenylamine (forms I and II) were obtained, and their structures were established by single-crystal X-ray diffraction. One of the crystal structures (form I) is non-centrosymmetric (space group P21212), which makes us assume possible application of the compound as non-linear optical material. In both of the crystal structures, the molecules form the same supramolecular synthon, a dimer built by two weak intermolecular H-bonds, a bonding O···O interaction between the acceptor atoms of the H-bond that is additionally stabilized by C-H···O interactions with the hydrogen atoms of the tolyl substituents. The differences in the conformation of the supramolecular synthons reflect the symmetry of the crystal structures: in the non-centrosymmetric form I, the dimer is located about a two-fold axis, while in the centrosymmetric structure II, two dimers formed by crystallographically independent molecules lie on the inversion centers. In addition, the geometry of the synthon is different for two independent molecules in form II, as in one of the pairs, the molecules are significantly shifted in direction that is perpendicular to the intramolecular H-bonded ring. The Quantum Theory of Atoms in Molecules (QTAIM) approach applied to the theoretical (PBE0-D3/POB-TZVP) electron density distribution shows that despite the difference in conformation, the set of bonding interactions in the synthons are the same in all of the structures, with the exception of one weak C-H···O bond. Both of the conformations of the supramolecular synthon with C2 and Ci symmetry were found to be energy minima, but with a very flat potential energy surface for molecular libration. Despite the contribution of the binding energy in the supramolecular synthon to the total lattice energy not exceeding 15%, the presence of the synthon in both of the polymorphs and the crystal structure of the related 2,4-dinitrodiphenylamine assumes its importance for crystal packing.
Interestingly, the unit cell parameters of the form I and those of 2,4-dinitrodiphenylamine exhibit a strong similarity. The comparison of the crystal packing shows that both of the structures contain a quasi-isostructural fragment, infinite π-stacks joined by weak non-directional intermolecular interactions. However, these fragments are linked together by the supramolecular synthons, which lead to a non-centrosymmetric structure in the case of polymorph I, but to a centrosymmetric structure (space group P21/n) of the phenyl analogue. Therefore, the addition of one substituent peripheral to the supramolecular synthon indirectly changes the geometry of the synthon and the overall symmetry of the crystal structure, leaving the quasi-isostructural fragment nearly unaffected.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst13020296/s1, Figure S1: Fragment of crystal packing of the polymorph I; Figure S2: Fragments of crystal packing of the polymorph II; Figure S3: Observed and calculated powder diffraction patterns for the crystal structure of form I; Figure S4: DSC curves for the powder sample of form I upon heating and cooling; Listing S1: Coordinates of form I optimized by PBE0-D3/POB-TZVP method; Listing S2: Coordinates of form II optimized by PBE0-D3/POB-TZVP method; Table S1: Bond critical points corresponding to intramolecular interactions in form I; Table S2: Bond critical points corresponding to intramolecular interactions in form I; Table S3: Bond critical points corresponding to intramolecular interactions in form II; Table S4: Bond critical points corresponding to intramolecular interactions in form II.

Author Contributions

Conceptualization, I.V.F. and A.I.S.; methodology, I.V.F. and A.I.S.; software, I.V.F.; validation, I.V.F. and A.I.S.; investigation, I.V.F. and A.I.S.; resources, A.I.S.; data curation, I.V.F. and A.I.S.; writing—original draft preparation, I.V.F.; writing—review and editing, I.V.F.; visualization, I.V.F.; sample synthesis, I.V.F.; supervision, I.V.F.; project administration, I.V.F.; funding acquisition, A.I.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Russian Science Foundation, grant no 22-23-00570.

Data Availability Statement

The data presented in this study are available in Supporting Information. to the Cambridge Structural Database, CCDC 1434708 and 1434709, containing the sup-plementary crystallographic data in this paper. These data can be obtained free of charge via https://www.ccdc.cam.ac.uk/structures/ (accessed on 1 January 2023).

Acknowledgments

The contribution of center for molecule composition studies of INEOS RAS is gratefully acknowledged.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Bernstein, J. Polymorphism in Molecular Crystals; International Union of Crystallography Monographs on Crystallography; Oxford University Press: Oxford, UK; Oxford Clarendon Press: New York, NY, USA, 2002; ISBN 0-19-850605-8. [Google Scholar]
  2. Bernstein, J. Crystal Growth, Polymorphism and Structure-Property Relationships in Organic Crystals. J. Phys. D Appl. Phys. 1993, 26, B66–B76. [Google Scholar] [CrossRef]
  3. Hilfiker, R. (Ed.) Polymorphism in the Pharmaceutical Industry; Wiley-VCH: Weinheim, Germany, 2006; ISBN 978-3-527-31146-0. [Google Scholar]
  4. Politzer, P.; Murray, J.S. Energetic Materials. Pt. 1, Decomposition, Crystal and Molecular Properties; Elsevier: Amsterdam, The Netherlands; Heidelberg, Germany, 2003; ISBN 0-444-51518-6. [Google Scholar]
  5. Ok, K.M.; Chi, E.O.; Halasyamani, P.S. Bulk Characterization Methods for Non-Centrosymmetric Materials: Second-Harmonic Generation, Piezoelectricity, Pyroelectricity, and Ferroelectricity. Chem. Soc. Rev. 2006, 35, 710. [Google Scholar] [CrossRef] [PubMed]
  6. McCrone, W.C. Polymorphism. In Physics and Chemistry of the Organic Solid State; Fox, D., Labes, M.M., Weissberger, A., Eds.; Interscience Publishers: London, UK, 1965; Volume 2, pp. 725–767. [Google Scholar]
  7. Price, S.L. Why Don’t We Find More Polymorphs? Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2013, 69, 313–328. [Google Scholar] [CrossRef] [PubMed]
  8. Cruz-Cabeza, A.J.; Bernstein, J. Conformational Polymorphism. Chem. Rev. 2014, 114, 2170–2191. [Google Scholar] [CrossRef] [PubMed]
  9. Desiraju, G.R. Supramolecular Synthons in Crystal Engineering—A New Organic Synthesis. Angew. Chem. Int. Ed. Engl. 1995, 34, 2311–2327. [Google Scholar] [CrossRef]
  10. Jetti, R.K.R.; Boese, R.; Sarma, J.A.R.P.; Reddy, L.S.; Vishweshwar, P.; Desiraju, G.R. Searching for a Polymorph: Second Crystal Form of 6-Amino-2-Phenylsulfonylimino-1,2-Dihydropyridine. Angew. Chem. Int. Ed. 2003, 42, 1963–1967. [Google Scholar] [CrossRef]
  11. Steiner, T. The Hydrogen Bond in the Solid State. Angew. Chem. Int. Ed. 2002, 41, 48–76. [Google Scholar] [CrossRef]
  12. Gilday, L.C.; Robinson, S.W.; Barendt, T.A.; Langton, M.J.; Mullaney, B.R.; Beer, P.D. Halogen Bonding in Supramolecular Chemistry. Chem. Rev. 2015, 115, 7118–7195. [Google Scholar] [CrossRef]
  13. Rijhwani, J.B.; Asthana, J.G. Synthesis and Antibacterial Activity of Some 2,4-Dinitrodiphenylamine Derivatives. Indian Drugs Pharm. Ind. 1978, 13, 41–42. [Google Scholar]
  14. Manea-Saghin, A.; Andreea Marin, C.; Pădurețu, C.; Kajzar, F. Third-Order Optical Nonlinearity of DNA-CTMA Complex Doped with Different Aromatic Moieties. Opt. Laser Technol. 2022, 149, 107863. [Google Scholar] [CrossRef]
  15. Cao, Y.; Wang, Z.; Zhong, X.; Huang, L.; Xue, W.; Li, M. Application of Powder Test to the Study of New Organic Materials for Frequency Doubling. Chin. J. Lasers Chin. 1992, 19, 627–633. [Google Scholar]
  16. Vizgert, R.V.; Davydov, B.L.; Kotovshchikov, S.G.; Starodubtseva, M.P. Generation of the Second Harmonic of a Neodymium Laser in Powders of Noncentrosymmetric Organic Compounds. Sov. J. Quantum Electron. 1982, 12, 214–215. [Google Scholar] [CrossRef]
  17. Hernández-Paredes, J.; Carrillo-Torres, R.C.; Hernández-Negrete, O.; Sotelo-Mundo, R.R.; Glossman-Mitnik, D.; Esparza-Ponce, H.E.; Alvarez-Ramos, M.E. Experimental and Theoretical Study on the Molecular Structure, Covalent and Non-Covalent Interactions of 2,4-Dinitrodiphenylamine: X-Ray Diffraction and QTAIM Approach. J. Mol. Struct. 2017, 1141, 53–63. [Google Scholar] [CrossRef]
  18. Ikramuddeen, T.M.; Chandrasekara, N.; Ramarajan, K.; Subramanian, K.A. Kinetics of Nucleophilic Substitution Reaction of 1-Chloro-2,4-Dinitrobenzene with Substituted Anilines. J. Indian Chem. Soc. 1989, 66, 342–344. [Google Scholar]
  19. Bruker. SAINT; Bruker AXS Inc.: Madison, WI, USA, 2013. [Google Scholar]
  20. Krause, L.; Herbst-Irmer, R.; Sheldrick, G.M.; Stalke, D. Comparison of Silver and Molybdenum Microfocus X-Ray Sources for Single-Crystal Structure Determination. J. Appl. Crystallogr. 2015, 48, 3–10. [Google Scholar] [CrossRef]
  21. Sheldrick, G.M. SHELXT—Integrated Space-Group and Crystal-Structure Determination. Acta Crystallogr. Sect. Found. Adv. 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
  22. Sheldrick, G.M. Crystal Structure Refinement with SHELXL. Acta Crystallogr. Sect. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef]
  23. Dovesi, R.; Erba, A.; Orlando, R.; Zicovich-Wilson, C.M.; Civalleri, B.; Maschio, L.; Rérat, M.; Casassa, S.; Baima, J.; Salustro, S.; et al. Quantum-Mechanical Condensed Matter Simulations with CRYSTAL. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1360. [Google Scholar] [CrossRef]
  24. Adamo, C.; Barone, V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
  25. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
  26. Peintinger, M.F.; Oliveira, D.V.; Bredow, T. Consistent Gaussian Basis Sets of Triple-Zeta Valence with Polarization Quality for Solid-State Calculations. J. Comput. Chem. 2013, 34, 451–459. [Google Scholar] [CrossRef] [PubMed]
  27. Boys, S.F.; Bernardi, F. The Calculation of Small Molecular Interactions by the Differences of Separate Total Energies. Some Procedures with Reduced Errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
  28. Bader, R.F.W. Atoms in Molecules—A Quantum Theory; Oxford University Press: Oxford, UK, 1990; ISBN 0-19-855168-1. [Google Scholar]
  29. Gatti, C.; Saunders, V.R.; Roetti, C. Crystal Field Effects on the Topological Properties of the Electron Density in Molecular Crystals: The Case of Urea. J. Chem. Phys. 1994, 101, 10686. [Google Scholar] [CrossRef]
  30. Keith, T.A. AIMAll, version 19.10.12; TK Gristmill Software: Overland Park, KS, USA, 2019. [Google Scholar]
  31. Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen Bond Strengths Revealed by Topological Analyses of Experimentally Observed Electron Densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
  32. Spackman, M.A. How Reliable Are Intermolecular Interaction Energies Estimated from Topological Analysis of Experimental Electron Densities? Cryst. Growth Des. 2015, 15, 5624–5628. [Google Scholar] [CrossRef]
  33. Ananyev, I.V.; Karnoukhova, V.A.; Dmitrienko, A.O.; Lyssenko, K.A. Toward a Rigorous Definition of a Strength of Any Interaction Between Bader’s Atomic Basins. J. Phys. Chem. A 2017, 121, 4517–4522. [Google Scholar] [CrossRef]
  34. Lyssenko, K.A. Analysis of Supramolecular Architectures: Beyond Molecular Packing Diagrams. Mendeleev Commun. 2012, 22, 1–7. [Google Scholar] [CrossRef]
  35. Bruno, I.J.; Cole, J.C.; Kessler, M.; Luo, J.; Motherwell, W.D.S.; Purkis, L.H.; Smith, B.R.; Taylor, R.; Cooper, R.I.; Harris, S.E.; et al. Retrieval of Crystallographically-Derived Molecular Geometry Information. J. Chem. Inf. Comput. Sci. 2004, 44, 2133–2144. [Google Scholar] [CrossRef]
  36. Bernstein, J.; Davis, R.E.; Shimoni, L.; Chang, N.-L. Patterns in Hydrogen Bonding: Functionality and Graph Set Analysis in Crystals. Angew. Chem. Int. Ed. Engl. 1995, 34, 1555–1573. [Google Scholar] [CrossRef]
  37. Etter, M.C. Encoding and Decoding Hydrogen-Bond Patterns of Organic Compounds. Acc. Chem. Res. 1990, 23, 120–126. [Google Scholar] [CrossRef]
  38. Fedyanin, I.V.; Lyssenko, K.A. New Hydrogen-Bond-Aided Supramolecular Synthon: A Case Study of 2,4,6-Trinitroaniline. CrystEngComm 2013, 15, 10086–10093. [Google Scholar] [CrossRef]
  39. Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 171–179. [Google Scholar] [CrossRef] [PubMed]
  40. Fedyanin, I.V.; Karnoukhova, V.A.; Lyssenko, K.A. Conformational Analysis of a Supramolecular Synthon: A Case Study of 8-Hydroxyquinoline. CrystEngComm 2018, 20, 652–660. [Google Scholar] [CrossRef]
  41. Macrae, C.F.; Sovago, I.; Cottrell, S.J.; Galek, P.T.A.; McCabe, P.; Pidcock, E.; Platings, M.; Shields, G.P.; Stevens, J.S.; Towler, M.; et al. Mercury 4.0: From Visualization to Analysis, Design and Prediction. J. Appl. Crystallogr. 2020, 53, 226–235. [Google Scholar] [CrossRef] [PubMed]
  42. Vologzhanina, A.V. Intermolecular Interactions in Functional Crystalline Materials: From Data to Knowledge. Crystals 2019, 9, 478. [Google Scholar] [CrossRef]
  43. Bombicz, P. The Way from Isostructurality to Polymorphism. Where Are the Borders? The Role of Supramolecular Interactions and Crystal Symmetries. Crystallogr. Rev. 2017, 23, 118–151. [Google Scholar] [CrossRef]
  44. Fedyanin, I.V. Control of Supramolecular Chirality in Co-Crystals of Achiral Molecules via Stacking Interactions and Hydrogen Bonding. CrystEngComm 2022, 24, 2591–2601. [Google Scholar] [CrossRef]
Crystals 13 00296 sch001 550
Scheme 1. Schematic representation of the molecules 1 and 2.
Scheme 1. Schematic representation of the molecules 1 and 2.
Crystals 13 00296 sch001
Crystals 13 00296 g001 550
Figure 1. (a): General view of the molecule 1 in crystal form I, anisotropic displacement parameters are drawn at 50% probability level; (b): overlay of molecules from crystal structures of forms I (green), II (light and dark blue) and crystal structure of 2,4-dinitrodiphenylamine 2 [17], red).
Figure 1. (a): General view of the molecule 1 in crystal form I, anisotropic displacement parameters are drawn at 50% probability level; (b): overlay of molecules from crystal structures of forms I (green), II (light and dark blue) and crystal structure of 2,4-dinitrodiphenylamine 2 [17], red).
Crystals 13 00296 g001
Crystals 13 00296 g002 550
Figure 2. Topological graphs of the H-bonded dimers in polymorphs I and II (two crystallographically independent molecules A and B). Bond critical points are drawn as orange spheres, bond paths for non-covalent interactions are drawn with dashed lines. The intermolecular R22(12) H-bonded graph set is shown with a green dotted line using form I as an example.
Figure 2. Topological graphs of the H-bonded dimers in polymorphs I and II (two crystallographically independent molecules A and B). Bond critical points are drawn as orange spheres, bond paths for non-covalent interactions are drawn with dashed lines. The intermolecular R22(12) H-bonded graph set is shown with a green dotted line using form I as an example.
Crystals 13 00296 g002
Crystals 13 00296 g003 550
Figure 3. Fragments of crystal packing of eight molecules in polymorph I of 1 (blue) and 2 (red), demonstrating partial quasi-isostructurality of the solids. The unit cell is taken from polymorph I, view along the crystallographic c axis (a) and crystallographic a axis (b). Symmetry elements that generate the second half of the unit cell on (a) are depicted by symbols of the corresponding color.
Figure 3. Fragments of crystal packing of eight molecules in polymorph I of 1 (blue) and 2 (red), demonstrating partial quasi-isostructurality of the solids. The unit cell is taken from polymorph I, view along the crystallographic c axis (a) and crystallographic a axis (b). Symmetry elements that generate the second half of the unit cell on (a) are depicted by symbols of the corresponding color.
Crystals 13 00296 g003
Table
Table 1. Experimental crystallographic data and refinement parameters for polymorphs of 1, forms I and II, and unit cell parameters of form 2 [17].
Table 1. Experimental crystallographic data and refinement parameters for polymorphs of 1, forms I and II, and unit cell parameters of form 2 [17].
Compound12
Form IForm II
Chemical formulaC13H11N3O4
M273.25
CCDC number/
CSD identifier		143470914347081491537/
QQQFGG02
Temperature, K100100100
Crystal shape and colorred needleorange prismred needle
Crystal size, mm0.24 × 0.07 × 0.050.12 × 0.10 × 0.08
Crystal systemorthorhombictriclinicmonoclinic
Space groupP21212P¯1P21/n
Z/Z’4/14/24/1
a, Å12.214(2)7.1979(4)3.7626(2)
b, Å26.118(5)12.8243(8)11.0374(5)
c, Å3.8006(7)13.1514(8)26.8216(12)
α, °9086.2870(10)
β, °9083.6270(10)90.273(2)
γ, °9086.2960(10)
V, Å31212.4(4)1201.93(12)1113.87(9)
dcalc, g cm−31.4971.510
μ (MoKα), mm−10.1140.115
2θ max (°)6060
Measured reflections830625991
Independent reflections35506939
R(int)0.0770.033
No. of parameters186371
Reflections with I > 2σ(I)20705500
R10.0550.053
wR20.0940.136
GOF0.991.03
ρmax/ρmin (e Ǻ−3)0.29/−0.300.44/−0.26
Table
Table 2. Geometric parameters of bonding interactions in forms I and II and characteristics of the electron density ρ(r) and its derivatives.
Table 2. Geometric parameters of bonding interactions in forms I and II and characteristics of the electron density ρ(r) and its derivatives.
III-AII-B
exp.DFTexp.DFTexp.DFT
Intramolecular H-bond
N···O, Å2.620(3)2.5932.6308(19)2.6062.6295(19)2.614
H···O, Å1.8131.8021.8671.8281.8771.842
N−H···O, °133.87132.04129.48130.80128.42130.21
ρ(r), e Å−3 0.266 0.252 0.244
∇2ρ(r), e Å−3 3.42 3.29 3.21
ε 0.02 0.02 0.04
EEML, kcal/mol 12.27 11.36 10.85
Intermolecular H-bond
N···O, Å3.330(3)3.4573.2558(19)3.3003.3865(19)3.436
H···O, Å2.4252.5642.3282.3892.5432.600
N−H···O, °148.22146.75151.58149.03140.33139.61
ρ(r), e Å−3 0.034 0.050 0.035
∇2ρ(r), e Å−3 0.54 0.83 0.53
ε 1.86 0.50 1.39
EEML, kcal/mol 0.86 1.31 0.86
Intermolecular O1···O1 contact
O1···O1, Å2.699(3)2.8912.683(2)2.7442.928(2)2.923
ρ(r), e Å−3 0.044 0.062 0.046
∇2ρ(r), e Å−3 0.87 1.25 0.85
ε 0.47 0.53 0.55
EEML, kcal/mol 1.45 2.33 1.43
Intermolecular C8-H8···O1 contact
C···O, Å3.504(4)3.5933.449(2)3.4293.541(2)3.629
H···O, Å2.8863.0482.8492.7922.6232.720
C-H···O, °115.97111.76114.64117.43141.43113.74
ρ(r), e Å−3 0.022 0.037 0.037
∇2ρ(r), e Å−3 0.32 0.50 0.49
ε 0.30 0.14 0.78
EEML, kcal/mol 0.47 0.87 0.87
Intermolecular C8-H8···O2 contact
C···O, Å3.659(4)3.7753.390(2)3.4583.431(2)3.510
H···O, Å3.2203.4182.7782.8772.4212.561
C-H···O, °105.15100.84115.34141.28145.04145.66
ρ(r), e Å−3 0.031 0.049
∇2ρ(r), e Å−3 0.44 0.64
ε 0.17 0.05
EEML, kcal/mol 0.73 1.17
The values of the electron density ρ(r), laplassian of the electron density ∇2ρ(r), and elliptisity ε are calculated in the corresponding bond critical point (BCP) using PBE0-D3/POB-TZVP data. Experimental N-H and C-H distances normalized to the average values of 1.014 and 1.090 Å taken from DFT calculations.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Fedyanin, I.V.; Samigullina, A.I. Two Crystal Forms of 4′-Methyl-2,4-dinitrodiphenylamine: Polymorphism Governed by Conformational Flexibility of a Supramolecular Synthon. Crystals 2023, 13, 296. https://doi.org/10.3390/cryst13020296

AMA Style

Fedyanin IV, Samigullina AI. Two Crystal Forms of 4′-Methyl-2,4-dinitrodiphenylamine: Polymorphism Governed by Conformational Flexibility of a Supramolecular Synthon. Crystals. 2023; 13(2):296. https://doi.org/10.3390/cryst13020296

Chicago/Turabian Style

Fedyanin, Ivan V., and Aida I. Samigullina. 2023. "Two Crystal Forms of 4′-Methyl-2,4-dinitrodiphenylamine: Polymorphism Governed by Conformational Flexibility of a Supramolecular Synthon" Crystals 13, no. 2: 296. https://doi.org/10.3390/cryst13020296

APA Style

Fedyanin, I. V., & Samigullina, A. I. (2023). Two Crystal Forms of 4′-Methyl-2,4-dinitrodiphenylamine: Polymorphism Governed by Conformational Flexibility of a Supramolecular Synthon. Crystals, 13(2), 296. https://doi.org/10.3390/cryst13020296

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop