Study of the Bandgap and Crystal Structure of Cu4TiSe4: Theory vs. Experiment
Abstract
1. Introduction
2. Materials and Methods
2.1. Solid State Synthesis
2.2. X-ray Diffraction
2.3. Scanning Electron Microscopy (SEM) and Energy-Dispersive X-ray Spectroscopy (EDX)
2.4. UV-Vis Spectrophotometry
2.5. Ab Initio and Uspex Calculations
- Optimized thermodynamic potential: enthalpy;
- Population size: 30;
- Size of initial population: 40;
- Maximal number of generations: 40;
- Portion of structures created by heredity: 0.5;
- Portion of structures created randomly: 0.2;
- Portion of structures created by atom mutations: 0.2;
- Portion of structures created by lattice mutations: 0.1;
- Number of relaxation steps: 5;
- Resolutions of the k-points grid for consecutive relaxations steps: 0.12, 0.11, 0.10, 0.09, and 0.08.
- (I)
- Heredity—it merges two geometrically similar parent structures (in reference to fractional coordinates) while the lattice parameters are the weighted average of the parents;
- (II)
- Permutation—it changes the kind of atom between two randomly picked atoms in the structure;
- (III)
- Mutation—it deforms the elemental cell shape using a random symmetric strain matrix.
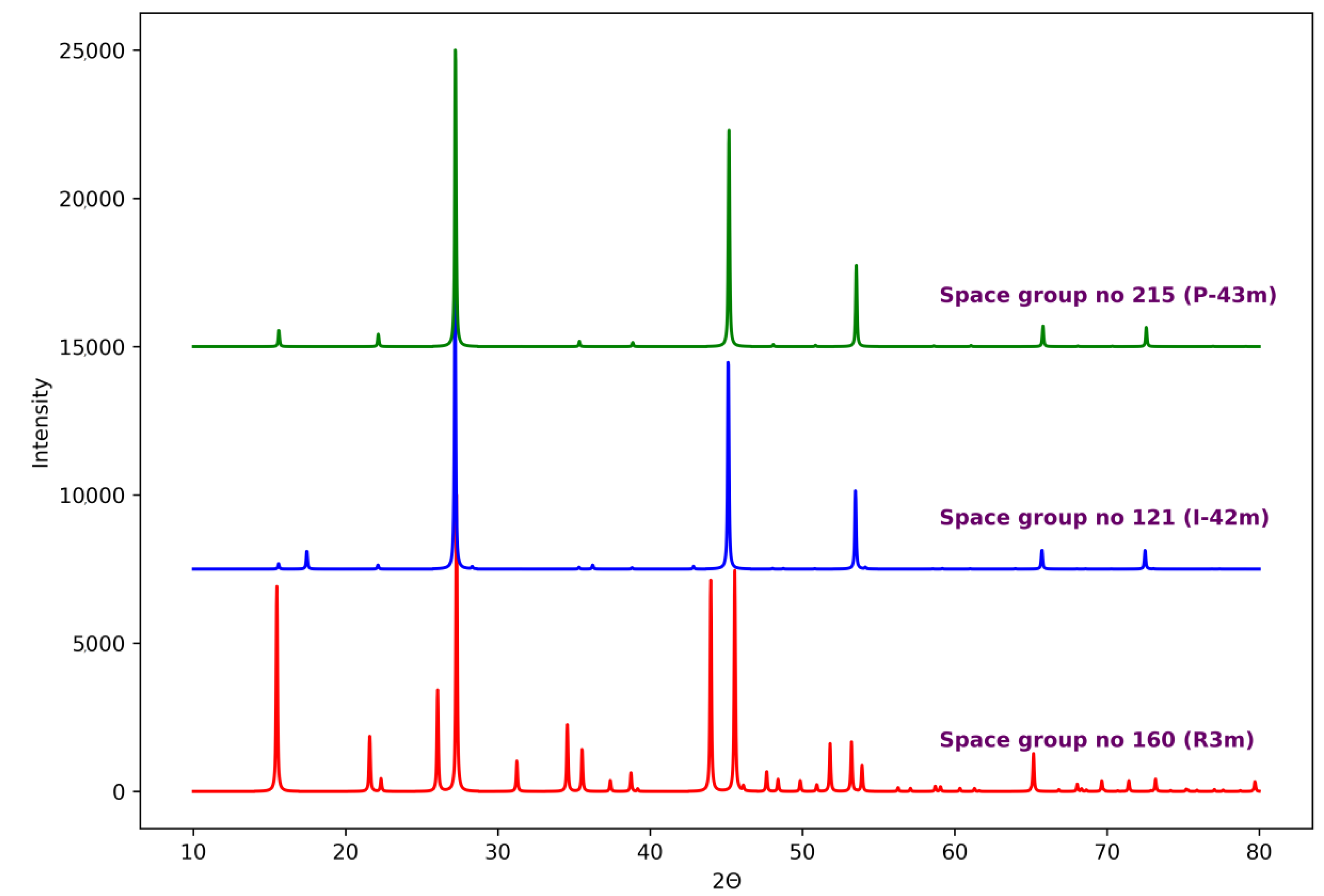
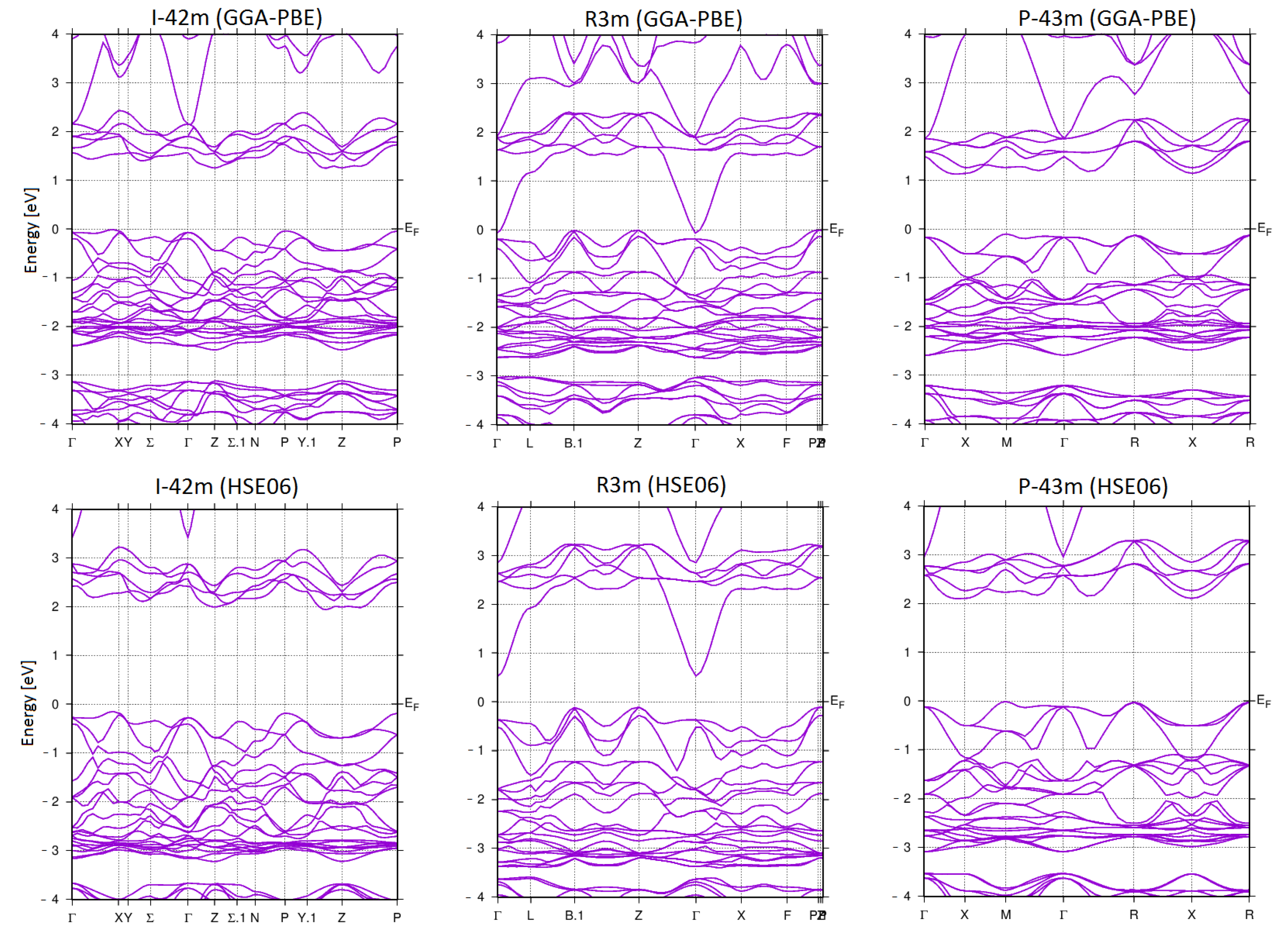
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Burton, L.A.; Colombara, D.; Abellon, R.D.; Grozema, F.C.; Peter, L.M.; Savenije, T.J.; Dennler, G.; Walsh, A. Synthesis, Characterization, and Electronic Structure of Single-Crystal SnS, Sn2S3, and SnS2. Chem. Mater. 2013, 25, 4908–4916. [Google Scholar] [CrossRef]
- Lewis, D.J.; Kevin, P.; Bakr, O.; Muryn, C.A.; Malik, M.A.; O’Brien, P. Routes to tin chalcogenide materials as thin films or nanoparticles: A potentially important class of semiconductor for sustainable solar energy conversion. Inorg. Chem. Front. 2014, 1, 577–598. [Google Scholar] [CrossRef]
- Reddy, N.K.; Devika, M.; Gopal, E.S.R. Review on Tin (II) Sulfide (SnS) Material: Synthesis, Properties, and Applications. Crit. Rev. Solid State 2015, 40, 359–398. [Google Scholar] [CrossRef]
- Zhang, Q.; Ma, S.; Zhang, R.; Tie, Y.; Pei, S. Optimization ethanol detection performance manifested by SnS/SnS2 nanoparticles. Mater. Lett. 2019, 258, 126783. [Google Scholar] [CrossRef]
- Wu, Y.-Q.; Yang, Y.; Pu, H.; Gao, R.-Z.; Meng, W.-J.; Yang, H.-X.; Zhao, D.-L. SnS2 nanoparticle-integrated graphene nanosheets as high-performance and cycle-stable anodes for lithium and sodium storage. J. Alloy Compd. 2020, 822, 153686. [Google Scholar] [CrossRef]
- Tian, H.; Fan, C.; Liu, G.; Yuan, S.; Zhang, Y.; Wang, M.; Li, E. Ultrafast broadband photodetector based on SnS synthesized by hydrothermal method. Appl. Surf. Sci. 2019, 487, 1043–1048. [Google Scholar] [CrossRef]
- Butler, K.T.; Davies, D.W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine learning for molecular and materials science. Nature 2018, 559, 547–555. [Google Scholar] [CrossRef]
- Schleder, G.R.; Padilha, A.C.M.; Acosta, C.M.; Costa, M.; Fazzio, A. From DFT to machine learning: Recent approaches to materials science—A review. J. Phys. Mater. 2019, 2, 032001. [Google Scholar] [CrossRef]
- Song, X.; Ji, X.; Li, M.; Lin, W.; Luo, X.; Zhang, H. A Review on Development Prospect of CZTS Based Thin Film Solar Cells. Int. J. Photoenergy 2014, 2014, 613173. [Google Scholar] [CrossRef]
- Wang, X.; Li, J.; Zhao, Z.; Huang, S.; Xie, W. Crystal structure and electronic structure of quaternary semiconductors Cu2ZnTiSe4 and Cu2ZnTiS4 for solar cell absorber. J. Appl. Phys. 2012, 112, 023701. [Google Scholar] [CrossRef]
- Klepp, K.O.; Eulenberger, G. Preparation and Crystal Structure of Tl4TiS4, Tl4SnS4, and Tl4TiSe4. Z. Naturforsch. B 1984, 39, 705–712. [Google Scholar] [CrossRef]
- Klepp, K.O. Preparation and Crystal Structure of Na4TiSe4. A Selenotitanate with Discrete Tetrahedral Anions. Z. Naturforsch. B 2000, 55, 39–44. [Google Scholar] [CrossRef]
- Chen, E.M.; Williams, L.; Olvera, A.; Zhang, C.; Zhang, M.; Shi, G.; Heron, J.T.; Qi, L.; Guo, L.J.; Kioupakis, E.; et al. Sustainable p-type copper selenide solar material with ultra-large absorption coefficient. Chem. Sci. 2018, 9, 5405–54144. [Google Scholar] [CrossRef] [PubMed]
- Koley, B.; Lakshan, A.; Raghuvanshi, P.R.; Singh, C.; Bhattacharya, A.; Jana, P.P. Ultralow Lattice Thermal Conductivity at Room Temperature in Cu4TiSe4. Angew. Chem. Int. Ed. 2020, 60, 9106–9113. [Google Scholar] [CrossRef]
- Matyszczak, G.; Sutuła, S.; Krawczyk, K.; Woźniak, K. Experimental and theoretical study of crystal structure and bandgap of CdBi2S4. J. Solid State Chem. 2021, 305, 122695. [Google Scholar] [CrossRef]
- Matyszczak, G.; Sutuła, S.; Januszewski, R.; Zakrzewska, A.; Cieślukowska, K.; Gołędowska, M.; Jóźwik, P.; Woźniak, K. Synthesis, characterization, crystal structure prediction, and ab initio study of bandgap of Cu3VSe4. J. Solid State Chem. 2021, 301, 122336. [Google Scholar] [CrossRef]
- CrysAlis CCD and CrysAlis RED; Oxford Diffraction Ltd.: Yarnton, UK, 2008.
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Cryst. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Sheldrick, G.M. SHELXT—Integrated space-group and crystal-structure determination. Acta Cryst. A 2015, 71, 3–8 . [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Cryst. C 2015, 71, 3–8 . [Google Scholar] [CrossRef]
- Zhang, W.; Oganov, A.R.; Goncharov, A.F.; Zhu, Q.; Boulfelfel, S.E.; Lyakhov, A.O.; Stavrou, E.; Somayazulu, M.; Prakapenka, V.B.; Konôpková, Z. Unexpected Stable Stoichiometries of Sodium Chlorides. Science 2013, 342, 1502–1505. [Google Scholar] [CrossRef]
- Zurek, E.; Hoffmann, R.; Ashcroft, N.W.; Oganov, A.R.; Lyakhov, A.O. A little bit of lithium does a lot for hydrogen. Proc. Natl. Acad. Sci. USA 2009, 106, 17640–17643. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes forab initiototal-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://uspex-team.org/en/uspex/documentation (accessed on 8 February 2023).
- Organov, A.R.; Ma, Y.; Glass, C.W.; Valle, M. Evolutionary crystal structure prediction: Overview of the USPEX method and some of its applications. PSI-K Newsl. 2007, 84, 142–171. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Phillips, J.C.; Kleinman, L. New Method for Calculating Wave Functions in Crystals and Molecules. Phys. Rev. 1959, 116, 287–294. [Google Scholar] [CrossRef]
- Lejaeghere, K.; Bihlmayer, G.; Björkman, T.; Blaha, P.; Blügel, S.; Blum, V.; Caliste, D.; Castelli, I.E.; Clark, S.J.; Corso, A.D.; et al. Reproducibility in density functional theory calculations of solids. Science 2016, 351, aad3000. [Google Scholar] [CrossRef]
- Chau, Y.-F.; Wu, F.-L.; Jiang, Z.-H.; Li, H.-Y. Evolution of the complete photonic bandgap of two-dimensional photonic crystal. Opt. Express 2011, 19, 4862–4867. [Google Scholar] [CrossRef]
- Macrae, C.F.; Edgington, P.R.; McCabe, P.; Pidcock, E.; Shields, G.P.; Taylor, R.; Towler, M.; van de Streek, J. Mercury: Visualization and analysis of crystal structures. J. Appl. Crystallogr. 2006, 39, 453–457. [Google Scholar] [CrossRef]
- Klepp, K.; Gurtner, D. Synthesis and crystal structure of Cu4TiS4: A novel chalcogenide with tetrahedrally coordinated titanium. J. Alloy Compd. 1996, 243, 19–22. [Google Scholar] [CrossRef]
- Keane, P.M.; Ibers, J.A. Synthesis, structure, and physical properties of the new group IV ternary tellurides, Cu2MTe3 (M = Ti, Zr, Hf). J. Solid State Chem. 1991, 93, 291–297. [Google Scholar] [CrossRef]
- Choudhury, A.; Mohapatra, S.; Asl, H.Y.; Lee, S.H.; Hor, Y.S.; Medvedeva, J.E.; McClane, D.L.; Hilmas, G.E.; McGuire, M.A.; May, A.F.; et al. New insights into the structure, chemistry, and properties of Cu4SnS4. J. Solid State Chem. 2017, 253, 192–201. [Google Scholar] [CrossRef]
- Anchena, X.; Onodaa, M.; Wada, H.; Satoa, A.; Nozakia, H.; Irmerb, R.H. Preparation, Electrical Properties, Crystal Structure, and Electronic Structure of Cu4GeS4. J. Solid State Chem. 1999, 145, 204–211. [Google Scholar] [CrossRef]
- van Arkel, A.E.; Crevecoeur, C. Quelques sulfures et seleniures complexes. J. Less Common Met. 1963, 5, 177–180. [Google Scholar] [CrossRef]
- Klepp, O.; Gurtner, D. Crystal structure of tricopper tetraselenidovanadate(V), Cu3VSe4. Z. Kristallogr. NCS 2000, 215, 4. [Google Scholar] [CrossRef]
- Koley, B.; Lakshan, A.; Jana, P.P. Temperature-Induced Phase Transition in Cu4TiSe4. Eur. J. Inorg. Chem. 2021, 2021, 5052–5059. [Google Scholar] [CrossRef]
- Matyszczak, G.; Zberecki, K. Application of artificial neural network and global optimization techniques for high throughput modeling of the crystal structure of stannites and kesterites. J. Comput. Chem. 2021, 42, 740–745. [Google Scholar] [CrossRef]
- Chen, S.; Gong, X.G.; Walsh, A.; Wei, S.-H. Crystal and electronic band structure of Cu2ZnSnX4 (X=S and Se) photovoltaic absorbers: First-principles insights. Appl. Phys. Lett. 2009, 94, 041903. [Google Scholar] [CrossRef]
- Shockley, W.; Queisser, H.J. Detailed Balance Limit of Efficiency of p-n Junction Solar Cells. J. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]


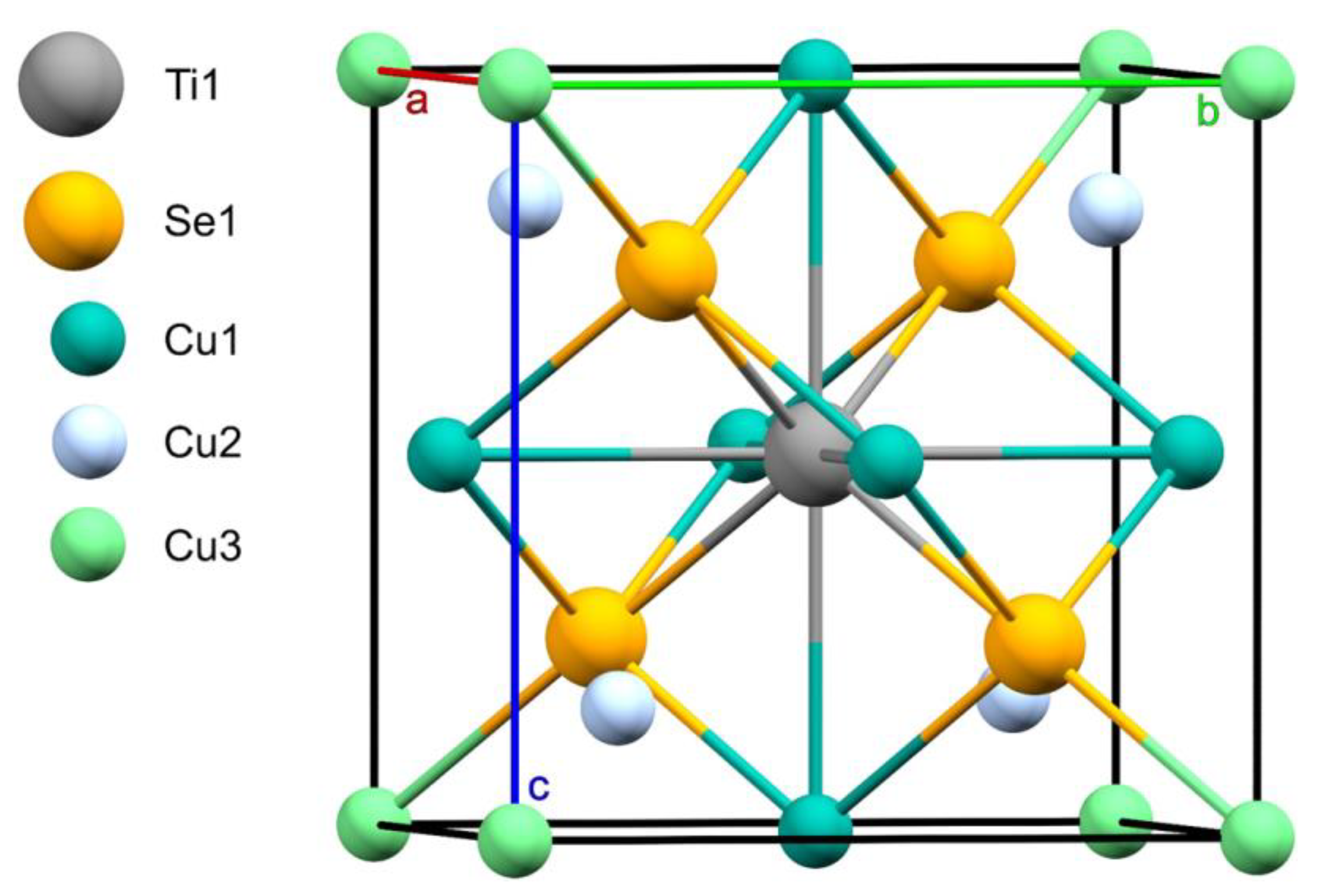
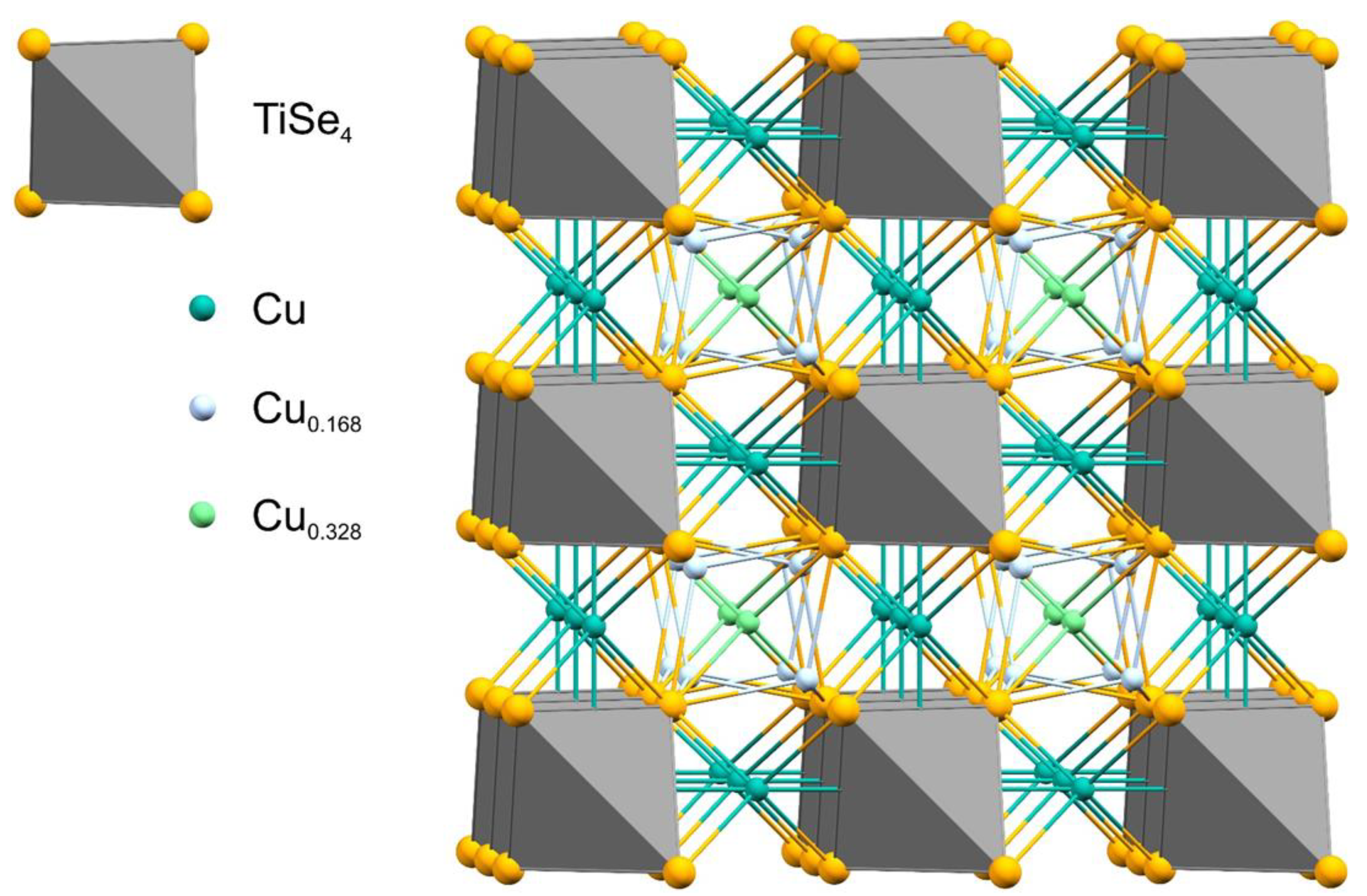


| Empirical Formula | Cu4Se4Ti |
|---|---|
| Formula weight | 617.90 |
| Temperature/K | 296.78(10) |
| Crystal system | cubic |
| Space group | P-43m |
| a/Å | 5.65180(10) |
| b/Å | 5.65180(10) |
| c/Å | 5.65180(10) |
| α/° | 90 |
| β/° | 90 |
| γ/° | 90 |
| Volume/Å3 | 180.535(10) |
| Z | 1 |
| ρcalc g/cm3 | 5.683 |
| μ/mm−1 | 32.692 |
| F(000) | 274.0 |
| Crystal size/mm3 | 0.173 × 0.169 × 0.155 |
| Radiation | MoKα (λ = 0.71073) |
| 2Θ range for data collection/° | 7.21 to 71.336 |
| Index ranges | −9 ≤ h ≤ 9, −9 ≤ k ≤ 9, −8 ≤ l ≤ 9 |
| Reflections collected | 4803 |
| Independent reflections | 194 [Rint = 0.0881, Rsigma = 0.0223] |
| Data/restraints/parameters | 194/0/12 |
| Goodness-of-fit on F2 | 1.239 |
| Final R indexes [I ≥ 2σ (I)] | R1 = 0.0224, wR2 = 0.0576 |
| Final R indexes [all data] | R1 = 0.0241, wR2 = 0.0596 |
| Largest diff. peak/hole/e Å−3 | 2.18/−0.49 |
| Flack parameter | 0.01(5) |
| Space Group Number (Symbol) | Lattice Parameters {Å} | Structure Type | Enthalpy {eV} |
|---|---|---|---|
| 121 (I-42m) | a = 5.677, c = 11.358 | Stannite | −41.262 |
| 215 (P-43m) | a = 5.672 | - | −41.199 |
| 160 (R3m) | a = 7.958, c = 10.258 | - | −41.335 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matyszczak, G.; Sutuła, S.; Jóźwik, P.; Krawczyk, K.; Woźniak, K. Study of the Bandgap and Crystal Structure of Cu4TiSe4: Theory vs. Experiment. Crystals 2023, 13, 331. https://doi.org/10.3390/cryst13020331
Matyszczak G, Sutuła S, Jóźwik P, Krawczyk K, Woźniak K. Study of the Bandgap and Crystal Structure of Cu4TiSe4: Theory vs. Experiment. Crystals. 2023; 13(2):331. https://doi.org/10.3390/cryst13020331
Chicago/Turabian StyleMatyszczak, Grzegorz, Szymon Sutuła, Paweł Jóźwik, Krzysztof Krawczyk, and Krzysztof Woźniak. 2023. "Study of the Bandgap and Crystal Structure of Cu4TiSe4: Theory vs. Experiment" Crystals 13, no. 2: 331. https://doi.org/10.3390/cryst13020331
APA StyleMatyszczak, G., Sutuła, S., Jóźwik, P., Krawczyk, K., & Woźniak, K. (2023). Study of the Bandgap and Crystal Structure of Cu4TiSe4: Theory vs. Experiment. Crystals, 13(2), 331. https://doi.org/10.3390/cryst13020331











