Conductivities in Yttrium-Doped Barium Zirconate: A First-Principles Study
Abstract
1. Introduction
2. Computational Methods and Materials
2.1. Calculation Details
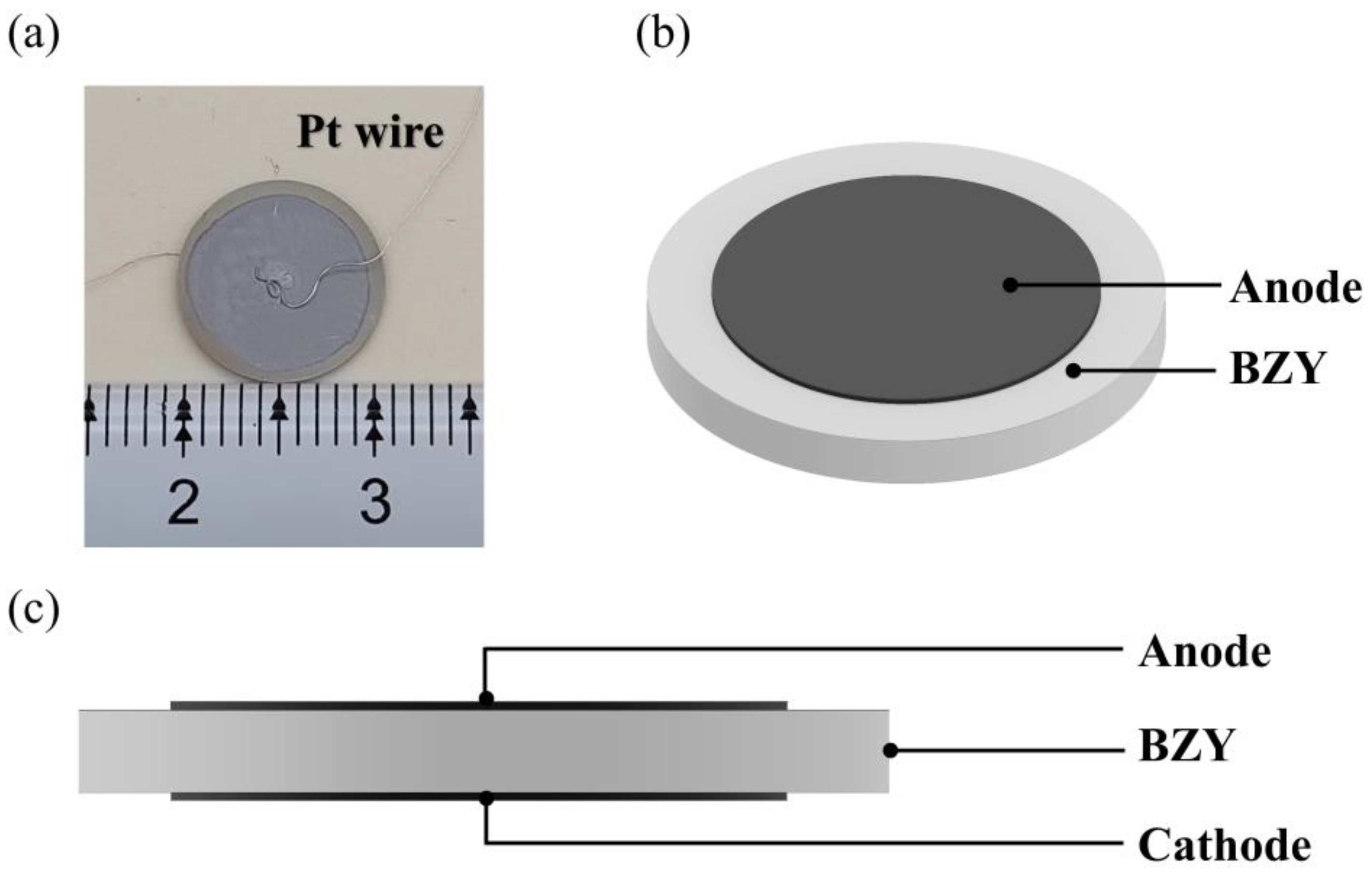
2.2. Fabrication and Testing of Samples
3. Results and Discussion
3.1. Computational Analysis
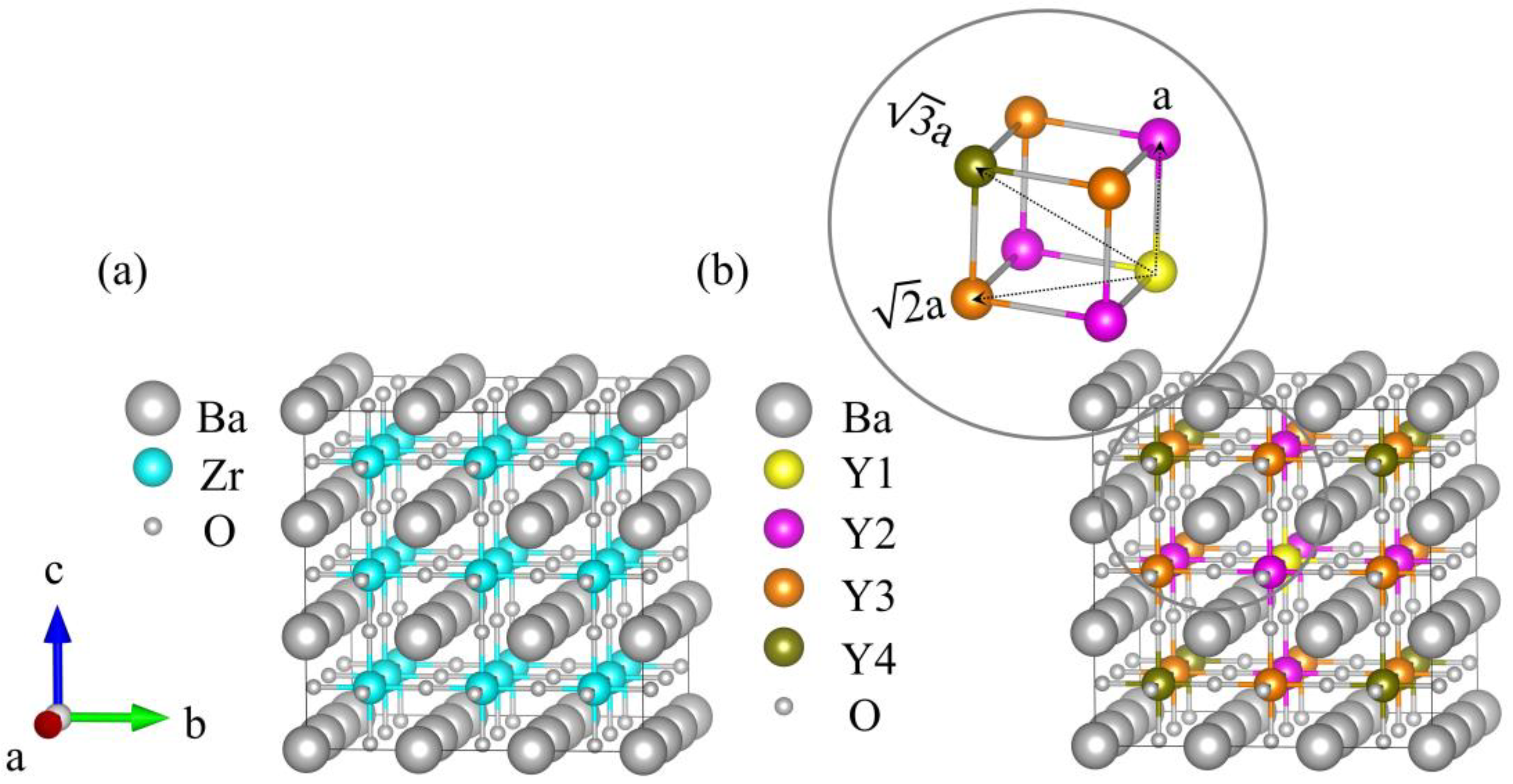
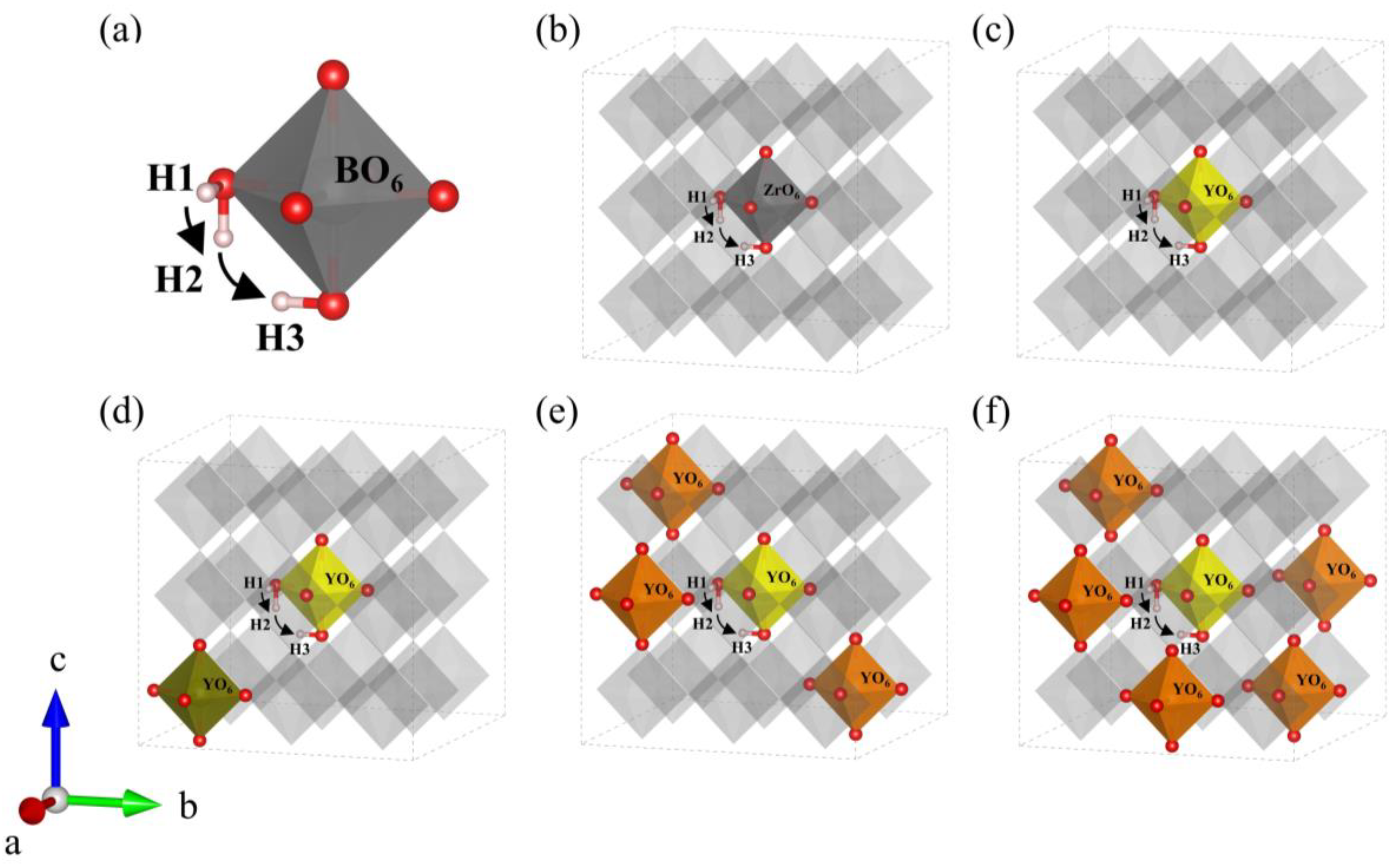
3.1.1. Supercell Structures
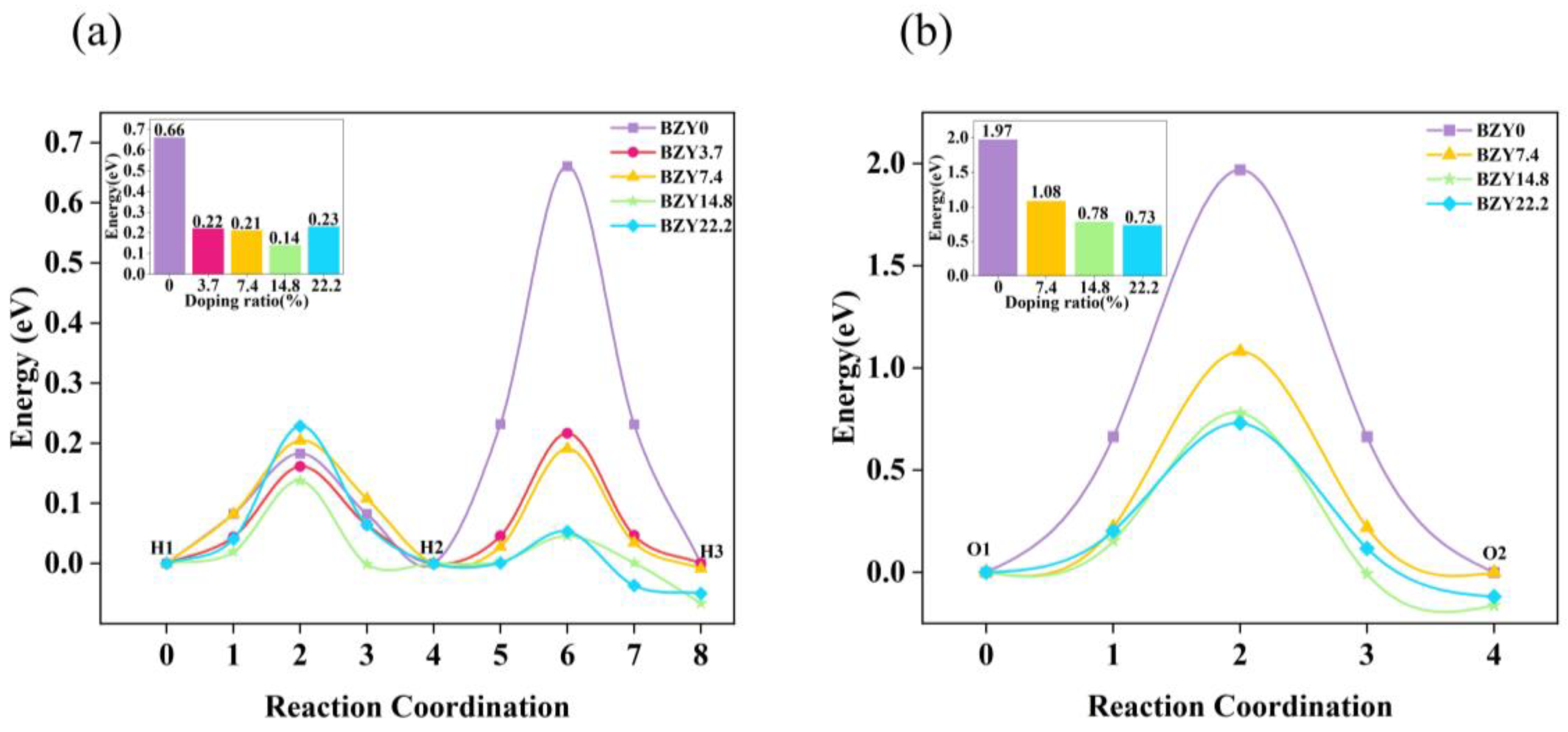
3.1.2. Proton Migration in BZYs
3.1.3. Oxygen Ion Migration in BZYs
3.1.4. Electronic Structure Analysis
3.2. Experimental Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ding, D.; Li, X.; Lai, S.Y.; Gerdes, K.; Liu, M. Enhancing SOFC cathode performance by surface modification through infiltration. Energy Environ. Sci. 2014, 7, 552–575. [Google Scholar] [CrossRef]
- Stambouli, A.B.; Traversa, E. Fuel cells, an alternative to standard sources of energy. Renew. Sust. Energ. Rev. 2002, 6, 295–304. [Google Scholar] [CrossRef]
- Stambouli, A.B.; Traversa, E. Solid oxide fuel cells (SOFCs): A review of an environmentally clean and efficient source of energy. Renew. Sust. Energ. Rev. 2002, 6, 433–455. [Google Scholar] [CrossRef]
- Haile, S.M. Fuel cell materials and components. Acta Mater. 2003, 51, 5981–6000. [Google Scholar] [CrossRef]
- Taylor, F.H.; Buckeridge, J.; Catlow, C.R.A. Defects and oxide ion migration in the solid oxide fuel cell cathode material LaFeO3. Chem. Mater. 2016, 28, 8210–8220. [Google Scholar] [CrossRef]
- Han, D.; Uda, T. The best composition of an Y-doped BaZrO3 electrolyte: Selection criteria from transport properties, microstructure, and phase behavior. J. Mater. Chem. A 2018, 6, 18571–18582. [Google Scholar] [CrossRef]
- Jacobson, A.J. Materials for Solid Oxide Fuel Cells. Chem. Mater. 2009, 22, 660–674. [Google Scholar] [CrossRef]
- Shi, H.; Su, C.; Ran, R.; Cao, J.; Shao, Z. Electrolyte materials for intermediate-temperature solid oxide fuel cells. Prog. Nat. Sci. 2020, 30, 764–774. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, Y.; Yan, M. A review on the preparation of thin-film YSZ electrolyte of SOFCs by magnetron sputtering technology. Sep. Purif. Technol. 2022, 298, 121627. [Google Scholar] [CrossRef]
- Chen, X.J.; Khor, K.A.; Chan, S.H.; Yu, L.G. Influence of microstructure on the ionic conductivity of yttria-stabilized zirconia electrolyte. Mater. Sci. Eng. A 2002, 335, 246–252. [Google Scholar] [CrossRef]
- Pavone, M.; Ritzmann, A.M.; Carter, E.A. Quantum-mechanics-based design principles for solid oxide fuel cell cathode materials. Energy Environ. Sci. 2011, 4, 4933. [Google Scholar] [CrossRef]
- Chen, G.; Luo, Y.; Sun, W.; Liu, H.; Ding, Y.; Li, Y.; Geng, S.; Yu, K.; Liu, G. Electrochemical performance of a new structured low temperature SOFC with BZY electrolyte. Int. J. Hydrog. Energy. 2018, 43, 12765–12772. [Google Scholar] [CrossRef]
- Fabbri, E.; Bi, L.; Pergolesi, D.; Traversa, E. Towards the next generation of solid oxide fuel cells operating below 600 °C with chemically stable proton-conducting electrolytes. Adv. Mater. 2012, 24, 195–208. [Google Scholar] [CrossRef]
- Fabbri, E.; Pergolesi, D.; Traversa, E. Materials challenges toward proton-conducting oxide fuel cells: A critical review. Chem. Soc. Rev. 2010, 39, 4355–4369. [Google Scholar] [CrossRef]
- Poulidi, D.; Metcalfe, I.S. Electrochemical promotion of a metal catalyst supported on a mixed-ionic conductor. Solid State Ion. 2006, 177, 2211–2215. [Google Scholar] [CrossRef]
- Iwahara, H.; Yajima, T.; Hibino, T.; Ozaki, K.; Suzuki, H. Protonic conduction in calcium, strontium and barium zirconates. Solid State Ion. 1993, 61, 65–69. [Google Scholar] [CrossRef]
- Kreuer, K.D. Proton-conducting oxides. Annu. Rev. Mater. Sci. 2003, 33, 333–359. [Google Scholar] [CrossRef]
- Steele, B.C.H.; Heinzel, A. Materials for fuel-cell technologies. Nature 2001, 414, 345–352. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhang, L.; Tang, Z.; Liu, M. Fast oxygen transport in bottlelike channels for y-doped BaZrO3: A reactive molecular dynamics investigation. J. Phys. Chem. C 2019, 123, 25611–25617. [Google Scholar] [CrossRef]
- Draber, F.M.; Denninger, J.R.; Müller, P.C.; Sommerfeld, I.K.; Martin, M. The Impact of Nanoscale Percolation in Yttrium-Doped BaZrO3 on the Oxygen Ion and Proton Conductivities: A Density Functional Theory and Kinetic Monte Carlo Study. Adv. Energy Sustain. Res. 2022, 3, 2200007. [Google Scholar] [CrossRef]
- Draber, F.M.; Ader, C.; Arnold, J.P.; Eisele, S.; Grieshammer, S.; Yamaguchi, S.; Martin, M. Nanoscale percolation in doped BaZrO3 for high proton mobility. Nat. Mater. 2020, 19, 338. [Google Scholar] [CrossRef]
- Merinov, B.; Goddard, W.A. Proton diffusion pathways and rates in Y-doped BaZrO3 solid oxide electrolyte from quantum mechanics. J. Chem. Phys. 2009, 130, 194707. [Google Scholar] [CrossRef] [PubMed]
- Yamazaki, Y.; Blanc, F.; Okuyama, Y.; Buannic, L.; Lucio-Vega, J.C.; Grey, C.P.; Haile, S.M. Proton trapping in yttrium-doped barium zirconate. Nat. Mater. 2013, 12, 647–651. [Google Scholar] [CrossRef] [PubMed]
- Gorelov, V.P.; Balakireva, V.B.; Kuz’min, A.V. Ionic, Proton, and Oxygen conductivities in the BaZr1–xYxO3–α system (x = 0.02–0.15) in humid air. Russ. J. Electrochem. 2010, 46, 890–895. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B Condens. Matter Mater. Phys. 1992, 46, 6671. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmuller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Stolbov, S.; Ortigoza, M.A.; Rahman, T.S. Application of density functional theory to CO tolerance in fuel cells: A brief review. J. Phys. Condens. Matter. 2009, 21, 474226. [Google Scholar] [CrossRef]
- Blochl, P.E. Projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Zaanen, A. Band theory and mott insulators: Hubbard U instead of stoner I. Phys. Rev. B Condens. Matter Mater. Phys. 1991, 44, 943–954. [Google Scholar] [CrossRef] [PubMed]
- Henkelman, G.; Jonsson, H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 2000, 113, 9978–9985. [Google Scholar] [CrossRef]
- Henkelman, G.; Uberuaga, B.P.; Jonsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
- Helal, M.A.; Kojima, S. Structural instability and phase transition in BaZrO3 single crystals: Brillouin scattering and DFT study. Mater. Sci. Eng. B 2021, 271, 115314. [Google Scholar] [CrossRef]
- Bilic, A.; Gale, J.D. Ground state structure of BaZrO3: A comparative first-principles study. Phys. Rev. B 2009, 79, 174107. [Google Scholar] [CrossRef]
- Bjorketun, M.E.; Sundell, P.G.; Wahnstrom, G.; Engberg, D. A kinetic Monte Carlo study of proton diffusion in disordered perovskite structured lattices based on first-principles calculations. Solid State Ion. 2005, 176, 3035–3040. [Google Scholar] [CrossRef]
- Nowick, A.S.; Du, Y. High-temperature protonic conductors with perovskite-related structures. Solid State Ion. 1995, 77, 137–146. [Google Scholar] [CrossRef]
- Agmon, N. The Grotthuss mechanism. Chem. Phys. Lett. 1995, 244, 456. [Google Scholar] [CrossRef]
- Gomez, M.A.; Griffin, M.A.; Jindal, S.; Rule, K.D.; Cooper, V.R. The effect of octahedral tilting on proton binding sites and transition states in pseudo-cubic perovskite oxides. J. Chem. Phys. 2005, 123, 094703. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.S.; Davies, R.A.; Gales, J.D. Proton migration and defect interactions in the CaZrO3 orthorhombic perovskite: A quantum mechanical study. Chem. Mater. 2001, 13, 2049–2055. [Google Scholar] [CrossRef]
- Munch, W.; Kreuer, K.D.; Seifert, G.; Maier, J. Proton diffusion in perovskites: Comparison between BaCeO3, BaZrO3, SrTiO3, and CaTiO3 using quantum molecular dynamics. Solid State Ion. 2000, 136, 183–189. [Google Scholar] [CrossRef]
- Lei, X.; Huang, K.; Qin, C. Enhanced interfacial proton migration on BaZr(Y)O3 by molten carbonate: A first principles study. Solid State Ion. 2016, 289, 48–54. [Google Scholar] [CrossRef]
- Munch, W.; Seifert, G.; Kreuer, K.D.; Maier, J. A quantum molecular dynamics study of the cubic phase of BaTiO3 and BaZrO3. Solid State Ion. 1997, 97, 39–44. [Google Scholar] [CrossRef]
- Rizwan, M.; Aleena, S.; Shakil, M.; Mahmood, T.; Zafar, A.A.; Hussain, T.; Farooq, M.H. A computational insight of electronic and optical properties of Cd-doped BaZrO3. Chinese J. Phys. 2020, 66, 318–326. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, X.; Liu, L.; Jiang, X.; Lv, J.; Li, Z.; Zou, Z. Synthesis and photocatalytic characterization of a new photocatalyst BaZrO3. Int. J. Hydrog. Energy 2008, 33, 5941–5946. [Google Scholar] [CrossRef]
- Fabbri, E.; Pergolesi, D.; Licoccia, S.; Traversa, E. Does the increase in Y-dopant concentration improve the proton conductivity of BaZr1–xYxO3-δ fuel cell electrolytes? Solid State Ion. 2010, 181, 1043–1051. [Google Scholar] [CrossRef]
- Uthayakumar, A.; Pandiyan, A.; Moorthy, S.B.K. Yttrium dependent space charge effect on modulating the conductivity of barium zirconate electrolyte for solid oxide fuel cell. Int. J. Hydrog. Energy 2018, 43, 23488–23499. [Google Scholar] [CrossRef]

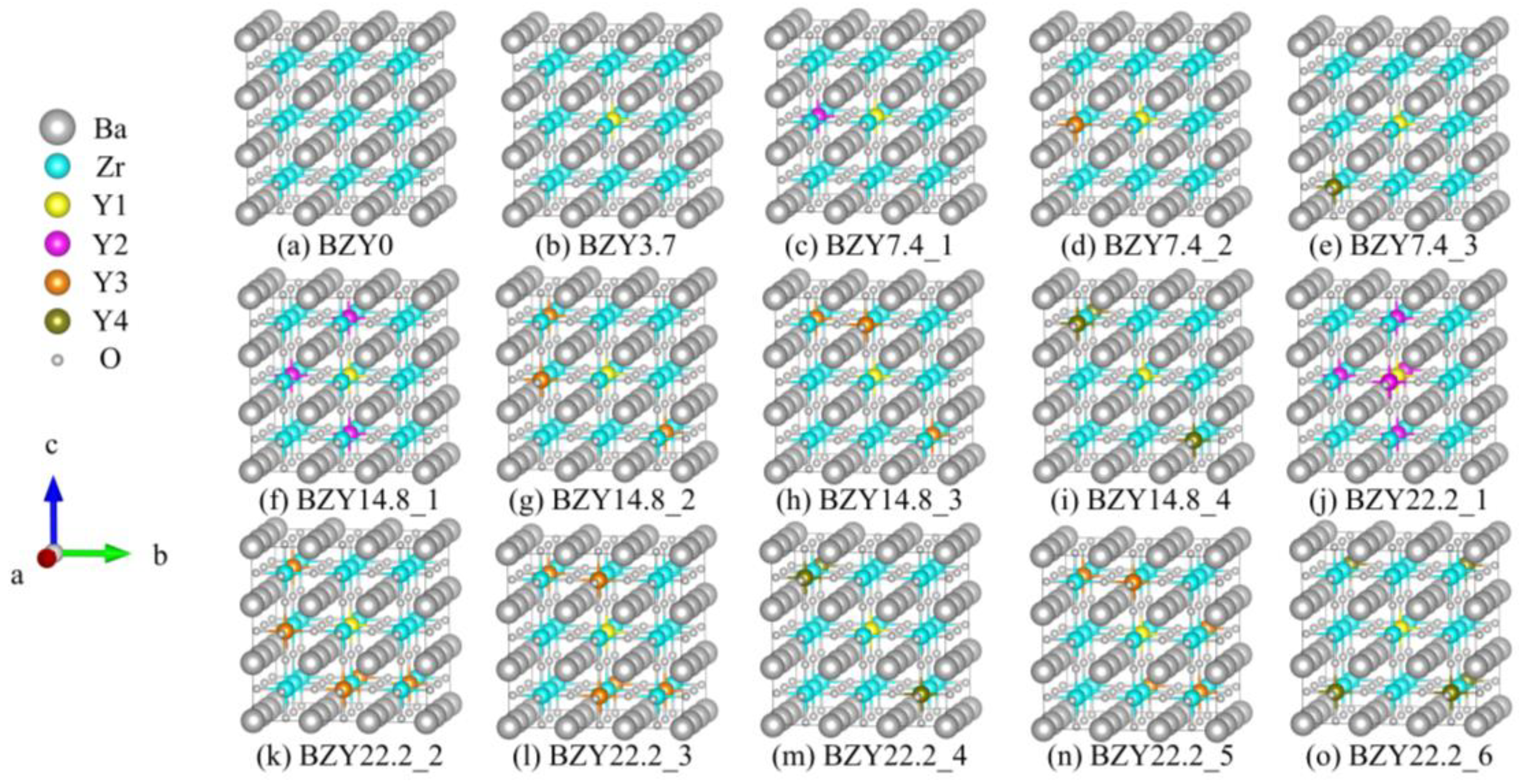
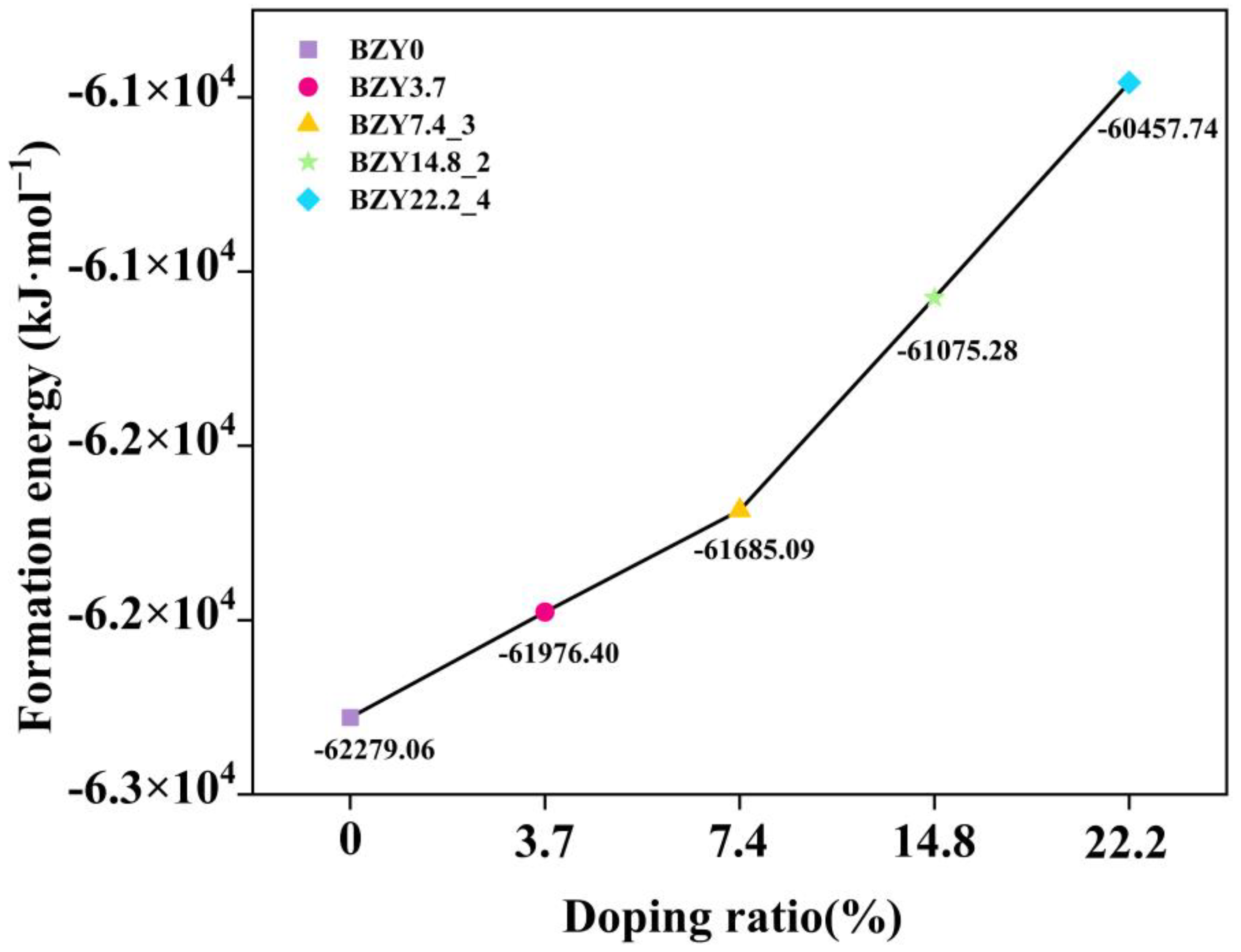




| # of Y | Dopant Concentration | Configurations | Formation Energy (kJ mol−1) |
|---|---|---|---|
| 2 | 7.4% | BZY7.4_1 | −61,663.86 |
| BZY7.4_2 | −61,681.23 | ||
| BZY7.4_3 | −61,685.09 | ||
| 4 | 14.8% | BZY14.8_1 | −61,015.45 |
| BZY14.8_2 | −61,075.28 | ||
| BZY14.8_3 | −61,075.28 | ||
| BZY14.8_4 | −61,066.59 | ||
| 6 | 22.2% | BZY22.2_1 | −60,354.50 |
| BZY22.2_2 | −60,441.34 | ||
| BZY22.2_3 | −60,423.00 | ||
| BZY22.2_4 | −60,457.74 | ||
| BZY22.2_5 | −60,456.77 | ||
| BZY22.2_6 | −60,398.88 |
| Transition State | dOH (Å) | ||||
|---|---|---|---|---|---|
| Initial | 1 | 2 | 3 | 4 | |
| H2-H3 in BZY0 | 0.98 | 1.02 | 1.94a | 1.02 | 0.98 |
| H2-H3 in BZY3.7 | 0.98 | 1.01 | 1.23a | 1.01 | 0.98 |
| H2-H3 in BZY7.4 | 0.98 | 1.01 | 1.23a | 1.01 | 0.98 |
| H2-H3 in BZY14.8 | 1.01 | 1.04 | 1.19a | 1.03 | 1.01 |
| H2-H3 in BZY22.2 | 1.01 | 1.03 | 1.20a | 1.03 | 1.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Zou, J.; Shan, L.; Jiang, X.; Ni, Y.; Li, X.; Qian, X.; Chen, W.; Zhou, Y.; Zhang, W.; et al. Conductivities in Yttrium-Doped Barium Zirconate: A First-Principles Study. Crystals 2023, 13, 401. https://doi.org/10.3390/cryst13030401
Hu H, Zou J, Shan L, Jiang X, Ni Y, Li X, Qian X, Chen W, Zhou Y, Zhang W, et al. Conductivities in Yttrium-Doped Barium Zirconate: A First-Principles Study. Crystals. 2023; 13(3):401. https://doi.org/10.3390/cryst13030401
Chicago/Turabian StyleHu, Huijia, Jie Zou, Liang Shan, Xiaoqing Jiang, Yongjian Ni, Xuebin Li, Xianwei Qian, Wenwen Chen, Yucun Zhou, Weifeng Zhang, and et al. 2023. "Conductivities in Yttrium-Doped Barium Zirconate: A First-Principles Study" Crystals 13, no. 3: 401. https://doi.org/10.3390/cryst13030401
APA StyleHu, H., Zou, J., Shan, L., Jiang, X., Ni, Y., Li, X., Qian, X., Chen, W., Zhou, Y., Zhang, W., Wei, S., & Jian, J. (2023). Conductivities in Yttrium-Doped Barium Zirconate: A First-Principles Study. Crystals, 13(3), 401. https://doi.org/10.3390/cryst13030401







