Numerical Simulations of Circular Dichroism and Polarization Conversion in VO2-Based Terahertz Metamaterials
Abstract
:1. Introduction
2. Structural Design and Methods
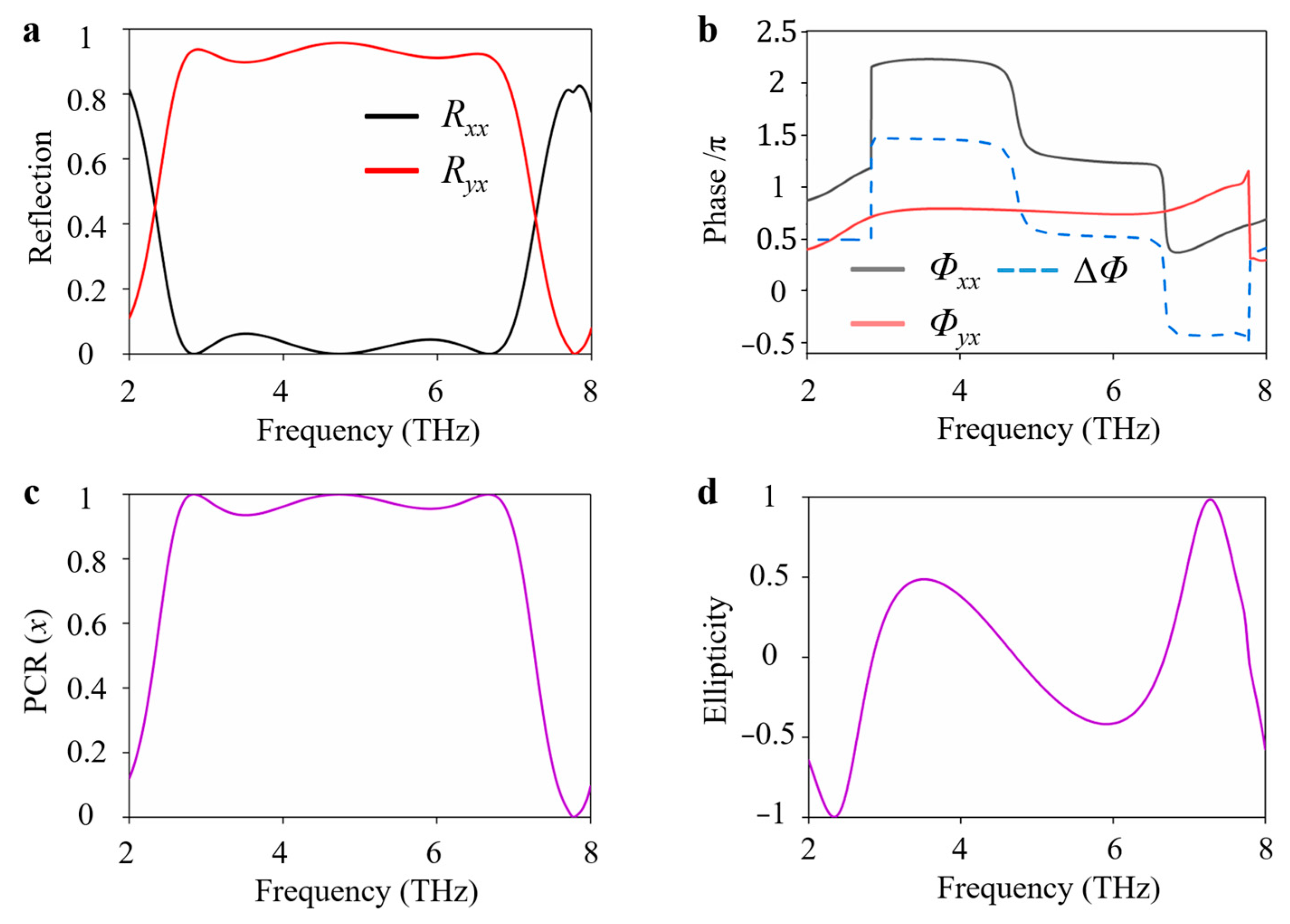
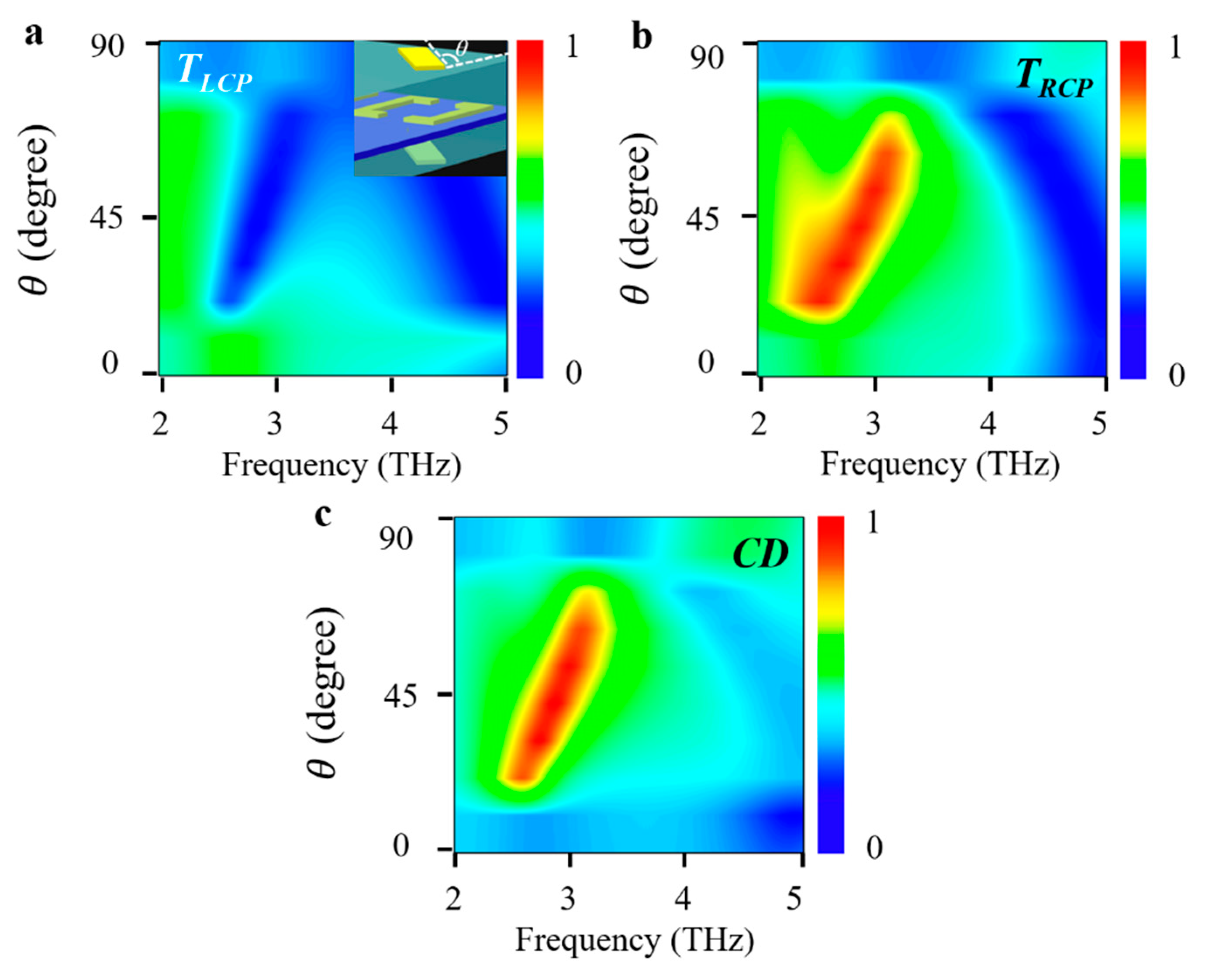
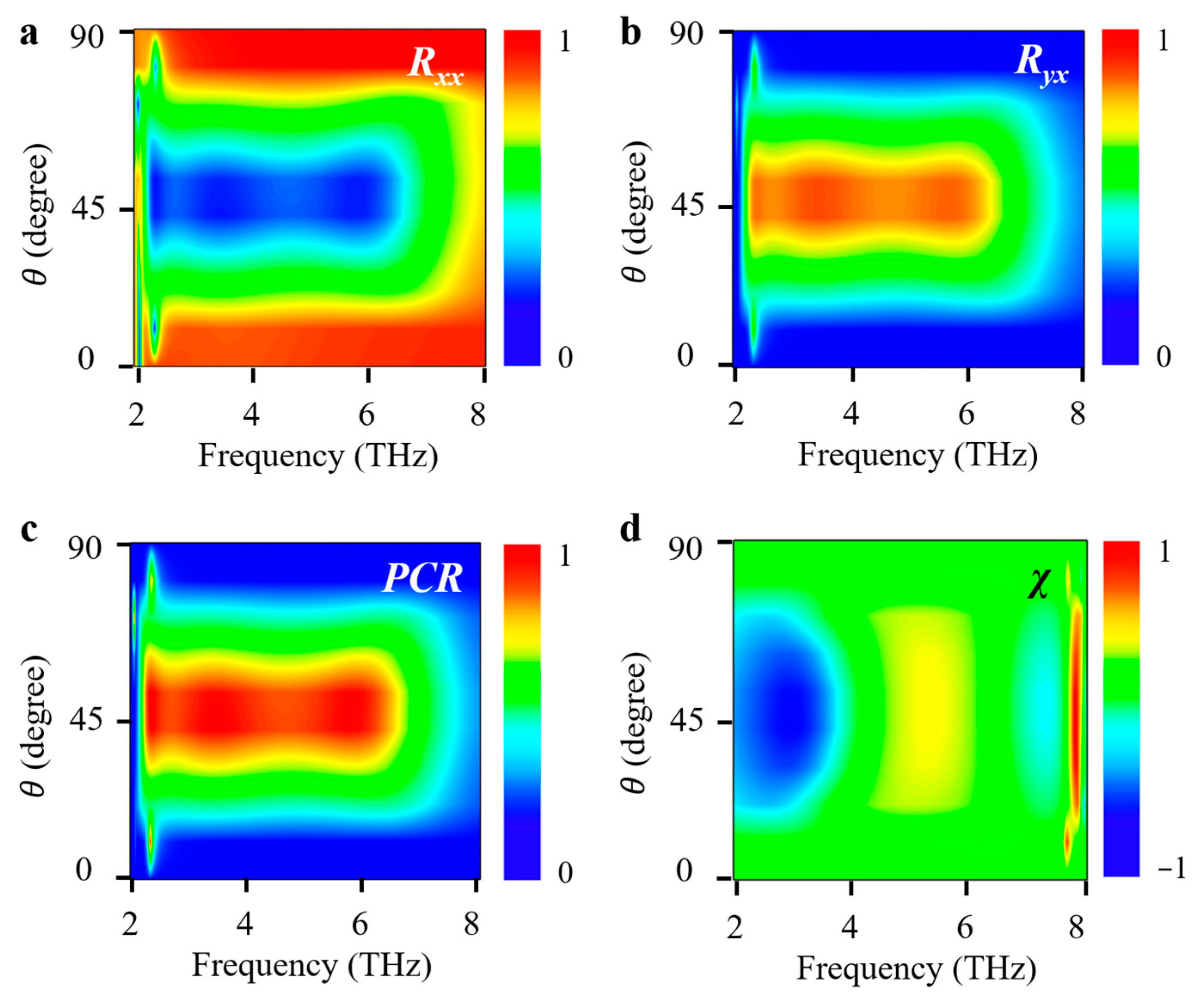
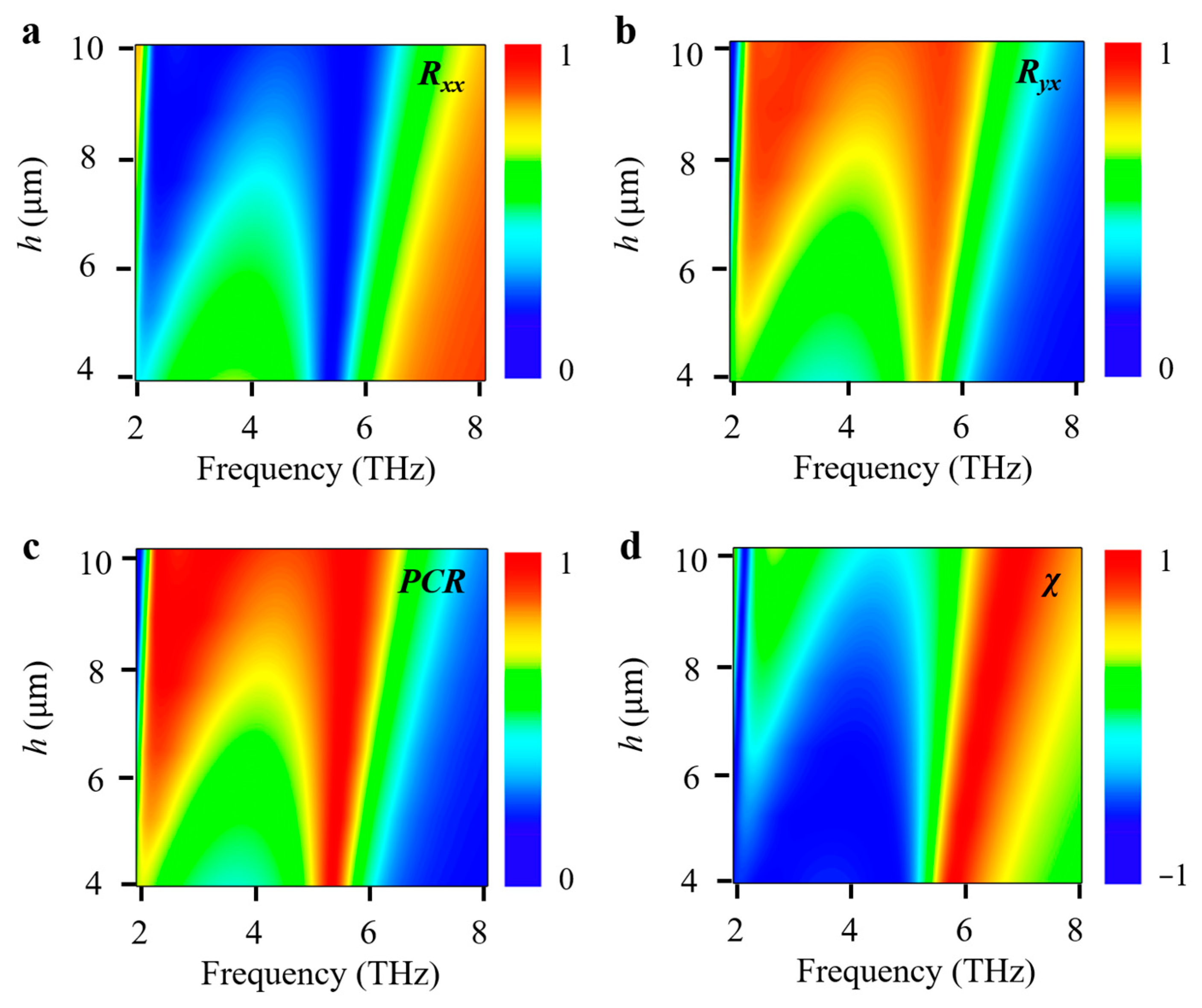
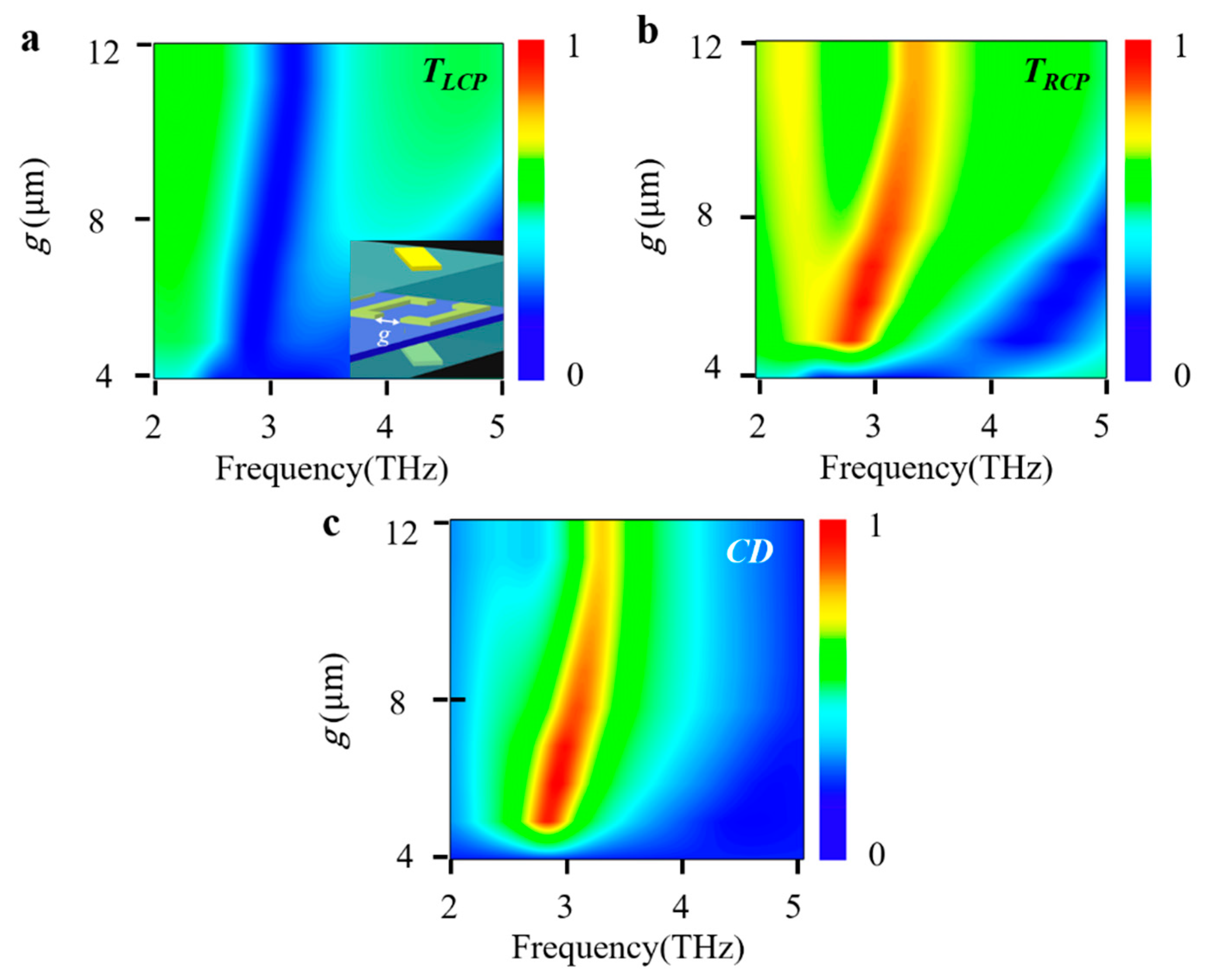
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cui, Y.; Kang, L.; Lan, S.; Rodrigues, S.; Cai, W. Giant Chiral Optical Response from a Twisted-Arc Metamaterial. Nano Lett. 2014, 14, 1021–1025. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Yao, K.; Su, G.; Ma, W.; Li, L.; Liu, Y.; Zhan, P.; Wang, Z. Graphene-metal hybrid metamaterials for strong and tunable circular dichroism generation. Opt. Lett. 2018, 43, 2636–2639. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Dong, G.; Zhao, R.; Wang, K.; Zhou, S.; Sun, L.; Li, P.; Zhu, Z.; Guan, C.; Shi, J. Dual-band asymmetric transmission and circular dichroism in hybrid coupled plasmonic metamaterials. J. Phys. D Appl. Phys. 2018, 51, 285105. [Google Scholar] [CrossRef]
- Ren, Y.; Jiang, C.; Tang, B. Asymmetric transmission in bilayer chiral metasurfaces for both linearly and circularly polarized waves. JOSA B 2020, 37, 3379–3385. [Google Scholar] [CrossRef]
- Tang, B.; Li, Z.; Palacios, E.; Liu, Z.; Butun, S.; Aydin, K. Chiral-Selective Plasmonic Metasurface Absorbers Operating at Visible Frequencies. IEEE Photon. Tech. Lett. 2017, 29, 295–298. [Google Scholar] [CrossRef]
- Rajaei, M.; Zeng, J.; Albooyeh, M.; Kamandi, M.; Hanifeh, M.; Capolino, F.; Wickramasinghe, H.K. Giant Circular Dichroism at Visible Frequencies Enabled by Plasmonic Ramp-Shaped Nanostructures. ACS Photonics 2019, 6, 924–931. [Google Scholar] [CrossRef]
- Huang, Y.; Yao, Z.; Hu, F.; Liu, C.; Yu, L.; Jin, Y.; Xu, X. Tunable circular polarization conversion and asymmetric transmission of planar chiral graphene-metamaterial in terahertz region. Carbon 2017, 119, 305–313. [Google Scholar] [CrossRef]
- Huang, Y.; Xie, X.; Pu, M.; Guo, Y.; Xu, M.; Ma, X.; Li, X.; Luo, X. Dual-Functional Metasurface toward Giant Linear and Circular Dichroism. Adv. Opt. Mater. 2020, 8, 1902061. [Google Scholar] [CrossRef]
- Amin, M.; Siddiqui, O.; Farhat, M. Linear and Circular Dichroism in Graphene-Based Reflectors for Polarization Control. Phys. Rev. Appl. 2020, 13, 024046. [Google Scholar] [CrossRef] [Green Version]
- Xiao, S.; Wang, T.; Liu, T.; Zhou, C.; Jiang, X.; Zhang, J. Active metamaterials and metadevices: A review. J. Phys. D Appl. Phys. 2020, 53, 503002. [Google Scholar] [CrossRef]
- Dănilă, O.; Bărar, A.; Vlădescu, M.; Mănăilă-Maximean, D. An extended k-surface framework for electromagnetic fields in artificial media. Materials 2021, 14, 7842. [Google Scholar] [CrossRef] [PubMed]
- Danila, O.; Manaila-Maximean, D. Bifunctional metamaterials using spatial phase gradient architectures: Generalized reflection and refraction considerations. Materials 2021, 14, 2201. [Google Scholar] [CrossRef] [PubMed]
- Tang, B.; Yang, N.; Song, X.; Jin, G.; Su, J. Triple-band anisotropic perfect absorbers based on α-phase MoO3 metamaterials in visible frequencies. Nanomaterials 2021, 11, 2061. [Google Scholar] [CrossRef]
- Tang, B.; Guo, Z.; Jin, G. Polarization-controlled and symmetry-dependent multiple plasmon-induced transparency in graphene-based metasurfaces. Opt. Express 2022, 30, 35554–35566. [Google Scholar] [CrossRef]
- Grady, N.K.; Heyes, J.E.; Chowdhury, D.R.; Zeng, Y.; Reiten, M.T.; Azad, A.K.; Taylor, A.J.; Dalvit, D.A.; Chen, H.-T. Terahertz metamaterials for linear polarization conversion and anomalous refraction. Science 2013, 340, 1304–1307. [Google Scholar] [CrossRef] [Green Version]
- Yu, Y.; Xiao, F.; He, C.; Jin, R.; Zhu, W. Double-arrow metasurface for dual-band and dual-mode polarization conversion. Opt. Express 2020, 28, 11797–11805. [Google Scholar] [CrossRef] [PubMed]
- Azzam, R.M.A.; Bashara, N.M. Ellipsometry and Polarized Light; North-Holland: New Yourk, NY, USA, 1977. [Google Scholar]
- Zheng, Q.; Guo, C.; Ding, J. Wideband Metasurface-Based Reflective Polarization Converter for Linear-to-Linear and Linear-to-Circular Polarization Conversion. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 1459–1463. [Google Scholar] [CrossRef]
- Wu, P.C.; Sokhoyan, R.; Shirmanesh, G.K.; Cheng, W.-H.; Atwater, H.A. Near-Infrared Active Metasurface for Dynamic Polarization Conversion. Adv. Opt. Mater. 2021, 9, 2100230. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, Y.; Zhao, J. Graphene-enabled tunable multifunctional metamaterial for dynamical polarization manipulation of broadband terahertz wave. Carbon 2020, 163, 244–252. [Google Scholar] [CrossRef]
- Jia, Z.; Huang, L.; Su, J.; Tang, B. Tunable electromagnetically induced transparency-like in graphene metasurfaces and its application as a refractive index sensor. J. Lightwave Technol. 2021, 39, 1544–1549. [Google Scholar] [CrossRef]
- Zhu, Y.; Tang, B.; Jiang, C. Tunable ultra-broadband anisotropic absorbers based on multi-layer black phosphorus ribbons. Appl. Phys. Express 2019, 12, 032009. [Google Scholar] [CrossRef]
- Quader, S.; Zhang, J.; Akram, M.R.; Zhu, W. Graphene-based high-efficiency broadband tunable linear-to-circular polarization converter for terahertz waves. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1–8. [Google Scholar] [CrossRef]
- Park, J.; Kang, J.-H.; Kim, S.J.; Liu, X.; Brongersma, M.L. Dynamic reflection phase and polarization control in metasurfaces. Nano Lett. 2017, 17, 407–413. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Lu, J.; Wang, X.R. Metamaterials based on the phase transition of VO2. Nanotechnology 2017, 29, 24002. [Google Scholar] [CrossRef]
- Kocer, H.; Butun, S.; Ba Nar, B.; Wang, K.; Tongay, S.; Wu, J.; Aydin, K. Thermal tuning of infrared resonant absorbers based on hybrid gold-VO2 nanostructures. Appl. Phys. Lett. 2015, 106, 161104. [Google Scholar] [CrossRef]
- Lei, L.; Lou, F.; Tao, K.; Huang, H.; Cheng, X.; Xu, P. Tunable and scalable broadband metamaterial absorber involving VO2-based phase transition. Photon. Res. 2019, 7, 734–741. [Google Scholar] [CrossRef]
- Ren, Y.; Zhou, T.; Jiang, C.; Tang, B. Thermally switching between perfect absorber and asymmetric transmission in vanadium dioxide-assisted metamaterials. Opt. Express 2021, 29, 7666–7679. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, H.; Zhang, Y.; Zhang, Y.; Cao, M. Tunable bifunctional terahertz metamaterial device based on Dirac semimetals and vanadium dioxide. Opt. Express 2020, 28, 17434–17448. [Google Scholar] [CrossRef]
- Song, Z.; Zhang, J. Achieving broadband absorption and polarization conversion with a vanadium dioxide metasurface in the same terahertz frequencies. Opt. Express 2020, 28, 12487–12497. [Google Scholar] [CrossRef]
- Yan, D.; Meng, M.; Li, J.; Li, J.; Li, X. Vanadium dioxide-assisted broadband absorption and linear-to-circular polarization conversion based on a single metasurface design for the terahertz wave. Opt. Express 2020, 28, 29843–29854. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, K.; Cao, A.; Liu, Y.; Kong, W. Bi-functional switchable broadband terahertz polarization converter based on a hybrid graphene-metal metasurface. Opt. Express 2020, 28, 26102–26110. [Google Scholar] [CrossRef] [PubMed]
- Mao, M.; Liang, Y.; Liang, R.; Zhao, L.; Xu, N.; Guo, J.; Wang, F.; Meng, H.; Liu, H.; Wei, Z. Dynamically Temperature-Voltage Controlled Multifunctional Device Based on VO2 and Graphene Hybrid Metamaterials: Perfect Absorber and Highly Efficient Polarization Converter. Nanomaterials 2019, 9, 1101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ren, Y.; Tang, B. Switchable Multi-Functional VO2-Integrated Metamaterial Devices in the Terahertz Region. J. Lightwave Technol. 2021, 39, 5864–5868. [Google Scholar] [CrossRef]
- Wang, R.; Tang, B. Tri-functional metamaterials integrated with vanadium dioxide in terahertz regions. Phys. E Low-Dimens. Syst. Nanostructures 2022, 144, 115414. [Google Scholar] [CrossRef]
- Qi, H.; Tang, B. Active tunable terahertz functional metamaterial based on hybrid-graphene vanadium dioxide. Phys. Chem. Chem. Phys. 2023. [Google Scholar] [CrossRef] [PubMed]
- Ding, F.; Zhong, S.; Bozhevolnyi, S.I. Vanadium Dioxide Integrated Metasurfaces with Switchable Functionalities at Terahertz Frequencies. Adv. Opt. Mater. 2018, 6, 1701204. [Google Scholar] [CrossRef]
- Luo, J.; Shi, X.; Luo, X.; Hu, F.; Li, G. Broadband switchable terahertz half-/quarter-wave plate based on metal-VO2 metamaterials. Opt. Express 2020, 28, 30861–30870. [Google Scholar] [CrossRef]
- Tang, B.; Ren, Y. Tunable and switchable multi-functional terahertz metamaterials based on a hybrid vanadium dioxide–graphene integrated configuration. Phys. Chem. Chem. Phys. 2022, 24, 8408–8414. [Google Scholar] [CrossRef]
- Zhao, J.; Song, J.; Xu, T.; Yang, T.; Zhou, J. Controllable linear asymmetric transmission and perfect polarization conversion in a terahertz hybrid metal-graphene metasurface. Opt. Express 2019, 27, 9773–9781. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, G.; Ren, Y.; Tang, B. Numerical Simulations of Circular Dichroism and Polarization Conversion in VO2-Based Terahertz Metamaterials. Crystals 2023, 13, 437. https://doi.org/10.3390/cryst13030437
Jin G, Ren Y, Tang B. Numerical Simulations of Circular Dichroism and Polarization Conversion in VO2-Based Terahertz Metamaterials. Crystals. 2023; 13(3):437. https://doi.org/10.3390/cryst13030437
Chicago/Turabian StyleJin, Gui, Yi Ren, and Bin Tang. 2023. "Numerical Simulations of Circular Dichroism and Polarization Conversion in VO2-Based Terahertz Metamaterials" Crystals 13, no. 3: 437. https://doi.org/10.3390/cryst13030437
APA StyleJin, G., Ren, Y., & Tang, B. (2023). Numerical Simulations of Circular Dichroism and Polarization Conversion in VO2-Based Terahertz Metamaterials. Crystals, 13(3), 437. https://doi.org/10.3390/cryst13030437





