The Reliability of the Complex Components under Temperature Cycling, Random Vibration, and Combined Loading for Airborne Applications
Abstract
:1. Introduction
2. Experimental Procedures and Simulation
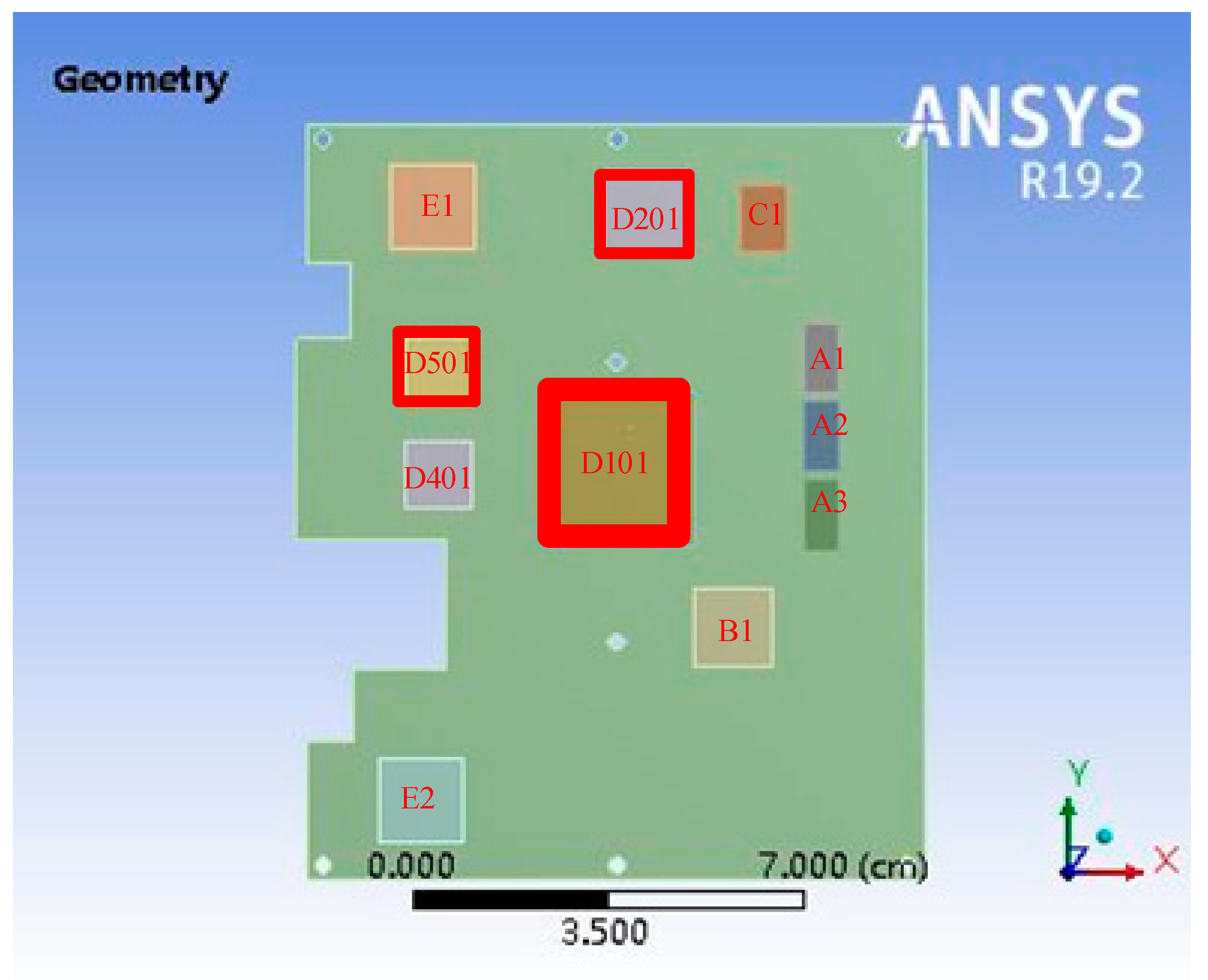
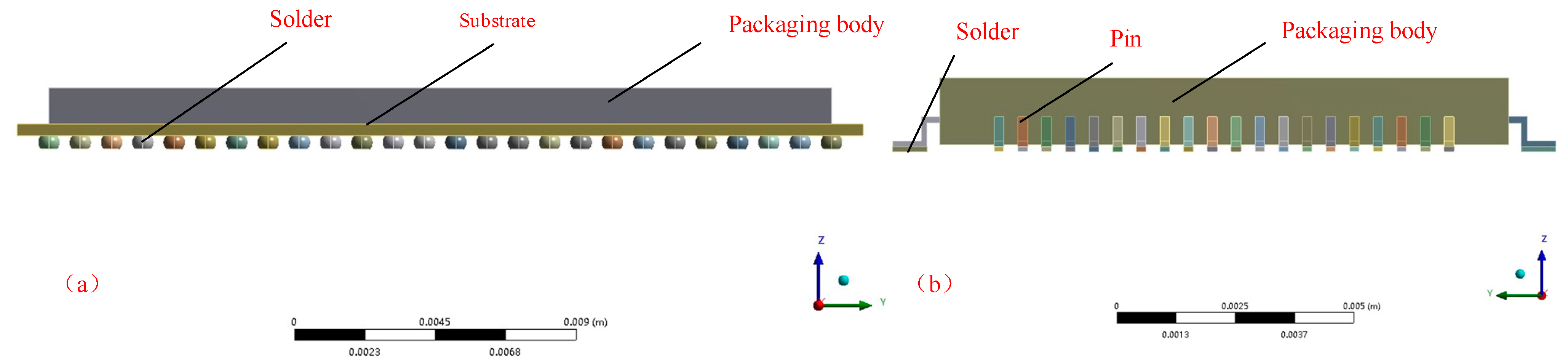
2.1. Specimen and Testing
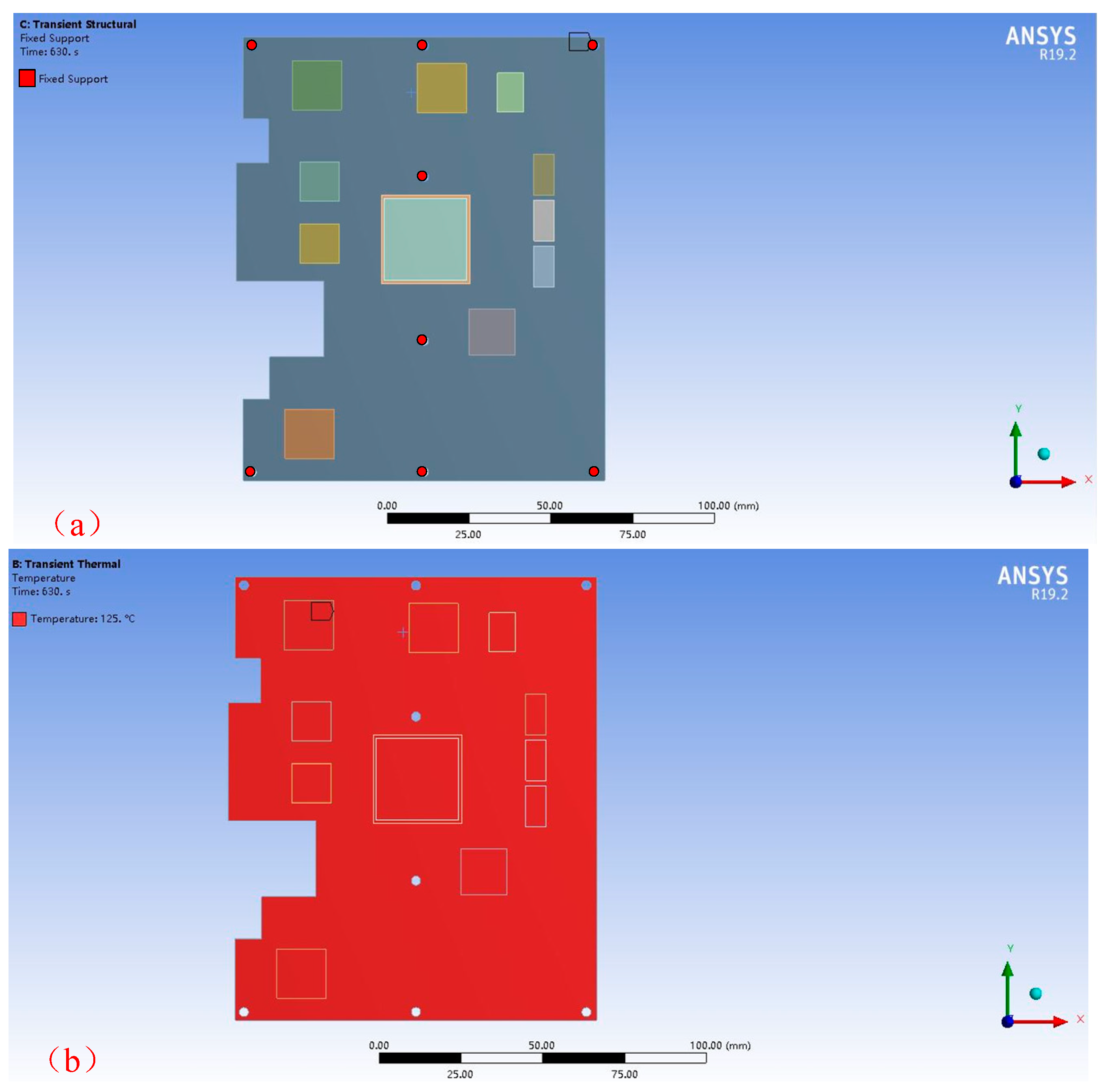
2.2. Simulation Approaches
3. Results and Discussion
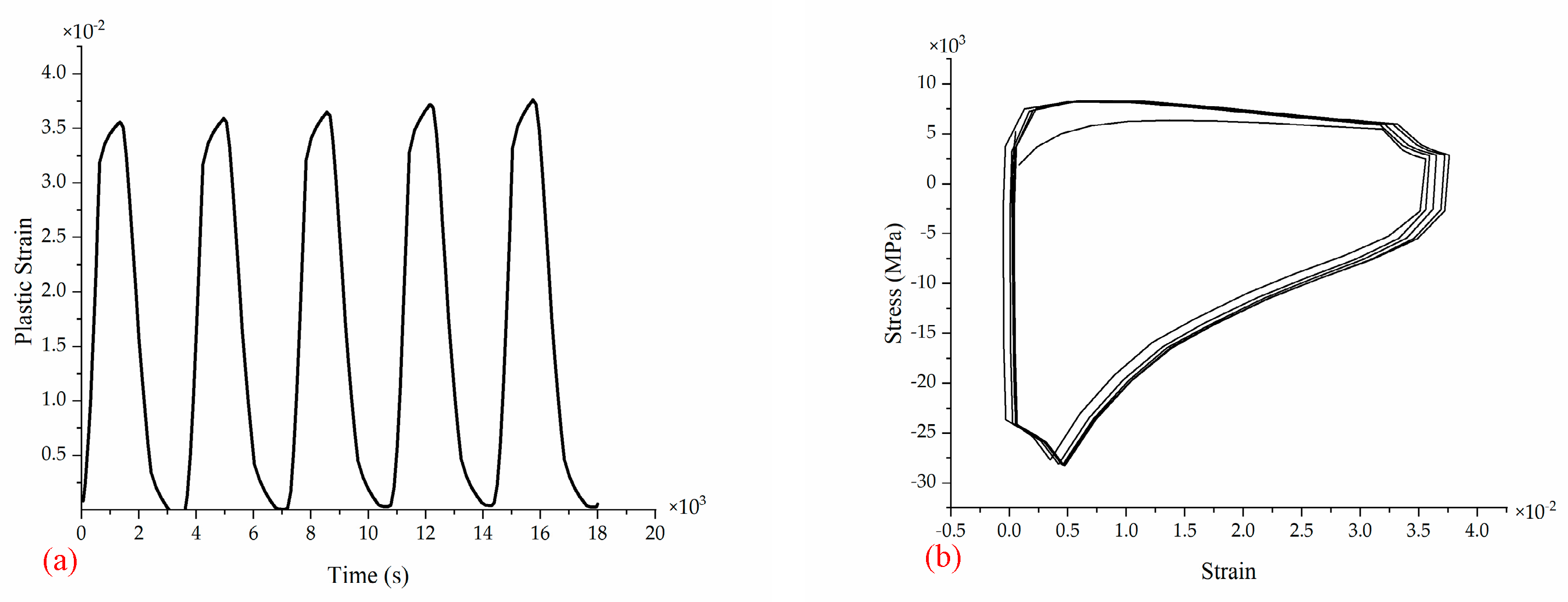
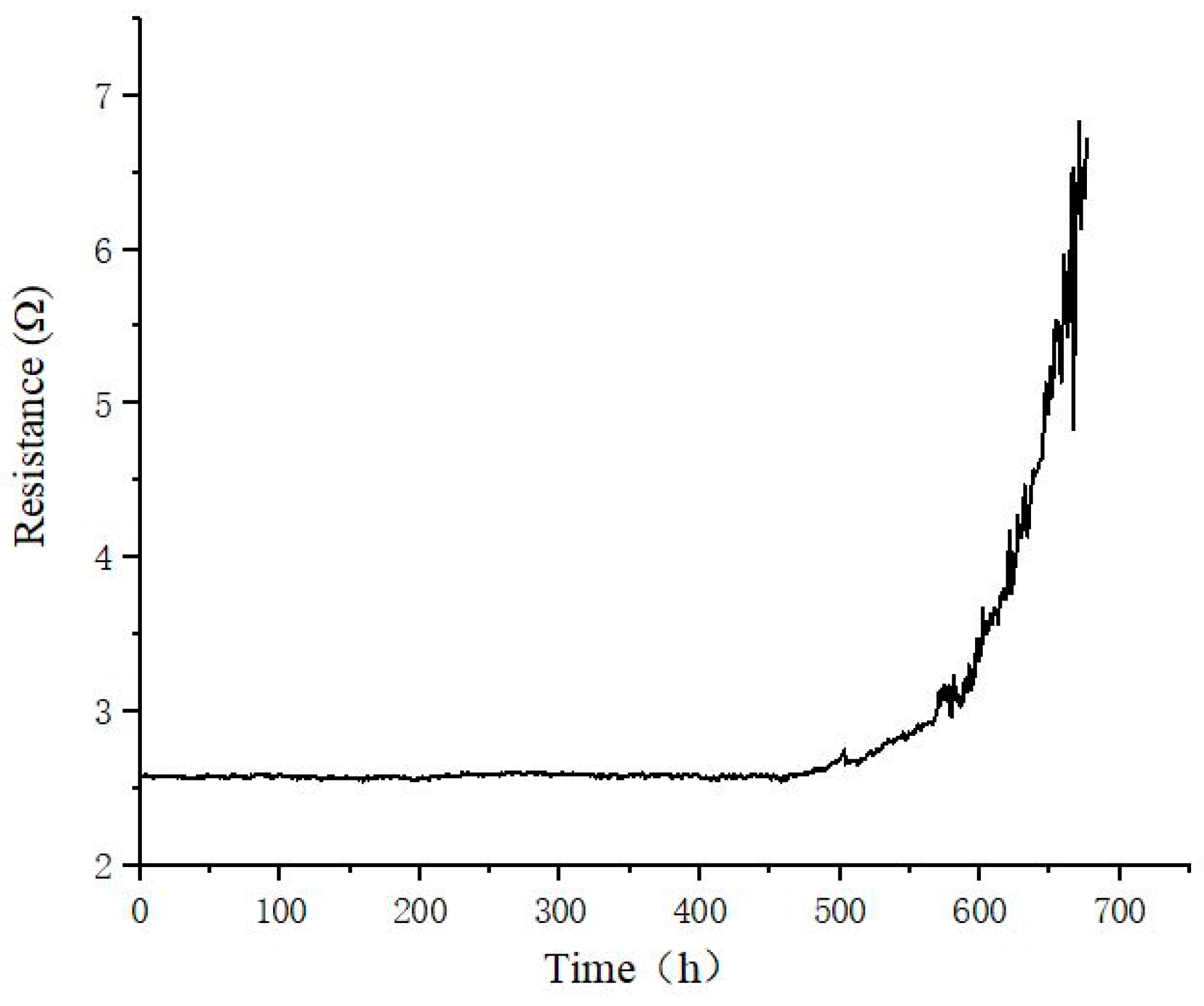
3.1. Temperature Cycling Test Analysis
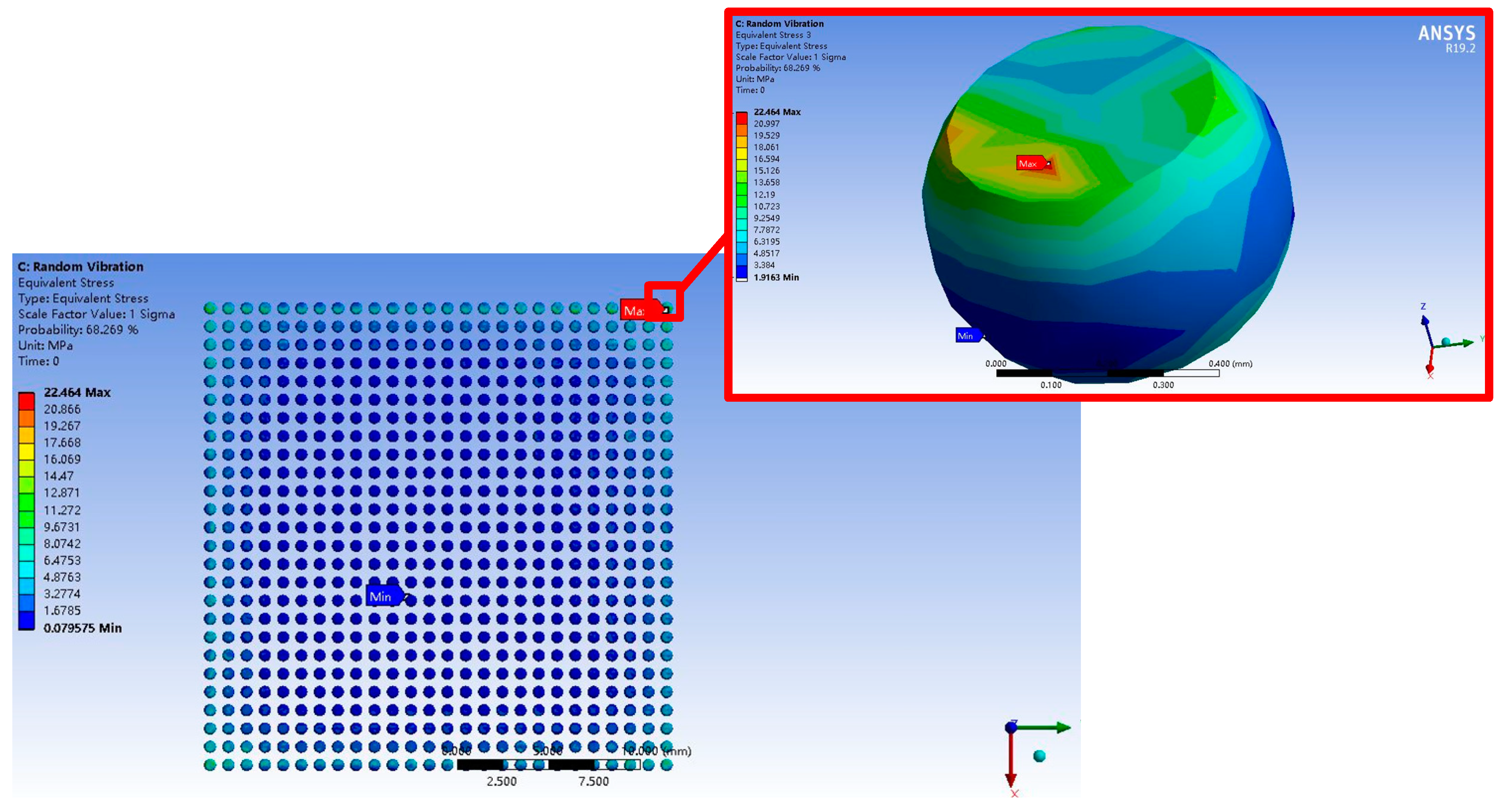
3.2. Random Vibration Test Analysis
3.3. The Combined Temperature Cycling and Random Vibration Analysis
4. Conclusions
- (1)
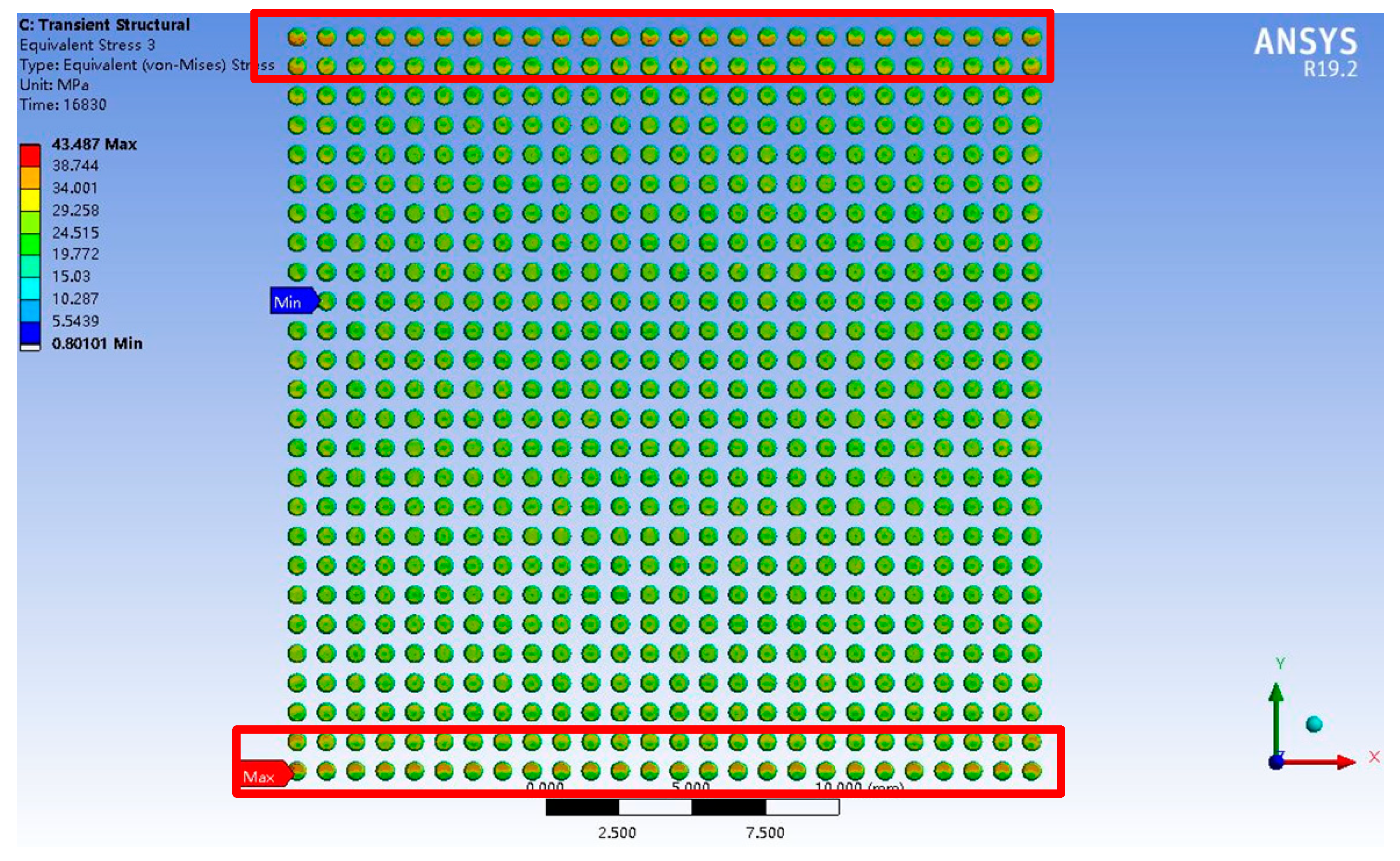
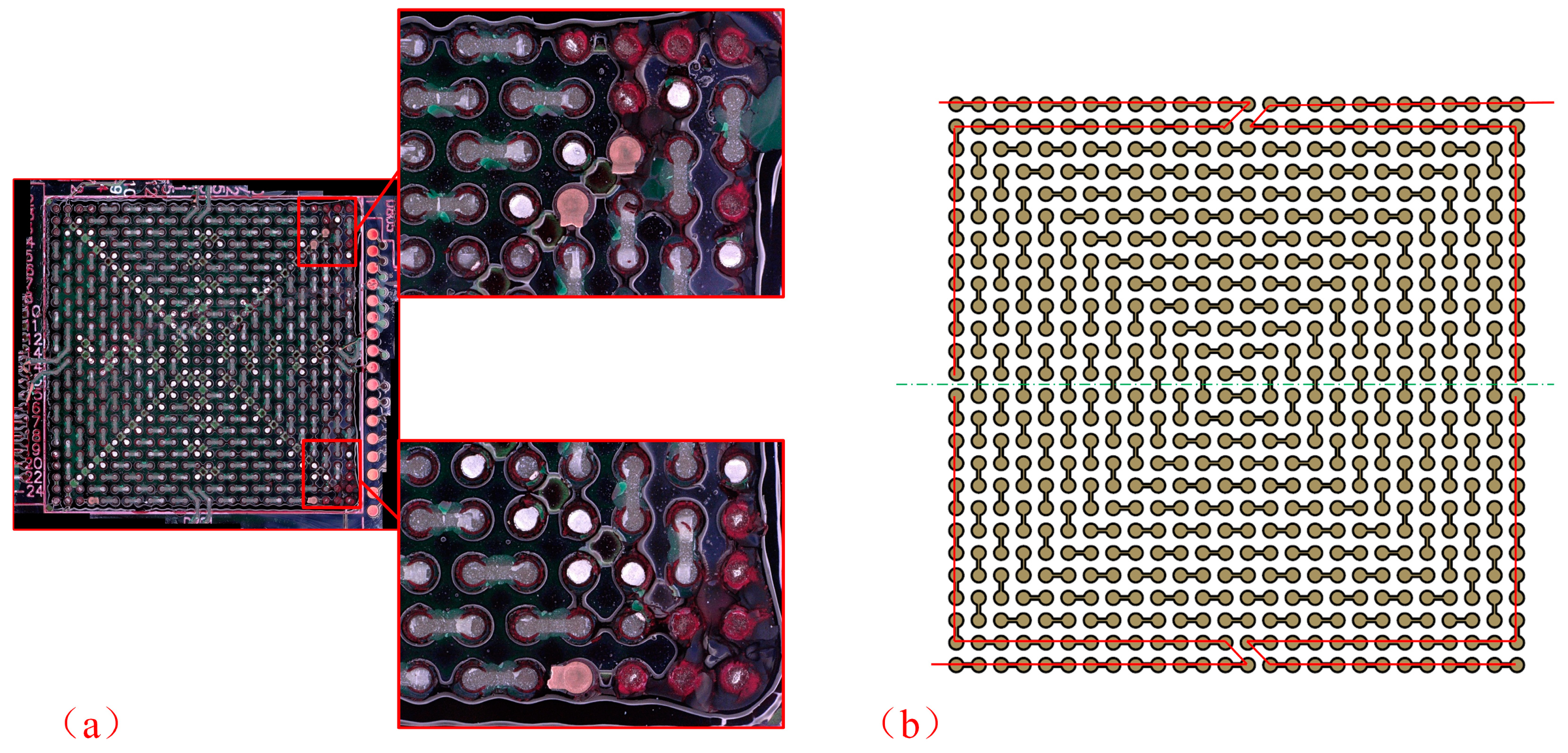
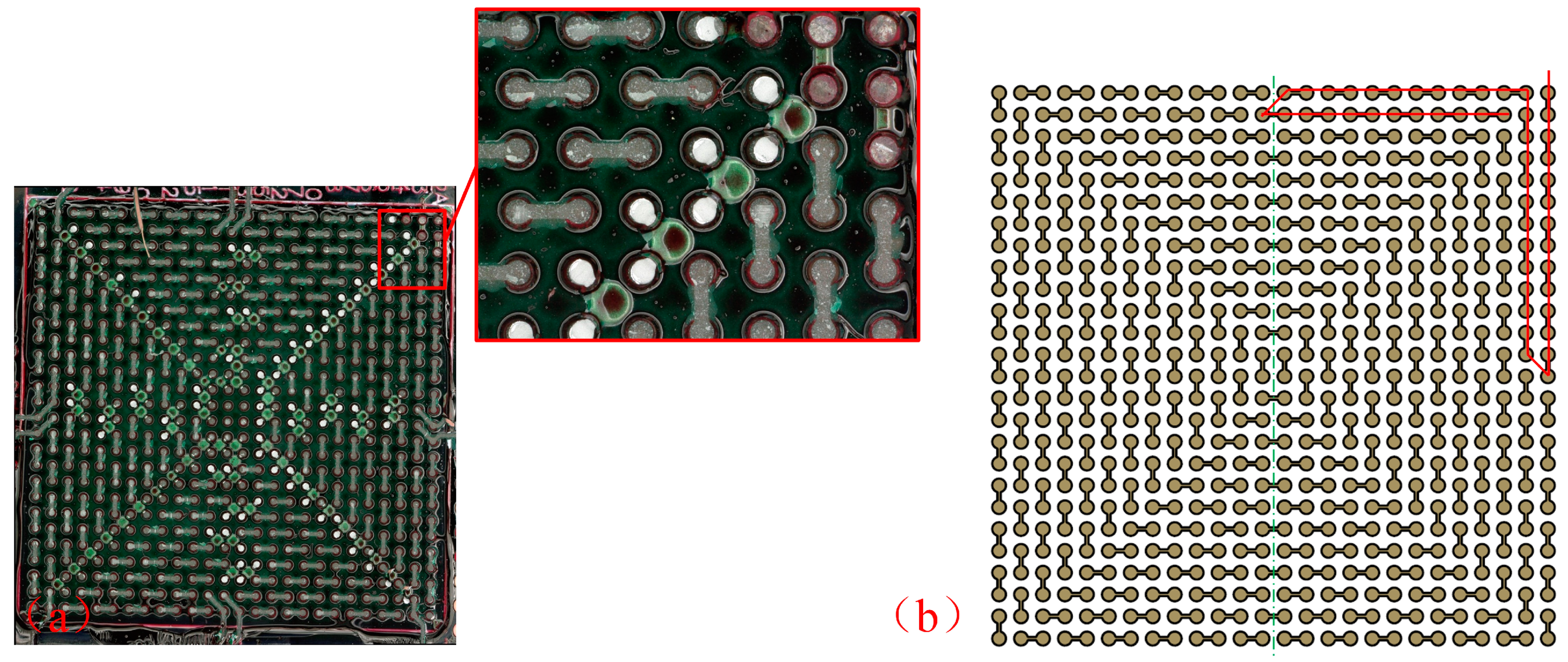
- For the temperature cycling test, the failed solder joints appeared on the corners, indicating that the experimental results accorded well with the simulation results. Thermal mismatch induced by the interconnection structure greatly affected the growth of cracks of bulk solder joints, especially on the component side. All specimens failed due to the increase in daisy chain resistance with a fatigue life above 500 h;
- (2)
- The fatigue life for the random vibration test was 13.36 h which was much shorter than the temperature cycling test of 589 h. A few open circuit phenomena could be observed above the test specimens. Miner’s linear fatigue damage criterion and Steinberg’s model could be fully used to predict an accurate fatigue life compared with the experimental result. The cracks were located on the component side, and the daisy chain resistance fluctuated between a narrow range and rapidly increased when the failure occurred;
- (3)
- The rapid life-prediction approach was able to accurately forecast the fatigue life with a minimal error when compared to the experimental result for the combined temperature cycling and random vibration test. The dependability design of the structure under coupled temperature cycling and random vibration loads may benefit from this technique;
- (4)
- All of the specimens failed owing to an open circuit once the QFP device failures were identified. Results showed that during the combined temperature cycling and random vibration testing, the solder junctions on the component side were more brittle and the pins shattered at the welding regions. Lowered stress levels and fatigue life in the solder joints were a result of the degradation of the yield strength of the solder brought on by temperature change. The designer should consider strengthening the protective measures at dangerous locations to improve reliability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| ρ (g/cm3) | Density |
| E (GPa) | Young’s modulus |
| v | Poisson’s ratio |
| α (1 × 10−6/K) | Coefficient of thermal expansion |
| s0 (MPa) | Initial value of deformation resistance |
| Q/R (1/K) | Activation energy |
| A (1/s) | Pre-exponential factor |
| ξ | Stress multiplier |
| m | Strain rate sensitivity of stress |
| h0 (MPa) | Hardening coefficient |
| ŝ (MPa) | Coefficient for deformation resistance saturation value |
| n | Strain rate sensitivity of saturation value |
| α | Strain rate sensitivity of hardening coefficient |
| Nf (h) | Fatigue lifetime |
| Δγp | Equivalent plastic strain |
| εf | Fatigue toughness coefficient |
| c | Fatigue toughness index |
| Δεt | Strain difference |
| σu | Tensile strength |
| niσ | Number of cycles under −iσ~ + iσ strain amplitudes. |
| Niσ | Number of cycles corresponding to iσ strain amplitudes |
| Pi (g2/Hz) | Power density spectrums |
| fi | i-order natural frequency |
| Ωi | i-order angular frequency |
| D | Total accumulating damage |
| ni | Cycles number |
| Ni (h) | Vibration fatigue life |
| Th (°C) | Highest temperature |
| Tl (°C) | Lowest temperature |
| Tav (°C) | Average temperature |
| th | Ratio of the highest temperature time to the total cycle time |
| tl | Ratio of the lowest temperature time to the total cycle time |
| tav | Ratio of the average temperature time to the total cycle time |
References
- Qi, H.; Osterman, M.; Pecht, M. A Rapid Life-Prediction Approach for PBGA Solder Joints Under Combined Thermal Cycling and Vibration Loading Conditions. IEEE Trans. Compon. Packag. Technol. 2009, 32, 283–292. [Google Scholar] [CrossRef]
- Arabi, F.; Gracia, A.; Delétage, J.Y.; Frémont, H. Sequential combined thermal cycling and vibration test and simulation of printed circuit board. Microelectron. Reliab. 2018, 88–90, 768–773. [Google Scholar] [CrossRef]
- Tian, W.; Cui, H.; Yu, W. Analysis and Experimental Test of Electrical Characteristics on Bonding Wire. Electronics 2019, 8, 365. [Google Scholar] [CrossRef] [Green Version]
- Jaafar, N.B.; Ching, E.W.L. Study on ultra low loop copper wire bonding process using 0.8 mils Cu wire for low profile package applications. In Proceedings of the 2015 IEEE 17th Electronics Packaging and Technology Conference (EPTC), Singapore, 2–4 December 2015; pp. 1–4. [Google Scholar]
- Cui, H.; Tian, W.; Zhao, X.; Chen, S.; Chen, Z. Effect of the reflow process on IMC growth for different devices and complex components. Smart Mater. Struct. 2022, 31, 115028. [Google Scholar] [CrossRef]
- Yuan, C.; Fan, X.; Zhang, G. Solder Joint Reliability Risk Estimation by AI-Assisted Simulation Framework with Genetic Algorithm to Optimize the Initial Parameters for AI Models. Materials 2021, 14, 4835. [Google Scholar] [CrossRef]
- Vieira, D.N.; Lima, A.; Santos, D.; Rodrigues, N.; Carvalho, V.; Puga, H.; Teixeira, S.F.C.F.; Teixeira, J.C. Prediction of Solder Joint Reliability with Applied Acrylic Conformal Coating. J. Electron. Mater. 2022, 51, 273–283. [Google Scholar] [CrossRef]
- Jayesh, S.; Elias, J. Experimental and finite element analysis on determining the fatigue life of pb-free solder joint (Sn-0.5Cu-3Bi-1Ag) used in electronic packages under harmonic loads. Int. J. Model. Simul. Sci. Comput. 2020, 11, 2050020. [Google Scholar] [CrossRef]
- Amalu, E.H.; Ekere, N.N. Damage of lead-free solder joints in flip chip assemblies subjected to high-temperature thermal cycling. Comput. Mater. Sci. 2012, 65, 470–484. [Google Scholar] [CrossRef]
- Kanai, H.; Kariya, Y.; Sugimoto, H.; Abe, Y.; Yokoyama, Y.; Ochi, K.; Hanada, R.; Soda, S. Fatigue Life Prediction of Die-Attach Joint in Power Semiconductors Subjected to Biaxial Stress by High-Speed Thermal Cycling. Mater. Trans. 2022, 63, 759–765. [Google Scholar] [CrossRef]
- Liu, D.S.; Chen, Y.W.; Tsai, C.Y. Thermal Stress Analysis of Chip Scale Packaging by Using Novel Multiscale Interface Element Method. Math. Probl. Eng. 2018, 2018, 4962498. [Google Scholar] [CrossRef]
- Pan, J.; Chou, T.; Bath, J.; Willie, D.; Toleno, B.J.J.S.; Technology, S.M. Effects of reflow profile and thermal conditioning on intermetallic compound thickness for SnAgCu soldered joints. Solder. Surf. Mt. Technol. 2009, 21, 32–37. [Google Scholar] [CrossRef] [Green Version]
- Kang, M.-S.; Jeon, Y.-J.; Kim, D.-S.; Shin, Y.-E. Degradation characteristics and Ni3Sn4 IMC growth by a thermal shock test in SAC305 solder joints of MLCCs applied in automotive electronics. Int. J. Precis. Eng. Manuf. 2016, 17, 445–452. [Google Scholar] [CrossRef]
- Dalton, E.; Ren, G.; Punch, J.; Collins, M.N. Accelerated temperature cycling induced strain and failure behaviour for BGA assemblies of third generation high Ag content Pb-free solder alloys. Mater. Des. 2018, 154, 184–191. [Google Scholar] [CrossRef]
- Wentlent, L.; Alghoul, T.M.; Greene, C.M.; Borgesen, P. Effects of Amplitude Variations on Deformation and Damage Evolution in SnAgCu Solder in Isothermal Cycling. J. Electron. Mater. 2018, 47, 2752–2760. [Google Scholar] [CrossRef]
- Xia, J.; Li, G.; Li, B.; Cheng, L.; Zhou, B. Fatigue life prediction of Package-on-Package stacking assembly under random vibration loading. Microelectron. Reliab. 2017, 71, 111–118. [Google Scholar] [CrossRef]
- Baishya, K.; Harvey, D.M.; Partida Manzanera, T.; Zhang, G.; Braden, D.R. Failure patterns of solder joints identified through lifetime vibration tests. Nondestruct. Test. Eval. 2022, 38, 147–171. [Google Scholar] [CrossRef]
- Xia, J.; Cheng, L.; Li, G.; Li, B. Reliability study of package-on-package stacking assembly under vibration loading. Microelectron. Reliab. 2017, 78, 285–293. [Google Scholar] [CrossRef]
- Kim, Y.K.; Hwang, D.S. PBGA packaging reliability assessments under random vibrations for space applications. Microelectron. Reliab. 2015, 55, 172–179. [Google Scholar] [CrossRef]
- Ding, Y.; Tian, R.; Wang, X.; Hang, C.; Yu, F.; Zhou, L.; Meng, X.; Tian, Y. Coupling effects of mechanical vibrations and thermal cycling on reliability of CCGA solder joints. Microelectron. Reliab. 2015, 55, 2396–2402. [Google Scholar] [CrossRef]
- Ghaderi, D. Reliability analysis for TO-247 multilayered power module packaging under mechanical oscillation based on finite element method. Microelectron. Reliab. 2021, 118, 114046. [Google Scholar] [CrossRef]
- Engelmaier, W. Fatigue Life of Leadless Chip Carrier Solder Joints During Power Cycling. IEEE Trans. Compon. Hybrids Manuf. Technol. 1983, 6, 232–237. [Google Scholar] [CrossRef]
- Yang, P.; Tang, X.; Liu, Y.; Wang, S.; Yang, J. Dynamic reliability approach of chip scale package assembly under vibration environment. Microelectron. Int. 2014, 31, 71–77. [Google Scholar] [CrossRef]
- Qi, H.; Osterman, M.; Pecht, M. Plastic Ball Grid Array Solder Joint Reliability for Avionics Applications. IEEE Trans. Compon. Packag. Technol. 2007, 30, 242–247. [Google Scholar] [CrossRef]









| Frequency (Hz) | PSD (g) |
|---|---|
| 15 | 0.03584 |
| 75 | 0.03584 |
| 105 | 0.16384 |
| 127 | 0.16384 |
| 152 | 0.05888 |
| 252 | 0.05888 |
| 295 | 0.04096 |
| 355 | 0.04096 |
| 407 | 0.23808 |
| 485 | 0.23808 |
| 525 | 0.0512 |
| 911 | 0.0512 |
| 1162 | 0.768 |
| 1380 | 0.768 |
| 2000 | 0.02304 |
| Instrument | Model | Manufacturer | Main Characteristics |
|---|---|---|---|
| Temperature cycling test chamber | RT1000-70W10L | WuHan Climate equipment Co., Ltd. Wuhan, China | Temperature range: −70~ + 150 °C Temperature rate: 5 °C/min Degree of uniformity: ≤2 °C |
| Accelerometers | MKFK320 | Deyike Instrument Co., Ltd. Wuxi, China | Dynamic range: ±50 g Sensitivity: ≤5% Shock tolerance: 2000 g |
| Resistance data loggers | HG2515B/TH2518 | Changzhou Tonghui Electronic Co., Ltd. Changzhou, China | Resistance range: 10 μΩ~200 KΩ Basic accuracy: 0.05% |
| Temperature and vibration comprehensive test chamber | ECE73310-10/ES50-445 | WuHan Climate equipment Co., Ltd. Wuhan, China | Temperature range: −70~ + 150 °C Temperature rate: 5 °C/min Frequency range: DC~4000 Hz Maximum acceleration: 350 m/s2 |
| Scanning electron microscope | MIRA3&elect plus | TESCAN CHINA, Ltd. Shanghai, China | Backscattered electron resolution: 2.0 nm@30 kV Acceleration voltage: 0.2–30 kV |
| Component | Parameter | Value (mm) |
|---|---|---|
| D101 | Length | 25 |
| Width | 25 | |
| Height | 1.17 | |
| D201 | Length | 15 |
| Width | 15 | |
| Height | 1.4 | |
| D401/D501 | Length | 12 |
| Width | 12 | |
| Height | 0.97 | |
| Length | 12.5 | |
| A1/A2/A3 | Width | 6.1 |
| Height | 1.1 | |
| Length | 14 | |
| B1 | Width | 14 |
| Height | 1.4 | |
| Length | 11.8 | |
| C1 | Width | 8 |
| Height | 1 | |
| Length | 15 | |
| E1/E2 | Width | 15 |
| Height | 2.82 | |
| Length | 135 | |
| PCB | Width | 110 |
| Height | 2 |
| Component | Materials | Density p (g/cm3) | Young’s modulus E (GPa) | Poisson’s Ratio v | CTE α (1 × 10−6/K) |
|---|---|---|---|---|---|
| Scheme 63 | 63Sn37Pb | 8.4 | 30 | 0.36 | 24.7 |
| PCB | FR4 | 1.859 | 11 | 0.28 | 13.6 |
| Packaging body | EMC | 1.820 | 8.7 | 0.3 | 12.4 |
| Substrate | BT | 1.7 | 23.1 | 0.21 | 12.4 |
| Pin/Pad | Cu | 8.92 | 117 | 0.34 | 16.6 |
| s0 (MPa) | 3.8 | Initial value of deformation resistance |
| Q/R (1/K) | 5509.87058 | Activation energy |
| A (1/s) | 392.39411 | Pre-exponential factor |
| ξ | 5.08 | Stress multiplier |
| m | 0.24 | Strain rate sensitivity of stress |
| h0 (MPa) | 40530.52 | Hardening coefficient |
| Ŝ (MPa) | 96.0765 | Coefficient for deformation resistance saturation value |
| n | 0.012 | Strain rate sensitivity of saturation value |
| α | 1.612549 | Strain rate sensitivity of hardening coefficient |
| Mesh Dividing Methods | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Node | 85484 | 101454 | 135584 | 553786 | 736879 | 2560397 |
| Element | 12880 | 15784 | 35274 | 98567 | 127413 | 548244 |
| Element quality | 0.875 | 0.835 | 0.798 | 0.962 | 0.973 | 0.980 |
| Natural modal between 0~3000 Hz | 13 | 13 | 14 | 15 | 15 | 15 |
| Computing time | 10s | 25s | 42s | 6 min 24 s | 9 min 10 s | 32 min 7 s |
| Specimen Number | Fatigue Life (h) |
|---|---|
| 29A | 467 |
| 31A | 479 |
| 18A | 488 |
| 9A | 489 |
| 30A | 493 |
| 13A | 495 |
| 28A | 498 |
| 15A | 510 |
| 32A | 528 |
| 17A | 533 |
| 14A | 540 |
| 1A | 550 |
| 19A | 577 |
| 3A | 584 |
| 27A | 588 |
| 16A | 589 |
| Modal Order | Natural Frequency (Hz) |
|---|---|
| 1 | 416.29 |
| 2 | 512.39 |
| 3 | 944.07 |
| 4 | 1013.5 |
| 5 | 1231.7 |
| 6 | 1444.2 |
| Mechanical Response | Strain | Damage (h−1) |
|---|---|---|
| 1σ | 0.000324 | 0.000144 |
| 2σ | 0.000649 | 0.00185 |
| 3σ | 0.000973 | 0.00865 |
| Specimen Number | Fatigue Life (h) | Failure Mode |
|---|---|---|
| 15B | 0.43 | Open circuit |
| 16B | 1.05 | / |
| 14B | 2.43 | Open circuit |
| 18B | 3.58 | / |
| 17B | 4.05 | / |
| 21B | 4.40 | / |
| 19B | 4.50 | / |
| 10B | 4.75 | / |
| 12B | 6.20 | / |
| 09B | 6.33 | / |
| 14B | 7.11 | / |
| 1B | 9.11 | / |
| 27B | 12.11 | / |
| 11B | 12.16 | / |
| 28B | 12.80 | / |
| 29B | 13.36 | / |
| Temperature (°C) | Mechanical Response | Strain | Damage (h−1) |
|---|---|---|---|
| 1σ | 0.000381 | 0.00052 | |
| −55 | 2σ | 0.000762 | 0.06721 |
| 3σ | 0.001143 | 0.31515 | |
| 1σ | 0.000380 | 0.00051 | |
| 35 | 2σ | 0.0007631 | 0.00662 |
| 3σ | 0.001143 | 0.31087 | |
| 1σ | 0.000339 | 0.00019 | |
| 125 | 2σ | 0.000679 | 0.02508 |
| 3σ | 0.001018 | 0.11724 |
| Specimen Number | Fatigue Life (h) | Failure Component |
|---|---|---|
| 18C | 2.02 | D501 |
| 11C | 2.16 | D501 |
| 7C | 2.21 | D101, D501 |
| 8C | 2.22 | D501 |
| 24C | 2.25 | D501 |
| 16C | 2.25 | D101 |
| 25C | 2.38 | D101 |
| 30C | 2.58 | D101 |
| 32C | 3.11 | D101 |
| 10C | 3.14 | D101 |
| 31C | 3.20 | D101 |
| 17C | 3.21 | D101 |
| 26C | 3.24 | D501 |
| 22C | 3.33 | D101 |
| 12C | 3.34 | D101 |
| 27C | 3.36 | D101 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, H.; Tian, W.; Xu, H.; Wang, H.; Huang, J.; Peng, C.; Chen, Z. The Reliability of the Complex Components under Temperature Cycling, Random Vibration, and Combined Loading for Airborne Applications. Crystals 2023, 13, 473. https://doi.org/10.3390/cryst13030473
Cui H, Tian W, Xu H, Wang H, Huang J, Peng C, Chen Z. The Reliability of the Complex Components under Temperature Cycling, Random Vibration, and Combined Loading for Airborne Applications. Crystals. 2023; 13(3):473. https://doi.org/10.3390/cryst13030473
Chicago/Turabian StyleCui, Hao, Wenchao Tian, Hanyang Xu, Heng Wang, Jiabo Huang, Chunxi Peng, and Zhiqiang Chen. 2023. "The Reliability of the Complex Components under Temperature Cycling, Random Vibration, and Combined Loading for Airborne Applications" Crystals 13, no. 3: 473. https://doi.org/10.3390/cryst13030473
APA StyleCui, H., Tian, W., Xu, H., Wang, H., Huang, J., Peng, C., & Chen, Z. (2023). The Reliability of the Complex Components under Temperature Cycling, Random Vibration, and Combined Loading for Airborne Applications. Crystals, 13(3), 473. https://doi.org/10.3390/cryst13030473






