Oxygen Vacancies in Zirconia and Their Migration: The Role of Hubbard-U Parameters in Density Functional Theory
Abstract
:1. Introduction
2. Computational Methods
3. Results
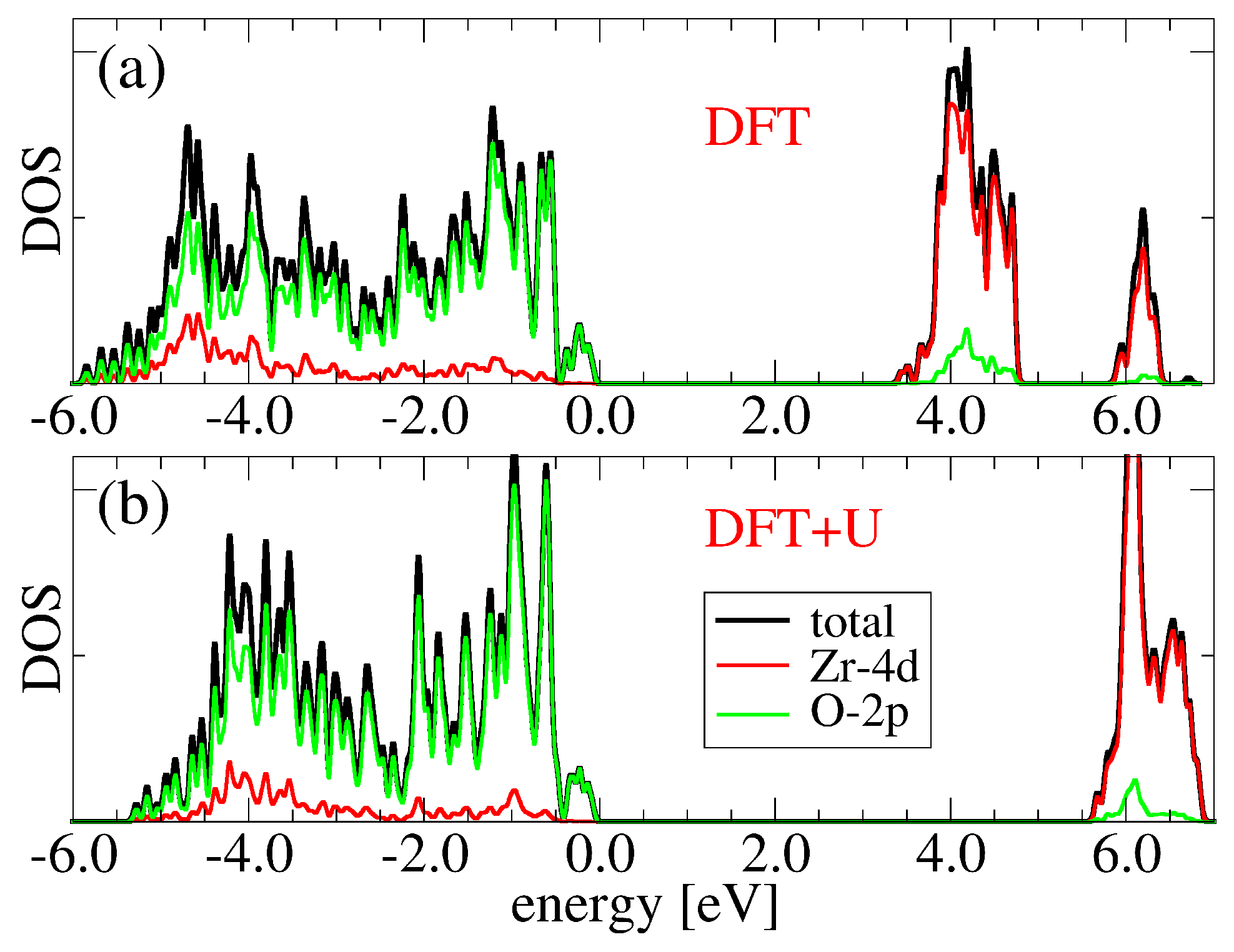
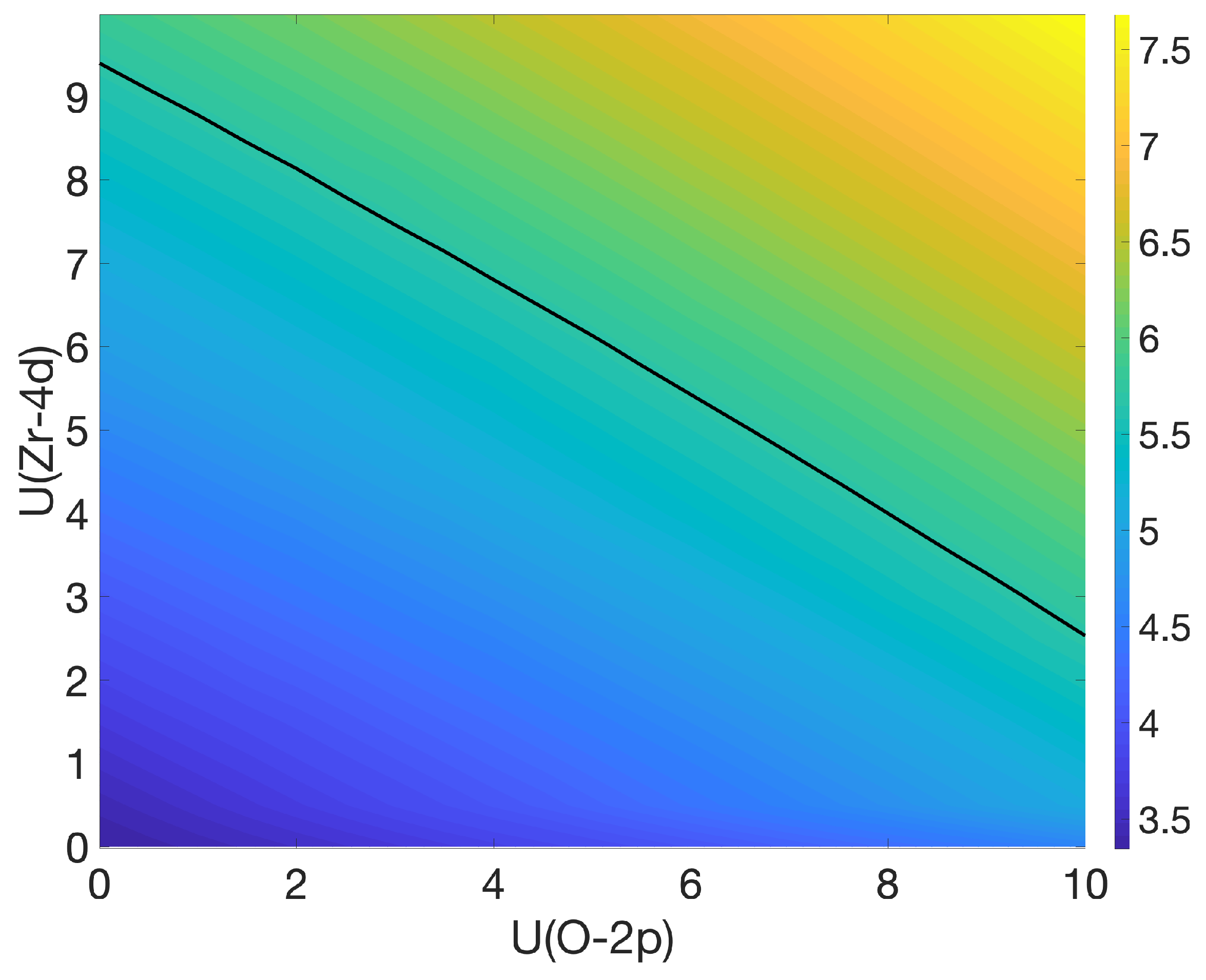
3.1. Bulk c-ZrO2
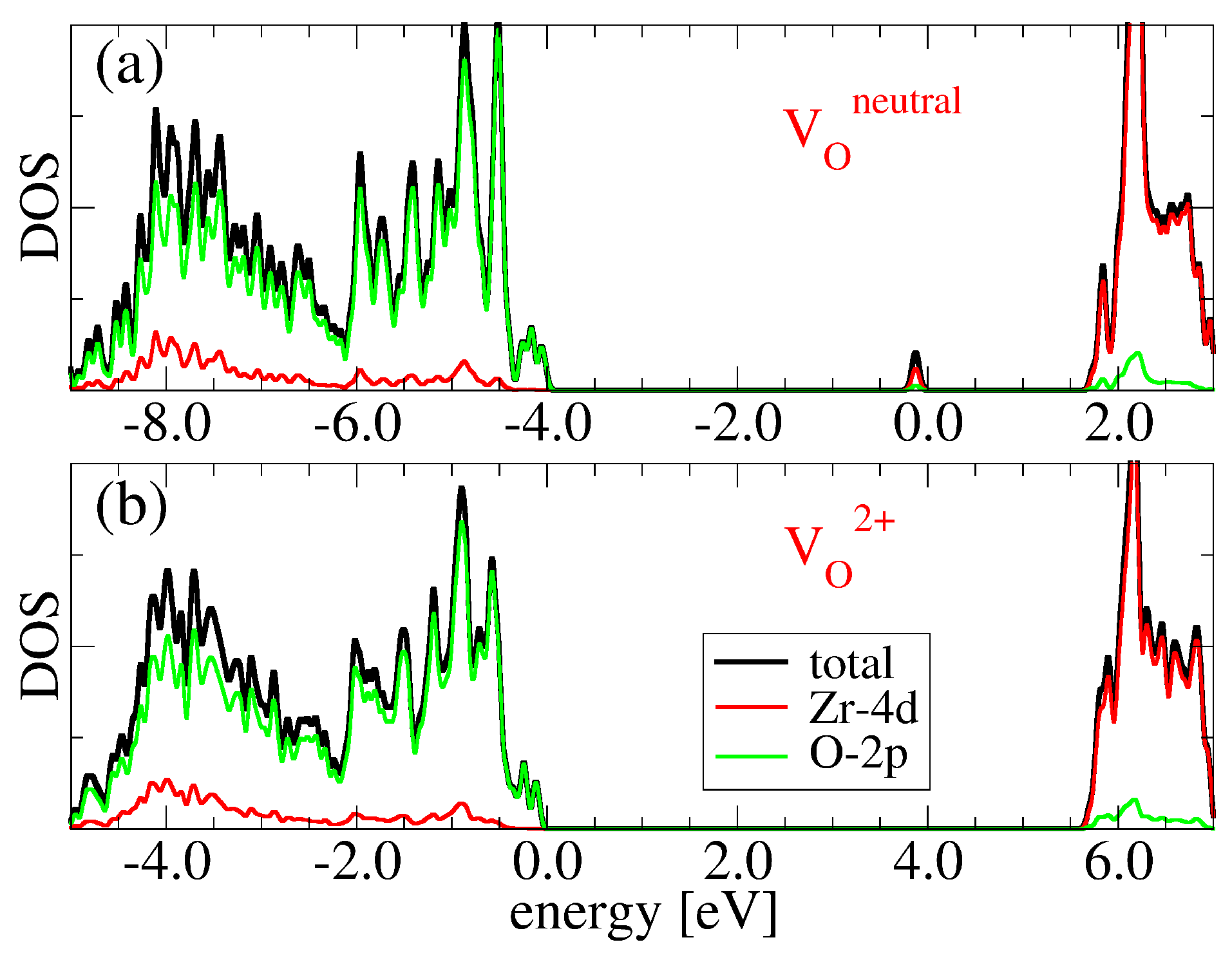
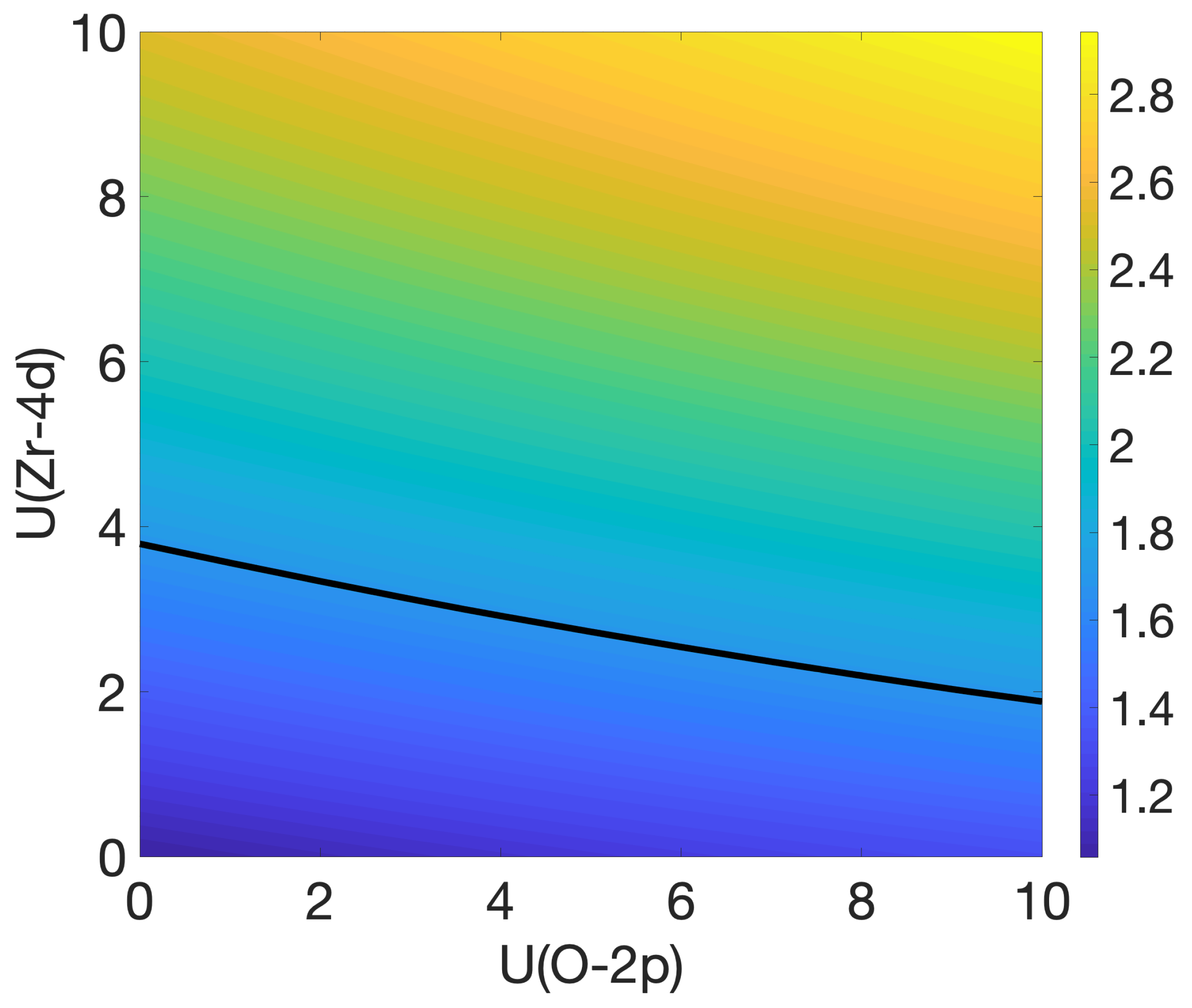
3.2. Oxygen Vacancies in c-ZrO2
4. Conclusions
Supplementary Materials
Funding
Conflicts of Interest
References
- Khattab, E.S.R.; Abd El Rehim, S.S.; Hassan, W.M.I.; El-Shazly, T.S. Band Structure Engineering and Optical Properties of Pristine and Doped Monoclinic Zirconia (m-ZrO2): Density Functional Theory Theoretical Prospective. ACS Omega 2021, 6, 30061–30068. [Google Scholar] [CrossRef] [PubMed]
- Lindgren, M.; Panas, I. Oxygen Vacancy Formation, Mobility, and Hydrogen Pick-up during Oxidation of Zirconium by Water. Oxid. Met. 2017, 87, 355–365. [Google Scholar] [CrossRef] [Green Version]
- Zhu, H.; Li, J.; Chen, K.; Yi, X.; Cheng, S.; Gan, F. Nature of charge transport and p-electron ferromagnetism in nitrogen-doped ZrO2: An ab initio perspective. Sci. Rep. 2015, 5, 8586. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raza, M.; Cornil, D.; Cornil, J.; Lucas, S.; Snyders, R.; Konstantinidis, S. Oxygen vacancy stabilized zirconia (OVSZ); a joint experimental and theoretical study. Scr. Mater. 2016, 124, 26–29. [Google Scholar] [CrossRef]
- Fabris, S. A stabilization mechanism of zirconia based on oxygen vacancies only. Acta Mater. 2002, 50, 5171–5178. [Google Scholar] [CrossRef] [Green Version]
- Oka, M.; Kamisaka, H.; Fukumura, T.; Hasegawa, T. Density functional theory-based ab initio molecular dynamics simulation of ionic conduction in N-/F-doped ZrO2 under epitaxial strain. Comput. Mater. Sci. 2018, 154, 91–96. [Google Scholar] [CrossRef]
- Lee, Y.L.; Duan, Y.; Morgan, D.; Sorescu, D.; Abernathy, H.; Hackett, G. Density functional theory modeling of cation diffusion in bulk tetragonal zirconia. Ceram. Trans. 2019, 266, 95–110. [Google Scholar] [CrossRef]
- Schultze, T.K.; Arnold, J.P.; Grieshammer, S. Ab Initio Investigation of Migration Mechanisms in La Apatites. ACS Appl. Energy Mater. 2019, 2, 4708–4717. [Google Scholar] [CrossRef]
- Koga, H.; Hayashi, A.; Ato, Y.; Tada, K.; Hosokawa, S.; Tanaka, T.; Okumura, M. Facile NO-CO elimination over zirconia-coated Cu (110) surfaces: Further evidence from DFT + U calculations. Appl. Surf. Sci. 2020, 508, 145252. [Google Scholar] [CrossRef]
- Mueller, M.P.; Pingen, K.; Hardtdegen, A.; Aussen, S.; Kindsmueller, A.; Hoffmann-Eifert, S.; De Souza, R.A. Cation diffusion in polycrystalline thin films of monoclinic HfO2 deposited by atomic layer deposition. APL Mater. 2020, 8, 081104. [Google Scholar] [CrossRef]
- Lee, Y.L.; Duan, Y.; Sorescu, D.C.; Morgan, D.; Abernathy, H.; Kalapos, T.; Hackett, G. Density functional theory modeling of cation diffusion in tetragonal bulk ZrO2: Effects of humidity and hydrogen defect complexes on cation transport. Phys. Rev. Res. 2021, 3, 013121. [Google Scholar] [CrossRef]
- Kumar, N.; Seriani, N.; Gebauer, R. DFT insights into electrocatalytic CO2 reduction to methanol on α-Fe2O3 (0001) surfaces. Phys. Chem. Chem. Phys. 2020, 22, 10819–10827. [Google Scholar] [CrossRef] [PubMed]
- Ulman, K.; Poli, E.; Seriani, N.; Piccinin, S.; Gebauer, R. Understanding the electrochemical double layer at the hematite/water interface: A first principles molecular dynamics study. J. Chem. Phys. 2019, 150, 041707. [Google Scholar] [CrossRef] [PubMed]
- Ahamed, I.; Ulman, K.; Seriani, N.; Gebauer, R.; Kashyap, A. Magnetoelectric e-Fe2O3: DFT study of a potential candidate for electrode material in photoelectrochemical cells. J. Chem. Phys. 2018, 148, 214707. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, M.T.; Gebauer, R. Graphene Supported on Hematite Surfaces: A Density Functional Study. J. Phys. Chem. C 2014, 118, 8455–8461. [Google Scholar] [CrossRef]
- Walker, B.G.; Hendy, S.C.; Gebauer, R.; Tilley, R.D. Application of Lanczos-based time-dependent density-functional theory approach to semiconductor nanoparticle quantum dots. Eur. Phys. J. B 2008, 66, 7–15. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Dal Corso, A. Pseudopotentials periodic table: From H to Pu. Comput. Mater. Sci. 2014, 95, 337–350. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ernzerhof, M.; Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 1996, 105, 9982–9985. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Mulliken, R.S. Electronic Population Analysis on LCAO–MO Molecular Wave Functions. I. J. Chem. Phys. 1955, 23, 1833–1840. [Google Scholar] [CrossRef] [Green Version]
- Bader, R.F.W. Atoms in Molecules—A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Sit, P.H.L.; Car, R.; Cohen, M.H.; Selloni, A. Simple, unambiguous theoretical approach to oxidation state determination via first-principles calculations. Inorg. Chem. 2011, 50, 10259–10267. [Google Scholar] [CrossRef]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.L.; Fan, X.L.; Liu, C.; Ran, R.X. First principles study of structural and electronic properties of cubic phase of ZrO2 and HfO2. Phys. B Condens. Matter 2014, 434, 7–13. [Google Scholar] [CrossRef]
- Cococcioni, M.; de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA+U method. Phys. Rev. B 2005, 71, 035105. [Google Scholar] [CrossRef] [Green Version]
- Timrov, I.; Marzari, N.; Cococcioni, M. Hubbard parameters from density-functional perturbation theory. Phys. Rev. B 2018, 98, 085127. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Meng, S.; Niu, J.; Lu, H. Electronic structures and optical properties of monoclinic ZrO2 studied by first-principles local density approximation + U approach. J. Adv. Ceram. 2017, 6, 43–49. [Google Scholar] [CrossRef] [Green Version]
- Henkelman, G.; Uberuaga, B.P.; Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef] [Green Version]


| ecutwfc | ecutrho | n | Lattice Parameter |
|---|---|---|---|
| 40 Ry | 400 Ry | 4 | 5.09 Å |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gebauer, R. Oxygen Vacancies in Zirconia and Their Migration: The Role of Hubbard-U Parameters in Density Functional Theory. Crystals 2023, 13, 574. https://doi.org/10.3390/cryst13040574
Gebauer R. Oxygen Vacancies in Zirconia and Their Migration: The Role of Hubbard-U Parameters in Density Functional Theory. Crystals. 2023; 13(4):574. https://doi.org/10.3390/cryst13040574
Chicago/Turabian StyleGebauer, Ralph. 2023. "Oxygen Vacancies in Zirconia and Their Migration: The Role of Hubbard-U Parameters in Density Functional Theory" Crystals 13, no. 4: 574. https://doi.org/10.3390/cryst13040574
APA StyleGebauer, R. (2023). Oxygen Vacancies in Zirconia and Their Migration: The Role of Hubbard-U Parameters in Density Functional Theory. Crystals, 13(4), 574. https://doi.org/10.3390/cryst13040574






