First-Principles Studies on the Physical Properties of the Half Heusler RbNbCd and RbNbZn Compounds: A Promising Material for Thermoelectric Applications
Abstract
:1. Introduction
2. Computational Method
3. Results and Discussion
3.1. Structural Properties
3.2. Elastic Properties
3.3. Magnetic Properties
3.4. Electronic Properties
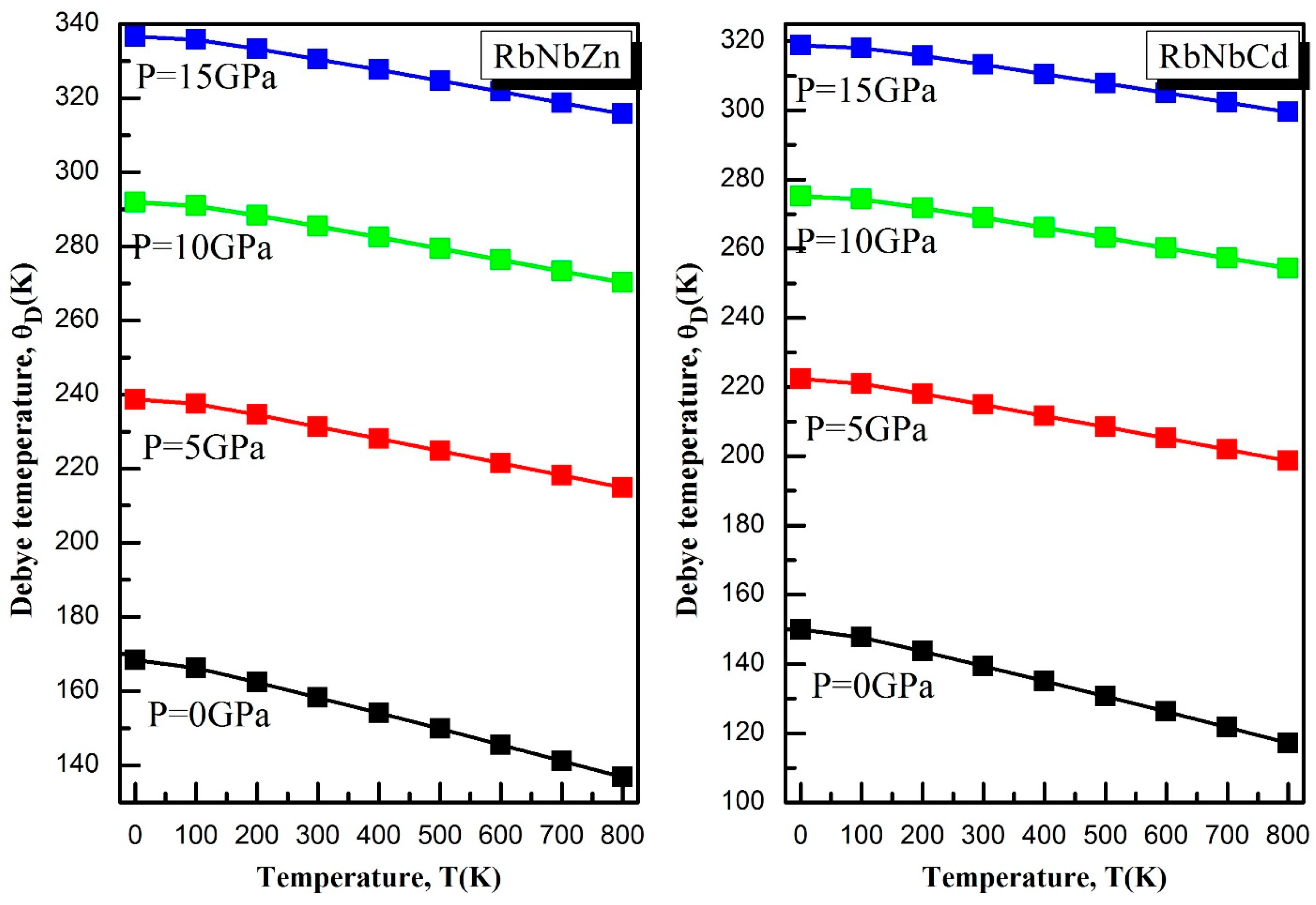
3.5. Thermodynamic Properties
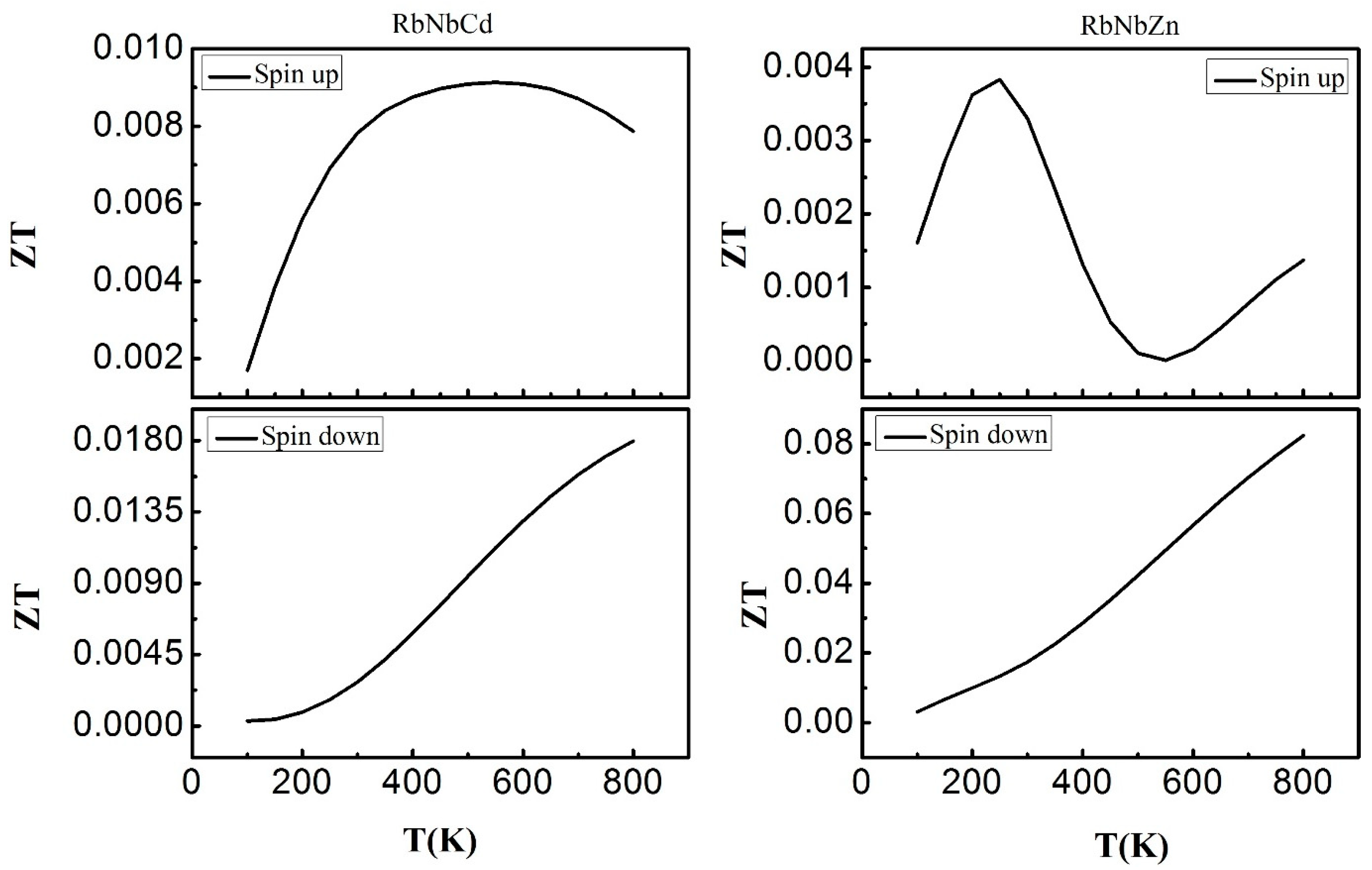
3.6. Thermoelectric Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haq, B.U.; Ahmed, R.; AlFaify, S.; Butt, F.K.; Shaari, A.; Laref, A. Exploring thermoelectric materials for renewable energy applications: The case of highly mismatched alloys based on AlBi1-xSbx and InBi1-xSbx. Intermetallics 2018, 93, 235–243. [Google Scholar] [CrossRef]
- Twidell, J. Renewable Energy Resources; Routledge: New York, NY, USA, 2021. [Google Scholar]
- Jarman, J.T.; Khalil, E.E.; Khalaf, E. Energy Analyses of Thermoelectric Renewable Energy Sources. Open J. Energy Effic. 2013, 2, 143–153. [Google Scholar] [CrossRef]
- Elsheikh, M.H.; Shnawah, D.A.; Sabri, M.F.M.; Said, S.B.M.; Hassan, M.H.; Bashir, M.B.A.; Mohamad, M. A review on thermoelectric renewable energy: Principle parameters that affect their performance. Renew. Sustain. Energy Rev. 2014, 30, 337–355. [Google Scholar] [CrossRef]
- Mamur, H.; Ahiska, R. A review: Thermoelectric generators in renewable energy. Int. J. Renew. Energy Res. 2014, 4, 128–136. [Google Scholar]
- Manzoor, M.; Behera, D.; Sharma, R.; Iqbal, M.W.; Mukherjee, S.K.; Khenata, R.; Alarfaji, S.S.; Alzahrani, H.A. Investigation of the structural, mechanical, optoelectronic and, thermoelectric characteristics of cubic GeTiO3: An ab initio study. Mater. Today Commun. 2023, 34, 105053. [Google Scholar] [CrossRef]
- Telkes, M. Solar thermoelectric generators. J. Appl. Phys. 1954, 25, 765–777. [Google Scholar] [CrossRef]
- Tohidi, F.; Holagh, S.G.; Chitsaz, A. Thermoelectric Generators: A comprehensive review of characteristics and applications. Appl. Therm. Eng. 2021, 201, 117793. [Google Scholar] [CrossRef]
- Jain, E.; Behera, D.; Agrawal, Y.; Yugbodh, K.; Abraham, J.A.; Sharma, R.; Mukherjee, S.K. First principles investigation on half metallic ferromagnetism properties of cubic VLaO3 compound. Mater. Today Proc. 2023; in press. [Google Scholar] [CrossRef]
- Sootsman, J.R.; Chung, D.Y.; Kanatzidis, M.G. New and Old Concepts in Thermoelectric Materials. Angew. Chem. Int. Ed. 2009, 48, 8616–8639. [Google Scholar] [CrossRef]
- Shakouri, A. Recent Developments in Semiconductor Thermoelectric Physics and Materials. Annu. Rev. Mater. Res. 2011, 41, 399–431. [Google Scholar] [CrossRef]
- Chen, G.; Dresselhaus, M.S.; Dresselhaus, G.; Fleurial, J.-P.; Caillat, T. Recent developments in thermoelectric materials. Int. Mater. Rev. 2003, 48, 45–66. [Google Scholar] [CrossRef]
- Behera, D.; Manzoor, M.; Sharma, R.; Salah, M.M.; Stich, I.; Mukherjee, S.K. A Comprehensive First-Principles Investigation of SnTiO3 Perovskite for Optoelectronic and Thermoelectric Applications. Crystals 2023, 13, 408. [Google Scholar] [CrossRef]
- Behera, D.; Mukherjee, S.K. First-principles calculations to investigate structural, optoelectronics and thermoelectric properties of lead free Cs2GeSnX6 (X = Cl, Br). Mater. Sci. Eng. B 2023, 292, 116421. [Google Scholar] [CrossRef]
- Casper, F.; Graf, T.; Chadov, S.; Balke, B.; Felser, C. Half-Heusler compounds: Novel materials for energy and spintronic applications. Semicond. Sci. Technol. 2012, 27, 63001. [Google Scholar] [CrossRef]
- Chen, S.; Ren, Z. Recent progress of half-Heusler for moderate temperature thermoelectric applications. Mater. Today 2013, 16, 387–395. [Google Scholar] [CrossRef]
- Dixit, A.; Saxena, A.; Behera, D.; Abraham, J.A.; Sharma, R.; Mukherjee, S.K. First principles study on structural, mechanical, and thermoelectric properties of half-Heusler alloy (KLiTe). Mater. Today Proc. 2023; in press. [Google Scholar] [CrossRef]
- Heusler, F.; Starck, W.; Haupt, E. Magnetisch-chemische studien. Verh. Dtsch. Phys. Ges. 1903, 5, 219–232. [Google Scholar]
- Huang, L.; Zhang, Q.; Yuan, B.; Lai, X.; Yan, X.; Ren, Z. Recent progress in half-Heusler thermoelectric materials. Mater. Res. Bull. 2016, 76, 107–112. [Google Scholar] [CrossRef]
- Bos, J.-W.; Downie, R.A. Half-Heusler thermoelectrics: A complex class of materials. J. Phys. Condens. Matter 2014, 26, 433201. [Google Scholar] [CrossRef]
- Tavares, S.; Yang, K.; Meyers, M.A. Heusler alloys: Past, properties, new alloys, and prospects. Prog. Mater. Sci. 2022, 132, 101017. [Google Scholar] [CrossRef]
- Bos, J.-W.G. Recent developments in half-Heusler thermoelectric materials. Thermoelectr. Energy Convers. 2021, 125–142. [Google Scholar] [CrossRef]
- Behera, D.; Abraham, J.A.; Sharma, R.; Mukerjee, S.K.; Jain, E. First Principles Study of New d0 Half-Metallic Ferromagnetism in CsBaC Ternary Half-Heusler Alloy. J. Supercond. Nov. Magn. 2022, 35, 3431–3437. [Google Scholar] [CrossRef]
- Mingo, N. Thermoelectric figure of merit and maximum power factor in III–V semiconductor nanowires. Appl. Phys. Lett. 2004, 84, 2652–2654. [Google Scholar] [CrossRef]
- Behera, D.; Manzoor, M.; Mukherjee, S.K. Incorporation of Te in enhancing thermoelectric response of AeAg2SeTe (Ae= Sr, Ba) compounds: A DFT insight. Comput. Condens. Matter 2022, 33, e00757. [Google Scholar] [CrossRef]
- Javed, M.; Sattar, M.A.; Benkraouda, M.; Amrane, N. Structural and mechanical stability, lattice dynamics and electronic structure of the novel CrVZ (Z= S, Se, & Te) half-Heusler alloys. Mater. Today Commun. 2020, 25, 101519. [Google Scholar]
- Zerrouki, T.; Rached, H.; Rached, D.; Caid, M.; Cheref, O.; Rabah, M. First-principles calculations to investigate structural stabilities, mechanical and optoelectronic properties of NbCoSn and NbFeSb half-Heusler compounds. Int. J. Quantum Chem. 2021, 121, e26582. [Google Scholar] [CrossRef]
- Ahmad, M.; Murtaza, G.; Khenata, R.; Omran, S.B.; Bouhemadou, A. Structural, elastic, electronic, magnetic and optical properties of RbSrX (C, SI, Ge) half-Heusler compounds. J. Magn. Magn. Mater. 2015, 377, 204–210. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Sorantin, P.; Trickey, S. Full-potential, linearized augmented plane wave programs for crystalline systems. Comput. Phys. Commun. 1990, 59, 399–415. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Madsen, G.K.H.; Kvasnicka, D.; Luitz, J. Wien2k, An Augmented Plane Wave+ Local Orbitals Program for Calculating Crystal Properties. Mater. Sci. Eng. 2001, 60, 1–302. [Google Scholar]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Wu, Z.; Cohen, R.E. More accurate generalized gradient approximation for solids. Phys. Rev. B 2006, 73, 235116. [Google Scholar] [CrossRef]
- Koller, D.; Tran, F.; Blaha, P. Improving the modified Becke-Johnson exchange potential. Phys. Rev. B 2012, 85, 155109. [Google Scholar] [CrossRef]
- Koller, D.; Tran, F.; Blaha, P. Merits and limits of the modified Becke-Johnson exchange potential. Phys. Rev. B 2011, 83, 195134. [Google Scholar] [CrossRef]
- Behera, D.; Mukherjee, S.K. Structural, elastic, electronic and thermoelectric properties of K2GeBr6: A first principle approach. Mater. Today Proc. 2023; in press. [Google Scholar] [CrossRef]
- Jamal, M.; Bilal, M.; Ahmad, I.; Jalali-Asadabadi, S. IRelast package. J. Alloys Compd. 2018, 735, 569–579. [Google Scholar] [CrossRef]
- Otero-De-La-Roza, A.; Luaña, V. Gibbs2: A new version of the quasi-harmonic model code. I. Robust treatment of the static data. Comput. Phys. Commun. 2011, 182, 1708–1720. [Google Scholar] [CrossRef]
- Madsen, G.K.; Singh, D.J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef]
- Hafner, J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. J. Comput. Chem. 2008, 29, 2044–2078. [Google Scholar] [CrossRef]
- Anand, S.; Xia, K.; Hegde, V.I.; Aydemir, U.; Kocevski, V.; Zhu, T.; Wolverton, C.; Snyder, G.J. A valence balanced rule for discovery of 18-electron half-Heuslers with defects. Energy Environ. Sci. 2018, 11, 1480–1488. [Google Scholar] [CrossRef]
- Katsura, T.; Tange, Y. A Simple Derivation of the Birch–Murnaghan Equations of State (EOSs) and Comparison with EOSs Derived from Other Definitions of Finite Strain. Minerals 2019, 9, 745. [Google Scholar] [CrossRef]
- Behera, D.; Mukherjee, S.K. Optoelectronics and Transport Phenomena in Rb2InBiX6 (X = Cl, Br) Compounds for Renewable Energy Applications: A DFT Insight. Chemistry 2022, 4, 1044–1059. [Google Scholar] [CrossRef]
- Behera, D.; Manzoor, M.; Maharana, M.; Iqbal, M.W.; Zahid, T.; Lakra, S.; Mukherjee, S.; Alarfaji, S.S. Structural, electronic, optical, and thermoelectric response of zintl phase AAg2S2 (A = Sr/Ba) compounds for renewable energy applications. Phys. B Condens. Matter 2023, 649, 414446. [Google Scholar] [CrossRef]
- Behera, D.; Manzoor, M.; Sharma, R.; Iqbal, M.W.; Mukherjee, S.K. First principle insight on structural, opto-electronic and transport properties of novel zintl-phase AMg2Bi2 (A = Sr, Ba). J. Solid State Chem. 2023, 320, 123860. [Google Scholar] [CrossRef]
- Birch, F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar] [CrossRef]
- Azzouz-Rached, A.; Hadi, M.; Rached, H.; Hadji, T.; Rached, D.; Bouhemadou, A. Pressure effects on the structural, elastic, magnetic and thermodynamic properties of Mn2AlC and Mn2SiC MAX phases. J. Alloys Compd. 2021, 885, 160998. [Google Scholar] [CrossRef]
- Azzouz-Rached, A.; Qureshi, M.W.; Ouadha, I.; Rached, H.; Hadji, T.; Rekab-Djabri, H. DFT analysis of physical properties of quaternary MAX phase nitrides:(Fe0. 5M0. 5) 2SiN (M= Cr & Mn). Comput. Condens. Matter 2022, 33, e00748. [Google Scholar]
- Born, M.; Huang, K.; Lax, M. Dynamical Theory of Crystal Lattices. Am. J. Phys. 1955, 23, 474. [Google Scholar] [CrossRef]
- Born, M.; Huang, K. Dynamical Theory of Crystal Lattices; Oxford University Press: Oxford, UK, 1954. [Google Scholar]
- Born, M. On the stability of crystal lattices. I. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1940; pp. 160–172. [Google Scholar]
- Waller, I. Dynamical theory of crystal lattices by M. Born and K. Huang. Acta Crystallogr. 1956, 9, 837–838. [Google Scholar] [CrossRef]
- Zuo, L.; Humbert, M.; Esling, C. Elastic properties of polycrystals in the Voigt-Reuss-Hill approximation. J. Appl. Crystallogr. 1992, 25, 751–755. [Google Scholar] [CrossRef]
- Behera, D.; Mukherjee, S.K. Theoretical Investigation of the Lead-free K2InBiX6 (X= Cl, Br) Double Perovskite Compounds Using First Principle Calculation. JETP Lett. 2022, 116, 537–546. [Google Scholar] [CrossRef]
- Azzouz-Rached, A.; Rached, H.; Babu, M.H.; Hadji, T.; Rached, D. Prediction of double transition metal (Cr1− xZrx) 2AlC MAX phases as thermal barrier coatings: Insight from density functional theory. Int. J. Quantum Chem. 2021, 121, e26770. [Google Scholar] [CrossRef]
- Behera, D.; Dixit, A.; Nahak, B.; Srivastava, A.; Sharma, R.; Khenata, R.; Bin-Omran, S.; Abdelmohsen, S.A.M.; Abdelbacki, A.M.M.; Mukherjee, S.K. Theoretical insight on the electronic band structure, mechanical, vibrational and thermodynamic characteristic of antiperovskites RE3InN (RE= Y and La). Mater. Today Commun. 2023, 35, 105618. [Google Scholar] [CrossRef]
- Pugh, S.F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Behera, D.; Sharma, R.; Mukherjee, S.K. Structural, phonon and elastic properties of semimetal YSb: A DFT study. Mater. Today Proc. 2023; in press. [Google Scholar] [CrossRef]
- Frantsevich, I.N. Elastic Constants and Elastic Moduli of Metals and Insulators; Reference Book; Naukova Dumka: Kyiv, Ukraine, 1982. [Google Scholar]
- Eberhart, M.E.; Jones, T.E. Cauchy pressure and the generalized bonding model for nonmagnetic bcc transition metals. Phys. Rev. B 2012, 86, 134106. [Google Scholar] [CrossRef]
- Manzoor, M.; Behera, D.; Sharma, R.; Iqbal, M.W.; Mukherjee, S. First principles insights on the structural, mechanical, dynamical, thermoelectric and thermodynamics properties of novel topological (ScSb) semi-metal. Mater. Sci. Eng. B 2023, 291, 116372. [Google Scholar] [CrossRef]
- Chung, D.H.; Buessem, W.R. The Elastic Anisotropy of Crystals. J. Appl. Phys. 1967, 38, 2010–2012. [Google Scholar] [CrossRef]
- Kube, C.M. Elastic anisotropy of crystals. AIP Adv. 2016, 6, 095209. [Google Scholar] [CrossRef]
- Ouadha, I.; Rached, H.; Azzouz-Rached, A.; Reggad, A.; Rached, D. Study of the structural, mechanical and thermodynamic properties of the new MAX phase compounds (Zr1-xTix) 3AlC2. Comput. Condens. Matter 2020, 23, e00468. [Google Scholar] [CrossRef]
- Behera, D.; Dixit, A.; Nahak, B.; Srivastava, A.; Dubey, S.; Sharma, R.; Mishra, A.K.; Mukherjee, S.K. Structural, electronic, elastic, vibrational and thermodynamic properties of antiperovskites Mg3NX (X = Ge, Sn): A DFT study. Phys. Lett. A 2022, 453, 128478. [Google Scholar] [CrossRef]
- Abraham, J.A.; Behera, D.; Kumari, K.; Srivastava, A.; Sharma, R.; Mukherjee, S.K. A comprehensive DFT analysis on structural, electronic, optical, thermoelectric, SLME properties of new Double Perovskite Oxide Pb2ScBiO6. Chem. Phys. Lett. 2022, 806, 139987. [Google Scholar] [CrossRef]
- Dugdale, J.S.; MacDonald, D.K.C. Lattice thermal conductivity. Phys. Rev. 1955, 98, 1751. [Google Scholar] [CrossRef]
- Andritsos, E.I.; Zarkadoula, E.; Phillips, A.E.; Dove, M.; Walker, C.J.; Brazhkin, V.V.; Trachenko, K. The heat capacity of matter beyond the Dulong–Petit value. J. Phys. Condens. Matter 2013, 25, 235401. [Google Scholar] [CrossRef] [PubMed]
- Fitzgerel, R.K.; Verhoek, F.H. The law of Dulong and Petit. J. Chem. Educ. 1960, 37, 545. [Google Scholar] [CrossRef]
- Inaba, H.; Yamamoto, T. Debye temperature of materials. Netsu Sokutei 1983, 10, 132–145. [Google Scholar]
- Saxena, A.; Dixit, A.; Behera, D.; Abraham, J.A.; Sharma, R.; Mukherjee, S.K. Insight on structural, electronic and thermoelectric properties of perovskite AgBaCl3 by an Ab-initio for solar cell and renewable energy. Mater. Today Proc. 2023; in press. [Google Scholar] [CrossRef]


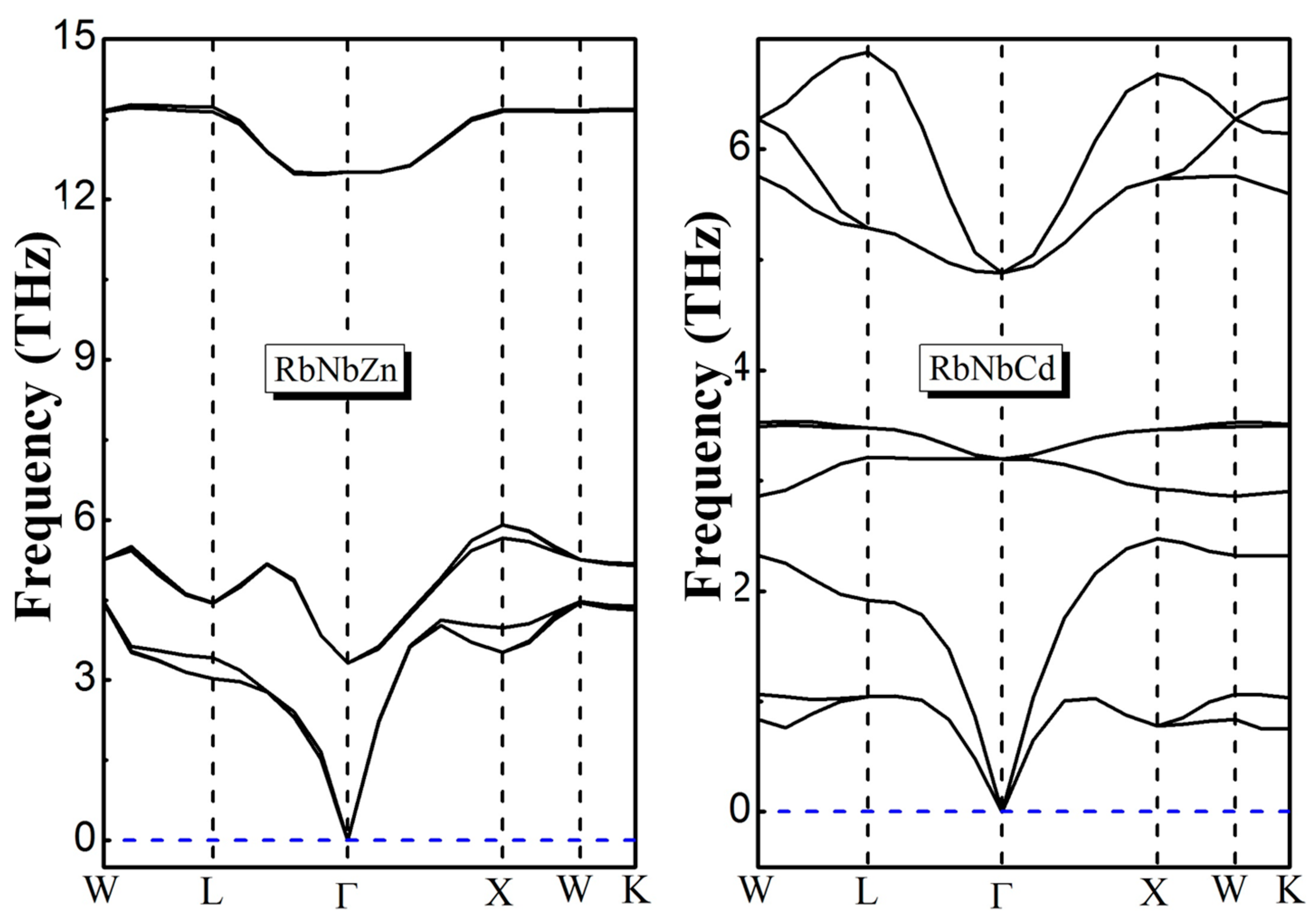
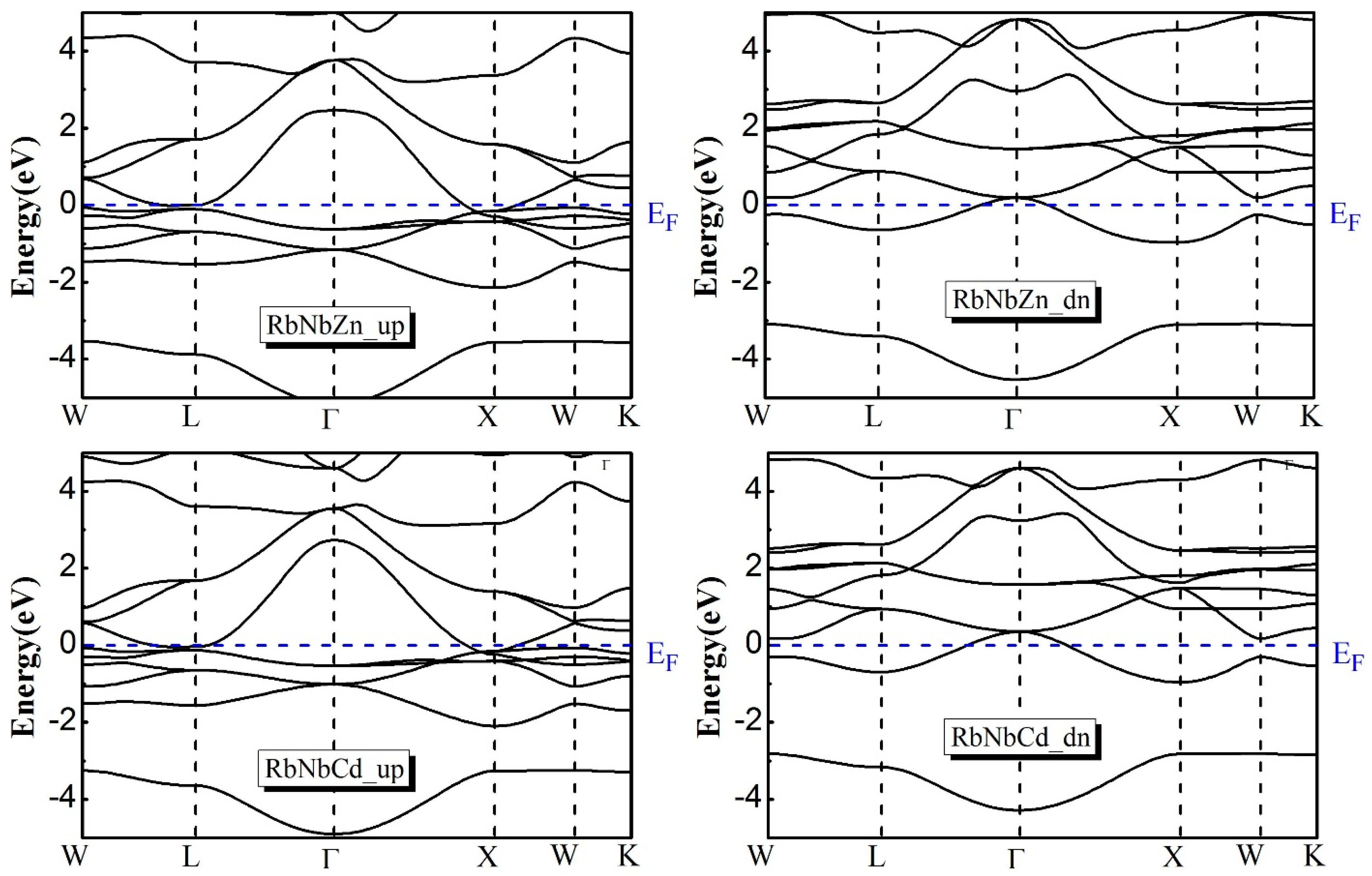
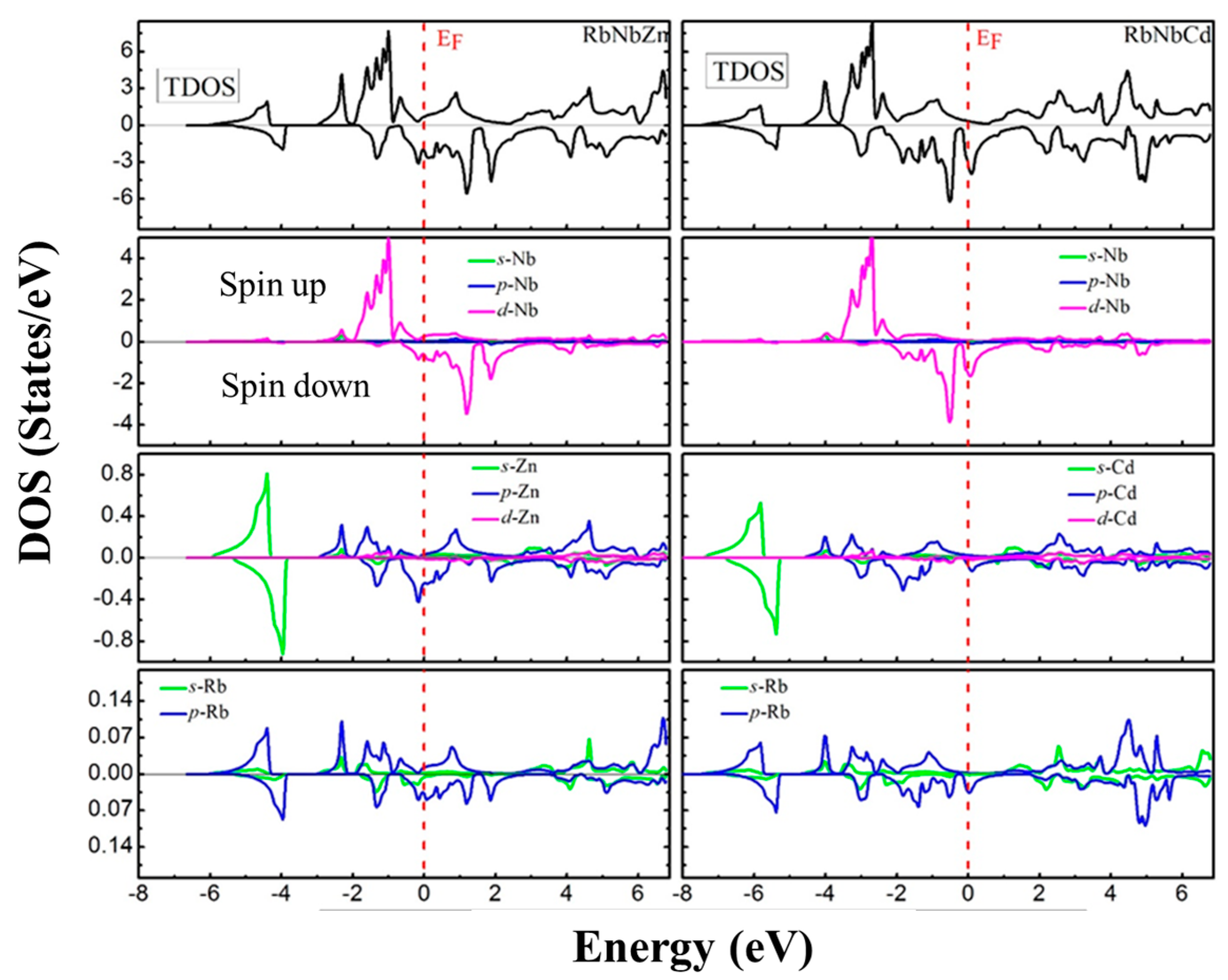


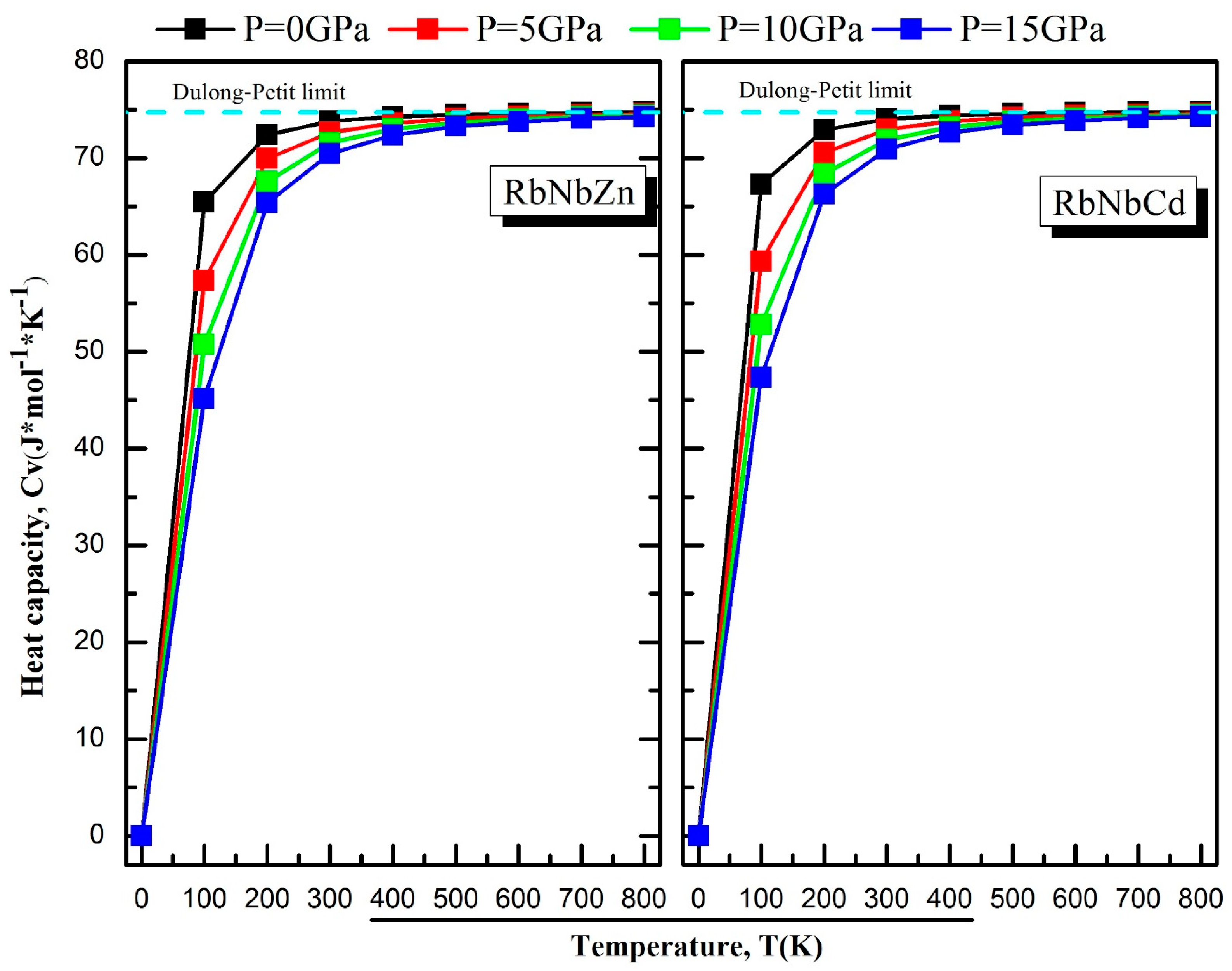



| Compounds | Phase | a (Å) | B (GPa) | B’ | Energy (eV) | Eform (eV/atom) | |
|---|---|---|---|---|---|---|---|
| RbNbCd | Alpha | NM | 7.27 | 18.07 | 5.59 | −337,359.50342 | 0.06 |
| FM | 8.06 | 7.43 | 4.43 | −337,360.48248 | −0.03 | ||
| Beta | NM | 7.21 | 24.78 | 4.68 | −337,361.02856 | −0.02 | |
| FM | 7.64 | 14.22 | 4.65 | −337,361.59782 | −0.30 | ||
| Gamma | NM | 7.42 | 24.57 | 4.68 | −337,360.98197 | −0.25 | |
| FM | 7.68 | 17.47 | 4.81 | −337,361.78735 | −0.95 | ||
| RbNbZn | Alpha | NM | 6.96 | 21.11 | 5.67 | −233,958.79599 | −1.03 |
| FM | 7.93 | 6.47 | 4.93 | −233,959.52525 | −1.03 | ||
| Beta | NM | 6.96 | 26.45 | 4.47 | −233,960.27421 | −1.03 | |
| FM | 7.37 | 14.06 | 5.49 | −233,960.67933 | −1.03 | ||
| Gamma | NM | 7.09 | 27.40 | 4.42 | −233,960.41307 | −1.03 | |
| FM | 7.39 | 19.13 | 4.46 | −233,961.06317 | −1.03 |
| Compound | C11 | C12 | C44 | B | G | G/B | E | υ | A | |
|---|---|---|---|---|---|---|---|---|---|---|
| RbNbCd | 30.7941 | 11.7813 | 9.6574 | 18.118 | 9.596 | 0.52 | 24.468 | 0.274 | 2.12 | 1.01 |
| RbNbZn | 36.1129 | 6.9461 | 7.8413 | 16.668 | 10.078 | 0.61 | 25.162 | 0.248 | −0.89 | 0.53 |
| Compounds | Total (μB) | Rb (μB) | Nb (μB) | Cd/Zn (μB) | Interstitial (μB) |
|---|---|---|---|---|---|
| RbNbCd | 4.05 | 0.03 | 2.52 | 0.04 | 1.44 |
| RbNbZn | 4.01 | 0.05 | 2.49 | 0.07 | 1.39 |
| Compounds | ρ(g/cm3) | kmin | kph | |||||
|---|---|---|---|---|---|---|---|---|
| RbNbCd | 4.2546 | 2695.51 | 1501.82 | 1672.28 | 148.309 | 734.309 | 0.161 | 0.701 |
| RbNbZn | 4.0022 | 2742.67 | 1586.86 | 1761.39 | 162.329 | 766.4272 | 0.098 | 0.947 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behera, D.; Azzouz-Rached, A.; Bouhenna, A.; Salah, M.M.; Shaker, A.; Mukherjee, S.K. First-Principles Studies on the Physical Properties of the Half Heusler RbNbCd and RbNbZn Compounds: A Promising Material for Thermoelectric Applications. Crystals 2023, 13, 618. https://doi.org/10.3390/cryst13040618
Behera D, Azzouz-Rached A, Bouhenna A, Salah MM, Shaker A, Mukherjee SK. First-Principles Studies on the Physical Properties of the Half Heusler RbNbCd and RbNbZn Compounds: A Promising Material for Thermoelectric Applications. Crystals. 2023; 13(4):618. https://doi.org/10.3390/cryst13040618
Chicago/Turabian StyleBehera, Debidatta, Ahmed Azzouz-Rached, Abdessalem Bouhenna, Mostafa M. Salah, Ahmed Shaker, and Sanat Kumar Mukherjee. 2023. "First-Principles Studies on the Physical Properties of the Half Heusler RbNbCd and RbNbZn Compounds: A Promising Material for Thermoelectric Applications" Crystals 13, no. 4: 618. https://doi.org/10.3390/cryst13040618
APA StyleBehera, D., Azzouz-Rached, A., Bouhenna, A., Salah, M. M., Shaker, A., & Mukherjee, S. K. (2023). First-Principles Studies on the Physical Properties of the Half Heusler RbNbCd and RbNbZn Compounds: A Promising Material for Thermoelectric Applications. Crystals, 13(4), 618. https://doi.org/10.3390/cryst13040618







