Temperature Dependence of the Hyperfine Magnetic Field at Fe Sites in Ba-Doped BiFeO3 Thin Films Studied by Emission Mössbauer Spectroscopy
Abstract
:1. Introduction
2. Materials and Methods
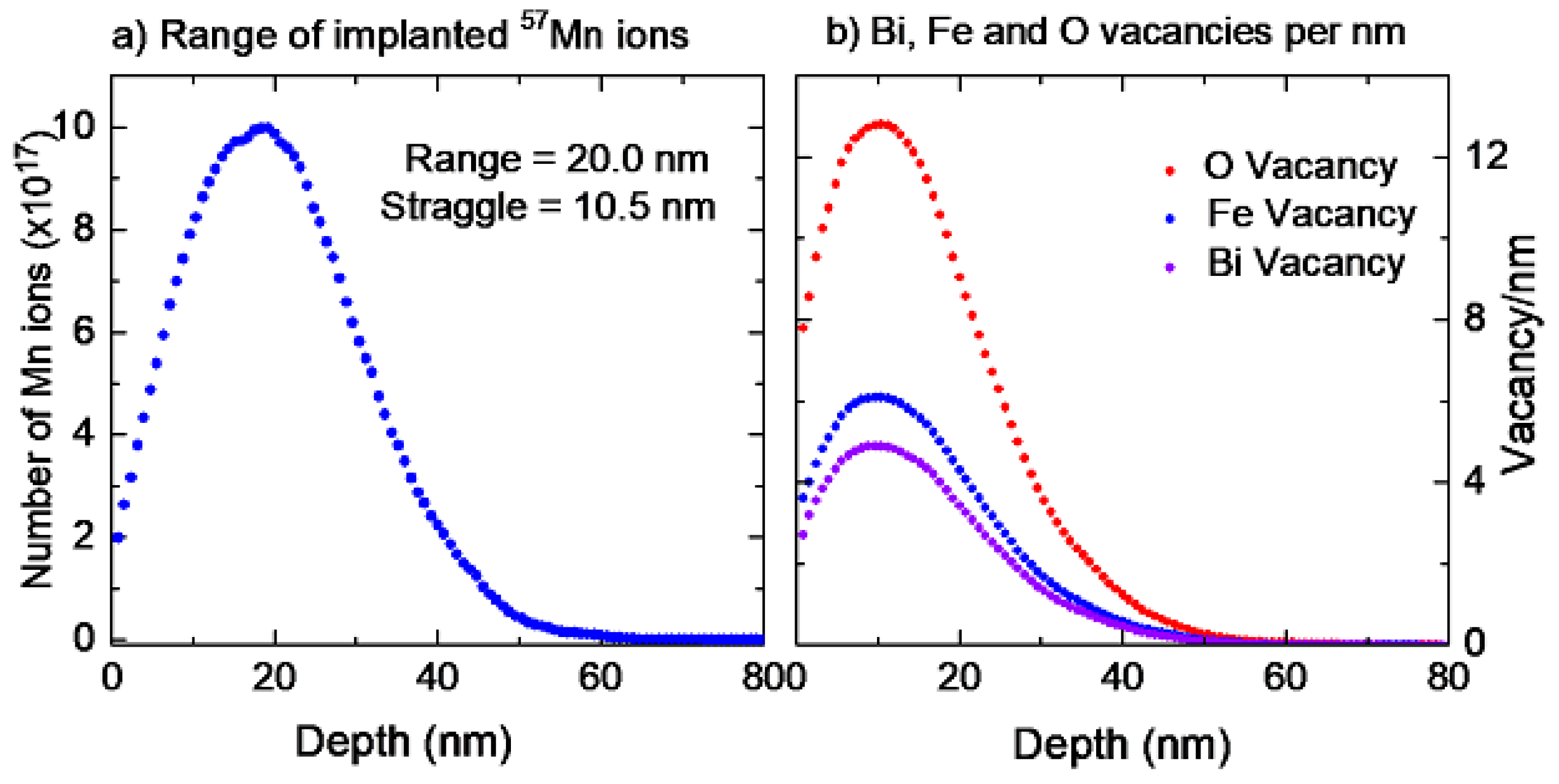
2.1. Sample Preparation and Ion Implantation
2.2. Emission Mössbauer Spectroscopy (eMS) Measurements
3. Results
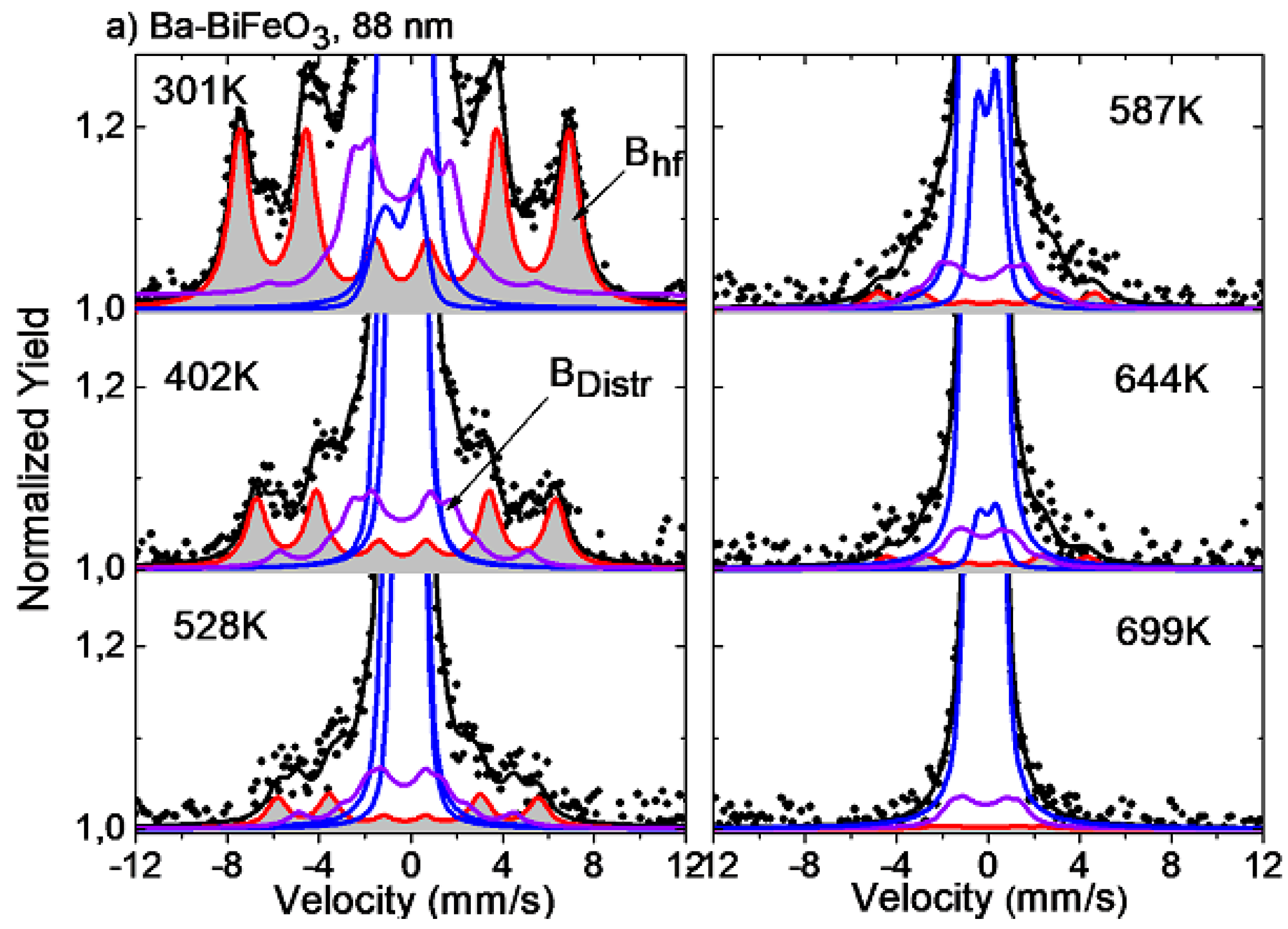
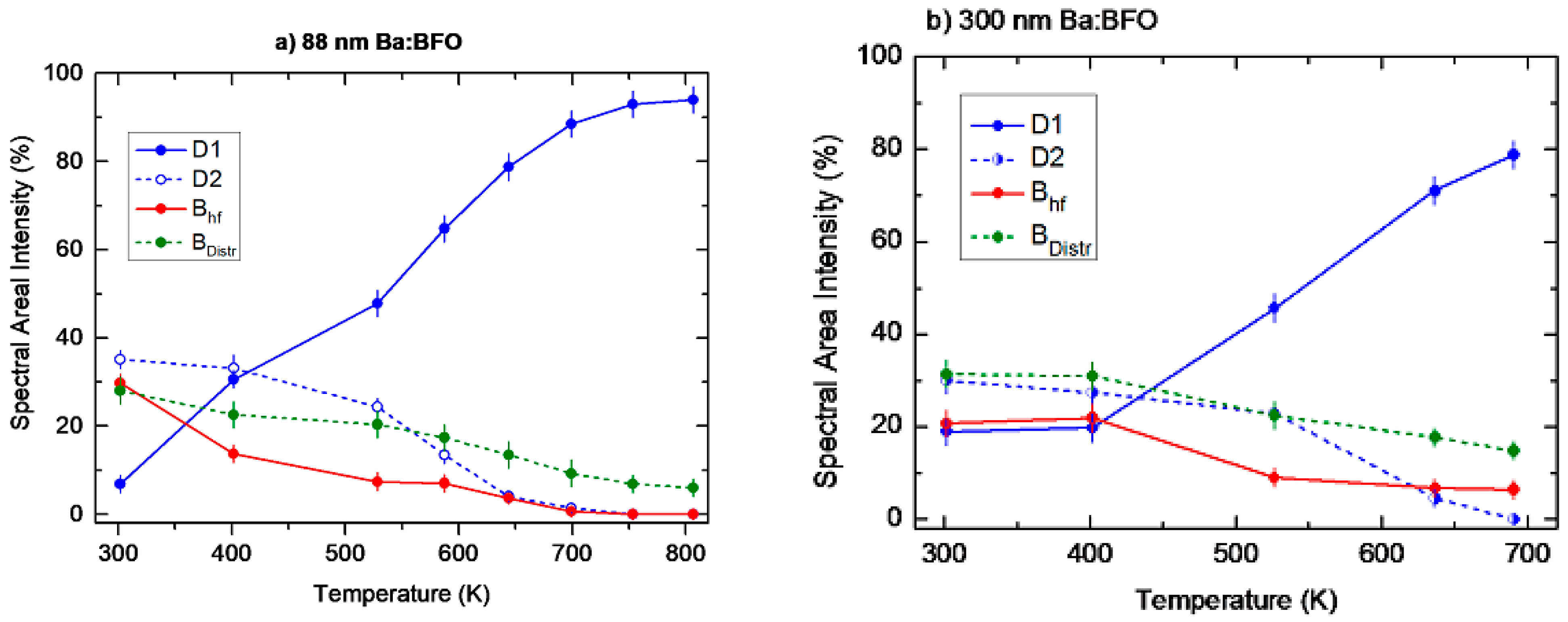
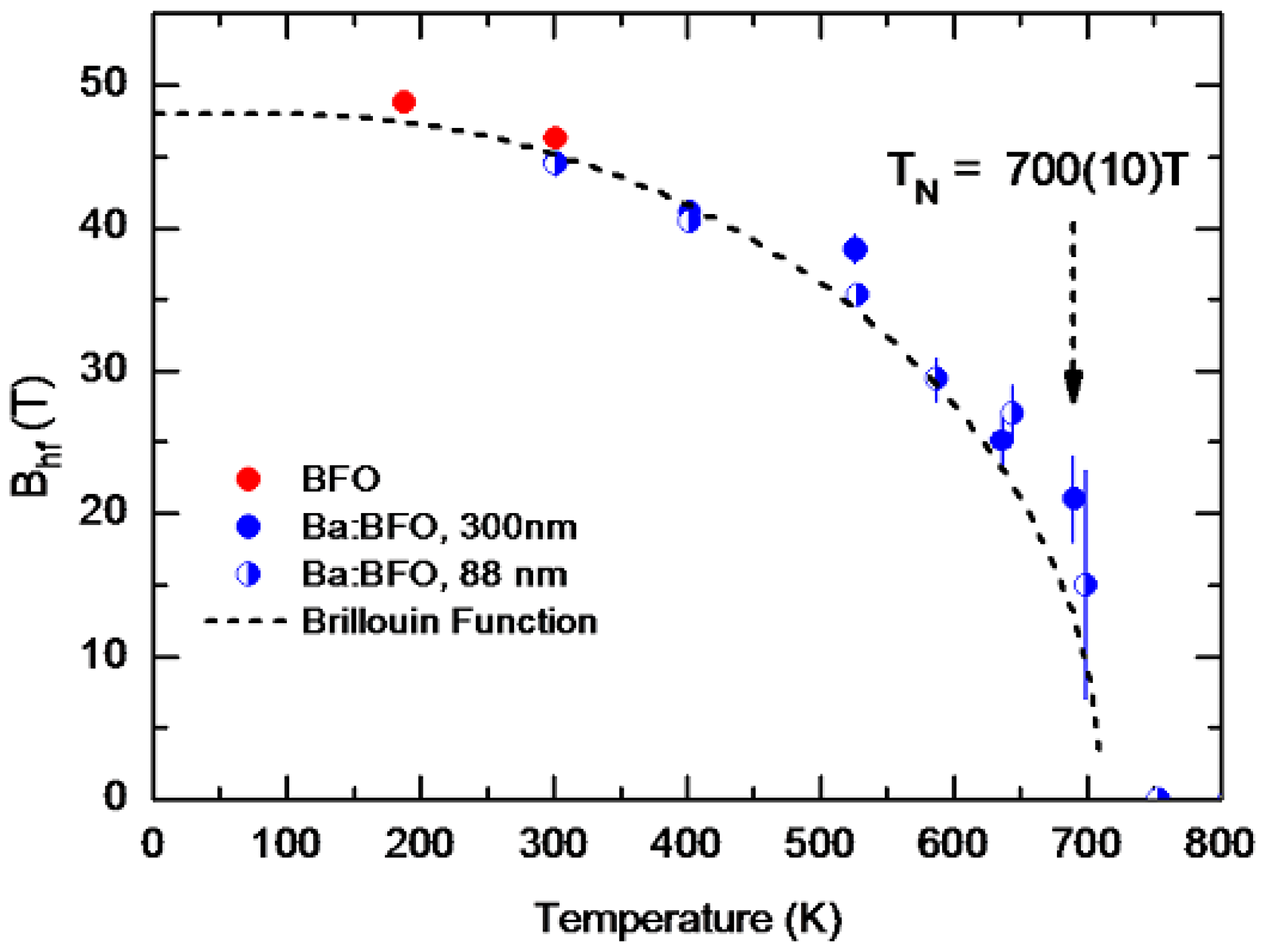
Temperature Dependence of the Hyperfine Magnetic Field Bhf
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Catalan, G.; Scott, J.F. Physics and Applications of Bismuth Ferrite. Adv. Mater. 2009, 21, 2463–2485. [Google Scholar] [CrossRef]
- Marschick, G.; Schell, J.; Stöger, B.; Gonçalves, J.N.; Karabasov, M.O.; Zyabkin, D.; Welker, A.; Escobar, C.M.; Gärtner, D.; Efe, I.; et al. Multiferroic bismuth ferrite: Perturbed angular correlation studies on its ferroic α−β phase transition. Phys. Rev. B 2020, 102, 224110. [Google Scholar] [CrossRef]
- Arnold, D.C.; Knight, K.S.; Morrison, F.D.; Lightfoot, P. Ferroelectric-Paraelectric Transition in BiFeO3: Crystal Structure of the Orthorhombic β Phase. Phys. Rev. Lett. 2009, 102, 027602. [Google Scholar] [CrossRef]
- Wei, J.; Wu, C.; Yang, T.; Lv, Z.; Xu, Z.; Wang, D.; Haumont, R.; Cheng, Z. Temperature-Driven Multiferroic Phase Transitions and Structural Instability Evolution in Lanthanum-Substituted Bismuth Ferrite. J. Phys. Chem. 2019, 123, 4457–4468. [Google Scholar] [CrossRef]
- Schell, J.; Schmuck, M.; Efe, I.; Dang, T.T.; Gonçalves, J.N.; Lewin, D.; Castillo, M.E.; Shvartsman, V.V.; Costa, Â.R.G.; Köster, U.; et al. Strong magnetoelectric coupling at an atomic nonmagnetic electromagnetic probe in bismuth ferrite. Phys. Rev. B 2022, 105, 094102. [Google Scholar] [CrossRef]
- Dang, T.T.; Schell, J.; Boa, A.G.; Lewin, D.; Marschick, G.; Dubey, A.; Escobar-Castillo, M.; Noll, C.; Beck, R.; Zyabkin, D.V.; et al. Temperature dependence of the local electromagnetic field at the Fe site in multiferroic bismuth ferrite. Phys. Rev. B 2022, 106, 054416. [Google Scholar] [CrossRef]
- Yang, C.-H.; Kan, D.; Takeuchi, I.; Nagarajan, V.; Seidel, J. Doping BiFeO3: Approaches and enhanced functionality. Phys. Chem. Chem. Phys. 2012, 14, 15953–15962. [Google Scholar] [CrossRef] [PubMed]
- Catherall, R.; Andreazza, W.; Breitenfeldt, M.; Dorsival, A.; Focker, G.; Gharsa, T.; Giles, T.; Grenard, J.; Locci, F.; Martins, P.; et al. The ISOLDE facility. J. Phys. G 2017, 44, 094002. [Google Scholar] [CrossRef]
- Johnston, K.; Schell, J.; Correia, J.; Deicher, M.; Gunnlaugsson, H.; Fenta, A.; David-Bosne, E.; Costa, A.; Lupascu, D.C. The solid state physics programme at ISOLDE. J. Phys. G 2017, 44, 104001. [Google Scholar] [CrossRef]
- Kim, W.; Kim, C.S. Mössbauer study of polycrystalline multiferroic Ba-doped BiFeO3 compound. J. Kor. Phys. Soc. 2010, 56, 607–610. [Google Scholar] [CrossRef]
- Mix, C.; Jakob, G. Multiferroic and structural properties of BiFeO3 close to the strain induced phase transition on different substrates. J. Appl. Phys. 2013, 113, 17D907. [Google Scholar] [CrossRef]
- Patterson, A.L. The Scherrer Formula for X-ray Particle Size Determination. Phys. Rev. 1939, 56, 978–982. [Google Scholar] [CrossRef]
- Porporati, A.A.; Tsuji, K.; Valant, M.; Axelsson, A.-K.; Pezzottia, G. Raman tensor elements for multiferroic BiFeO3 with rhombohedral R3c symmetry. J. Raman Spectrosc. 2010, 41, 84–87. [Google Scholar] [CrossRef]
- Iliev, M.; Litvinchuk, A.; Hadjiev, V.G.; Gospodinov, M.M.; Skumryev, V.; Ressouche, E. Phonon and magnon scattering of antiferromagnetic Bi2Fe4O9. Phys. Rev. B 2010, 81, 024302. [Google Scholar] [CrossRef]
- Weyer, G.; ISOLDE Collaboration. Mössbauer spectroscopy at ISOLDE. Hyperfine Interact. 2000, 129, 371–390. [Google Scholar] [CrossRef]
- Weyer, G. Defects in semiconductors—Results from Mössbauer spectroscopy. Hyperfine Interact. 2007, 177, 1–13. [Google Scholar] [CrossRef]
- Schell, J.; Zyabkin, D.; Bharuth-Ram, K.; Gonçalves, J.N.; Díaz-Guerra, C.; Gunnlaugsson, H.P.; Martín-Luengo, A.T.; Schaaf, P.; Bonanni, A.; Masenda, H.; et al. Anisotropy of the Electric Field Gradient in Two-Dimensional α-MoO3 Investigated by 57Mn(57Fe) Emission Mössbauer Spectroscopy. Crystals 2022, 12, 942. [Google Scholar] [CrossRef]
- Gunnlaugsson, H.P. Spreadsheet based analysis of Mössbauer spectra. Hyperfine Interact. 2016, 237, 79. [Google Scholar] [CrossRef]
- Ziegler, J.F. Interactions of Ions with Matter. SRIM-2008 Software Package. Available online: http://www.srim.org (accessed on 26 March 2023).
- Papaefthymiou, G.C.; Viescas, A.J.; Le Breton, J.-M.; Chiron, H.; Juraszek, J.; Park, T.-J.; Wong, S.S. Magnetic and Mössbauer characterization of the magnetic properties of single-crystalline sub-micron sized Bi2Fe4O9 cubes. Curr. Appl. Phys. 2015, 15, 417–422. [Google Scholar] [CrossRef]
- Sobolev, A.V.; Rusakov, V.S.; Gapochka, A.M.; Glazkoa, I.S.; Gubaidulina, T.V.; Matsnev, M.E.; Belik, A.A.; Presniakov, I.A. 57Fe Mössbauer spectroscopy study of cycloidal spin arrangements and magnetic transitions in BiFe1−xCoxO3. Phys. Rev. B 2020, 101, 224409-(1)–224409-(13). [Google Scholar] [CrossRef]
- Gütlich, P.; Bill, E.; Trautwein, A.X. Mössbauer Spectroscopy and Transition Metal Chemistry: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Kothari, D.; Reddy, V.R.; Gupta, A.; Phase, D.M.; Lakshmi, N.; Deshpande, S.K.; Awasti, A.M. Study of the effect of Mn doping on the BiFeO3 system. J. Phys. Condens. Matter 2007, 19, 136202-(1)–136202-(8). [Google Scholar] [CrossRef]
- El-Desoky, M.; Ayoua, M.; Mostafa, M.; Ahmed, M. Multiferroic properties of nanostructured barium doped bismuth ferrite. J. Magn. Magn. Mater. 2016, 404, 68–73. [Google Scholar] [CrossRef]
- Das, R.; Mandal, K. Magnetic, ferroelectric and magnetoelectric properties of Ba-doped BiFeO3. J. Magn. Magn. Mater. 2012, 324, 1913–1918. [Google Scholar] [CrossRef]
- Kumar, A.; Denev, S.; Zeches, R.J.; Vlahos, E.; Podraza, N.J.; Melville, A.; Schlom, D.G.; Ramesh, R.; Gopalan, V. Probing mixed tetragonal/rhombohedral-like monoclinic phases in strained bismuth ferrite films by optical second harmonic generation. Appl. Phys. Lett. 2010, 97, 112903. [Google Scholar] [CrossRef]
- Mehedi, H.; Hakim, M.A.; Basith, M.A.; Hossain, M.S.; Ahmmad, B.; Zubair, M.A.; Hussain, A.; Islam, M.F. Size dependent magnetic and electrical properties of Ba-doped nanocrystalline BiFeO3. AIP Adv. 2016, 6, 035314. [Google Scholar]
- Li, M.; Ning, M.; Ma, Y.; Wu, Q.; Ong, C.K. Room temperature ferroelectric, ferromagnetic and magnetoelectric properties of Ba-doped BiFeO3 thin films. J. Phys. D 2007, 40, 1603–1607. [Google Scholar] [CrossRef]
- Godara, S.; Kumar, B. Effect of Ba–Nb co-doping on the structural, dielectric, magnetic and ferroelectric properties of BiFeO3 nanoparticles. Ceram. Int. 2015, 44, 6912–6919. [Google Scholar] [CrossRef]
- Cheng, G.F.; Huang, Y.H.; Ge, J.J.; Lv, B.; Wu, X.S. Effects of local structural distortion on magnetization in BiFeO3 with Pr, Ba co-doping. J. Appl. Phys. 2012, 111, 07C707. [Google Scholar] [CrossRef]
- Jayakumar, O.D.; Achary, S.N.; Girija, K.G.; Tyagi, A.K.; Sudakar, C.; Lawes, G.; Naik, R.; Nisar, J.; Peng, X.; Ahuja, R. Theoretical and experimental evidence of enhanced ferromagnetism in Ba and Mn cosubstituted BiFeO3. Appl. Phys. Lett. 2010, 96, 032903. [Google Scholar] [CrossRef]
- Si, Y.H.; Xia, Y.; Shang, S.K.; Xiong, X.B.; Zeng, X.R.; Zhou, J.; Li, Y.Y. Enhanced Visible Light Driven Photocatalytic Behavior of BiFeO3/Reduced Graphene Oxide Composites. Nanomaterials 2018, 8, 526. [Google Scholar] [CrossRef]
- Quan, Z.C.; Hu, H.; Xu, S.; Liu, W.; Fang, G.J.; Li, M.Y.; Zhao, X.Z. Surface chemical bonding states and ferroelectricity of Ce-doped BiFeO3 thin films prepared by sol–gel process. J. Sol-Gel Sci. Technol. 2008, 48, 261–266. [Google Scholar] [CrossRef]
- Li, Z.J.; Hou, Z.L.; Song, W.L.; Liu, X.D.; Cao, W.Q.; Shao, X.H.; Cao, M.S. Unusual continuous dual absorption peaks in Ca-doped BiFeO3 nanostructures for broadened microwave absorption. Nanoscale 2016, 8, 10415–10424. [Google Scholar] [CrossRef] [PubMed]
- Yiyi, Z.; Chuye, Q.; Yuhui, M.; Qi, W.; Weiwei, M.; Xingfu, W.; Jian, Z.; Yonggang, M.; Jianping, Y.; Xingao, L.; et al. Effect of Eu, Mn co-doping on structural, optical and magnetic properties of BiFeO3 nanoparticles. Mater. Sci. Semicond. Process. 2017, 57, 178–184. [Google Scholar]
- Dutta, D.P.; Jayakumar, O.D.; Tyagi, A.K.; Girija, K.G.; Pillai, C.G.S.; Sharma, G. Effect of doping on the morphology and multiferroic properties of BiFeO3 nanorods. Nanoscale 2010, 2, 1149–1154. [Google Scholar] [CrossRef] [PubMed]
- Burns, S.R.; Paull, O.; Jurasek, J.; Nagarajan, V.; Sando, D. The Experimentalist’s Guide to the Cycloid, or Noncollinear Antiferromagnetism in Epitaxial BiFeO3. Adv. Mater. 2020, 32, 2003711. [Google Scholar] [CrossRef] [PubMed]
- Kim, C.S.; Min, B.K.; An, S.Y.; Uhm, Y.R. Mössbauer studies of Y3Fe4.75Al0.25O12. J. Magn. Magn. Mater. 2002, 239, 54–56. [Google Scholar] [CrossRef]
- Kim, C.S.; Min, B.K.; Kim, S.J.; Yoon, S.R.; Uhm, Y.R. Crystallographic and magnetic properties of Y3Fe5−xAlxO12. J. Magn. Magn. Mater. 2003, 254–255, 553–555. [Google Scholar] [CrossRef]
- Catalan, G.; Sardar, K.; Church, N.S.; Scott, J.F.; Harrison, J.; Redfern, S.A. Effect of chemical substitution on the Néel temperature of multiferroic Bi1−xCaxFeO3. Phys. Rev. B 2009, 79, 212415. [Google Scholar] [CrossRef]
- Suresh, P.; Srinath, S. Effect of La substitution on structure and magnetic properties of sol-gel prepared BiFeO3. J. Appl. Phys. 2013, 113, 17D920. [Google Scholar] [CrossRef]


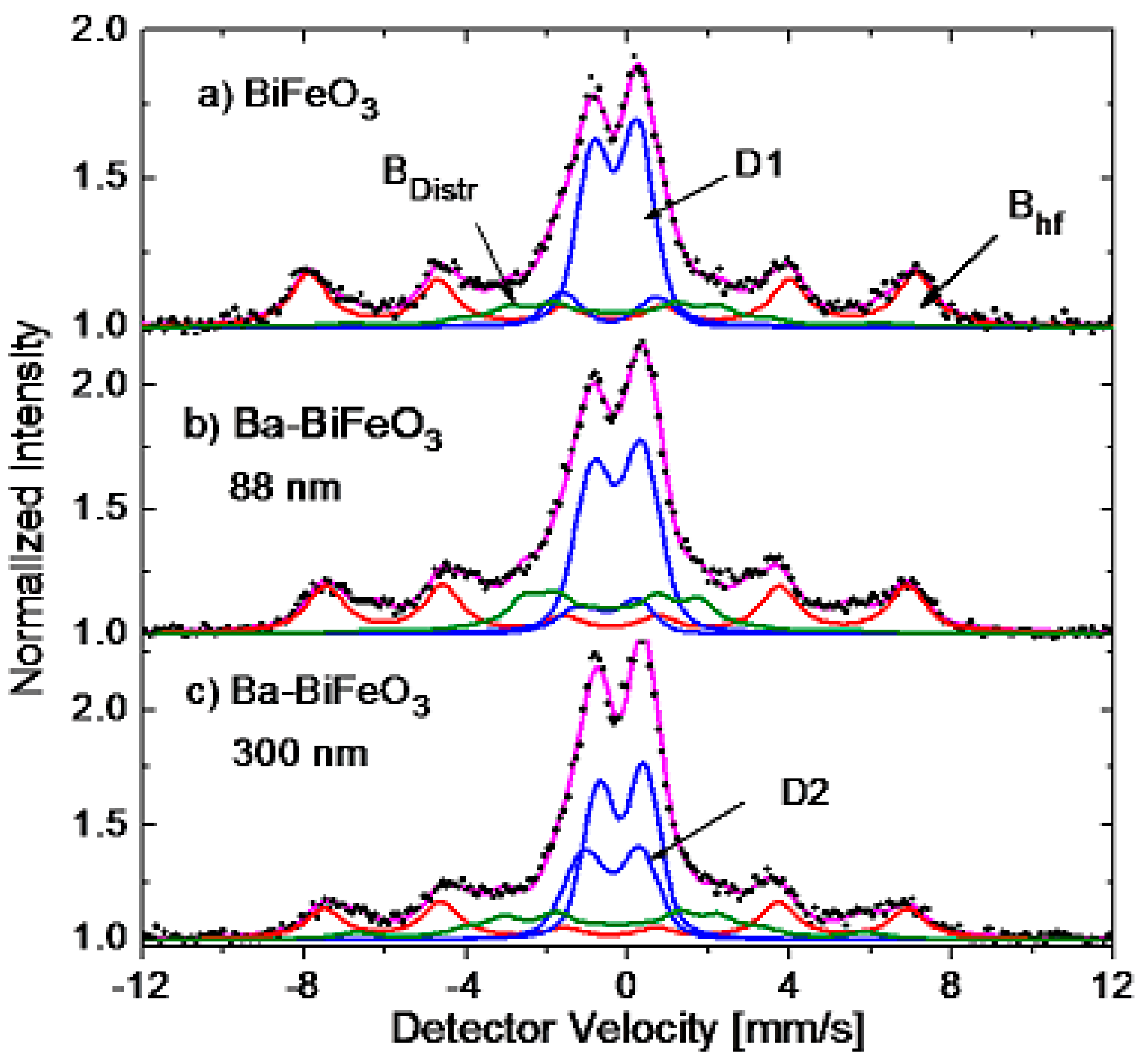

| Sample | Spectral Component | δ (mm/s) | ΔEQ/ε (mm/s) | Bhf (T) | Area Fraction (%) |
|---|---|---|---|---|---|
| BiFeO3 | D1 | 0.31(1) | 1.10(1) | - | 35(1) |
| D2 | 0.45(1) | 2.3(2) | - | 7(1) | |
| Bhf | 0.37(1) | 0.033(3) | 46.3(3) | 32(1) | |
| BDistr | 0.32(5) | 0.015(4) | 40-16 | 26(2) | |
| Ba-BiFeO3 88 nm | D1 | 0.45(6) | 1.66(2) | - | 7(1) |
| D2 | 0.26(1) | 1.20(1) | - | 35(1) | |
| Bhf | 0.35(1) | 0.14(2) | 44.5(9) | 30(1) | |
| BDistr | 0.42(4) | 0.04(5) | 37-13 | 29(2) | |
| Ba-BiFeO3300 nm | D1 | 0.38(3) | 1.38(4) | - | 19(1) |
| D2 | 0.16(1) | 1.12(1) | - | 29(1) | |
| Bhf | 0.37(2) | 0.15(3) | 44.6(2) | 21(1) | |
| BDistr | 0.35(4) | 0.12(5) | 39-16 | 31(2) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heiniger-Schell, J.; Bharuth-Ram, K.; Naicker, K.; Masondo, V.; Dang, T.T.; Escobar, M.; Díaz-Guerra, C.; Marschick, G.; Masenda, H.; Gunnlaugsson, H.P.; et al. Temperature Dependence of the Hyperfine Magnetic Field at Fe Sites in Ba-Doped BiFeO3 Thin Films Studied by Emission Mössbauer Spectroscopy. Crystals 2023, 13, 724. https://doi.org/10.3390/cryst13050724
Heiniger-Schell J, Bharuth-Ram K, Naicker K, Masondo V, Dang TT, Escobar M, Díaz-Guerra C, Marschick G, Masenda H, Gunnlaugsson HP, et al. Temperature Dependence of the Hyperfine Magnetic Field at Fe Sites in Ba-Doped BiFeO3 Thin Films Studied by Emission Mössbauer Spectroscopy. Crystals. 2023; 13(5):724. https://doi.org/10.3390/cryst13050724
Chicago/Turabian StyleHeiniger-Schell, Juliana, Krish Bharuth-Ram, Kimara Naicker, Vusumuzi Masondo, Thien Thanh Dang, Marianela Escobar, Carlos Díaz-Guerra, Georg Marschick, Hilary Masenda, Haraldur P. Gunnlaugsson, and et al. 2023. "Temperature Dependence of the Hyperfine Magnetic Field at Fe Sites in Ba-Doped BiFeO3 Thin Films Studied by Emission Mössbauer Spectroscopy" Crystals 13, no. 5: 724. https://doi.org/10.3390/cryst13050724
APA StyleHeiniger-Schell, J., Bharuth-Ram, K., Naicker, K., Masondo, V., Dang, T. T., Escobar, M., Díaz-Guerra, C., Marschick, G., Masenda, H., Gunnlaugsson, H. P., Qi, B., Unzueta, I., Ólafsson, S., Adhikari, R., Peters, G., Naidoo, D., Schaaf, P., Zyabkin, D., Johnston, K., ... Jakob, G. (2023). Temperature Dependence of the Hyperfine Magnetic Field at Fe Sites in Ba-Doped BiFeO3 Thin Films Studied by Emission Mössbauer Spectroscopy. Crystals, 13(5), 724. https://doi.org/10.3390/cryst13050724










