Band Broadening of Terahertz Photonic Crystals Circulator Using Two Symmetrical Hexagonal Aluminum Sheets
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Design of PC Circulator
2.3. Ultra-Wideband PBG of the PCs
3. Numerical Results for the Designed THz PC Circulator
3.1. Theoretical Model of PC Circulator
3.2. Numerical Simulations and Results
4. Discussion
5. Conclusions
- In order to improve the bandwidth of the PC circulator to meet the needs of the future terahertz communication systems, a novel ultra-wideband circulator is proposed by using two hexagonal metal sheets. Not only is the impedance of the circulator coarse-tuned by changing the radius of the circumscribing circle in the two hexagonal sheets, but it also can be fine-tuned by rotating the angle of the hexagonal metal sheets in the junction.
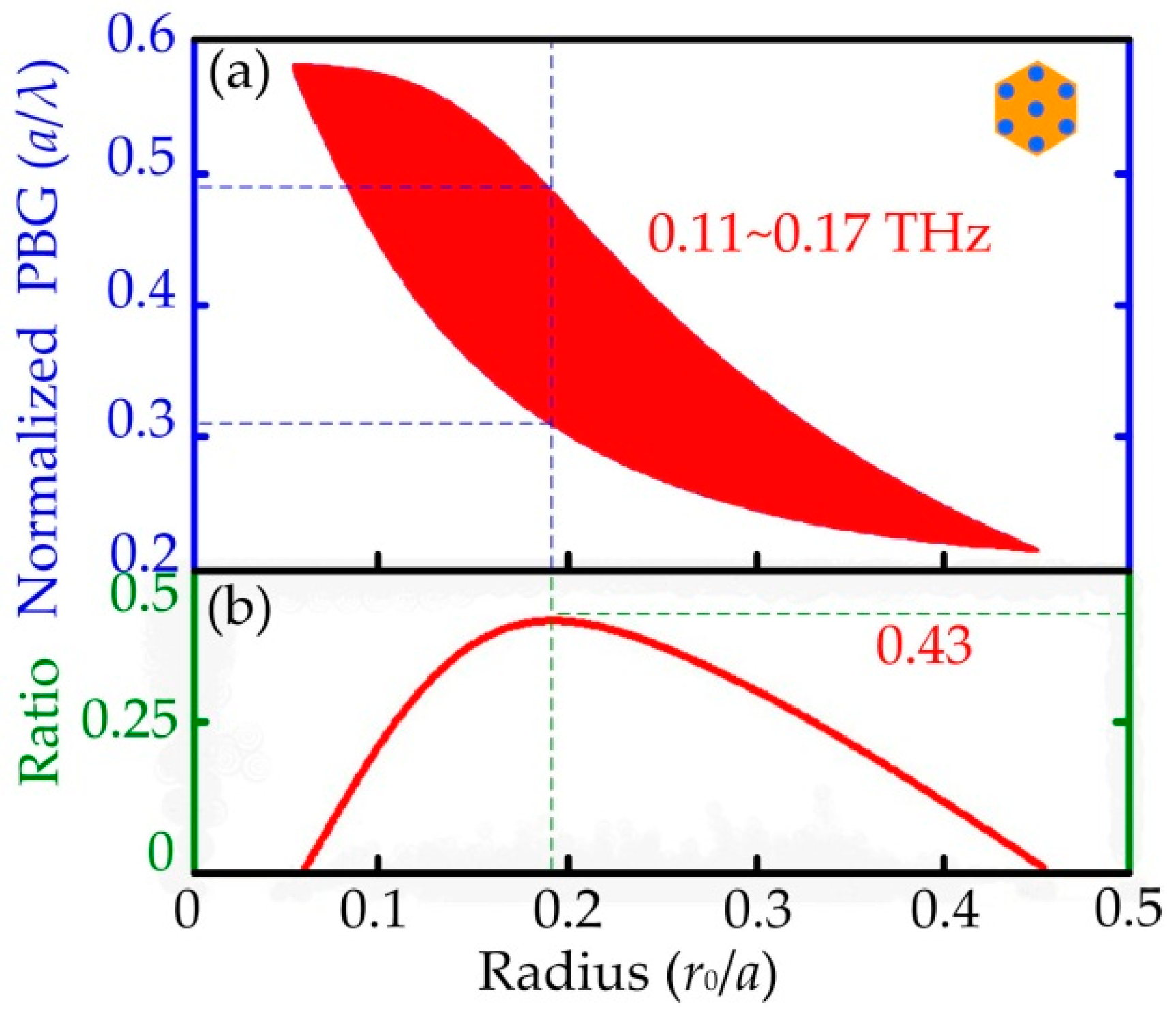
- Through adjusting the proportional relationship between the radius of the dielectric rods and the lattice constant to be 0.19, the PBG is optimized to be 0.11 to 0.17 THz via PWEM for the Al2O3 PCs.
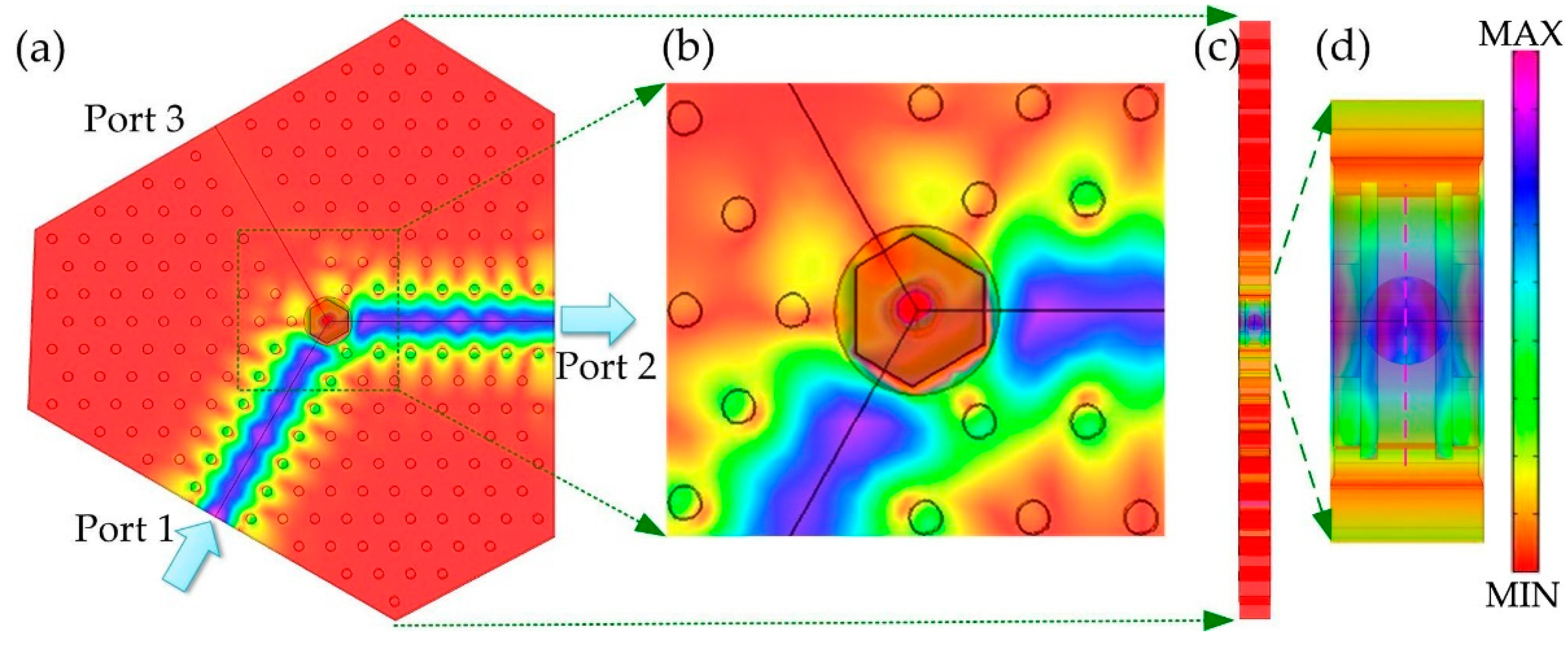
- The transmission of the THz signals for the PC circulator is simulated through FEM in the frequency domain of the PBG. At a central frequency of 0.144 THz, the transmission path of the THz wave is investigated in the designed circulator, and the power is evenly distributed in both hemispheres of the ferrite sphere.
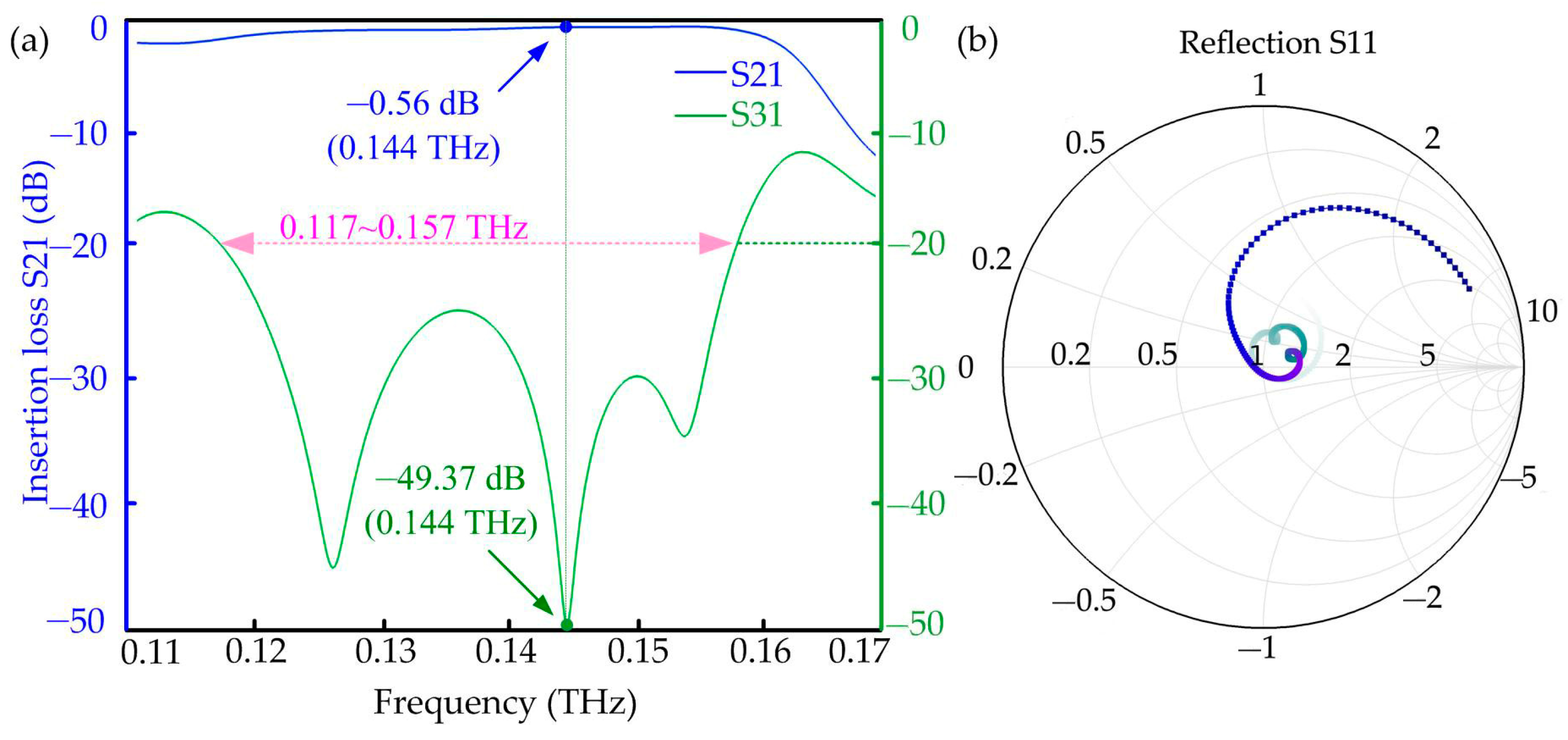
- When one side of the hexagon is perpendicular to the direction of propagation of the signal, the bandwidth of the circulator is assuredly extended to 40 GHz by using EMBM, in which the peak values of the insertion loss and isolation are 0.56 dB and 49.37 dB, respectively.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tonouchi, M. Cutting-edge terahertz technology. Nat. Photonics 2007, 1, 97–105. [Google Scholar] [CrossRef]
- Katyba, G.M.; Kurlov, V.N.; Zaytsev, K.I. Terahertz Photonic Crystal Waveguides Based on Sapphire Shaped Crystals. IEEE Trans. Terahertz Sci. Technol. 2016, 6, 576–582. [Google Scholar]
- Soltanian, M.; Amiri, I.S.; Alavi, S.E.; Ahmad, H. Dual-wavelength erbium-doped fiber laser to generate terahertz radiation using photonic crystal fiber. J. Light. Technol. 2015, 3, 5038–5046. [Google Scholar] [CrossRef]
- Campion, J.; Xenidis, N.; Smirnov, S.; Ivanov, R.; Oberhammer, J.; Hussainova, I. Ultra-wideband integrated graphene-based absorbers for terahertz waveguide systems. Adv. Electron. Mater. 2022, 9, 8. [Google Scholar] [CrossRef]
- European Vision for the 6G Network Ecosystem. Available online: https://5g-ppp.eu/wp-content/uploads/2021/06/WhitePaper-6G-Europe.pdf (accessed on 30 May 2021).
- Wang, Y.; Xu, B.G.; Zhang, D.G.; Xu, S.X.; Dong, Z.; Zeng, X.K.; Lu, X.W.; Pei, J.H. Magneto-optical isolator based on ultra-wideband photonic crystals waveguide for 5G communication. Crystals 2019, 9, 570. [Google Scholar] [CrossRef]
- Hiroyuki, T.; Sajeev, J. Compact optical one-way waveguide isolators for photonic-band-gap microchips. Phys. Rev. A 2008, 78, 023804. [Google Scholar]
- Liu, L.; Hesler, J.L.; Xu, H.; Lichtenberger, A.W.; Weikle, R.M. A broadband quasi-optical terahertz detector utilizing a zero bias schottky diode. IEEE Microw. Wirel. Compon. Lett. 2010, 20, 504–506. [Google Scholar] [CrossRef]
- Spagnolo, V.; Patimisco, P.; Pennetta, R. THz Quartz-enhanced photoacoustic sensor for H2S trace gas detection. Opt. Express 2015, 23, 7574–7582. [Google Scholar] [CrossRef]
- Deal, W.R.; Mei, X.B.; Radisic, V. Demonstration of a 0.48 THz amplifier module using InP HEMT transistors. IEEE Microw. Wirel. Compon. Lett. 2010, 20, 289–291. [Google Scholar] [CrossRef]
- Wang, P.Y.; Lai, Y.C.; Cheng, Y.C. Spatial beam filtering with auto-cloned photonic crystals. Crystals 2019, 9, 585. [Google Scholar] [CrossRef]
- Bruyant, A.; Lérondel, G.; Reece, P.J.; Gal, M. Allsilicon omnidirectional mirrors based on one-dimensional photonic crystals. Appl. Phys. Lett. 2003, 82, 3227–3229. [Google Scholar] [CrossRef]
- Happ, T.D.; Markard, A.; Kamp, M. InP-based short cavity lasers with 2D photonic crystal mirror. Electron. Lett. 2001, 37, 428–429. [Google Scholar] [CrossRef]
- Jao, R.F.; Lin, M.C. Quantitative analysis of photon density of states for one-dimensional photonic crystals in a rectangular waveguide. Crystals 2019, 9, 576. [Google Scholar] [CrossRef]
- Chutinan, A.; Okano, M.; Noda, S. Waveguides and waveguide bends in two-dimensional photonic crystal slabs. Appl. Phys. Lett. 2002, 80, 1698–1700. [Google Scholar] [CrossRef]
- Duan, S.Q.; Chen, Y.P.; Li, G.Z.; Zhu, C.Y.; Chen, X.F. Broadband polarization beam splitter based on a negative refractive lithium niobate photonic crystal slab. Chin. Opt. Lett. 2016, 14, 042301–042304. [Google Scholar] [CrossRef]
- Kato, H.; Matsushita, T.; Takayama, A.; Egawa, M.; Nishimura, K.; Inoue, M. Properties of one-dimensional magnetophotonic crystals for use in optical isolator devices. IEEE Trans. Magn. 2002, 28, 3246–3248. [Google Scholar] [CrossRef]
- Fang, K.; Yu, Z.; Liu, V.; Fan, S. Ultracompact nonreciprocal optical isolator based on guided resonance in a magneto-optical photonic crystal slab. Opt. Lett. 2011, 36, 4254–4256. [Google Scholar] [CrossRef]
- Pligovka, A.; Poznyak, A.; Norek, M. Optical Properties of Porous Alumina Assisted Niobia Nanostructured Films–Designing 2-D Photonic Crystals Based on Hexagonally Arranged Nanocolumns. Micromachines 2021, 12, 589. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, D.; Wang, Y.; Hong, B.; Shu, G.; He, W. A Terahertz Circulator Based on Magneto Photonic Crystal Slab. Photonics 2023, 10, 360. [Google Scholar] [CrossRef]
- Jin, C.; Cheng, B.; Li, Z. Two-dimensional metallic photonic crystal in the THz range. Opt. Commun. 1999, 166, 9–13. [Google Scholar] [CrossRef]
- Hasanuzzaman, G.; Rana, S.; Habib, M.S. A novel low loss, highly birefringent photonic crystal fiber in THz regime. IEEE Photonics Technol. Lett. 2016, 28, 899–902. [Google Scholar] [CrossRef]
- Letizia, R.; Mineo, M.; Paoloni, C. Photonic crystal-structures for THz vacuum electron devices. IEEE Trans. Electron. Devices 2014, 62, 178–183. [Google Scholar] [CrossRef]
- Jin, G.; Ren, Y.; Tang, B. Numerical simulations of circular dichroism and polarization conversion in VO2-based terahertz metamaterials. Crystals 2023, 13, 437. [Google Scholar] [CrossRef]
- Fan, F.; Chang, S.J.; Niu, C.; Hou, Y.; Wang, X.H. Magnetically tunable silicon ferrite photonic crystals for terahertz circulator. Opt. Commun. 2012, 285, 3763–3769. [Google Scholar] [CrossRef]
- Dmitriev, V.; Portela, G.; Martins, L. Photonic crystal-based circulators with three and four ports for sub-terahertz region. Photonic Netw. Commun. 2017, 33, 303–312. [Google Scholar] [CrossRef]
- Wang, Q.; Ouyang, Z.B. Multiport photonic crystal circulators created by cascading magneto-optical cavities. Opt. Soc. Am. B 2011, 28, 703–708. [Google Scholar] [CrossRef]
- Dmitriev, V.; Kawakatsu, M.N.; Souza, F.J.M. Compact three-port optical two-dimensional photonic crystal-based circulator of W-format. Opt. Lett. 2012, 37, 3192–3194. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Fan, S.H. Optical circulators in two-dimensional magneto-optical photonic crystals. Opt. Lett. 2005, 15, 1989–1991. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, D.G.; Xu, B.G.; He, W.L.; Ian, H. Ultra-wideband terahertz circulator with a ferrite-sphere filled triangle photonic crystal. Mater. Sci. Eng. B 2022, 277, 115603. [Google Scholar] [CrossRef]
- Zhang, D.G.; Yung, E.K.N.; Yang, S.W.; Liu, S.Z. 8mm T-junction waveguide circulator with a ferrite sphere. IEE Electron. Lett. 1995, 31, 2185–2187. [Google Scholar] [CrossRef]
- Piotrowski, W.S.; Raue, J.E. Low-loss broad-band EHF circulator. IEEE Trans. Microw. Theory Tech. 2003, 24, 863–866. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, D.G.; Xu, S.X.; Xu, B.G.; Dong, Z.; Huang, T. Experimental evidence of photonic crystal waveguide with wide bandwidth in two-dimensional Al2O3 rods-array. Chin. Opt. Lett. 2017, 15, 062301. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, D.G.; Xu, S.X.; Xu, B.G.; Dong, Z. H-plane cross-shaped waveguide circulator in magneto-photonic crystals with five ferrite posts. Chin. Opt. Lett. 2017, 15, 111601. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Xu, B.; Chang, K.; Huang, H.; Xu, Z.; He, W.; Wang, W. Band Broadening of Terahertz Photonic Crystals Circulator Using Two Symmetrical Hexagonal Aluminum Sheets. Crystals 2023, 13, 779. https://doi.org/10.3390/cryst13050779
Wang Y, Xu B, Chang K, Huang H, Xu Z, He W, Wang W. Band Broadening of Terahertz Photonic Crystals Circulator Using Two Symmetrical Hexagonal Aluminum Sheets. Crystals. 2023; 13(5):779. https://doi.org/10.3390/cryst13050779
Chicago/Turabian StyleWang, Yong, Biaogang Xu, Kaiming Chang, Hongwei Huang, Zhuozi Xu, Wenlong He, and Wenli Wang. 2023. "Band Broadening of Terahertz Photonic Crystals Circulator Using Two Symmetrical Hexagonal Aluminum Sheets" Crystals 13, no. 5: 779. https://doi.org/10.3390/cryst13050779
APA StyleWang, Y., Xu, B., Chang, K., Huang, H., Xu, Z., He, W., & Wang, W. (2023). Band Broadening of Terahertz Photonic Crystals Circulator Using Two Symmetrical Hexagonal Aluminum Sheets. Crystals, 13(5), 779. https://doi.org/10.3390/cryst13050779





