Phase Field Modeling of Crack Growth with Viscoplasticity
Abstract
1. Introduction
2. Viscoplastic Phase Field Model
2.1. Viscoplastic Constitutive
2.2. Viscoplastic Phase Field Model
2.3. Implicit Integration for Viscoplasticity
2.4. Numerical Implementation
3. Numerical Examples
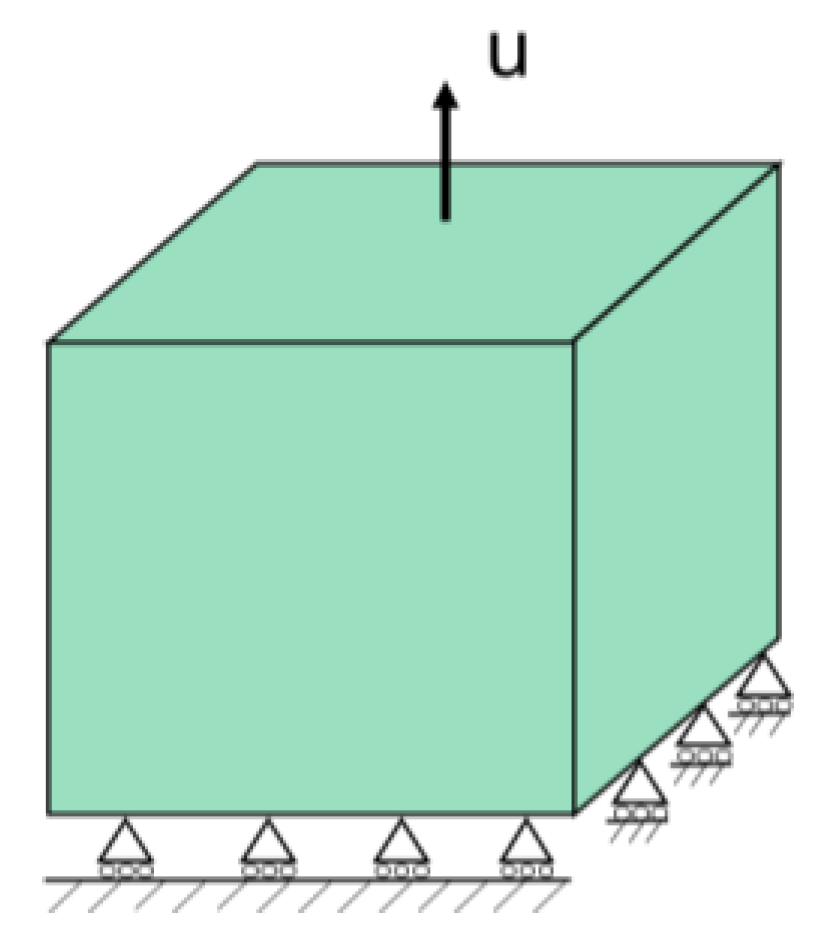
3.1. One-Dimensional Viscoplastic Test
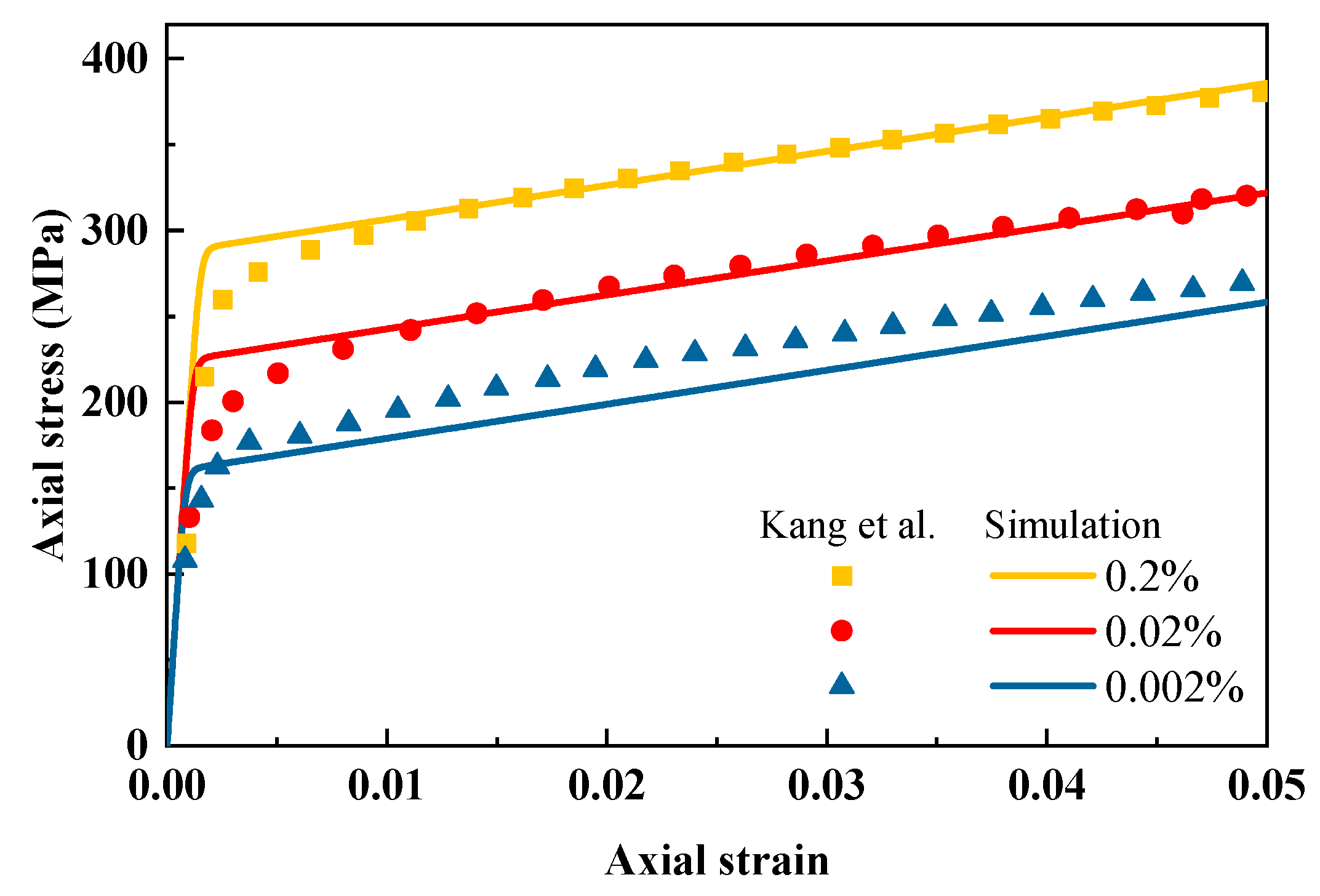
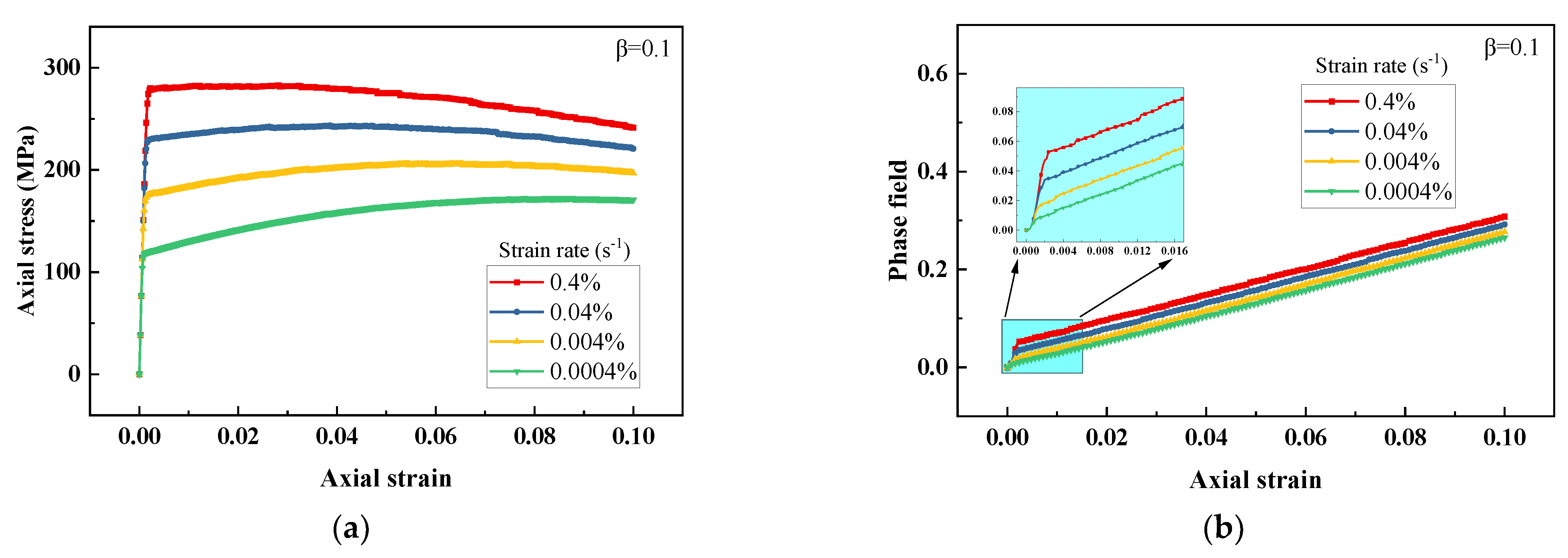
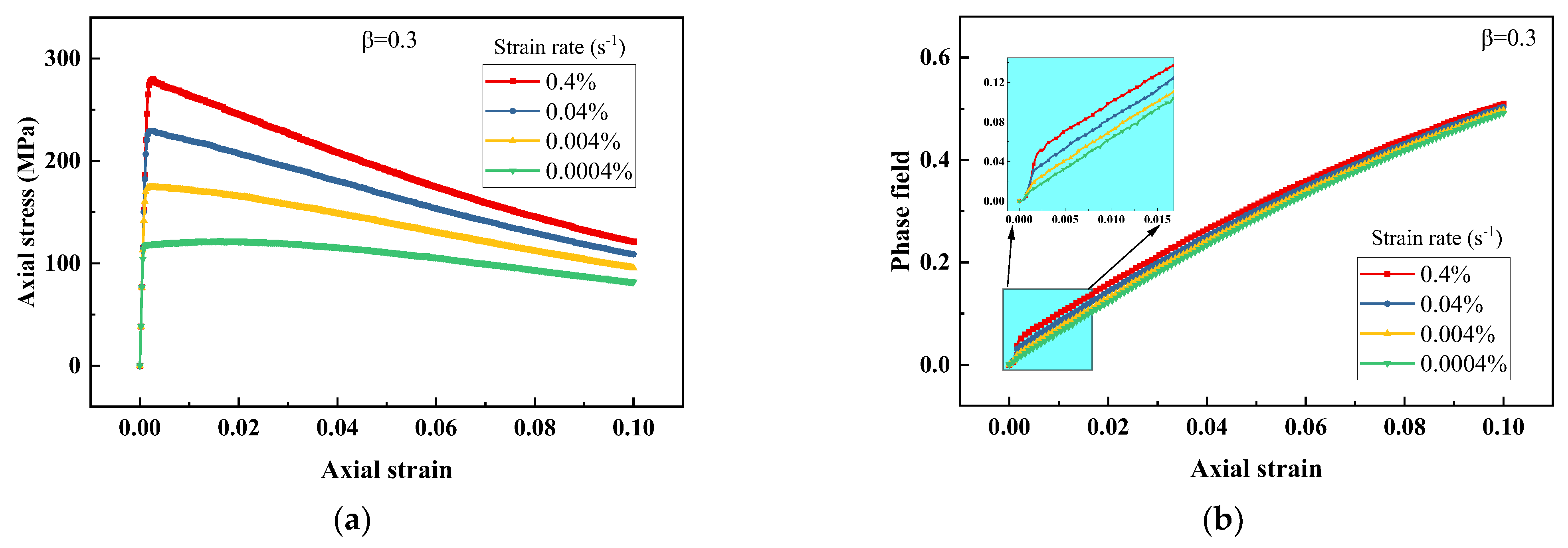
3.1.1. Strain Rate Test
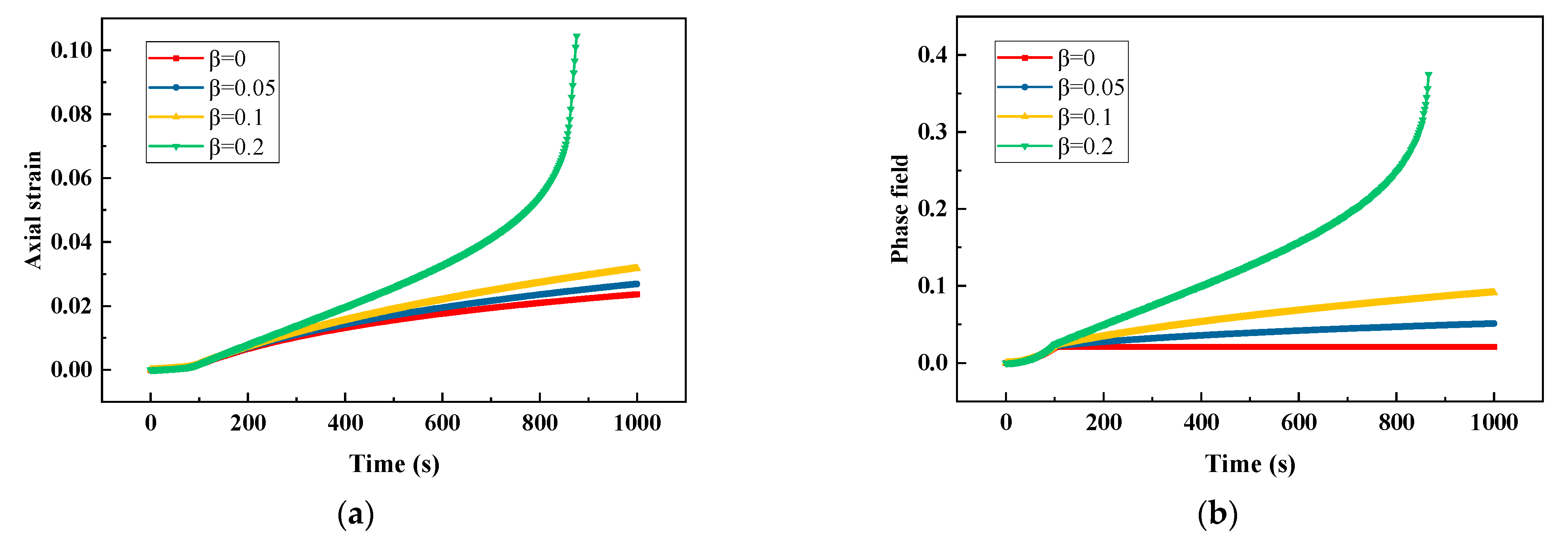
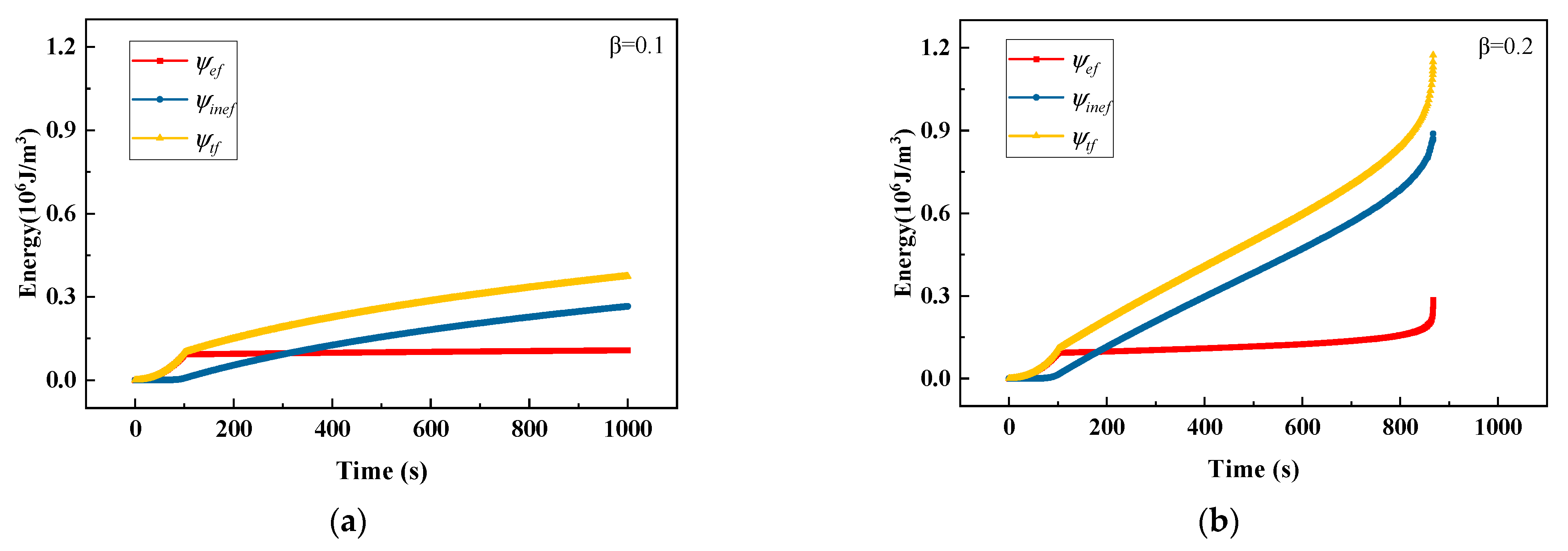
3.1.2. Creep Test
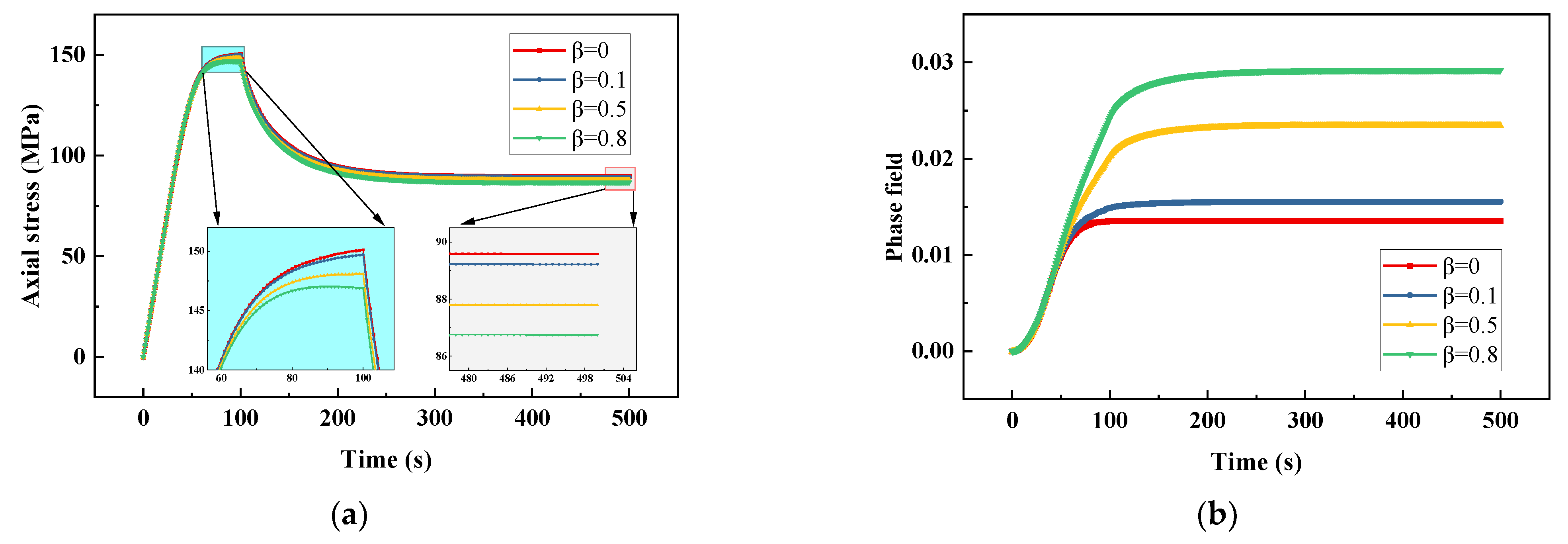
3.1.3. Stress Relaxation Test
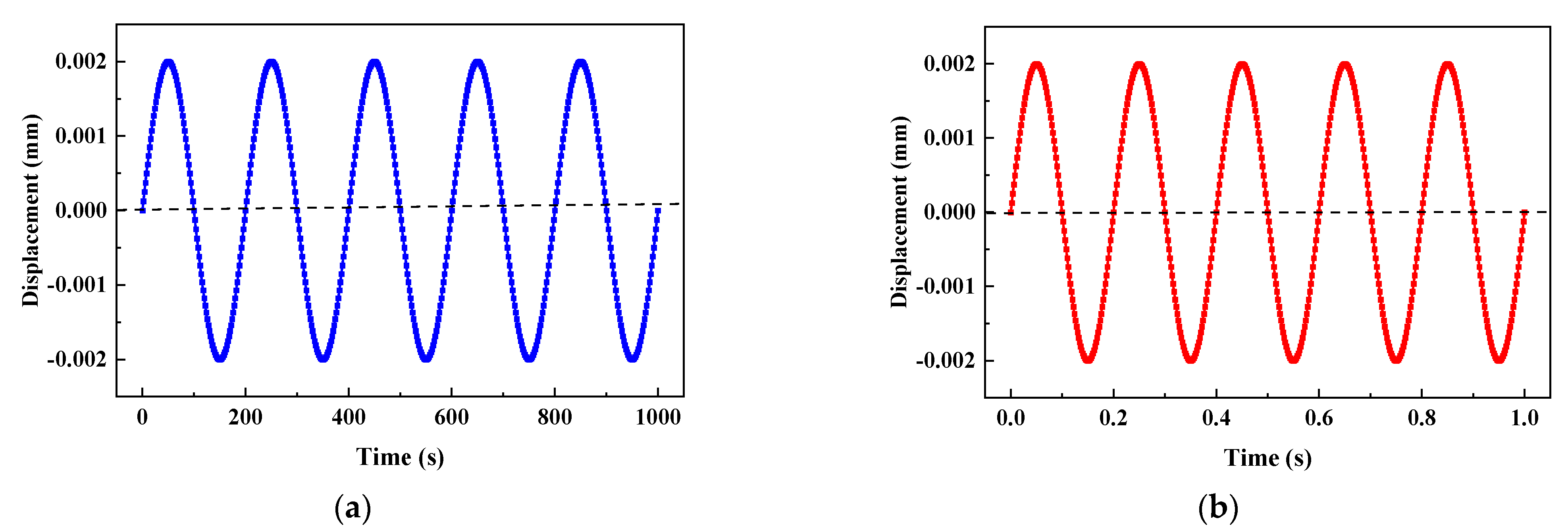
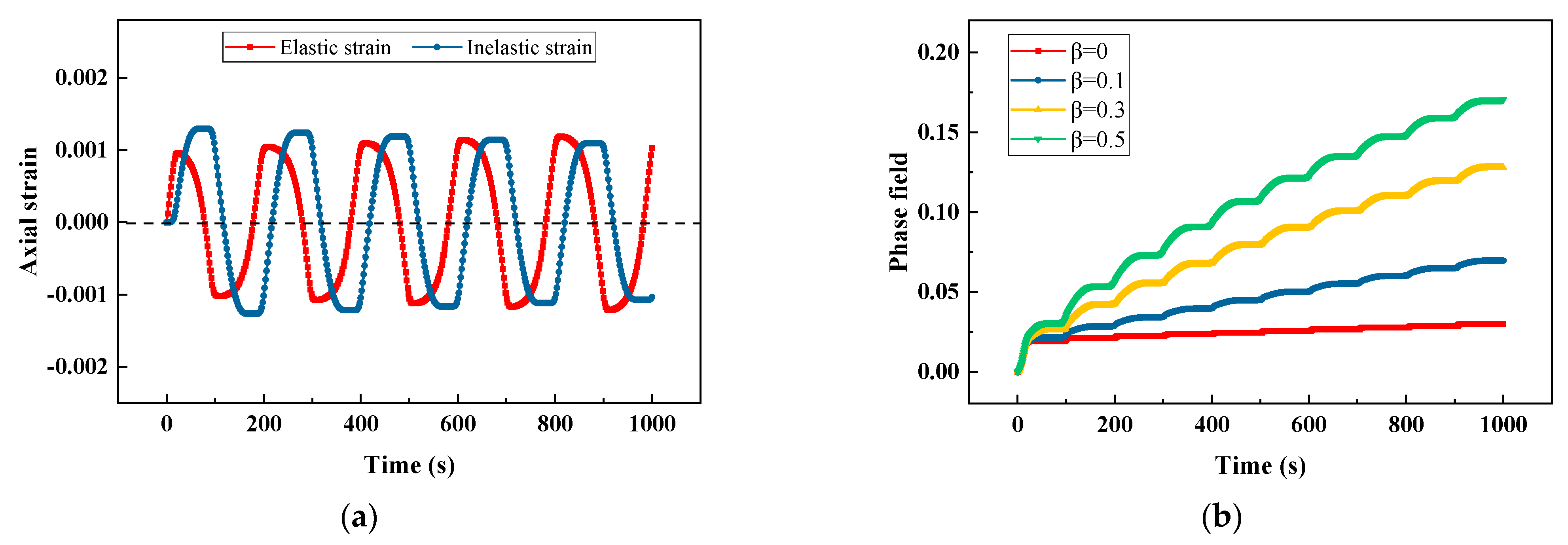
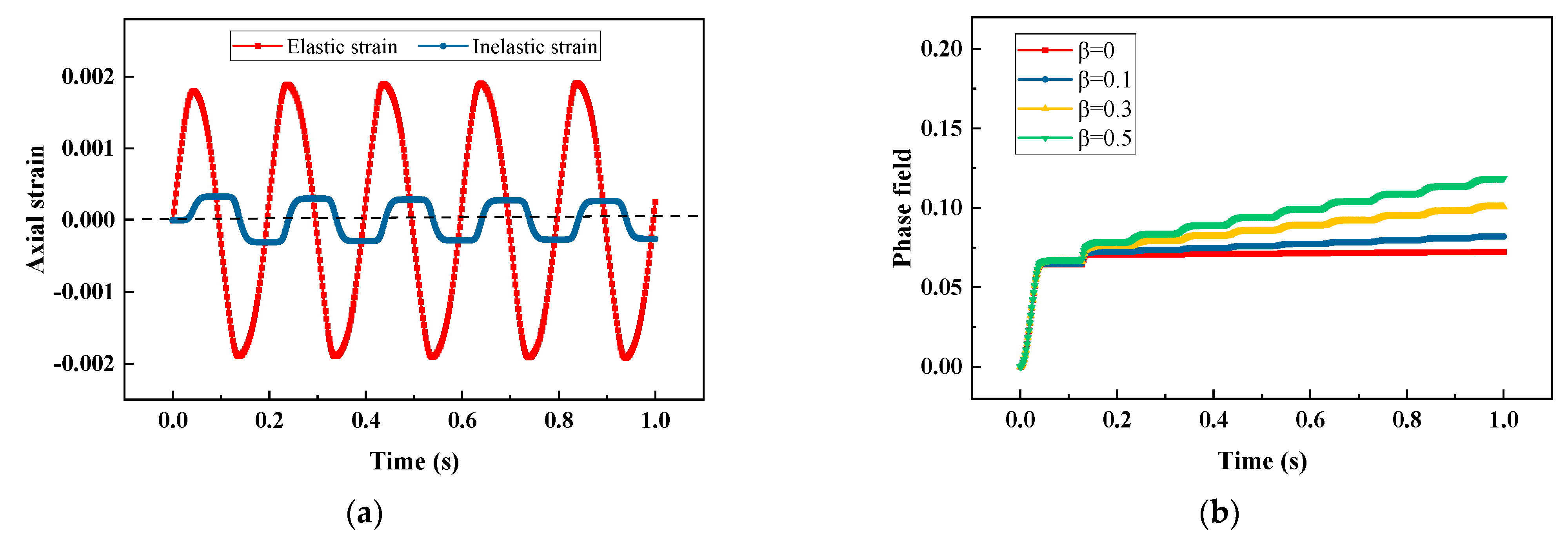
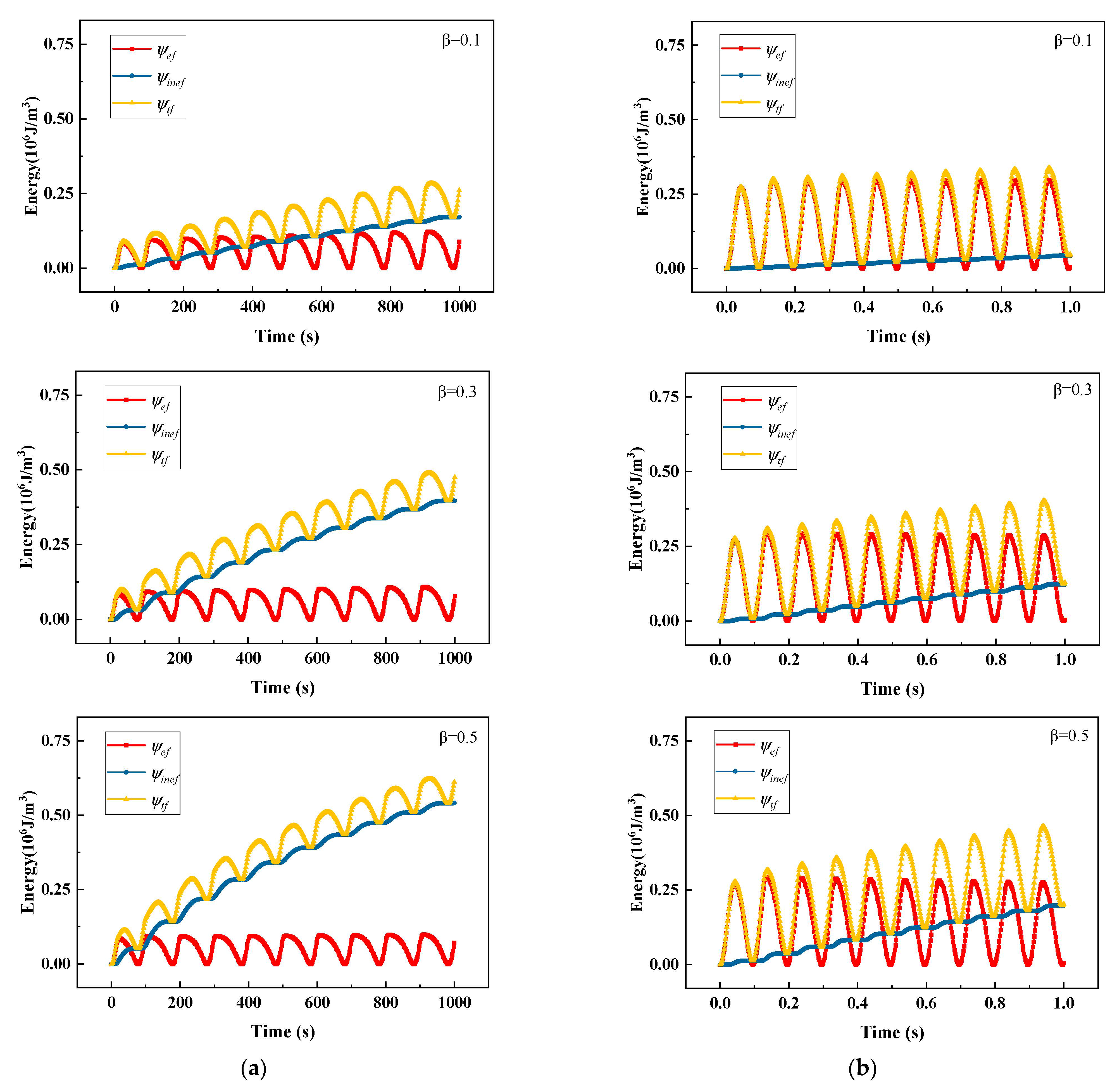
3.1.4. Cyclic Load Test
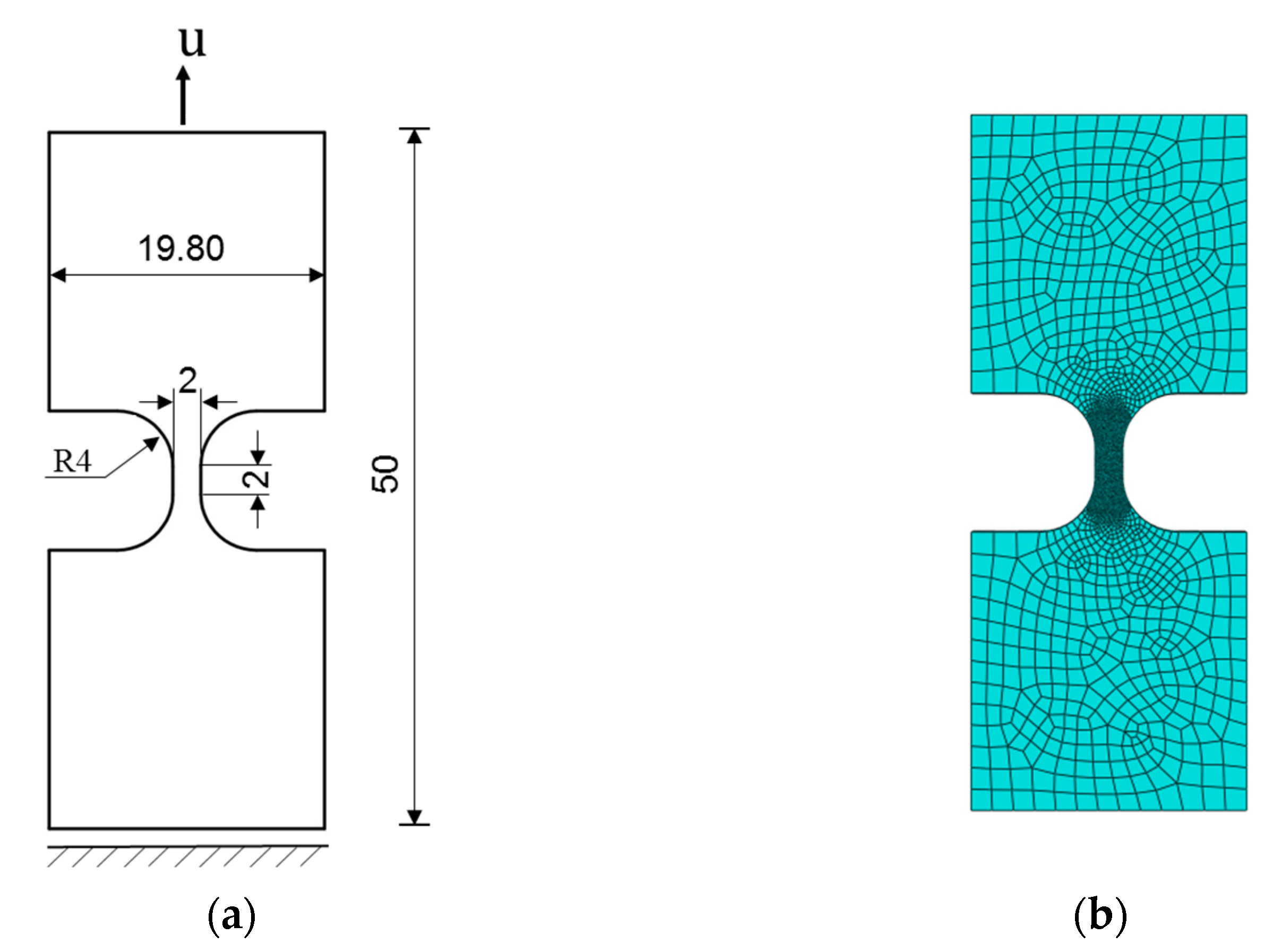
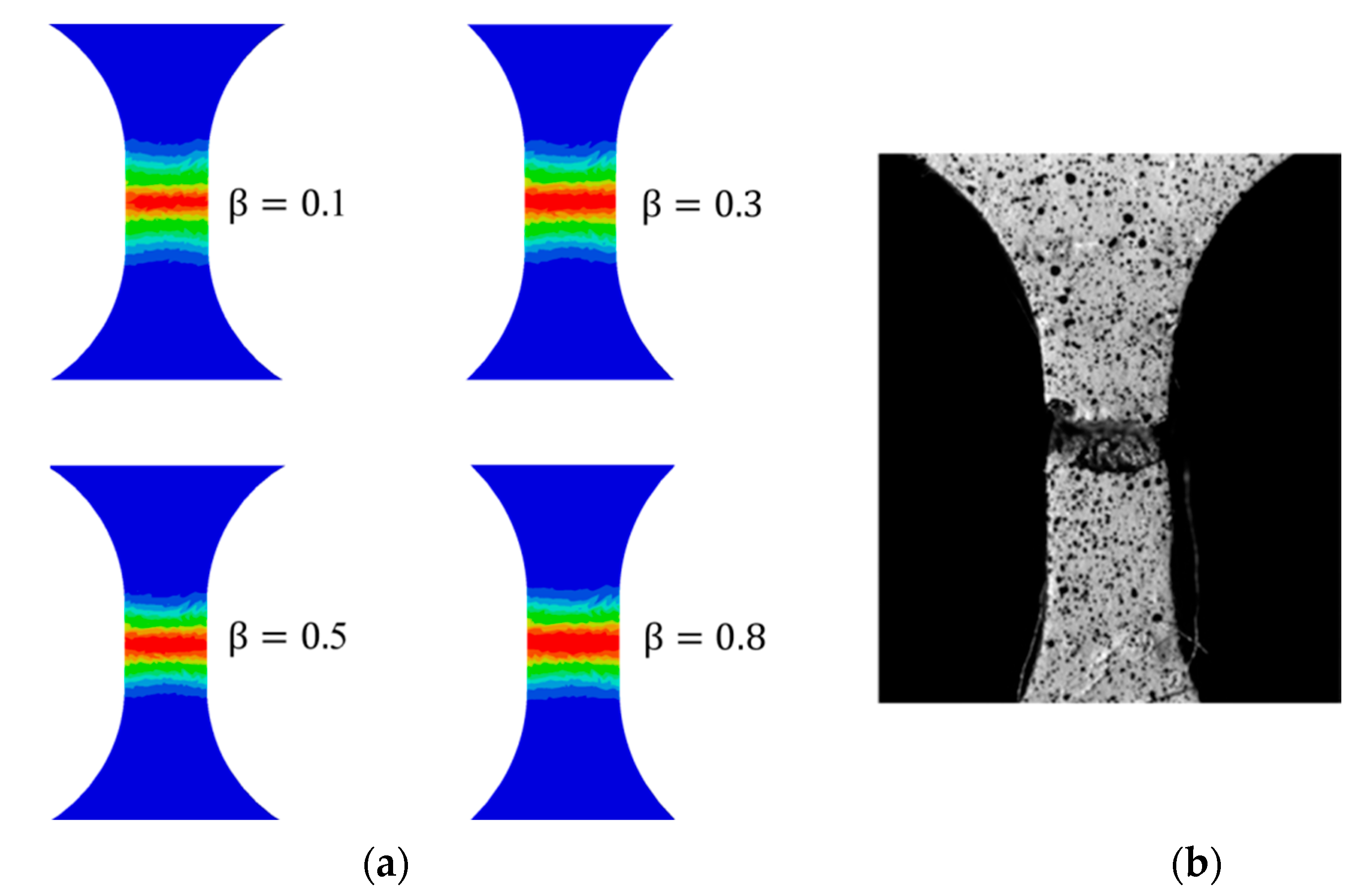
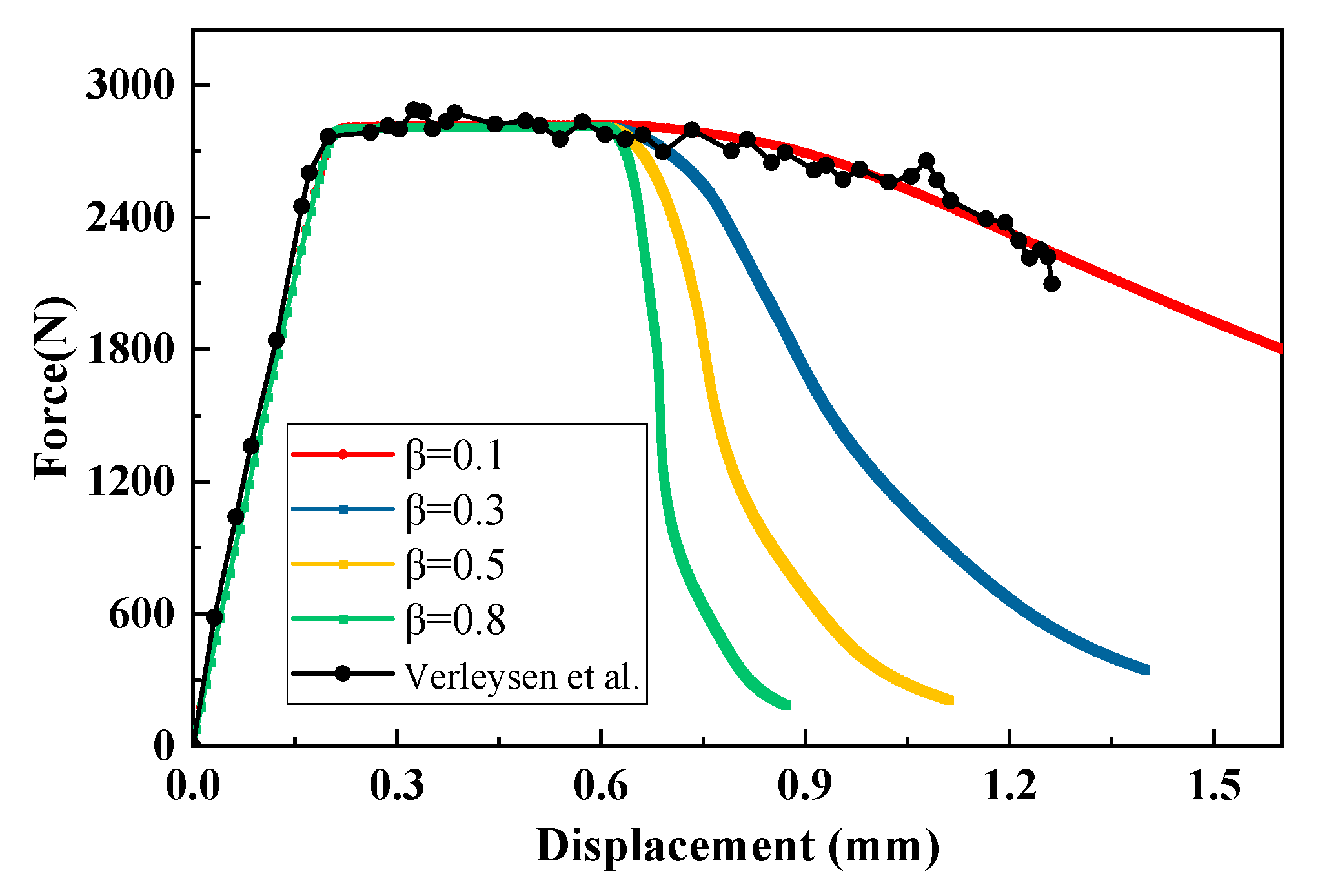
3.2. Stainless-Steel Plate Tensile Test
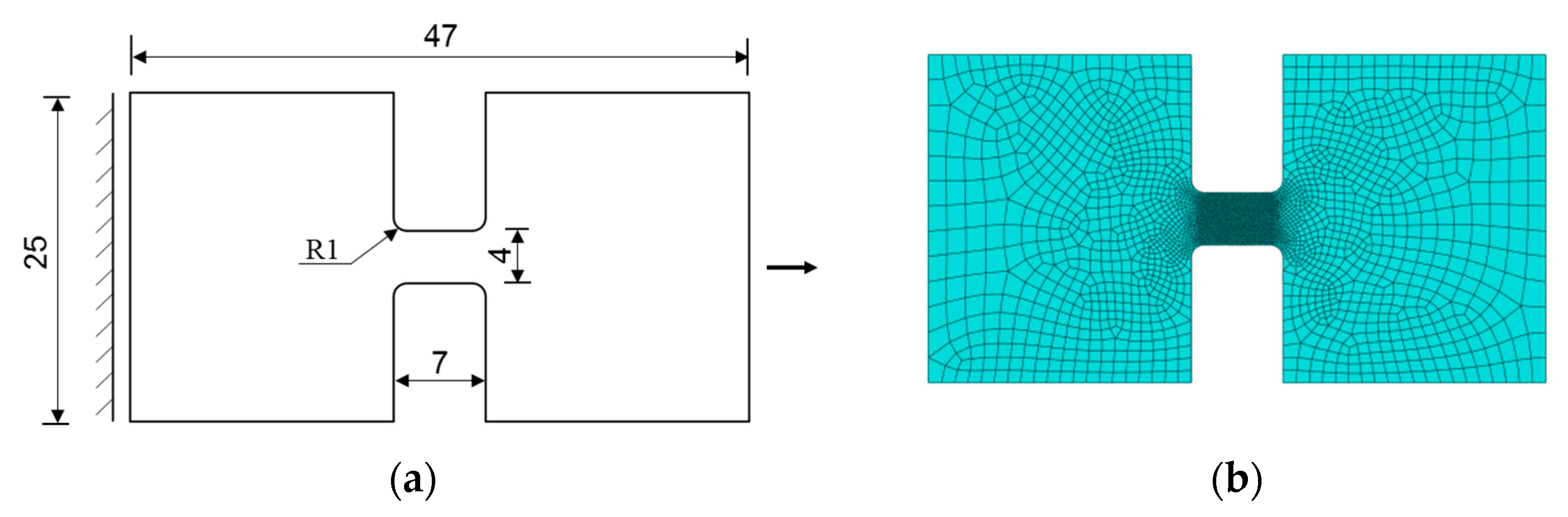
3.3. Titanium Alloy Plate Tensile Test
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A, B | model parameters of sinh-type viscoplastic constitutive |
| gradient operators of the shape functions | |
| displacement field | |
| degraded stress tensors | |
| undegraded stress tensors | |
| von-Mises stress | |
| uniaxial stress considering viscoplasticity | |
| initial yield stress | |
| trial stress | |
| trial stress tensor | |
| deviatoric stress tensor | |
| effective inelastic strain rate | |
| equivalent inelastic strain increment | |
| total strain increment tensor | |
| elastic strain increment tensor | |
| inelastic strain increment tensor | |
| hardening stress | |
| d | phase field |
| elastic stiffness matrix | |
| yield function | |
| G | shear modulus |
| critical energy release rate | |
| K, m | viscous material constants |
| length scale | |
| stiffness degradation function | |
| shape functions associated with node i | |
| tangent stiffness matrix | |
| identity tensor | |
| residual forms of the nodal displacement and phase field variables | |
| energy density threshold | |
| total strain rate tensor | |
| elastic strain rate tensor | |
| inelastic strain tensors | |
| weight factor of inelastic energy | |
| Lame constant | |
| gradient operator | |
| elastic strain energy density | |
| inelastic strain energy density | |
| elastic crack driving energy | |
| inelastic crack driving energy | |
| total crack driving energy | |
| an arbitrary domain | |
| external boundary | |
| discrete crack set | |
| total energy history field | |
| elastic energy history field | |
| functional form of equivalent inelastic strain rate | |
References
- Ambati, M.; Gerasimov, T.; De Lorenzis, L. Phase-field modeling of ductile fracture. Comput. Mech. 2015, 55, 1017–1040. [Google Scholar] [CrossRef]
- Zhou, F.; Molinari, J.F. Dynamic crack propagation with cohesive elements: A methodology to address mesh dependency. Int. J. Numer. Methods Eng. 2004, 59, 1–24. [Google Scholar] [CrossRef]
- Peng, G.L.; Wang, Y.H. A Node Split Method for Crack Growth Problem. In Applied Mechanics and Materials; Trans. Tech. Publications Ltd.: Stafa-Zurich, Switzerland, 2012; Volume 182–183, pp. 1524–1528. [Google Scholar] [CrossRef]
- Azevedo, N.M.; Lemos, J. Hybrid discrete element/finite element method for fracture analysis. Comput. Methods Appl. Mech. Eng. 2006, 195, 4579–4593. [Google Scholar] [CrossRef]
- Fang, J.; Wu, C.; Li, J.; Liu, Q.; Wu, C.; Sun, G. Phase field fracture in elasto-plastic solids: Variational formulation for multi-surface plasticity and effects of plastic yield surfaces and hardening. Int. J. Mech. Sci. 2019, 156, 382–396. [Google Scholar] [CrossRef]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Meth. Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Moës, N.; Gravouil, A.; Belytschko, T. Non-planar 3D crack growth by the extended finite element and level sets-Part I: Mechanical model. Int. J. Numer. Methods Eng. 2002, 53, 2549–2568. [Google Scholar] [CrossRef]
- Mueller, R.; Maugin, G.A. On material forces and finite element discretizations. Comput. Mech. 2002, 29, 52–60. [Google Scholar] [CrossRef]
- Miehe, C.; Gürses, E.; Birkle, M. A computational framework of configurational-force-driven brittle fracture based on incremental energy minimization. Int. J. Fract. 2007, 145, 245–259. [Google Scholar] [CrossRef]
- Fang, J.; Wu, C.; Rabczuk, T.; Wu, C.; Ma, C.; Sun, G.; Li, Q. Phase field fracture in elasto-plastic solids: Abaqus implementation and case studies. Theor. Appl. Fract. Mech. 2019, 103, 102252. [Google Scholar] [CrossRef]
- Tvergaard, V.; Needleman, A. Analysis of the cup-cone fracture in a round tensile bar. Acta Met. 1984, 32, 157–169. [Google Scholar] [CrossRef]
- Lemaitre, J. A Continuous damage mechanics model for ductile fracture. ASME J. Eng. Mater. Technol. 1985, 107, 83–89. [Google Scholar] [CrossRef]
- Peerlings, R.; Borst, R.; Brekelmans, W.; Vree, J.; Spee, I. Some observations on localisation in non-local and gradient damage models. Eur. J. Mech. A Solids 1996, 15, 937–953. [Google Scholar]
- Ambati, M.; Kruse, R.; De Lorenzis, L. A phase-field model for ductile fracture at finite strains and its experimental verification. Comput. Mech. 2016, 57, 149–167. [Google Scholar] [CrossRef]
- Oh, Y.-R.; Nam, H.-S.; Kim, Y.-J.; Miura, N. Application of the GTN model to ductile crack growth simulation in through-wall cracked pipes. Int. J. Press. Vessel. Pip. 2018, 159, 35–44. [Google Scholar] [CrossRef]
- Griffith, A.A. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. Lond. Ser. A 1921, 221, 163–198. [Google Scholar]
- Francfort, G.A.; Marigo, J.-J. Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 1998, 46, 1319–1342. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.A.; Marigo, J.-J. Numerical experiments in revisited brittle fracture. J. Mech. Phys. Solids 2000, 48, 797–826. [Google Scholar] [CrossRef]
- Shi, Q.; Yu, H.; Guo, L.; Hao, L.; Huang, K. A phase field model with plastic history field for fracture of elasto-plastic materials. Eng. Fract. Mech. 2022, 268, 108447. [Google Scholar] [CrossRef]
- Shen, R.; Waisman, H.; Guo, L. Fracture of viscoelastic solids modeled with a modified phase field method. Comput. Methods Appl. Mech. Eng. 2019, 346, 862–890. [Google Scholar] [CrossRef]
- Yin, B.; Kaliske, M. Fracture simulation of viscoelastic polymers by the phase-field method. Comput. Mech. 2020, 65, 293–309. [Google Scholar] [CrossRef]
- Huang, K.; Yan, J.; Shen, R.; Wan, Y.; Li, Y.; Ge, H.; Yu, H.; Guo, L. Investigation on fracture behavior of polymer-bonded explosives under compression using a viscoelastic phase-field fracture method. Eng. Fract. Mech. 2022, 266, 108411. [Google Scholar] [CrossRef]
- Dammaß, F.; Ambati, M.; Kästner, M. A unified phase-field model of fracture in viscoelastic materials. Contin. Mech. Thermodyn. 2021, 33, 1907–1929. [Google Scholar] [CrossRef]
- Valverde-González, A.; Reinoso, J.; Jha, N.K.; Merodio, J.; Paggi, M. A phase field approach to fracture for hyperelastic and visco-hyperelastic materials applied to pre-stressed cylindrical structures. Mech. Adv. Mater. Struct. 2022, 29, 1–20. [Google Scholar] [CrossRef]
- Hojjat, B.; Elahe, E.; Mohammed, M. A phase field model for rate-dependent ductile fracture. Metals 2017, 7, 180. [Google Scholar]
- Gmati, H. Phase Field Modelling of Fracture of Elastic and Elasto-Viscoplastic Solid Materials. Ph.D. Thesis, HESAM Université, Paris, France, 2020. [Google Scholar]
- Wang, M.; Yu, Z.; Shen, W.; Shao, J. Numerical study of time-dependent deformation and cracking in brittle rocks with phase-field method and application to slope instability analysis. Int. J. Rock Mech. Min. Sci. 2022, 155, 105144. [Google Scholar] [CrossRef]
- Hai, L.; Li, J. A rate-dependent phase-field framework for the dynamic failure of quasi-brittle materials. Eng. Fract. Mech. 2021, 252, 107847. [Google Scholar] [CrossRef]
- Xie, Q.; Qi, H.; Li, S.; Yang, X.; Shi, D.; Li, F. Phase-field fracture modeling for creep crack. Theor. Appl. Fract. Mech. 2023, 124, 103798. [Google Scholar] [CrossRef]
- Arash, B.; Exner, W.; Rolfes, R. A finite deformation phase-field fracture model for the thermo-viscoelastic analysis of polymer nanocomposites. Comput. Methods Appl. Mech. Eng. 2021, 381, 113821. [Google Scholar] [CrossRef]
- Arash, B.; Wibke, E.; Raimund, R. Effect of moisture on the nonlinear viscoelastic fracture behavior of polymer nanocompsites: A finite deformation phase-field model. Eng. Comput. 2023, 39, 773–790. [Google Scholar] [CrossRef]
- Ullah, A.; ZeinEldin, R.A.; Khalifa, H.A.E.-W. Investigation of the Three-Dimensional Hybrid Casson Nanofluid Flow: A Cattaneo–Christov Theory. ACS Omega 2023, 8, 10991–11002. [Google Scholar] [CrossRef]
- ZeinEldin, R.A.; Ullah, A.; Khalifa, H.A.E.-W.; Ayaz, M. Analytical Study of the Energy Loss Reduction during Three-Dimensional Engine Oil-Based Hybrid Nanofluid Flow by Using Cattaneo–Christov Model. Symmetry 2023, 15, 166. [Google Scholar] [CrossRef]
- Borden, M.J.; Hughes, T.J.; Landis, C.M.; Anvari, A.; Lee, I.J. A phase-field formulation for fracture in ductile materials: Finite deformation balance law derivation, plastic degradation, and stress triaxiality effects. Comput. Methods Appl. Mech. Eng. 2016, 312, 130–166. [Google Scholar] [CrossRef]
- Dunne, F. Introduction to Computational Plasticity; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Amor, H.; Marigo, J.-J.; Maurini, C. Regularized formulation of the variational brittle fracture with unilateral contact: Numerical experiments. J. Mech. Phys. Solids 2009, 57, 1209–1229. [Google Scholar] [CrossRef]
- Liu, G.; Li, Q.; Msekh, M.A.; Zuo, Z. Abaqus implementation of monolithic and staggered schemes for quasi-static and dynamic fracture phase-field model. Comput. Mater. Sci. 2016, 121, 35–47. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Bourdin, B. Numerical implementation of the variational formulation for quasi-static brittle fracture. Interfaces Free Boundaries 2007, 9, 411–430. [Google Scholar] [CrossRef]
- Burke, S.; Ortner, C.; Süli, E. An adaptive finite element approximation of a variational model of brittle fracture. SIAM J. Numer. Anal. 2010, 48, 980–1012. [Google Scholar] [CrossRef]
- Brun, M.K.; Wick, T.; Berre, I.; Nordbotten, J.M.; Radu, F.A. An iterative staggered scheme for phase field brittle fracture propagation with stabilizing parameters. Comput. Methods Appl. Mech. Eng. 2020, 361, 112752. [Google Scholar] [CrossRef]
- Jeong, H.; Signetti, S.; Han, T.-S.; Ryu, S. Phase field modeling of crack propagation under combined shear and tensile loading with hybrid formulation. Comput. Mater. Sci. 2018, 155, 483–492. [Google Scholar] [CrossRef]
- Msekh, M.A.; Sargado, J.M.; Jamshidian, M.; Areias, P.M.; Rabczuk, T. Abaqus implementation of phase-field model for brittle fracture. Comput. Mater. Sci. 2015, 96, 472–484. [Google Scholar] [CrossRef]
- Kang, G.; Kan, Q. Constitutive modeling for uniaxial time-dependent ratcheting of SS304 stainless steel. Mech. Mater. 2007, 39, 488–499. [Google Scholar] [CrossRef]
- Azinpour, E.; Cruz, D.J.; Cesar de Sa, J.M.A.; Santos, A. Phase-field approach in elastoplastic solids: Application of an iterative staggered scheme and its experimental validation. Comput. Mech. 2021, 68, 255–269. [Google Scholar] [CrossRef]
- Verleysen, P.; Peirs, J. Quasi-static and high strain rate fracture behaviour of Ti6Al4V. Int. J. Impact Eng. 2017, 108, 370–388. [Google Scholar] [CrossRef]

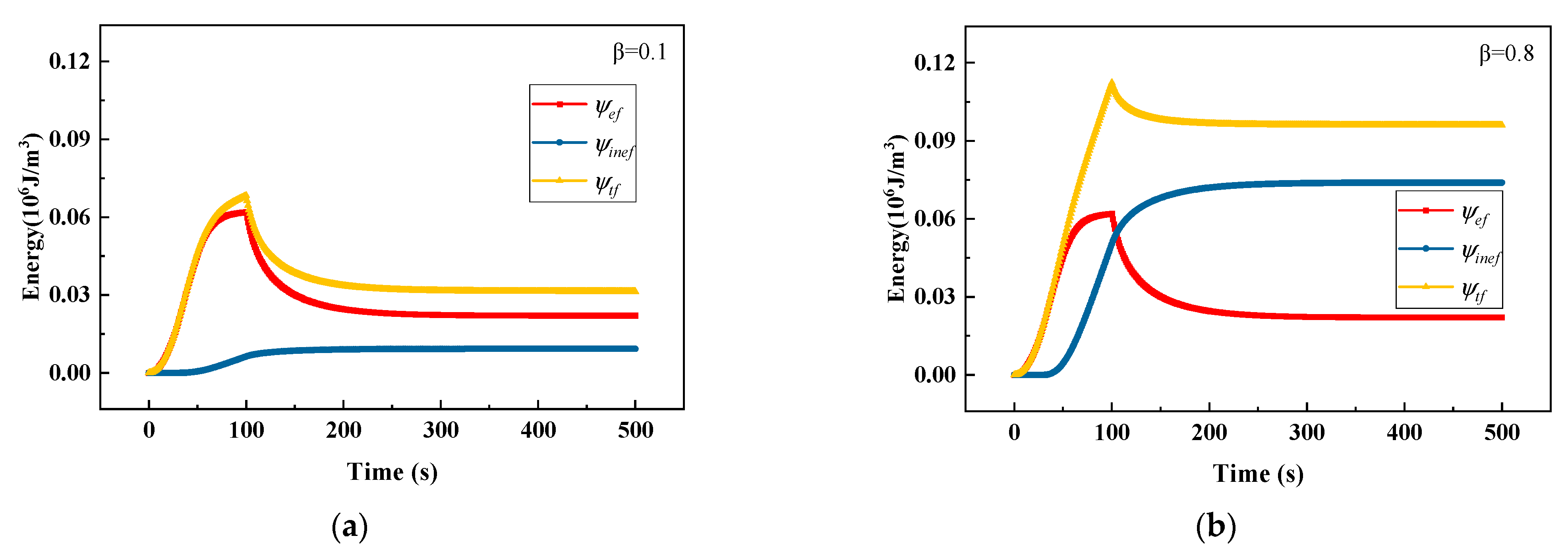

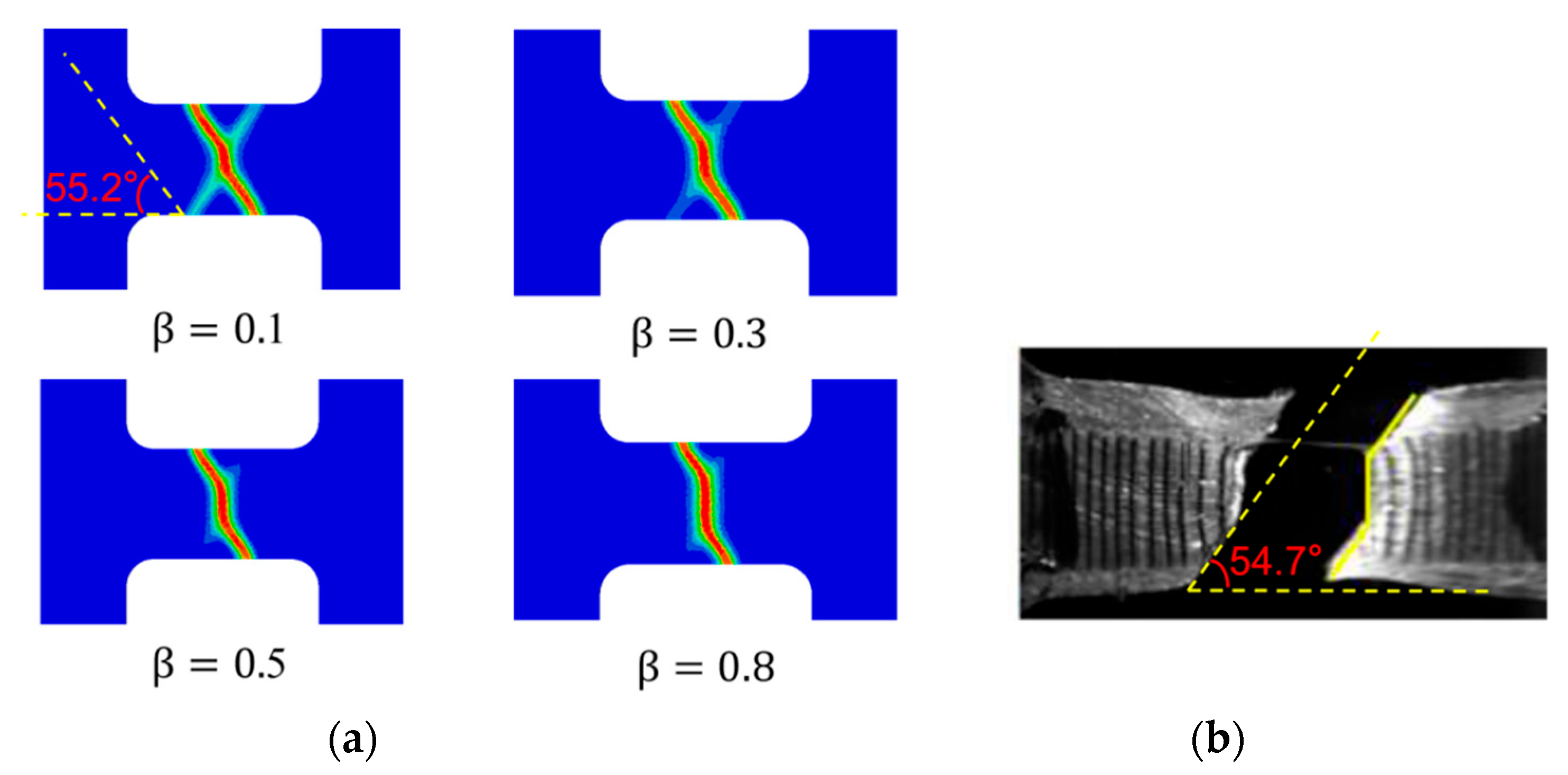
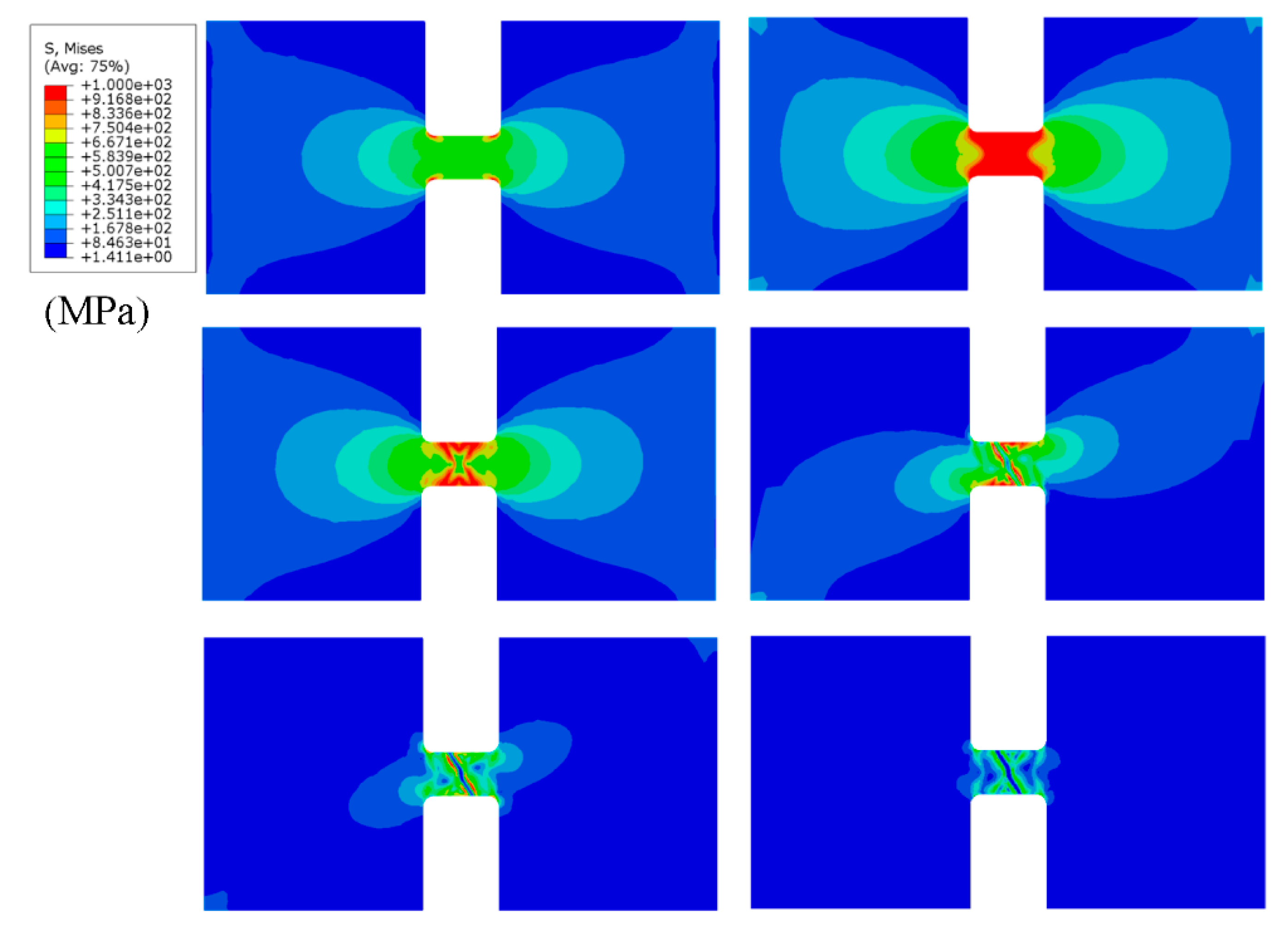
| Parameter | Name | Values |
|---|---|---|
| E | Young’ modulus | 192 (GPa) |
| Poisson’ ratio | 0.33 | |
| Initial yield stress | 90 (MPa) | |
| h | Hardening modulus | 2001.09 (MPa) |
| Gc | Critical energy release rate | 18 (N/mm) |
| A | Material constant | 3.16 × 10−6 |
| B | Material constant | 0.03572 |
| Energy density threshold | 0 (MPa) | |
| l | Length scale | 2 mm |
| Parameter | Name | Values |
|---|---|---|
| E | Young’ modulus | 192 (GPa) |
| Poisson’ ratio | 0.33 | |
| Initial yield stress | 402 (MPa) | |
| h | Hardening modulus | 1708 (MPa) |
| Gc | Critical energy release rate | 25 (N/mm) |
| A | Material constant | 6.1 × 10−4 |
| B | Material constant | 0.04 |
| Energy density threshold | 40 (MPa) | |
| l | Length scale | 0.2 mm |
| Parameter | Name | Values |
|---|---|---|
| E | Young’ modulus | 117 (GPa) |
| Poisson’ ratio | 0.3 | |
| Initial yield stress | 951 (MPa) | |
| h | Hardening modulus | 40 (MPa) |
| Gc | Critical energy release rate | 50 (N/mm) |
| A | Material constant | 1.3 × 10−4 |
| B | Material constant | 0.055 |
| Energy density threshold | 120 (MPa) | |
| l | Length scale | 0.12 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Q.; Yu, H.; Wang, X.; Huang, K.; Han, J. Phase Field Modeling of Crack Growth with Viscoplasticity. Crystals 2023, 13, 854. https://doi.org/10.3390/cryst13050854
Shi Q, Yu H, Wang X, Huang K, Han J. Phase Field Modeling of Crack Growth with Viscoplasticity. Crystals. 2023; 13(5):854. https://doi.org/10.3390/cryst13050854
Chicago/Turabian StyleShi, Qianyu, Hongjun Yu, Xiangyuhan Wang, Kai Huang, and Jian Han. 2023. "Phase Field Modeling of Crack Growth with Viscoplasticity" Crystals 13, no. 5: 854. https://doi.org/10.3390/cryst13050854
APA StyleShi, Q., Yu, H., Wang, X., Huang, K., & Han, J. (2023). Phase Field Modeling of Crack Growth with Viscoplasticity. Crystals, 13(5), 854. https://doi.org/10.3390/cryst13050854






