Electro-Elastic Modeling of Multi-Step Transitions in Two Elastically Coupled and Sterically Frustrated 1D Spin Crossover Chains
Abstract
:1. Introduction
2. The 1D Electro-Elastic Model
2.1. The Model Hamiltonian without Frustration
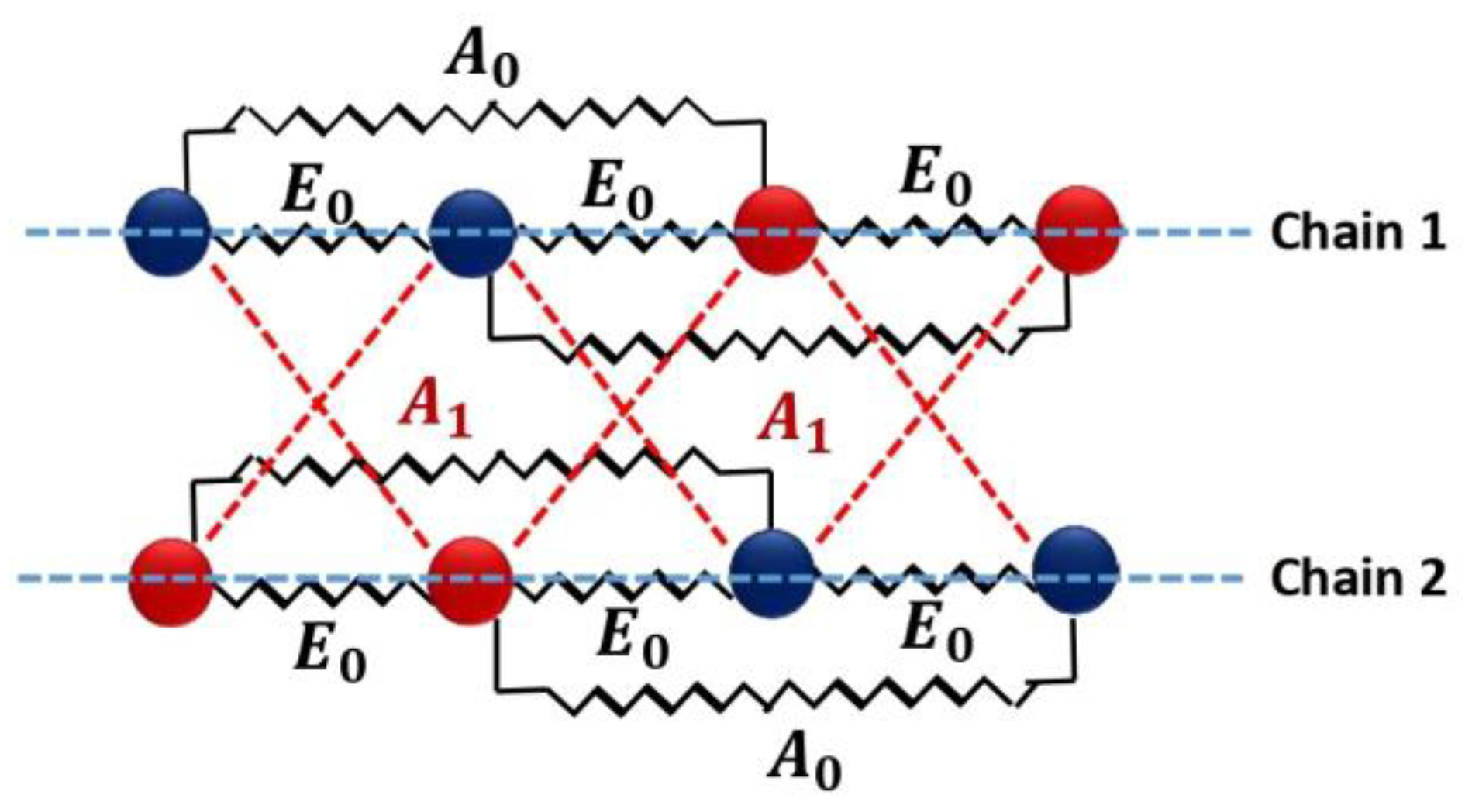
2.2. Introduction of the Elastic Frustration
2.3. Model Parameters and Resolution Method
3. Results and Discussions
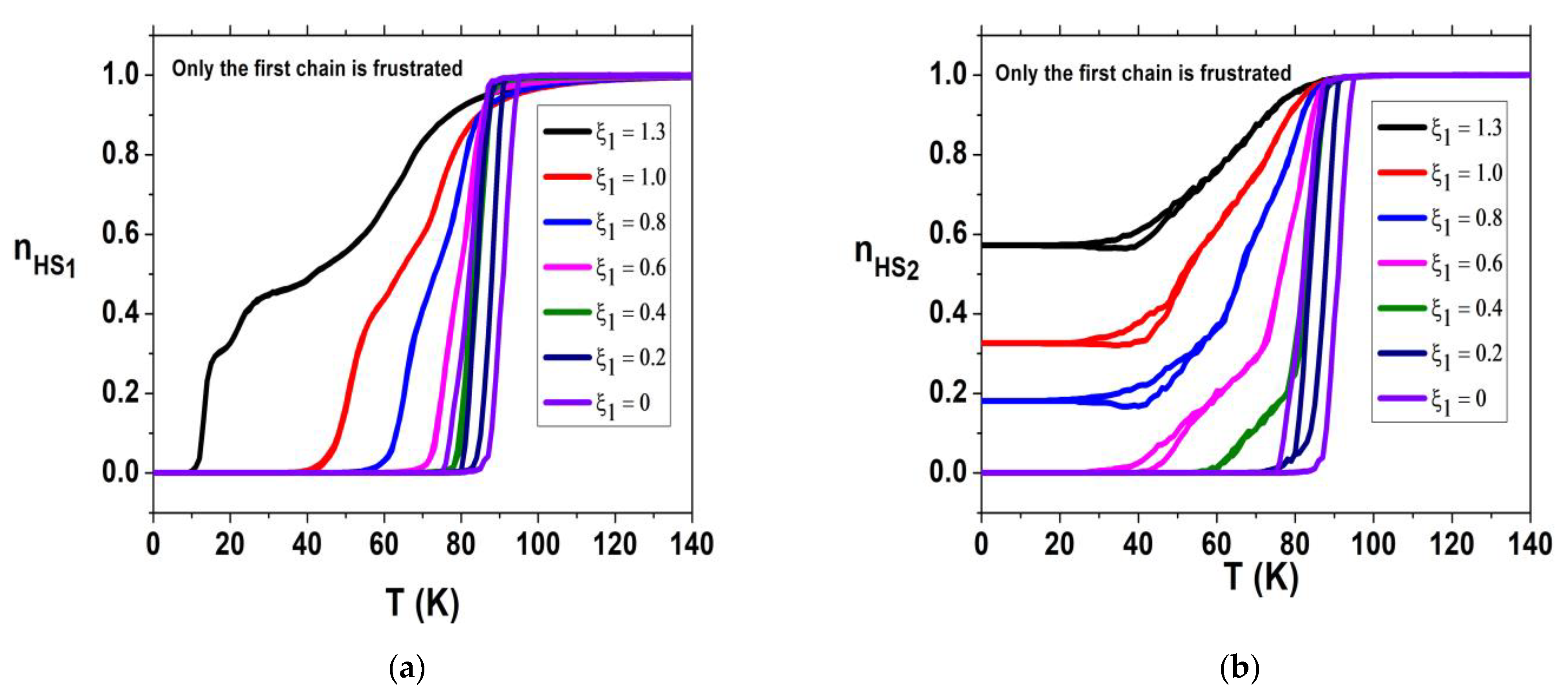
3.1. Frustration of the First Chain
3.1.1. Thermal Dependence of the HS Fraction
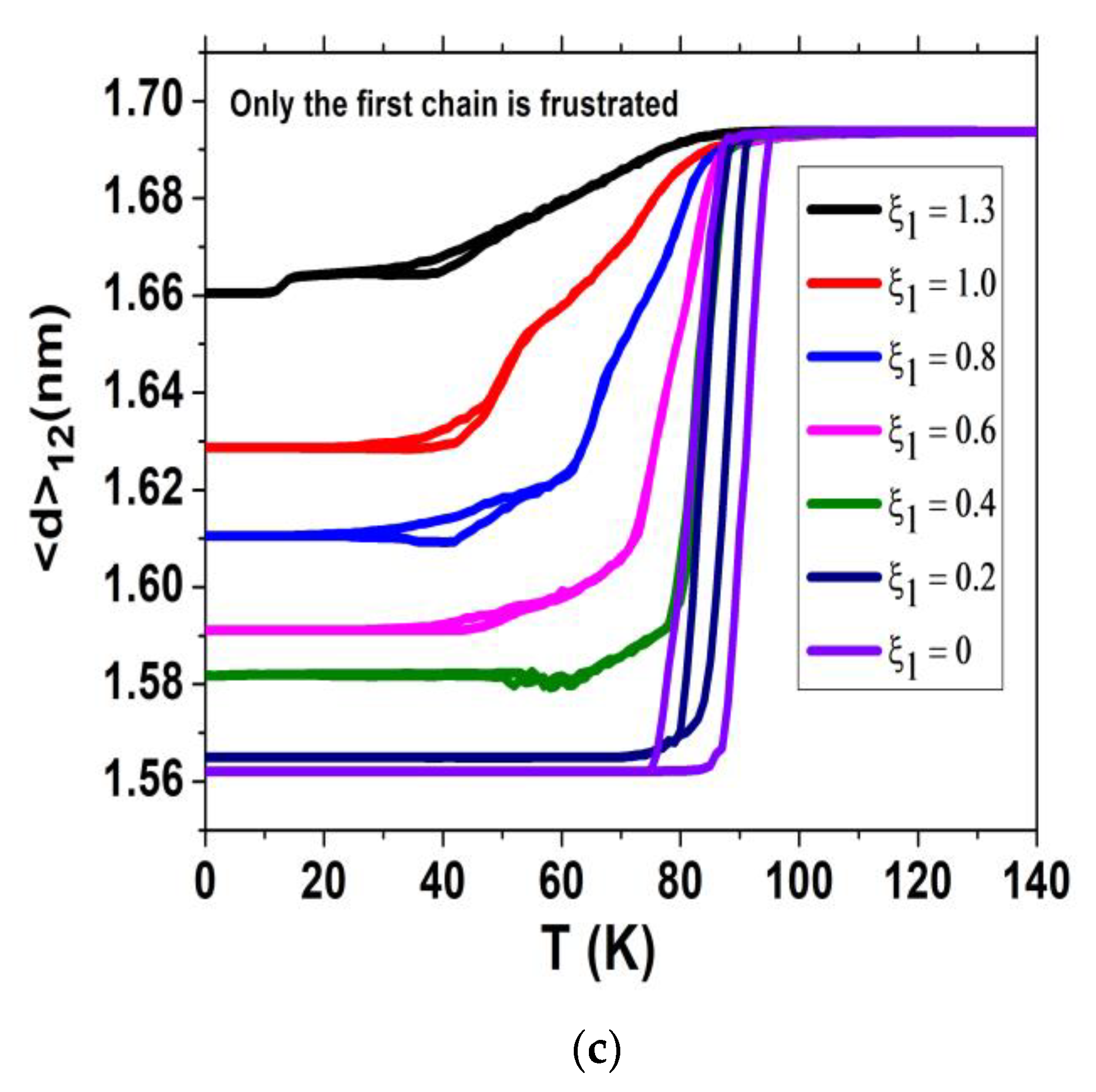
3.1.2. Thermal Dependence of the Lattice Bond Lengths
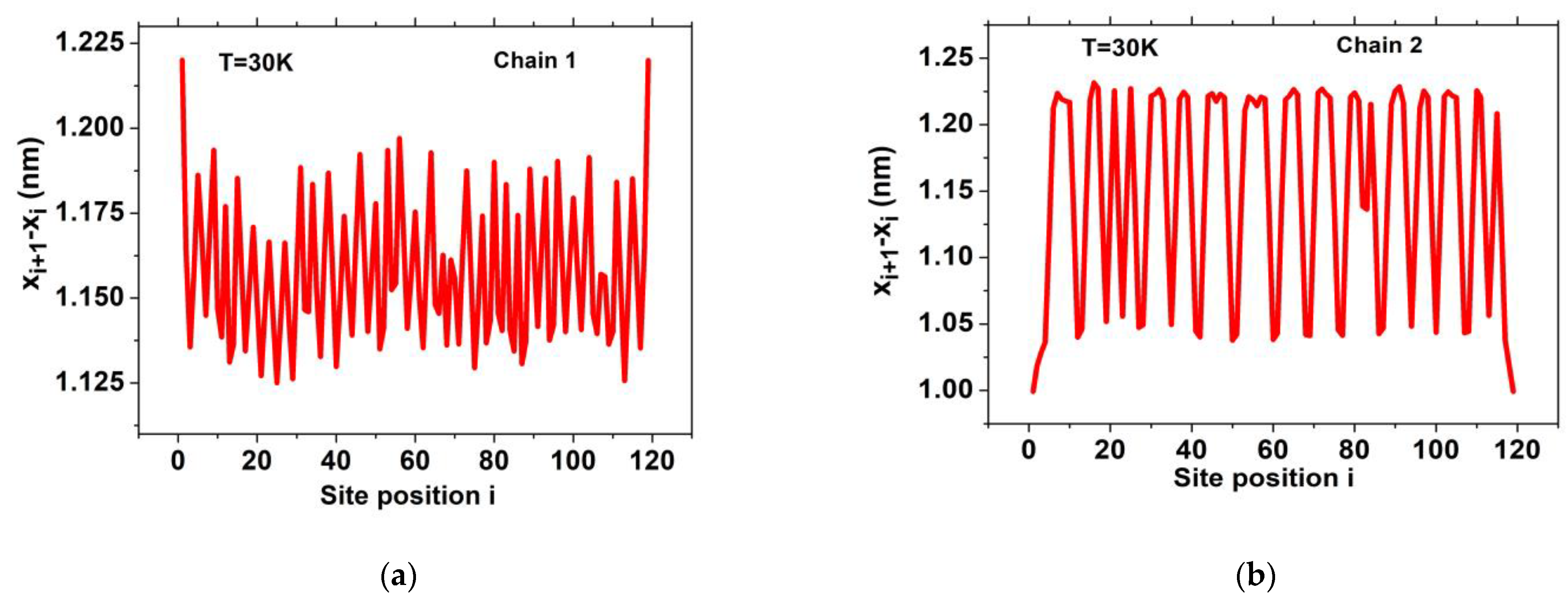
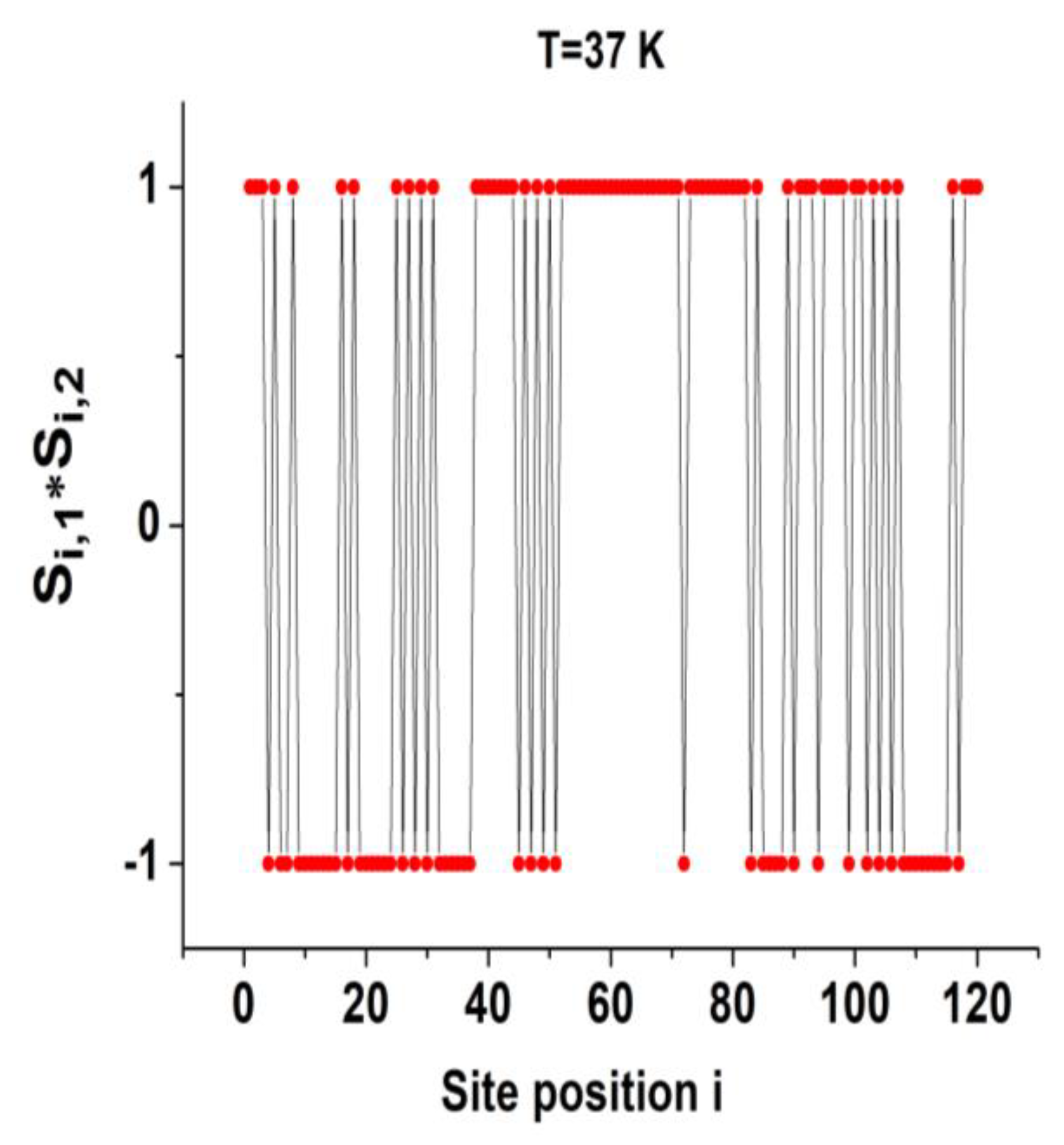
3.1.3. Self-Organization of the Spin States and Lattice Bond Lengths
3.2. Both Chains Are Frustrated
3.2.1. Thermal Dependence of the HS Fraction
3.2.2. Self-Organization of the Spin States in the Plateau Regions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Phan, H.; Benjamin, S.M.; Steven, E.; Brooks, J.S.; Shatruk, M. Photomagnetic Response in Highly Conductive Iron(II) Spin Crossover Complexes with TCNQ Radicals. Angew. Chem. Int. Ed. 2015, 54, 823. [Google Scholar] [CrossRef]
- Ohkoshi, S.I.; Tokoro, H. Photomagnetism in Cyano-Bridged Bimetal Assemblies. Acc. Chem. Res. 2012, 45, 1749. [Google Scholar] [CrossRef]
- Coronado, E.; Galán-Mascarós, J.R.; Monrabal-Capilla, M.; García-Martínez, J.; Pardo-Ibáñez, P. Bistable Spin-Crossover Nanoparticles Showing Magnetic Thermal Hysteresis near Room Temperature. Adv. Mater. 2007, 19, 1359. [Google Scholar] [CrossRef]
- Kahn, O.; Jay-Martinez, C. Spin-Transition Polymers: From Molecular Materials. Towar. Mem. Devices Sci. 1998, 279, 44. [Google Scholar]
- Gütlich, P.; Hauser, A.; Spiering, H. Thermal and Optical Switching of Iron(II) Complexes. Angew. Chem. Int. Ed. 1994, 33, 2024–2054. [Google Scholar] [CrossRef]
- Gütlich, P.; Goodwin, H.A. Spin Crossover in Transition Metal Compounds Iron(II); Springer: Berlin/Heidelberg, Germany, 2004; Volume 233, pp. 234–235. [Google Scholar]
- Olguín, J.; Brooker, S. Spin Crossover Active Iron(II) Complexes of Selected Pyrazole-Pyridine/Pyrazine Ligands. Coord. Chem. Rev. 2011, 255, 203–240. [Google Scholar] [CrossRef]
- Gütlich, P.; Gaspar, A.B.; Garcia, Y. Spin State Switching in Iron Coordination Compounds. Beilstein. J. Org. Chem. 2013, 9, 342–391. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Z.Y.; Dai, J.W.; Shiota, Y.; Yoshizawa, K.; Kanegawa, S.; Sato, O. Multi-Step Spin Crossover Accompanied by Symmetry Breaking in an Fe(III) Complex: Crystallographic Evidence and DFT Studies. Chem. Eur. J. 2013, 19, 12948–12952. [Google Scholar] [CrossRef] [PubMed]
- Jureschi, C.M.; Linares, J.; Rotaru, A.; Ritti, M.H.; Parlier, M.; Dîrtu, M.M.; Wolff, M.; Garcia, Y. Pressure Sensor via Optical Detection Based on a 1D Spin Transition Coordination Polymer. Sensors 2015, 15, 2388–2398. [Google Scholar] [CrossRef] [Green Version]
- Decurtins, S.; Gütlich, P.; Hasselbach, K.M.; Hauser, A.; Spiering, H. Light-induced excited-spin-state trapping in Iron(II) spin-crossover systems. Optical spectroscopic and magnetic susceptibility study. Inorg. Chem. 1985, 24, 2174–2178. [Google Scholar] [CrossRef]
- Hauser, A. Reversibility of light-induced excited spin state trapping in the Fe(ptz)6(BF4)2, and the Zn1-xFex(ptz)6(BF4)2 spin-crossover systems. Chem. Phys. Lett. 1986, 124, 543–548. [Google Scholar] [CrossRef]
- Hauser, A.; Adler, J.; Gütlich, P. Light-induced excited spin state trapping (LIESST) in [ Fe(2-mephen)3]+2 embedded in polymer matrices. Chem. Phys. Lett. 1988, 152, 468–472. [Google Scholar] [CrossRef]
- Gütlich, P.; Garcia, Y.; Goodwin, H.A. Spin crossover phenomena in Fe(II) complexes. Chem. Soc. Rev. 2000, 29, 419–427. [Google Scholar] [CrossRef]
- Hauser, A. Light-Induced Spin Crossover and the High-Spin Low-Spin Relaxation. In Spin Crossover in Transition Metal Compounds; Topics in Current Chemistry; Springer: New York, NY, USA, 2004; Volume 234, pp. 155–198. [Google Scholar]
- Mahfoud, T.; Molnar, G.; Bonhommeau, S.; Cobo, S.; Salmon, L.; Demont, P.; Tokoro, H.; Ohkoshi, S.; Boukheddaden, K.; Bousseksou, A. Electric-Field-Induced Charge-Transfer Phase Transition: A Promising Approach Toward Electrically Switchable Devices. J. Am. Chem. Soc. 2009, 131, 15049–15054. [Google Scholar] [CrossRef]
- Rotaru, A.; Dugay, J.; Tan, R.P.; Guralskiy, I.A.; Salmon, L.; Demont, P.; Carrey, J.; Molnar, G.; Respaud, M.; Bousseksou, A. Nanoelectromanipulation of Spin Crossover Nanorods: Towards Switchable Nanoelectronic. Devices Adv. Mater. 2013, 25, 1745–1749. [Google Scholar] [CrossRef] [Green Version]
- Prins, F.; Monrabal-Capilla, M.; Osorio, E.A.; Coronado, E.; van der Zant, H.S. Room-Temperature Electrical Addressing of a Bistable Spin-Crossover Molecular System. Adv. Mater. 2011, 23, 1545–1549. [Google Scholar] [CrossRef]
- Slimani, A.; Boukheddaden, K.; Varret, F.; Oubouchou, H.; Nishino, M.; Miyashita, S. Microscopic spin-distortion model for switchable molecular solids: Spatiotemporal study of the deformation field and local stress at the thermal spin transition. Phys. Rev. B 2013, 87, 014111. [Google Scholar] [CrossRef]
- Moussa, N.O.; Ostrovskii, D.; Garcia, V.M.; Molnár, G.; Tanaka, K.; Gaspar, A.B.; Real, J.A.; Bousseksou, A. Bidirectional photoswitching of the spin state of iron(II) ions in a triazol based spin crossover complex within the thermal hysteresis loop. Chem. Phys. Lett. 2009, 477, 156–159. [Google Scholar] [CrossRef]
- Shepherd, H.J.; Rosa, P.; Fallis, I.A.; Guionneau, P.; Howard, J.A.K.; Goeta, A.E. Structural origin of the gradual spin transition in a mononuclear iron(II) complex. Phys. Chem. Solids 2012, 73, 193–197. [Google Scholar] [CrossRef]
- Takahashi, K.; Mori, H.; Kobayashi, H.; Sato, O. Mechanism of reversible spin transition with a thermal hysteresis loop in [FeIII(qsal)2][Ni(dmise)2] · 2CH3CN: Selenium analogue of the precursor of an Fe(III) spin-crossover molecular conducting system. Polyhedron 2009, 28, 1776. [Google Scholar] [CrossRef]
- Fedaoui, D.; Bouhadja, Y.; Kaiba, K.; Guionneau, P.; Létard, J. Complexation of 2,6-Bis(3-pyrazolyl)pyridine–Bis(thiocyanato)iron(II) with a Bridging 4,40-Bipyridine: A New Example of a Dinuclear Spin Crossover Complex. Eur. J. Inorg. Chem. 2008, 7, 1022–1023. [Google Scholar] [CrossRef]
- De Gaetano, Y.; Jeanneau, E.; Verat, A.Y.; Rechignat, L.; Bousseksou, A.; Matouzenko, G.S. Ligand-Induced Distortions and Magneto-Structural Correlations in a Family of Dinuclear Spin Crossover Compounds with Bipyridyl-Like Bridging Ligands. Eur. J. Inorg. Chem. 2013, 2013, 1015–1023. [Google Scholar] [CrossRef]
- Sciortino, N.F.; Scherl-Gruenwald, K.R.; Chastanet, G.; Halder, G.J.; Chapman, K.W.; Létard, J.F.; Kepert, C.J. Hysteretic Three-Step Spin Crossover in a Thermo-and Photochromic 3D Pillared Hofmann-type Metal–Organic Framework. Angew. Chem. Int. Ed. Engl. 2012, 124, 10301–10305. [Google Scholar] [CrossRef]
- Romstedt, H.; Spiering, H.; Gütlich, P. Modelling of two step high spinlow spin transitions using the cluster variation method. J. Phys. Chem. Solids 1998, 59, 1353–1362. [Google Scholar] [CrossRef]
- Piñeiro-López, L.; Valverde-Muñoz, F.J.; Trzop, E.; Muñoz, M.C.; Seredyuk, M.; Castells-Gil, J.; da Silva, I.; Martí-Gastaldo, C.; Collet, E.; Real, J.A. Guest induced reversible on-off switching of elastic frustration in a 3D spin crossover coordination polymer with room temperature hysteretic behaviour. Chem. Sci. 2020, 12, 1317–1326. [Google Scholar] [CrossRef]
- Watanabe, H.; Tanaka, k.; Bréfuel, N.; Cailleau, H.; Létard, J.-F.; Ravy, S.; Fertey, P.; Nishino, M.; Miyashita, S.; Collet, E. Ordering phenomena of high-spin/low-spin states in stepwise spin-crossover materials described by the ANNNI model. Phys. Rev. B 2016, 93, 014419. [Google Scholar] [CrossRef]
- Pittala, N.; Cuza, E.; Pinkowicz, D.; Magott, M.; Marchivie, M.; Boukheddaden, K.; Triki, S. Antagonist elastic interactions tuning spin crossover and LIESST behaviours in FeII trinuclear-based one-dimensional chains. Inorg. Chem. Front. 2022, 9, 6468–6481. [Google Scholar] [CrossRef]
- Ndiaye, M.; Yogendra, S.; Fourati, H.; Sy, M.; Lo, B.; Boukheddaden, K. Isomorphism between the Electro-Elastic Modelling of the Spin Transition and Ising-like Model with Competing Interactions. J. Appl. Phys. 2021, 129, 153901. [Google Scholar] [CrossRef]
- Ndiaye, M.; Boukheddaden, K. Electro-elastic Modelling of the Two-Step High-Spin to Low-Spin Relaxation with Transient Self-Organized Spin States in 2D Spin Crossover Solids. J. Phys. Soc. Jpn. 2020, 89, 014004. [Google Scholar] [CrossRef]
- Nishino, M.; Yogendra, S.; Boukheddaden, K.; Miyashita, S. Tutorial on elastic interaction models for multistep spin-crossover. J. Appl. Phys. 2021, 130, 141102. [Google Scholar] [CrossRef]
- Paez-Espejo, M.; Sy, M.; Boukheddaden, K. Elastic Frustration Causing Two-Step and Multistep Transitions in Spin-Crossover Solids: Emergence of Complex Antiferroelastic Structures. J. Am. Chem. Soc. 2016, 138, 3202–3210. [Google Scholar] [CrossRef]
- Pillet, S.; Bendeif, E.-E.; Bonnet, S.; Shepherd, H.J.; Guionneau, P. Multimetastability, phototrapping, and thermal trapping of a metastable commensurate superstructure in a FeII spin-crossover compound. Phys. Rev. B Condens. Matter Mater. 2012, 86, 064106. [Google Scholar] [CrossRef] [Green Version]
- Collet, E.; Watanabe, H.; Brefuel, N.; Palatinus, L.; Roudaut, L.; Toupet, L.; Tanaka, K.; Tu-chagues, J.-P.; Fertey, P.; Ravy, S.; et al. Aperiodic Spin State Ordering of Bistable Molecules and Its Photoinduced Erasing. Phys. Rev. Lett. 2012, 109, 257206. [Google Scholar] [CrossRef]
- Milin, E.; Patinec, V.; Triki, S.; Bendeif, E.; Pillet, S.; Marchivie, M.; Chastanet, G.; Boukheddaden, K. Hidden Hysteresis Revealed by Photo-Switching in a Multi-Stable Two-Dimensional Hoffman-Like Spin-Crossover Metal-Organic Framework. Inorg. Chem. 2016, 55, 11652–11661. [Google Scholar] [CrossRef]
- Bousseksou, A.; Nasser, J.; Linares, J.; Boukheddaden, K.; Varret, F. Ising-like model for the two-step spin-crossover. J. Phys. I 1992, 2, 1381–1403. [Google Scholar] [CrossRef]
- Boukheddaden, K.; Linares, J.; Codjovi, E.; Varret, F.; Niel, V.; Real, J.A. Dynamical ising-like model for the two-step spin-crossover systems. J. Appl. Phys. 2003, 93, 7103–7105. [Google Scholar] [CrossRef] [Green Version]
- Singh, Y.; Oubouchou, H.; Nishino, M.; Miyashita, S.; Boukheddaden, K. Elastic-frustration-driven unusual magnetoelastic properties in a switchable core-shell spin-crossover nanostructure. Phys. Rev. B 2020, 101, 054105. [Google Scholar] [CrossRef]
- Affes, k.; Slimani, A.; Singh, Y.; Maalej, A.; Boukheddaden, K. Magnetoelastic properties of a spin-crossover membrane deposited on a substrate. J. Phys. Cond. Matt. 2020, 32, 255402. [Google Scholar] [CrossRef]
- Singh, Y.; Affes, K.; Belmouri, N.-I.; Boukheddaden, K. Clamping of Spin-Crossover Solid Inducing Crystal Bending and Spatial Spin Organization. Mater. Today Phys. 2022, 27, 100842. [Google Scholar] [CrossRef]
- Traiche, R.; Sy, M.; Boukheddaden, K. Elastic Frustration in 1D Spin-Crossover Chains: Evidence of Multi-Step Transitions and Self-Organizations of the Spin States. J. Phys. Chem. C 2018, 122, 4083–4096. [Google Scholar] [CrossRef]
- Traiche, R.; Oubouchou, H.; Boukhedaden, K. Elastic Modeling of Two-Step Transitions in Sterically Frustrated 1D Binuclear Spin-Crossover Chains. Symmetry 2021, 13, 1836. [Google Scholar] [CrossRef]
- Boukheddaden, K.; Traiche, R.; Oubouchou, H.; Linares, J. Multistep Relaxations in a Spin-Crossover Lattice with Defect: A Spatiotemporal Study of the Domain Propagation. Magnetochemistry 2016, 2, 17. [Google Scholar] [CrossRef] [Green Version]
- Ndiaye, M.; Belmouri, N.; Linares, J.; Boukheddaden, K. Elastic Origin of the Unsymmetrical Thermal Hysteresis in Spin Crossover Materials: Evidence of Symmetry Breaking. Symmetry 2021, 13, 828. [Google Scholar] [CrossRef]
- Di Scala, N.; Belmouri, N.; Paez-Espejo, M.; Boukheddaden, K. Explaining the origin of the orientation of the front transformation in spin-transition crystals. Phys. Rev. B 2022, 106, 144107. [Google Scholar] [CrossRef]
- Affes, K.; Singh, Y.; Boukheddaden, K. Electro-Elastic Modeling of Thermal Spin Transition in Diluted Spin-Crossover Single Crystals. Int. J. Mol. Sci. 2022, 23, 13854. [Google Scholar] [CrossRef] [PubMed]
- Miyashita, S.; Konishi, Y.; Nishino, M.; Tokoro, H.; Rikvold, P.A. Realization of the mean-field universality class in spin-crossover materials. Phys. Rev. B Condens, Matter Mater. Phys. 2008, 77, 014105. [Google Scholar] [CrossRef] [Green Version]
- di Scala, N.; Belmouri, N.E.I.; Espejo, M.A.P.; Boukheddaden, K. Three-Dimensional Electroelastic Modeling of the Nucleation and Propagation of the Spin Domains in Spin-Crossover Materials. Phys. Rev. B 2022, 106, 014422. [Google Scholar] [CrossRef]
- Decurtins, S.; Gutlich, P.; Kohler, C.P.; Spiering, H. New examples of light-induced excited spin state trapping (LIESST) in iron(II) spin-crossover systems. J. Chem. Soc. Chem. Commun. 1985, 7, 430–432. [Google Scholar] [CrossRef]
- Desaix, A.; Roubeau, O.; Jeftić, J.; Haasnoot, J.G. Light-induced bistability in spin transition solids leading to thermal and optical hysteresis. Eur. Phys. J. B–Condens. Matter Complex Syst. 1998, 6, 183–193. [Google Scholar] [CrossRef]
- Létard, J.F.; Guionneau, P.; Rabardel, L.; Howard, J.A.K.; Goeta, A.E.; Chasseau, D.; Kahn, O. Structural, Magnetic, and Photomagnetic Studies of a Mononuclear Iron(II) Derivative Exhibiting an Exceptionally Abrupt Spin Transition. Light-Induced Thermal Hysteresis Phenomenon. Inorg. Chem. 1998, 37, 4432–4441. [Google Scholar] [CrossRef]
- Oke, T.D.; Ndiaye, M.; Hontinfinde, F.; Boukheddaden, K. Magnetic-field induced multi-step transitions in ferromagnetic spin-crossover solids within the BEG model. Eur. Phys. J. B 2021, 94, 38. [Google Scholar] [CrossRef]
- Felts, A.C.; Cain, J.M.; Andrus, M.J.; Ahir, A.R.; Abboud, K.A.; Slimani, A.; Meisel, M.W.; Boukheddaden, K.; Talham, D.R. Control of the Speed of a Light-Induced Spin Transition through Mesoscale Core–Shell Architecture. J. Am. Chem. Soc. 2018, 140, 5814−5824. [Google Scholar] [CrossRef] [PubMed]
- Sadhukhan, P.; Qi Wu, S.; Long, J.I.; Nakanishi, T. Manipulating electron redistribution to achieve electronic pyroelectricity in molecular [FeCo] crystals. Nat. Commun. 2021, 12, 4836. [Google Scholar] [CrossRef] [PubMed]
- Carbonera, C.; Dei, A.; Létard, J.-F.; Sangregorio, C.; Sorace, L. Thermally and light-induced valence tautomeric transition in a dinuclear cobalt–tetraoxolene com-plex. Angew. Chem. Int. Ed. 2004, 43, 3136–3138. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, R.D.; Shultz, D.A.; Martin, J.D. Magnetic bistability in a cobalt bis (dioxo-lene) complex: Long-lived photoinduced valence tautomerism. Inorg. Chem. 2010, 49, 3162–3168. [Google Scholar] [CrossRef]
- Tao, J.; Maruyama, H.; Sato, O. Valence tautomeric transitions with thermal hystere-sis around room temperature and photoinduced effects observed in a co-balt−tetraoxolene complex. J. Am. Chem. Soc. 2003, 128, 1790–1791. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Traiche, R.; Oubouchou, H.; Boukheddaden, K. Electro-Elastic Modeling of Multi-Step Transitions in Two Elastically Coupled and Sterically Frustrated 1D Spin Crossover Chains. Crystals 2023, 13, 937. https://doi.org/10.3390/cryst13060937
Traiche R, Oubouchou H, Boukheddaden K. Electro-Elastic Modeling of Multi-Step Transitions in Two Elastically Coupled and Sterically Frustrated 1D Spin Crossover Chains. Crystals. 2023; 13(6):937. https://doi.org/10.3390/cryst13060937
Chicago/Turabian StyleTraiche, Rachid, Hassane Oubouchou, and Kamel Boukheddaden. 2023. "Electro-Elastic Modeling of Multi-Step Transitions in Two Elastically Coupled and Sterically Frustrated 1D Spin Crossover Chains" Crystals 13, no. 6: 937. https://doi.org/10.3390/cryst13060937




