A Combination of Virtual and Experimental Screening Tools for the Prediction of Nitrofurantoin Multicomponent Crystals with Pyridine Derivatives
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Crystallization Procedure
2.3. Liquid-Assisted Grinding (LAG)
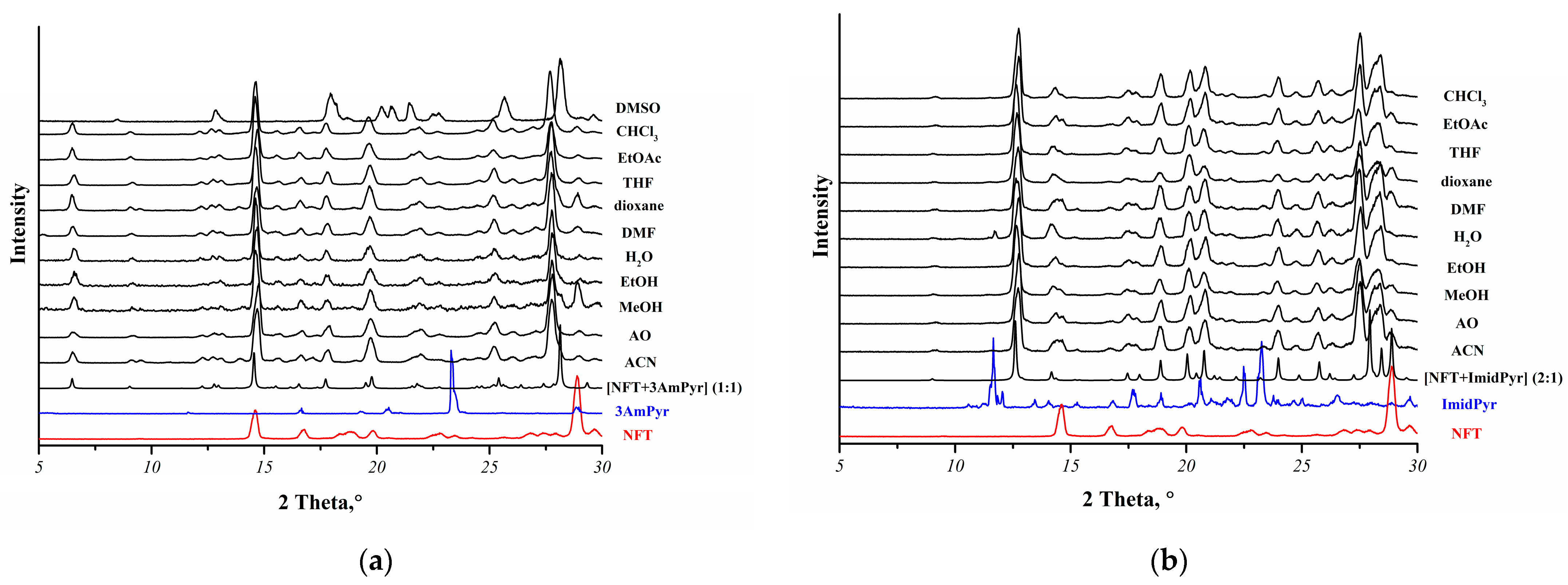
2.4. Powder X-ray Diffraction (PXRD)
2.5. Single Crystal X-ray Diffraction (SCXRD)
2.6. Thermogravimetric Analysis
2.7. Computational Details
2.7.1. Molecular Complementarity (MC)
2.7.2. Hydrogen Bond Propensity (HBP)
2.7.3. Crystal Similarity Analysis Using XPac
2.7.4. Molecular Electrostatic Potential (MEP) Calculations
2.7.5. Hirshfeld Surface Analysis
2.7.6. Periodic DFT Computations
2.7.7. Lattice Energy Evaluation
3. Results
3.1. Experimental Screening
3.2. Virtual Screening
3.2.1. Molecular Complementary (MC) Calculation Method
3.2.2. Hydrogen-Bond Propensity (HBP) Calculation Method
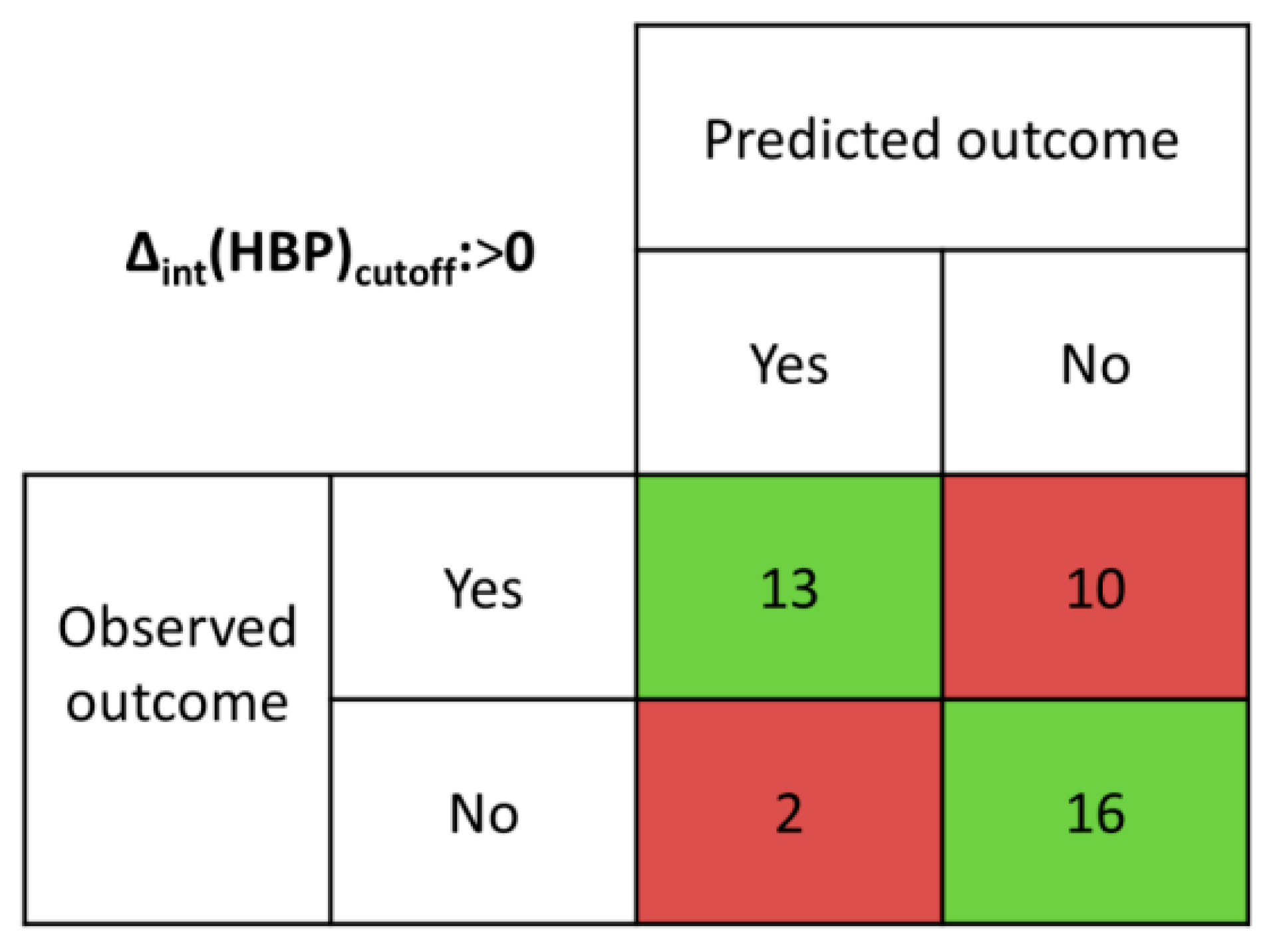
3.2.3. Integrated Hydrogen-Bond Propensity (intHBP) Calculation Method
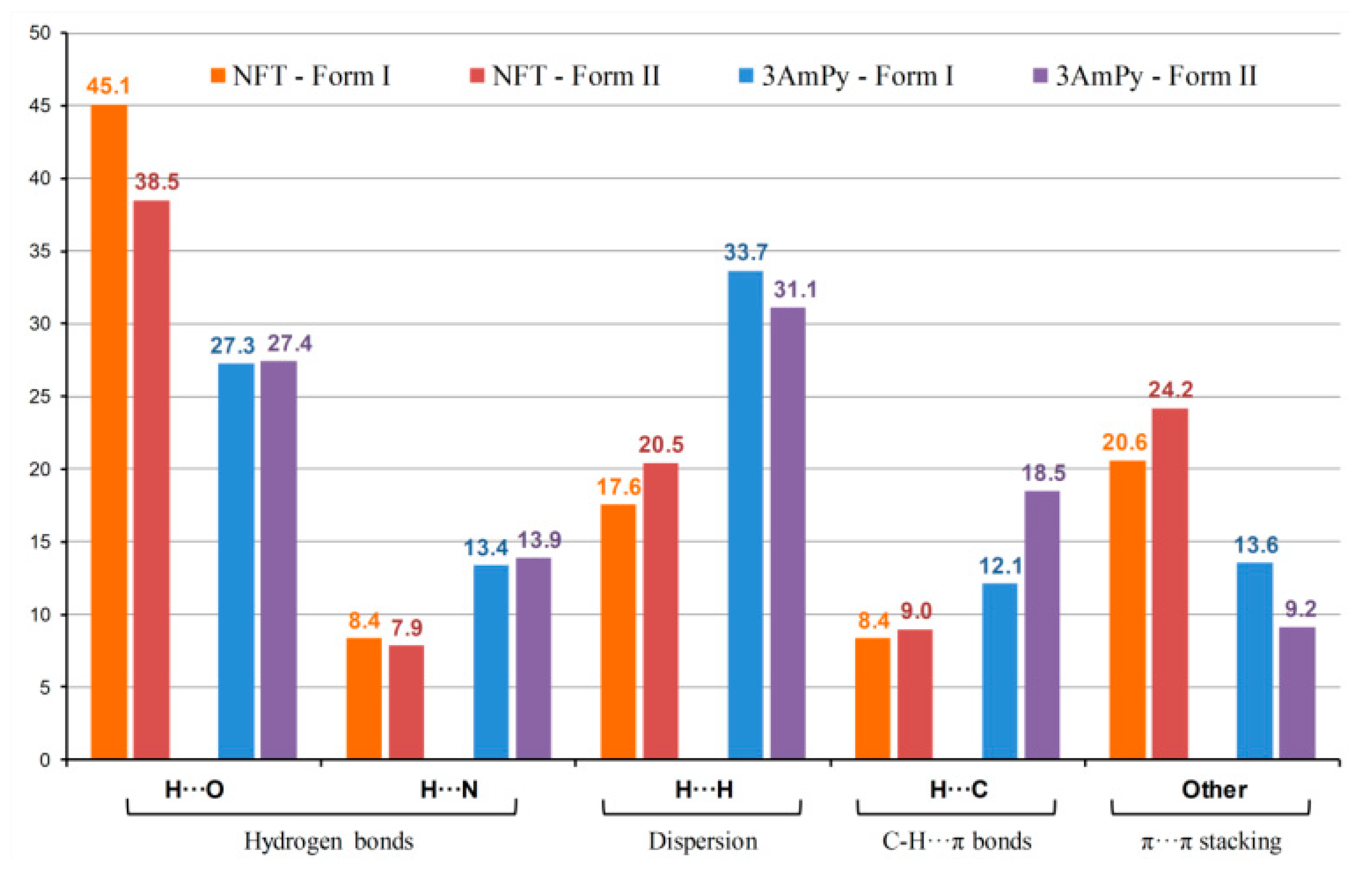
3.3. Crystal Structure Analysis
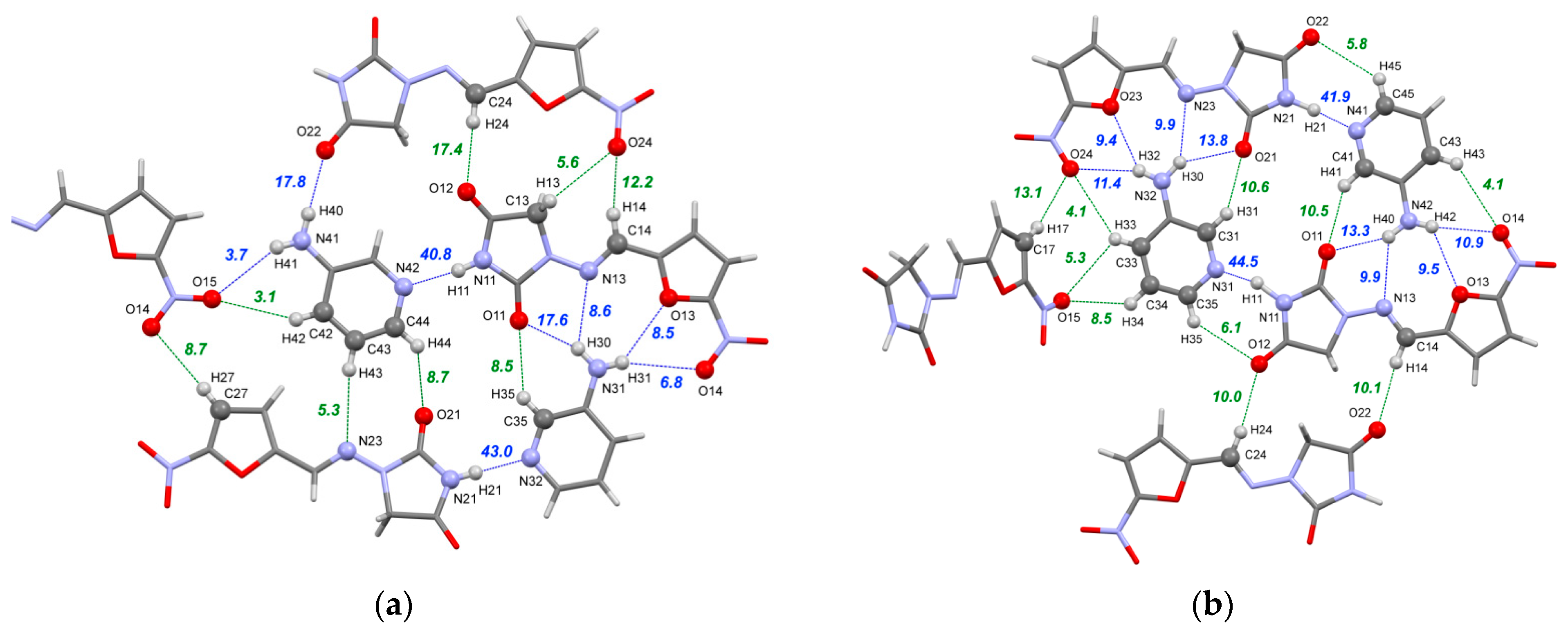
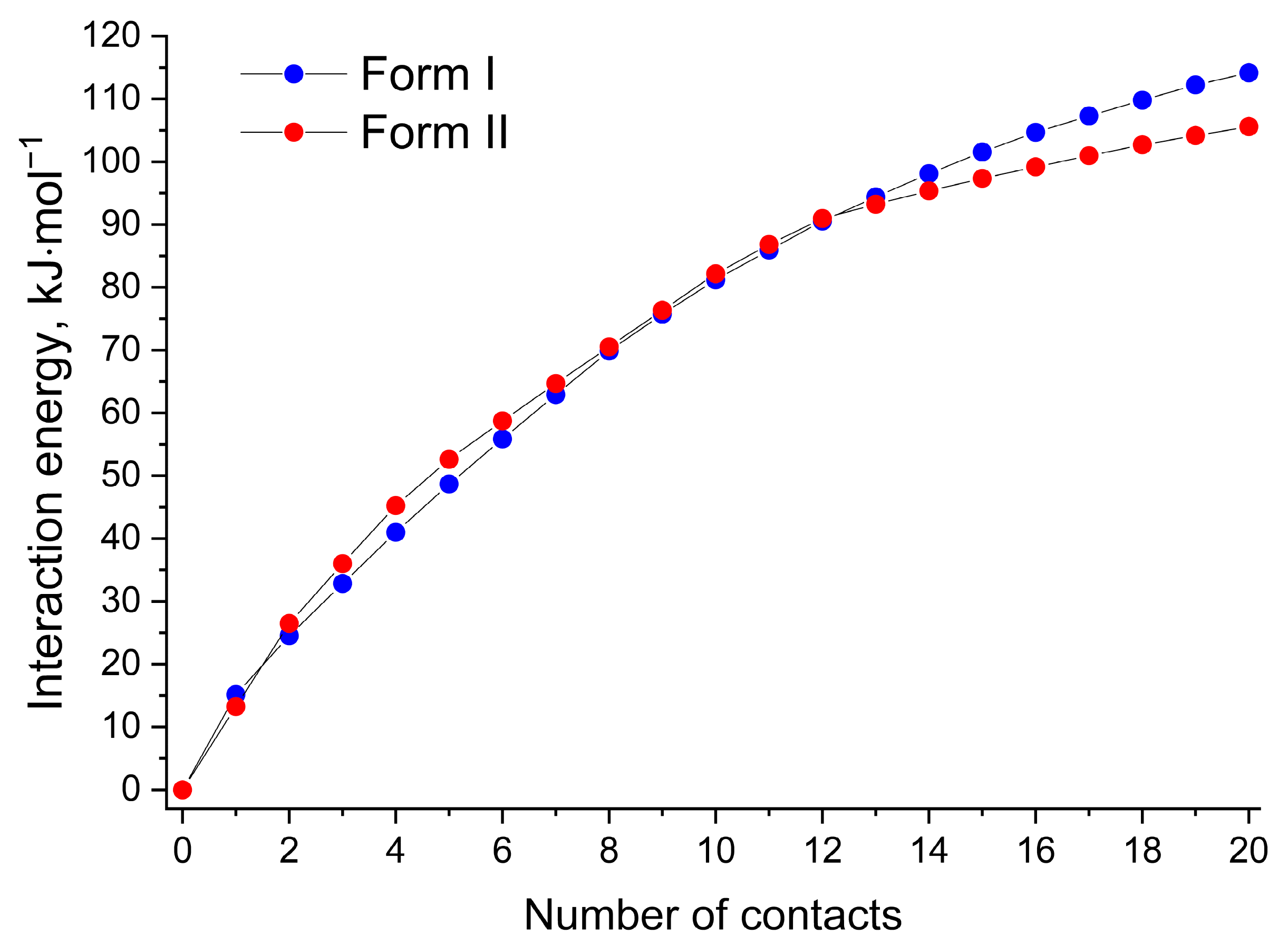
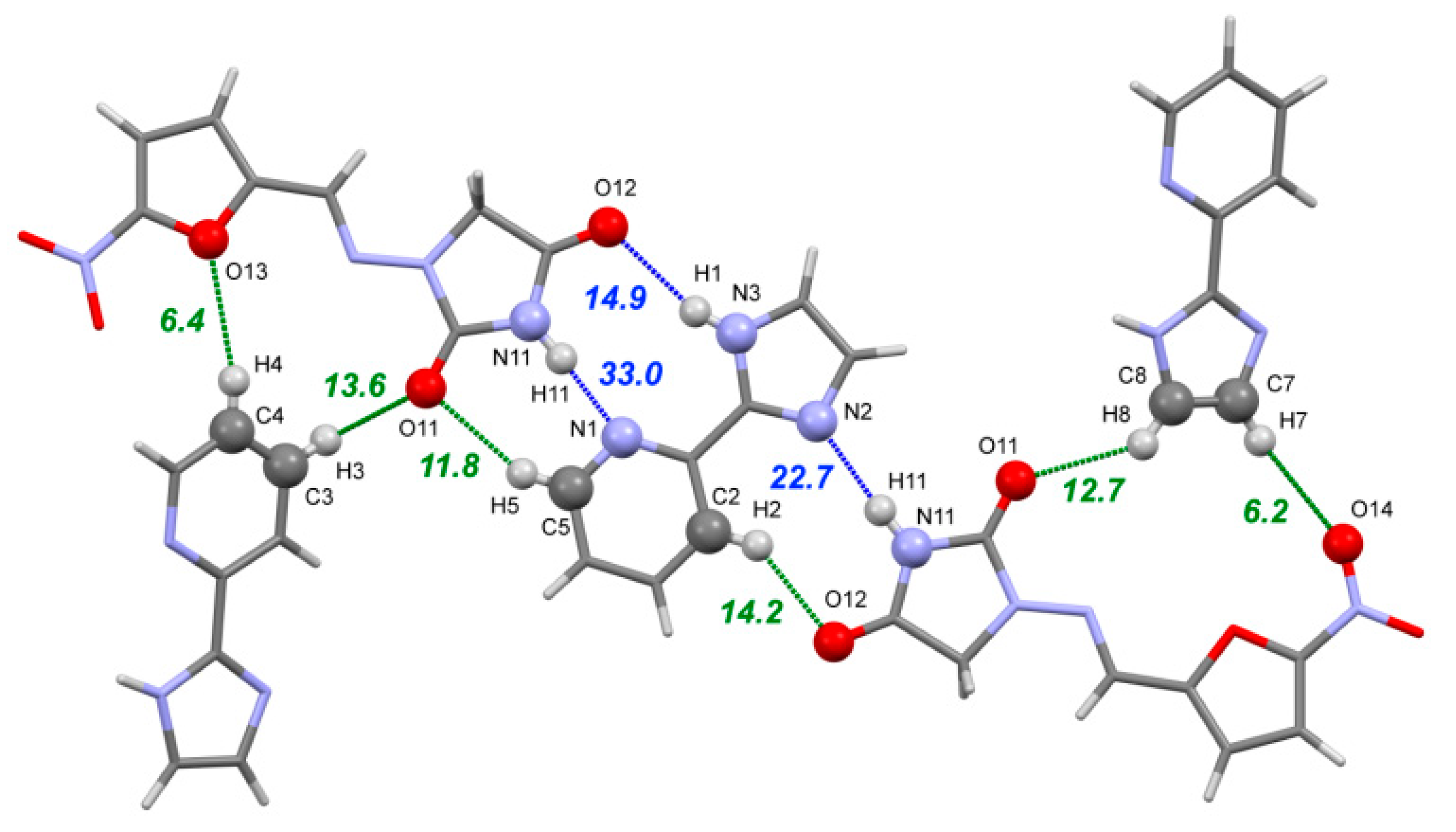
3.3.1. [NFT+3AmPy] Cocrystals (1:1) Forms I and II
3.3.2. [NFT+ImidPy] Cocrystal (2:1)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, Q.T.; Li, T. Formulation and Manufacturing of Solid Dosage Forms. Pharm. Res. 2018, 36, 16. [Google Scholar] [CrossRef] [PubMed]
- Thayer, A.M. Finding Solutions. Chem. Eng. News Arch. 2010, 88, 13–18. [Google Scholar] [CrossRef]
- Aakeröy, C.B.; Fasulo, M.E.; Desper, J. Cocrystal or Salt: Does It Really Matter? Mol. Pharm. 2007, 4, 317–322. [Google Scholar] [CrossRef]
- Nangia, A.; Desiraju, G.R. Supramolecular Synthons and Pattern Recognition. In Design of Organic Solids. Topics in Current Chemistry; Weber, E., Aoyama, Y., Caira, M.R., Desiraju, G.R., Glusker, J.P., Hamilton, A.D., Meléndez, R.E., Nangia, A., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; Volume 198, pp. 57–95. ISBN 978-3-540-69178-5. [Google Scholar]
- Corpinot, M.K.; Bučar, D.-K. A Practical Guide to the Design of Molecular Crystals. Cryst. Growth Des. 2019, 19, 1426–1453. [Google Scholar] [CrossRef]
- Fleischman, S.G.; Kuduva, S.S.; McMahon, J.A.; Moulton, B.; Bailey Walsh, R.D.; Rodríguez-Hornedo, N.; Zaworotko, M.J. Crystal Engineering of the Composition of Pharmaceutical Phases: Multiple-Component Crystalline Solids Involving Carbamazepine. Cryst. Growth Des. 2003, 3, 909–919. [Google Scholar] [CrossRef]
- Desiraju, G.R. Supramolecular Synthons in Crystal Engineering—A New Organic Synthesis. Angew. Chem. Int. Ed. Engl. 1995, 34, 2311–2327. [Google Scholar] [CrossRef]
- Kavuru, P.; Aboarayes, D.; Arora, K.K.; Clarke, H.D.; Kennedy, A.; Marshall, L.; Ong, T.T.; Perman, J.; Pujari, T.; Wojtas, Ł.; et al. Hierarchy of Supramolecular Synthons: Persistent Hydrogen Bonds between Carboxylates and Weakly Acidic Hydroxyl Moieties in Cocrystals of Zwitterions. Cryst. Growth Des. 2010, 10, 3568–3584. [Google Scholar] [CrossRef]
- Bučar, D.-K.; Henry, R.F.; Zhang, G.G.Z.; MacGillivray, L.R. Synthon Hierarchies in Crystal Forms Composed of Theophylline and Hydroxybenzoic Acids: Cocrystal Screening via Solution-Mediated Phase Transformation. Cryst. Growth Des. 2014, 14, 5318–5328. [Google Scholar] [CrossRef]
- Gołdyn, M.; Larowska, D.; Nowak, W.; Bartoszak-Adamska, E. Synthon Hierarchy in Theobromine Cocrystals with Hydroxybenzoic Acids as Coformers. CrystEngComm 2019, 21, 7373–7388. [Google Scholar] [CrossRef]
- Bolla, G.; Nangia, A. Supramolecular Synthon Hierarchy in Sulfonamide Cocrystals with Syn-Amides and N-Oxides. IUCrJ 2019, 6, 751–760. [Google Scholar] [CrossRef]
- Malamatari, M.; Ross, S.A.; Douroumis, D.; Velaga, S.P. Experimental Cocrystal Screening and Solution Based Scale-up Cocrystallization Methods. Adv. Drug Deliv. Rev. 2017, 117, 162–177. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Nanda, A. In-Silico Methods of Cocrystal Screening: A Review on Tools for Rational Design of Pharmaceutical Cocrystals. J. Drug Deliv. Sci. Technol. 2021, 63, 102527. [Google Scholar] [CrossRef]
- Khalaji, M.; Potrzebowski, M.J.; Dudek, M.K. Virtual Cocrystal Screening Methods as Tools to Understand the Formation of Pharmaceutical Cocrystals—A Case Study of Linezolid, a Wide-Range Antibacterial Drug. Cryst. Growth Des. 2021, 21, 2301–2314. [Google Scholar] [CrossRef]
- Galek, P.T.A.; Allen, F.H.; Fábián, L.; Feeder, N. Knowledge-Based H-Bond Prediction to Aid Experimental Polymorph Screening. CrystEngComm 2009, 11, 2634–2639. [Google Scholar] [CrossRef]
- Delori, A.; Galek, P.T.; Pidcock, E.; Patni, M.; Jones, W. Knowledge-Based Hydrogen Bond Prediction and the Synthesis of Salts and Cocrystals of the Anti-Malarial Drug Pyrimethamine with Various Drug and GRAS Molecules. CrystEngComm 2013, 15, 2916. [Google Scholar] [CrossRef]
- Fábián, L. Cambridge Structural Database Analysis of Molecular Complementarity in Cocrystals. Cryst. Growth Des. 2009, 9, 1436–1443. [Google Scholar] [CrossRef]
- Mohammad, M.A.; Alhalaweh, A.; Velaga, S.P. Hansen Solubility Parameter as a Tool to Predict Cocrystal Formation. Int. J. Pharm. 2011, 407, 63–71. [Google Scholar] [CrossRef]
- Abramov, Y.A.; Loschen, C.; Klamt, A. Rational Coformer or Solvent Selection for Pharmaceutical Cocrystallization or Desolvation. J. Pharm. Sci. 2012, 101, 3687–3697. [Google Scholar] [CrossRef]
- Musumeci, D.; Hunter, C.A.; Prohens, R.; Scuderi, S.; McCabe, J.F. Virtual Cocrystal Screening. Chem. Sci. 2011, 2, 883–890. [Google Scholar] [CrossRef]
- Cappuccino, C.; Cusack, D.; Flanagan, J.; Harrison, C.; Holohan, C.; Lestari, M.; Walsh, G.; Lusi, M. How Many Cocrystals Are We Missing? Assessing Two Crystal Engineering Approaches to Pharmaceutical Cocrystal Screening. Cryst. Growth Des. 2022, 22, 1390–1397. [Google Scholar] [CrossRef]
- Braga, D.; Maini, L.; Grepioni, F. Mechanochemical Preparation of Co-Crystals. Chem. Soc. Rev. 2013, 42, 7638–7648. [Google Scholar] [CrossRef] [PubMed]
- Boycov, D.E.; Manin, A.N.; Drozd, K.V.; Churakov, A.V.; Perlovich, G.L. Thermal Method Usage Features for Multicomponent Crystal Screening. CrystEngComm 2022, 24, 2280–2290. [Google Scholar] [CrossRef]
- Friščić, T.; Childs, S.L.; Rizvi, S.A.A.; Jones, W. The Role of Solvent in Mechanochemical and Sonochemical Cocrystal Formation: A Solubility-Based Approach for Predicting Cocrystallisation Outcome. CrystEngComm 2009, 11, 418–426. [Google Scholar] [CrossRef]
- Pawar, N.; Saha, A.; Nandan, N.; Parambil, J.V. Solution Cocrystallization: A Scalable Approach for Cocrystal Production. Crystals 2021, 11, 303. [Google Scholar] [CrossRef]
- Manin, A.N.; Drozd, K.V.; Surov, A.O.; Churakov, A.V.; Volkova, T.V.; Perlovich, G.L. Identification of a Previously Unreported Co-Crystal Form of Acetazolamide: A Combination of Multiple Experimental and Virtual Screening Methods. Phys. Chem. Chem. Phys. 2020, 22, 20867–20879. [Google Scholar] [CrossRef]
- Sarkar, N.; Gonnella, N.C.; Krawiec, M.; Xin, D.; Aakeröy, C.B. Evaluating the Predictive Abilities of Protocols Based on Hydrogen-Bond Propensity, Molecular Complementarity, and Hydrogen-Bond Energy for Cocrystal Screening. Cryst. Growth Des. 2020, 20, 7320–7327. [Google Scholar] [CrossRef]
- Grecu, T.; Adams, H.; Hunter, C.A.; McCabe, J.F.; Portell, A.; Prohens, R. Virtual Screening Identifies New Cocrystals of Nalidixic Acid. Cryst. Growth Des. 2014, 14, 1749–1755. [Google Scholar] [CrossRef]
- Cherukuvada, S.; Babu, N.J.; Nangia, A. Nitrofurantoin–P-aminobenzoic Acid Cocrystal: Hydration Stability and Dissolution Rate Studies. J. Pharm. Sci. 2011, 100, 3233–3244. [Google Scholar] [CrossRef]
- Maity, D.K.; Paul, R.K.; Desiraju, G.R. Drug–Drug Binary Solids of Nitrofurantoin and Trimethoprim: Crystal Engineering and Pharmaceutical Properties. Mol. Pharm. 2020, 17, 4435–4442. [Google Scholar] [CrossRef]
- Wijma, R.A.; Fransen, F.; Muller, A.E.; Mouton, J.W. Optimizing Dosing of Nitrofurantoin from a PK/PD Point of View: What Do We Need to Know? Drug Resist. Updates 2019, 43, 1–9. [Google Scholar] [CrossRef]
- Rosenberg, H.A.; Bates, T.R. The Influence of Food on Nitrofurantoin Bioavailability. Clin. Pharmacol. Ther. 1976, 20, 227–232. [Google Scholar] [CrossRef] [PubMed]
- Vangala, V.R.; Chow, P.S.; Tan, R.B.H. Characterization, Physicochemical and Photo-Stability of a Co-Crystal Involving an Antibiotic Drug, Nitrofurantoin, and 4-Hydroxybenzoic Acid. CrystEngComm 2011, 13, 759–762. [Google Scholar] [CrossRef]
- Alhalaweh, A.; George, S.; Basavoju, S.; Childs, S.L.; Rizvi, S.A.A.; Velaga, S.P. Pharmaceutical Cocrystals of Nitrofurantoin: Screening, Characterization and Crystal Structure Analysis. CrystEngComm 2012, 14, 5078–5088. [Google Scholar] [CrossRef]
- Vangala, V.R.; Chow, P.S.; Tan, R.B.H. The Solvates and Salt of Antibiotic Agent, Nitrofurantoin: Structural, Thermochemical and Desolvation Studies. CrystEngComm 2013, 15, 878–889. [Google Scholar] [CrossRef]
- Vangala, V.R.; Chow, P.S.; Tan, R.B.H. Co-Crystals and Co-Crystal Hydrates of the Antibiotic Nitrofurantoin: Structural Studies and Physicochemical Properties. Cryst. Growth Des. 2012, 12, 5925–5938. [Google Scholar] [CrossRef]
- Surov, A.O.; Voronin, A.P.; Drozd, K.V.; Volkova, T.V.; Vasilev, N.; Batov, D.; Churakov, A.V.; Perlovich, G.L. Extending the Range of Nitrofurantoin Solid Forms: Effect of Molecular and Crystal Structure on Formation Thermodynamics and Physicochemical Properties. Cryst. Growth Des. 2022, 22, 2569–2586. [Google Scholar] [CrossRef]
- Tutughamiarso, M.; Bolte, M.; Wagner, G.; Egert, E. Five Pseudopolymorphs and a Cocrystal of Nitrofurantoin. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 2011, 67, 18–25. [Google Scholar] [CrossRef]
- Segalina, A.; Pavan, B.; Ferretti, V.; Spizzo, F.; Botti, G.; Bianchi, A.; Pastore, M.; Dalpiaz, A. Cocrystals of Nitrofurantoin: How Coformers Can Modify Its Solubility and Permeability Across Intestinal Cell Monolayers. Cryst. Growth Des. 2022, 22, 3090–3106. [Google Scholar] [CrossRef]
- Sheldrick, G.M. SADABS, Programs for Scaling and Absorption Correction of Area Detector Data; University of Gottingen: Gottingen, Germany, 1997. [Google Scholar]
- Sheldrick, G.M. A Short History of SHELX. Acta Crystallogr. Sect. A 2008, 64, 112–122. [Google Scholar] [CrossRef]
- Wood, P.A.; Feeder, N.; Furlow, M.; Galek, P.T.A.; Groom, C.R.; Pidcock, E. Knowledge-Based Approaches to Co-Crystal Design. CrystEngComm 2014, 16, 5839–5848. [Google Scholar] [CrossRef]
- MacRae, C.F.; Sovago, I.; Cottrell, S.J.; Galek, P.T.A.; McCabe, P.; Pidcock, E.; Platings, M.; Shields, G.P.; Stevens, J.S.; Towler, M.; et al. Mercury 4.0: From Visualization to Analysis, Design and Prediction. J. Appl. Crystallogr. 2020, 53, 226–235. [Google Scholar] [CrossRef] [PubMed]
- Pidcock, E.; Motherwell, W.D.S. A New Model of Crystal Packing. Chem. Commun. 2003, 24, 3028–3029. [Google Scholar] [CrossRef] [PubMed]
- Taylor, R.; Wood, P.A. A Million Crystal Structures: The Whole Is Greater than the Sum of Its Parts. Chem. Rev. 2019, 119, 9427–9477. [Google Scholar] [CrossRef] [PubMed]
- Gelbrich, T.; Hursthouse, M.B. A Versatile Procedure for the Identification, Description and Quantification of Structural Similarity in Molecular Crystals. CrystEngComm 2005, 7, 324–336. [Google Scholar] [CrossRef]
- Gelbrich, T.; Hursthouse, M.B. Systematic Investigation of the Relationships between 25 Crystal Structures Containing the Carbamazepine Molecule or a Close Analogue: A Case Study of the XPac Method. CrystEngComm 2006, 8, 448–460. [Google Scholar] [CrossRef]
- Murray, J.S.; Politzer, P. Hydrogen Bonding: A Coulombic σ-Hole Interaction. J. Indian Inst. Sci. 2020, 100, 21–30. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C. 01; Gaussian Inc.: Wallingford, CT, USA, 2016; Volume 1. [Google Scholar]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Spackman, M.A.; Jayatilaka, D. Hirshfeld Surface Analysis. CrystEngComm 2009, 11, 19–32. [Google Scholar] [CrossRef]
- Spackman, P.R.; Turner, M.J.; McKinnon, J.J.; Wolff, S.K.; Grimwood, D.J.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer: A Program for Hirshfeld Surface Analysis, Visualization and Quantitative Analysis of Molecular Crystals. J. Appl. Crystallogr. 2021, 54, 1006–1011. [Google Scholar] [CrossRef]
- Dovesi, R.; Erba, A.; Orlando, R.; Zicovich-Wilson, C.M.; Civalleri, B.; Maschio, L.; Rérat, M.; Casassa, S.; Baima, J.; Salustro, S.; et al. Quantum-Mechanical Condensed Matter Simulations with CRYSTAL. WIREs Comput. Mol. Sci. 2018, 8, e1360. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Becke, A. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Manin, A.N.; Voronin, A.P.; Drozd, K.V.; Perlovich, G.L. Thermodynamic Properties of Nalidixic and Oxolinic Acids: Experimental and Computational Study. Thermochim. Acta 2019, 682, 178411. [Google Scholar] [CrossRef]
- Surov, A.O.; Manin, A.N.; Voronin, A.P.; Boycov, D.E.; Magdysyuk, O.V.; Perlovich, G.L. New Pharmaceutical Cocrystal Forms of Flurbiprofen: Structural, Physicochemical, and Thermodynamic Characterization. Cryst. Growth Des. 2019, 19, 5751–5761. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The Calculation of Small Molecular Interactions by the Differences of Separate Total Energies. Some Procedures with Reduced Errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Surov, A.O.; Voronin, A.P.; Vener, M.V.; Churakov, A.V.; Perlovich, G.L. Specific Features of Supramolecular Organisation and Hydrogen Bonding in Proline Cocrystals: A Case Study of Fenamates and Diclofenac. CrystEngComm 2018, 20, 6970–6981. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Tsirelson, V.G.; Ozerov, R.P. Electron Density and Bonding in Crystals: Principles, Theory and X-ray Diffraction Experiments in Solid State Physics and Chemistry; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Shahbazian, S. Why Bond Critical Points Are Not “Bond” Critical Points. Chem. A Eur. J. 2018, 24, 5401–5405. [Google Scholar] [CrossRef]
- Gatti, C.; Saunders, V.R.; Roetti, C. Crystal Field Effects on the Topological Properties of the Electron Density in Molecular Crystals: The Case of Urea. J. Chem. Phys. 1994, 101, 10686–10696. [Google Scholar] [CrossRef]
- Mata, I.; Alkorta, I.; Espinosa, E.; Molins, E. Relationships between Interaction Energy, Intermolecular Distance and Electron Density Properties in Hydrogen Bonded Complexes under External Electric Fields. Chem. Phys. Lett. 2011, 507, 185–189. [Google Scholar] [CrossRef]
- Manin, A.N.; Voronin, A.P.; Manin, N.G.; Vener, M.V.; Shishkina, A.V.; Lermontov, A.S.; Perlovich, G.L. Salicylamide Cocrystals: Screening, Crystal Structure, Sublimation Thermodynamics, Dissolution, and Solid-State DFT Calculations. J. Phys. Chem. B 2014, 118, 6803–6814. [Google Scholar] [CrossRef] [PubMed]
- Gavezzotti, A. Are Crystal Structures Predictable? Acc. Chem. Res. 1994, 27, 309–314. [Google Scholar] [CrossRef]
- Gavezzotti, A.; Filippini, G. Geometry of the Intermolecular X–H···Y (X, Y=N, O) Hydrogen Bond and the Calibration of Empirical Hydrogen-Bond Potentials. J. Phys. Chem. 1994, 98, 4831–4837. [Google Scholar] [CrossRef]
- Boycov, D.E.; Drozd, K.V.; Manin, A.N.; Churakov, A.V.; Perlovich, G.L. New Solid Forms of Nitrofurantoin and 4-Aminopyridine Salt: Influence of Salt Hydration Level on Crystal Packing and Physicochemical Properties. Molecules 2022, 27, 8990. [Google Scholar] [CrossRef]
- Manin, A.N.; Drozd, K.V.; Churakov, A.V.; Perlovich, G.L. Hydrogen Bond Donor/Acceptor Ratios of the Coformers: Do They Really Matter for the Prediction of Molecular Packing in Cocrystals? The Case of Benzamide Derivatives with Dicarboxylic Acids. Cryst. Growth Des. 2018, 18, 5254–5269. [Google Scholar] [CrossRef]
- Khodov, I.; Dyshin, A.; Efimov, S.; Ivlev, D.; Kiselev, M. High-Pressure NMR Spectroscopy in Studies of the Conformational Composition of Small Molecules in Supercritical Carbon Dioxide. J. Mol. Liq. 2020, 309, 113113. [Google Scholar] [CrossRef]
- Khodov, I.; Efimov, S.; Krestyaninov, M.; Kiselev, M. Exposing Hidden Conformations of Carbamazepine Appearing Due to Interaction with the Solid Phase by 2D 1H-15N HMBC NMR Spectroscopy. J. Pharm. Sci. 2021, 110, 1533–1539. [Google Scholar] [CrossRef]
- Sarkar, N.; Sinha, A.S.; Aakeröy, C.B. Systematic Investigation of Hydrogen-Bond Propensities for Informing Co-Crystal Design and Assembly. CrystEngComm 2019, 21, 6048–6055. [Google Scholar] [CrossRef]
- Barua, H.; Gunnam, A.; Yadav, B.; Nangia, A.; Shastri, N.R. An Ab Initio Molecular Dynamics Method for Cocrystal Prediction: Validation of the Approach. CrystEngComm 2019, 21, 7233–7248. [Google Scholar] [CrossRef]
- Sandhu, B.; McLean, A.; Sinha, A.S.; Desper, J.; Sarjeant, A.A.; Vyas, S.; Reutzel-Edens, S.M.; Aakeröy, C.B. Evaluating Competing Intermolecular Interactions through Molecular Electrostatic Potentials and Hydrogen-Bond Propensities. Cryst. Growth Des. 2018, 18, 466–478. [Google Scholar] [CrossRef]
- Vener, M.V.; Levina, E.O.; Koloskov, O.A.; Rykounov, A.A.; Voronin, A.P.; Tsirelson, V.G. Evaluation of the Lattice Energy of the Two-Component Molecular Crystals Using Solid-State Density Functional Theory. Cryst. Growth Des. 2014, 14, 4997–5003. [Google Scholar] [CrossRef]
- Manin, A.N.; Voronin, A.P.; Shishkina, A.V.; Vener, M.V.; Churakov, A.V.; Perlovich, G.L. Influence of Secondary Interactions on the Structure, Sublimation Thermodynamics, and Solubility of Salicylate: 4-Hydroxybenzamide Cocrystals. Combined Experimental and Theoretical Study. J. Phys. Chem. B 2015, 119, 10466–10477. [Google Scholar] [CrossRef]
- Taylor, R. Identifying Intermolecular Atom···atom Interactions That Are Not Just Bonding but Also Competitive. CrystEngComm 2020, 22, 7145–7151. [Google Scholar] [CrossRef]
- Garcia, M.R.; Iribarren, I.; Rozas, I.; Trujillo, C. Simultaneous Hydrogen Bonds with Different Binding Modes: The Acceptor “Rules” but the Donor “Chooses”. Chem. A Eur. J. 2023, 29, e202300717. [Google Scholar] [CrossRef]
- Etter, M.C. Encoding and Decoding Hydrogen-Bond Patterns of Organic Compounds. Acc. Chem. Res. 1990, 23, 120–126. [Google Scholar] [CrossRef]
- Gatti, C. Chemical Bonding in Crystals: New Directions. Z. Krist. Cryst. Mater. 2005, 220, 399–457. [Google Scholar] [CrossRef]
- Vener, M.V.; Churakov, A.V.; Voronin, A.P.; Parashchuk, O.D.; Artobolevskii, S.V.; Alatortsev, O.A.; Makhrov, D.E.; Medvedev, A.G.; Filarowski, A. Comparison of Proton Acceptor and Proton Donor Properties of H2O and H2O2 in Organic Crystals of Drug-like Compounds: Peroxosolvates vs. Crystallohydrates. Molecules 2022, 27, 717. [Google Scholar] [CrossRef] [PubMed]
- Desiraju, G.R.; Gavezzotti, A. Crystal Structures of Polynuclear Aromatic Hydrocarbons. Classification, Rationalization and Prediction from Molecular Structure. Acta Crystallogr. Sect. B 1989, 45, 473–482. [Google Scholar] [CrossRef]
- Burger, A.; Ramberger, R. On the Polymorphism of Pharmaceuticals and Other Molecular Crystals. II. Microchim. Acta 1979, 72, 273–316. [Google Scholar] [CrossRef]
- Perlovich, G.; Surov, A. Polymorphism of Monotropic Forms: Relationships between Thermochemical and Structural Characteristics. Acta Crystallogr. Sect. B 2020, 76, 65–75. [Google Scholar] [CrossRef] [PubMed]
- Civiš, S.; Lamanec, M.; Špirko, V.; Kubišta, J.; Špet’ko, M.; Hobza, P. Hydrogen Bonding with Hydridic Hydrogen–Experimental Low-Temperature IR and Computational Study: Is a Revised Definition of Hydrogen Bonding Appropriate? J. Am. Chem. Soc. 2023, 145, 8550–8559. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Xiao, H.; Liu, N.; Zhang, B.; Shi, Q. Three New Compounds Derived from Nitrofurantoin: X-ray Structures and Hirshfeld Surface Analyses. Open J. Inorg. Chem. 2015, 5, 63–73. [Google Scholar] [CrossRef]


| Method | |||||
|---|---|---|---|---|---|
| MCP | HBP | intHBP | |||
| Hit Rate ≥ 50% | >−0.08 | >0 | >0.08 | >0 | |
| εΣ, % | 50.0 | 61.8 | 55.9 | 58.8 | 76.5 |
| εTP, % | 57.1 | 80.9 | 61.9 | 38.1 | 61.9 |
| εTN, % | 38.4 | 30.7 | 46.2 | 92.4 | 100 |
| [NFT+3AmPy] (1:1) Form I | [NFT+3AmPy] (1:1) Form II | [NFT+ImidPy] (2:1) | |
|---|---|---|---|
| Crystal data | |||
| Chemical formula | C8H6N4O5·C5H6N2 | C8H6N4O5·C5H6N2 | 2(C8H6N4O5)·C8H7N3 |
| Mr | 332.29 | 332.29 | 621.50 |
| Crystal system, space group | Monoclinic, P21/c | Orthorhombic, P212121 | Monoclinic, P21/c |
| Temperature (K) | 150 | 150 | 100 |
| a (Å) | 7.2192 (4) | 6.9736 (5) | 6.5662 (4) |
| b (Å) | 24.3322 (13) | 13.9724 (10) | 13.7101 (8) |
| c (Å) | 16.4729 (8) | 30.187 (2) | 14.3019 (7) |
| α (°) | 90 | 90 | 90 |
| β (°) | 91.087 (2) | 90 | 101.218 (2) |
| γ (°) | 90 | 90 | 90 |
| V (Å3) | 2893.1 (3) | 2941.8 (4) | 1262.90 (12) |
| Z | 8 | 8 | 2 |
| Radiation type | Mo Kα | Mo Kα | Mo Kα |
| μ (mm−1) | 0.121 | 0.119 | 0.131 |
| ρ (mg·m−3) | 1.526 | 1.501 | 1.634 |
| Crystal size (mm) | 0.40 × 0.30 × 0.20 | 0.22 × 0.03 × 0.02 | 0.30 × 0.20 × 0.20 |
| Data collection | |||
| Diffractometer | Bruker SMART APEX II | Bruker D8 Venture | Bruker D8 Venture |
| Absorption correction | Multi-scan SADABS (Bruker, 2016) | ||
| Measured reflns. | 9928 | 5552 | 4788 |
| Independent reflns. | 6312 | 5775 | 3039 |
| observed reflns. with [I > 2σ(I)] | 5283 | 4614 | 2113 |
| Rint | 0.056 | 0.055 | 0.1217 |
| Refinement | |||
| R[F2 > 2σ(F2)] | 0.0605 | 0.0529 | 0.0406 |
| wR(F2) | 0.1315 | 0.1081 | 0.0839 |
| S | 1.14 | 1.06 | 1.06 |
| No. of reflections | 6312 | 5775 | 3039 |
| No. of parameters | 429 | 458 | 203 |
| CCDC No. | 2169245 | 2169244 | 2169243 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manin, A.N.; Voronin, A.P.; Boycov, D.E.; Drozd, K.V.; Churakov, A.V.; Perlovich, G.L. A Combination of Virtual and Experimental Screening Tools for the Prediction of Nitrofurantoin Multicomponent Crystals with Pyridine Derivatives. Crystals 2023, 13, 1022. https://doi.org/10.3390/cryst13071022
Manin AN, Voronin AP, Boycov DE, Drozd KV, Churakov AV, Perlovich GL. A Combination of Virtual and Experimental Screening Tools for the Prediction of Nitrofurantoin Multicomponent Crystals with Pyridine Derivatives. Crystals. 2023; 13(7):1022. https://doi.org/10.3390/cryst13071022
Chicago/Turabian StyleManin, Alex N., Alexander P. Voronin, Denis E. Boycov, Ksenia V. Drozd, Andrei V. Churakov, and German L. Perlovich. 2023. "A Combination of Virtual and Experimental Screening Tools for the Prediction of Nitrofurantoin Multicomponent Crystals with Pyridine Derivatives" Crystals 13, no. 7: 1022. https://doi.org/10.3390/cryst13071022
APA StyleManin, A. N., Voronin, A. P., Boycov, D. E., Drozd, K. V., Churakov, A. V., & Perlovich, G. L. (2023). A Combination of Virtual and Experimental Screening Tools for the Prediction of Nitrofurantoin Multicomponent Crystals with Pyridine Derivatives. Crystals, 13(7), 1022. https://doi.org/10.3390/cryst13071022












