Many-Body Calculations of Excitons in Two-Dimensional GaN
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussion
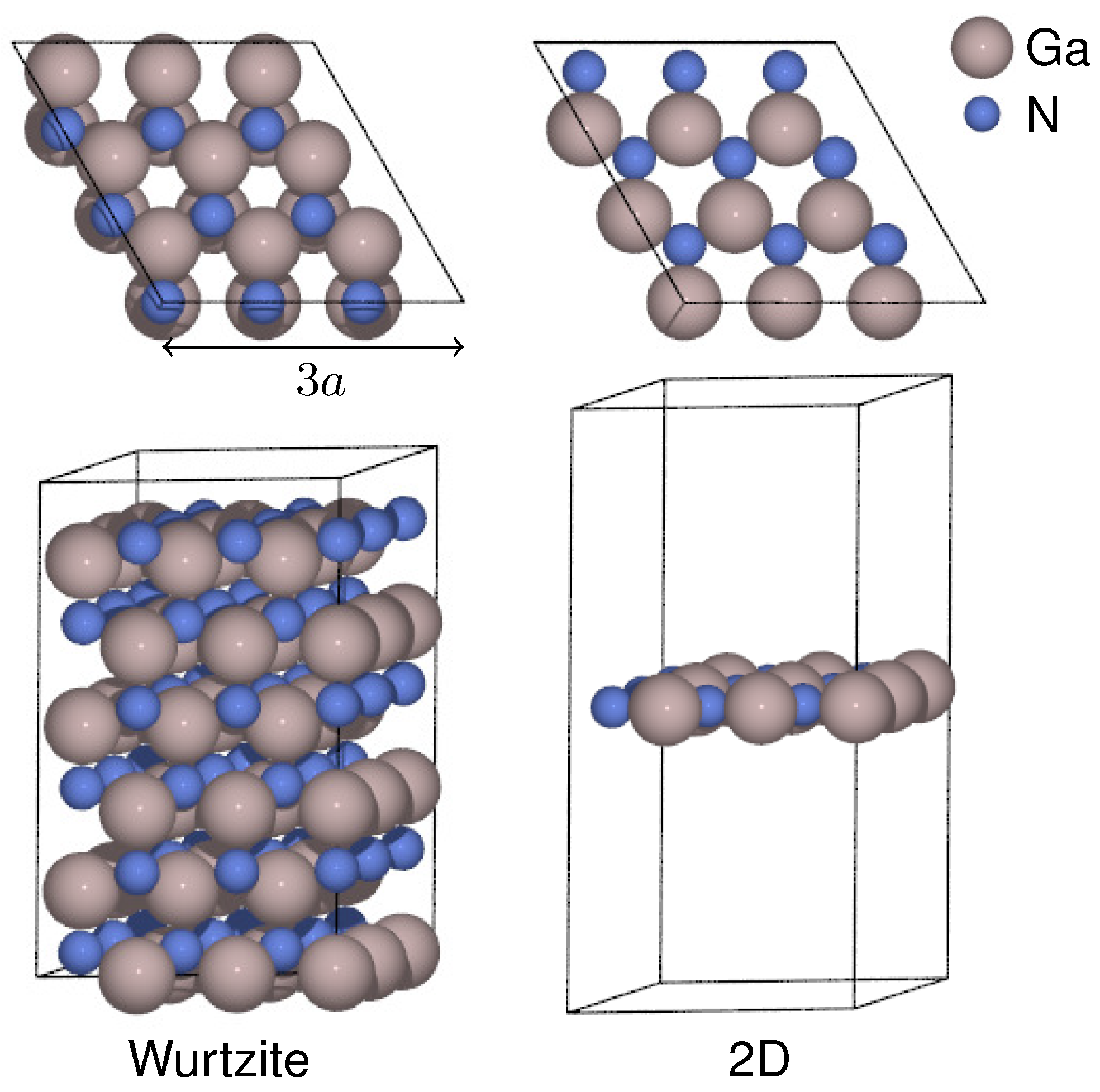
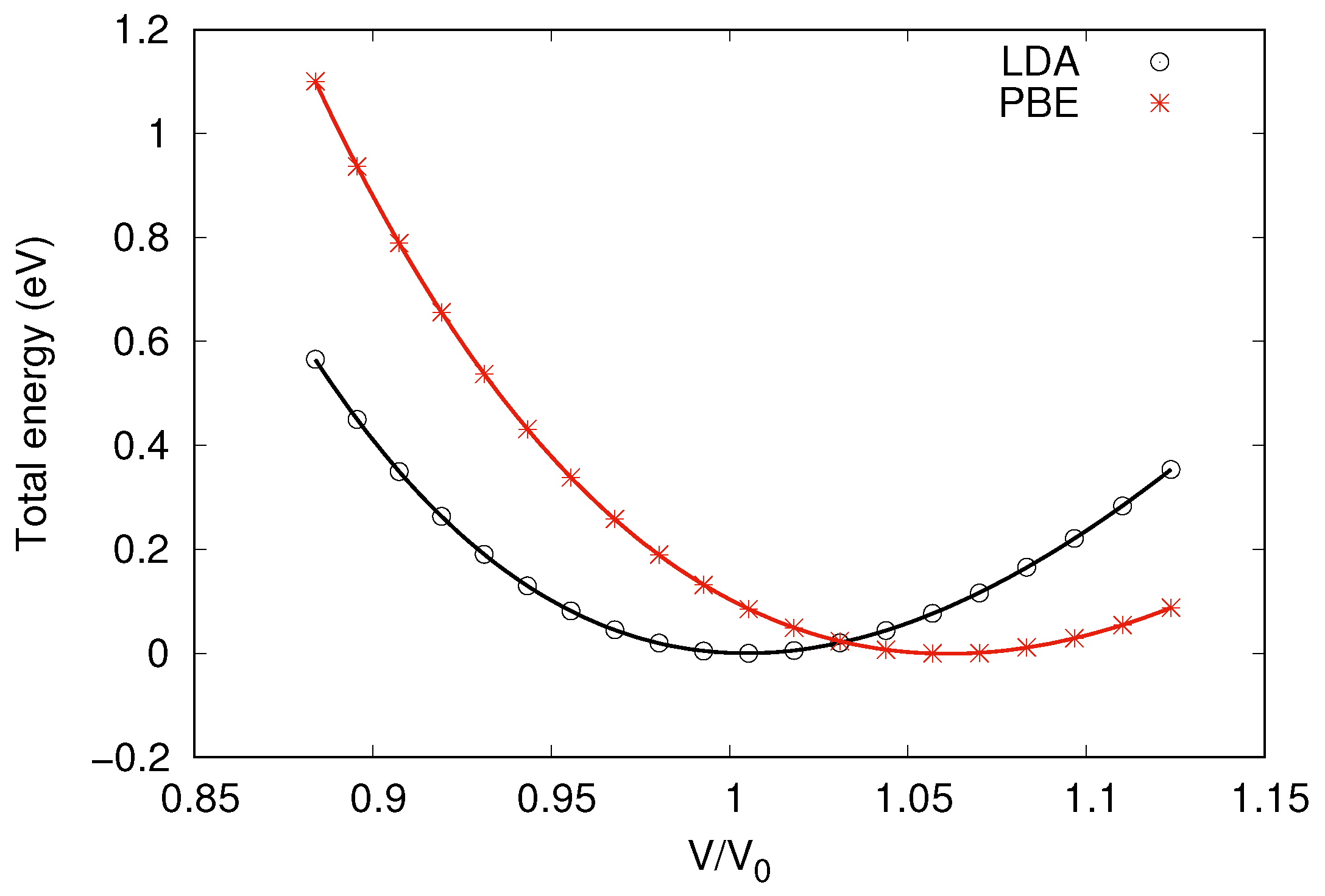
3.1. Atomic Structures
| Material | LDA | PBE | Other Work | Expt. |
|---|---|---|---|---|
| Wurtzite GaN 1 | 3.195 | 3.254 | 3.196/3.252 (LDA/PBE) [62] | 3.190 [61] |
| 2D GaN | 3.218 | 3.272 | 3.21 (PBE) [64] | – |
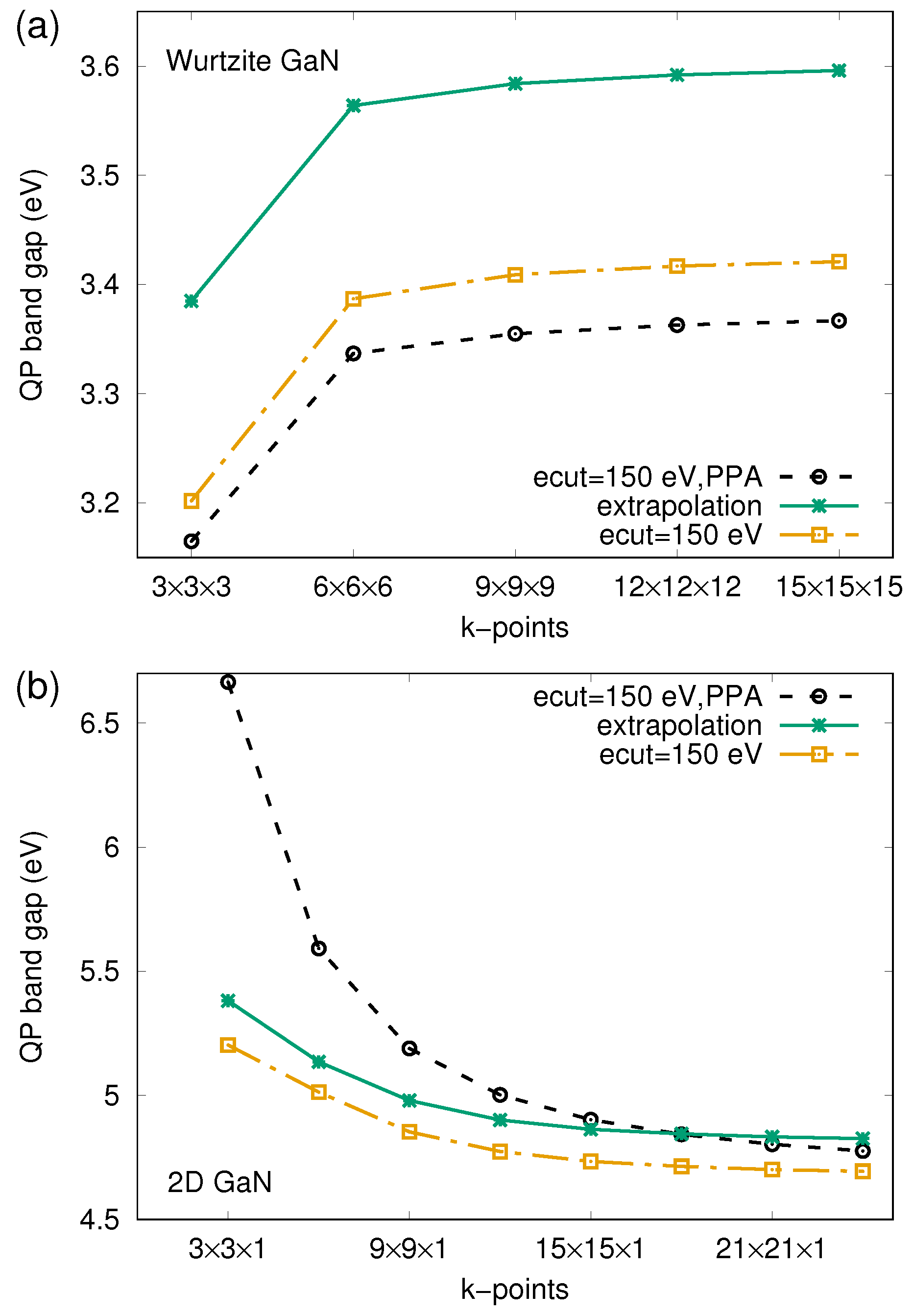
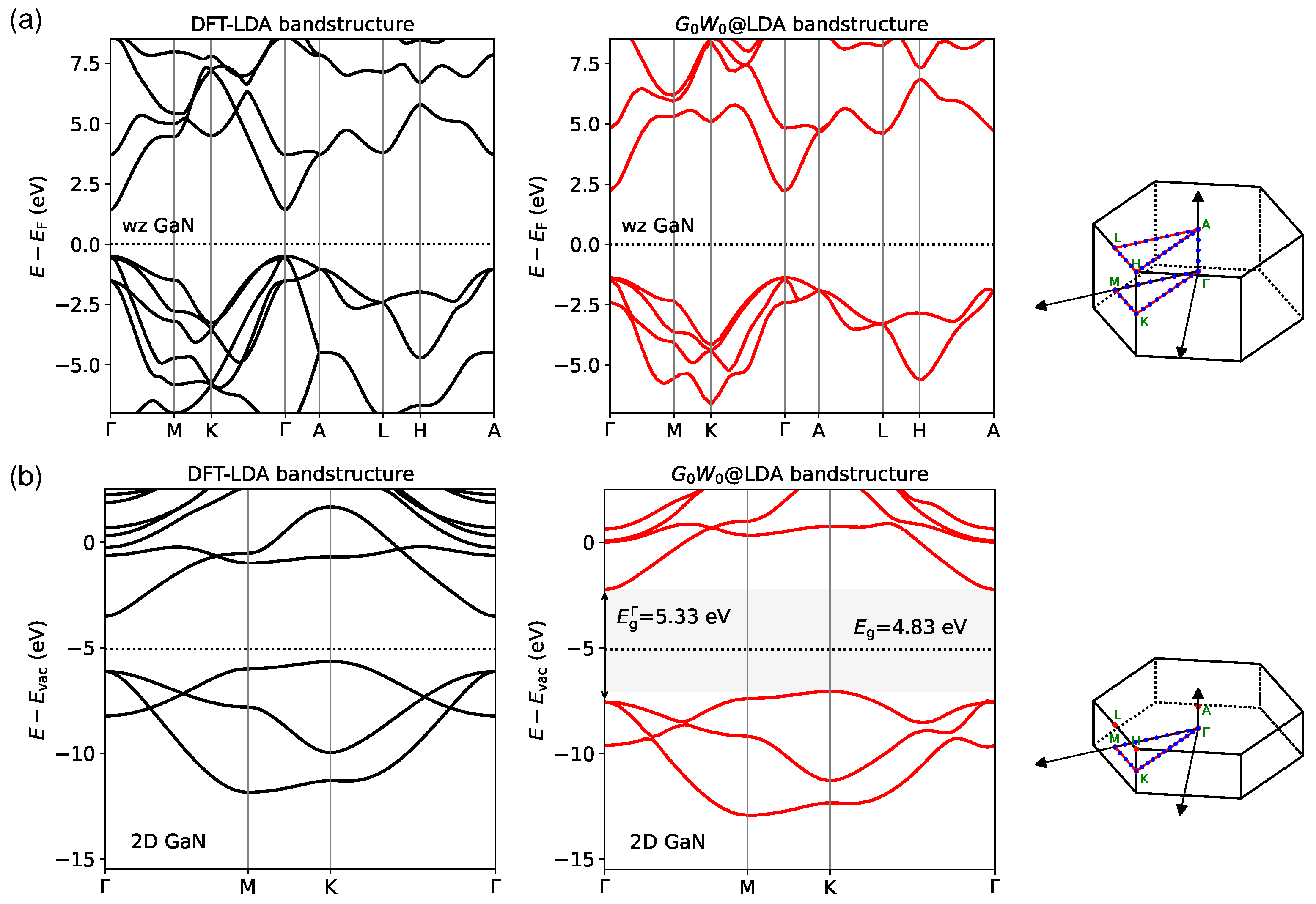
3.2. Quasiparticle Bandstructures
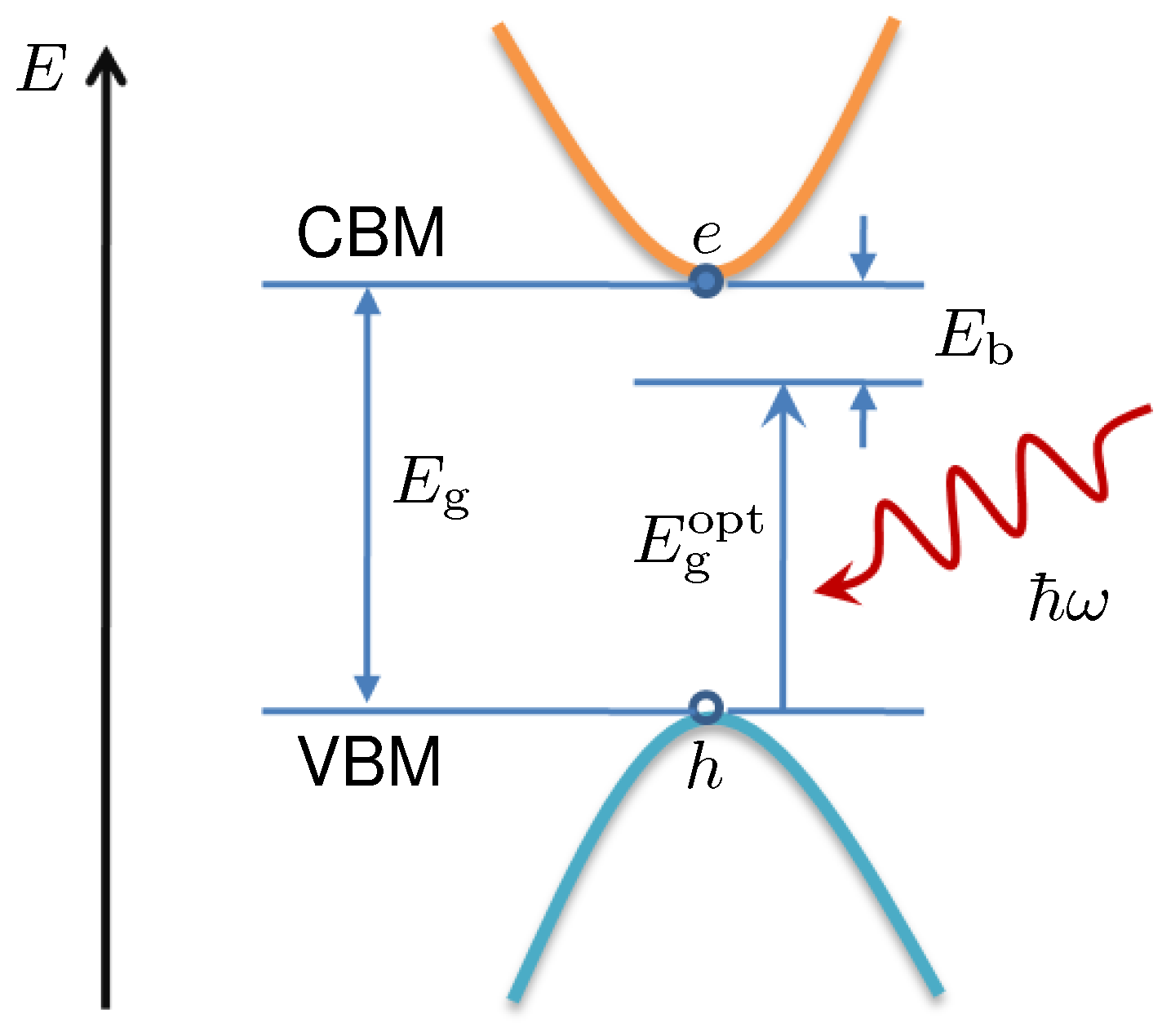
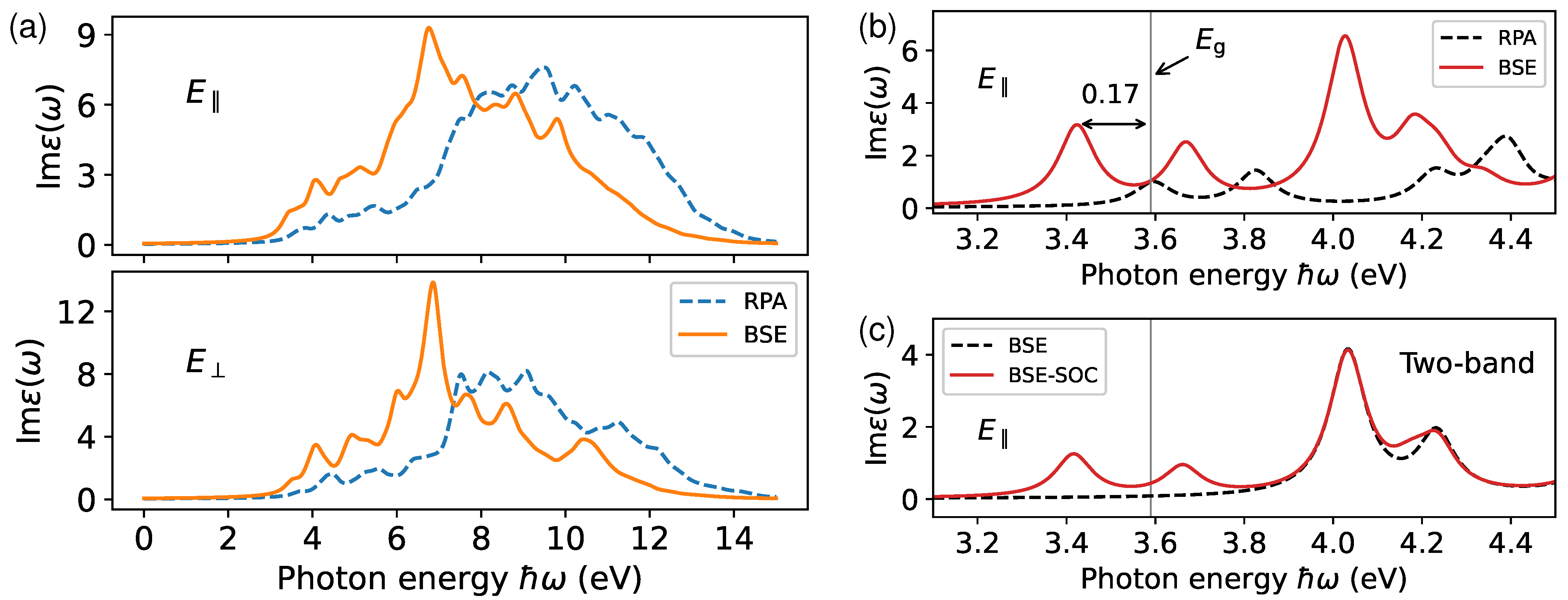
3.3. Excitons
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 2D | Two-dimensional |
| DFT | Density-functional theory |
| BSE | Bethe–Salpeter Equation |
| QP | Quasiparticle |
| RPA | Random-phase approximation |
| PPA | Plasmon-pole approximation |
| PW | Plane wave |
| CBM | Conduction band minimum |
| VBM | Valence band maximum |
| SOC | Spin–orbit coupling |
References
- Strite, S.; Morkoç, H. GaN, AlN, and InN: A review. J. Vac. Sci. Technol. B 1992, 10, 1237–1266. [Google Scholar] [CrossRef]
- Wu, J. When group-III nitrides go infrared: New properties and perspectives. J. Appl. Phys. 2009, 106, 011101. [Google Scholar] [CrossRef]
- Fu, W.Y.; Choi, H.W. Progress and prospects of III-nitride optoelectronic devices adopting lift-off processes. J. Appl. Phys. 2022, 132, 060903. [Google Scholar] [CrossRef]
- Yamada, M.; Mitani, T.; Narukawa, Y.; Shioji, S.; Niki, I.; Sonobe, S.; Deguchi, K.; Sano, M.; Mukai, T. InGaN-Based Near-Ultraviolet and Blue-Light-Emitting Diodes with High External Quantum Efficiency Using a Patterned Sapphire Substrate and a Mesh Electrode. Jpn. J. Appl. Phys. 2002, 41, L1431. [Google Scholar] [CrossRef]
- Mi, Z.; Zhao, S. Extending group-III nitrides to the infrared: Recent advances in InN. Phys. Status Solidi B 2015, 252, 1050–1062. [Google Scholar] [CrossRef]
- Nakamura, S.; Pearton, S.; Fasol, G. The Blue Laser Diode: The Complete Story; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Pushpakaran, B.N.; Subburaj, A.S.; Bayne, S.B. Commercial GaN-Based Power Electronic Systems: A Review. J. Electron. Mater. 2020, 49, 6247. [Google Scholar] [CrossRef]
- Musa, A.Z.; Isa, M.M.; Ahmad, N.; Taking, S.; Musa, F.A. Normally-off GaN HEMT for high power and high-frequency applications. AIP Conf. Proc. 2021, 2347, 020121. [Google Scholar] [CrossRef]
- Bermudez, V. The fundamental surface science of wurtzite gallium nitride. Surf. Sci. Rep. 2017, 72, 147–315. [Google Scholar] [CrossRef]
- Mohanty, S.; Khan, K.; Ahmadi, E. N-polar GaN: Epitaxy, properties, and device applications. Prog. Quant. Electron. 2023, 87, 100450. [Google Scholar] [CrossRef]
- Laskowski, R.; Christensen, N.E.; Santi, G.; Ambrosch-Draxl, C. Ab initio calculations of excitons in GaN. Phys. Rev. B 2005, 72, 035204. [Google Scholar] [CrossRef]
- Adachi, K.; Ogi, H.; Nagakubo, A.; Nakamura, N.; Hirao, M.; Imade, M.; Yoshimura, M.; Mori, Y. Elastic constants of GaN between 10 and 305 K. J. Appl. Phys. 2016, 119, 245111. [Google Scholar] [CrossRef]
- Al Balushi, Z.Y.; Wang, K.; Ghosh, R.K.; Vilá, R.A.; Eichfeld, S.M.; Caldwell, J.D.; Qin, X.; Lin, Y.C.; DeSario, P.A.; Stone, G.; et al. Two-dimensional gallium nitride realized via graphene encapsulation. Nat. Mater. 2016, 15, 1166. [Google Scholar] [CrossRef] [PubMed]
- Bayerl, D.; Islam, S.; Jones, C.M.; Protasenko, V.; Jena, D.; Kioupakis, E. Deep ultraviolet emission from ultra-thin GaN/AlN heterostructures. Appl. Phys. Lett. 2016, 109, 241102. [Google Scholar] [CrossRef]
- Alaal, N.; Roqan, I.S. Tuning the Electronic Properties of Hexagonal Two-Dimensional GaN Monolayers via Doping for Enhanced Optoelectronic Applications. ACS Appl. Nano Mater. 2019, 2, 202–213. [Google Scholar] [CrossRef] [Green Version]
- Geim, A.K.; Grigorieva, I.V. Van der Waals heterostructures. Nature 2013, 499, 419. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Attia, A.A.; Jappor, H.R. Tunable electronic and optical properties of new two-dimensional GaN/BAs van der Waals heterostructures with the potential for photovoltaic applications. Chem. Phys. Lett. 2019, 728, 124–131. [Google Scholar] [CrossRef]
- Sang, L.; Sumiya, M.; Liao, M.; Koide, Y.; Yang, X.; Shen, B. Polarization-induced hole doping for long-wavelength In-rich InGaN solar cells. Appl. Phys. Lett. 2021, 119, 202103. [Google Scholar] [CrossRef]
- Aggarwal, N.; Gupta, G. Enlightening gallium nitride-based UV photodetectors. J. Mater. Chem. C 2020, 8, 12348–12354. [Google Scholar] [CrossRef]
- Moun, M.; Kumar, M.; Garg, M.; Pathak, R. Understanding of MoS2/GaN Heterojunction Diode and its Photodetection Properties. Sci. Rep. 2018, 8, 11799. [Google Scholar] [CrossRef] [Green Version]
- Goswami, L.; Aggarwal, N.; Vashishtha, P.; Jain, S.; Nirantar, S.; Ahmed, J.; Khan, M.; Pandey, R.; Gupta, G. Fabrication of GaN nano-towers based self-powered UV photodetector. Sci. Rep. 2021, 11, 10859. [Google Scholar] [CrossRef]
- Roldán, R.; Chirolli, L.; Prada, E.; Silva-Guillén, J.A.; San-Jose, P.; Guinea, F. Theory of 2D crystals: Graphene and beyond. Chem. Soc. Rev. 2017, 46, 4387–4399. [Google Scholar] [CrossRef] [Green Version]
- Thygesen, K.S. Calculating excitons, plasmons, and quasiparticles in 2D materials and van der Waals heterostructures. 2D Mater. 2017, 4, 022004. [Google Scholar] [CrossRef]
- Onida, G.; Reining, L.; Rubio, A. Electronic Excitations: Density-Functional versus Many-Body Green’s-Function Approaches. Rev. Mod. Phys. 2002, 74, 601–659. [Google Scholar] [CrossRef] [Green Version]
- Blase, X.; Duchemin, I.; Jacquemin, D.; Loos, P.F. The Bethe-Salpeter Equation Formalism: From Physics to Chemistry. J. Phys. Chem. Lett. 2020, 11, 7371–7382. [Google Scholar] [CrossRef] [PubMed]
- Vorwerk, C.; Aurich, B.; Cocchi, C.; Draxl, C. Bethe-Salpeter equation for absorption and scattering spectroscopy: Implementation in the exciting code. Electron. Struct. 2019, 1, 037001. [Google Scholar] [CrossRef]
- Crowley, J.M.; Tahir-Kheli, J.; Goddard, W.A. Resolution of the Band Gap Prediction Problem for Materials Design. J. Phys. Chem. Lett. 2016, 7, 1198–1203. [Google Scholar] [CrossRef]
- Perdew, J.P.; Levy, M. Physical Content of the Exact Kohn-Sham Orbital Energies: Band Gaps and Derivative Discontinuities. Phys. Rev. Lett. 1983, 51, 1884–1887. [Google Scholar] [CrossRef]
- Mori-Sánchez, P.; Cohen, A.J.; Yang, W. Localization and Delocalization Errors in Density Functional Theory and Implications for Band-Gap Prediction. Phys. Rev. Lett. 2008, 100, 146401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rasmussen, F.A.; Thygesen, K.S. Computational 2D Materials Database: Electronic Structure of Transition-Metal Dichalcogenides and Oxides. J. Phys. Chem. C 2015, 119, 13169–13183. [Google Scholar] [CrossRef]
- Yakovkin, I.N. Dirac Cones in Graphene, Interlayer Interaction in Layered Materials, and the Band Gap in MoS2. Crystals 2016, 6, 143. [Google Scholar] [CrossRef] [Green Version]
- Rasmussen, F.A.; Schmidt, P.S.; Winther, K.T.; Thygesen, K.S. Efficient many-body calculations for two-dimensional materials using exact limits for the screened potential: Band gaps of MoS2, h-BN, and phosphorene. Phys. Rev. B 2016, 94, 155406. [Google Scholar] [CrossRef] [Green Version]
- Haastrup, S.; Strange, M.; Pandey, M.; Deilmann, T.; Schmidt, P.S.; Hinsche, N.F.; Gjerding, M.N.; Torelli, D.; Larsen, P.M.; Riis-Jensen, A.C.; et al. The Computational 2D Materials Database: High-throughput modeling and discovery of atomically thin crystals. 2D Mater. 2018, 5, 042002. [Google Scholar] [CrossRef]
- Massicotte, M.; Vialla, F.; Schmidt, P.; Lundeberg, M.B.; Latini, S.; Haastrup, S.; Danovich, M.; Davydovskaya, D.; Watanabe, K.; Taniguchi, T.; et al. Dissociation of two-dimensional excitons in monolayer WSe2. Nat. Commun. 2018, 9, 1633. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sanders, N.; Bayerl, D.; Shi, G.; Mengle, K.A.; Kioupakis, E. Electronic and Optical Properties of Two-Dimensional GaN from First-Principles. Nano Lett. 2017, 17, 7345–7349. [Google Scholar] [CrossRef] [PubMed]
- Peng, B.; Zhang, H.; Shao, H.; Xu, K.; Ni, G.; Wu, L.; Li, J.; Lu, H.; Jin, Q.; Zhu, H. Room-Temperature Bound Exciton with Long Lifetime in Monolayer GaN. ACS Photonics 2018, 5, 4081–4088. [Google Scholar] [CrossRef]
- Shu, H.; Niu, X.; Ding, X.; Wang, Y. Effects of strain and surface modification on stability, electronic and optical properties of GaN monolayer. Appl. Surf. Sci. 2019, 479, 475–481. [Google Scholar] [CrossRef]
- Prete, M.S.; Grassano, D.; Pulci, O.; Kupchak, I.; Olevano, V.; Bechstedt, F. Giant excitonic absorption and emission in two-dimensional group-III nitrides. Sci. Rep. 2020, 10, 10719. [Google Scholar] [CrossRef]
- Andersen, K.; Latini, S.; Thygesen, K.S. Dielectric Genome of van der Waals Heterostructures. Nano Lett. 2015, 15, 4616–4621. [Google Scholar] [CrossRef] [Green Version]
- Latini, S.; Winther, K.T.; Olsen, T.; Thygesen, K.S. Interlayer Excitons and Band Alignment in MoS2/hBN/WSe2 van der Waals Heterostructures. Nano Lett. 2017, 17, 938–945. [Google Scholar] [CrossRef] [Green Version]
- Elliott, J.D.; Colonna, N.; Marsili, M.; Marzari, N.; Umari, P. Koopmans Meets Bethe–Salpeter: Excitonic Optical Spectra without GW. J. Chem. Theory Comput. 2019, 15, 3710–3720. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Jin, Y.; Su, N.Q.; Yang, W. Combining localized orbital scaling correction and Bethe-Salpeter equation for accurate excitation energies. J. Chem. Phys. 2022, 156, 154101. [Google Scholar] [CrossRef]
- Orton, J.W. Exciton spectra and spin-orbit splitting in GaN epitaxial films. Semicond. Sci. Technol. 1997, 12, 64. [Google Scholar] [CrossRef]
- Ren, G.B.; Liu, Y.M.; Blood, P. Valence-band structure of wurtzite GaN including the spin-orbit interaction. Appl. Phys. Lett. 1999, 74, 1117–1119. [Google Scholar] [CrossRef]
- Jhalani, V.A.; Chen, H.Y.; Palummo, M.; Bernardi, M. Precise radiative lifetimes in bulk crystals from first principles: The case of wurtzite gallium nitride. J. Phys. Condens. Matter 2019, 32, 084001. [Google Scholar] [CrossRef]
- Enkovaara, J.; Rostgaard, C.; Mortensen, J.J.; Chen, J.; Dułak, M.; Ferrighi, L.; Gavnholt, J.; Glinsvad, C.; Haikola, V.; Hansen, H.A.; et al. Electronic Structure Calculations with GPAW: A Real-Space Implementation of the Projector Augmented-Wave Method. J. Phys. Condens. Matter 2010, 22, 253202. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perdew, J.P.; Wang, Y. Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Hedin, L. New Method for Calculating the One-Particle Green’s Function with Application to the Electron-Gas Problem. Phys. Rev. 1965, 139, A796–A823. [Google Scholar] [CrossRef]
- Aryasetiawan, F.; Gunnarsson, O. The GW method. Rep. Prog. Phys. 1998, 61, 237–312. [Google Scholar] [CrossRef] [Green Version]
- Hybertsen, M.S.; Louie, S.G. Electron correlation in semiconductors and insulators: Band gaps and quasiparticle energies. Phys. Rev. B 1986, 34, 5390–5413. [Google Scholar] [CrossRef] [PubMed]
- Hüser, F.; Olsen, T.; Thygesen, K.S. Quasiparticle GW calculations for solids, molecules, and two-dimensional materials. Phys. Rev. B 2013, 87, 235132. [Google Scholar] [CrossRef] [Green Version]
- Rasmussen, A.; Deilmann, T.; Thygesen, K.S. Towards fully automated GW band structure calculations: What we can learn from 60.000 self-energy evaluations. npj Comput. Mater. 2021, 7, 22. [Google Scholar] [CrossRef]
- Yan, J.; Jacobsen, K.W.; Thygesen, K.S. Optical properties of bulk semiconductors and graphene/boron nitride: The Bethe-Salpeter equation with derivative discontinuity-corrected density functional energies. Phys. Rev. B 2012, 86, 045208. [Google Scholar] [CrossRef] [Green Version]
- Salpeter, E.E.; Bethe, H.A. A Relativistic Equation for Bound-State Problems. Phys. Rev. 1951, 84, 1232–1242. [Google Scholar] [CrossRef]
- Latini, S. Excitons in van der Waals Heterostructures: A Theoretical Study. Ph.D. Thesis, Technical University of Denmark, Kongens Lyngby, Denmark, 2016. [Google Scholar]
- Olsen, T. Designing in-plane Heterostructures of Quantum Spin Hall Insulators from First Principles: 1T′-MoS2 with Adsorbates. Phys. Rev. B 2016, 94, 235106. [Google Scholar] [CrossRef] [Green Version]
- Alchagirov, A.B.; Perdew, J.P.; Boettger, J.C.; Albers, R.C.; Fiolhais, C. Energy and pressure versus volume: Equations of state motivated by the stabilized jellium model. Phys. Rev. B 2001, 63, 224115. [Google Scholar] [CrossRef]
- Larsen, A.H.; Mortensen, J.J.; Blomqvist, J.; Castelli, I.E.; Christensen, R.; Dułak, M.; Friis, J.; Groves, M.N.; Hammer, B.; Hargus, C.; et al. The atomic simulation environment—A Python library for working with atoms. J. Phys. Condens. Matter 2017, 29, 273002. [Google Scholar] [CrossRef] [Green Version]
- Magnuson, M.; Mattesini, M.; Höglund, C.; Birch, J.; Hultman, L. Electronic structure of GaN and Ga investigated by soft x-ray spectroscopy and first-principles methods. Phys. Rev. B 2010, 81, 085125. [Google Scholar] [CrossRef] [Green Version]
- Rosa, A.L.; Neugebauer, J. First-principles calculations of the structural and electronic properties of clean GaN (0001) surfaces. Phys. Rev. B 2006, 73, 205346. [Google Scholar] [CrossRef]
- Maniš, J.; Mach, J.; Bartošík, M.; Šamořil, T.; Horák, M.; Čalkovský, V.; Nezval, D.; Kachtik, L.; Konečný, M.; Šikola, T. Low temperature 2D GaN growth on Si(111) 7 × 7 assisted by hyperthermal nitrogen ions. Nanoscale Adv. 2022, 4, 3549–3556. [Google Scholar] [CrossRef] [PubMed]
- Onen, A.; Kecik, D.; Durgun, E.; Ciraci, S. GaN: From three- to two-dimensional single-layer crystal and its multilayer van der Waals solids. Phys. Rev. B 2016, 93, 085431. [Google Scholar] [CrossRef]
- Hüser, F.; Olsen, T.; Thygesen, K.S. How dielectric screening in two-dimensional crystals affects the convergence of excited-state calculations: Monolayer MoS2. Phys. Rev. B 2013, 88, 245309. [Google Scholar] [CrossRef] [Green Version]
- Latini, S.; Olsen, T.; Thygesen, K.S. Excitons in van der Waals heterostructures: The important role of dielectric screening. Phys. Rev. B 2015, 92, 245123. [Google Scholar] [CrossRef] [Green Version]
- Ullah, S.S.; Farooq, M.; Din, H.U.; Alam, Q.; Idrees, M.; Bilal, M.; Amin, B. First principles study of electronic and optical properties and photocatalytic performance of GaN-SiS van der Waals heterostructure. RSC Adv. 2021, 11, 32996–33003. [Google Scholar] [CrossRef]
- Rubio, A.; Corkill, J.L.; Cohen, M.L.; Shirley, E.L.; Louie, S.G. Quasiparticle band structure of AlN and GaN. Phys. Rev. B 1993, 48, 11810–11816. [Google Scholar] [CrossRef]
- Reimann, K.; Steube, M.; Fröhlich, D.; Clarke, S. Exciton binding energies and band gaps in GaN bulk crystals. J. Cryst. Growth 1998, 189–190, 652–655. [Google Scholar] [CrossRef]
- Yeo, Y.C.; Chong, T.C.; Li, M.F. Electronic band structures and effective-mass parameters of wurtzite GaN and InN. J. Appl. Phys. 1998, 83, 1429–1436. [Google Scholar] [CrossRef]
- Kuisma, M.; Ojanen, J.; Enkovaara, J.; Rantala, T.T. Kohn-Sham potential with discontinuity for band gap materials. Phys. Rev. B 2010, 82, 115106. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y. Photocatalytic activity of MoS2 with water monolayers: Global optimization. J. Chem. Phys. 2022, 157, 184703. [Google Scholar] [CrossRef]
- Chaves, A.; Azadani, J.G.; Alsalman, H.; da Costa, D.R.; Frisenda, R.; Chaves, A.J.; Song, S.H.; Kim, Y.D.; He, D.; Zhou, J.; et al. Bandgap engineering of two-dimensional semiconductor materials. npj 2D Mater. Appl. 2020, 4, 29. [Google Scholar] [CrossRef]
- Ben, J.; Liu, X.; Wang, C.; Zhang, Y.; Shi, Z.; Jia, Y.; Zhang, S.; Zhang, H.; Yu, W.; Li, D.; et al. 2D III-Nitride Materials: Properties, Growth, and Applications. Adv. Mater. 2021, 33, 2006761. [Google Scholar] [CrossRef] [PubMed]
- Goano, M.; Bellotti, E.; Ghillino, E.; Ghione, G.; Brennan, K.F. Band structure nonlocal pseudopotential calculation of the III-nitride wurtzite phase materials system. Part I. Binary compounds GaN, AlN, and InN. J. Appl. Phys. 2000, 88, 6467–6475. [Google Scholar] [CrossRef]
- Poncé, S.; Jena, D.; Giustino, F. Hole mobility of strained GaN from first principles. Phys. Rev. B 2019, 100, 085204. [Google Scholar] [CrossRef] [Green Version]
- Prete, M.S.; Mosca Conte, A.; Gori, P.; Bechstedt, F.; Pulci, O. Tunable electronic properties of two-dimensional nitrides for light harvesting heterostructures. Appl. Phys. Lett. 2017, 110, 012103. [Google Scholar] [CrossRef]
- Dong, Y.; Li, E.; Cui, Z.; Shen, Y.; Ma, D.; Wang, F.; Yuan, Z.; Yang, K. Electronic properties and photon scattering of buckled and planar few-layer 2D GaN. Vacuum 2023, 210, 111861. [Google Scholar] [CrossRef]
- Li, J.; Jin, Y.; Rinke, P.; Yang, W.; Golze, D. Benchmark of GW Methods for Core-Level Binding Energies. J. Chem. Theory Comput. 2022, 18, 7570–7585. [Google Scholar] [CrossRef]
- Kovalev, D.; Averboukh, B.; Volm, D.; Meyer, B.K.; Amano, H.; Akasaki, I. Free exciton emission in GaN. Phys. Rev. B 1996, 54, 2518–2522. [Google Scholar] [CrossRef]
- Hägele, D.; Zimmermann, R.; Oestreich, M.; Hofmann, M.; Rühle, W.; Meyer, B.; Amano, H.; Akasaki, I. Energy loss rate of excitons in GaN. Physica B 1999, 272, 409–411. [Google Scholar] [CrossRef]
- Olsen, T.; Latini, S.; Rasmussen, F.; Thygesen, K.S. Simple Screened Hydrogen Model of Excitons in Two-Dimensional Materials. Phys. Rev. Lett. 2016, 116, 056401. [Google Scholar] [CrossRef] [Green Version]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y. Many-Body Calculations of Excitons in Two-Dimensional GaN. Crystals 2023, 13, 1048. https://doi.org/10.3390/cryst13071048
Zhang Y. Many-Body Calculations of Excitons in Two-Dimensional GaN. Crystals. 2023; 13(7):1048. https://doi.org/10.3390/cryst13071048
Chicago/Turabian StyleZhang, Yachao. 2023. "Many-Body Calculations of Excitons in Two-Dimensional GaN" Crystals 13, no. 7: 1048. https://doi.org/10.3390/cryst13071048
APA StyleZhang, Y. (2023). Many-Body Calculations of Excitons in Two-Dimensional GaN. Crystals, 13(7), 1048. https://doi.org/10.3390/cryst13071048







