Next Article in Journal
Colored PDLC Films with Wide Gamut Range
Next Article in Special Issue
One Pot Synthesis, Surface, and Magnetic Properties of Ni–NiO@C Nanocomposites
Previous Article in Journal
Effect of Ultrasonic Rolling on the Organization and Properties of a High-Speed Laser Cladding IN 718 Superalloy Coating
Previous Article in Special Issue
Rapid Bio-Assisted Synthesis and Magnetic Behavior of Zinc Oxide/Carbon Nanoparticles
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 13
Issue 8
10.3390/cryst13081215
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Electronic and Optical Properties of Finite Gallium Sulfide Nano Ribbons: A First-Principles Study

by
Omar H. Abd-Elkader
1,*,
Hazem Abdelsalam
2,3,
Mahmoud A. S. Sakr
4,
Nahed H. Teleb
5 and
Qinfang Zhang
2,*
1
Department of Physics and Astronomy, College of Science, King Saud University, P.O. Box 2455, Riyadh 11451, Saudi Arabia
2
School of Materials Science and Engineering, Yancheng Institute of Technology, Yancheng 224051, China
3
Theoretical Physics Department, National Research Centre, El-Buhouth Str., Dokki, Giza 12622, Egypt
4
Center of Basic Science (CBS), Misr University for Science and Technology (MUST), 6th October City 12566, Egypt
5
Electron Microscope and Thin Films Department, National Research Centre, El-Buhouth Str., Dokki, Giza 12622, Egypt
*
Authors to whom correspondence should be addressed.
Crystals 2023, 13(8), 1215; https://doi.org/10.3390/cryst13081215
Submission received: 27 May 2023 / Revised: 27 July 2023 / Accepted: 29 July 2023 / Published: 5 August 2023
(This article belongs to the Special Issue Crystalline Magnetic Compounds)
Browse Figures
Versions Notes

Abstract

:
The electronic and optical properties of finite GaS nanoribbons are investigated using density functional theory calculations. The effect of size, edge termination, and chemical modification by doping and edge passivation are taken into account. The dynamical stability is confirmed by the positive vibration frequency from infrared spectra; further, the positive binding energies ensure the stable formation of the considered nanoribbons. Accurate control of the energy gap has been achieved. For instance, in armchair nanoribbons, energy gaps ranging from ~ 1 to 4 eV were obtained in varying sizes. Moreover, the energy gap can be increased by up to 5.98 eV through edge passivation with F-atoms or decreased to 0.98 eV through doping with Si-atoms. The density of states shows that the occupied molecular orbitals are dominated by S-atoms orbitals, while unoccupied ones are mostly contributed to by Ga orbitals. Thus, S-atoms will be the electron donor sites, and Ga-atoms will be the electron acceptors in the interactions that the nanoribbons might undergo. The nature of electron–hole interactions in the excited states was investigated using various indices, such as electron–hole overlapping, charge–transfer length, and hole–electron Coulomb attraction energy. The UV-Vis absorption spectra reveal a redshift by increasing the size in the armchair or the zigzag directions. Chemical functionalization shows a significant influence on the absorption spectra, where a redshift or blueshift can be achieved depending on the dopant or the attached element.

1. Introduction

Two-dimensional (2D) materials showed and still show exceptional physical and chemical properties that make them one of the top candidates for next-generation technology [1,2,3,4,5,6,7]. Two-dimensional materials are ultrathin and ultralight materials from a single layer, e.g., graphene [8], silicene [9], transition metal dichalcogenides (TMD) [10], and mxenes [11], or a few layers, such as layered graphene [12], phosphorene [13], and heterostructures [14,15]. Their unique properties render them promising in a wide range of applications, including electronics [16,17], optoelectronics [18,19], spintronics [20,21], quantum computing [22,23], sensors [24,25], catalysis [26,27], energy storage [28,29], and photovoltaic [30,31]. Among 2D materials, monolayer GaS has been recently investigated and introduced for different applications, such as hydrogen evolution reactions [32], Li-ion batteries [33], nonlinear optics [34], photodetectors [35], and gas sensors [36]. A monolayer of GaS consists of S-Ga-Ga-S, which is two inner layers from Ga-atoms sandwiched between two layers of S-atoms. It is a semiconductor with a wide band gap of ~3.33 eV that is wider than its bulk counter [37,38]. The electronic, magnetic, and mechanical properties of monolayer GaS have been extensively investigated [38,39,40,41,42]. However, the effect of size, edge termination, and doping on the electronic and optical properties of 2D-GaS quantum dots is still unexplored.
Two-dimensional quantum dots (2DQDs) are small-sized 2D materials ~20 nm or lower with additional control over their properties by size and edge type [43,44,45,46,47]. In these nanodots, the electronic and optical properties can be tuned by tuning the size, where decreasing the size of a material increases its electronic and optical energy gap [48,49,50,51,52]. Another important factor that can improve the properties of quantum dots toward the required application is chemical functionalization which can be achieved by doping [53], vacancies [54,55], or attaching chemical groups [56,57,58,59]. The capacity to control the physical and chemical properties using these factors has greatly widened the application range of 2DQDs. For instance, hBN quantum dots modified with different chemical groups show a high capacity to detect metal ions with boosted adsorption energy compared to the pristine nanodots [60] and noticeable fluorescence quenching [61]. Additionally, chemically modified graphene, phosphorene, TMD, and mxenes quantum dots have also been investigated for sensing and removal of different pollutants [62,63,64,65,66,67]. Two-dimensional quantum dots are promising for catalysis because of their abundant active sites, large specific surface area, energy gap engineering, superior photo-trapping, multi exciton generation [68]. For instance, Mohanty et al. reported that MoS2 QDs are highly performant catalysts for oxygen evolution reaction (OER) with a low overpotential of ~0.37 e [69]. Antimonene nanoclusters show an even lower overpotential of ~0.31 V for OER at the edges [70]. In the field of photovoltaic, three main characteristics are required to achieve highly efficient solar cells. (a) Charge separation on donor and acceptor layers for efficient collection of electrons and holes at the terminals, (b) tiny conduction band offset, and (c) suitable donor energy gap for the adsorption of incident sunlight. These requirements have been achieved in edge-functionalized phosphorene [71] and graphene/silicene [72] quantum dots with noticeable high power conversion efficiency.
In this article, we study the electronic and optical properties of GaS quantum dots or, more specifically, finite nanoribbons. The effect of size, edge termination, and doping are taken into account. The pristine nanoribbons are semiconductors characterized by a wide energy gap that can be decreased to 0.98 eV by doping with Si-atoms or increased to 5.98 eV by edge passivation with F-atoms. Consequently, a wide range of applications can be offered for these finite GaS nanoribbons. The optical properties are also affected by chemical modification, where redshift or blueshift in the UV-Vis spectra can be obtained depending on the dopant or the edge passivation element.

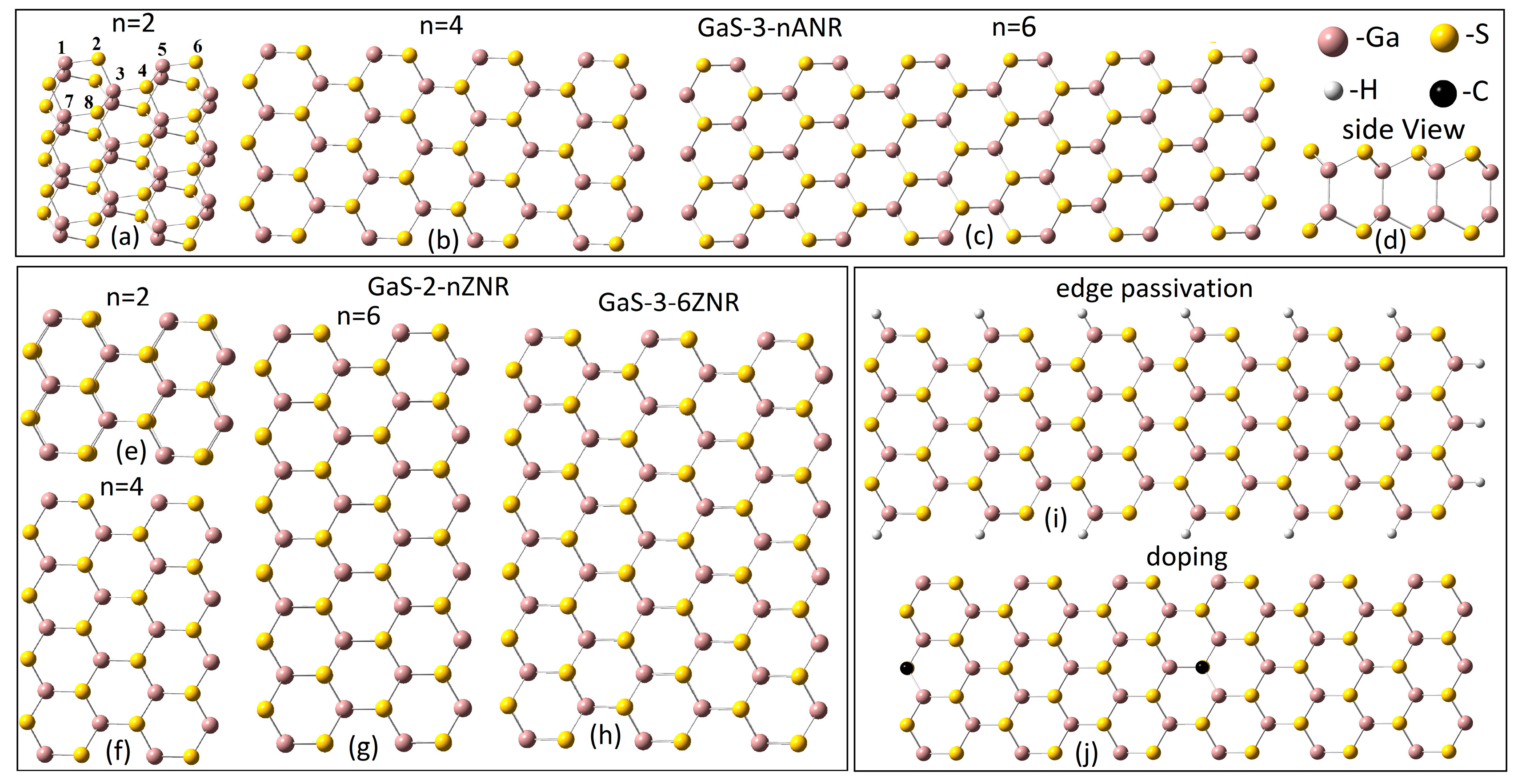
2. Computational Model

The structure optimization, electronic, and optical properties are investigated using density functional theory (DFT) calculations as implemented in Gaussian 16 [73]. The considered functional is the long-range-corrected WB97XD that yields improved accuracy for non-covalent interactions [74,75]. We also consider the LANL2DZ basis set [76] that gives acceptable results accuracy at moderate computational power [77,78]. The considered structures are fully optimized through the minimization of the energy by setting the self-consistent field (SCF) conversion criterion to 10−8. This means that the SCF convergence requires both <10−8 root-mean-square (RMS) change in the density matrix and <10−6 maximum change in the density matrix. All the investigated nanoribbons were built using Gauss View [79]. The optical calculations are performed using time-dependent DFT calculations for the first twenty excited states. For a review of the nature of the excited states and how they are predicted using TD-DFT calculations, see [80,81]. All the hole and electron parameters, such as the overlap between electron and hole density distributions (Sr index), used to describe the nature of the excited states are calculated using Multiwfn software [82].

3. Results and Discussion

Figure 1 shows the finite nanoribbons before and after chemical modification. The GaS nanoribbons with armchair termination are shown in Figure 1a–c. The effect of the armchair edge size is taken into account by considering nanoribbons with two (a), four (b), and six (c) hexagons on the armchair edge. The acronym “GaS-3-nANR” will be used to define the GaS nanoribbons with armchair termination, where three is the fixed number of edge hexagons in the zigzag direction, and n is the number of armchair edge hexagons, n = 2, 4, and 6. The zigzag nanoribbons (GaS-2-nZNR) and the wider one (GaS-3-6ZNR) are shown in Figure 1e–h, respectively. We then select the GaS-3-6ANR for further chemical modifications, namely edge passivation and doping. In order to clearly introduce the considered structures, their molecular formulas are calculated. For instance, the GaS-3-2ANR shown in Figure 1a,d consists of 28 Ga atoms and 28 S atoms, and its molecular formula is then Ga28S28. The molecular formulas of all the considered nanoribbons are provided in Table A2 in Appendix D.

3.1. Structure Stability

The stability of the GaS nanoribbons is investigated by calculating the binding energy and by performing frequency calculations. The binding energy (Eb) is calculated from the equation; Eb = (NGaEGa + NSES + NdEd + NpEp − Et)/Nt. With NGa, NS, and Nt are the numbers of Ga, S, and the total number of atoms, respectively. In cases of chemical modifications, Nd and Np represent the number of dopant and passivating atoms, respectively. EGa, ES, Ed, Ep, and Et are the corresponding total energies of the Ga, S, d, and p atoms and the final compound, respectively. The calculated binding energies are positive, and their values range from 3.7 to 3.9 (eV). These values are also shown for each structure in Figure A1 of Appendix A. The positive values indicate the stable formation of GaS nanoribbons with comparable values to that of other two-dimensional quantum dots such as phosphorene and antimonene nanodots [65,83]. This considerable binding energy is a result of the strong covalently bonded S-Ga-Ga-S atoms that facilitated the fabrication of stable two-dimensional GaS nanoflakes [35]. The values of Eb in Figure A1 show that increasing the length of the nanoribbon in both armchair and zigzag directions leads to an increase in the binding energy. Furthermore, passivation with hydrogen slightly decreases Eb, while doping with two carbon atoms increases it. The infrared (IR) spectra obtained from frequency calculations are the second tool used here to confirm the dynamical stability of the considered structure. The positive vibrational frequencies obtained from the IR spectra shown in Figure A1 indicate that there are no saddle points on the potential energy surface, and all the structures are dynamically stable. It can also be used as a characteristic tool to identify the GaS nanoribbons in experimental synthesis, where the pristine GaS nanoribbon has its vibrational IR peaks at low frequencies, around 500 (cm−1), as seen in Figure A1. While doping with 2O atoms, for instance, introduces two IR peaks at frequencies equal to 600 and 800 cm−1. Furthermore, edge passivation with H-atoms introduces two IR peaks at a frequency of ~2000 cm−1.
The structural properties are also investigated by calculating the bond length, dihedral, and bond angle. Table 1 depicts the optimized structural parameters of GaS-nanoribbons and provides information on bond lengths, bond angles, and dihedral angles. None of the analyzed nanoribbons have a flat surface, as indicated by dihedral angles ranging from 21.290 to 174.94 degrees. Variations in chemical compositions among the nanoribbons result in differences in intermolecular bond lengths and bond angles. For example, increasing the length of armchair edges leads to increased Ga1-S2, Ga3-S4, and Ga7-S8 bond lengths, as given in Table 1. See Figure 1a for the selected eight atoms. Passivating GaS-3-6ANR with hydrogen causes changes in bond lengths. Some bond lengths, such as Ga1-S2 and Ga7-S8, increase, while others, such as Ga3-S4 and S4-Ga5, decrease. Doping GaS-3-6ANR with 2C (presumably carbon) leads to increased Ga1-S2, Ga3-S4, S4-Ga5, and Ga7-S8 bond lengths. None of the systems under study (GaS-3-2ANR, GaS-3-4ANR, GaS-3-6ANR, GaS-2-2ZNR, GaS-2-4ZNR, GaS-2-6ZNR, GaS-3-6ANR-H, and GaS-3-6ANR-2C) exhibit planar side views. This implies that no Ga atom lies in the same plane as any other S atom. To summarize, the findings indicate that the bond angles in GaS-nanoribbons fall within a specific range. Passivation with hydrogens and doping with carbon have contrasting effects on bond lengths. Additionally, the structures of the analyzed nanoribbons are not planar, with Ga and S atoms occupying different planes.

3.2. Electronic Properties

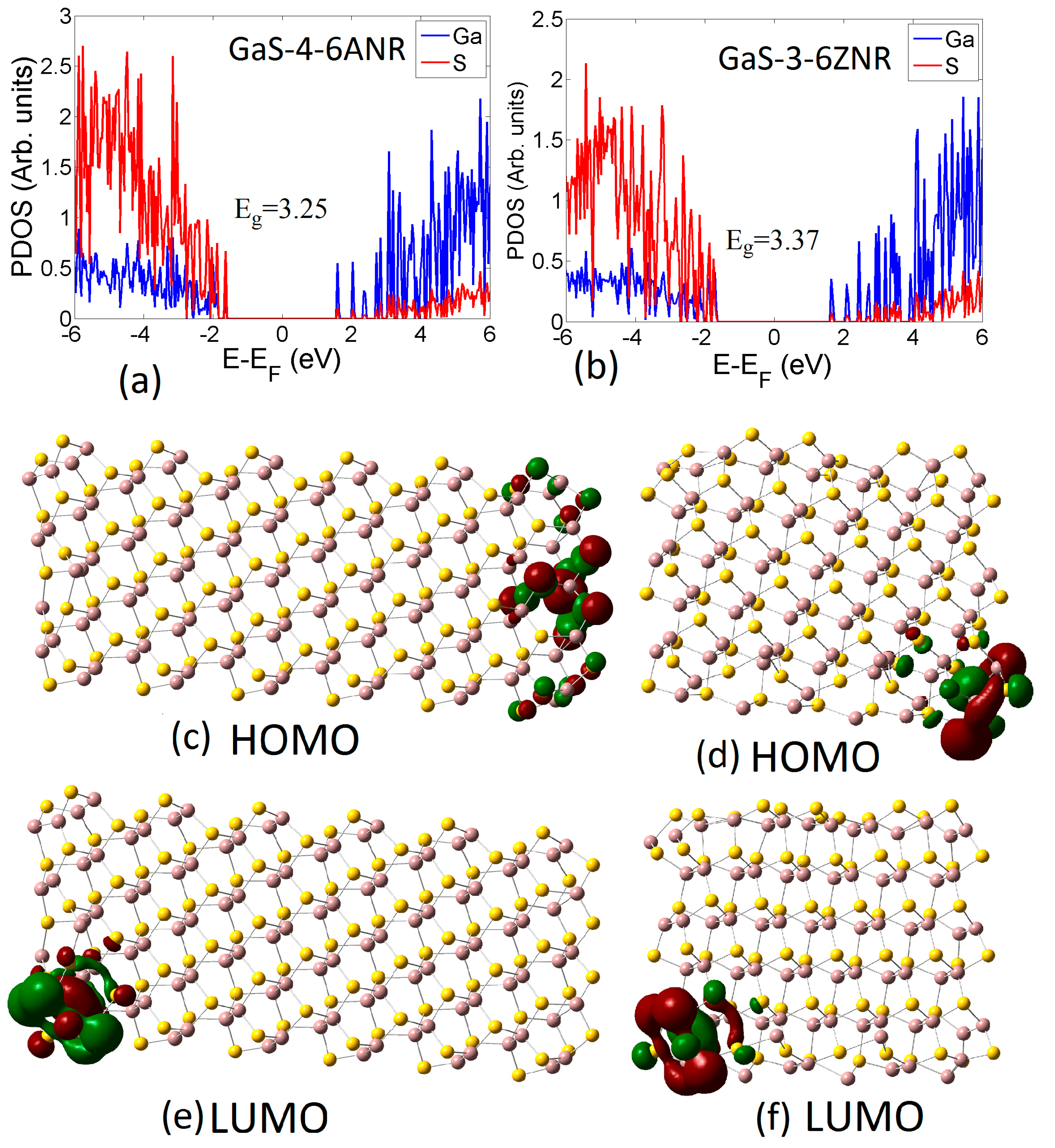
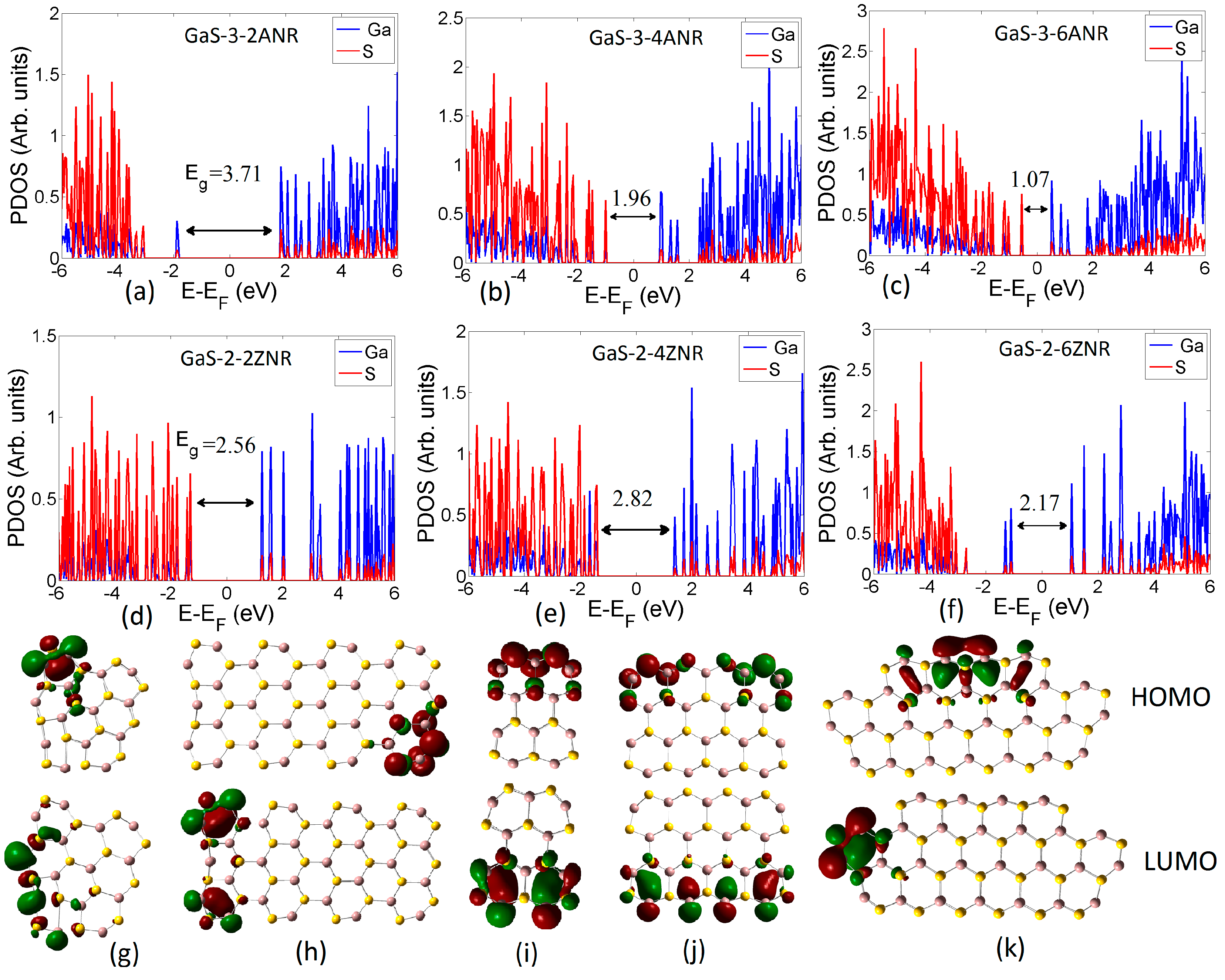
3.2.1. Pristine Nanoribbons

In order to study the electronic properties, the partial density of states (PDOS) and the highest occupied/lowest unoccupied molecular orbitals (HOMO/LUMO) are employed. The PDOS shown in Figure 2a–f was obtained by further analysis of the Gaussian output file using the GaussSum software that calculates the percent contribution of each atom to the molecular orbitals [84]. The PDOS spectra are shifted to 0 eV by setting the x-axis to E-EF, with EF being the Fermi level, EF = EHOMO + ELUMO/2. It is observed from the PDOS that the occupied molecular orbitals are mostly contributed to by S-atoms (red peaks) in both armchair and zigzag GaS nanoribbons. On the other hand, the unoccupied molecular orbitals are mainly contributed to by Ga-atoms, as seen by the blue peaks above the 0 energy in Figure 2a–f. These results are also found in the HOMO/LUMO distributions shown in Figure 2h–j. Where the HOMO cubs mostly distribute on S-atoms and the LUMO cubs on Ga atoms. For example, Figure 2i,j shows that the HOMO distributes on the edge G-atoms while the LUMO distributes on S-atoms on the other side. The HOMO/LUMO of GaS-3-6ANR is not shown because it is similar to that of GaS-3-4ANR in (h). The localized distribution of HOMO cubes explains their origin from the lone pairs electrons in S atoms, while the LUMO shows extended distribution mostly on the Ga-Ga bond. Only in a few cases, such as Figure 2a,f, the HOMO is mainly by Ga atoms at the edges (see Figure 2g,k) due to the high deformation, especially at the edges.
The energy gap (Eg), which is defined as the difference between the energy of the LUMO (ELUMO) and the energy of the HOMO (EHOMO), is also shown in PDOS plots. We found that Eg decreases by increasing the size of the ANR (see Figure 2a–c, which agrees with the quantum size effect. The case of ZNR is slightly different, where the energy gap increases from 2.56 eV in GaS-2-2ZNR to 2.82 eV in GaS-2-4ZNR and then decreases to 2.17 eV in GaS-2-6ZNR. To figure out the main trend of the energy gap, we perform additional calculations on GaS-2-8ZNR and found that Eg decreases to 2.01 eV. Furthermore, calculations on the wide-ZNR in Figure 1h confirm that the energy gap decreases by increasing the size in the zigzag direction. Thus, the energy gap decreases by increasing size in the armchair or zigzag directions.
In contrast, increasing the width of the ANR or ZNR, see Figure A2 of Appendix B, leads to an increase in the energy gap which disagrees with the quantum confinement effect. This peculiar behavior is a result of the edge effect, where in thinner nanoribbons, the edge atoms have higher deformation than in wider ones which in turn results in the formation of low-energy molecular orbitals that decreases the energy gap in the first case. For instance, the edge reconstruction of GaS-2-6ZNR (Figure 2k) after optimization leads to the formation of interactive Ga-atoms at the edge with low-energy molecular orbitals that forms the HOMO and the LUMO. While in the case of GaS-3-6ANR, as shown in Figure A2, the optimized structure is not highly deformed. Furthermore, the HOMO and LUMO distribute on S and G-atoms, respectively, not only on G-atoms.

3.2.2. Chemical Modification

The chemical modification that could occur during experimental synthesis or precisely added is an efficient tool to manipulate the electronic properties of the pristine GaS nanoribbons. It is considered here by (a) substitutional doping of 2S atoms with 2B, 2C, 2Si, 2N, 2O, and 2S atoms and (b) edge passivation of Ga-atoms with H, F, and Cl atoms. Doping and edge passivation have a significant effect on the electronic properties, as shown by PDOS and the HOMO/LUMO distributions in Figure 3. For example, the energy gap of the pristine GaS-3-6ANR increases from 1.07 eV to 2.78 or 3.72 eV by doping with 2B or 2O atoms, see Figure 3a,b. In contrast, it can be decreased to 0.98 eV by doping with 2Si atoms. In the case of increasing the energy gap, the dopant acts like a passivating element with a negligible contribution to the PDOS (Figure 3a,b). Thus the dopants replace the low energy S- peaks with their peaks that are deeper in the valance band, and eventually, the energy gap increases. This is also seen in the HOMO distribution on the S atoms and not on the dopants in Figure 3d,e. On the other hand, dopants that decrease the band gap, such as Si, participate by some of their molecular orbitals to the low energy orbitals, as seen in Figure 3g,j. By edge passivation, a further increase in the energy gap, up to 5.98 eV, can be achieved by attaching F-atoms to Ga at edges, see Figure 3f. Therefore, the electronic properties of GaS nanoribbons can be efficiently tuned to be a semiconductor with tiny, wide, or even insulator energy gaps by chemical modification.
It is worth mentioning that we also calculated the vertical ionization potential (IP) and the vertical electron affinity (EA) to test the accuracy of the DFT calculations. IP is calculated as the difference between the ground state energy of the cation and that of the neutral structure. EA is the difference between the ground state energy of the neutral and the anion. Then the energy of the HOMO (EH) is compared with IP, and the HOMO-LUMO energy gap is compared with the fundamental energy gap (Eg0 = IP-EA). These comparisons are made for selected structures, namely GaS-3-6ANR, GaS-3-6ANR-2B, GaS-3-6ANR-2C, and GaS-3-6ANR-H. The calculations given in Table A1 of Appendix C indicate that the values of IP and Eg0 are slightly different from the corresponding EH and Eg, respectively, for structures with wide energy gaps such as GaS-3-6ANR-2B and GaS-3-6ANR-H. On the other hand, this difference increases in structures with low energy gaps, as shown in Table A1 for GaS-3-6ANR and GaS-3-6ANR-2C. This little correlation between ionization potential/electron affinity and EH/EL is expected in DFT calculations due to the approximation employed for the exchange–correlation function [85].

3.2.3. Quantum Stability

Important quantum stability chemical (QSC) parameters such as dipole moment (μ), chemical potential (ρ), electronegativity (χ), and chemical hardness (η) were calculated using the HOMO energy (EH) and the LUMO (EL) [86,87,88,89]. These QSC parameters are obtained from the following equations ρ = E H + E L 2   , χ = − E H + E L 2 , a n d η = E L − E H 2 . It is important to note that structures with high values of μ exhibit an asymmetry in their electronic charge distribution. Among the structures examined, GaS-3-6ANR has the highest magnitude of μ, as indicated in Table 2, followed by GaS-3-6ANR-2C. This suggests that GaS-3-6ANR experiences more active intramolecular charge transfer compared to other structures. On the other hand, GaS-2-4ZNR has the most negative ρ value with respect to other systems, implying that it has higher electrons escaping than other structures. Electronegativity, which is a measure of the tendency of an atom or a structure to attract electrons, has high values, which indicates that GaS nanoribbons have a high tendency to attract electrons. The highest values of χ were observed in nanoribbons with zigzag termination and doped ones, namely GaS-2-4ZNR with χ = 6.22 and GaS-3-6ANR-2C with χ = 5.91. Passivation with H-atoms decreases χ to 5.21, which is a result of the passivation of edge Ga-atoms. Since chemical hardness (η) is a measure of the resistance to charge transfer, then GaS-3-6ANR-H has the highest resistance toward charge transfer, while GaS-3-6ANR has the lowest resistance. Therefore, we conclude that the reactivity increases by increasing size and doping and decreases by passivation. In the first case, there is an increase in the active sites coming from edge atoms or the dopant that eventually boosts electronegativity and decreases the chemical hardness. In the second case, these decrease by passivating edge atoms.

3.3. Characterization of Excited States

The characterization of excited states plays a crucial role in understanding the electronic structure and properties of molecules. Various indices have been developed to describe the nature of excited states, including overlap between electron and hole density distributions (Sr index), centroid coordinates of holes and electrons (D index), hole–electron Coulomb attraction energy (Ec), hole–electron degree of separation (t index), and charge–transfer length (∆r). Table 3 presents data on various indices, including D, Sr, t, Ec, and Δr. To select representative states, the first excitation state, S1, has been chosen. The ∆r index measures the charge–transfer length during electron excitation. Excitations can be categorized as local excitation (LE) if a hole and an electron are found nearby. Or it can be charge–transfer excitation (CT) when there is significant spatial separation resulting in noticeable charge density displacement. Based on the values of Δr, it can be inferred that the transitions from the ground state (S0) to the excited state S1 in GaS-2-2ZNR predominantly exhibit local excitations (LE). This is evident from the significantly low Δr indices, with a suggested criterion of 2.0 Å to distinguish between LE and CT excitations according to the original paper on Δr [90]. On the other hand, for the other molecular structures listed in Table 3, the Δr indices are higher than 2, indicating the predominance of CT excitations. This finding is supported by the D index values in Table 3, where the distances between the centers of the hole and electron isosurfaces (Chole and Cele centroids) are considerably close to each other in GaS-2-2ZNR, resulting in a small D index value for S1 compared to the other states. These results provide evidence for LE excitation in GaS-2-2ZNR and CT excitation in the other GaS-based materials in their S1 excited states.
The Sr index is then examined, and it is observed that the Sr indices for GaS- are relatively large compared to the other molecular structures. This is attributed to the low value of the D index. Further, In the S0→S1 transition of GaS-2-4ZNR, the Sr value is high, reaching 0.89. This indicates an overlapping between the hole and electron in GaS-2-4ZNR in the S1 excited state, unlike the other studied molecular structures in the same excited state (see Table 3). The t-indices for the excitations from the ground state (S0) to the S1 excited state are negative for GaS-2-2ZNR, GaS-3-6ANR-H, GaS-3-6ANR-F, GaS-3-6ANR-2O, and GaS-3-6ANR-2B. This suggests a very low degree of separation between the holes and electrons in the S1 state of these structures. Conversely, the positive t-index values for the other studied molecular structures indicate a high degree of separation between the holes and electrons in their S1 excited states. The hole–electron Coulomb attractive energy listed in Table 3 is closely related to the characteristics of electron excitation, with the D-index being the most influential factor. As the D-index increases, the Coulomb attractive energy weakens. As shown in Table 3, the hole–electron Coulomb’s attractive energy for GaS-2-4ZNR (Ec = 4.10 eV) in the S1 state is larger than that in the other studied structures. This observation is consistent with the lower D-index value in the S1 state of GaS-2-4ZNR compared to the other studied structures, suggesting a stronger Coulomb attraction between the hole and electron.

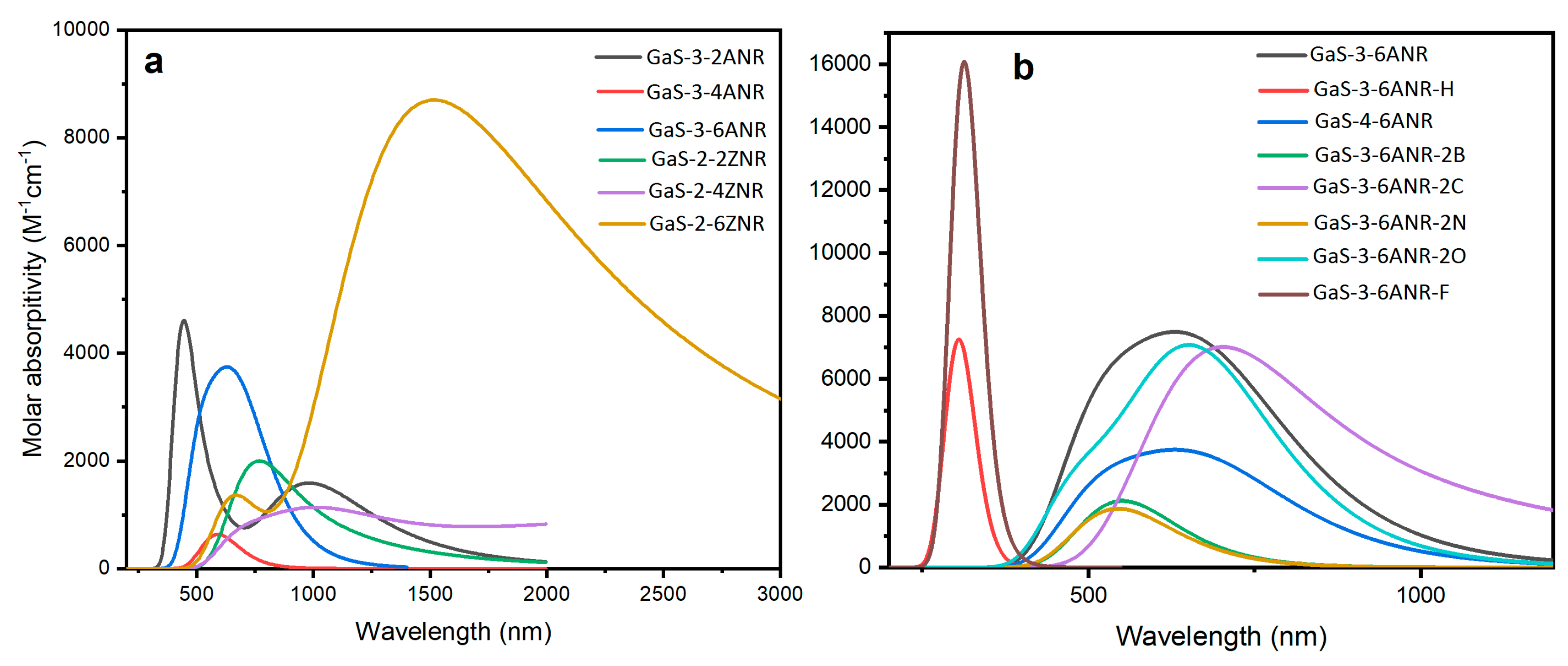
3.4. Optical Properties

In this section, we study the UV-Vis absorption spectra of different GaS nanoribbons. Specifically, GaS-3-2ANR, GaS-3-4ANR, GaS-3-6ANR, GaS-3-6ANR-H, GaS-3-6ANR-F, GaS-3-6ANR-2C, GaS-3-6ANR-2N, GaS-3-6ANR-2O, GaS-3-6ANR-2B, GaS-4-6ANR, GaS-2-2ZNR, GaS-2-4ZNR, and GaS-2-6ZNR. The resulting spectra are shown in Figure 4, and the relevant parameters are provided in Table 4. Our main objective in this section is to investigate the influence of increasing the length of both the armchair and the zigzag edges on the computed electronic absorption spectra. Additionally, we explore the impact of passivation with hydrogen and fluoride, as well as doping with carbon, nitrogen, oxygen, and boron, on the UV-Vis absorption spectra of GaS-3-6ANR.
Since the absorption spectra originate from the electronic transitions between occupied and unoccupied molecular orbitals (MOs), the effects due to size and chemical modification on the optical absorption peaks should agree with the effects observed in the electronic properties. For the effect of increasing the size in the armchair or the zigzag directions, it is observed that the main absorption peak is redshifted to higher wavelengths in agreement with the decrease in the electronic energy gap. Namely, the maximum absorbance wavelengths (λmax) for GaS-3-2ANR, GaS-3-4ANR, and GaS-3-6ANR are 454.34 nm, 590.58 nm, and 616.13 nm, respectively. The corresponding electronic transitions are H-4→L, H-29→L, and H-49→L, respectively, as seen in Table 4. This means that the low energy transitions (H→L and neighbors) are not the main transitions for GaS-nANR, especially for GaS-3-6ANR. Similarly, λmax increases by increasing the zigzag edge size, as shown in Figure 4 and listed in Table 4. Chemical modifications show a significant influence on the absorption spectra of GaS-3-6ANR, where a redshift or a blueshift can be achieved, as shown in Figure 4b. For instance, passivating GaS-3-6ANR with hydrogen and fluoride atoms results in a blueshift in the absorption spectrum; namely, λmax becomes 304.04 and 313.38 nm, respectively. Doping with 2N and 2B leads to a blueshift to lower wavelengths of 541.14 and 558.25 nm, respectively, which agrees with the behavior of the electronic energy gap after passivation and doping. In contrast, doping with 2C and 2O causes a redshift. The case of doping with 2O atoms does not agree with the increase in electronic energy gap by doping with 2O atoms. This is because the main optical transition is from H-1→L+11; thus, the optical excitation energy is now defined by the energy difference between these states and not between the H→L as in the ideal case with the electronic energy gap.

4. Conclusion

In summary, the structure stability and electronic and optical properties of finite GaS-nanoribbons are investigated using density functional theory calculations. The effects of the size, edge type, and chemical modification are taken into account. The stability of the considered structures is confirmed by two factors (a) the positive binding energy and (b) the positive vibrational frequencies responsible for the infrared absorption peaks. The considered nanoribbons are semiconductors with an energy gap that can be smoothly tuned by size (in the range from 1 eV to 3.7 eV) or by chemical functionalization (in the range from 0.98 to 6 eV). For example, passivating Ga-atoms at the edges by F-atoms significantly increases the energy gap to ~ 5.98 eV, while doping the pristine GaS nanoribbon with Si-atoms decreases the energy gap to 0.98 eV. The partial density of states reveals that the density peaks representing the occupied orbitals are mostly contributed to by S-orbitals, while the unoccupied ones are dominated by Ga molecular orbitals. This means that sulfur atoms are the electron-donating sites, and the Ga-atoms are the electron-acceptor ones. The distributions of the highest occupied and lowest unoccupied molecular orbitals confirm the results. Several indices have been calculated, such as charge–transfer length (∆r), electron–hole overlaying (Sr), and hole–electron Coulomb attraction energy (Ec), that help in understanding electron–hole interactions in the excited states. The calculated UV-Vis absorption spectra indicate a redshift toward higher wavelengths by increasing the size in the zigzag or armchair direction, which agrees with the decrease in the electronic energy gap by size increasing. On the other hand, redshift (by doping with C atoms) or blueshift (passivation with H-atoms) can be achieved by chemical functionalization.

Author Contributions

Conceptualization, H.A.; methodology, H.A. and Q.Z.; software, Q.Z.; validation, H.A.; formal analysis, O.H.A.-E.; investigation, H.A.; resources, O.H.A.-E.; data curation, H.A.; writing—original draft preparation, O.H.A.-E., M.A.S.S., N.H.T. and H.A.; writing—review and editing, O.H.A.-E. and Q.Z.; visualization, O.H.A.-E., N.H.T. and M.A.S.S.; supervision, O.H.A.-E. and Q.Z.; project administration, O.H.A.-E. and H.A.; funding acquisition, O.H.A.-E. and Q.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported by the National Natural Science Foundation of China (No. 12274361), the Natural Science Foundation of Jiangsu Province (BK20211361), and College Natural Science Research Project of Jiangsu Province (20KJA430004). This work is supported also by Researchers Supporting Project number (RSP2023R468), King Saud University, Riyadh, Saudi Arabia.

Data Availability Statement

The data presented in this study are available on request from the corresponding authors.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (No. 12274361), the Natural Science Foundation of Jiangsu Province (BK20211361), and College Natural Science Re-search Project of Jiangsu Province (20KJA430004). This work is supported also by Researchers Supporting Project number (RSP2023R468), King Saud University, Riyadh, Saudi Arabia.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

The infrared (IR) spectra of the pristine and chemically modified GaS finite nanoribbons are shown here. It is observed that all the considered structures have positive vibrational frequencies responsible for the IR absorption peaks. It is also observed that pristine GaS nanoribbons have several IR absorption peaks distributing at low frequencies ~ from 300–500 cm−1. The chemical modification introduces additional IR peaks at higher frequencies. For instance, the additional two peaks appear around 2000 cm−1 after passivation with H-atoms, see Figure A1i.
Crystals 13 01215 g0a1
Figure A1. (a–f) The infrared spectra of GaS nanoribbons with different sizes. (g–i) The IR spectra of the selected chemically modified structure.
Figure A1. (a–f) The infrared spectra of GaS nanoribbons with different sizes. (g–i) The IR spectra of the selected chemically modified structure.
Crystals 13 01215 g0a1

Appendix B

The partial density of states (PDOS) and the corresponding HOMO/LUMO of the wider armchair and zigzag nanoribbons are shown in Figure A2.
Crystals 13 01215 g0a2
Figure A2. (a,b) PDOS of the wider armchair and zigzag GaS finite nanoribbons. (c–f) Their HOMO and LUMO distributions.
Figure A2. (a,b) PDOS of the wider armchair and zigzag GaS finite nanoribbons. (c–f) Their HOMO and LUMO distributions.
Crystals 13 01215 g0a2

Appendix C

In this section, we provide the calculated values of the ionization potential (IF), electron affinity (EA), and the fundamental energy gap (Eg0) to compare them with the HOMO, LUMO energies, and the HOMO-LUMO energy gap.
Table A1. The energy of HOMO (EH), the energy of LUMO (EL), the ionization potential (IP), the electron affinity (EF), the HOMO-LUMO energy gap (Eg), and the IP-EF fund energy gap (Eg0).
Table A1. The energy of HOMO (EH), the energy of LUMO (EL), the ionization potential (IP), the electron affinity (EF), the HOMO-LUMO energy gap (Eg), and the IP-EF fund energy gap (Eg0).
CompoundsEH (eV)EL (eV)IP (eV)EF (eV)Eg (eV)Eg0 (eV)
GaS-3-6ANR−6.31−5.235.935.781.070.15
GaS-3-6ANR-2C−6.62−5.196.145.451.430.69
GaS-3-6ANR-2B−7.67−4.897.185.182.782.04
GaS-3-6ANR-H−7.70−2.727.493.164.984.34

Appendix D

For a better understanding of the atomic composition of the investigated structures, their molecular formulas are given in Table A2.
Table A2. The molecular formulas for the considered GaS nanoribbons.
Table A2. The molecular formulas for the considered GaS nanoribbons.
NanoribbonMolecular FormulaNanoribbonMolecular Formula
GaS-3-2ANRGa28S28GaS-3-6ANR-FGa84S84F20
GaS-3-4ANRGa56S56GaS-3-6ANR-2CGa84S82C2
GaS-3-6ANRGa84S84GaS-3-6ANR-2NGa84S82N2
GaS-2-2ZNRGa20S20GaS-3-6ANR-2OGa84S82O2
GaS-2-4ZNRGa36S36GaS-3-6ANR-2BGa84S82B2
GaS-2-6ZNRGa52S52GaS-4-6ANRGa108S108
GaS-3-6ANR-HGa84S84H20GaS-3-6ZNRGa78S78

References

  1. Fiori, G.; Bonaccorso, F.; Iannaccone, G.; Palacios, T.; Neumaier, D.; Seabaugh, A.; Banerjee, S.K.; Colombo, L. Electronics based on two-dimensional materials. Nat. Nanotechnol. 2014, 9, 768–779. [Google Scholar] [CrossRef]
  2. Butler, S.Z.; Hollen, S.M.; Cao, L.; Cui, Y.; Gupta, J.A.; Gutiérrez, H.R.; Heinz, T.F.; Hong, S.S.; Huang, J.; Ismach, A.F. Progress, challenges, and opportunities in two-dimensional materials beyond graphene. ACS Nano 2013, 7, 2898–2926. [Google Scholar] [CrossRef]
  3. Akinwande, D.; Brennan, C.J.; Bunch, J.S.; Egberts, P.; Felts, J.R.; Gao, H.; Huang, R.; Kim, J.-S.; Li, T.; Li, Y. A review on mechanics and mechanical properties of 2D materials—Graphene and beyond. Extrem. Mech. Lett. 2017, 13, 42–77. [Google Scholar] [CrossRef] [Green Version]
  4. Liu, C.; Chen, H.; Wang, S.; Liu, Q.; Jiang, Y.-G.; Zhang, D.W.; Liu, M.; Zhou, P. Two-dimensional materials for next-generation computing technologies. Nat. Nanotechnol. 2020, 15, 545–557. [Google Scholar] [CrossRef] [PubMed]
  5. Hou, L.; Cui, X.; Guan, B.; Wang, S.; Li, R.; Liu, Y.; Zhu, D.; Zheng, J. Synthesis of a monolayer fullerene network. Nature 2022, 606, 507–510. [Google Scholar] [CrossRef] [PubMed]
  6. Kang, S.; Lee, D.; Kim, J.; Capasso, A.; Kang, H.S.; Park, J.-W.; Lee, C.-H.; Lee, G.-H. 2D semiconducting materials for electronic and optoelectronic applications: Potential and challenge. 2D Mater. 2020, 7, 022003. [Google Scholar] [CrossRef]
  7. Jiang, X.; Liu, Q.; Xing, J.; Liu, N.; Guo, Y.; Liu, Z.; Zhao, J. Recent progress on 2D magnets: Fundamental mechanism, structural design and modification. Appl. Phys. Rev. 2021, 8, 031305. [Google Scholar] [CrossRef]
  8. Geim, A.K. Graphene: Status and prospects. Science 2009, 324, 1530–1534. [Google Scholar]
  9. Vogt, P.; De Padova, P.; Quaresima, C.; Avila, J.; Frantzeskakis, E.; Asensio, M.C.; Resta, A.; Ealet, B.; Le Lay, G. Silicene: Compelling experimental evidence for graphenelike two-dimensional silicon. Phys. Rev. Lett. 2012, 108, 155501. [Google Scholar] [CrossRef]
  10. Manzeli, S.; Ovchinnikov, D.; Pasquier, D.; Yazyev, O.V.; Kis, A. 2D transition metal dichalcogenides. Nat. Rev. Mater. 2017, 2, 17033. [Google Scholar] [CrossRef]
  11. Naguib, M.; Barsoum, M.W.; Gogotsi, Y. Ten years of progress in the synthesis and development of MXenes. Adv. Mater. 2021, 33, 2103393. [Google Scholar] [CrossRef] [PubMed]
  12. Kim, H.W.; Yoon, H.W.; Yoon, S.-M.; Yoo, B.M.; Ahn, B.K.; Cho, Y.H.; Shin, H.J.; Yang, H.; Paik, U.; Kwon, S. Selective gas transport through few-layered graphene and graphene oxide membranes. Science 2013, 342, 91–95. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  13. Zhang, S.; Yang, J.; Xu, R.; Wang, F.; Li, W.; Ghufran, M.; Zhang, Y.-W.; Yu, Z.; Zhang, G.; Qin, Q. Extraordinary photoluminescence and strong temperature/angle-dependent Raman responses in few-layer phosphorene. ACS Nano 2014, 8, 9590–9596. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  14. Gibertini, M.; Koperski, M.; Morpurgo, A.F.; Novoselov, K.S. Magnetic 2D materials and heterostructures. Nat. Nanotechnol. 2019, 14, 408–419. [Google Scholar] [CrossRef] [Green Version]
  15. Pham, P.V.; Bodepudi, S.C.; Shehzad, K.; Liu, Y.; Xu, Y.; Yu, B.; Duan, X. 2D heterostructures for ubiquitous electronics and optoelectronics: Principles, opportunities, and challenges. Chem. Rev. 2022, 122, 6514–6613. [Google Scholar] [CrossRef]
  16. Britnell, L.; Gorbachev, R.; Jalil, R.; Belle, B.; Schedin, F.; Mishchenko, A.; Georgiou, T.; Katsnelson, M.; Eaves, L.; Morozov, S. Field-effect tunneling transistor based on vertical graphene heterostructures. Science 2012, 335, 947–950. [Google Scholar] [CrossRef] [Green Version]
  17. Zeng, S.; Tang, Z.; Liu, C.; Zhou, P. Electronics based on two-dimensional materials: Status and outlook. Nano Res. 2021, 14, 1752–1767. [Google Scholar] [CrossRef]
  18. Choi, M.S.; Qu, D.; Lee, D.; Liu, X.; Watanabe, K.; Taniguchi, T.; Yoo, W.J. Lateral MoS2 p–n junction formed by chemical doping for use in high-performance optoelectronics. ACS Nano 2014, 8, 9332–9340. [Google Scholar] [CrossRef]
  19. Liu, Z.; Alshareef, H.N. MXenes for optoelectronic devices. Adv. Electron. Mater. 2021, 7, 2100295. [Google Scholar] [CrossRef]
  20. Ahn, E.C. 2D materials for spintronic devices. Npj 2D Mater. Appl. 2020, 4, 17. [Google Scholar] [CrossRef]
  21. Han, W.; Kawakami, R.K.; Gmitra, M.; Fabian, J. Graphene spintronics. Nat. Nanotechnol. 2014, 9, 794–807. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  22. Iannaccone, G.; Bonaccorso, F.; Colombo, L.; Fiori, G. Quantum engineering of transistors based on 2D materials heterostructures. Nat. Nanotechnol. 2018, 13, 183–191. [Google Scholar] [CrossRef] [PubMed]
  23. Sun, Z.; He, J.; Yuan, M.; Lin, L.; Zhang, Z.; Kang, Z.; Liao, Q.; Li, H.; Sun, G.; Yang, X. Li+-clipping for edge S-vacancy MoS2 quantum dots as an efficient bifunctional electrocatalyst enabling discharge growth of amorphous Li2O2 film. Nano Energy 2019, 65, 103996. [Google Scholar] [CrossRef]
  24. Zhan, B.; Li, C.; Yang, J.; Jenkins, G.; Huang, W.; Dong, X. Graphene field-effect transistor and its application for electronic sensing. Small 2014, 10, 4042–4065. [Google Scholar] [CrossRef] [PubMed]
  25. Anichini, C.; Czepa, W.; Pakulski, D.; Aliprandi, A.; Ciesielski, A.; Samorì, P. Chemical sensing with 2D materials. Chem. Soc. Rev. 2018, 47, 4860–4908. [Google Scholar] [CrossRef] [Green Version]
  26. Lukowski, M.A.; Daniel, A.S.; Meng, F.; Forticaux, A.; Li, L.; Jin, S. Enhanced hydrogen evolution catalysis from chemically exfoliated metallic MoS2 nanosheets. J. Am. Chem. Soc. 2013, 135, 10274–10277. [Google Scholar] [CrossRef]
  27. Gao, G.; O’Mullane, A.P.; Du, A. 2D MXenes: A new family of promising catalysts for the hydrogen evolution reaction. Acs Catal. 2017, 7, 494–500. [Google Scholar] [CrossRef] [Green Version]
  28. Pomerantseva, E.; Gogotsi, Y. Two-dimensional heterostructures for energy storage. Nat. Energy 2017, 2, 17089. [Google Scholar] [CrossRef]
  29. Li, G.; Zhang, D.; Qiao, Q.; Yu, Y.; Peterson, D.; Zafar, A.; Kumar, R.; Curtarolo, S.; Hunte, F.; Shannon, S. All the catalytic active sites of MoS2 for hydrogen evolution. J. Am. Chem. Soc. 2016, 138, 16632–16638. [Google Scholar] [CrossRef]
  30. Suragtkhuu, S.; Sunderiya, S.; Myagmarsereejid, P.; Purevdorj, S.; Bati, A.S.; Bold, B.; Zhong, Y.L.; Davaasambuu, S.; Batmunkh, M. Graphene-Like Monoelemental 2D Materials for Perovskite Solar Cells. Adv. Energy Mater. 2023, 13, 2204074. [Google Scholar] [CrossRef]
  31. Shao, M.; Bie, T.; Yang, L.; Gao, Y.; Jin, X.; He, F.; Zheng, N.; Yu, Y.; Zhang, X. Over 21% efficiency stable 2D perovskite solar cells. Adv. Mater. 2022, 34, 2107211. [Google Scholar] [CrossRef]
  32. Harvey, A.; Backes, C.; Gholamvand, Z.; Hanlon, D.; McAteer, D.; Nerl, H.C.; McGuire, E.; Seral-Ascaso, A.; Ramasse, Q.M.; McEvoy, N. Preparation of gallium sulfide nanosheets by liquid exfoliation and their application as hydrogen evolution catalysts. Chem. Mater. 2015, 27, 3483–3493. [Google Scholar] [CrossRef]
  33. Zhang, C.; Park, S.H.; Ronan, O.; Harvey, A.; Seral-Ascaso, A.; Lin, Z.; McEvoy, N.; Boland, C.S.; Berner, N.C.; Duesberg, G.S. Enabling flexible heterostructures for Li-ion battery anodes based on nanotube and liquid-phase exfoliated 2D gallium chalcogenide nanosheet colloidal solutions. Small 2017, 13, 1701677. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  34. Ahmed, S.; Cheng, P.K.; Qiao, J.; Gao, W.; Saleque, A.M.; Al Subri Ivan, M.N.; Wang, T.; Alam, T.I.; Hani, S.U.; Guo, Z.L. Nonlinear Optical Activities in Two-Dimensional Gallium Sulfide: A Comprehensive Study. ACS Nano 2022, 16, 12390–12402. [Google Scholar] [CrossRef] [PubMed]
  35. Zappia, M.I.; Bianca, G.; Bellani, S.; Curreli, N.; Sofer, Z.k.; Serri, M.; Najafi, L.; Piccinni, M.; Oropesa-Nuñez, R.; Marvan, P. Two-dimensional gallium sulfide nanoflakes for UV-selective photoelectrochemical-type photodetectors. J. Phys. Chem. C 2021, 125, 11857–11866. [Google Scholar] [CrossRef]
  36. Opoku, F.; Akoto, O.; Asare-Donkor, N.K.; Adimado, A.A. Defect-engineered two-dimensional layered gallium sulphide molecular gas sensors with ultrahigh selectivity and sensitivity. Appl. Surf. Sci. 2021, 562, 150188. [Google Scholar] [CrossRef]
  37. Ho, C.; Lin, S. Optical properties of the interband transitions of layered gallium sulfide. J. Appl. Phys. 2006, 100, 083508. [Google Scholar] [CrossRef]
  38. Lu, Y.; Warner, J.H. Synthesis and applications of wide bandgap 2D layered semiconductors reaching the green and blue wavelengths. ACS Appl. Electron. Mater. 2020, 2, 1777–1814. [Google Scholar] [CrossRef]
  39. Chen, H.; Li, Y.; Huang, L.; Li, J. Influential electronic and magnetic properties of the gallium sulfide monolayer by substitutional doping. J. Phys. Chem. C 2015, 119, 29148–29156. [Google Scholar] [CrossRef]
  40. Yagmurcukardes, M.; Senger, R.T.; Peeters, F.M.; Sahin, H. Mechanical properties of monolayer GaS and GaSe crystals. Phys. Rev. B 2016, 94, 245407. [Google Scholar] [CrossRef] [Green Version]
  41. Rai, J.; Gautam, S. Computational quantum chemical analysis of structural and electronic properties of functionalized gallium sulfide (GaS) nanoflakes. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
  42. Stolbov, S. Local defects in two-dimensional gallium sulfide as potential single-photon emitters: First-principles evaluation. Phys. Rev. B 2022, 106, 245205. [Google Scholar] [CrossRef]
  43. Sun, H.; Wu, L.; Wei, W.; Qu, X. Recent advances in graphene quantum dots for sensing. Mater. Today 2013, 16, 433–442. [Google Scholar] [CrossRef]
  44. Abdelsalam, H.; Talaat, M.H.; Lukyanchuk, I.; Portnoi, M.; Saroka, V. Electro-absorption of silicene and bilayer graphene quantum dots. J. Appl. Phys. 2016, 120, 014304. [Google Scholar] [CrossRef] [Green Version]
  45. Saroka, V.; Lukyanchuk, I.; Portnoi, M.; Abdelsalam, H. Electro-optical properties of phosphorene quantum dots. Phys. Rev. B 2017, 96, 085436. [Google Scholar] [CrossRef] [Green Version]
  46. Jing, F.M.; Zhang, Z.Z.; Qin, G.Q.; Luo, G.; Cao, G.; Li, H.O.; Song, X.X.; Guo, G.P. Gate-Controlled Quantum Dots Based on 2D Materials. Adv. Quantum Technol. 2022, 5, 2100162. [Google Scholar] [CrossRef]
  47. Abdelsalam, H.; Zhang, Q.F. Properties and applications of quantum dots derived from two-dimensional materials. Adv. Phys. X 2022, 7, 2048966. [Google Scholar] [CrossRef]
  48. Tang, L.; Ji, R.; Li, X.; Teng, K.S.; Lau, S.P. Size-dependent structural and optical characteristics of glucose-derived graphene quantum dots. Part. Part. Syst. Charact. 2013, 30, 523–531. [Google Scholar] [CrossRef]
  49. Zhang, Z.; Chang, K.; Peeters, F. Tuning of energy levels and optical properties of graphene quantum dots. Phys. Rev. B 2008, 77, 235411. [Google Scholar] [CrossRef] [Green Version]
  50. Saroka, V.; Abdelsalam, H.; Demin, V.; Grassano, D.; Kuten, S.; Pushkarchuk, A.; Pulci, O. Absorption in finite-length chevron-type graphene nanoribbons. Semiconductors 2018, 52, 1890–1893. [Google Scholar] [CrossRef]
  51. Kundu, S.; Pillai, V.K. Synthesis and characterization of graphene quantum dots. Phys. Sci. Rev. 2019, 5, 20190013. [Google Scholar] [CrossRef]
  52. Abdelsalam, H.; Saroka, V.A.; Atta, M.M.; Osman, W.; Zhang, Q. Tunable electro-optical properties of doped chiral graphene nanoribbons. Chem. Phys. 2021, 544, 111116. [Google Scholar] [CrossRef]
  53. Kundu, S.; Yadav, R.M.; Narayanan, T.; Shelke, M.V.; Vajtai, R.; Ajayan, P.M.; Pillai, V.K. Synthesis of N, F and S co-doped graphene quantum dots. Nanoscale 2015, 7, 11515–11519. [Google Scholar] [CrossRef] [PubMed]
  54. Zhang, J.; Xu, W.; Wang, L.; Zheng, Z.; Liu, F.; Yu, P.; Yang, G. Colossal Vacancy Effect of 2D CuInP2S6 Quantum Dots for Enhanced Broadband Photodetection. Cryst. Growth Des. 2023, 23, 1259–1268. [Google Scholar] [CrossRef]
  55. Ali, S.R.; De, M. Defect-Engineered Functionalized MoS2 Quantum Dots with Enhanced Antibacterial Activity. ACS Appl. Nano Mater. 2023, 6, 2193–2202. [Google Scholar] [CrossRef]
  56. Abdelsalam, H.; Elhaes, H.; Ibrahim, M.A. Tuning electronic properties in graphene quantum dots by chemical functionalization: Density functional theory calculations. Chem. Phys. Lett. 2018, 695, 138–148. [Google Scholar] [CrossRef]
  57. Abdelsalam, H.; Saroka, V.A.; Ali, M.; Teleb, N.H.; Elhaes, H.; Ibrahim, M.A. Stability and electronic properties of edge functionalized silicene quantum dots: A first principles study. Phys. E Low-Dimens. Syst. Nanostructures 2019, 108, 339–346. [Google Scholar] [CrossRef]
  58. Gui, R.; Jin, H.; Wang, Z.; Li, J. Black phosphorus quantum dots: Synthesis, properties, functionalized modification and applications. Chem. Soc. Rev. 2018, 47, 6795–6823. [Google Scholar] [CrossRef]
  59. Musselman, K.P.; Ibrahim, K.H.; Yavuz, M. Research Update: Beyond graphene—Synthesis of functionalized quantum dots of 2D materials and their applications. APL Mater. 2018, 6, 120701. [Google Scholar] [CrossRef]
  60. Abdelsalam, H.; Younis, W.; Saroka, V.; Teleb, N.; Yunoki, S.; Zhang, Q. Interaction of hydrated metals with chemically modified hexagonal boron nitride quantum dots: Wastewater treatment and water splitting. Phys. Chem. Chem. Phys. 2020, 22, 2566–2579. [Google Scholar] [CrossRef]
  61. Liu, B.; Yan, S.; Song, Z.; Liu, M.; Ji, X.; Yang, W.; Liu, J. One-step synthesis of boron nitride quantum dots: Simple chemistry meets delicate nanotechnology. Chem.–Eur. J. 2016, 22, 18899–18907. [Google Scholar] [CrossRef] [PubMed]
  62. Zhou, C.; Jiang, W.; Via, B.K. Facile synthesis of soluble graphene quantum dots and its improved property in detecting heavy metal ions. Colloids Surf. B Biointerfaces 2014, 118, 72–76. [Google Scholar] [CrossRef] [PubMed]
  63. Abdelsalam, H.; Teleb, N.; Yahia, I.; Zahran, H.; Elhaes, H.; Ibrahim, M. First principles study of the adsorption of hydrated heavy metals on graphene quantum dots. J. Phys. Chem. Solids 2019, 130, 32–40. [Google Scholar] [CrossRef]
  64. Prasongkit, J.; Shukla, V.; Grigoriev, A.; Ahuja, R.; Amornkitbamrung, V. Ultrahigh-sensitive gas sensors based on doped phosphorene: A first-principles investigation. Appl. Surf. Sci. 2019, 497, 143660. [Google Scholar] [CrossRef]
  65. Abdelsalam, H.; Saroka, V.A.; Younis, W.O. Phosphorene quantum dot electronic properties and gas sensing. Phys. E Low-Dimens. Syst. Nanostructures 2019, 107, 105–109. [Google Scholar] [CrossRef] [Green Version]
  66. Guo, Y.; Li, J. MoS2 quantum dots: Synthesis, properties and biological applications. Mater. Sci. Eng. C 2020, 109, 110511. [Google Scholar] [CrossRef] [PubMed]
  67. Khan, K.; Tareen, A.K.; Iqbal, M.; Ye, Z.; Xie, Z.; Mahmood, A.; Mahmood, N.; Zhang, H. Recent Progress in Emerging Novel MXenes Based Materials and their Fascinating Sensing Applications. Small 2023, 19, 2206147. [Google Scholar] [CrossRef]
  68. Su, H.; Wang, W.; Shi, R.; Tang, H.; Sun, L.; Wang, L.; Liu, Q.; Zhang, T. Recent advances in quantum dot catalysts for hydrogen evolution: Synthesis, characterization, and photocatalytic application. Carbon Energy 2023, e280. [Google Scholar] [CrossRef]
  69. Mohanty, B.; Ghorbani-Asl, M.; Kretschmer, S.; Ghosh, A.; Guha, P.; Panda, S.K.; Jena, B.; Krasheninnikov, A.V.; Jena, B.K. MoS2 quantum dots as efficient catalyst materials for the oxygen evolution reaction. Acs Catal. 2018, 8, 1683–1689. [Google Scholar] [CrossRef]
  70. Abdelsalam, H.; Teleb, N.; Wang, B.; Yunoki, S.; Zhang, Q. The electronic, adsorption, and catalytic properties of Bi-, Sb-, and As-nanoclusters. Catal. Today 2021, 376, 126–133. [Google Scholar] [CrossRef]
  71. Hu, W.; Lin, L.; Yang, C.; Dai, J.; Yang, J. Edge-modified phosphorene nanoflake heterojunctions as highly efficient solar cells. Nano Lett. 2016, 16, 1675–1682. [Google Scholar] [CrossRef]
  72. Abdelsalam, H.; Atta, M.M.; Osman, W.; Zhang, Q. Two-dimensional quantum dots for highly efficient heterojunction solar cells. J. Colloid Interface Sci. 2021, 603, 48–57. [Google Scholar] [CrossRef]
  73. Frisch, M.; Trucks, G.; Schlegel, H.; Scuseria, G.; Robb, M.; Cheeseman, J.; Scalmani, G.; Barone, V.; Petersson, G.; Nakatsuji, H. Gaussian 16 Revision C. 01. 2016; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  74. Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  75. Chen, Z.; Li, Y.; He, Z.; Xu, Y.; Yu, W. Theoretical investigations on charge transport properties of tetrabenzo [a, d, j, m] coronene derivatives using different density functional theory functionals (B3LYP, M06-2X, and wB97XD). J. Chem. Res. 2019, 43, 293–303. [Google Scholar] [CrossRef]
  76. Hay, P.J.; Wadt, W.R. Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg. J. Chem. Phys. 1985, 82, 270–283. [Google Scholar] [CrossRef]
  77. Abdelsalam, H.; Abd-Elkader, O.H.; Zaghloul, N.S.; Zhang, Q. Magnetic and Electronic Properties of Edge-Modified Triangular WS2 and MoS2 Quantum Dots. Crystals 2023, 13, 251. [Google Scholar] [CrossRef]
  78. Wang, S.; Han, C.; Ye, L.; Zhang, G.; Hu, Y.; Li, W.; Jiang, Y. Electronic properties of triangle molybdenum disulfide (Mos2) clusters with different sizes and edges. Molecules 2021, 26, 1157. [Google Scholar] [CrossRef]
  79. Dennington, R.; Keith, T.A.; Millam, J.M. GaussView, Version 6.0. 16; Semichem Inc.: Shawnee Mission, KS, USA, 2016. [Google Scholar]
  80. Adamo, C.; Jacquemin, D. The calculations of excited-state properties with Time-Dependent Density Functional Theory. Chem. Soc. Rev. 2013, 42, 845–856. [Google Scholar] [CrossRef] [PubMed]
  81. Laurent, A.D.; Adamo, C.; Jacquemin, D. Dye chemistry with time-dependent density functional theory. Phys. Chem. Chem. Physics 2014, 16, 14334–14356. [Google Scholar] [CrossRef] [PubMed]
  82. Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
  83. Osman, W.; Saad, M.; Ibrahim, M.; Yahia, I.; Abdelsalam, H.; Zhang, Q. Electronic, optical, and catalytic properties of finite antimonene nanoribbons: First principles study. Phys. Scr. 2022, 97, 035802. [Google Scholar] [CrossRef]
  84. O’boyle, N.M.; Tenderholt, A.L.; Langner, K.M. Cclib: A library for package-independent computational chemistry algorithms. J. Comput. Chem. 2008, 29, 839–845. [Google Scholar] [CrossRef] [PubMed]
  85. Hamel, S.; Duffy, P.; Casida, M.E.; Salahub, D.R. Kohn–Sham orbitals and orbital energies: Fictitious constructs but good approximations all the same. J. Electron Spectrosc. Relat. Phenom. 2002, 123, 345–363. [Google Scholar] [CrossRef]
  86. Gece, G. The use of quantum chemical methods in corrosion inhibitor studies. Corros. Sci. 2008, 50, 2981–2992. [Google Scholar] [CrossRef]
  87. Bourass, M.; Benjelloun, A.T.; Benzakour, M.; Mcharfi, M.; Hamidi, M.; Bouzzine, S.M.; Bouachrine, M. DFT and TD-DFT calculation of new thienopyrazine-based small molecules for organic solar cells. Chem. Cent. J. 2016, 10, 67. [Google Scholar] [CrossRef] [Green Version]
  88. Abd-Elkader, O.H.; Abdelsalam, H.; Sakr, M.A.; Shaltout, A.A.; Zhang, Q. First-Principles Study of MoS2, WS2, and NbS2 Quantum Dots: Electronic Properties and Hydrogen Evolution Reaction. Crystals 2023, 13, 994. [Google Scholar] [CrossRef]
  89. Sakr, M.A.; Sherbiny, F.F.; El-Etrawy, A.-A.S. Hydrazone-based materials; DFT, TD-DFT, NBO analysis, fukui function, MESP analysis, and solar cell applications. J. Fluoresc. 2022, 32, 1857–1871. [Google Scholar] [CrossRef] [PubMed]
  90. Guido, C.A.; Cortona, P.; Mennucci, B.; Adamo, C. On the metric of charge transfer molecular excitations: A simple chemical descriptor. J. Chem. Theory Comput. 2013, 9, 3118–3126. [Google Scholar] [CrossRef]
Crystals 13 01215 g001
Figure 1. (a–d) GaS nanoribbons with an armchair edge (GaS-3-nANR) and (e–h) zigzag edge. The chemical modifications by edge hydrogenation (GaS-3-ANR-H) and doping (GaS-3-ANR-2C) are shown in (i) and (j), respectively.
Figure 1. (a–d) GaS nanoribbons with an armchair edge (GaS-3-nANR) and (e–h) zigzag edge. The chemical modifications by edge hydrogenation (GaS-3-ANR-H) and doping (GaS-3-ANR-2C) are shown in (i) and (j), respectively.
Crystals 13 01215 g001
Crystals 13 01215 g002
Figure 2. The partial density of states and the corresponding HOMO/LUMO distributions of GaS-3-nANR and GaS-2-nZNR, n = 2, 4, and 6.
Figure 2. The partial density of states and the corresponding HOMO/LUMO distributions of GaS-3-nANR and GaS-2-nZNR, n = 2, 4, and 6.
Crystals 13 01215 g002
Crystals 13 01215 g003
Figure 3. Partial density of states of GaS-3-6ANR after substitutional doping with 2Band 2O (a,b) and the corresponding HOMO (c,d). PDOS after doping with 2Si (e) and passivation with F (f), the related HOMO and LUMO are given in (g–j).
Figure 3. Partial density of states of GaS-3-6ANR after substitutional doping with 2Band 2O (a,b) and the corresponding HOMO (c,d). PDOS after doping with 2Si (e) and passivation with F (f), the related HOMO and LUMO are given in (g–j).
Crystals 13 01215 g003
Crystals 13 01215 g004
Figure 4. (a,b) The UV-Vis absorption spectra of GaS-nanoribbons show the effect of size increase in the armchair (ANR) and zigzag (ZNR) directions. The absorption spectra of GaS-3-6ANR before and after width increasing (GaS-4-6ANR), doping (with 2B, 2C, 2N, 2O), and edge passivation with H- and F-atoms.
Figure 4. (a,b) The UV-Vis absorption spectra of GaS-nanoribbons show the effect of size increase in the armchair (ANR) and zigzag (ZNR) directions. The absorption spectra of GaS-3-6ANR before and after width increasing (GaS-4-6ANR), doping (with 2B, 2C, 2N, 2O), and edge passivation with H- and F-atoms.
Crystals 13 01215 g004
Table 1. Some important structural properties for GaS-3-2ANR, GaS-3-4ANR, GaS-3-6ANR, GaS-2-2ZNR, GaS-2-4ZNR, GaS-2-6ZNR, GaS-3-6ANR-H, and GaS-3-6ANR-2C such as bond length (Å), dihedral, and bond angles (°).
Table 1. Some important structural properties for GaS-3-2ANR, GaS-3-4ANR, GaS-3-6ANR, GaS-2-2ZNR, GaS-2-4ZNR, GaS-2-6ZNR, GaS-3-6ANR-H, and GaS-3-6ANR-2C such as bond length (Å), dihedral, and bond angles (°).
DesignGa1-S2 (Å)Ga3-S4
(Å)		S4-Ga5
(Å)		Ga7-S8
(Å)		Ga1-S2-Ga3 (°)S4-Ga5-S6 (°)Ga1-S2-Ga3-S4 (°)Ga1-S2-Ga3-S8 (°)Ga3-S4-Ga5-S6 (°)
NRs
GaS-3-2ANR2.2752.4272.4162.32590.454109.2170.160.1167.9
GaS-3-4ANR2.2802.4412.3272.33889.550113.4172.464.7170.8
GaS-3-6ANR2.2782.4342.3292.33489.455113.5172.264.5170.4
GaS-2-2ZNR2.3312.5912.2942.71887.868109.5172.766.2174.9
GaS-2-4ZNR2.3292.5312.2972.60688.799109.6173.966.8173.9
GaS-2-6ZNR2.5412.3742.3814.94493.307113.9174.362.3158.1
GaS-3-6ANR-H2.3352.3782.3212.383115.37120.386.021.2135.6
GaS-3-6ANR-2C2.2792.4432.3322.33689.151114.5158.147.3171.6
Table 2. The HOMO energy (EH), the LUMO energy (EL), chemical potential (ρ), electronegativity (χ), chemical hardness (η), and dipole moment (μ) for selected GaS nanoribbons with and without chemical modification.
Table 2. The HOMO energy (EH), the LUMO energy (EL), chemical potential (ρ), electronegativity (χ), chemical hardness (η), and dipole moment (μ) for selected GaS nanoribbons with and without chemical modification.
CompoundsEH (eV)EL (eV)ρ (eV)χ (eV)η (eV)μ (D)
GaS-3-2ANR−7.29−3.58−5.445.441.8518.0
GaS-3-4ANR−6.71−4.75−5.735.730.9891.1
GaS-3-6ANR−6.31−5.23−5.775.770.54164.5
GaS-2-2ZNR−7.30−4.74−6.026.021.2834.6
GaS-2-4ZNR−7.63−4.81−6.226.221.4148.3
GaS-2-6ZNR−6.42−4.26−5.345.341.0820.3
GaS-3-6ANR-H−7.70−2.72−5.215.212.4965.1
GaS-3-6ANR-2C−6.62−5.19−5.915.910.72141.9
Table 3. Charge–transfer length (∆r), centroid coordinates of holes and electrons (D), electron–hole overlap (Sr), hole–electron degree of separation (t), and hole–electron Coulomb attraction energy (Ec) for GaS nanoribbons in S1 excited state.
Table 3. Charge–transfer length (∆r), centroid coordinates of holes and electrons (D), electron–hole overlap (Sr), hole–electron degree of separation (t), and hole–electron Coulomb attraction energy (Ec) for GaS nanoribbons in S1 excited state.
CompoundsΔr (Å)D (Å)Sr (au)t (Å)Ec (eV)
GaS-3-2ANR12.684.660.302.482.63
GaS-3-4ANR39.9320.630.00218.760.68
GaS-3-6ANR20.788.730.244.791.89
GaS-2-2ZNR14.206.500.164.611.74
GaS-2-4ZNR1.930.140.89−1.674.10
GaS-2-6ZNR20.788.730.244.791.89
GaS-3-6ANR-H19.563.750.34−2.220.67
GaS-3-6ANR-F5.663.580.17−1.630.27
GaS-3-6ANR-2C63.9433.840.00032.030.41
GaS-3-6ANR-2N12.316.180.340.580.97
GaS-3-6ANR-2O6.100.850.43−1.332.92
GaS-3-6ANR-2B15.431.190.44−2.241.54
GaS-3-6ANR-W8.844.310.292.492.79
Table 4. The calculated excited state (ES), maximum wavelength (λmax), transition energy (TE), electronic transition (ET), oscillator strength (f), and transition coefficient (TC).
Table 4. The calculated excited state (ES), maximum wavelength (λmax), transition energy (TE), electronic transition (ET), oscillator strength (f), and transition coefficient (TC).
NanoribbonESλmaxTE (eV)ETfTC
GaS-3-2ANR14454.342.72H-4→L0.0380.35
GaS-3-4ANR16590.582.09H-29→L0.010.25
GaS-3-6ANR3616.132.01H-49→L0.060.21
GaS-2-2ZNR13773.361.60H-5→L0.030.47
GaS-2-4ZNR81088.11.14H-2→L+10.010.23
GaS-2-6ZNR31504.150.82H→L0.190.18
GaS-3-6ANR-H9304.043.95H-27→L0.010.10
GaS-3-6ANR-F13313.383.96H-28→L0.040.19
GaS-3-6ANR-2C14692.021.79H-2→L+20.400.71
GaS-3-6ANR-2N8541.142.29H-1→L+20.010.68
GaS-3-6ANR-2O4644.091.93H-1→L+110.090.37
GaS-3-6ANR-2B7558.252.22H-1→L+20.020.66
GaS-4-6ANR3616.162.01H-49→L0.0010.10
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Abd-Elkader, O.H.; Abdelsalam, H.; Sakr, M.A.S.; Teleb, N.H.; Zhang, Q. Electronic and Optical Properties of Finite Gallium Sulfide Nano Ribbons: A First-Principles Study. Crystals 2023, 13, 1215. https://doi.org/10.3390/cryst13081215

AMA Style

Abd-Elkader OH, Abdelsalam H, Sakr MAS, Teleb NH, Zhang Q. Electronic and Optical Properties of Finite Gallium Sulfide Nano Ribbons: A First-Principles Study. Crystals. 2023; 13(8):1215. https://doi.org/10.3390/cryst13081215

Chicago/Turabian Style

Abd-Elkader, Omar H., Hazem Abdelsalam, Mahmoud A. S. Sakr, Nahed H. Teleb, and Qinfang Zhang. 2023. "Electronic and Optical Properties of Finite Gallium Sulfide Nano Ribbons: A First-Principles Study" Crystals 13, no. 8: 1215. https://doi.org/10.3390/cryst13081215

APA Style

Abd-Elkader, O. H., Abdelsalam, H., Sakr, M. A. S., Teleb, N. H., & Zhang, Q. (2023). Electronic and Optical Properties of Finite Gallium Sulfide Nano Ribbons: A First-Principles Study. Crystals, 13(8), 1215. https://doi.org/10.3390/cryst13081215

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop