Formation of Tesseract Time Crystals on a Quantum Computer
Abstract
:1. Introduction
2. Discrete Time Crystals
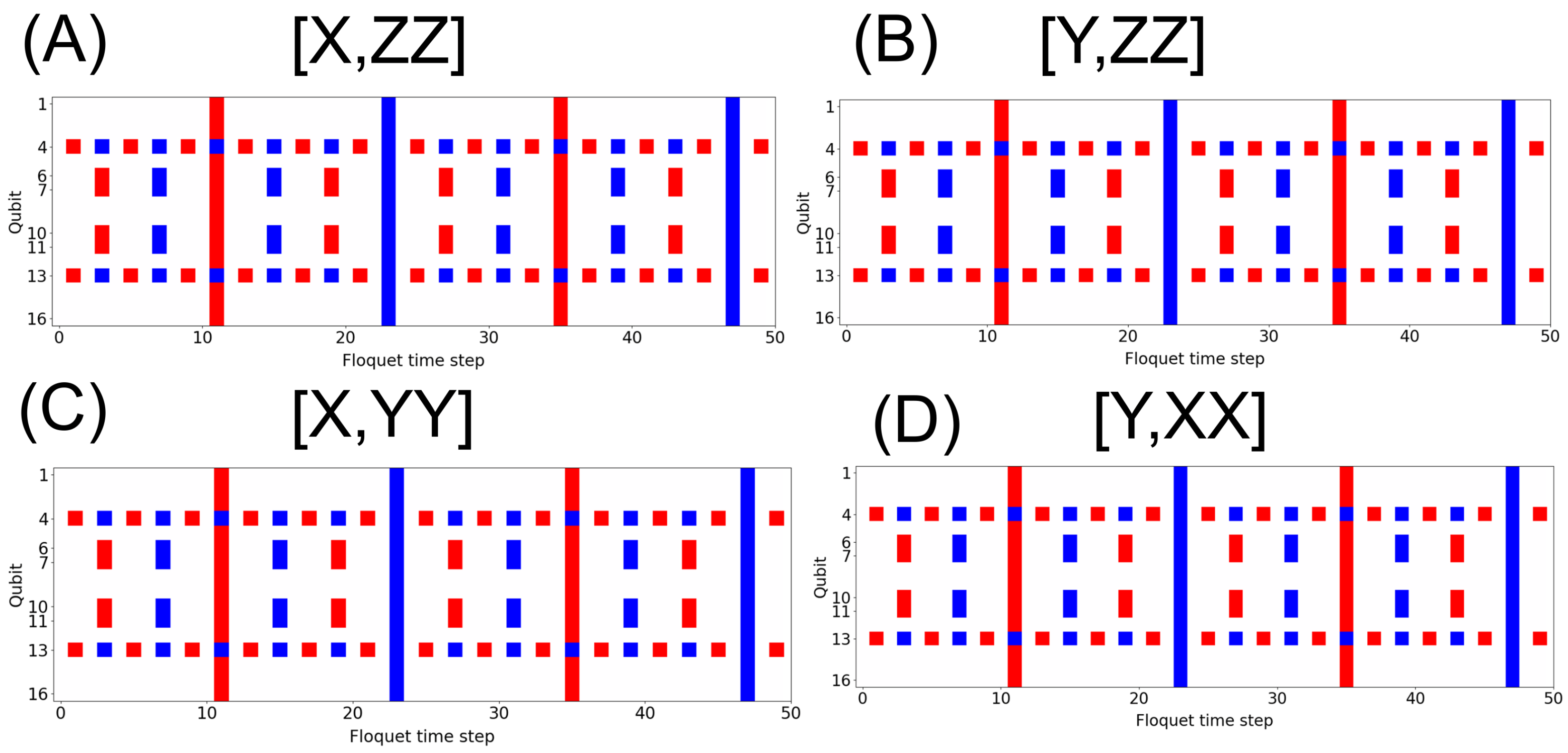
3. A 4D Discrete Time Crystal
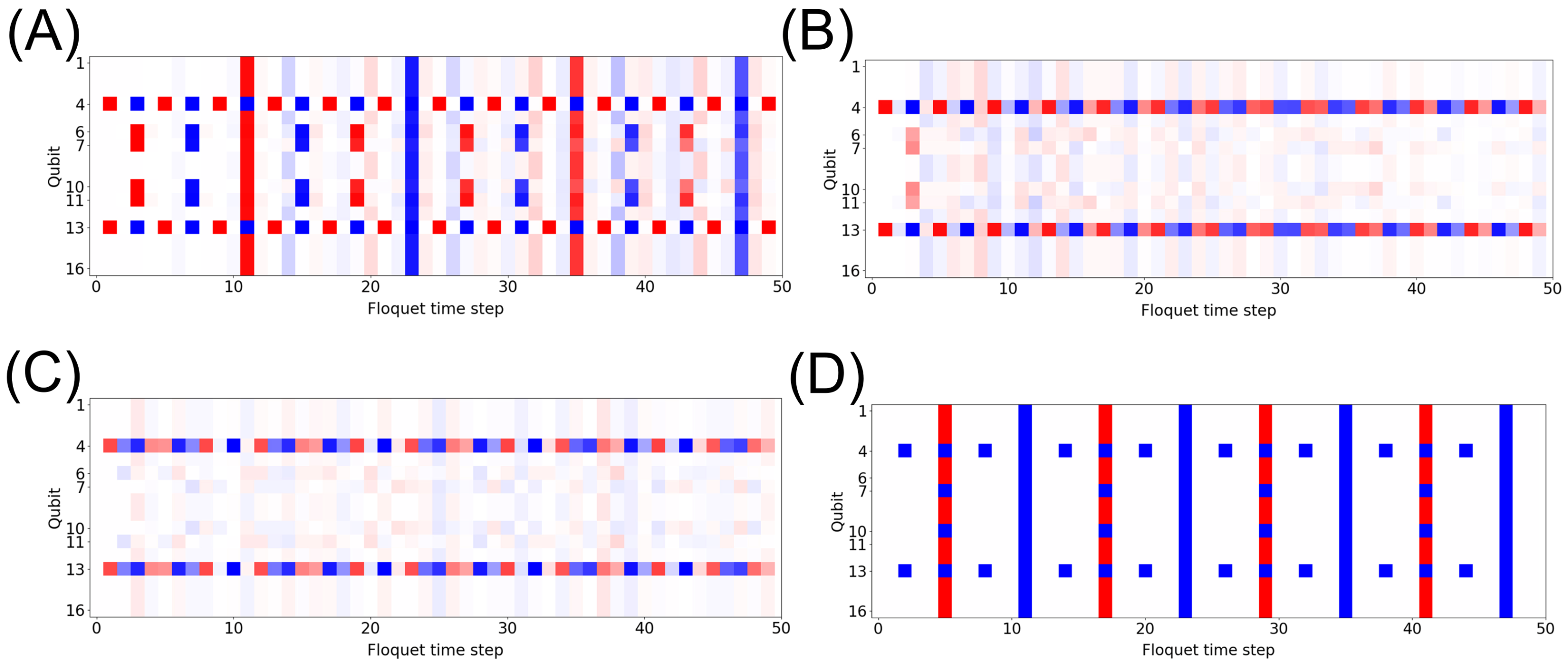
4. Prethermal Phase
4.1. Thermalization
4.2. Onsite Disorder
5. Discussion
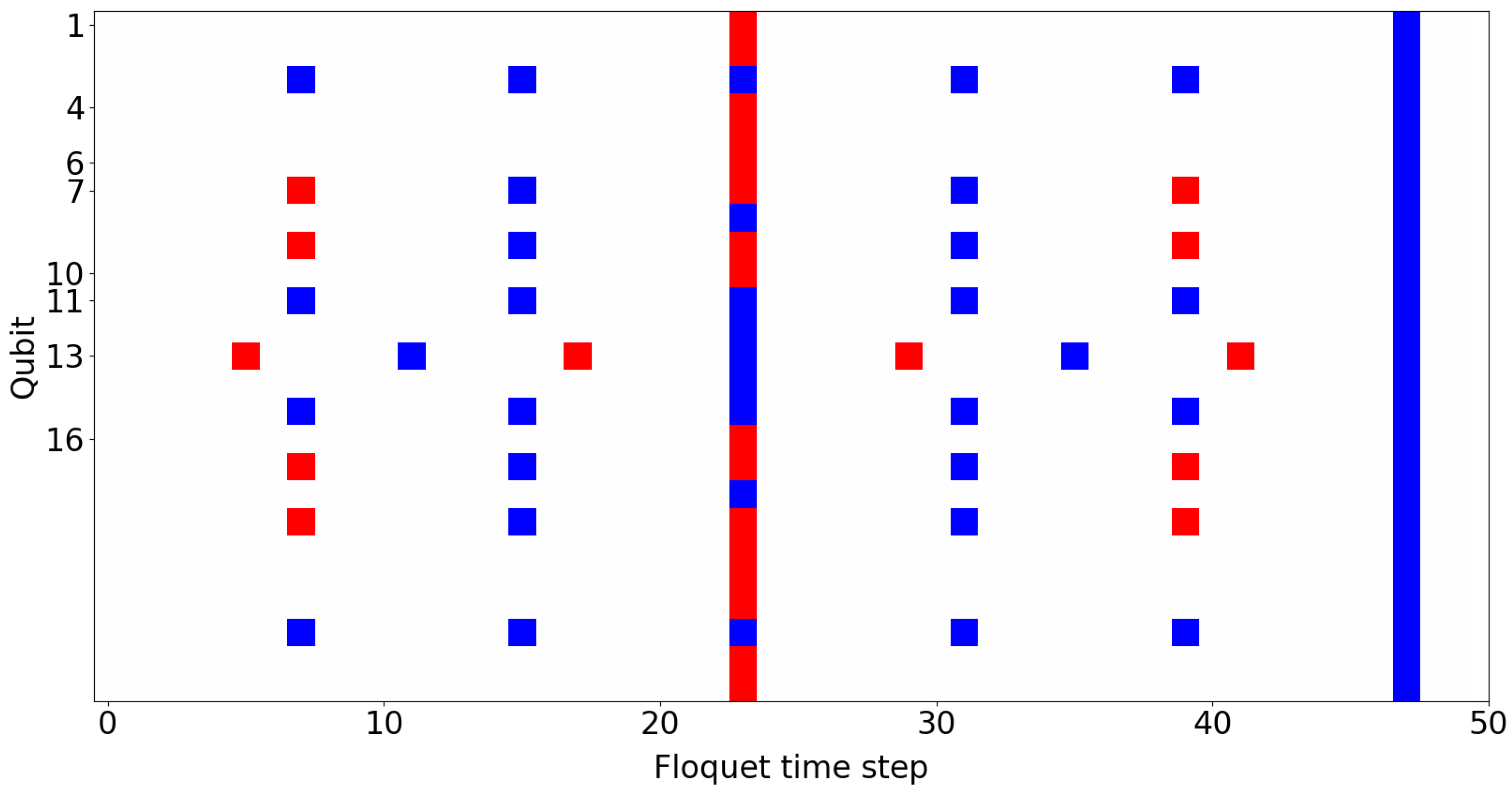
6. Methods
6.1. Simulation
6.2. Edge State
6.3. Circuits
7. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Wang, Y.H.; Steinberg, H.; Jarillo-Herrero, P.; Gedik, N. Observation of Floquet-Bloch States on the Surface of a Topological Insulator. Science 2013, 342, 453–457. [Google Scholar] [CrossRef] [PubMed]
- Bukov, M.; D’Alessio, L.; Polkovnikov, A. Universal high-frequency behavior of periodically driven systems: From dynamical stabilization to Floquet engineering. Adv. Phys. 2015, 64, 139–226. [Google Scholar] [CrossRef]
- Harper, F.; Roy, R.; Rudner, M.S.; Sondhi, S. Topology and Broken Symmetry in Floquet Systems. Annu. Rev. Condens. Matter Phys. 2020, 11, 345–368. [Google Scholar] [CrossRef]
- Titum, P.; Berg, E.; Rudner, M.S.; Refael, G.; Lindner, N.H. Anomalous Floquet-Anderson Insulator as a Nonadiabatic Quantized Charge Pump. Phys. Rev. X 2016, 6, 021013. [Google Scholar] [CrossRef]
- Gómez-León, A.; Platero, G. Floquet-Bloch Theory and Topology in Periodically Driven Lattices. Phys. Rev. Lett. 2013, 110, 200403. [Google Scholar] [CrossRef]
- Else, D.V.; Bauer, B.; Nayak, C. Floquet Time Crystals. Phys. Rev. Lett. 2016, 117, 090402. [Google Scholar] [CrossRef]
- von Keyserlingk, C.W.; Khemani, V.; Sondhi, S.L. Absolute stability and spatiotemporal long-range order in Floquet systems. Phys. Rev. B 2016, 94, 085112. [Google Scholar] [CrossRef]
- Sacha, K.; Zakrzewski, J. Time crystals: A review. Rep. Prog. Phys. 2017, 81, 016401. [Google Scholar] [CrossRef]
- Wilczek, F. Quantum Time Crystals. Phys. Rev. Lett. 2012, 109, 160401. [Google Scholar] [CrossRef]
- Watanabe, H.; Oshikawa, M. Absence of Quantum Time Crystals. Phys. Rev. Lett. 2015, 114, 251603. [Google Scholar] [CrossRef]
- Huse, D.A.; Nandkishore, R.; Oganesyan, V.; Pal, A.; Sondhi, S.L. Localization-protected quantum order. Phys. Rev. B 2013, 88, 014206. [Google Scholar] [CrossRef]
- Pekker, D.; Refael, G.; Altman, E.; Demler, E.; Oganesyan, V. Hilbert-Glass Transition: New Universality of Temperature-Tuned Many-Body Dynamical Quantum Criticality. Phys. Rev. X 2014, 4, 011052. [Google Scholar] [CrossRef]
- Ge, R.C.; Koshkaki, S.R.; Kolodrubetz, M.H. Cavity induced many-body localization. arXiv 2022, arXiv:2208.06898. [Google Scholar]
- Koshkaki, S.R.; Kolodrubetz, M.H. Inverted many-body mobility edge in a central qudit problem. Phys. Rev. B 2022, 105, l060303. [Google Scholar] [CrossRef]
- Zhang, J.; Hess, P.W.; Kyprianidis, A.; Becker, P.; Lee, A.; Smith, J.; Pagano, G.; Potirniche, I.D.; Potter, A.C.; Vishwanath, A.; et al. Observation of a discrete time crystal. Nature 2017, 543, 217–220. [Google Scholar] [CrossRef]
- Choi, S.; Choi, J.; Landig, R.; Kucsko, G.; Zhou, H.; Isoya, J.; Jelezko, F.; Onoda, S.; Sumiya, H.; Khemani, V.; et al. Observation of discrete time-crystalline order in a disordered dipolar many-body system. Nature 2017, 543, 221–225. [Google Scholar] [CrossRef]
- Rovny, J.; Blum, R.L.; Barrett, S.E. Observation of Discrete-Time-Crystal Signatures in an Ordered Dipolar Many-Body System. Phys. Rev. Lett. 2018, 120, 180603. [Google Scholar] [CrossRef]
- Wang, X.; Mirmoosa, M.S.; Asadchy, V.S.; Rockstuhl, C.; Fan, S.; Tretyakov, S.A. Metasurface-based realization of photonic time crystals. Sci. Adv. 2023, 9, eadg7541. [Google Scholar] [CrossRef]
- Kongkhambut, P.; Skulte, J.; Mathey, L.; Cosme, J.G.; Hemmerich, A.; Keßler, H. Observation of a continuous time crystal. Science 2022, 377, 670–673. [Google Scholar] [CrossRef]
- Yoshida, M.; Suzuki, R.; Zhang, Y.; Nakano, M.; Iwasa, Y. Memristive phase switching in two-dimensional 1T-TaS crystals. Sci. Adv. 2015, 1, e1500606. [Google Scholar] [CrossRef]
- Gao, F.Y.; Zhang, Z.; Sun, Z.; Ye, L.; Cheng, Y.H.; Liu, Z.J.; Checkelsky, J.G.; Baldini, E.; Nelson, K.A. Snapshots of a light-induced metastable hidden phase driven by the collapse of charge order. Sci. Adv. 2022, 8, eabp9076. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Zhang, T.; Zhao, D.; Chen, C.; Ding, S.; Yang, W.; Wang, X.; Li, C.; Wang, H.; Feng, D.; et al. Real-space observation of incommensurate spin density wave and coexisting charge density wave on Cr (001) surface. Nat. Commun. 2022, 13, 445. [Google Scholar] [CrossRef]
- Lee, J.; Bang, J.; Kang, J. Nonequilibrium Charge-Density-Wave Melting in 1T-TaS Triggered by Electronic Excitation: A Real-Time Time-Dependent Density Functional Theory Study. J. Phys. Chem. Lett. 2022, 13, 5711–5718. [Google Scholar] [CrossRef] [PubMed]
- Heim, B.; Rønnow, T.F.; Isakov, S.V.; Troyer, M. Quantum versus classical annealing of Ising spin glasses. Science 2015, 348, 215–217. [Google Scholar] [CrossRef]
- Schmitt, M.; Rams, M.M.; Dziarmaga, J.; Heyl, M.; Zurek, W.H. Quantum phase transition dynamics in the two-dimensional transverse-field Ising model. Sci. Adv. 2022, 8, eabl6850. [Google Scholar] [CrossRef]
- Mi, X.; Ippoliti, M.; Quintana, C.; Greene, A.; Chen, Z.; Gross, J.; Arute, F.; Arya, K.; Atalaya, J.; Babbush, R.; et al. Time-crystalline eigenstate order on a quantum processor. Nature 2021, 601, 531–536. [Google Scholar] [CrossRef]
- Kuroś, A.; Mukherjee, R.; Mintert, F.; Sacha, K. Controlled preparation of phases in two-dimensional time crystals. Phys. Rev. Res. 2021, 3, 043203. [Google Scholar] [CrossRef]
- Pizzi, A.; Nunnenkamp, A.; Knolle, J. Classical Prethermal Phases of Matter. Phys. Rev. Lett. 2021, 127, 140602. [Google Scholar] [CrossRef]
- Pizzi, A.; Nunnenkamp, A.; Knolle, J. Classical approaches to prethermal discrete time crystals in one, two, and three dimensions. Phys. Rev. B 2021, 104, 094308. [Google Scholar] [CrossRef]
- Frey, P.; Rachel, S. Realization of a discrete time crystal on 57 qubits of a quantum computer. Sci. Adv. 2022, 8, eabm7652. [Google Scholar] [CrossRef]
- Sims, C. Simulation of Higher-Dimensional Discrete Time Crystals on a Quantum Computer. Crystals 2023, 13, 1188. [Google Scholar] [CrossRef]
- Nandkishore, R.; Huse, D.A. Many-Body Localization and Thermalization in Quantum Statistical Mechanics. Annu. Rev. Condens. Matter Phys. 2015, 6, 15–38. [Google Scholar] [CrossRef]
- Abanin, D.A.; Altman, E.; Bloch, I.; Serbyn, M. Colloquium: Many-body localization, thermalization, and entanglement. Rev. Mod. Phys. 2019, 91, 021001. [Google Scholar] [CrossRef]
- Ponte, P.; Papić, Z.; Huveneers, F.; Abanin, D.A. Many-Body Localization in Periodically Driven Systems. Phys. Rev. Lett. 2015, 114, 140401. [Google Scholar] [CrossRef]
- Lazarides, A.; Das, A.; Moessner, R. Fate of Many-Body Localization Under Periodic Driving. Phys. Rev. Lett. 2015, 115, 030402. [Google Scholar] [CrossRef]
- Bordia, P.; Lüschen, H.; Schneider, U.; Knap, M.; Bloch, I. Periodically driving a many-body localized quantum system. Nat. Phys. 2017, 13, 460–464. [Google Scholar] [CrossRef]
- Throckmorton, R.E.; Sarma, S.D. Studying many-body localization in exchange-coupled electron spin qubits using spin–spin correlations. Phys. Rev. B 2021, 103, 165431. [Google Scholar] [CrossRef]
- Alet, F.; Laflorencie, N. Many-body localization: An introduction and selected topics. C. R. Phys. 2018, 19, 498–525. [Google Scholar] [CrossRef]
- Chen, C.; Chen, Y.; Wang, X. Many-body localization in the infinite-interaction limit and the discontinuous eigenstate phase transition. NPJ Quantum Inf. 2022, 8, 142. [Google Scholar] [CrossRef]
- Hu, T.; Xue, K.; Li, X.; Zhang, Y.; Ren, H. Excited-state fidelity as a signal for the many-body localization transition in a disordered Ising chain. Sci. Rep. 2017, 7, 577. [Google Scholar] [CrossRef] [PubMed]
- Kjäll, J.A.; Bardarson, J.H.; Pollmann, F. Many-Body Localization in a Disordered Quantum Ising Chain. Phys. Rev. Lett. 2014, 113, 107204. [Google Scholar] [CrossRef] [PubMed]
- Hauke, P.; Heyl, M. Many-body localization and quantum ergodicity in disordered long-range Ising models. Phys. Rev. B 2015, 92, 134204. [Google Scholar] [CrossRef]
- Bayraktar, H.; Charara, A.; Clark, D.; Cohen, S.; Costa, T.; Fang, Y.L.L.; Gao, Y.; Guan, J.; Gunnels, J.; Haidar, A.; et al. cuQuantum SDK: A High-Performance Library for Accelerating Quantum Science. arXiv 2023, arXiv:2308.01999. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sims, C. Formation of Tesseract Time Crystals on a Quantum Computer. Crystals 2023, 13, 1265. https://doi.org/10.3390/cryst13081265
Sims C. Formation of Tesseract Time Crystals on a Quantum Computer. Crystals. 2023; 13(8):1265. https://doi.org/10.3390/cryst13081265
Chicago/Turabian StyleSims, Christopher. 2023. "Formation of Tesseract Time Crystals on a Quantum Computer" Crystals 13, no. 8: 1265. https://doi.org/10.3390/cryst13081265




