Enumeration of Self-Avoiding Random Walks on Lattices as Model Chains in Polymer Crystals

Abstract

Recent simulation studies have revealed a wealth of distinct crystal polymorphs encountered in the self-organization of polymer systems driven by entropy or free energy. The present analysis, based on the concept of self-avoiding random walks (SAWs) on crystal lattices, is useful to calculate upper bounds for the entropy difference of the crystals that are formed during polymer crystallization and thus to predict the thermodynamic stability of distinct polymorphs. Here, we compare two pairs of crystals sharing the same coordination number, n_coord: hexagonal close-packed (HCP) and face centered cubic (FCC), both having n_coord = 12 and the same packing density, and the less dense simple hexagonal (HEX) and body centered cubic (BCC) lattices, with n_coord = 8. In both cases, once a critical number of steps is reached, one of the crystals shows a higher number of SAWs compatible with its geometry. We explain the observed trends in terms of the bending and torsion angles as imposed by the geometric constraints of the crystal lattice.

1. Introduction

The term “soft matter” refers to a class of physical systems which includes polymers, colloids, granular media, surfactants, and gels. The common feature of all these diverse materials is that they consist of units whose size is significantly larger than the constituent atoms [1]. One of the main characteristics of soft matter is the existence of thermal fluctuations which are mainly manifested as Brownian motion of atoms, particles, and molecules. Due to this, the molecular shape and size are constantly changing even under conditions of equilibrium. Thus, to describe equilibrium local and global structure, a statistical approach is required. Additionally, soft matter systems are characterized by spontaneous self-assembly, self-organization, and phase transitions. An important tool to aid in the statistical description of mesoscopic structure, but also of phenomena and processes relevant to soft matter, in general, and polymer science, in particular, is the concept of random walk (RW) and its variation in the form of self-avoiding random walk (SAW) [2].

The mathematical concept of a SAW corresponds to a trajectory of fixed step length that grows randomly on a lattice under the condition that it cannot visit the same point twice. In a strict mathematical sense, several salient aspects of SAW are still unknown or only partially resolved [2]. Still, this has not been an obstacle for its successful application in a very wide range of physical systems and topics in chemistry, physics, polymer science, material technology, mathematics, process optimization, computer science, and biology [3,4,5,6,7,8,9,10,11,12]. Over the years, significant advances have been made in the algorithms related to SAW identification and enumeration, further evolving its usage in diverse problems, especially ones related to synthetic and biological macromolecules. The excluded volume effect in polymer melts and solutions is, in fact, intimately related to the condition of self-avoidance in random walks [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29].

Self-avoiding random walks (SAWs) and polygons (SAPs) have been studied extensively on 2D and 3D lattices [30] with specific examples being the honeycomb [31,32,33,34], square [35,36], triangular [37], simple cubic [35,38,39,40], body centered cubic (BCC) [41], and face centered cubic (FCC) [41,42] lattices. Due to their importance and general applicability, significant algorithmic and theoretical advances have been made in the enumeration, characterization, identification, and scaling behavior of SAWs, SAPs, and their variants [19,20,33,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62]. It is interesting to notice that while the simple cubic (SC), BCC, and FCC crystals have been extensively studied in the literature, no such wealth of information exists for the hexagonal close-packed (HCP) one. This could be attributed to a possible assumption that the HCP and FCC crystals are characterized by the same number of SAWs, independent of the step size [63], because both crystals have the same coordination number (n_coord = 12) and packing density (φ = $\pi \sqrt{2}/6$). As will be demonstrated in the continuation, such a claim is not valid: beyond a certain SAW length (number of steps) the number of SAWs compatible with the HCP crystal becomes marginally higher than the one for the FCC crystal, the difference increasing as the number of SAW steps grows.

In the past, we employed a SAW-based analysis to enumerate the possible configurations of single-chain crystals and thus explain their thermodynamic stability in regular lattices in slits (tubes) [64] and plates [65]. These studies have been motivated by the spontaneous, entropy-driven crystallization of chains of tangent hard spheres as demonstrated in Monte Carlo (MC) simulations of dense packings under various conditions of spatial confinement [66,67,68]. Very recently, it was documented that starting from random (disordered) packings, freely jointed chains of hard spheres in the bulk show a transition to the ordered state following Ostwald’s rule of stages [69]: initially a random hexagonal close-packed (rHCP) morphology is formed of mixed HCP and FCC character [70,71]. Given enough observation time, the rHCP ordered morphology is eventually succeeded by an almost defect-free (perfect) FCC crystal [71]. In parallel modeling efforts, a wealth of distinct crystal polymorphs, including non-compact crystals like the body centered cubic (BCC) and holoedric 6/mmm (simple hexagonal, HEX), has also been encountered in the (free) energy-driven self-assembly of freely jointed chains of tangent monomers interacting with the square well potential under very dilute conditions [72].

With respect to the stability of the HCP and FCC crystals made of athermal polymer chains, semi-analytical calculations were presented in [70], based on the separation of translational and conformational degrees of freedom. Resulting upper-bound estimates demonstrate that the conformational entropy of an HCP crystal of hard-sphere polymers is higher than the one of the FCC crystal by a margin of 0.331 × 10⁻⁵ k per monomer, where k is Boltzmann’s constant. However, this minute difference is significantly smaller than the free energy advantage of the FCC crystal in terms of translational entropy. The latter can be assumed to be very similar, if not identical, to the translational entropy of monomers disregarding the constraints imposed by chain connectivity. A widely accepted value for the entropic difference between FCC and HCP crystals for monomeric hard spheres, corresponding to approximately 112 × 10⁻⁵ k per monomer, has been established in the literature [73,74,75], depending further on packing density [76]. The semi-analytical predictions of [70] have been supported by extremely long molecular simulations based on Monte Carlo algorithms demonstrating FCC perfection in athermal polymer crystallization of entangled chains [66,77].

In the present contribution, we further support the semi-analytical calculations of [70] by exhaustive enumeration of the self-avoiding random walks (SAWs) compatible with the inter-site geometry as encountered in the FCC and HCP crystals. We also analyze the SAW statistics, including the local geometry (bending and torsion angles) and the global size (distribution and mean of the end-to-end distance). Two additional crystals, the HEX and BCC, both having n_coord = 8, encountered in simulations of chains whose monomers interact with the square well potential [72], are considered in the current work.

The manuscript is organized as follows: Section 2 presents the model, the reference crystals and the method employed for the SAW enumeration. Section 3 hosts the results on the local and global properties of SAWs on the HCP, FCC, HEX, and BCC lattices. The discussion of the results can be found in Section 4. The manuscript is concluded with Section 5 summarizing the main conclusions and listing future extensions.

2. Materials and Methods

As reported in the Introduction, the present work forms part of an ongoing modeling study of (free) energy- [72,78] and entropy-driven [70,71,79,80] self-organization of idealized systems based on polymers interacting with the hard sphere or the square well potential [81]. Four different crystals have been considered in this work: the hexagonal close-packed (HCP), face centered cubic (FCC), body centered cubic (BCC or BC), and holoedric 6/mmm (simple hexagonal, HEX), whose periodic structure and salient characteristics can be found in [77,82]. The HCP and FCC ones have been selected because they compete as emerging and resulting structures in the disorder–order transition of freely jointed chains of hard spheres at sufficiently high packing densities [70,71,79,80]. The HEX and BCC crystals, along with the HCP and FCC crystals and the Frank–Kasper [83,84] phase, are encountered as final stable morphologies in the crystallization of clusters formed from chains interacting with the square well attractive potential [72,78] at dilute conditions. Density-based [85,86] and geometric [72] arguments can accurately explain the dominance of non-compact crystals in specific ranges of the interaction potential in two and three dimensions.

In the present work, a polymer is represented as a linear chain of strictly tangent hard spheres. This chain is grown on the sites of a crystal, so its bonded geometry is defined by the linear architecture of the chain, the tangency condition of the bonded atoms, and the spatial constraints imposed by the crystal sites. As in our past works [64,65], “monomer” refers to each of the hard spheres that constitute the polymer chain, while “site” refers to the each of the sites of the ideal crystal. A single chain is grown on each reference lattice, with a monomer occupying a single site, and bonded monomers lying on adjacent sites, which are thus separated by a bond/step length. With respect to bond geometry, bending (θ) and torsion (ϕ) angles are formed by successive triplets and quartets of monomers along the chain backbone. These angles must respect the connectivity and geometry of each lattice. Accordingly, bending and torsion angles along the polymer chain are different for different crystal types, as can be seen in

Table 1. Bending angles, θ, which are compatible with each reference crystal. Compatibility and incompatibility are indicated by the “+” and “−” symbols, respectively.

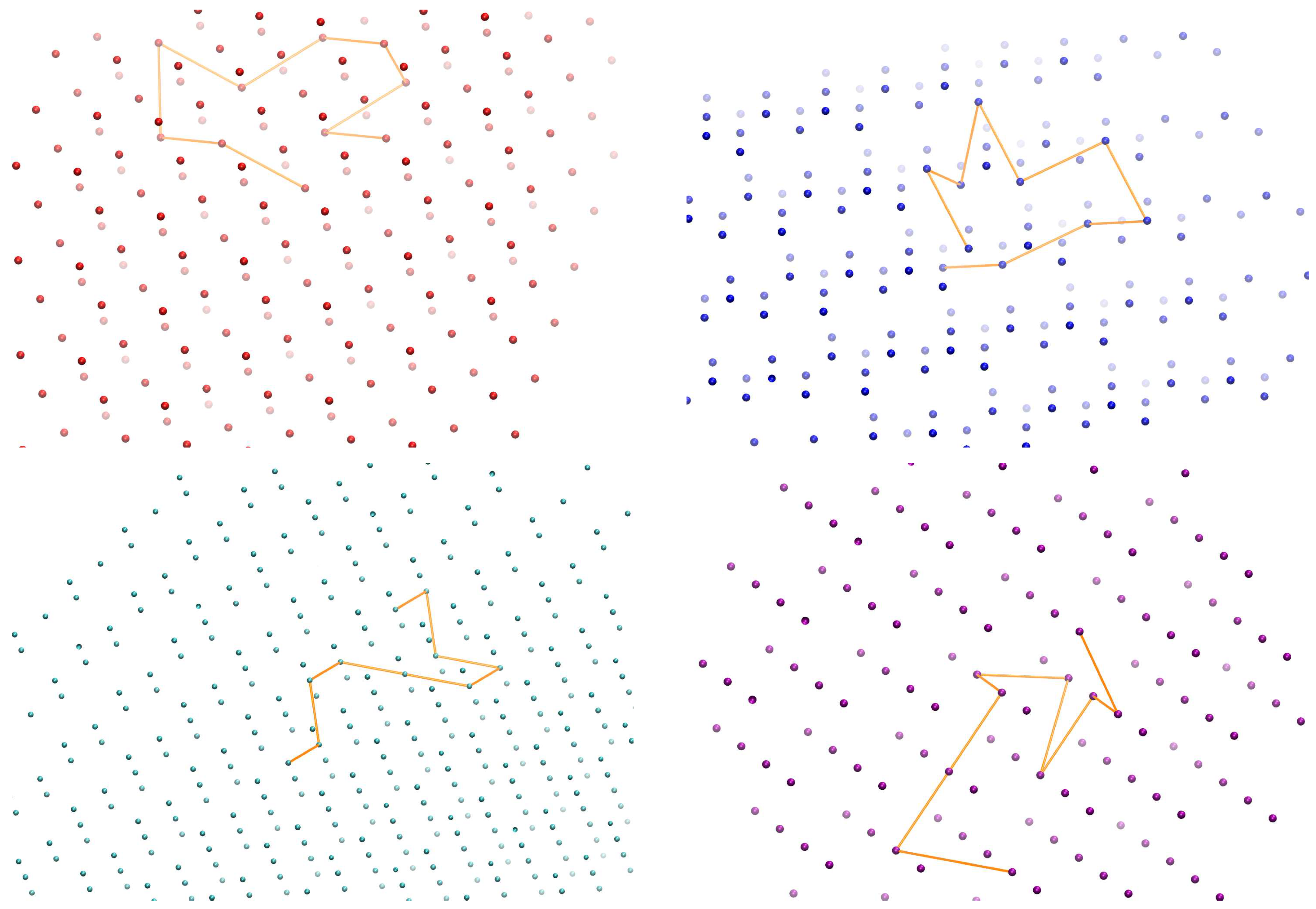
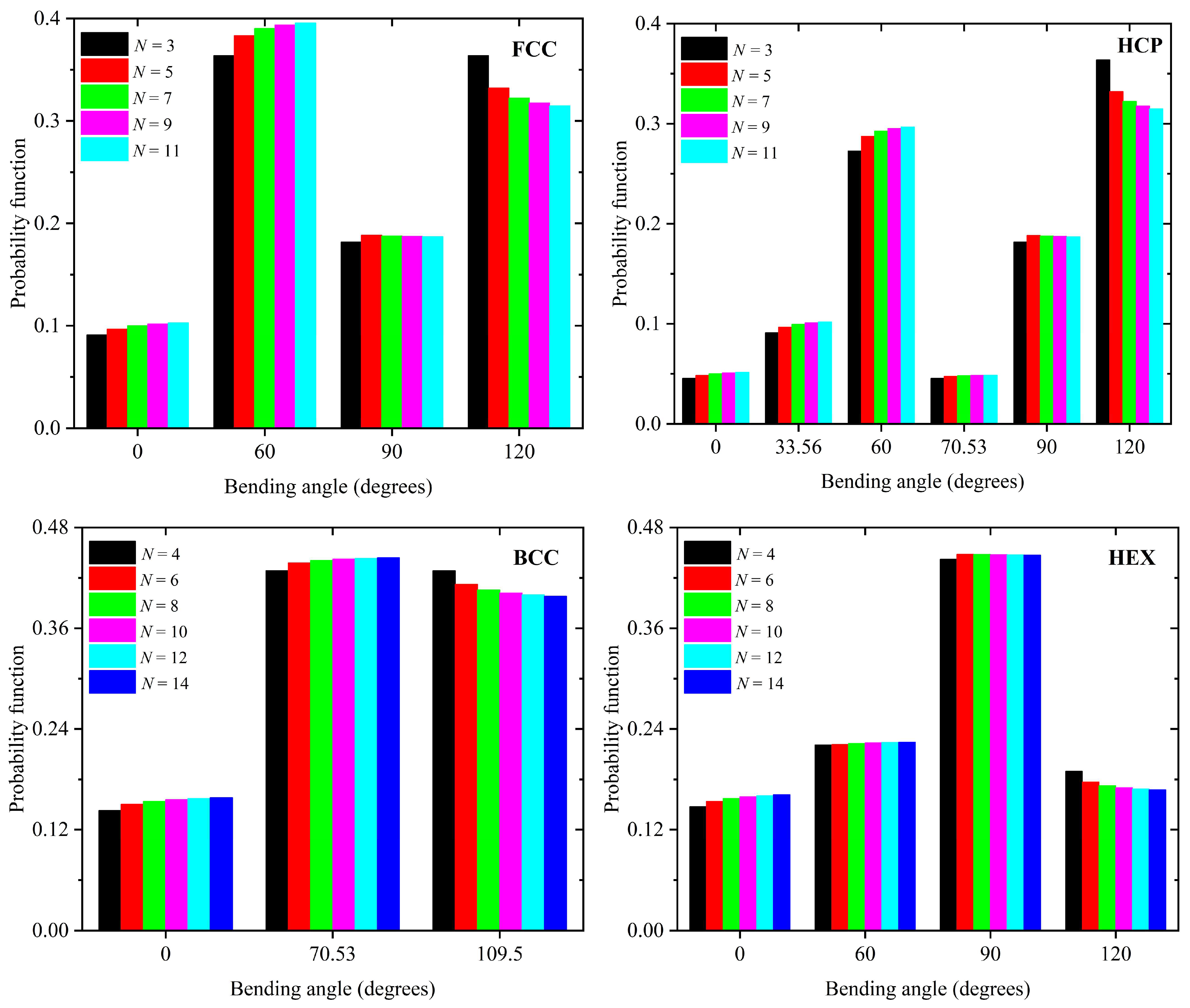
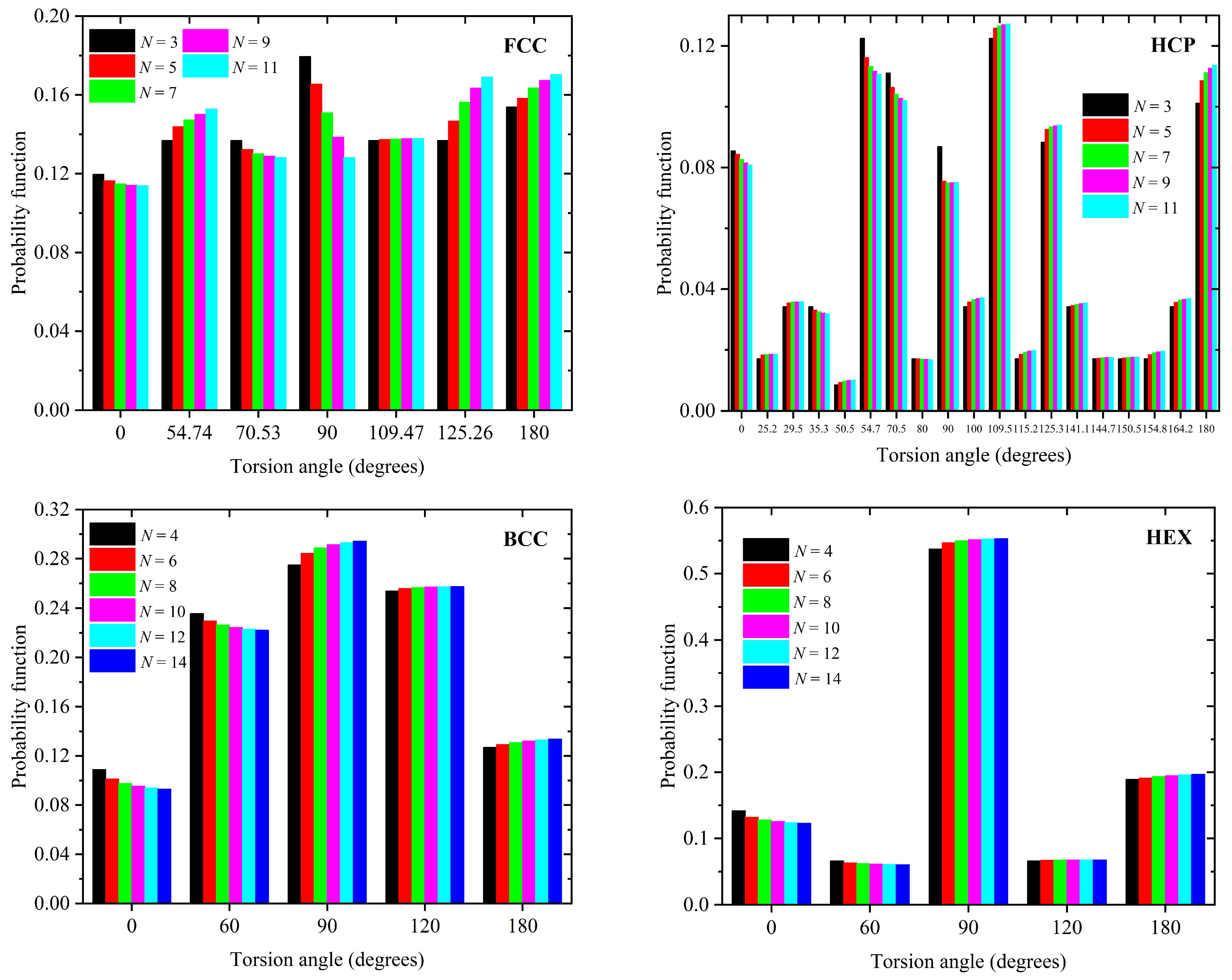
θ (Degrees)	FCC	HCP	BCC	HEX
0.000	+	+	+	+
33.56	−	+	−	−
60.00	+	+	−	+
70.53	−	+	+	−
90.00	+	+	−	+
109.47	−	−	+	−
120.00	+	+	−	+

(bending angles) and

Table 2. Torsion angles, ϕ, which are compatible with each reference crystal. Compatibility and incompatibility are indicated by the “+” and “−” symbols, respectively.

ϕ	FCC	HCP	BCC	HEX
0.000	+	+	+	+
25.24	−	+	−	−
29.50	−	+	−	−
35.26	−	+	−	−
50.48	−	+	−	−
54.74	+	+	−	−
60.00	−	−	+	+
70.53	+	+	−	−
79.98	−	+	−	−
90.00	+	+	+	+
100.02	−	+	−	−
109.47	+	+	−	−
115.24	−	+	−	−
120.00	−	−	+	+
125.26	+	+	−	−
141.06	−	+	−	−
144.74	−	+	−	−
150.50	−	+	−	−
154.76	−	+	−	−
164.21	−	+	−	−
180.00	+	+	+	+

(torsion angles). Chains on the HCP crystal show the largest variety, with 6 and 19 distinct bending and torsion angles, respectively, while SAWs on the BCC crystal have only 3 compatible bending angles.

Our homemade algorithm is based on direct enumeration of SAWs, as also implemented in our past works on SAWs under confinement [64,65]. The approach includes the exhaustive identification of all possible sequences of steps which fulfil two essential conditions: (1) the geometry imposed by the neighbor connectivity of the corresponding crystal, and (2) the self-avoidance of the random walk according to which the same crystal site cannot be visited twice by different segments (steps) of the SAW. The step length of the SAW is taken as unity and coincides with the distance between nearest neighbors in the crystal. Since the SAW growth is subjected only to the two conditions mentioned above, the selected bending (between two successive steps) and torsion (between three successive steps) angles adopt discrete values according to the imposed neighbor geometry of the corresponding crystals (as reported in Table 1 and Table 2). Figure 1 hosts segments of the four reference crystals (HCP, FCC, BCC, and HEX) along with a SAW of 9 steps (N = 9) grown on each one of them. Crystal sites are represented as spheres while the SAW steps are shown as orange lines.

A SAW of N steps consists of the ordered sequence of sites ω^N(0), ω^N(1), …, ω^N(N − 1), ω^N(N) with ω^N(0) being the SAW origin. In contrast to SAWs on spatially restricted lattices [64,65], the ones studied here correspond to the unconstrained bulk case. Thus, any site can be selected as the origin of the SAW, ω^N(0), due to the maximal symmetry of the bulk lattice. Self-avoidance of the random walk (or equivalently excluded volume of polymer) is fulfilled as ω^N(i) ≠ ω^N(j) for all i ≠ j. Bond tangency is satisfied as |ω^N(i + 1) − ω^N(i)| = 1, with i $\in$ [0, 1, …, N − 1] and |ω| = (ω·ω)^(1/2) denoting the Euclidean norm. The size of the SAW is quantified by the square end-to-end distance: |ω^N|² = (ω^N(N) − ω^N(0)). (ω^N(N) − ω^N(0)).

For a given number of steps, N, and a reference crystal X (HCP, FCC, HEX, or BCC) our algorithm is based on the direct enumeration of the total number of distinct SAWs, c_N(X), and proceeds with the calculation of all bending and torsion angles and of the square end-to-end distance of each identified SAW. Accordingly, for a SAW of N steps, the mean square end-to-end distance, 〈|ω^N|² 〉(X), can be readily calculated as:

$$\langle {\left|{\mathsf{\omega }}^N\right|}^2\rangle \left(X\right)=\frac{1}{c_N}{{\displaystyle \sum }}_{c_N}{\left|{\mathsf{\omega }}^N\right|}^2.$$

(1)

The scaling of the number of distinct SAWs, c_N, and of the average SAW size, 〈|ω^N|² 〉, as a function of the number of SAW steps is given by exponential-power-law asymptotic expressions [2,36,38,39,40,60,88]:

$$c_N\left(X\right)~A{\mu }^N{N}^{\gamma -1},$$

(2)

$$\langle {\left|{\mathsf{\omega }}^N\right|}^2\rangle \left(X\right)~D{N}^{2v},$$

(3)

where A and D are the critical amplitudes, μ is the connective constant, and γ and ν are the critical exponents. The critical exponents are considered universal, while the values of A, D, and μ are lattice dependent.

Starting from the work of Orr [22], elegant methods and efficient algorithms have been developed over the years to tackle the exponentially difficult SAW enumeration problem [6,9,36,38,39,61,62,89,90], reaching various high-N SAWs in distinct lattices. We should note here that our SAW enumeration algorithm is not as efficient as the state-of-the-art methods described above, and thus our analysis is limited to SAWs of intermediate number of steps. However, this should not be considered as a potential disadvantage as extensive off-lattice simulations, under a wide variety of conditions, have clearly demonstrated that, beyond a moderate value, chain length has practically no effect on the crystallization of athermal packings of fully flexible chains. The phase behavior and the established ordered morphologies are the same, independent of the average length of chains being as low as 12 or as high as 1000 monomers, the former value corresponding to short oligomers while the latter to well-entangled chains, deep in the polymeric regime [67,79,80].

The main objective of the present work is to provide a quantitative basis for the study of the thermodynamic stability of the HCP and FCC crystals made of fully flexible, athermal polymers. As mentioned in the Introduction, by assuming independence of the translational and conformational degrees of freedom, an argument which is analyzed in detail in [70], the total entropy of the crystal can be considered as the summation of two distinct contributions: the conformational one, ΔS_conf, dictated by chain connectivity respecting the geometric constraints of the reference crystal, and the translational one, ΔS_tran, which should be very similar to the one of monomeric systems of hard spheres, which are free of any constraints imposed by chain connectivity. Accordingly, the entropy difference of the HCP and FCC crystals can be written as [70]:

$$\Delta S^{FCC-HCP}=\Delta S_{\mathrm{conf}}^{FCC-HCP}+\Delta S_{\mathrm{tran}}^{FCC-HCP}=\ln \frac{\left|{\Xi }^{FCC}\right|}{\left|{\Xi }^{HCP}\right|}+\Delta S_{\mathrm{tran}}^{FCC-HCP}$$

(4)

where Ξ is the complete set (partition function) of all multichain configurations compatible with the polymer model (here, freely jointed chains of tangent hard spheres) and the lattice geometry (here, HCP or FCC), and || denote the cardinality of a set [70]. The translational contribution is known from past studies on monomeric analogs [73,74,75]. Thus, the evaluation of Ξ for the multichain configurations is required to arrive at an accurate estimate for $\Delta S^{FCC-HCP}$. However, such information is not available for any of the crystals. Accordingly, we need to establish an upper-bound, single-chain estimation. The concept of random walks (RWs) would not shed any light given that both the HCP and FCC crystals have the same coordination number and as such the same number of RWs over the whole range of steps. Toward this end, as a more refined criterion, we resort to self-avoiding random walks (SAWs), providing a tighter and more discriminating upper-bound estimate for the difference in the configurational entropy as [70]:

$$\frac{\left|{\Xi }^{HCP}\right|}{\left|{\Xi }^{FCC}\right|}<{\left(\frac{c_N\left(HCP\right)}{c_N\left(FCC\right)}\right)}^N\underset{}{\iff }\ln \left(\frac{\left|{\Xi }^{HCP}\right|}{\left|{\Xi }^{FCC}\right|}\right)=\frac{1}{N}ln\left(\frac{c_N\left(HCP\right)}{c_N\left(FCC\right)}\right).$$

(5)

3. Results

Table 3. Distinct number of SAWS, c_N, and mean square end-to-end distance, 〈|ω^N|²〉, as a function of number of SAW steps, N, for the FCC and HCP crystals. The difference in the number of SAWs Δc_N = c_N(HCP) − c_N(FCC) is also reported. Within the reported accuracy, there is no difference in the mean square end-to-end distance between the HCP and the FCC crystals.

N	FCC		HCP		Difference
	cN	〈|ωN|2〉	cN	〈|ωN|2〉	ΔcN
1	12	1.000	12	1.000	0
2	132	2.182	132	2.182	0
3	1404	3.496	1404	3.496	0
4	14,700	4.908	14,700	4.908	0
5	152,532	6.397	152,532	6.397	0
6	1,573,716	7.950	1,573,728	7.950	12
7	16,172,148	9.556	16,172,340	9.556	192
8	165,697,044	11.21	165,699,744	11.21	2700
9	1,693,773,924	12.90	1,693,809,348	12.90	35,424
10	17,281,929,564	14.64	17,282,367,084	14.64	437,520
11	176,064,704,412	16.41	176,069,916,384	16.41	5,211,972
12	1,791,455,071,068	18.21	1,791,515,688,168	18.21	60,617,100

presents the total number of distinct SAWs, c_N, and the mean square end-to-end distance, 〈|ω^N|²〉, as a function of SAW steps, N, for the FCC and HCP lattices, along with the difference in the number of SAWs, Δc_N (=c_N(HCP) − c_N(FCC)). The corresponding data for the BCC and HEX crystals are presented in

Table 4. Distinct number of SAWS, c_N, and mean square end-to-end distance, 〈|ω^N|²〉, as a function of number of SAW steps, N, for the BCC and HEX crystals. The differences Δc_N = c_N(BCC) − c_N(HEX) and Δ〈|ω^N|²〉 = 〈|ω^N|²〉 (BCC) − 〈|ω^N|²〉 (HEX) are also reported.

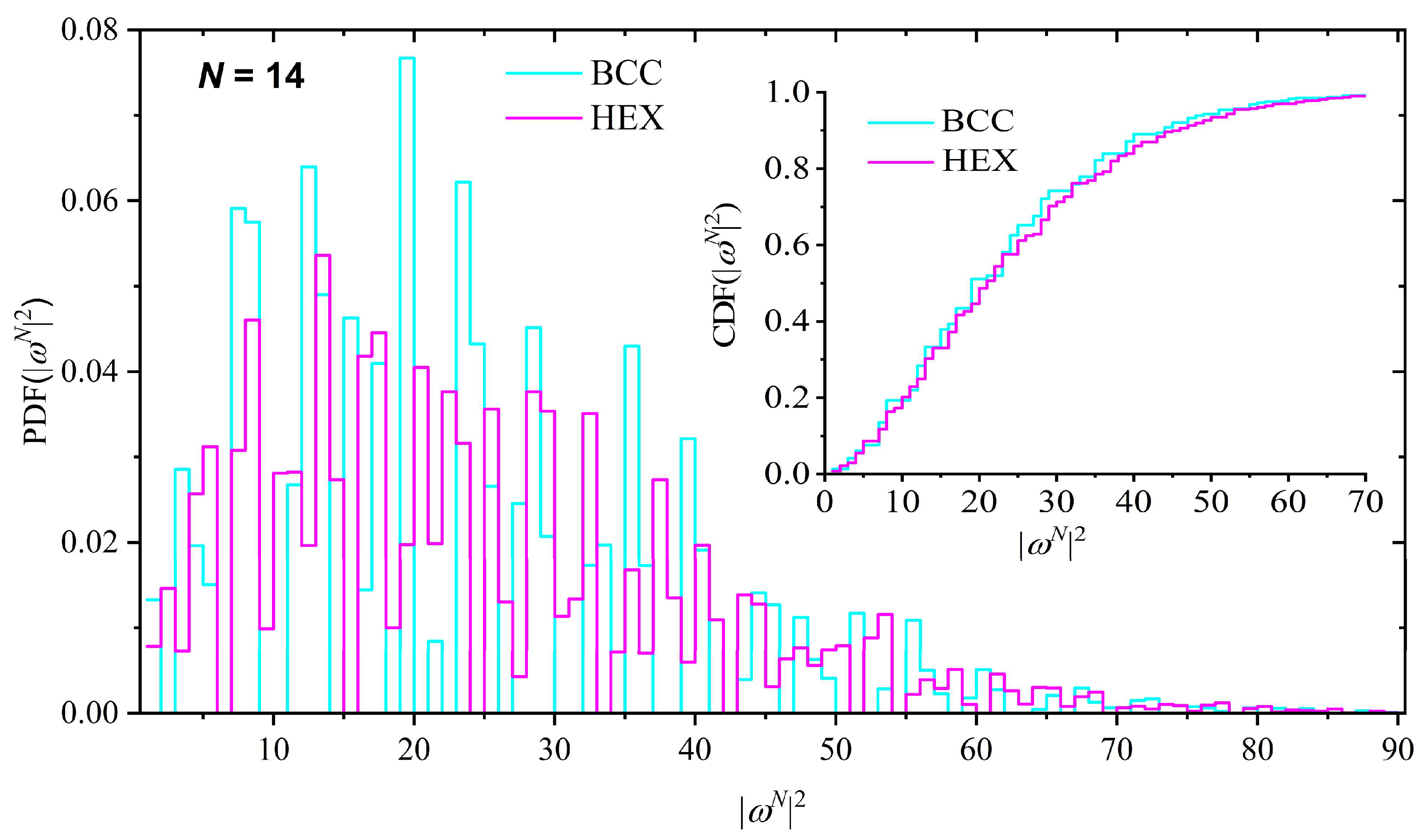
N	BCC		HEX		Difference
	cN	${\left|{\mathsf{\omega }}^{\mathit{N}}\right|}^2$	cN	${\left|{\mathsf{\omega }}^{\mathit{N}}\right|}^2$	ΔcN	$\Delta {\left|{\mathsf{\omega }}^{\mathit{N}}\right|}^2$
1	8	1.000	8	1.000	0	0.000
2	56	2.286	56	2.286	0	0.000
3	392	3.612	380	3.726	12	−0.114
4	2648	5.124	2540	5.280	108	−0.156
5	17,960	6.645	16,844	6.918	1116	−0.274
6	120,056	8.294	111,068	8.628	8988	−0.334
7	804,824	9.940	729,524	10.40	75,300	−0.458
8	5,351,720	11.69	4,777,628	12.22	574,092	−0.533
9	35,652,680	13.43	31,217,552	14.09	4,435,128	−0.661
10	236,291,096	15.26	203,608,520	16.01	32,682,576	−0.747
11	1,568,049,560	17.08	1,326,015,428	17.96	242,034,132	−0.879
12	10,368,669,992	18.97	8,625,090,800	19.95	1,743,579,192	−0.973
13	68,626,647,608	20.86	56,043,338,096	21.97	12,583,309,512	−1.11
14	453,032,542,040	22.81	363,826,528,532	24.02	89,206,013,508	−1.21

, which further hosts a column showcasing the difference in the mean square end-to-end distance. No such column exists in Table 3 because within the reported accuracy (four significant digits) there is no difference in the average SAW size between the HCP and the FCC crystals.

The FCC and HCP crystals show the same number of SAWs up to N = 5 steps. However, for N ≥ 6, the number of SAWs on the two lattices starts to deviate with the HCP crystal showing systematically more SAWs than the FCC one. At N = 6, Δc_N = 12, the relative difference is approximately 7.6 × 10⁻⁶. For the longest SAW studied here (N = 12) Δc_N = 60,617,100, which corresponds to a relative difference of 3.4 × 10⁻⁵, showing increasing trends as the SAW grows in length. In parallel, as can be seen by the comparison of the related rows in Table 3, the average size of the SAWs in the HCP and FCC lattices is the same within a tolerance of 10⁻⁵ for all values of N.

Similar trends are observed in the comparison of the BCC and HEX crystals as listed in Table 4. For N = 3, the BCC crystal has 12 more SAWs compared to the HEX crystal with the relative difference being 0.031, significantly higher than the one observed for the HCP-FCC pair at the corresponding deviation point (N = 6). For the longest SAW studied here (N = 14), the absolute and relative differences for the BCC-HEX pair increase to 89,206,013,508 and 0.20, respectively. Accordingly, even if both lattices have the same coordination number (n_coord = 8) the single-chain conformations, as quantified by the number of SAWs, are significantly fewer in HEX compared to BCC. With respect to the average size, the polymer grown on the HEX lattice is systematically longer than the one on the BCC with the relative difference being approximately 0.053 for N = 14.

The left panel of Figure 2 shows the logarithm of the total number of distinct SAWs, c_N, as a function of the logarithm of the total number of SAW steps, N, for all lattices studied here. The differences of the two pairs are also shown. On the right panel of Figure 2, we can observe the dependence of the logarithm of the mean square end-to-end distance, 〈|ω^N|² 〉(X), as calculated from Equation (1), on the logarithm of the number of SAW steps, N. Furthermore, we have fitted all available data with best linear fits corresponding to the scaling formula of Equation (3). Figure 2 shows one such best linear fit corresponding to the data for the HEX crystal, with the reliability fitting coefficient being practically equal to 1. The complete set of the parameter values, according to Equations (2) and (3), as obtained from best linear fits on current SAW data, are reported in

Table 5. Critical amplitudes, A and D, critical exponents, γ and v, and connective constant, μ, as calculated from best linear fits using the SAW enumeration data as reported in Table 3 and Table 4 and Figure 2 for the HCP, BCC, and HEX lattices. Due to the minimal differences between the HCP and FCC crystals in Section 4 (Discussion), we present the correlation of the difference.

Lattice	A	μ	γ	D	v
HCP	1.19	10.07	1.134	0.977	0.587
BCC	1.21	6.565	1.124	0.995	0.593
HEX	1.24	6.436	1.129	0.994	0.603

. Very little variation is observed for both the critical amplitude and exponent between the different lattices, especially when the FCC and HCP crystals are compared. A minimal trend suggests that the exponent increases slightly for the crystals of the lower coordination number, while the opposite behavior is observed for the amplitude. Given the short or intermediate length of the studied SAWs, the universal exponent of 0.588 is nicely matched for the HCP and FCC crystals. Between the HCP and the FCC crystal there is no appreciable difference suggesting that the corresponding SAW sizes will be very similar, but strictly not identical, for the limit of infinitely long chains (N → ∞).

The distribution of the discrete bending angles, which are compatible with each lattice studied here, is given in Figure 3 as a function of the number of SAW steps. For all crystal types, as N grows, the population of obtuse angles experiences small decreases in favor of the acute ones because of the self-avoidance condition. The fraction of bending angles with 90°, where available (HCP, FCC, and HEX), rapidly reaches a stable plateau. Extrapolating the current trends, to longer N, the most probable bending angle is 60°, 60°, 70.53°, and 90° for the FCC, HCP, BCC, and HEX crystals, respectively.

Figure 4 hosts the corresponding results for the distribution of discrete torsion angles which are compatible with each lattice crystal. For FCC, as N increases, the populations at 54.7, 125.3, and 180° increase, while the one at 90° shows a significant reduction. Compared to other crystals, the SAWs on the HCP lattice show a richer behavior with the primary angles resting at 54.7°, 70.5°, 109.5°, and 180°. The HEX crystal is the one that shows the smallest variation with increasing number of SAW steps.

The distribution of SAW size, as quantified by the square end-to-end distance, |ω^N|², is shown in Figure 5 and Figure 6 for the HCP–FCC and BCC–HEX pairs, respectively. The probability distribution function (PDF) is presented in the main figure while the cumulative distribution function (CDF) is shown in the inset. Given the major differences in the bonded geometry between HCP and FCC lattices, it is not surprising that the distribution of the SAW size shows significant deviations. However, it is interesting to notice that in spite of these variations, the global SAW size, on average, is indistinguishable between the close-packed FCC and HCP crystals, as shown in Table 1, and further confirmed by the CDF trends in the inset of Figure 5. On the other hand, SAWs on the BCC lattice have a smaller size than the ones on the HEX as indicated by the concentrated maxima of the BCC distribution at small values of the square end-to-end distance.

4. Discussion

We enumerate and describe the self-avoiding random walks, SAWs, grown on different crystals, characterized by the same coordination number (n_coord = 12 or 8). We observe that for the HCP and FCC pair, once a critical number of steps is reached (N = 6) the number of distinct SAWs becomes different. In relative numbers, this difference is minute but definitely non-zero with the HCP crystal showing a larger number of SAWs compared to FCC (c_N(HCP) > c_N(FCC) for N > 5). The present finding is clear evidence that the SAW behavior in the HCP and FCC crystals should not be considered as identical even though both are characterized by the same coordination number and packing density. In parallel, the average size of SAWs on these two crystals is indistinguishable for the whole range of studied SAW steps even if the internal chain/SAW bonded geometry, as quantified by the bending and torsion angles, is significantly different: the HCP crystal shows a much richer variety in bond geometry and same is true for the size distribution as quantified by the end-to-end distance.

The data presented here in Table 3 and Table 4, and Figure 2 for the HCP-FCC and BCC-HEX pairs clearly identify a difference in the number of SAWs once a critical number of steps is reached. The ratio of the SAWs in Equation (5) can be fitted using an asymptotic formula:

$$\frac{\frac{c_N\left(X\right)}{c_N\left(Y\right)}-1}{N}=A_1-B{e}^{-dN}$$

(6)

where X and Y are the two crystals to be compared and A₁, B, and d are the fitting parameters. Fittings using the exponential formula of Equation (6) on available SAW enumeration data are reported in Figure 7.

Both pairs suggest an asymptotic behavior of the conformational entropy difference per monomer. For the HCP and FCC crystals, the established behavior is far from the asymptotic regime and significantly longer SAWs are required, pointedly increasing the computational complexity of the problem. However, application of the exponential formula (Equation (6)) allows for the prediction of the ratio for very long SAWs from short and intermediate values as the ones presented here. The fitting parameters for the HCP/FCC and BCC/HEX are summarized in

Table 6. Fitting parameters A₁, B, and d of the asymptotic formula (Equation (6)) applied on the current SAW enumeration data for the HCP/FCC and BCC/HEX pairs of crystal lattices.

Pair of Crystals	A1	B	d	Range of Validity
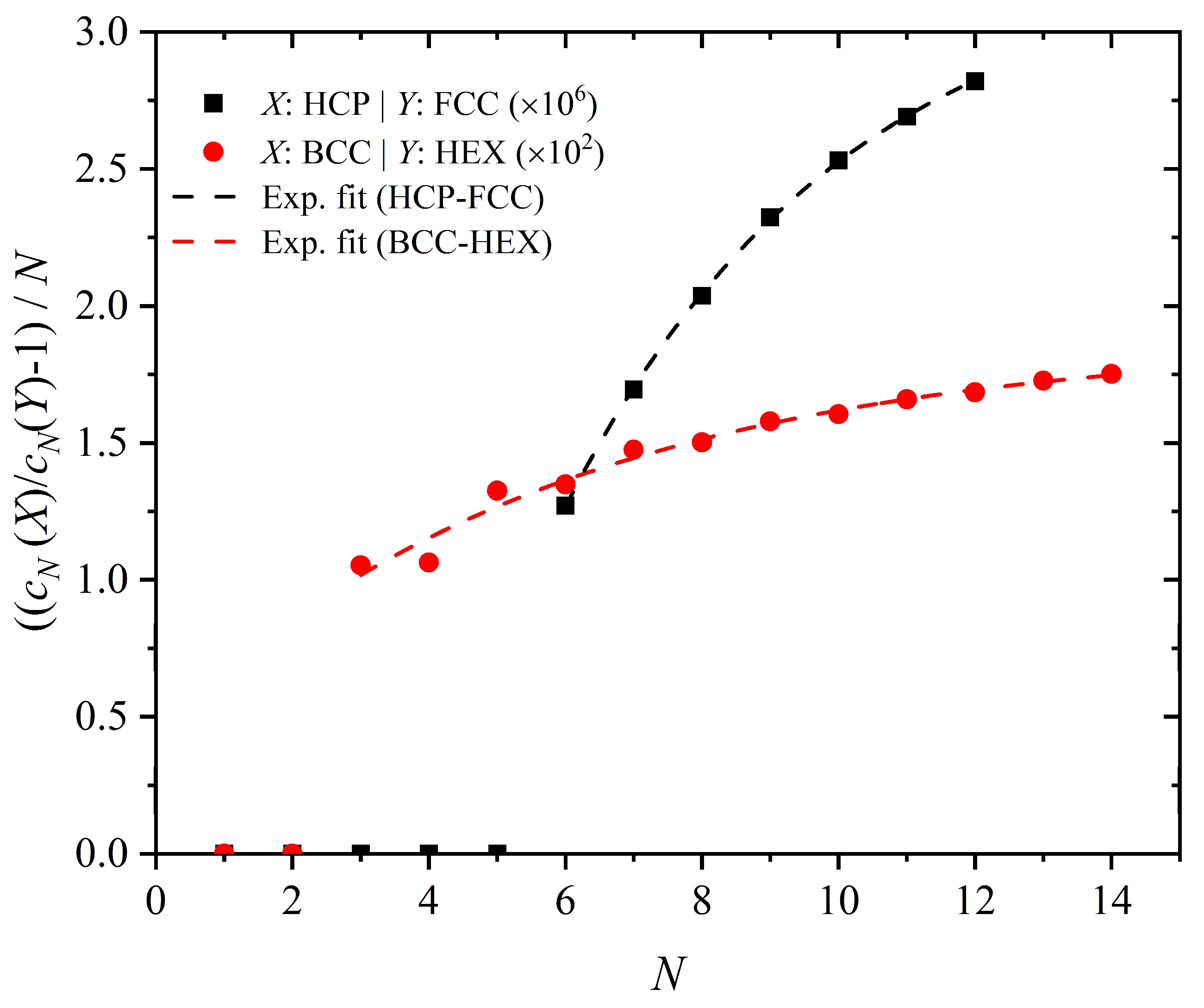
HCP-FCC	3.31 × 10−6	8.63 × 10−6	0.24	N > 5
BCC-HEX	0.0188	0.0144	0.17	N > 2

. Although the maximum chain length for which we could exhaustively enumerate SAWs is moderate, the quality of the fit in Figure 7 suggests that the values of the parameter A₁ in Table 6 are a quite accurate approximation to the asymptotic value, i.e., for infinite chain length, which is the physically relevant quantity for long polymers.

Concentrating on the HCP-FCC pair, which is the main focus of the present study, placing the asymptotic formula in Equation (5) and considering the limit of very long chains provides an upper-bound estimate, $\Delta S_{\mathrm{conf}}^{FCC-HCP}\approx -0.331\times {10}^{-5}$ k, as the HCP polymer crystal has a higher conformational entropy than the FCC one. However, this value is significantly lower than the translational entropy $\Delta S_{\mathrm{trans}}^{FCC-HCP}\approx 112\times {10}^{-5}$ k. Accordingly, the FCC is the most stable crystal among the polymorphs for freely jointed polymers of tangent hard spheres.

5. Conclusions

Prediction of the thermodynamic stability of crystals made of athermal polymers is significantly more complicated than for monomeric analogs due to the presence of constraints imposed by chain connectivity. Here, we demonstrate that once a critical number of steps is reached, the HCP crystal has more self-avoiding random walks than the FCC one. Accordingly, a tight upper-bound estimate of the conformational entropic advantage of the HCP crystal suggests that this lead is not sufficient to overcome the significantly larger translational advantage of the FCC crystal [70]. Hence, the FCC crystal is the thermodynamically most stable athermal polymer crystal and should prevail among competing polymorphs, as confirmed by recent off-lattice simulations of freely jointed chains of hard spheres [71]. The present work is currently being extended to tackle freely rotating chains on crystals in two and three dimensions.