Virtual Work Principle for Piezoelectric Semiconductors and Its Application on Extension and Bending of ZnO Nanowires
Abstract
:1. Introduction
2. Three-Dimensional Framework for PSs
2.1. The PVW for PSs
2.2. Constitutive Relations for PSs
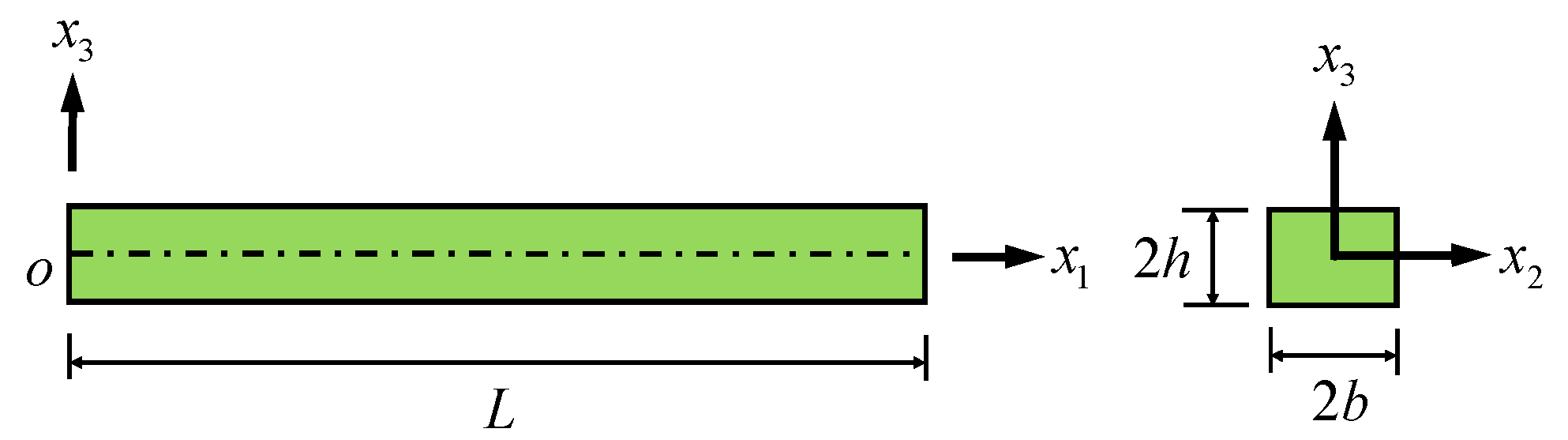
3. One-Dimensional Model for PS Nanowires
3.1. Field Equations for PS Nanowires
3.2. One-Dimensional Constitutive Relations
4. Examples
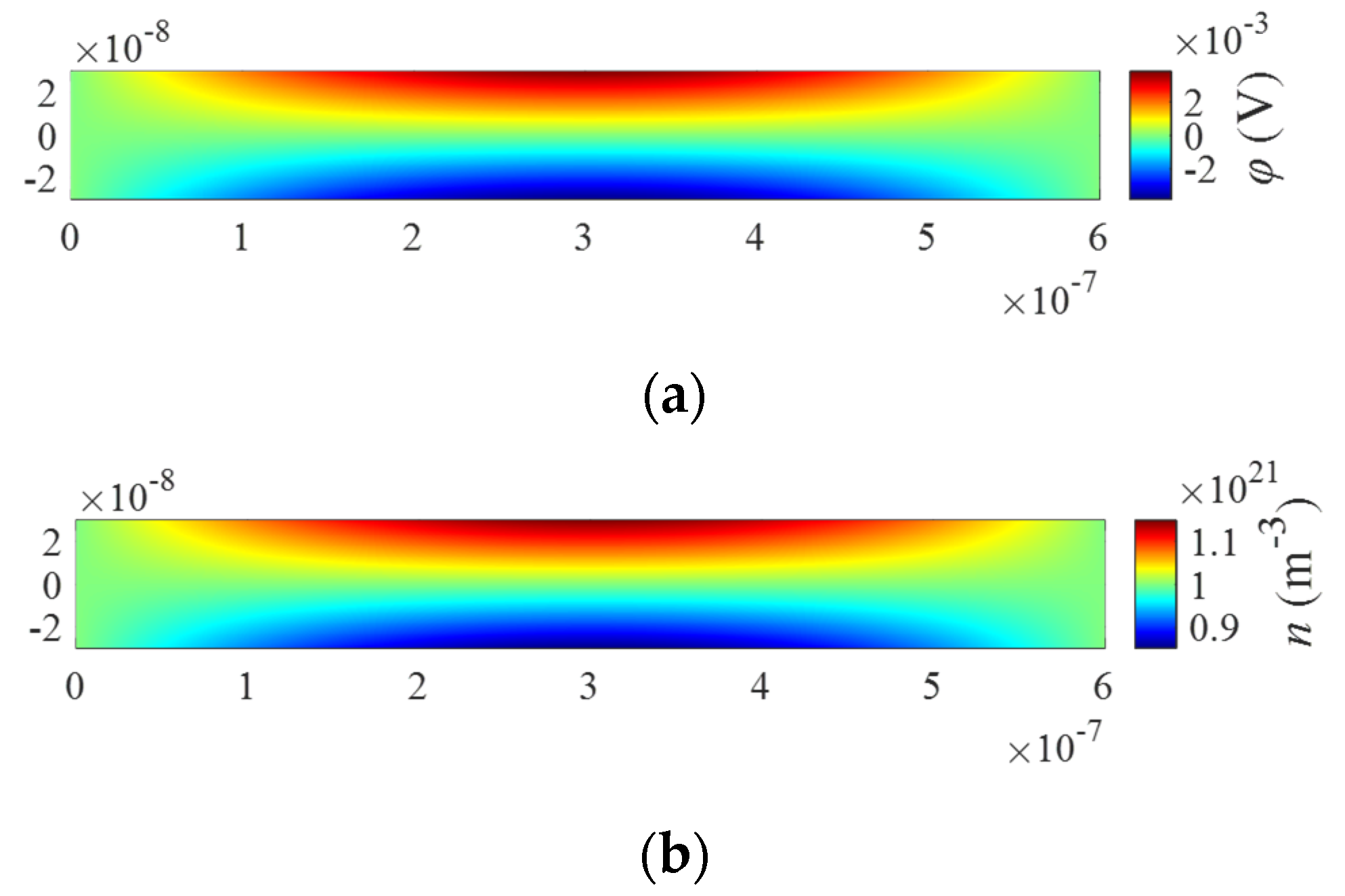
4.1. Extension of ZnO Nanowires
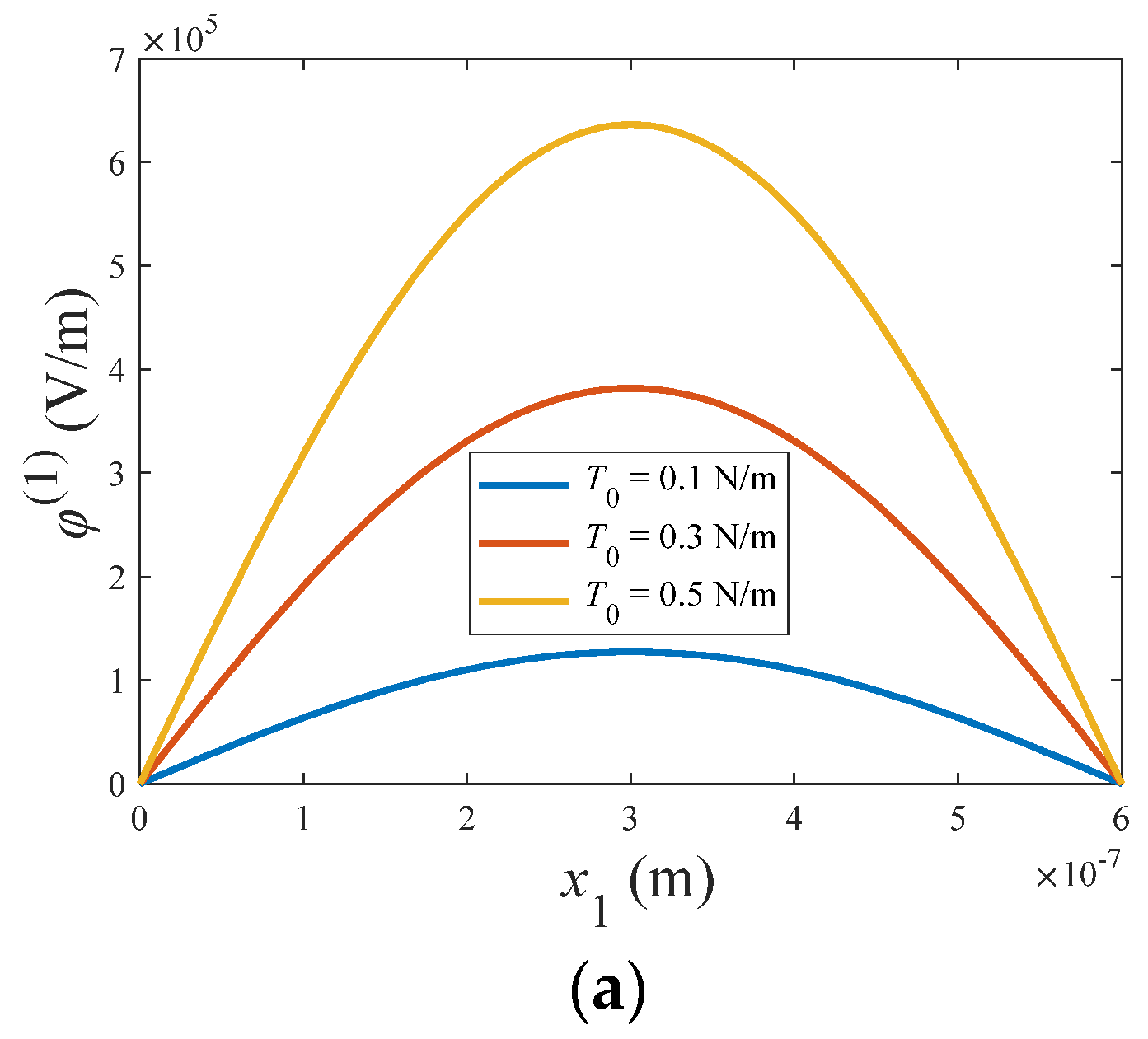
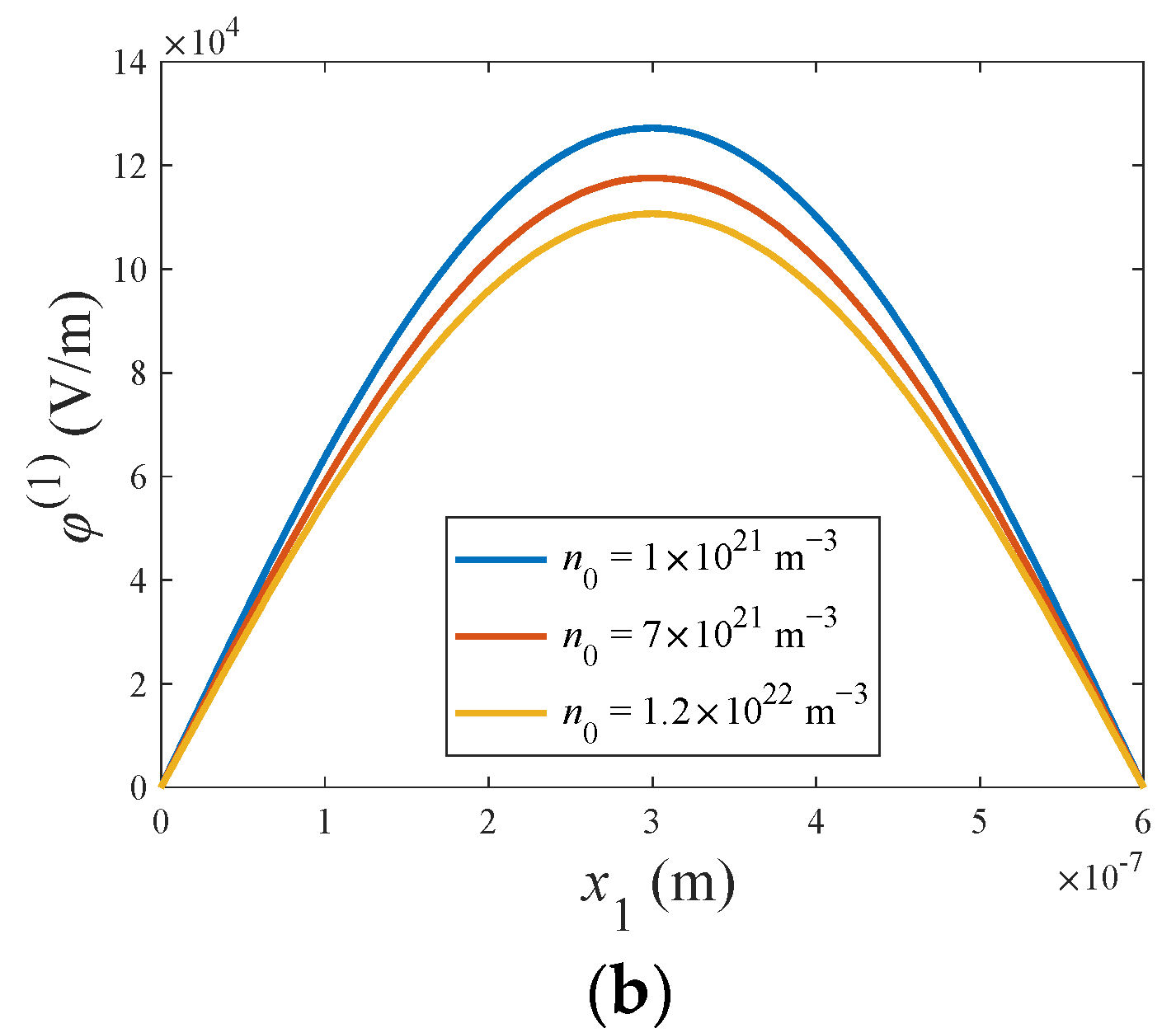
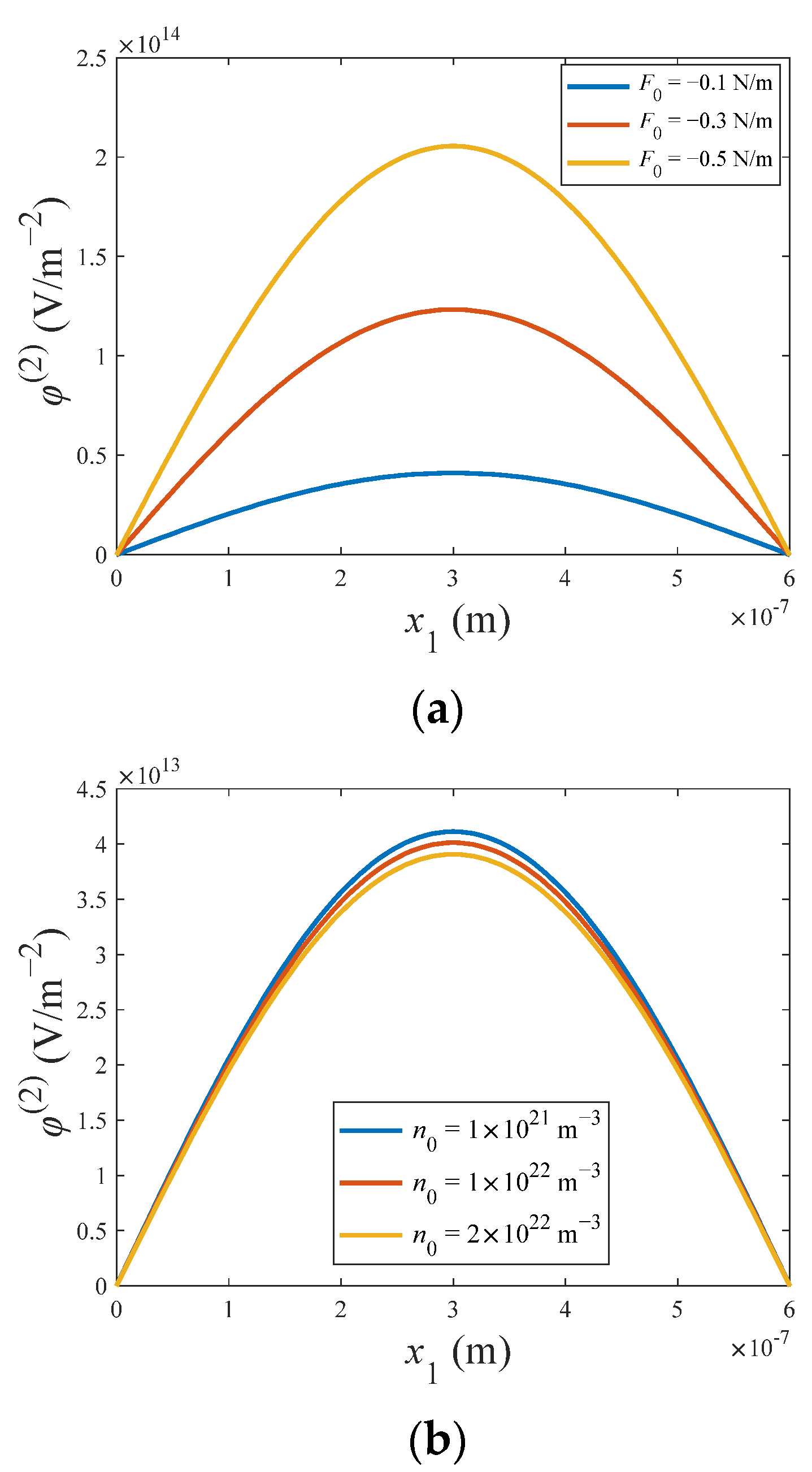
4.2. Bending of ZnO Nanowires
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Auld, B.A. Acoustic Fields and Waves in Solids; John Wiley & Sons: New York, NY, USA, 1973. [Google Scholar]
- Hickernell, F.S. The piezoelectric semiconductor and acoustoelectronic device development in the sixties. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 737–745. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.L. Nanobelts, nanowires, and nanodiskettes of semiconducting oxides—From materials to nanodevices. Adv. Mater. 2003, 15, 432–436. [Google Scholar] [CrossRef]
- Lao, C.S.; Liu, J.; Gao, P.; Zhang, L.; Davidovic, D.; Tummala, R.; Wang, Z.L. ZnO nanobelt/nanowire Schottky diodes formed by dielectrophoresis alignment across Au electrodes. Nano Lett. 2006, 6, 263–266. [Google Scholar] [CrossRef]
- Kim, K.K.; Kim, H.S.; Hwang, D.K.; Lim, J.H.; Park, S.J. Realization of p-type ZnO thin films via phosphorus doping and thermal activation of the dopant. Appl. Phys. Lett. 2003, 83, 63–65. [Google Scholar] [CrossRef]
- Wang, Z.L. Piezotronics and Piezo-Phototronics; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Wang, Z.L.; Song, J. Piezoelectric nanogenerators based on zinc oxide nanowire arrays. Science 2006, 312, 242–246. [Google Scholar] [CrossRef]
- Sharma, J.N.; Sharma, K.K.; Kumar, A. Surface waves in a piezoelectric–semiconductor composite structure. Int. J. Solids Struct. 2010, 47, 816–826. [Google Scholar] [CrossRef]
- Tian, R.; Liu, J.; Pan, E.; Wang, Y.; Soh, A.K. Some characteristics of elastic waves in a piezoelectric semiconductor plate. J. Appl. Phys. 2019, 126, 125701. [Google Scholar] [CrossRef]
- Cao, X.; Hu, S.; Liu, J.; Shi, J. Generalized Rayleigh surface waves in a piezoelectric semiconductor half space. Meccanica 2019, 54, 271–281. [Google Scholar] [CrossRef]
- Gokhale, V.J.; Rais-Zadeh, M. Phonon-electron interactions in piezoelectric semiconductor bulk acoustic wave resonators. Sci. Rep. 2014, 4, 1–10. [Google Scholar] [CrossRef]
- Sladek, J.; Sladek, V.; Pan, E.; Young, D.L. Dynamic anti-plane crack analysis in functional graded piezoelectric semiconductor crystals. CMES 2014, 99, 273–296. [Google Scholar]
- Fan, C.; Yan, Y.; Xu, G.; Zhao, M. Piezoelectric-conductor iterative method for analysis of cracks in piezoelectric semiconductors via the finite element method. Eng. Fract. Mech. 2016, 165, 183–196. [Google Scholar] [CrossRef]
- Qin, G.; Lu, C.; Zhang, X.; Zhao, M. Electric current dependent fracture in GaN piezoelectric semiconductor ceramics. Materials 2018, 11, 2000. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.L.; Luo, Y.X.; Cheng, R.R.; Wang, X.Y. Electromechanical fields in piezoelectric semiconductor nanofibers under an axial force. MRS Adv. 2017, 2, 3421. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, X.; Chen, W.; Yang, J. An analysis of the extension of a ZnO piezoelectric semiconductor nanofiber under an axial force. Smart Mater. Struct. 2017, 26, 025030. [Google Scholar] [CrossRef]
- Jin, L.S.; Yan, X.H.; Wang, X.F.; Hu, W.J.; Zhang, Y.; Li, L.J. Dynamic model for piezotronic and piezo-phototronic devices under low and high frequency external compressive stresses. J. Appl. Phys. 2018, 123, 025709. [Google Scholar] [CrossRef]
- Qu, Y.L.; Jin, F.; Yang, J.S. Torsion of a piezoelectric semiconductor rod of cubic crystals with consideration of warping and in-plane shear of its rectangular cross section. Mech. Mater. 2022, 172, 104407. [Google Scholar] [CrossRef]
- Fang, K.; Qian, Z.; Yang, J. Piezopotential in a composite cantilever of piezoelectric dielectrics and nonpiezoelectric semiconductors produced by shear force through e15. Mater. Res. Express 2019, 6, 115917. [Google Scholar] [CrossRef]
- Ren, C.; Wang, K.F.; Wang, B.L. Adjusting the electromechanical coupling behaviors of piezoelectric semiconductor nanowires via strain gradient and flexoelectric effects. J. Appl. Phys. 2020, 128, 215701. [Google Scholar] [CrossRef]
- Yang, J.S. Analysis of Piezoelectric Semiconductor Structures; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Qu, Y.L.; Jin, F.; Yang, J.S. Stress-induced electric potential barriers in thickness-stretch deformations of a piezoelectric semiconductor plate. Acta Mech. 2021, 232, 4533–4543. [Google Scholar] [CrossRef]
- Qu, Y.L.; Jin, F.; Yang, J.S. Buckling of a Reissner–Mindlin plate of piezoelectric semiconductors. Meccanica 2022, 57, 2797–2807. [Google Scholar] [CrossRef]
- Xu, C.; Wei, P.; Wei, Z.; Guo, X. Rayleigh wave in layered piezoelectric semiconductor with consideration of PN junction effects. Math. Mech. Solids 2022, 28, 1817–1833. [Google Scholar] [CrossRef]
- Xu, C.; Wei, P.; Wei, Z.; Guo, X. Effects of Schottky junction on surface waves in a piezoelectric semiconducting film over a metal substrate. Math. Mech. Solids 2023. Online. [Google Scholar] [CrossRef]
- Qu, Y.L.; Pan, E.N.; Zhu, F.; Jin, F.; Roy, A.K. Modeling thermoelectric effects in piezoelectric semiconductors: New fully coupled mechanisms for mechanically manipulated heat flux and refrigeration. Int. J. Eng. Sci. 2023, 182, 103775. [Google Scholar] [CrossRef]
- Zhou, J.; Fei, P.; Gao, Y.; Gu, Y.; Liu, J.; Bao, G.; Wang, Z.L. Mechanical-electrical triggers and sensors using piezoelectric micowires/nanowires. Nano Lett. 2008, 8, 2725–2730. [Google Scholar] [CrossRef]
- Liang, C.; Zhang, C.; Chen, W.; Yang, J. Static buckling of piezoelectric semiconductor fibers. Mater. Res. Express 2020, 6, 125919. [Google Scholar] [CrossRef]
- Zhang, Z.; Liang, C.; Wang, Y.; Xu, R.; Gao, C.; Zhang, C. Static bending and vibration analysis of piezoelectric semiconductor beams considering surface effects. J. Vib. Eng. Technol. 2021, 9, 1789–1800. [Google Scholar] [CrossRef]
- Zhang, Z.; Liang, C.; Kong, D.; Xiao, Z.; Zhang, C.; Chen, W. Dynamic buckling and free bending vibration of axially compressed piezoelectric semiconductor rod with surface effect. Int. J. Appl. Mech. 2023, 238, 107823. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, C.; Chen, W.; Yang, J. Piezopotential in a bended composite fiber made of a semiconductive core and of two piezoelectric layers with opposite polarities. Nano Energy 2018, 54, 341–348. [Google Scholar] [CrossRef]
- Maugin, G.A. The method of virtual power in continuum mechanics: Application to coupled fields. Acta Mech. 1980, 35, 1–70. [Google Scholar] [CrossRef]
- Daher, N.; Maugin, G.A. Virtual power and thermodynamics for electromagnetic continua with interfaces. J. Math. Phys. 1986, 27, 3022–3035. [Google Scholar] [CrossRef]
- Maugin, G.A. The principle of virtual power: From eliminating metaphysical forces to providing an efficient modelling tool: In memory of Paul Germain (1920–2009). Continuum Mech. Therm. 2013, 25, 127–146. [Google Scholar] [CrossRef]
- Falsone, G.; La Valle, G. A homogenized theory for functionally graded Euler–Bernoulli and Timoshenko beams. Acta Mech. 2019, 230, 3511–3523. [Google Scholar] [CrossRef]
- Ascione, A.; Gherlone, M.; Orifici, A.C. Nonlinear static analysis of composite beams with piezoelectric actuator patches using the Refined Zigzag Theory. Compos. Struct. 2022, 282, 115018. [Google Scholar] [CrossRef]
- Germain, P. The method of virtual power in the mechanics of continuous media, I: Second-gradient theory. Math. Mech. Complex Sy. 2020, 8, 153–190. [Google Scholar] [CrossRef]
- Qu, Y.L.; Zhang, G.Y.; Fan, Y.M.; Jin, F. A non-classical theory of elastic dielectrics incorporating couple stress and quadrupole effects: Part I – reconsideration of curvature-based flexoelectricity theory. Math. Mech. Solids 2021, 26, 1647–1659. [Google Scholar] [CrossRef]
- Yang, J.S. The Mechanics of Piezoelectric Structures; World Scientific: Singapore, 2006. [Google Scholar]
- Gao, X.-L.; Mall, S. Variational solution for a cracked mosaic model of woven fabric composites. Int. J. Solids Struct. 2001, 38, 855–874. [Google Scholar] [CrossRef]
- Qu, Y.L.; Jin, F.; Yang, J.S. Flexoelectric effects in second-order extension of rods. Mech. Res. Commun. 2021, 111, 103625. [Google Scholar] [CrossRef]
- Zhang, G.Y.; Guo, Z.W.; Qu, Y.L.; Gao, X.L.; Jin, F. A new model for thermal buckling of an anisotropic elastic composite beam incorporating piezoelectric, flexoelectric and semiconducting effects. Acta Mech. 2022, 233, 1719–1738. [Google Scholar] [CrossRef]
- Qu, Y.L.; Zhang, G.Y.; Gao, X.L.; Jin, F. A new model for thermally induced redistributions of free carriers in centrosymmetric flexoelectric semiconductor beams. Mech. Mater. 2022, 171, 104328. [Google Scholar] [CrossRef]
- Sze, S.M.; Ng, K.K. Physics of Semiconductor Devices; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Wang, G.; Liu, J.; Liu, X.; Feng, W.; Yang, J. Extensional vibration characteristics and screening of polarization charges in a ZnO piezoelectric semiconductor nanofiber. J. Appl. Phys. 2018, 124, 094502. [Google Scholar] [CrossRef]
- Zhang, G.Y.; Qu, Y.L.; Guo, Z.W.; Jin, F. Magnetically induced electric potential in first-order composite beams incorporating couple stress and its flexoelectric effects. Acta Mech. Sin. 2021, 37, 1509–1519. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Zhang, G.; Li, D.; Qu, Y. Virtual Work Principle for Piezoelectric Semiconductors and Its Application on Extension and Bending of ZnO Nanowires. Crystals 2023, 13, 1368. https://doi.org/10.3390/cryst13091368
Chen J, Zhang G, Li D, Qu Y. Virtual Work Principle for Piezoelectric Semiconductors and Its Application on Extension and Bending of ZnO Nanowires. Crystals. 2023; 13(9):1368. https://doi.org/10.3390/cryst13091368
Chicago/Turabian StyleChen, Jingbo, Gongye Zhang, Dongbo Li, and Yilin Qu. 2023. "Virtual Work Principle for Piezoelectric Semiconductors and Its Application on Extension and Bending of ZnO Nanowires" Crystals 13, no. 9: 1368. https://doi.org/10.3390/cryst13091368
APA StyleChen, J., Zhang, G., Li, D., & Qu, Y. (2023). Virtual Work Principle for Piezoelectric Semiconductors and Its Application on Extension and Bending of ZnO Nanowires. Crystals, 13(9), 1368. https://doi.org/10.3390/cryst13091368






