Effect of Ultrasonic Vibration on Tensile Mechanical Properties of Mg-Zn-Y Alloy

Abstract

Ultrasonic vibration assisted (UVA) plastic forming technology has proven to be a highly effective processing method, particularly for materials that are challenging to deform. In this research, UVA tensile tests were carried out on Mg_98.5Zn_0.5Y₁ alloy at different vibration frequencies and amplitudes. The experimental results indicate that, compared with conventional tensile tests, the yield strength and tensile strength of Mg_98.5Zn_0.5Y₁ alloy exhibit a decrease. Furthermore, the application of ultrasonic vibration demonstrates an ability to enhance the material’s elongation and plasticity. In order to further predict the stress-strain relationship in the metal tensile process, a hybrid constitutive model coupling the frequency and amplitude of ultrasonic vibration was developed based on the modified Johnson Cook model. The calculated results of the constitutive equation are in good agreement with the experimental results, indicating that the established constitutive equation can accurately predict the trend of alloy stress change at different amplitudes and frequencies. It establishes a theoretical foundation for scrutinizing the deformation mechanisms of the alloy under ultrasonic vibration. Furthermore, Abaqus finite element analysis software was employed to simulate and analyze the UVA tensile process, elucidating the impact of ultrasonic vibration on stress distribution, strain patterns, and material flow in the tensile behavior of Mg_98.5Zn_0.5Y₁ alloys.

1. Introduction

As a light structural material, magnesium alloy has a very good application prospect in the automobile, aerospace, national defense, biomedicine and other industries. It should be noted that the Mg-Zn-Y alloy has generated great interest due to its good combination of strength and ductility [1,2]. However, the poor formability of magnesium alloys at room temperature limits their wide application. Such poor formability of Mg alloys mainly comes from their crystal structure being hcp with a limited number of deformation systems [3]. The problem concerning how to improve the plastic formability of magnesium alloys is the key to expand their application range. Previous studies [4] have shown that although it is a common practice to increase the number of active slip systems by thermal deformation, there are many shortcomings to this approach. For instance, magnesium alloy’s low specific heat makes it challenging to maintain a steady temperature during processing. Additionally, the repeated annealing and high-temperature processing will result in a complicated forming process and considerable energy usage. As a result, many researchers are dedicated to developing short and environmentally friendly processing methods [5,6]. Among them, ultrasonic vibration assisted (UVA) plastic forming technology is considered as a relatively mature metal forming technology. Following the seminal work of Blaha and Longenecker [7], which demonstrated the substantial reduction of flow stress in the tensile testing of single zinc crystals under ultrasonic vibration, a series of studies have been conducted to delve into UVA plastic forming and scrutinize the influence of ultrasonic vibration on material properties. Compared with the traditional forming process, the superposition of vibration on the die or workpiece can reduce the forming load of the material, improve the plasticity and fracture limit, and effectively improve the mechanical properties of the material [8,9]. Ultrasonic vibration, known for its high frequency, rapid speed, short cycles, user-friendliness, environmental friendliness, and controllability, has emerged as a highly effective method for surface strengthening and stress relief in various metal-plastic forming processes. To date, processing technologies such as ultrasonic assisted drawing [10], ultrasonic assisted extrusion [11] and ultrasonic assisted deep drawing [12] have been developed. The advantage of UVA plastic deformation of metals is that it cannot only reduce the forming force of materials and improve the forming quality of materials, but also reduce the friction between specimens and molds and improve the surface quality of materials. It can effectively refine the grains [13,14] and promote the dislocation slip [15]. Moreover, the softening effect induced by ultrasonic vibration is not only more efficient, but also more energy-saving compared to traditional heating-induced softening [16].

Ultrasonic vibration in metal UVA plastic deformations induces two primary effects: the volume effect [17] and the surface effect [18]. The volume effect primarily signifies the impact of ultrasonic vibration on physical properties, such as the internal structure of materials. Meanwhile, the surface effect primarily reflects the influence of friction between the die and the blank during vibration. Based on various explanations of UVA plastic deformation, many scholars have proposed the constitutive model of metal deformation under ultrasonic vibration. Yao et al. [19] established acoustic softening and acoustic residual hardening models of aluminum under ultrasonic vibration based on thermal activation model and dislocation evolution theory in metal plastic deformation, which can accurately predict the stress-strain relationship of aluminum under high-frequency vibration. Prabhakar [20] expanded the constitutive model according to the acoustic softening of aluminum alloys under ultrasonic vibration, and successfully predicted the acoustic softening behavior of aluminum alloys under different vibration conditions. Sedaghat et al. [21] proposed a new constitutive model to predict the acoustic plastic behavior of materials based on the deformation behavior of aluminum alloys under ultrasonic vibration, combined with the dislocation dynamics and acoustic energy conversion mechanism of materials under ultrasonic vibration. Meng et al. [22] established the ultrasonic vibration constitutive model of materials at high temperature according to the plastic deformation behavior of Inconel 718 alloy under ultrasonic vibration and the dislocation evolution theory of materials. The outcomes reveal that the predicted results align well with the experimental findings, demonstrating the model’s effectiveness in describing the material’s behavior under these conditions. Lin et al. [23] established the constitutive relationship of pure titanium under ultrasonic vibration using the original Johnson cook and its modified model according to the compression deformation of pure titanium under different strain rates and different amplitudes. This model can accurately predict the material flow behavior under different amplitudes and strain rates.

In the present work, the effect of frequencies, amplitudes and strain rates on tensile properties of Mg-Zn-Y alloy was systematically studied. The stress-strain relationship of Mg-Zn-Y alloy under different conditions was compared. Additionally, the effect of ultrasonic vibration on material dislocations and dislocation motion evolution in forming process were analyzed. As a result, we developed a constitutive model that incorporates both frequencies and amplitudes to better understand and describe the material’s behavior under ultrasonic vibration.

2. Experimental Procedures

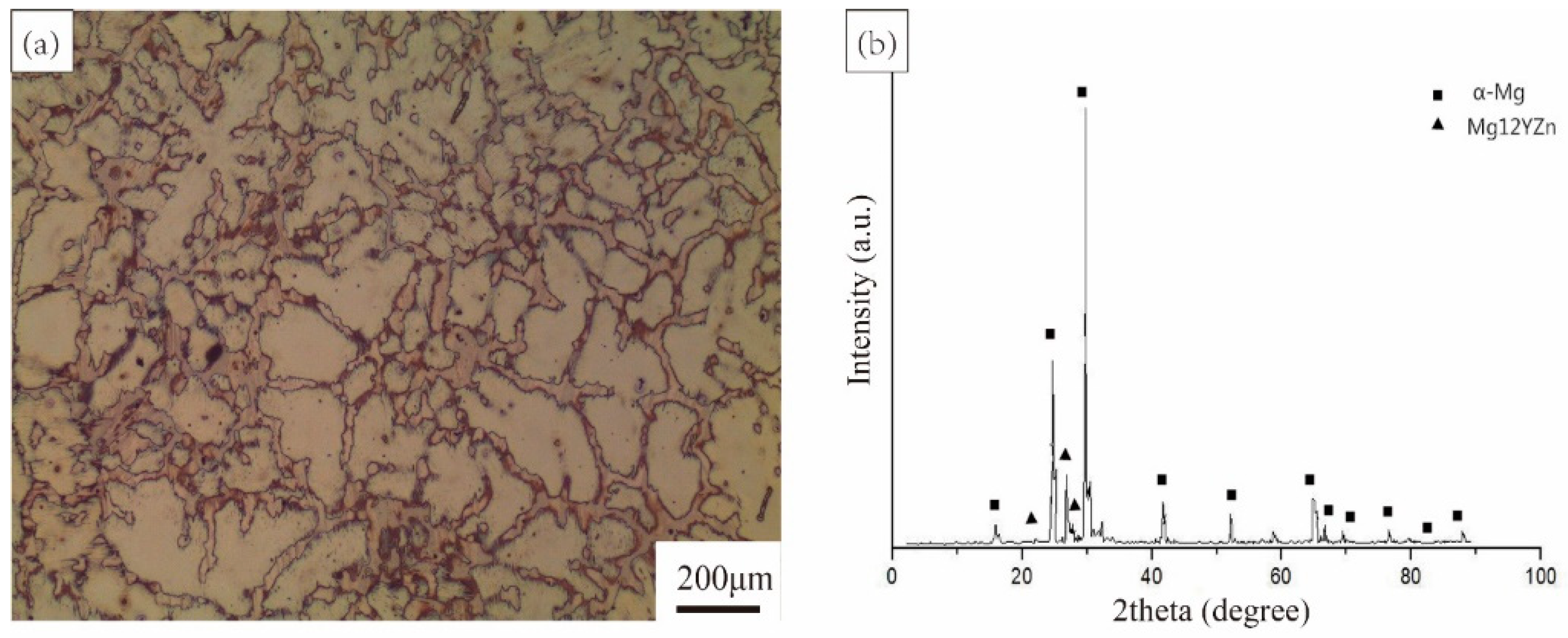
2.1. Specimen Preparation

The Mg_98.5Zn_0.5Y₁ alloy used in the experiment was melted by pure magnesium (99.99 wt%), pure zinc (99.99 wt%) and Mg-25 wt% Y alloy. The alloy is smelted in SXL-1200 resistance furnace filled with argon. The ingots were homogenized at 500 °C for 16 h and then cooled in air. The composition of alloy ingot was measured by X-ray fluorescence spectrometer. The alloy’s chemical composition is detailed in

Table 1. Chemical composition of Mg_98.5Zn_0.5Y₁ alloy.

Nominal Alloy	Actual Composition (at %)
Mg98.5Zn0.5Y1	Mg	Zn	Y	Y/Zn
	98.5	0.5	1	2

. The microstructure was examined using optical microscopy (OM, Carl Zeiss Axio Observer. 5m) (Carl Zeiss, Oberkochen, Germany). X-ray diffractometry (XRD) (Shimadzu, Kyoto, Japan) was carried out in a θ–2θ diffractometer Philips 1810 using Cu Kα radiation, voltage of 35 kV, and current of 50 mA. Figure 1 shows the microstructure of the Mg_98.5Zn_0.5Y₁ alloy. The average grain size, as illustrated in Figure 1a, is 146 μm. Additionally, Figure 1b indicates that the primary phase of the Mg_98.5Zn_0.5Y₁ alloy is Mg₁₂YZn (LPSO).

2.2. Experimental Setup

The UVA tensile test of Mg-Zn-Y alloy was carried out on an EAST testing machine. The ultrasonic vibration system includes an ultrasonic generator, a sound transducer, and a horn. The ultrasonic vibration device was installed on the tensile testing machine, as presented in Figure 2. A 10 mm diameter hole is milled to fix the end of the specimen by a bolt. The other end of the specimen was attached to the lower clamp with bolts. Throughout the tensile tests, the horn amplified ultrasonic vibration and transmitted ultrasonic energy to the specimens. The wavelength of the ultrasonic vibration was used to calculate the length of the horn. Given the limited space available in the test system, the resonance frequencies were chosen to be 20, 25 and 30 kHz, respectively. The ultrasonic generator had the capability to adjust the ultrasonic amplitude, directly proportional to the ultrasonic energy. The sets of experimental parameters are detailed in

Table 2. Experimental variables and conditions of tensile test.

Category	Frequency/kHz	Amplitude/μm	Strain Rate/s−1
Tensile test	No vibration	————	0.001
			0.01
			0.1
			1
	20 kHz/25 kHz/30 kHz	3 μm/5 μm/7 μm	0.001
			0.01
			0.1
			1

.

3. Results and Discussion

3.1. Effect of the Ultrasonic Vibration on Flow Stress

The experiments encompass three distinct ultrasonic vibration amplitudes and frequencies, offering a comprehensive exploration of the coupling effects between frequency and amplitude on the material’s performance. The stress-strain curves for both conventional and UVA tensile tests are illustrated in Figure 3 and Figure 4. From the figures, one can easily observe that the flow stress falls once ultrasonic vibration is applied. To quantitatively assess the impact of vibration amplitude and frequency on flow stress, the yield stress under various conditions is presented in

Table 3. Yield stress at different amplitudes and frequency (MPa).

Frequency	Amplitude	Initial Strain Rate/s−1
		0.001	0.01	0.1	1
No vibration	——	131.96	145.15	152.16	165.98
20 kHz	3 μm	126.78	137.77	147.55	161.40
	5 μm	119.33	131.78	142.80	151.81
	7 μm	107.56	119.37	127.68	139.89
25 kHz	3 μm	125.97	134.67	146.35	159.78
	5 μm	116.01	128.35	139.89	149.22
	7 μm	105.46	116.67	124.87	135.67
30 kHz	3 μm	123.63	132.41	145.76	157.91
	5 μm	115.33	125.31	137.24	147.82
	7 μm	105.23	115.62	123.02	133.56

. It can be clearly seen that the yield stress decreases with the increase of the vibration amplitude and frequency. For instance, the most significant reduction in yield stress is 29.1 MPa when the vibration amplitude is 7 μm, the frequency is 30 kHz, and the stress rate is 0.001 s⁻¹, constituting 19% of the yield stress.

It can be concluded that the tensile curves under different conditions exhibit almost the same trend of change. The acoustic softening and stress superposition are the main reasons for the flow stress reduction [24]. The acoustic softening means that the dislocation in the alloy will absorb enough acoustic energy through the application of high frequency ultrasonic vibrations, so that the dislocation is more likely to deviate from its equilibrium position. Stress superposition refers to the phenomenon where the oscillating stress, which initially reaches peak levels, is reduced to an average stress due to the elastic deformation of the specimens. On the other hand, there are lattice defects in the alloy, which are easier to absorb sound energy [25]. We can infer that the combined impact of the two reasons leads to a decrease in tensile stress. From the comparison of the stress-strain diagram, it can also be concluded that the application of ultrasonic vibration improves the ductility of the Mg-Zn-Y alloy. It is reported [15] that ultrasonic vibration can promote the slip and rearrangement of dislocations, which reduces the stacking of dislocations in the alloy and increases the proportion of dynamic recrystallization, thereby improving the plasticity of the alloy.

3.2. Effects of Ultrasonic Vibration on Microstructure

3.2.1. Microstructure

Figure 5 shows the crystal orientation distribution and the orientation angle distribution of the specimens with different situation. As seen from the images, there is no significant difference between the grain size and the crystal orientation distribution. It can be calculated that the average size of the grains is 30 μm. The grain size and grain orientation distribution of alloy are not appreciably altered by ultrasonic vibration. Simultaneously, it can be seen from the figure that there are small recrystallized grains and tension twins in the specimen without UV. It is worth noting that the recrystallization and twining of the alloy after ultrasonic vibration is not obvious. Namely, after the application of ultrasonic vibration, there is a decrease in the quantity of both recrystallized and twinned grains. By comparing the statistical distribution of orientation angles, it can be easily deduced that the application of ultrasonic vibration significantly influences the formation of small-angle grain boundaries during the deformation.

In order to better understand the effect of UV on small-angle grain boundaries, we compared the composition of small-angle grain boundaries in different states of specimens, as displayed in Figure 6. By statistics, after tensile deformation, the percentage of small angle grain boundaries in the specimen is 14.8%. When ultrasonic vibration is applied, the content of small-angle grain boundaries in the alloy is reduced to 13.2%. This suggests that ultrasonic vibration contributes to a decrease in the number of small-angle grain boundaries. As we all know, fewer small-angle grain boundaries indicate lower dislocation density, which means better plasticity of the material [26]. This phenomenon is consistent with the softening of the material observed in the previous experiments. In this paper, the acoustic softening effect is considered as main reason. Ultrasonic vibrations increase the vibrational energy of atoms, making it easier for crystal defects such as dislocations to be created and move [15,16]. Ultrasonic vibration enhances the coordination and uniformity of plastic deformation in the material. The sooner ultrasonic vibration is applied, the less dislocation entanglement and plugging occur within the material. Consequently, the material exhibits a weaker hardening tendency in the subsequent molding process, marking the primary cause of the “acoustic residual softening effect” [27]. A detailed analysis will be conducted by Section 3.2.2.

KAM (Kernel average misorientation) is a common method to characterize the degree of plastic deformation of metallic materials by calculating the orientation difference between the target pixel point and its surrounding pixel points and then determining the average value of these differences, resulting in the KAM value. The KAM value can qualitatively reflect the degree of homogenization of plastic deformation. The higher value of the location indicates a higher degree of plastic deformation or a higher density of defects [28]. Figure 7 depicts the KAM maps of Mg-Zn-Y alloy during tensile deformation at room temperature.

From Figure 7, it can be seen that the KAM values of deformed specimens without vibration are not uniformly distributed. KAM values are generally higher at grain boundaries and lower within most individual grains. This observation suggests that, in the absence of vibration, plastic deformation in the material primarily occurs near the grain boundaries, and not all grains are involved in the deformation. With the application of UV, KAM values become higher and are uniformly distributed both at grain boundaries and within most individual grains. This observation signifies that, after introducing ultrasonic vibration, a greater number of grains participate in the plastic deformation process, leading to a more even distribution of plastic deformation across different grains. The above-mentioned difference indicates that ultrasonic vibration can promote grain refinement and grain rotation, thus enhancing the coordination of deformation between grains. In conclusion, ultrasonic vibration promotes coordinated intra- and intergranular deformation of the material, leading to a reduction in deformation resistance and enhanced uniformity, ultimately improving formability.

3.2.2. Dislocation Structure

In order to better analyze the mechanism of the influence of UV on material dislocations, the bright-fields TEM images were acquired, as shown in Figure 8. Figure 8a illustrates that in the absence of ultrasonic vibration, the sample exhibits a high dislocation density with a random and disorderly distribution, resulting in significant dislocation pile-ups. Figure 8b displays the dislocations within the sample under conditions of 30 kHz frequency and 7 µm amplitude. Notably, the dislocation lines are mostly parallel and appear to be straight. This results in a more organized and regular distribution of dislocations in contrast to those observed without UV.

It has been reported that ultrasound energy has a propensity to concentrate on localized dislocations [15]. After the application of UV, these dislocations, which have absorbed energy, become more mobile and tend to distribute themselves in a more organized and even manner. This phenomenon subsequently leads to a reduction in dislocation pile-ups, resulting in a decrease in material strength and an increase in plasticity.

The two primary explanations that can be used to explain the aforementioned phenomena are as follows, as illustrated in Figure 9. The first is the dislocation annihilation brought on by ultrasonic vibrations, which, as the physical model in Figure 9a illustrates, reduces the dislocation density. With a review of the reported investigations [29,30,31], it is obvious that superimposed ultrasonic vibrations can increase the dislocation mobility. This phenomenon aids dislocations located near grain boundaries in moving further and propagating over longer distances within the grains. This raises the possibility of dislocations with opposing signals coming into contact with one another, which could ultimately lead to dislocation annihilation.

Another reason is the enhancement of lattice rotation brought about by ultrasonic vibrations, which causes the LAGBs to become HAGBs, as depicted in Figure 9b. This was also found in Deng’s study [32]. When ultrasonic oscillations are applied, dislocations with the same signal are dispersed and moved until they aggregate along the LAGBs, leading to stronger dislocation walls. In this case, lattice rotation is more likely to occur due to the coupling effect of strain and ultrasonic oscillation stresses. This offers a reasonable explanation for the notable decline in the percentage of LAGBs in the presence of ultrasonic vibration, as shown in Figure 6.

It is reported that during ultrasound-assisted vibratory processing, energy is mainly absorbed by defective locations such as dislocations and vacancies within the material [25]. This absorption results in the contraction of extended dislocations, allowing helical dislocations to cross-slip without the need for thermal activation [33]. In contrast, during thermoforming, thermal energy is uniformly absorbed throughout the entire specimen region. Consequently, the efficiency of acoustic softening is remarkably higher, approximately 107 times more effective than thermal softening [34]. Crystal defects such as dislocations can absorb energy during vibration loading and promote dislocation movement, thus causing a decrease in stress. These microscopic observations offer valuable insights into the mechanisms behind the phenomenon of vibration-induced softening. Nevertheless, it’s important to note that the vibration-induced softening effect is temporary and vanishes once the vibration is removed. Additionally, it is challenging to observe the vibration-induced softening phenomenon in situ. This inherent transience and difficulty in real-time observation are the primary reasons why a unified theory explaining the mechanism of vibration-induced softening has remained elusive for an extended period.

3.2.3. Fracture Morphology

The fracture morphology without UV is presented in Figure 10a. This fracture morphology reveals that the wedge-shaped edge is flat and sharp, and the two material parts separate smoothly during the final stages of the fracture. With the application of ultrasonic vibration (UV), as evident in Figure 10a, the fracture surface appears rough and irregular, and there is an absence of a distinct wedge-shaped edge. The fracture surface is mainly composed of some irregularly shaped fiber zone contours, especially when the grain size is larger. In this case, the width of the fiber zone is notably wider. This phenomenon indicates that after loading ultrasonic vibration, the material undergoes a violent deformation at the fracture separation stage. After necking, there is a rapid reduction in the local cross-sectional area of the specimen. This reduction leads to an increase in the energy density of ultrasonic vibration per unit volume in this particular region. The repeated loading and unloading at high intensity prevent the material from undergoing a smooth separation process, ultimately resulting in the formation of complex and irregular fracture morphologies.

By comparing the fracture morphology, we can also determine that a large number of dimples appear in the fracture without UV. However, when the UV is applied, the number of dimples decreases. This is mainly due to the fact that when the ultrasonic vibration is applied, the ultrasonic energy impacts defects such as grain boundaries, thereby relieving dislocation blockages. This is less conducive to the initiation and growth of voids, resulting in a reduced number of dimples. It should be noted in particular that, with the application of UV, there is a decrease in the presence of tear ridges on the fracture surface, and the size and depth of the dimples increase. This observation is indicative of the high ductility of the material. The analysis of the fracture morphology aligns well with the statistical results of elongation, confirming the material’s enhanced ductility under the influence of ultrasonic vibration.

4. Discussion

The above experimental results describe the influence of parameters, such as vibration frequencies, amplitudes, and strain rates, on the microstructure and mechanical properties of Mg_98.5Zn_0.5Y₁ alloy, giving us a good basis for modeling. In this section, the constitutive equation of Mg_98.5Zn_0.5Y₁ alloy under ultrasonic vibration is established using the Johnson-Cook and its modified model. It’s worth noting that the frequency and amplitude parameters were introduced to modify the model. The resulting constitutive equation for Mg_98.5Zn_0.5Y₁ alloy effectively captures the plastic deformation characteristics under ultrasonic vibration. This equation aligns well with the observed plastic deformation behavior of Mg_98.5Zn_0.5Y₁ alloy when subjected to ultrasonic vibration.

4.1. Johnson–Cook Model of Mg_98.5Zn_0.5Y₁ Alloy without Vibration

The Johnson-Cook (JC) model is an empirical metal constitutive model proposed by Johnson and Cook in 1983 [35]. Due to its simple formula and high prediction accuracy, the JC model has become one of the most widely used flow stress models. By coupling metal strain hardening, strain rate, and thermal softening, the model can effectively predict the metal stress-strain relationship at different strain rates and temperatures. The original JC model can be described as,

$$\sigma =\left(A+B{\epsilon }^n\right)\left(1+\mathit{Cln}\frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}\right)(1-T^{*m})$$

(1)

where σ is the equivalent flow stress and A is the yield stress at the reference strain rate, indicating the stress resistance to micro plastic deformation. B is the coefficient of strain-hardening, ε is the equivalent plastic strain; and n represents the strain-hardening exponent, describing the strain hardening behavior. C is the coefficient of strain-rate hardening, which reflects the sensitivity of material to strain rate. $\dot{\epsilon }$ and ${\dot{\epsilon }}_0$ are the strain rate and strain rate reference, respectively. T refers to the homogenization temperature; m is the thermal softening index of the material. To enhance the prediction of material properties for magnesium alloys and address the significant deviation in the traditional JC model in describing stress-strain behavior, we incorporated an improved J-C model [23]. This improved model includes a quadratic term of strain and considers the coupling effect of temperature and strain rate on the flow behaviors. With these enhancements, we aim to achieve more accurate and reliable predictions for the material’s response under different conditions. Given that the experiment is conducted at room temperature, the temperature component is omitted from the model. The improved J-C model can be expressed as follows:

$$\sigma =\left[A+B_1\epsilon +B_2{\epsilon }^2+B_3{\epsilon }^3\right]\left(1+Cln\frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}\right)$$

(2)

where B₁, B₂, and B₃ are the strain-hardening coefficients. C is the strain rate hardening factor. The remaining parameter definitions are consistent with the original J-C model. The values of the above parameters need to be determined in combination with experimental data. In this study, the reference strain rate is taken as the minimum value of 0.001 s⁻¹, and the improved J-C model can be written as follows:

$$\sigma =\left[A+B_1\epsilon +B_2{\epsilon }^2+B_3{\epsilon }^3\right]$$

(3)

By fitting the stress-strain curves under the reference strain rate, as shown in Figure 11, the values of A, B₁, B₂, and B₃ can be obtained as 110.18 MPa, 521.72 MPa, −1659.45 MPa and 1561.44 MPa, respectively. Equation (2) can be transformed into:

$$\sigma =C·\left(A+B_1\epsilon +B_2{\epsilon }^2+B_3{\epsilon }^3\right)·ln\frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}+\left(A+B_1\epsilon +B_2{\epsilon }^2+B_3{\epsilon }^3\right)$$

(4)

Combining formula (4) and experimental data, the values of different strain rates under certain strains can be obtained. In order to determine the value of the strain rate coefficient C, in this experiment, the strain is set in the range of 0.1–0.4, and the strain increment is 0.05. The formula σ–$ln\dot{\epsilon }/{\dot{\epsilon }}_0$ is linearly fitted to obtain the slope of $ln\dot{\epsilon }/{\dot{\epsilon }}_0$, which is C (A + B₁ε + B₂ε² + B₃ε³). The fitting results are shown in Figure 12. The constitutive equation of the Mg-Zn-Y alloy without vibration, based on the average value of the seven different C values (calculated to be 0.0287), can be expressed as follows:

$$\sigma =\left[110.18+521.72\epsilon -1659.45{\epsilon }^2+1561.44{\epsilon }^3\right]\left(1+0.0287\mathit{ln}\frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}\right)$$

(5)

4.2. Johnson–Cook Model of Mg_98.5Zn_0.5Y₁ Alloy with Vibration

According to the tensile curves of Mg-Zn-Y alloys under different vibration conditions, the values of parameters under different amplitudes and frequencies were obtained using the experimental method described in Section 4.1. The results are shown in

Table 4. Material constants in the modified JC model at 20 kHz.

Amplitude/μm	A/MPa	B1/MPa	B2/MPa	B3/MPa	C
0	110.18	521.72	−1659.45	1561.44	0.0287
3	113.98	624.06	−1764.68	2304.7	0.0296
5	70.22	817.34	−2957.88	3085.99	0.0338
7	60.34	736.83	−2587.12	2721.06	0.0362

,

Table 5. Material constants in the modified JC model at 25 kHz.

Amplitude/μm	A/MPa	B1/MPa	B2/MPa	B3/MPa	C
0	110.18	521.72	−1659.45	1561.44	0.0287
3	99.94	483.64	−1411.37	1100.37	0.0302
5	71.04	756.17	−2661.68	2678.3	0.0337
7	54.51	805.57	−2931.22	3209.02	0.0371

and

Table 6. Material constants in the modified JC model at 30 kHz.

Amplitude/μm	A/MPa	B1/MPa	B2/MPa	B3/MPa	C
0	124.43	160.91	−778.08	730.22	0.082
3	87.35	651.5	−2209.28	2576.18	0.031
5	69.99	739.15	−2591.32	2611.52	0.0343
7	59.29	691.36	−2414.21	2437.48	0.0384

:

In this study, the constitutive model of Mg-Zn-Y alloy under vibration conditions is established according to the material parameter values under different frequency and amplitude conditions. In order to demonstrate the impact of the amplitude on the material constants, the subscripts ‘0’ and ‘v’ are used to indicate the separation and recording of the material constants with and without oscillation, respectively. Thus, the A₀, B₁, B₂, and B₃ and C₀ represent the parameter values with no vibration. Concurrently, the A_V, B_1V, B_2V, B_3V, and C_V represent the parameter values with vibration. The variation of A₀/A_v, B_1v/B₁, B_2v/B₂, B_3v/B₃, and C_v/C₀ with amplitude can be computed and plotted in Figure 13 and Figure 14.

Figure 13 and Figure 14 depict the amplitude-based trends for A₀/A_v, C_v/C₀, B_1v/B₁, B_2v/B₂, and B_3v/B₃ in sequential order. Notably, the ratio increases with higher vibration amplitudes. Based on the variation of material parameter values and amplitude shown in the figures, we propose the relations (6)–(10). Here, ‘a’ represents the amplitude parameter, while the coefficients K, H, and L are derived from the calculation results. The fitting curves in red on Figure 13 and Figure 14 illustrate the outcomes of the fitting process, and the corresponding parameter values are presented in

Table 7. Values of the material parameters at 20, 25 and 30 kHz after fitting.

f/kHz	K1	K2	K3	K4	K5	H	L1	L2	L3	L4	L5
20	−0.02	0.07	0.10	0.12	0.04	0.02	0.97	1.03	0.97	1.08	0.97
25	−0.03	0.08	0.11	0.14	0.04	0.03	0.98	1.00	0.97	1.05	0.97
30	0.008	0.05	0.07	0.08	0.04	0.07	0.99	1.05	1.07	1.17	0.97

.

$$A_0/A_v=K_1{a}^2+Ha+L_1$$

(6)

$$B_{1v}/B_1=K_{2}a+L_2$$

(7)

$$B_{2v}/B_2=K_{3}a+L_3$$

(8)

$$B_{3v}/B_3=K_{4}a+L_4$$

(9)

$$C_v/C_0 =K_{5}a+L_5$$

(10)

According to the calculation results in Table 7, the relationship equation for the variation of material parameters with amplitude at 20 kHz frequency can be derived as shown in Equation (11):

$$\sigma =\left[\frac{110.18}{-0.02a^2+0.02a+0.97}+\left(36.52a+537.37\right)\epsilon -\left(165.95a+1609.67\right){\epsilon }^2 \left(187.37a+1686.36\right){\epsilon }^3\right]\left[1+\left(0.0011a+0.0278\right)ln\frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}\right]$$

(11)

Using the same method described above, we can derive the vibrational equations of Mg-Zn-Y alloy under the 25 kHz and 30 kHz frequency conditions, as illustrated in Equations (12) and (13).

$$\sigma =\left[\frac{110.18}{-0.08a^2+0.03a+0.98}+\left(41.74a+521.72\right)\epsilon -\left(182.54a+1609.67\right){\epsilon }^2+\left(218.54a+1639.05\right){\epsilon }^3\right]\left[1+\left(0.0011a+0.0278\right)ln\frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}\right]$$

(12)

$$\sigma =\left[\frac{110.18}{0.008a^2+0.07a+0.99}+\left(26.09a+547.81\right)\epsilon -\left(116.16a+1775.61\right){\epsilon }^2+\left(124.92a+1826.88\right){\epsilon }^3\right]\left[1+\left(0.0011a+0.0278\right)ln\frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}\right]$$

(13)

By comparing Equations (11), (12), and (13), it becomes evident that the parameters of the material’s vibration constitutive equation undergo changes at different frequencies. Nonetheless, it is a common practice in academic research to concentrate primarily on constitutive equations at a single, specific frequency, with limited exploration of variations in frequency. The calculations presented above clearly demonstrate that changes in vibration frequencies have a substantial impact on the parameters of the vibration equation. Therefore, it becomes imperative to consider the influence of frequency and amplitude on the constitutive equation’s parameters for ultrasonic vibration. Notably, the strain rate hardening coefficient remains almost entirely unaffected by the vibration frequency, as evidenced by Equations (11)–(13).

Referring to the literature, it is known that the acoustic energy density in the sample can be calculated using the formula E = a²(2πf)²ρ/2 [36,37]. Additionally, Longenecker’s research revealed that the reduction of metal stress under ultrasonic vibration is proportional to the input of sound energy [25]. Building on this understanding, we assume that the material’s flow stress reduction under ultrasonic vibration is proportional to the product of vibration amplitude squared and frequency squared, denoted as a²f². Consequently, new parameter relationship Equations (14)–(17) are proposed accordingly. In Equations (14)–(17), a and f represent the amplitude and frequency of ultrasonic vibration, respectively. D, E, G, and I represent the coefficients of the parameter relational equation. By combining this information with the data presented in Table 4, Table 5 and Table 6, the results of the coupling between frequency and amplitude are depicted in in

Table 8. Parameter values after fitting the amplitude and frequency.

A0/Av		B1v/B1		B2v/B2		B3v/B3
D1	1.8 × 10−5	E1	0.07	G1	0.1	I1	0.12
D2	0.083	E2	−0.005	G2	−0.001	I2	−0.007
D3 D4	−0.004 1.03	E3	1.14	G3	1.04	I3	1.29

.

$$A_0/A_v=D_1{a}^2{f}^2+D_{2}a+D_{3}f+D_4$$

(14)

$$B_{1v}/B_1=E_{1}a+E_{2}f+E_3$$

(15)

$$B_{2v}/B_2=G_{1}a+G_{2}f+G_3$$

(16)

$$B_{3v}/B_3=I_{1}a+I_{2}f+I_3$$

(17)

Based on the fitting results presented in Table 8, the constitutive equation of the Mg-Zn-Y alloy under ultrasonic vibration is ultimately determined as follows:

$$\sigma =\left[\frac{110.18}{1.8\times {10}^{-5}{a}^2{f}^2+0.083a-0.004f+1.03}+\left(36.52a-2.61f+594.76\right)\epsilon -\left(165.95a-1.66f+1725.83\right){\epsilon }^2+\left(187.32a-10.93f+2013.69\right){\epsilon }^3\right]\left[1+\left(0.0011a+8.61\times {10}^{-5}f+0.025\right)ln\frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}\right]$$

(18)

4.3. Verification of the Constitutive Equations

After establishing the ultrasonic vibration constitutive model at the reference temperature, we conducted an evaluation of the material fluidity prediction for the Mg-Zn-Y alloy. The results of this evaluation are depicted in Figure 15a. Evidently, the predicted values from the constitutive model align well with the data obtained from experimental measurements. In order to further compare the accuracy of the model to predict material flow, the maximum error between the predicted stress value σ_p and the measured value σ_m can be expressed as:

$$\mathrm{E}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r} \mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}=\frac{|{\sigma }_p-{\sigma }_m|}{{\sigma }_m}\times 100\%$$

After calculation, the error rate between the improved models σ_p and σ_m are shown in Figure 15b–d. It is evident from the results that the flow stress estimate has a maximum error of only 2.62. In addition, when compared to the original and modified Johnson-Cook models, the improved model offers a more precise estimation of the flow behavior. These results demonstrate that the enhanced Johnson-Cook model presented in this work is appropriate for modeling the Mg-Zn-Y alloys’ tensile behavior.

By combining the experimental findings mentioned above, it’s apparent that the improved Johnson-Cook’s model performs significantly better at predicting the material flow behavior of Mg-Zn-Y alloys under typical tensile conditions. This model exhibits a significant degree of concordance with the experimental results, particularly when it comes to predicting the stress-strain curves of the constitutive equation for Mg-Zn-Y alloys.

5. Finite Element Simulation

5.1. Effect of Ultrasonic Vibration on Stress-Strain Distribution during the Tensile Process

Finite element analysis serves as a potent tool for investigating the plastic forming process of metals. To gain a more profound understanding of the deformation mechanism of Mg-Zn-Y alloy under the influence of ultrasonic vibration, finite element simulations were conducted for both conventional tensile tests and ultrasonic vibration-assisted tensile tests using Abaqus software. In this study, discrete rigid body modeling was employed for the tensile fixture part, and reference points were strategically placed to facilitate the application of boundary conditions. The grid of the tensile specimen part was configured as C3D8R, as depicted in Figure 16. Accounting for the influence of strain rate on stress, the tensile rate was set to 0.001 s⁻¹. Additionally, the frequency was set to 20 kHz and 30 kHz, while the amplitude was varied between 0 μm, 3 μm, 5 μm, and 7 μm.

Figure 17 and Figure 18 present a cloud diagram illustrating the stress-strain distribution of the specimen during the stretching process at various amplitude frequencies. In comparison to conventional tensile tests, the introduction of ultrasonic vibration leads to a reduction in the flow stress of the metal material. Importantly, the extent of this reduction is directly correlated with the amplitude of the applied ultrasonic vibration, with larger amplitudes resulting in more substantial reductions in flow stress. Figure 18 displays the magnitude distribution of strain under various amplitude frequency conditions. It is evident that after applying ultrasonic vibration, the maximum strain of the specimen increases with higher frequencies, while variations in amplitude have a relatively smaller impact on strain.

5.2. Effect of Ultrasonic Vibration on Material Flow Behavior

Figure 19 depict the velocity distribution fields of Mg-Zn-Y alloy specimens under various conditions. Given the immobility of the specimen’s bottom during conventional stretching, the velocity at the base remains at zero. However, the material within the stretched portion of the specimen undergoes flow in tandem with the stretching process. After applying ultrasonic vibration, the material’s flow velocity undergoes significant transformation. Notably, the flow velocity’s direction no longer aligns with the tensile direction; instead, in certain material sections, the flow velocity opposes the tensile direction. By comparing the velocity clouds, it becomes evident that the maximum flow velocity of the material is shifted from the upper part to the main deformed part in the middle of the specimen. Given that vibration primarily demonstrates stress superposition effects within finite element analysis, the vibration frequency exerts a relatively minor influence on stress. However, altering the frequency can induce shifts in material flow velocity. Notably, the figure highlights that an increase in frequency corresponds to an elevation in the material’s maximum flow velocity.

As depicted in Figure 19, with an amplitude of 5 μm, the maximum flow velocity experiences an upsurge as the frequency increases. Remarkably, the material attains a peak flow velocity of 1216 mm·s⁻¹ at 30 kHz. Similar to amplitude, frequency incites only an instantaneous rate alteration, resulting in a relatively minor shift in the average flow rate throughout the deformation process.

6. Conclusions

Ultrasonic vibration assisted tension was performed on Mg-Zn-Y alloy. The mechanical behavior and microstructure evolution of the sheet at different amplitudes and frequencies were examined. The constitutive equation of Mg-Zn-Y alloy under tension with vibration is constructed using the modified JC model. Based on the experimental results, the following conclusions can be drawn:

(1)

In the ultrasonic vibration stretching process, both the amplitude and frequency of vibration affected the flow behavior of Mg_98.5Zn_0.5Y₁ alloy during the stretching process. The acoustic softening effect caused by ultrasonic vibration is gradually obvious with the increase of amplitude. A comparison of the stress-strain curves at various frequencies and amplitudes leads to the conclusion that amplitude has a more significant effect on the flow stresses of Mg_98.5Zn_0.5Y₁ alloy when compared to vibration frequency.

(2)

A hybrid constitutive model coupling the frequency and amplitude of ultrasonic vibration is developed based on the modified Johnson Cook model. Comparing to the measured stress, it is evident that the proposed Johnson-Cook model aligns well with the experimental data, exhibiting a maximum error in the flow stress estimate of only 2.62. That indicates the proposed JC model is very suitable for the flow behavior prediction of Mg_98.5Zn_0.5Y₁ alloy with and without UV.

(3)

The finite element analysis results show that ultrasonic vibration has a great influence on the stress-strain distribution in the stretching process. There is great potential in applying vibration-assisted ultrasonic vibration methods to the thermal processing of magnesium alloys. Examples of such applications include vibration-assisted additive manufacturing and vibration-assisted stamping. It can effectively improve the formability of magnesium alloy and improve the quality of formed parts.