Wulff Constructions for an Equilibrium MFI-Type Zeolite Shape Modelling under Different Conditions

Abstract

As an MFI-type zeolite, ZSM-5 zeolite has wide applications in industry, such as in the fine chemical, petrochemical, and coal chemical industries. However, shape control of ZSM-5 nanocrystals constitutes one of the major challenges of current nanotechnology. Here, the MFI framework structure was used as the theoretical model of pure silicon ZSM-5 to investigate the surface energy and Wulff shape. The models with different crystal surfaces were simulated by molecular dynamics (MD) with the assistance of machine learning potentials (MLPs). The factors influencing the crystal surface energy, such as temperature, pH, and ionic concentration, have been studied in detail. Depending on the calculated surface energies, the crystal surface morphology and its ratio were obtained by means of the Wulff theorem. The results show that the area in the equilibrium shape of the (110) surface is usually the largest, and its proportion varies with external conditions. A high temperature and high concentration of the aluminum source promoted the growth of the (110) crystal surface, and the theoretical value of the crystal surface ratio was as high as 90%. This study provides theoretical insight into the synthesis of zeolites with different morphologies of all-silicon or low-aluminum.

1. Introduction

Zeolites with ordered networks of micropores have been extensively applied as heterogeneous catalysts in the petrochemical, fine chemical and coal chemical industries due to their large surface areas, high adsorption capacities, hydrothermal stability, and so on [1,2,3,4]. As an important type of zeolite, ZSM-5 is often used in various catalytic reactions, such as alkylation, aromatization, isomerization, etc., owing to its appropriate acidity and well-defined pore sizes with excellent shape selectivity [5,6,7]. Note that different crystal faces of ZSM-5 have different channel environments, which results in differences in their properties, such as the diffusion of reactants and products, as well as surface acidity [8,9,10]. Thus, it is necessary to study the growth mechanism of ZSM-5, that is, the growth and ablation of crystal faces in different external environments.

There are many synthesis strategies for ZSM-5, among which the one-step synthesis method has good research and development prospects due to its simple processing, energy savings, high efficiency, environmental friendliness, and feasibility [11,12,13,14]. Zhang et al. prepared ZSM-5 crystals by a one-step method from pre-seeded mesoporous aluminosilicate spheres (MASSs) via in situ vapour phase transformation [14]. Che’s group reported a coffin-shaped hollow ZSM-5 zeolite with a hollow diameter of 1.5 μm by a one-pot method [15]. Zhu et al. proposed a simple one-step strategy to synthesize high-quality bow-like hollow ZSM-5 without additional templates [16]. However, during the one-step synthesis of ZSM-5 zeolite, the crystal faces of the grains exhibit different growth trends due to differences in their stability. Some crystal faces undergo ablation under certain reaction conditions, while other faces continue to grow, forming a specific grain structure. In other words, reasonable adjustments in reaction conditions, such as temperature, pH and the ionic concentration of alkaline solution, can, in principle, lead to the regulation of ZSM-5 zeolite growth and ablation, which is crucial for guiding practical industry applications.

The surface energy is an important parameter for describing the stability of a crystal face and can be used to predict the growth of ZSM-5 zeolite [17,18]. Once all surface energies of a crystal are provided, the equilibrium shape that minimizes the total surface energy at a constant volume can be provided by Wulff’s theorem [19,20]. For example, α-tetragonal (α-t) boron has been shown to be more stable than α-rhombohedral (α-rh), β-rhombohedral (β-rh), or β-tetragonal (β-t) boron due to its lower surface energy. Then, the equilibrium shapes of the born crystals were determined using Wulff’s theorem [21]. Using density functional theory (DFT) calculations, Jiang et al. obtained the surface energies of six low-index stoichiometries of TiO₂. Based on DFT calculations, the authors determined the surface energies of six low-index stoichiometric facets of TiO₂ following the calibration of the crystal structure. A geometric model of equilibrium rutile TiO₂ was built based on the calculated surface energy calculations and Wulff’s principles [22]. Tian et al. calculated the surface energies of asymmetric and nonstoichiometric surface terminations of MoP catalysts by using the concepts of cleavage energy and relaxation energy as well as DFT calculations. The relative stability of symmetric MoP surfaces under different preparation conditions was revealed [23]. To investigate the changes in MgO crystal shapes from dry to wet environments, Geysermans et al. employed the DFT method to calculate the surface energies of the (100), (110) and (111) planes at different water partial pressures [24]. In addition, Seif and coauthor applied the density functional perturbation theory (DFPT) to compute the phonon density of states and vibrational contributions to entropy based on DFT calculations. This approach allowed direct simulation of the thermodynamic effects on the W surface topography [25]. Interestingly, Tran et al. constructed a large database of surface energies and Wulff shapes for more than 100 polymorphic systems by combining high-throughput calculations and DFT calculations. The elemental crystals included all polymorphic systems in the Materials Project, and the chemistries covered both metals and nonmetals [26]. The results were used as an input to construct the equilibrium Wullf shapes of MgO crystals [24]. These works show that DFT calculations are widely used in theoretical studies of crystal surface morphology [25,27]. However, the crystal structure of ZSM-5 zeolite has a more complex spatial topology than that of pure metals or metal oxides. Owing to this structural property, surface energy calculations require the use of larger surface model structures. Thus, calculating the surface energy of ZSM-5 with a nanoscale crystal size by first-principles calculations is quite time-consuming. On the other hand, the surface energy of large-scale systems can be obtained by molecular dynamics (MD), but it is difficult to obtain satisfactory accuracy via molecular force field. The rapid rise of machine learning techniques provides the possibility for high-precision simulation of large-scale systems. In particular, the MD method with the assistance of machine learning potentials (MLPs) can compensate for the shortcomings in computational speed while maintaining good accuracy.

In the present study, the morphological control of MFI-type ZSM-5 zeolite in different growth environments was investigated theoretically, as shown in Scheme 1. A comprehensive low-index stoichiometric facet model based on the MFI was constructed. The method of combining MD and MLPs was used for structure relaxation to ensure calculation efficiency and accuracy. Different external factors, such as temperature, pH, and ionic concentration, were considered during the process of MD. Subsequently, the surface energies of the MFI framework were evaluated, and the equilibrium shapes were obtained by Wulff’s theorem. The influence of the ion concentration, pH, and temperature on the growth mechanism of MFI-type ZSM-5 zeolite was revealed, which provides fundamental theoretical guidance for the surface analysis and surface modification of ZSM-5 zeolite.

2. Methods

2.1. Surface Energy

The surface energy considering the adsorbate ${\gamma }_{adsorbate}^0$ is given by [17]

$${\gamma }_{adsorbate}^0={\gamma }_s+\frac{{BE}_{adsorbate}}{A}$$

(1)

where γ_s is the surface energy, BE_adsorbate is the adsorption energy, and A is the surface area.

The surface energy γ_s, which describes the stability of a surface, is the energy needed to cleave a surface from a bulk crystal. It is given by [18]

$${\gamma }_s=\frac{(E_{slab}-N·E_{bulk})}{2A}$$

(2)

where E_slab is the energy of the corresponding slab, E_bulk is the energy of the bulk crystal, and N is the number of bulk units in the slab. The lower the surface energy is, the greater the surface stability.

The adsorption energies (BE_adsorbates) were calculated with respect to the solution as follows:

$${BE}_{adsorbate}=(E_{s-adsorbate}-E_s-E_{adsorbate}^{solv})$$

(3)

where E_{s−adsorbate} is the energy of the surface covered with adsorbate molecules, E_s is the energy of the clean surface, and $E_{adsorbate}^{solv}$ is the energy of the solvated adsorbate.

2.2. Wulff’s Theorem

Wulff’s theorem is broadly applied to grain growth and requires a minimum surface energy in the terminal geometrical shape of the crystal grain. When all the surface energies γ_s of a crystal are provided, the equilibrium shape corresponding to the lowest surface energy at a constant volume can be determined by Wulff’s theorem [19,20]. Herein, the Wullf shape represents the appearance of the crystal without other constraints, which is consistent with the crystal point group symmetry [21]. Wulff’s theorem states that the distance h_(ijk) from the center of the crystallite to the surface is proportional to its surface energy γ_s(ijk) per unit area. Hence, surfaces with low energy are closer to the center and exhibit a larger area. On the whole, it is preferred that the crystal planes with low surface energy be exposed during growth. Due to the faster growth rate of the crystal in the normal direction, the high-energy plane is usually covered by other adjacent planes during crystal growth. The crystal planes with lower surface energies are invariably low-index facets, which means that the final exposed plane is always contributed by the low-index facet.

$$\frac{{\gamma }_{s\left(ijk\right)}}{h_{\left(ijk\right)}}=constant$$

(4)

2.3. Global Neural Network (G-NN) Potential and Molecular Dynamics

To perform long-term atomic simulations of ZSM-5 under different growth conditions, the latest Al-Si-P-O-Na-H global neural network (G-NN) potential generated by machine learning techniques was utilized, as implemented in the Large-scale Atomic Simulation with Neural Network Potential (LASP, www.lasphub.com, accessed on 20 May 2023) program developed by Liu’s group [28]. The potential of Al-Si-P-O-Na-H G-NN is generated by self-learning the global potential energy surface (PES) dataset, which is openly available on the LASP website [29]. The dataset contains 50,052 structures with an accuracy for the G-NN potential of 2.900 meV/atom for the root-mean-square (RMS) error in energy and 0.105 eV/Å for the force. The NVT canonical ensemble was employed for molecular dynamics calculations. The time step interval, equilibrium time, and total time were set to 1.0 fs, 2 ps, and 200 ps, respectively. The temperature was set to 300 K, 500 K, or 700 K and controlled with a Nose–Hoover heating bath [30]. After the dynamic trajectory tended to stabilize, the energies of the systems were evaluated by the statistical average of the energies during MD in combination with MLPs [31].

2.4. Computational Model

MFI-type zeolite is an important siliceous zeolite that not only is a promising membrane material but is also often used as a model system to illuminate the mechanism of crystal growth [32,33,34]. Hence, the MFI framework structure was used as the theoretical model of pure silicon ZSM-5. The space group of the MFI unit cell is P21/nma, with lattice parameters of a = 20.02 Å, b = 19.90 Å, and c = 13.38 Å, and is an orthorhombic crystal system. Each Si atom is fourfold coordinated to the O atom with a Si-O bond length of approximately 1.59 Å. We considered several low-index stoichiometric facets of MFI, (100), (010), and (001), and the open surfaces that might be present in growth structures, that is, the (110), (101), (011), and (111) planes. The main crystal surface topography was determined by using VESTA 3 [35] software, and the results are presented in Figure S1. Supercells consisting of 1 × 1 × 2 unit cells were used, and the directions of the extended cells were selected along the normal direction of the cutting planes. For three-dimensional (3D) periodic geometry, the vacuum spaces in the out-of-plane direction were set to 15 Å for all the crystal systems.

3. Results and Discussion

The factors influencing the growth and ablation of MFI-type zeolites include temperature, pH, and ionic concentration. In Figure S1, seven different low-index facets of MFI were considered: the (100), (010), (001), (110), (101), (011), and (111) planes. First, the energies of the bulk crystal, surface covered with adsorbate molecules, clean surface, and solvated adsorbate were calculated by structure relaxation using the MD-MLPs method. When the crystal nanoparticles are in different external environments, the surface atoms are affected by unbalanced intermolecular forces compared with the internal atoms, resulting in significant changes in the surface energy. Next, the surface energies were obtained under different conditions. Then, the equilibrium shape corresponding to the different surface energies at a constant volume can be determined by Wulff’s theorem. Finally, the growth mechanism of MFI can be theoretically predicted.

3.1. Effect of Temperature

The temperature plays a crucial role in the crystal growth process [36,37]. The growth of crystals requires the right temperature, which can enhance the movement of solute molecules, increase the ease of generating crystal structures, and prevent the deformation of the crystal structure. It should be noted that the current work does not directly study the growth rate of crystals at different temperatures but qualitatively predicts the direction of crystal growth by analyzing the shape and exposed surface of the MFI. MD-MLPs of MFI with different crystal plane orientations were first analyzed at different temperatures, 300 K, 500 K, and 700 K. The calculated surface energies are shown in Figure 1a. There is no doubt that the surface energy of the (110) surface is the lowest among all the surfaces at 300 K (0.93 J/m²; Figure 1a), resulting in the largest surface ratio (52.34%; Figure 1b) and exhibiting the largest area in the equilibrium shape (Figure 1c). In addition, the (111) and (001) surfaces in equilibrium shapes according to Wullf’s theorem appear relatively large (Figure 1c) due to their moderate surface energies (1.19 and 1.22 J/m², Figure 1a). As shown in Figure 1b, as the temperature increases, the proportion of the (111) surface increases, and the proportions of the (110) and (001) surfaces decrease. Therefore, as the temperature increases, the (111) surface gradually becomes the most dominant surface. Taken together, these findings show that the MFI-type zeolite mainly exposes (110) and (111) surfaces in the absence of external factors, and changes in temperature significantly affect the proportions of (110) and (111) planes. These temperature-dependent differences on the exposed surfaces (110) and (111) are caused by changes in the surface energy. This is due to the increased thermal motion of atoms at higher temperatures, which can lead to a variation in the cohesive forces at the surface. Additionally, changes in temperature can affect the arrangement of atoms at the surface, influencing the overall surface energy.

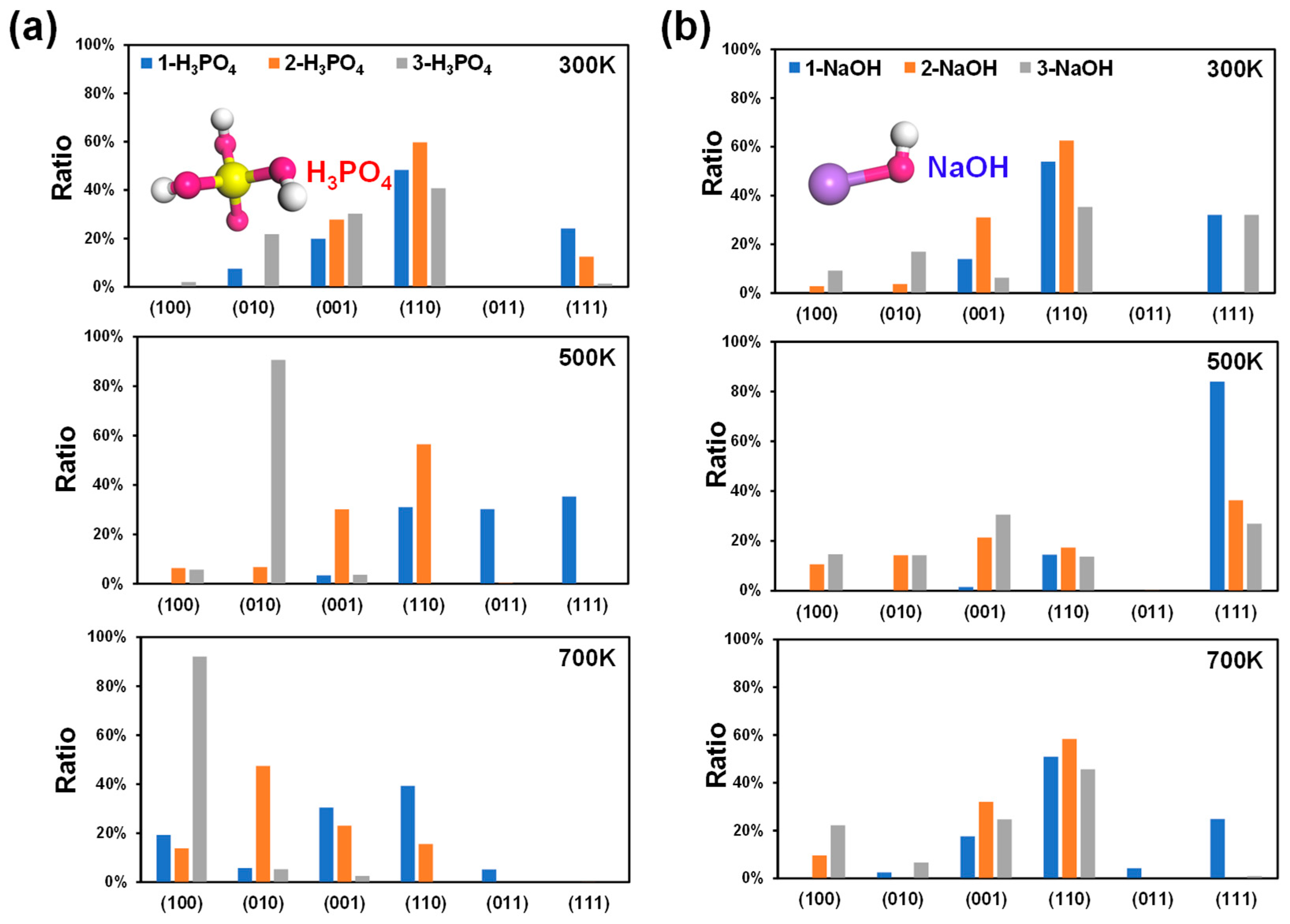
3.2. Effect of pH at Different Temperatures

It has been shown in laboratories that pH affects the growth and ablation of ZSM-5 zeolite [38]. This is because pH affects solute solubility or molecular interactions, which in turn affect crystal formation. To investigate the surface morphology of MFI under different degrees of acidic and alkaline conditions, H₃PO₄ and NaOH molecules were added to the surface to simulate acidic/alkaline conditions. Different molecular numbers represent different pH values.

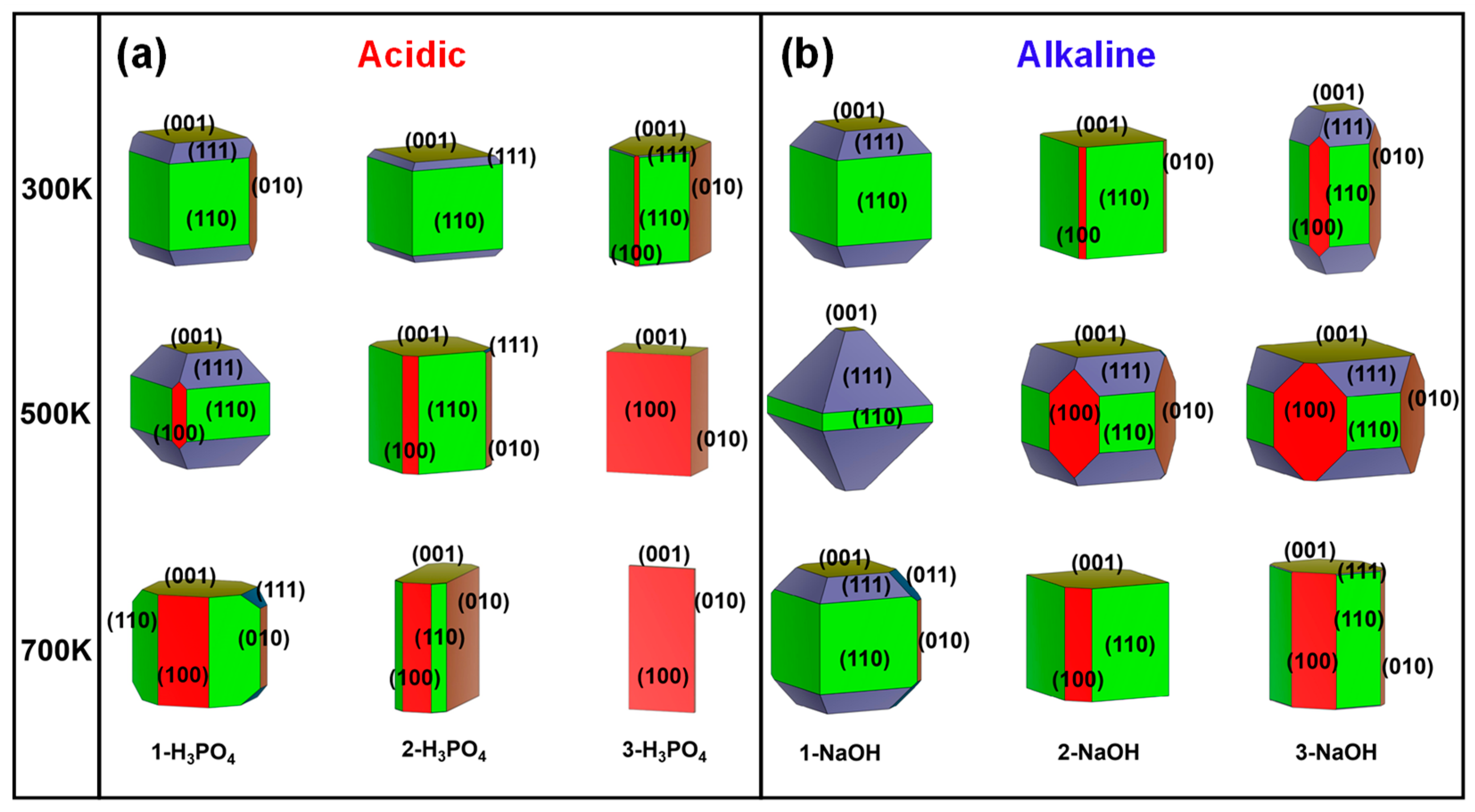
3.2.1. Effect of Acidic Conditions

As the number of H₃PO₄ molecules on the surface of MFI increases, the acidity of the environment increases, i.e., the pH decreases. The 1-H₃PO₄, 2-H₃PO₄, and 3-H₃PO₄ models were selected to simulate acidic conditions. The surface energies of MFI at 300 K, 500 K, and 700 K were calculated (Figure S2), and the corresponding crystal surface ratios (Figure 2a) were obtained. At 300 K, the (110) plane has the lowest surface energy (0.83, 0.64 and 0.52 J/m²; Figure S2) and the highest proportion of crystal planes (48.37%, 59.75%, and 40.75%; Figure 2a), regardless of the 1-H₃PO₄, 2-H₃PO₄, or 3-H₃PO₄ model. These findings illustrate that the growth of MFI is dominated by the (110) crystal plane under acidic conditions at room temperature and that the proportion of the (110) surface first increases and then decreases with increasing acidity (Figure 3a).

With the increase in the number of H₃PO₄ molecules at different temperatures, the proportion of the (111) surfaces decreased (Figure 2a), which indicated that the growth of (111) surfaces with greater acidity was inhibited. Once the acidity is increased to a certain extent (in the 3-H₃PO₄ models), the main growth plane changes from the (110) to the (010) and then to the (100) crystal plane as the temperature increases (Figure 2a). The aforementioned results demonstrated that the MFI-type zeolite mainly exposes the (110) surface under acidic conditions at room temperature, and changes in acidity and temperature significantly affect the proportions of the (110), (010), and (100) planes (Figure 3a). These acidity-dependent differences in the exposed surfaces change with surface energy. The surface energy may be affected by the protonation of the unsaturated facets with the H atom in the H3PO4 molecules.

3.2.2. Effect of Alkaline Conditions

Like in the above situation, three simple models (1-NaOH, 2-NaOH, 3-NaOH) were selected to simulate alkaline conditions. A greater number of NaOH molecules indicates a more strongly alkaline environment, i.e., a greater pH. The surface energies, crystal surface ratios, and surface morphologies of MFI for different models at 300 K, 500 K, and 700 K are shown in Figure S3, Figure 2b, and Figure 3b, respectively. At 300 K, the ratio of the (110) surface was still the highest among the three models (53.90%, 62.57%, and 35.36%; Figure 2b), with corresponding surface energies of 0.82, 0.61, and 0.46 J/m², respectively (Figure S3). This means that the (110) crystal plane of MFI plays an important role in the growth process under alkaline conditions at room temperature (Figure 2b and Figure 3b), and its surface ratio first increases and then decreases with increasing strength in an alkaline environment, similar to that in an acidic environment (Figure 2a).

In contrast to acidic environments (Figure 2a), the crystal surface ratio of the (111) plane in the alkaline environment is significantly greater, especially for the 1-NaOH model at 500 K (Figure 2b). However, at high temperatures of 500 K and 700 K, the ratio of the (111) plane decreases with increasing number of NaOH molecules (Figure 2b). That is, the growth of the (111) crystal surface requires reasonable control of the alkaline environment and temperature, and blindly increasing these factors is not suitable for the growth of this surface. The above results indicated that the MFI-type zeolite mainly exposes the (110) surface under alkaline conditions at room temperature, and changes in alkalinity and temperature significantly affect the proportions of (110), (111), and (001) (Figure 3b). The above phenomenon could be attributed to the different interactions between the unsaturated low-value surface and the OH group in the NaOH molecule, as well as the influence of the difference in the pore environment.

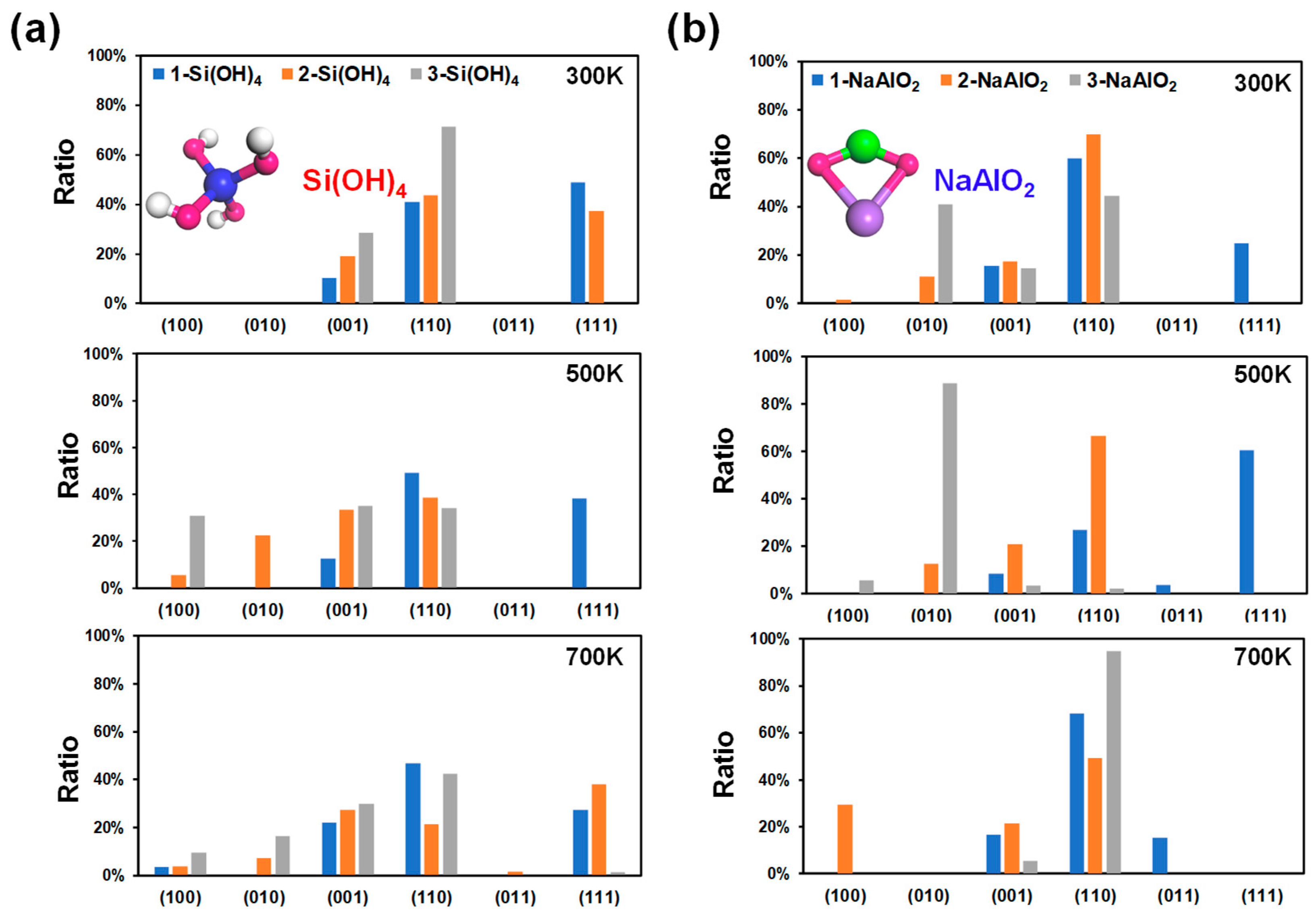
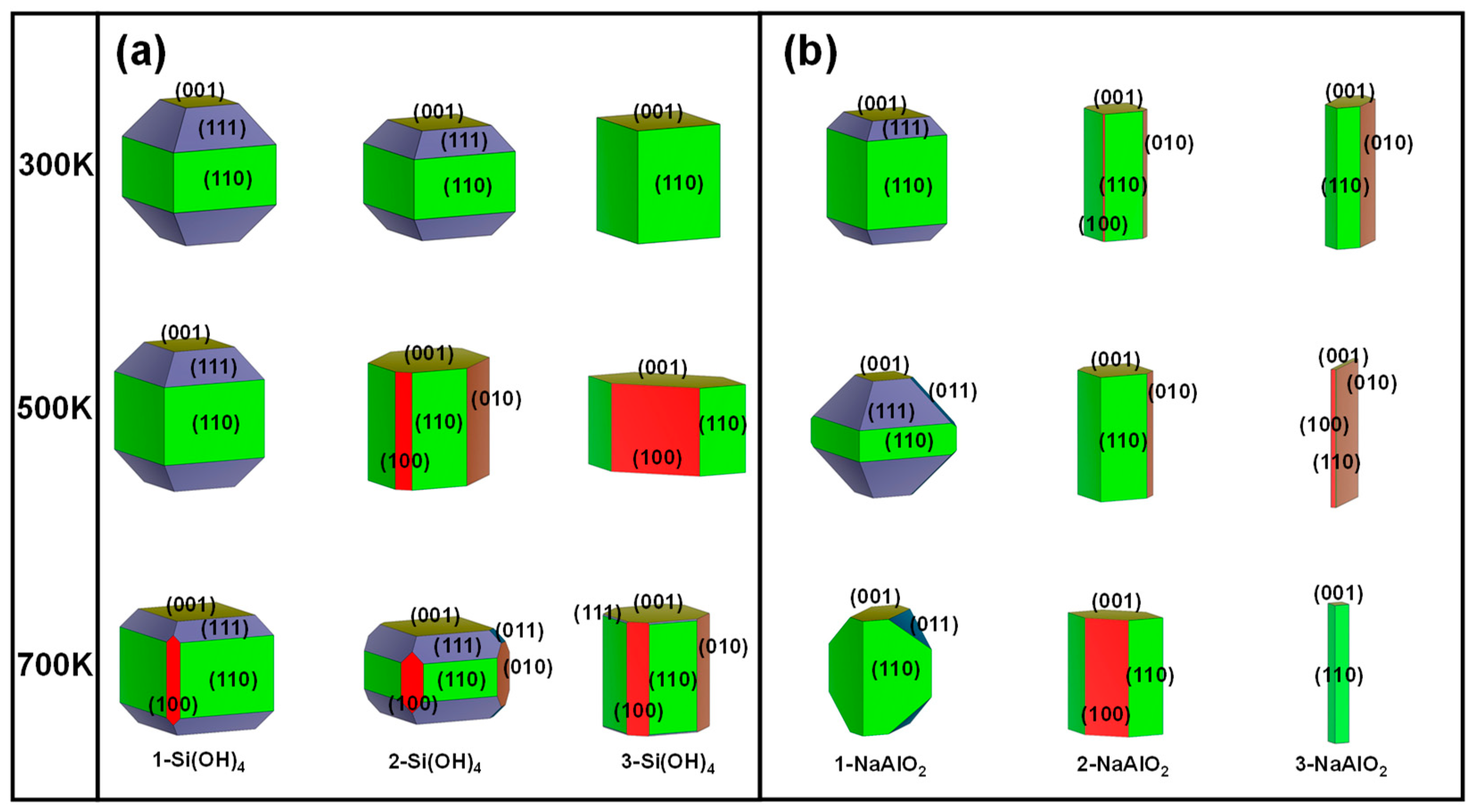
3.3. Effect of Si/Al Concentration at Different Temperatures

In addition to the acid-base environment, the growth and ablation laws of crystal faces are usually affected by ionic concentration [38]. The different types and concentrations of ions have different effects on the growth of crystals. In particular, the silicon or aluminum (Si/Al) concentration has a great influence on the morphology and catalytic performance (e.g., desulfurization) of ZSM-5 [39]. Herein, different amounts of Si(OH)₄ and NaAlO₂ were chosen for the Si and Al sources to investigate the effect of the Si/Al concentration on the growth mechanism of MFI. The calculated surface energies, crystal surface ratios, and morphologies of MFI under different Si and Al sources at 300 K, 500 K, and 700 K are shown in Figures S4 and S5, Figure 4 and Figure 5, respectively.

To simplify the model, an increase in the concentration of the unilateral Si source was considered to describe the increase in the Si concentration. As shown in Figure 4a, the (110), (111), and (001) surfaces dominate in the low-index planes under the Si source environment. At 300 K, the proportion of the (111) surface in the 1-Si(OH)₄ model is the highest among the other planes (48.83%, Figure 4a), with a surface energy of 0.98 J/m² (Figure S4). Nevertheless, with an increase in the number of Si(OH)₄ molecules, the (111) plane was inhibited. In contrast, the surface ratios of the (110) (40.95~71.37%) and (001) (10.22~28.63%) planes increase with increasing number of Si(OH)₄ molecules at 300 K. When the temperature increases to 500 K or even 700 K, with an increase in the number of Si(OH)₄ molecules, the proportion of the (111) surface decreases rapidly and tends toward 0%, while the portion of the (001) surface has a slight upwards trend. However, in this situation, the variation law of the (110) surface ratio is no longer clear (Figure 4a). The above findings imply that the MFI-type zeolite mainly exposes the (110) and (111) surfaces under moderate Si source and room temperature conditions. A high Si concentration can strongly inhibit the growth of the (111) surface and reduce the dominance of the (111) plane with increasing temperature (Figure 5a).

The decrease in the Al concentration can be simplistically expressed by an increase in the number of NaAlO₂ molecules. The (110) surface in the 1-NaAlO₂ model still occupied an important proportion at 300 K, and its surface ratio reached 59.81% (Figure 4b). Additionally, the ratio of the (110) surface increases first and then decreases with increasing NaAlO₂. This phenomenon is especially evident at 500 K (Figure 4b). Surprisingly, the ratio of the (110) plane under the 3-NaAlO₂ model is abnormally high (> 90%) at 700 K (Figure 4b). This is a good illustration of the high-temperature conditions combined with the high concentration of Al sources, which strongly promoted the growth of the (110) crystal surface. In addition, the ratio of the (010) surface under the 3-NaAlO₂ model exceeded 80% at 500 K, indicating that a high proportion of the (010) surface is expected to be obtained under a high concentration of Al when heated to an appropriate temperature. Finally, a high concentration of Al is also unsuitable for the growth of the (111) surface. From the above results, it can be inferred that in a high-Al concentration environment, high temperatures can facilitate the growth of the (110) crystal plane; appropriate heating can promote the growth of the (010) plane.

Overall, the Si/Al concentration of a solution has a significant impact on the surface energy of MFI, particularly for surfaces that interact with Si/Al atoms in the surrounding environment. In the case of charged surfaces, changes in ionic concentration influence the distribution of ions at the surface, leading to alterations in the surface energy. Moreover, due to the structural differences in the facets, the proportions of some low-value surfaces increase with increasing temperature, while the proportions of some low-value surfaces decrease with increasing temperature.

4. Conclusions

In this paper, the surface energies and nanocrystal morphologies of a pure-silicon MFI frame were investigated as a research model under different external conditions, including temperature, pH, and ionic concentration. Molecular dynamics and machine learning potentials were used to evaluate the surface energy. Subsequently, the calculated crystal surface ratio and the morphology determined by Wulff’s theorem were obtained and used to predict the growth process of ZSM-5. The results show that a reasonable setting of the concentration of Al or Si sources, temperature, and pH can regulate the growth of crystal planes:

(I)

Simply increasing the temperature in the absence of external factors greatly reduces the ratio of the dominant (110) surface, while the (111) proportion increases significantly.

(II)

In a more acidic environment, the main growth plane changes from the (110) to the (010) and then to the (100) crystal plane as the temperature increases.

(III)

Moderate alkalinity and temperature conditions can achieve substantial growth of the (111) surface.

(IV)

A high Al concentration combined with a high temperature can facilitate the growth of the (110) crystal plane.

Finally, our theoretical calculations provide theoretical guidance for the surface analysis and surface modification of MFI-type zeolite materials from experimental research to industrial manufacture. In further work, we will conduct a more detailed study of the growth mechanism of MFI by high-resolution transmission electron microscopy (HRTEM) in variable chemical environments at finite temperatures.